Imaging Electrically Evoked Micromechanical Motion within the Organ of Corti of the Excised Gerbil Cochlea

Abstract

The outer hair cell (OHC) of the mammalian inner ear exhibits an unusual form of somatic motility that can follow membrane-potential changes at acoustic frequencies. The cellular forces that produce this motility are believed to amplify the motion of the cochlear partition, thereby playing a key role in increasing hearing sensitivity. To better understand the role of OHC somatic motility in cochlear micromechanics, we developed an excised cochlea preparation to visualize simultaneously the electrically-evoked motion of hundreds of cells within the organ of Corti (OC). The motion was captured using stroboscopic video microscopy and quantified using cross-correlation techniques. The OC motion at ∼2–6 octaves below the characteristic frequency of the region was complex: OHC, Deiter's cell, and Hensen's cell motion were hundreds of times larger than the tectorial membrane, reticular lamina (RL), and pillar cell motion; the inner rows of OHCs moved antiphasic to the outer row; OHCs pivoted about the RL; and Hensen's cells followed the motion of the outer row of OHCs. Our results suggest that the effective stimulus to the inner hair cell hair bundles results not from a simple OC lever action, as assumed by classical models, but by a complex internal motion coupled to the RL.

INTRODUCTION

Gold, in 1948 (1), was the first to hypothesize that cochlear tuning and sensitivity were the result of a feedback system. In this system, in-phase correspondence between the feedback force and the basilar membrane (BM) velocity would lead to an enhancement of the cochlear tuning by canceling the viscous forces acting on the BM. It is currently hypothesized that voltage-dependent OHC length changes function as a key component of this feedback system.

OHCs are one of the major types of cochlear sensory cells located in the organ of Corti (OC) of the inner ear. Evidence for direct involvement of OHCs in cochlear function came with the observation that eliminating the OHCs and leaving the rest of the OC intact leads to a significant loss of sensitivity (2–4). Stimulation of cochlear efferents, which terminate mostly on OHCs, altered the production of distortion-product emissions (5) and tuning of inner hair cells (IHCs) (6). The discovery of electrically-evoked otoacoustic emissions (7) and of voltage-dependent length changes in isolated OHCs (8,9) provided more evidence for the active role of OHCs in cochlear function. Recently, OHC electromotility has been attributed to the voltage-sensitive motor protein prestin (10). Prestin-mutant mice have a 40- to 60-dB hearing loss and lack OHC somatic motility in vitro (11), further supporting the idea of OHCs as key players in cochlear amplification.

There is currently little understanding on how OHC length changes affect the vibration characteristics of the cochlear partition and contribute to cochlear tuning. The intricate anatomy of the OC and the diverse mechanical properties of the cellular components (see, e.g., Olson and Mountain (12,13), Naidu and Mountain (14), and Scherer and Gummer (15)) suggest that the OC vibration pattern can be complex. Moreover, both the anatomy and the mechanical properties of individual cells in the OC change along the length of the cochlea. Therefore, to understand the micromechanical motion of the OC in response to OHC length changes, measurements have to be made at multiple positions within the organ and along the cochlea for multiple stimulus conditions.

To investigate OC mechanics, most researchers have made measurements across the BM (16–22), or the reticular lamina (RL) and/or the tectorial membrane (TM) (17,22–30). Some of this work is reviewed by Ulfendahl (31) and Robles and Ruggero (32). Little information is available on the internal micromechanical motion of the OC due to OHC contractions. Measurement of this internal motion is important to our understanding of the mechanical role of OHC somatic motility but has been a challenge because the internal structure of the OC is not optically accessible. Few attempts have been made to make such internal OC measurements. Richter et al. (33), Hu et al. (25), and Cai et al. (34) used a hemicochlea preparation which allowed visualization of the radial profile of the OC, and reported that the vibration pattern is complex. Fridberger et al. (35) used an excised cochlea preparation combined with confocal microscopy to reconstruct the radial deformation of the OC. In response to static pressure changes, the authors reported a complex deformation pattern in the apical turn of the guinea pig cochlea. These studies, however, did not isolate the effect of OHC somatic motility on OC motion, and the data were limited to one radial location.

In this study, we wanted to quantify the internal micromechanical motion of the OC due to OHC contractions in a semi-intact cochlea preparation. We developed an excised cochlea preparation that allowed us to image, in the same cochlear preparation, the responses of hundreds of cells located at many radial locations and multiple focal levels, starting at the TM level and moving down to the BM level, at 2-μm intervals. We present data from the apical and middle turns for low-stimulus frequencies, because at these frequencies the observed motions were larger and easier to quantify. Using our system, we have been able to collect data (not included here) up to 9 kHz for selected cells within the OC (36,37). For the work presented here, the term “low frequency” refers to frequencies ∼2–6 octaves below the characteristic frequency (CF) of the measurement location. Stimulus frequency and CF are indicated in the figures as needed. The CF of our measurement locations was estimated using the place-frequency map of the gerbil cochlea (38) and ranged from 0.4 to 4 kHz. We show that in response to electrically-evoked OHC contractions, the motion of the OC at low frequencies is complex, and is qualitatively similar in both the apical and middle turns of the gerbil cochlea. We also show, using a simple electroanatomical model of the cochlea, that the magnitude of OHC length change in this study is similar to that observed in isolated OHC studies.

METHODS

Surgical preparation of gerbil cochleae

Young female Mongolian gerbils were decapitated after being anesthetized (no paw-withdrawal reflex and no corneal reflex) with an intraperitoneal injection of sodium pentobarbital (60 mg/kg, Steris Laboratories, Phoenix, AZ) or using a mixture of ketamine (160 mg/kg, Fort Dodge Animal Health, Fort Dodge, IA) and xylazine (8 mg/kg, Bayer, Shawnee Mission, KS). The procedures followed an institutionally approved protocol with guidelines provided by the Laboratory Animal Care Facility at Boston University. All chemicals were purchased from Sigma Chemicals (St. Louis, MO) unless noted otherwise. Both temporal bones were excised, and muscular and brain tissue was removed. After opening the bulla, the bones were immersed in oxygenated culture medium (Leibovitz L-15) supplemented with 5 mM D-glucose. The pH of the solution was adjusted to 7.3 at the beginning of each experiment using NaHCO₃ (J.T. Baker Chemical Company, Phillipsburg, NJ). In later experiments, the medium was a Cl⁻-modified perilymph-like solution composed of 140 mM D-gluconic acid, 6.6 mM NaCl, 100 μM CaCl₂, 3 mM KCl, 5 mM NaH₂PO₄, 100 μM MgCl₂, 5 mM D-glucose, and 5 mM HEPES (298 mOsm, pH 7.3, adjusted using 1 M NaOH). Both solutions were at room temperature (∼18°C) during the experiment. The later solution was formulated to improve the condition of the preparation and the viability of the cells. Using this solution, we were able to reliably collect data for a maximum of 9 h after decapitation.

The next step in the surgical procedure was to transfer the immersed bone under a dissecting scope (AO570, American Optical, Buffalo, NY) and remove the tympanic membrane, the malleus, the incus, and part of the semicircular canals. Most of the temporal bone was left intact and was used to hold the cochlea. We then exposed the turn of interest without damaging Reissner's membrane, and removed as much of the bone surrounding the scala tympani of the lower turn as necessary to establish a better optical path.

For experiments in the apical (low-frequency) turn, the round window membrane was removed along with most of the bone surrounding the basal (high-frequency) turn. This allowed access to the modiolus between the basal and middle turns. The modiolus was then cut with a pair of forceps and the basal turn was removed along with the bone of the scala tympani and sometimes the scala media (SM) of the middle turn. Next, a hole was made with a sharp pick at the very tip of the apical turn. Using the band of stria vascularis as a guide, the bone covering the scala vestibuli (SV) was removed using a thin pair of forceps, and the apical turn was exposed. This procedure ensured that the SM remained intact.

For experiments in the middle turn, the basal turn of the cochlea was removed and a hole was made in the apical turn as before. Using a thin pair of forceps, the apical turn was completely removed and the bone covering the SV of the middle turn was carefully peeled away. As mentioned previously, this procedure ensured that the SM was anatomically preserved (Fig. 1). The average time for the surgical procedure after decapitation was 20 min.

FIGURE 1.

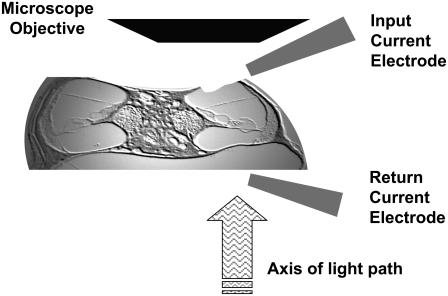
Midmodiolar cross section of a gerbil cochlea (slide provided by J. C. Adams, Harvard Medical School, 2000) to illustrate our middle-turn preparation. The apical and basal turns have been removed and a small opening has been made in the SV above the region of interest. Note that Reissner's membrane is intact and therefore the anatomical architecture of the entire turn is preserved. Also shown is the relative electrode placement for the electrical stimulation paradigm.

Video microscopy system

After dissection, the preparation was mounted in a custom-made chamber with a cover-glass bottom and then placed on the stage of an upright microscope (BX50WI, Olympus, Melville, NY). The microscope was sitting on a vibration-isolation table with a second degree of isolation provided by a steel slab supported on tennis balls. In later experiments, the cochlea holder was modified to allow manual rotation in three dimensions, which permitted control over the viewing angle of the organ. A 4×, 0.13 NA lens (Olympus) was used for orienting the cochlea and later positioning the electrodes (described in the next section). Fig. 2 shows the view of the cochlea using the 4× objective for a middle-turn experiment. A 20×, 0.5 NA, or a 60×, 0.9 NA water immersion lens (Olympus) with an additional 2× magnification was used for detailed observation of the OC in the regions of interest. The microscope objective was connected to a nanopositioner (PIFOC P-723, Physik Instrumente, Auburn, MA) equipped with a piezoelectric driver. The PIFOC driver was controlled remotely via a programmable amplifier module (E-662, Physik Instrumente), and allowed precise control over the focal level. Fig. 3 (see also Supplementary Material, Movie 1) shows a view of the cochlea at different focal levels using the 20× objective. The resolution of the images using this objective was 432 nm/pixel. A CCD camera (C2400-77, Hamamatsu, Bridgewater, NJ) was mounted on the phototube of the microscope. Analog contrast enhancement and brightness enhancement was accomplished using an image processor (Argus-20, Hamamatsu). The output of the image processor was connected to an externally triggered frame grabber (AG-5, Scion Corporation, Frederick, MD) for real-time frame capture and averaging.

FIGURE 2.

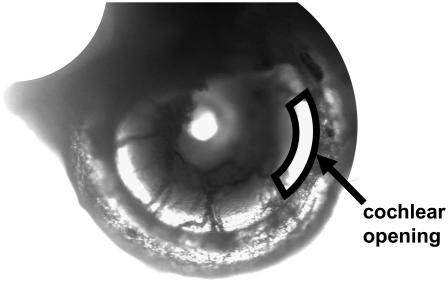
Low-magnification surface view of our excised cochlea preparation. This is a middle turn preparation of a left cochlea and it spirals clockwise toward the apex. Notice that the entire turn of interest is present. The arrow points to the opening of the SV above the region of interest. The opening is outlined for clarity.

FIGURE 3.

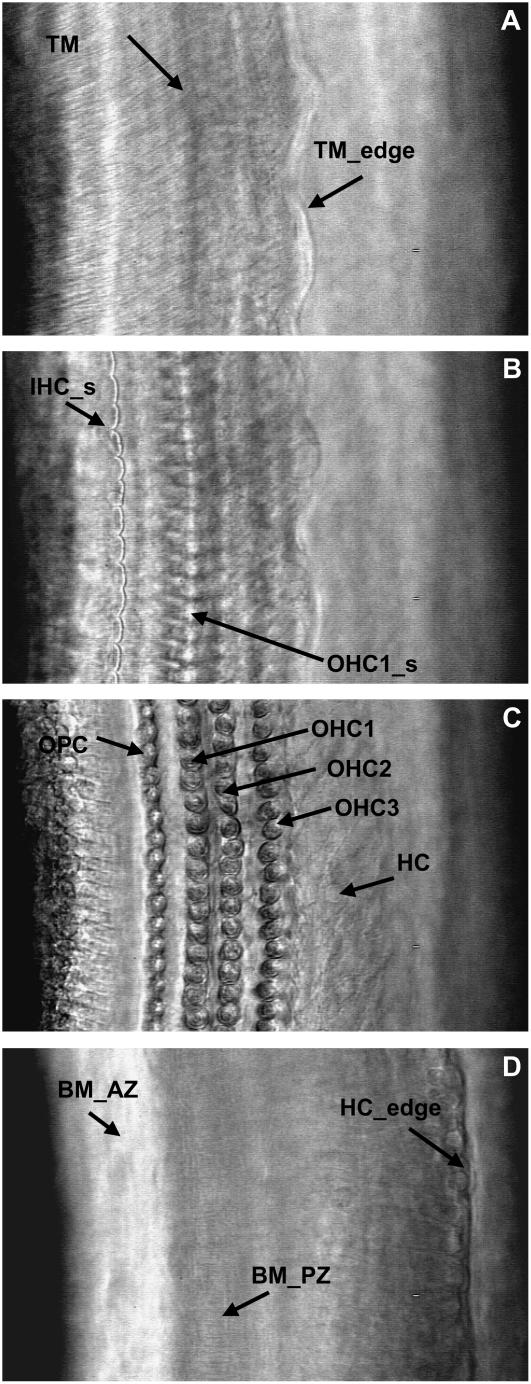
High-magnification surface views of our excised cochlea preparation. All views are from the same cochlea location and were acquired by focusing the objective at different depths of the OC. (A) Tectorial membrane (TM) level. Arrows point to the TM radial fibers and the edge of the TM (TM_edge). (B) Cuticular plate level. Arrows point to the IHC (IHC_s) and OHC1 (OHC1_s) hair bundles. (C) OHC-basal-end level. Arrows point to the outer pillar cells (OPC), first through third rows of OHCs (OHC1, OHC2, and OHC3, respectively), and Hensen's cells (HC). (D) Basilar membrane level. Arrows point to the arcuate zone of the BM (BM_AZ), the radial fibers of the pectinate zone of the BM (BM_PZ), and the edge of the HC (HC_edge).

Electrical stimulation: hardware and software

Alternating current was delivered through glass pipettes filled with 3 M NaCl. The input current electrode was placed in the SV of the same turn in which responses were measured. The return-current electrode was placed near the former location of SV in the next more basal turn (Fig. 1). The pipettes were sealed with agar (Agarose, Type III: High EEO, Sigma Chemicals) at their tips to prevent NaCl leakage and were connected to an optically isolated constant (high-impedance) current source (BSI-1, BAK Electronics, Mount Airy, MD). The inner diameter of the pipettes ranged from 100 to 300 μm. The injected current was monitored by measuring the voltage across a 100-Ω resistor in the current return path. A computer controlled analog interface (System II, Tucker-Davis Technologies, Alachua, FL) was used to generate the input to the current source and to store the stimulating-current waveform. During electrical stimulation, current levels ranged between 0.1 and 4 mA to prevent tissue damage. Our current stimulus is expected to cause a 0.8- to 4-mV/mA OHC transmembrane voltage drop (see Appendix B, Model predictions). This gives an OHC transmembrane voltage drop of 0.08–16 mV, which is comparable to that used in isolated OHC preparations (<100 mV) and also similar to the one used recently by other groups using excised cochlea preparations (e.g., Nowotny and Gummer (30) used 0.6–1.7 mV).

The stimuli were sine waves with frequencies from 30 to 120 Hz. Movements synchronized to the stimulus frequency were captured using stroboscopic illumination. A custom-made current source was used to deliver current pulses of 200-mA peak to a light-emitting diode (AND190AYP, Purdy Electronics, Sunnyvale, CA) emitting more than 50 Cd at a 4° viewing angle. The light-emitting diode was mounted on a holder designed to replace the light source of the microscope. The input pulses to the strobe system were generated using the Tucker-Davis Technologies system. The pulses occurred at fixed phases within the period of the stimulus, with duration equal to 10% of the stimulus period.

Data were collected for eight equally spaced, randomized phases and for two conditions: 1), with the stimulating current present, and 2), with the stimulating current turned off, referred to as the “no-stimulus condition”. The no-stimulus condition gave us an estimate of the magnitude of the minimum resolvable motion of our system and also verified that the motions observed were due to the current being present. For each stimulus period, pulses occurred only at one particular phase. Thus, to collect data from eight phases, the same frequency was played eight times. For each frequency-phase combination the stimulus was on for 1 s to provide enough images for subsequent averaging. Typically, we used a 16-frame average. The video frames of interest were subsequently digitized and animations of the observed motion were created by playing the images from each phase in succession.

Voltage measurements

To quantify the voltage drop in the fluid between our stimulating electrodes, we performed voltage measurements using glass pipettes filled with 3 M NaCl, which had the same inner diameter as the current electrodes (∼300 μm). The ground-voltage electrode was placed next to the return-current electrode. The active-voltage electrode was placed first next to the input-current electrode and then was sequentially moved to locations away from the input-current electrode. The voltage electrodes were connected to a direct current-coupled differential amplifier (Tektronix, Richardson, TX). The output of the amplifier was connected to an analog to digital interface (AD2, Tucker-Davis Technologies) used to store the resulting waveforms.

The voltage measurements were performed using a current stimulus of 1 mA at five frequencies: 60 Hz, 120 Hz, 450 Hz, 810 Hz, and 1200 Hz. Measurements at higher frequencies (>1200 Hz) were not practical due to contamination from capacitive coupling between the electrodes.

Image processing and motion estimation

Electrically evoked motion was estimated using two-dimensional (2D) cross-correlation. In traditional signal processing, cross-correlation is performed to obtain a measure of similarity between two signals f₁(t) and f₂(t) as a function of a scanning parameter τ. This parameter is usually the time shift of one signal with respect to the other. An important application of cross-correlation in image processing is in the area of template matching, where the goal is to find the closest match between an unknown image and a set of known images (39). The scanning parameter in this case is the spatial shift of one image with respect to the other. Since we are interested in 2D discrete images, the spatial shift applies for any combination of x (radial dimension) and y (longitudinal dimension) on the image plane. For the discrete 2D case the cross correlation of two images f(x,y) and g(x,y) is given by

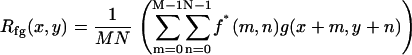(1)

for x = 0,1,2,…, M − 1 and y = 0,1,2,…, N − 1. The symbols M, N refer to the image's radial and longitudinal dimensions, respectively. The following cross correlation theorem,

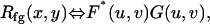(2)

holds for u=0,1,2,…, M − 1 and v = 0,1,2,…, N − 1. The functions F, G are the frequency domain representations of f, g. The theorem states that the cross-correlation of two images in the spatial frequency domain is the result of a simple multiplication of their spatial Fourier transforms. The asterisk indicates that the complex conjugate of the function is taken. Cross-correlation functions computed with fast Fourier transforms (FFTs) are often referred to as circular cross-correlation functions, since the FFT treats the image as though it represents a periodic pattern. As a result, the computed cross-correlation is periodic. Since the motions in our experiments were small compared to the extraction size, the largest peak near the origin was chosen for the displacement estimate. If the displacement was larger than half the image size, then the peak was wrapped around to the origin and the phase adjusted accordingly.

Cross-correlation was used to estimate radial and longitudinal displacements, and it is demonstrated in Fig. 4 for the one-dimensional case. In this method, two images taken under different conditions are considered at a time. In our case, one of those images is the one taken at the no-stimulus condition of a particular phase and is considered as the reference image. The other image is the one taken at the phase corresponding to the no-stimulus condition. Cross-correlation between the two images was performed by first extracting a portion of the image containing a feature of interest like the edge of a hair cell (Fig. 4 A). The same portion was extracted from an image taken at a different stimulus phase. (Fig. 4, B–D).

FIGURE 4.

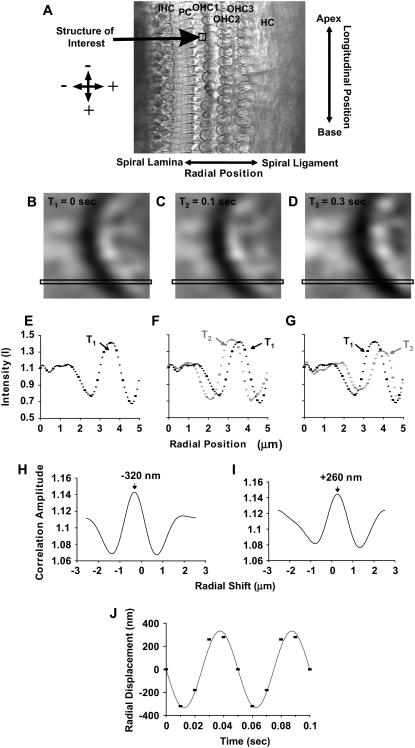
(A) High-magnification surface view of the OC captured with our video stroboscopy system at one particular phase of the stimulus (exp. 131). Several structures of interest are shown: the basal end of IHCs, the head of the pillar cells (PC), the three rows of OHCs, and the area of the HC. In all our images, the radial dimension is from spiral lamina to spiral ligament and the longitudinal dimension from base to apex. Radial motions toward the spiral ligament and longitudinal motions toward the base are positive by convention. To estimate these motions, a portion of the image containing a feature of interest like the edge of a hair cell was extracted from each of the eight phases and the corresponding no-stimulus conditions. For simplicity, we present the analysis for three time points. (B–D) Shown are three time frames of the edge of an OHC. Each panel is a matrix of 16 × 16 pixels (432-nm resolution). For illustration purposes, the analysis is shown for one row of pixels (illustrated in each time frame), but during motion estimation the analysis is done for the entire extracted image. (E–G) The intensity of each pixel across one row is plotted as a function of radial position (solid squares). Note that the shape of the intensity profile could be similar (but not identical) from one time frame to the next but shifted with respect to the radial position. The next step was to quantify this shift. Because the motion of interest was usually less than a pixel, interpolation was used (solid circles between squares). The resulting images had a resolution of 27 nm/pixel. (H and I) Cross-correlation computed with fast Fourier transforms was used to quantify the shift that yields the best fit between two images. For the curves shown in E and F, the best fit was at a shift of 320 nm toward the left and for the curves in E and G, the best fit was at a shift of 260 nm toward the right. (J) Cross-correlation was repeated for all the stimulus phases to derive the time waveform of the displacement shown by the squares. Fourier analysis was then performed on the time waveform and from the fundamental component we estimated the peak amplitude and phase of motion for each stimulus frequency.

It is important to note that the extractions of interest were chosen to have a well defined edge, and thus their resulting intensity profiles were single-peaked (Fig. 4, E–G, solid squares). Single-peaked profiles had the advantage of giving a well defined cross-correlation peak. Also, in Fig. 4, E–G, notice that the beginning and the end of the intensity profiles do not have the same value. We found that this caused errors in the estimation of motion. To solve this problem, and accurately extract the peak of the intensity profile, the images were high-pass filtered (not shown in Fig. 4) using the following kernels:

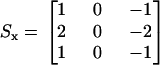(3)

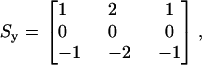(4)

where S_x refers to the kernel applied in the radial direction, and S_y to the kernel applied in the longitudinal direction. These kernels are also known as Sobel operators (39) and were chosen over other gradient operators because they can detect edges while also having a smoothing effect, therefore reducing additional noise introduced by high-pass filtering the images. Both kernels operated on a pixel-by-pixel basis.

Because the motion of interest was usually less than our pixel size, the next step was to interpolate the extracted images. For simplicity, we outline our methodology for the one-dimensional case (for example, the radial dimension). A detailed analysis of this procedure is given in Oppenheim and Schafer (40). Our objective was to up-sample the image I[m] to I_i[m] as given by

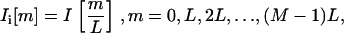(5)

where I_i[m] is the interpolated version of I[m], L is the interpolation factor, and M is the radial length of the image. One way to derive I_i[m] is by first using an expander on I[m] such that

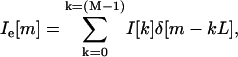(6)

where I_e[m] is the expanded version of I[m] and δ is the unit impulse function. I_i[m] is then obtained by low-pass filtering I_e[m] with a cutoff frequency of π/L and gain equal to L. We implemented this procedure in the spatial-frequency domain. Notice that the Fourier transform of I[m] and I_e[m] is given by

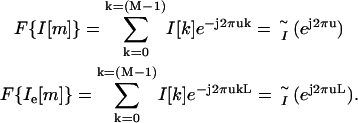(7)

From Eq. 7, we see that 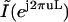is a frequency-scaled version of 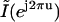.We therefore expanded the Fourier transform of our extracted image in the spatial-frequency domain by appending zeros to expand it to the desired interpolation size. We then calculated the inverse Fourier transform of the image to obtain the interpolated version of our original image. Notice that in our analysis our images are band limited; therefore, the form of the low-pass filter is rectangular. Such a filter is ideal, since the amount of distortion in the added samples is zero. We used a 16× interpolation factor and with that, our final pixel resolution was 27 nm. The resulting interpolated intensity profiles for the images shown in Fig. 4, B–D, are shown in Fig. 4, E–G (solid circles between squares) (here, the interpolation factor is limited to 4× for visualization purposes).

Once the extracted images were interpolated, the cross-correlation between two images was computed using FFTs. The location of the cross-correlation peak, with respect to the origin, gave us an estimate of the magnitude and direction of motion between the original images (Fig. 4, H and I). This procedure was then repeated for all the stimulus phases to derive the time waveform of the motion (Fig. 4 J).

Fourier analysis was then performed on the time series to estimate the peak magnitude and the phase of motion for each frequency. Specifically we used the complex exponential Fourier series (41) to reconstruct the time waveform, as given by

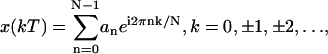(8)

where N is the number of samples per period, n is the harmonic number, k is the discrete increment of time, i.e., t = kT, where T is the sampling interval, and finally

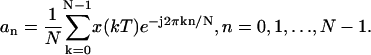(9)

We then computed the magnitude and the phase of motion of the fundament (n = 1) by

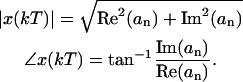(10)

Conventional Fourier analysis references phase to a cosine; we therefore added 90° to our motion-phase data to reference them to our sine wave stimuli. From this 2D analysis, we were able to estimate motion in two directions. The first was the radial direction (referring to the axis running from spiral lamina to spiral ligament) and the second was the longitudinal direction (referring to the axis running along the OC from base to apex). By convention, positive displacements are toward the spiral ligament in the radial direction, and toward the base in the longitudinal direction (Fig. 4 A).

There are several implicit assumptions in our method for motion estimation: 1), the motion is much smaller than the analysis window; 2), the motion is periodic, with frequency equal to the stimulus frequency; and 3), changes in the shape of the region of interest (ROI) are smaller than the displacement of that region.

Estimation of noise

Several factors contributed to variability in our measurements. One was functional differences between the cells related to the physiological state of each cell. Functional differences might show up as differences in the amplitude and phase of motion between individual cells. Another factor was low-frequency vibration and drift in the cochlear holder. Finally, another source of variability was noise within the images.

To estimate the noise in our measurements, we assumed that the measured response was the vectorial sum of a sinusoidal signal with fixed amplitude and phase plus a noise with fixed amplitude but random phase (Fig. 5 A). The presence of noise will affect both the magnitude and the phase of the measured response. In our experiments, the magnitude of the response across cells exhibited more variability than the phase. We believe that this is due to the cells differing in their absolute sensitivity (i.e., being frequency-independent), which would affect the magnitude but not the phase. We therefore decided to consider the effect of noise on just the phase of the measured response.

FIGURE 5.

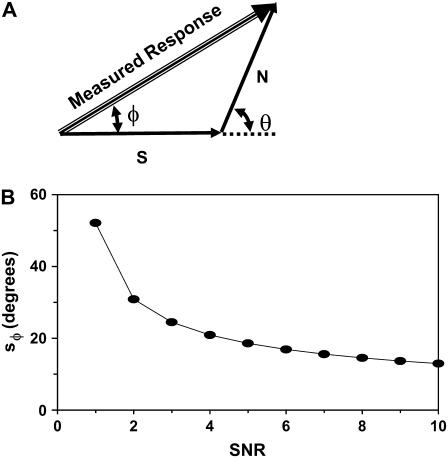
Estimation of the SNR from the standard deviation of the phase of our measured response. (A) The measured response is the vectorial sum of the signal (S) and a randomly varying noise (N). The magnitude and the phase (φ) of the measured response depend on the phase of the noise (θ). (B) Standard deviation of φ (s_φ) as a function of SNR.

The phase variation of the measured response due to a randomly varying noise is given by

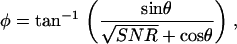(11)

where θ is the phase of the noise and SNR is defined as the signal²/noise². We solved Eq. 11 numerically for θ uniformly distributed from −π to +π and for the SNR ranging from 1 to 10 and estimated the standard deviation of φ as a function of the SNR. The results of this calculation are plotted in Fig. 5 B. Note that when the SNR is <1, the measured responses are below the noise level and the standard deviation of the phase is >52°.

Therefore, to estimate the noise in our experiments, we calculated the standard deviation of the phase of the displacements across multiple cells as a function of stimulus level or frequency. We then recorded the corresponding magnitude of the displacements where the standard deviation of the phase was >52° and set the noise level to be equal to that displacement. In general, the noise level ranged from 10 to 100 nm peak-to-peak. In our motion measurements, the noise level was different across experiments and cell structures. It is important to note that the conclusions of this work do not rely on measurements near the noise level.

Alternative methods of estimating the SNR would have been to compare the stimulus-frequency response to “sidebands” or to collect matching data sets with the stimulus turned off. Since our technique only sampled one period of the response, all Fourier components (other than direct current) are harmonics of the stimulus and are potentially nonlinear responses to the stimulus. In other words, we have no sidebands in the Fourier transform. We did not use the approach of using matching data sets with the stimulus turned off, because this would have doubled our data collection time and we felt that it was important to collect the data from multiple focal planes as quickly as possible to prevent artifacts due to drift in the position of the preparation or in the condition of the cells.

Control experiments

Electrical stimulation

At the beginning of each experiment, after positioning the electrodes, a test stimulus was presented at a frequency of 120 Hz with the strobe flashing at 126 Hz. If the electrodes were positioned correctly and the preparation was in good condition, we observed a 6-Hz motion. If no response was observed within the 0.5–4 mA stimulus range, then the electrodes were repositioned and the test stimulus repeated. The level of the stimulus was kept to a minimum (i.e., displacements were just visually detectable) to avoid overstimulation of the tissue.

Motion artifacts

During data collection, low-frequency building vibrations and drift in the cochlear holder introduced mechanical noise in our measurements. The impact of drift was minimized by collecting a no-stimulus condition before each stimulus phase. Cross-correlation was then performed between the image at a particular phase and the image at the corresponding no-stimulus condition. This control also verified that the motions observed were due to the applied current. In addition, cross correlation was performed among the no-stimulus-condition images to quantify any mechanical drift.

Frame grabber and image processing algorithm

The following experiment was designed to test whether the frame grabber captured the correct frames and whether the motion estimation algorithm gave accurate results. A piezoelectric probe (12) was used to produce a known sinusoidal displacement magnitude for frequencies ranging from 30 Hz to 3 kHz. Images of the force probe were collected using our stroboscopic system. The displacement of the probe was then estimated from these images using our cross-correlation technique. The displacement of the probe was also measured using a motion transducer system (Angstrom Resolver Model 201, Opto Acoustic Sensors, Raleigh, NC), and the results were compared with the displacements obtained using our motion estimation algorithm. The magnitude results were within 1.5 dB and the phase results were within 15° for frequencies between 30 and ∼2 kHz. Above this frequency range, the response of the force probe was not reliable due to its own resonance.

Anatomical orientation

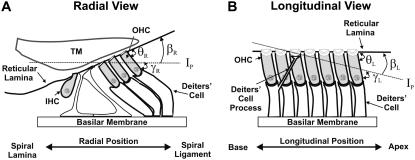
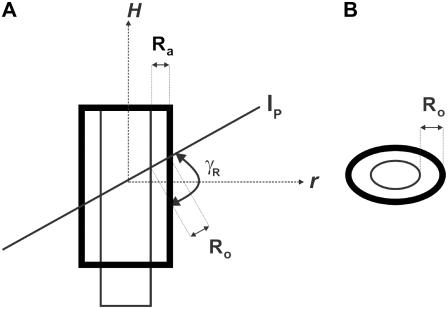
Typically, at the end of each experiment, images were collected at multiple focal levels to establish the anatomical orientation of our excised cochlea preparation with respect to our imaging plane (I_p). To interpret our motion estimation results, it was important to know the anatomical orientation of our preparation for each experiment. In Fig. 6, we show cartoons of the radial and longitudinal view of the OC and identify the angles of interest that will be used in the analysis of our results. The long axis of the OHCs is oriented at an oblique angle with respect to the RL in both the radial direction (θ_R) and the longitudinal direction (θ_L). Because the I_p is not always parallel to the RL, an additional angle is introduced between the I_p and the RL (β_R for the radial direction, β_L for the longitudinal direction) and between the I_p and the long axis of the OHC (γ_R for the radial direction, γ_L for the longitudinal direction). By convention, when (in the radial direction) the spiral ligament or (in the longitudinal direction) the apical end of the I_p is below the RL (as shown in Fig. 6), then the angle β is negative. The relationship between the angles is

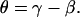(12)

FIGURE 6.

Anatomical cartoons showing the radial and longitudinal views of the OC. Also, shown are possible orientations of our imaging plane (I_p) to illustrate the different angles that are important for understanding the motion estimation results from our surface views. In the radial and longitudinal directions, respectively, θ_R and θ_L indicate the angle between the long axis of the OHCs and the RL; β_R and β_L the angle between the I_p and RL; and γ_R and γ_L the angle between the I_p and the long axis of the OHCs.

Using images taken at multiple focal levels, we were able to estimate γ_R, γ_L, and β_R, β_L, and use these angles to calculate θ_R, θ_L. To estimate γ_R and γ_L, we extracted the same ROI (i.e., the edge of a cell) from all the focal levels. We used our 2D cross-correlation technique to estimate the radial and longitudinal position of the edge of a cell at a given focal depth relative to its corresponding position at the RL level. We repeated this analysis for multiple ROIs and from all three rows of OHCs, and plotted the computed displacements as a function of focal depth. We then computed the slope between successive points in all curves by dividing the incremental change in the radial (ΔR) and the longitudinal dimension (ΔL) by the incremental change in the vertical dimension (ΔH). The angle of interest, γ_R, γ_L between successive points was then computed by

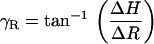(13)

and

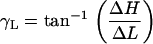(14)

A histogram of all the angles was plotted and the mode of the histograms was chosen as our estimate of γ_R, γ_L.

To estimate β_R, β_L, we used our multiple focal level images and identified those focal depths where key structures such as the hair bundles of the IHCs and OHCs first came into focus. We assumed that when the I_p is parallel to the RL in the radial dimension, we would see the IHC and OHC hair bundles in focus at the same time. Similarly, when the I_p is parallel to the RL in the longitudinal dimension, we would see the entire row of a given structure in our field of view (e.g., the entire row of IHC hair bundles) in focus at the same time. For example, in Fig. 4 A, notice that the three rows of OHCs are all in focus at the same time for both the radial and longitudinal directions. In addition, for this experiment, when we focused at the level of the stereocilia they were all in focus at the same time. This means that the I_p is parallel to the RL in both the radial and longitudinal dimensions. The next step in estimating β_R, β_L was to measure the vertical distance (H) between the focal levels at which the identified structures came into focus and the radial (R) or longitudinal (L) distance between those structures. Using these distances, β_R, β_L were calculated by

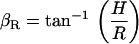(15)

and

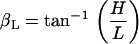(16)

RESULTS

Voltage measurements in SV

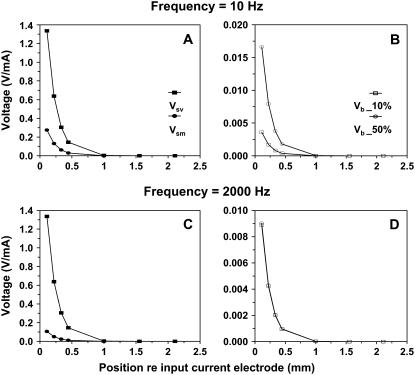
Fig. 7 shows the voltage in the fluid as a function of longitudinal distance from the input-current electrode, for an apical-turn experiment. The input current was 1 mA. We were not able to measure the voltage closer than 300 μm from the input-current electrode due to the large tip diameter of the electrodes. Therefore, in Fig. 7, although the input-current electrode was at 0 μm, the first voltage measurement was 300 μm away. For any given frequency, the voltage decreased as we moved away from the input-current electrode. The decrease was similar for all frequencies tested (i.e., 60, 120, 450, 810, and 1200 Hz). In Fig. 7, we plot the average voltage and corresponding standard deviation for all frequencies. As the distance from the input-current electrode increased, the standard deviation of the voltage at that location also increased.

FIGURE 7.

Voltage in the fluid between the input- and ground-current electrode as a function of longitudinal distance from the input-current electrode, for an apical turn experiment. Each point represents the average voltage of the frequencies tested (i.e., 60, 120, 450, 810, and 1200 Hz) using a 1-mA current stimulus. The vertical lines above and below each point are the average value ± 1 SD. The line is the resulting exponential fit using Eq. 17.

We were able to fit the data using a decaying exponential of the form

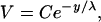(17)

where V is the voltage, C is a constant, y is the longitudinal distance from the input current electrode, and λ is the space constant describing the rate at which the voltage decreases with longitudinal distance from the input-current electrode. For the fit shown in Fig. 7, C = 2.8 V and λ = 150 μm. The space constant indicates that the voltage will drop to 37% of its maximum value at 150 μm away from the input source.

Effect of current level on OHC displacement

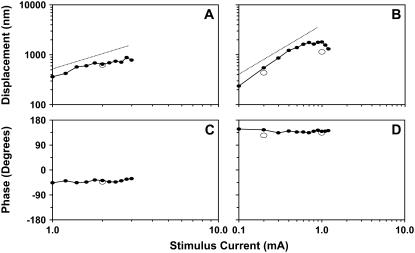
In Fig. 8, we show the magnitude and phase of radial displacements, as a function of stimulus level, for two OHCs. The magnitude of the second and third harmonics was >40 dB below the primary component at all frequencies and stimulus levels. The response magnitude of OHCs increased as the stimulus current increased. At low stimulus levels (when the motion of the cells could just be detected visually), the responses increased linearly with current. As the stimulus level increased further, the responses saturated and, at very high stimulus levels, decreased. The phase of the responses remained constant for all stimulus levels. The radial motion of the first row of OHCs (OHC1) was 180° out of phase with the motion of the third row (OHC3). This phase difference was observed in all of our experiments and will be further addressed in the following sections.

FIGURE 8.

Peak-to-peak magnitude and phase of radial displacements as a function of stimulus current. The stimulus frequency was 120 Hz. Dotted line has unity slope. (A and C) Responses from an apical turn OHC1 (OHC1b, exp. 615). (B and D) Responses from a middle-turn OHC3 (OHC3a, exp. 614). Note that the current axis ranges from 1 to 10 mA in A and C, and from 0.1 to 10 mA in B and D. Repeated measurements (∼25 min later, open circles) were used to evaluate the effect of time on OHC responses.

In Fig. 8, we also show the response at a few selected current levels (circled points in the graphs). These measurements were collected at the end of each experiment to evaluate the effect of time on the responses. Some of these points matched the ones collected ∼25 min earlier; others—like the one shown for the 1-mA current in B—showed a decreased response. Usually, as the current level increases, cells start to swell and stop contracting within minutes.

Finally, note that the current levels used are different for the two cells shown in Fig. 8. In our preparation, the minimum current needed to evoke detectable OHC motion depended on two factors. The first was the exact position of the input-current electrode with respect to the OHCs of the imaging location, and the second was the condition of the preparation. If the input electrode was close to the SV of the imaging location and the preparation was in good condition, the amount of current needed to stimulate the OHCs was small. A preparation was considered to be in good condition when the cells were not swollen and responses of adjacent cells in the same row were in phase. Also note that in all of the preparations used for data collection the TM was intact and extended above the OC as expected in vivo (Fig. 3, A and B; also see Discussion). Typically, the stimulus currents ranged from 0.1 to 4 mA, and for that range of currents, displacements up to ∼2 μm were in the linear regime.

Anatomical measurements

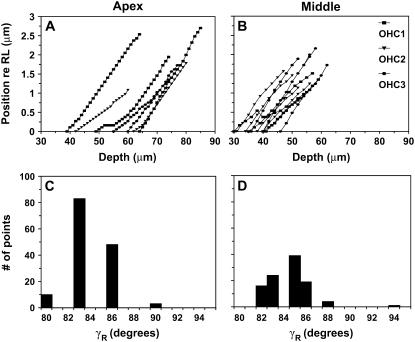
Figs. 8 and 9 illustrate results from two (one apical- and one middle-turn) of the four (two apical- and two middle-turn) experiments in which we estimated γ_R, γ_L, β_R, and β_L. The calculation of these angles was described in Methods. Fig. 9, A and B, shows the apparent radial position of individual OHC1, second row of OHC (OHC2), and OHC3 as a function of focal depth. As we focused from the RL toward the BM level, the radial position of all structures shifted toward the spiral ligament. Fig. 9, C and D, shows the histograms of γ_R, which correspond to the apical- and middle-turn experiment shown in Fig. 9, A and B, respectively. The average γ_R for each turn was taken to be the mode of the distribution shown in the histograms. For the experiments shown, γ_R = 83° in the apical turn and 85° in the middle turn. Finally, for these experiments, β_R = −9° in the apical-turn and +14° in the middle-turn experiment.

FIGURE 9.

Measurements to estimate γ_R in the apex (exp. 1008, CF ∼0.4 kHz) and middle turn (exp. 1011, CF ∼4 kHz). (A and B) Peak radial displacement of individual OHCs from each of the three rows as a function of depth from the RL to the BM. The displacements are positive, indicating that as we focused lower into the organ the cells shifted toward the spiral ligament. Due to the large longitudinal tilt in this experiment, the cells came into focus at different focal levels, and hence the extractions do not all start from the same focal level. In general, extractions from the middle-turn experiments span fewer levels, since the OHCs in this turn are shorter than those from the apical turn. (C and D) Histogram of the angles calculated from A and B (see text).

Fig. 10, A and B, shows the longitudinal displacement of the same structures shown in Fig. 9, A and B. For both the apical- and middle-turn experiments, the longitudinal position of the structures was shifted toward the apex (which by convention is the negative longitudinal direction). Fig. 10, C and D, shows the histograms of γ_L, which correspond to the apical- and middle-turn experiments of Fig. 10, A and B, respectively. The average γ_L for each turn was taken to be the mode of all the angles shown in the histograms. For the experiments shown, γ_L = 87° in the apical turn and γ_R = 89° in the middle turn. Finally, for these experiments β_L = −6° for both experiments.

FIGURE 10.

Measurements to estimate γ_L in the apex (exp. 1008, CF ∼0.4 kHz) and middle turn (exp. 1011, CF ∼3 kHz). (A and B) Peak longitudinal displacement of individual OHCs from each of the three rows as a function of depth from the RL to the BM. The displacements are negative, indicating that as we focused lower into the organ the cells shifted toward the apex. Due to the large longitudinal tilt in this experiment, the cells came into focus at different focal levels, and hence the extractions do not all start from the same focal level. In general, extractions from the middle-turn experiments span fewer levels, since the OHCs in this turn are shorter than those from the apical turn. (C and D) Histogram of the angles calculated from A and B (see text).

Using the above numerical results and Eq. 12, we calculated that for the apical-turn experiment, θ_R = 92° and θ_L = 93°, and for the middle-turn experiment, θ_R = 71° and θ_L = 95°. Similar results were seen in the other two experiments we analyzed.

Apparent diameter changes

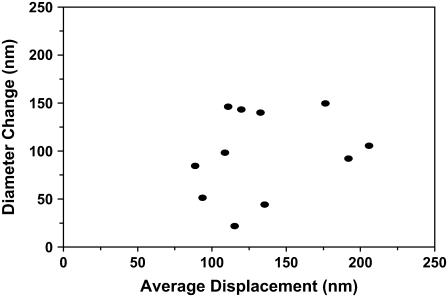
For most of our experiments, we were able to analyze motion for either the spiral-lamina (referring to the side of the cell toward the spiral lamina) or the spiral-ligament (the side toward the spiral ligament) side of a cell. For example, in Fig. 4 A, the structure of interest is the lamina side of the cell. To maximize the SNR, we analyzed the motion of the side of the cell with the greatest contrast. For some experiments, we were able to analyze both sides of the cell for all three rows of OHCs.

In Fig. 11, we show results from a middle-turn experiment where we were able to estimate the radial displacements from both the lamina (R_lam) and ligament (R_lig) edges of individual cells from each of the three rows. We plot the absolute difference (apparent diameter change) between motions of the two edges (ΔR) as a function of the mean displacement (R_mean). Each point in the graph corresponds to a different cell. R_mean ranged from 90 to 200 nm and ΔR from 20 to 150 nm. For all cells, the R_lam side of the cell moved in phase with the R_lig side of the cell (not shown in Fig. 11). For OHC1 and OHC2, R_lam > R_lig, whereas for OHC3, R_lig > R_lam. Similar to our previous findings from the apical turn (42), OHC1 and OHC2 moved in phase (toward the spiral lamina) and OHC3 moved 180° out of phase with respect to the other two rows (toward the spiral ligament).

FIGURE 11.

Absolute difference (diameter change) between the spiral-lamina edge of the cell and the spiral-ligament edge of the cell as a function of the average displacement of the two edges. All data points are from the same middle-turn experiment (exp. 1011, CF∼4 kHz). The stimulus frequency was 60 Hz.

Responses from multiple focal levels at low frequencies

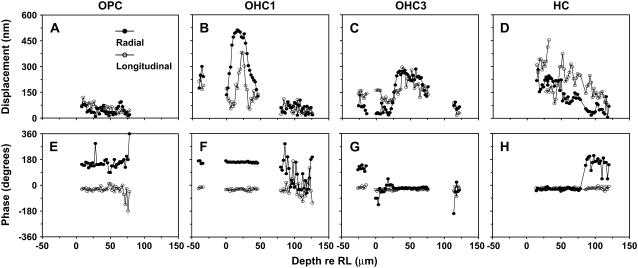
Fig. 12 illustrates electrically-evoked displacement measurements from multiple focal levels in one of our five middle-turn experiments (CF ∼4 kHz). To simplify the presentation of these results we show the motion of all the structures encountered as we focused from the TM to the BM level, for specific radial locations. We present here four such radial locations near the outer pillar cells (OPC), OHC1, OHC3, and the Hensen's cells (HC) region. The OHC2 region (not shown) was similar to OHC1. Notice that in each of the panels, data points are missing for some of the levels. Missing data points indicate that the contrast in these regions was too low for motion analysis. Data are in the noise level when successive phase data are different by >52° (see Methods, Estimation of noise), unless points indicate different structures within the same radial location (i.e., in Fig. 12 G, the first cluster of points refers to TM measurements and the second cluster of points refers to OHC3 and Dieter's cells (DC) measurements).

FIGURE 12.

Peak-to-peak radial (solid symbols) and longitudinal (open symbols) displacements as a function of depth relative to the RL, for four radial locations. All responses are from the middle-turn region (CF ∼4 kHz) from the same animal (exp. 1026). The stimulus frequency was 60 Hz. For this experiment γ_R = 91° and γ_L = 90°. Zero-degrees phase indicates motion toward the spiral ligament in the radial direction and toward the base in the longitudinal direction. (A and E) Magnitude and phase of OPC region displacements, with RL defined as the top of the OPC. (B and F) Magnitude and phase of OHC1 region displacements, with RL defined as the top of the OHC1 hair bundles. (C and G) Magnitude and phase of OHC3 region displacement, with RL defined as the top of the OHC3 hair bundles. (D and H) Magnitude and phase of HC region displacement, with RL defined as the top of OHC3 hair bundles.

The results shown in Fig. 12 are typical for all of our middle-turn experiments. The magnitude of the OC motion near the TM level (Fig. 12, focal depth <0 μm) and near the BM level (depth ∼110–140 μm) was hundreds of times smaller compared to the magnitude of the OC motion near the basal end of the OHCs at their junction with the DCs (depth ∼40–60 μm; see also Supplementary Material, Movie 2). This observation is most obvious for the OHC1 and OHC3 radial locations. For these locations, also note that the magnitude of the radial component of motion was generally around four times smaller compared to the magnitude of the longitudinal component. The magnitude of the motions observed at all focal depths of the OPC region was generally hundreds of times smaller compared to the magnitude of motion near the basal end of the OHCs. We often saw a small increase (∼100 nm) in the magnitude of the radial OPC motion close to the basal end of the OHCs (Fig. 12 A, focal depth ∼25 μm).

The phase of the longitudinal component of the OC motion (Fig. 12, E–H, open symbols) was the same for all structures: during the depolarizing phase of our stimulus (OHCs contracting, see Discussion), all the structures were displaced toward the basal end of the cochlea. The phase of the radial component of the OC motion (Fig. 12, E–H, solid symbols) was more complex: during the depolarizing phase of our stimulus, the TM, OPC, OHC1, basal end of the third row of DC, and HC were displaced toward the spiral lamina, whereas the OHC3 and the adjacent HC region (up to ∼75 μm below the RL) were displaced toward the spiral ligament.

We also measured the responses of the edge of the TM (TM_edge), the inner pillar cell (IPC), and the IHC hair bundles. Motion of all these structures was usually near or below the noise floor of our measurements. We sometimes saw motion in the IHC hair bundles and the TM_edge. During the depolarizing phase of our stimulus, the IHC hair bundles were displaced toward the spiral ligament. The phase of the radial motion of the TM_edge was toward the spiral ligament (i.e., in phase with OHC3 and out of phase with the rest of the TM).

Fig. 13 shows the corresponding data from our one apical-turn experiment (CF ∼0.4 kHz). Similar to the middle-turn data, the magnitude of motion near the TM level (Fig. 13, focal depth <0 μm) and near the BM level (depth ∼100–130 μm) was hundreds of times smaller compared to the magnitude of the OC motion near the basal end of the OHCs at their junction with the DCs (depth ∼40–70 μm). This observation is most obvious for the OHC1 and OHC3 radial locations. Unlike in the middle turn, the magnitude of the radial component of motion in the apical turn was usually around four times larger than and sometimes similar to the magnitude of the longitudinal component. The magnitude of motion observed at all focal depths of the OPC region was generally hundreds of times smaller compared to that near the basal end of the OHCs. We often saw a small increase (∼100 nm) in the magnitude of the radial OPC motion close to the basal end of the OHCs (Fig. 13 A, focal depth ∼70 μm).

FIGURE 13.

Peak-to-peak radial (solid symbols) and longitudinal (open symbols) displacements as a function of depth relative to the RL, for four radial locations. All responses are from the apical turn region (CF ∼0.4 kHz) from the same animal (exp. 325). The stimulus frequency was 30 Hz. For this experiment, γ_R = 73° and γ_L = 95°. Zero-degrees phase indicates motion toward the spiral ligament in the radial direction and toward the base in the longitudinal direction. (A and E) Magnitude and phase of OPC region displacements, with RL defined as the top of the OPC. (B and F) Magnitude and phase of OHC1 region displacements, with RL defined as the top of the OHC1 hair bundles. (C and G) Magnitude and phase of OHC3 region displacement, with RL defined as the top of the OHC3 hair bundles. (D and H) Magnitude and phase of HC region displacement, with RL defined as the top of OHC3 hair bundles.

Finally, similar to the middle-turn data, the phase of the longitudinal component of motion was the same for all structures (Fig. 13, E–H, open symbols): during the depolarizing phase of our stimulus, all the structures were displaced toward the basal end of the cochlea. The phase of the radial component of the OC motion (Fig. 13, E–H, solid symbols) was more complex: during the depolarizing phase of our stimulus, the TM, OPC, OHC1, and HC were displaced toward the spiral lamina, whereas the OHC3 and the adjacent HC region up to ∼75 μm below the RL were displaced toward the spiral ligament. In the apical turn, we did not observe the phase shift observed in the middle turn at the basal end of the DC region (focal depth ∼75 μm (Fig. 12 G)). This may be due to the fact that we were not able to image as deeply in the DC region for the apical turn as for the middle turn.

The magnitude of motion of the IHC hair bundles and the IPC was hundreds of times smaller (usually near the noise of our measurements) compared to the magnitude of motion near the basal end of the OHCs. When motion was seen in the IHC hair bundles, it was similar in phase with the motion seen in the middle turn, i.e., during the depolarizing phase of our stimulus, the IHC hair bundles were displaced toward the spiral ligament. Unlike in the middle turn, we were not able to image the TM_edge effectively in the apical turn, so no motion measurements were made for this structure.

DISCUSSION

Excised cochlea preparation

The major advantage of the excised cochlea preparation is that video microscopy can be used to observe, in the same experimental preparation, the responses of hundreds of cells in the OC simultaneously. Therefore, the relative motion of these cells in response to OHC electromotility can be investigated directly. This is especially important in vibration analysis, which requires the direct comparison of the relative magnitude and phase of motion of several points along the plane of interest and between different planes.

On the other hand, the use of an excised cochlea preparation poses some questions as to how the results can be related back to an intact cochlea. Some of the concerns associated with the excised cochlea preparation are that 1), the endocochlear potential decreases (43) as soon as the animal is decapitated; 2), when the cochlea is opened, the fluid mass acting on the cochlear partition can present a significant load and reduce the amplitude of the vibrations at low frequencies (44–46); 3), during the experiment, the mechanical properties of the cells can change.

When the endocochlear potential decreases, the forward transduction process is compromised. As a result, the gain of the feedback loop in which the OHCs are involved is reduced. This can be used to our advantage if we are interested in investigating the effect of OHC electromotility in the vibration pattern of the OC. By opening the feedback loop, we can directly stimulate the reverse transduction process and understand its contribution to cochlear micromechanics (16).

The vibration pattern of any complex structure depends on the mechanical properties of its individual components, on the anatomical architecture of the structure, and on the type and level of excitation (47). To relate our findings to intact cochlea preparations, we need to address how each of these factors in our excised cochlea preparation relates to intact cochleae.

Naidu and Mountain (14) have measured the stiffness of the excised gerbil OC and found it to agree with in vivo measurements performed on the same species by Olson and Mountain (12,13). Naidu and Mountain (14) also reported that the stiffness measurements were stable over 3 h after decapitation. It was concluded that the mechanical properties of the organ must also remain constant for this time period. Although we were not able to assess the structure of the organ at the subcellular level, we are confident that at the cellular level, the anatomical architecture of the OC was very close to in vivo conditions. This was accomplished by keeping Reissner's membrane intact, thus preserving the anatomy of SM for the entire turn of interest. In addition, using the Cl⁻-modified gluconate-based culture medium, we inhibited cell swelling for the duration of the data collection, thus further preserving the anatomy of the OC.

How is in vitro cochlear electrical excitation relevant to in vivo cochlear excitation? The input to the intact cochlea is the pressure difference between the scala tympani and SV. This differential pressure, in combination with the mechanical properties of the cochlea, sets up a traveling wave on the BM. Thus, the BM vibrates and causes bending of the IHC and OHC stereocilia. The bending of the stereocilia changes the ionic conductance at the surface of the cells, allowing positive ions to flow into the cells, depolarizing their membrane and causing them to contract. The precise phase and magnitude of this contraction is currently thought to shape the vibration pattern of the OC. We will refer to the OHC-driven OC vibration as the “OHC-driven component” and to the pressure-driven OC vibration as the “pressure-driven component”. The relative contribution of these two components to the total vibration of the OC depends on the type and level of excitation (48). We argue that with our electrical stimulation paradigm we emphasize the OHC-driven component. In the intact cochlea, the contribution of the OHCs appears to dominate at low sound levels; therefore, we expect that the OHC-driven component would be a dominant contributor (albeit not the only one) to the total vibration pattern at low sound levels.

Our data suggest that during the depolarizing phase (positive current into SV) of our stimulus, the OHCs contract. From our multiple plane surface views, we have been able to create low-resolution radial cross sections of the OC; from these new sets of images, we observed that during the depolarizing phase of the stimulus, the OHC3 increased in diameter and moved toward the spiral ligament. During the depolarizing phase of the stimulus, the cells were displaced toward the base; this type of longitudinal displacement could only occur if the cells were contracting (see our discussion of the longitudinal motion). Other studies using electrical stimulation, with similar electrode configurations, showed that during the depolarizing phase of the stimulus, the BM moves toward SV; this phase of motion occurred due to the OHCs contracting and pulling on the BM (16,18).

Although the current path in these experiments is unknown, the most likely path for the current is to go into the cell through the apical channels and out through the basolateral membrane channels. This path agrees with our observation that the OHCs contract during the depolarizing phase of the stimulus. Another possible route for the current would be through the RL, into the hair cell via the lateral membrane, and exiting either via the opposite lateral membrane or the basal portion of the membrane. This latter route appears to be less likely due to the high resistance of the tight junctions that exist between the cells (for a review, see Slepecky (49); also, see Mountain and Hubbard (50)).

Effect of tissue condition on responses

In our early experiments, the excised cochlea was immersed in oxygenated culture medium (Leibovitz L-15) that resembled perilymph. Using this medium, OHC swelling was observed in all of our preparations. The swelling process was accelerated when electrical current was applied, leading to complete loss of motility within a few minutes. Zeddies et al. (51) reported that cell swelling in excised mammalian preparations can be inhibited for up to 3 h if the Cl⁻ in the culture medium is replaced with a less permeable, larger anion, like lactobionate or gluconate. Gluconate was also found to be effective with lizard cochlea preparations (52,53). When we used gluconate as a Cl⁻ substitute, we were able to inhibit cell swelling for up to 9 h postmortem.

Cell swelling can affect both the motility of the cell and the response characteristics. In most preparations with swollen cells, OHC motility was completely lost. In a few of these preparations, motion could still be evoked (for a few minutes) if sufficiently high currents were used. It is difficult to know the exact physiological condition of these cells. Swollen cells might have leaky membranes, and therefore larger currents would be needed to stimulate the cells. In addition, cell swelling alters membrane tension, which can lead to a shift in the voltage dependence of the OHC motor complex (54). Similar dependence between membrane tension and voltage shift has been measured for the OHC motor protein prestin (55,56).

Swollen cells from the same row, when motile, moved out of phase with each other. Probably, in these cases, some cells that still exhibited motility displaced the cells that did not respond and those nonresponsive cells passively moved around in random directions. Similar responses have been reported in organ cultures of guinea pig cochleae in response to electric stimulation (57). Although the authors did not comment on the cell swelling, they mentioned that these asynchronously moving cells seemed to be partially detached from surrounding cells.

For all experiments presented in this article, the cells were in good condition. By that, we mean that 1), the majority of the cells within the turn of interest were not swollen during the course of the data collection; and 2), all OHC cells in the same row moved synchronously.

Data repeatability and variability

During our experiments, continuous current stimulation caused the preparation to deteriorate with time. The degree and the time course of this deterioration depended on current level. As shown in Fig. 8, the results were repeatable when the current was kept to a minimum. In fact, in some of our longest experiments (∼5 h) with low-stimulus currents, the magnitude of the displacement of a given structure across time was within 2.5 dB and the phase within a few degrees.

Sources of variability among different experiments could be related to 1), the distance between the electrode and the imaging location, and 2), the orientation of the imaging plane with respect to the long axis of the cell (γ_R, γ_L). The distance between the electrode and the imaging location depended on the amount of bone surrounding the SM of the location of interest (Fig. 1). Often, after dissection, there was too much bone surrounding the SM, which did not allow us to place the electrode very close to the location of interest, and therefore larger currents were needed to stimulate the OHCs. The orientation of the imaging plane with respect to the long axis of the cell was adjusted manually. This course adjustment did not allow a precise control on the cochlear orientation. Therefore, γ_R and γ_L varied among experiments and could cause variability in our estimates of the magnitude of the radial and longitudinal components of motion (see Appendix A). Given the experimental range of γ_R and γ_L (Figs. 9 and 10), variability due to orientation differences between our experiments was within 1.5% and has no impact on our conclusions.

Anatomical measurements

Our anatomical measurements (see Results) show that the OHCs in the apical and middle turns are oriented approximately perpendicular to the RL in the longitudinal dimension. The two turns differ in the radial orientation of the OHCs with respect to the RL. The apical-turn OHCs were oriented approximately perpendicular to the RL and the middle turn OHCs oriented at ∼70° with respect to the RL with their basal end tilted toward the spiral ligament.

We have found no other studies with in vitro measurements of the longitudinal orientation of the OHCs in the gerbil. We compared our findings regarding the radial orientation of the OHCs with those of the unfixed gerbil hemicochlea (58). Using the images shown in Fig. 4 of Edge et al. (58), we estimated that in the hemicochlea preparation the OHCs are oriented at ∼60° with respect to the RL in both the apical and middle turns. We currently cannot explain the difference in the apical-turn radial orientation of the OHCs between the two studies. One possibility is that the apical-turn location in these studies is significantly different.

Knowing the anatomical orientation of the OHCs within the OC is important for modeling studies of cochlear function. Some models have assumed that the longitudinal tilt of the OHC is important in cochlear amplification (for example, Geisler and Sang (59)). These models would appear to be inapplicable for the gerbil cochlea given the fact that the OHCs show little longitudinal tilt.

Estimates of length change

Our experimental data combined with our modeling results (Appendix B) indicate that, depending on the open probability of the transduction channels, the OHC transmembrane voltage change in our excised cochlea preparation ranged between 0.8 and 4 mV/mA near our imaging location (see Fig. 20, location 0.3 μm) and decreased as we moved away from the electrode location. As mentioned in Methods, our currents were as high as 4 mA, so the maximum transmembrane voltage change in our preparation was ∼16 mV. This voltage is comparable to or less than the voltage used in isolated hair cell studies (for example, see Santos-Sacchi (60)), which has been as high as 100 mV, and it was still in the linear range of the OHC voltage-length curve (60). Santos-Sacchi (60) has also inferred that the voltage sensitivity of the length change at around the resting potential of the OHC is ∼10 nm/mV. Assuming that the resting potential of the OHCs in our preparation is the same as in the isolated hair cell studies, we would have expected length changes as high as 160 nm. This is within an order of magnitude of the responses we measured (see length change estimate below). We can therefore proceed to compare our estimated range of OHC length changes to that of isolated OHC studies.

Assuming that the OHC is cylindrical and that the volume of the cell is conserved during contraction, the range of percent length changes that corresponds to the apparent diameter changes shown in Fig. 11 is ∼0.7–3.6%. In this calculation, the assumptions are that in the middle turn of the gerbil cochlea the length of the OHC is 40 μm (58) and the diameter of the OHC is 8 μm (our own estimates). This range is of the same order of magnitude as the expected length changes for isolated hair cells. For example, according to Santos-Sacchi (60), the range of percent length changes in guinea pig OHCs, estimated from Fig. 2 of their article, is 0.75–3%, depending on the membrane potential. We expected that the loading effects of surrounding cells on the OHCs would decrease the displacement magnitude of the OHCs with respect to that in isolated OHC studies. The fact that our estimates of percent length change are of the same order of magnitude as those estimated from the isolated hair cell studies suggests that OHC motility in an intact cochlea can significantly affect OC motion.

OHCs pivot about the RL

Most of the data presented are from regions of interest that included either the spiral lamina or the ligament edge of the OHCs. In Fig. 11, we presented results from experiments where extractions from both sides of the cell were possible. The fact that both sides of the cells moved in phase, coupled with our observation that the magnitude of the displacements of the OHCs near the RL level were hundreds of times smaller compared to the magnitude of the displacements at the basal end of the OHCs, leads to the conclusion that the cells pivot around a center of rotation that is close to the RL.

Even if the cells were not contracting, there would be an apparent diameter change due to the rotation of the cell. In the following paragraphs, we give a quantitative analysis of the apparent diameter change due to rotation and how it would affect our measurements of diameter change due to contraction.

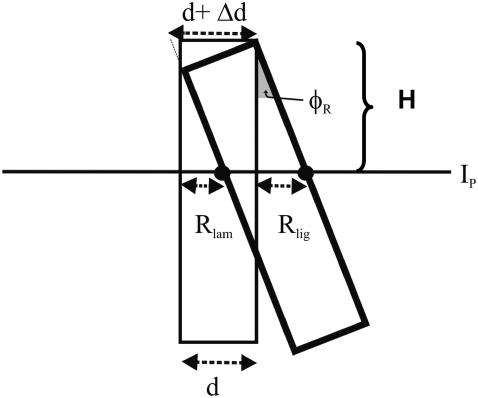
In Fig. 14, we assume that an OHC3 is not contracting and show the motion due to pivoting. The cell is illustrated in the resting state (thin line) and during maximum displacement resulting from pivoting around the top right corner of the rectangle (thick line). In the simplest case, where the imaging plane, I_p, is perpendicular to the long axis of the cell, the change in diameter caused by rotation, will be given by

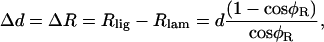(18)

where R_lig and R_lam are the radial displacement of the ligament and lamina edge of the cell, respectively, d is the diameter of the cell, and φ_R is the pivoting angle. Notice that we assume Δd = ΔR, due to the radial symmetry of the cell. The only unknown in Eq. 18 is φ_R, which can be calculated by

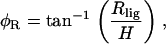(19)

where H is the vertical distance between the pivoting point and the location of I_p. Similarly, for OHC1 and OHC2,

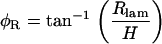(20)

FIGURE 14.

Schematic drawing of an OHC radial cross section. The cell is shown at rest (thin line) and after it has rotated about the upper right edge (thick line). The angle of rotation (pivoting angle) is indicated by φ_R. d, diameter of cell; Δd, observed change in diameter of the cell due to pivoting; R_lig, radial displacement of the ligament-side edge of the cell; R_lam, radial displacement of the lamina-side edge of the cell.

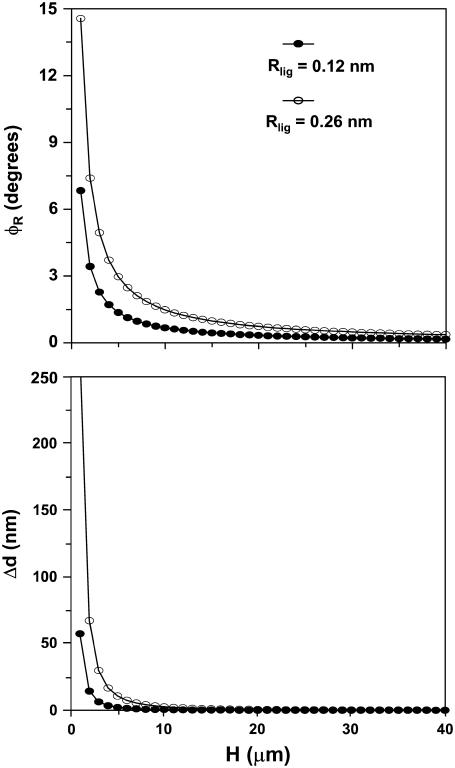
From the data presented in Fig. 11, the range of R_lig (for OHC3) and R_lam (for OHC1 and OHC2) was 120–260 nm, and the range of H was 0–40 μm. Notice that in this experiment γ_R ≈ 85°; therefore, the maximum number for H was set to be equal to the length of the OHCs. For the middle turn of the gerbil cochlea, this length was estimated to be 40 μm from the data of Edge et al. (58). Using the above values and Eq. 19, we calculated φ_R as a function of H. Fig. 15 shows the results of this calculation. Depending on the location of I_p (which in this experiment is equal to H), φ_R ranges from 0.2° to 7° for R_lig/lam = 120 nm, and from 0.4° to 14° for R_lig/lam = 260 nm.

FIGURE 15.

Calculation of φ_R and Δd from Eqs. 19 and 18 using data from Fig. 11. For each calculation, we used the minimum and maximum R_lig to estimate a range of φ_R and Δd.

We then calculated the expected diameter change of the cell due to pivoting using Eq. 18. The only unknown in this equation was the diameter of the OHC, which from our images and also from Edge et al. (58) was estimated to be 8 μm. The results are shown in Fig. 15. Depending on H, Δd ranges from 0.04 nm to 57 nm, for R_lam/lig = 120 nm, and from 0.17 nm to 266 nm, for R_lam/lig = 260 nm. Using our multiple-level images, we estimated that our imaging plane was 30 μm below the RL. Therefore, in this experiment, the expected Δd due to pivoting would range from 0.06 nm to 0.3 nm. This value is very small and below the noise level of our system. In fact, for any H > 4 μm, the resulting Δd < 17 nm, which is a very small value. Therefore, the difference in the motion of the two edges of the OHCs shown in Fig. 11 (26–∼150 nm) should be a reliable estimate of the diameter change due to OHC contraction.

Finally, note that our calculation of the mean displacement (Fig. 11) corresponds to the displacement of the center of the cell during pivoting. This ranged from 75 nm to 200 nm. These numbers correspond to a range of pivot angles of 0.14–0.38° (for H = 30 μm). These angles are in agreement with the expected pivot angles shown in Fig. 15, for H = 30 μm.

The longitudinal motion of the OC at low frequencies is simple

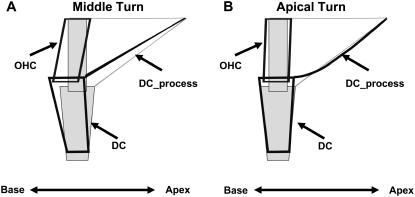
During the depolarizing phase of our stimulus, the OHCs contracted and all structures moved in phase toward the base of the cochlea. The large longitudinal motion in the middle turn (compared to the apical turn) was not expected because our anatomical measurements showed that the OHCs in both turns were oriented perpendicular to the RL. It may be that this longitudinal motion results from constraints imposed by the DCs. Each OHC sits on the apical end of a DC. The DC sends a process toward the RL, which extends apically and, together with the cuticular plate of the OHCs, forms part of the RL (Fig. 6 B). Although in many species the third-row DC process arches to form the outer tunnel, in gerbils it passes up to the RL, as do the processes of the other two rows of DCs (61,62). Within the cytoskeleton of the DC, there are microfilaments and microtubules that run from the basal end of the DC to the apical end, and also extend to the RL through the DC process. (For a complete list of references, see Slepecky (49) and Spicer and Schulte (63).) This specialization of the DC cytoskeleton has been referred to as the microtubule stalk (63) and is also present in the pillar cells. In both structures, the stalk adds structural rigidity.

Based on the above information, we assume that during OHC contraction the DC process does not bend. Therefore, during contraction, we expect the OHC base to be displaced longitudinally toward the base of the cochlea. This motion is illustrated in Fig. 16 A. Note that, for simplicity, we also assumed that during OHC contraction the RL remains fixed and the DC moves in the vertical dimension due to the length change of the OHC. Even if this assumption was relaxed, and the length change of the OHC displaced both the RL and the BM, our prediction of Fig. 16 A, i.e., that during OHC contraction the OHC base is displaced longitudinally toward the base of the cochlea, would remain the same.

FIGURE 16.

Schematic drawing of an OHC/DC complex shown at rest (gray fill, fine lines) and during maximum contraction (no fill, thick lines). (A) Expected OHC/DC displacement without bending of the DC_process. (B) Expected OHC/DC displacement with bending of the DC_process.

The above arguments however, do not explain the differences in the relative magnitude of the radial and longitudinal OHC component, between the apical and middle turns. Spicer and Schulte (64) showed that there are structural differences in the DC body along the length of the cochlea. These differences are such that the DC stiffness decreases from base to apex (14,64). If a similar argument holds for the DC process, then we expect that in more apical regions the DC process would be more compliant, and could bend during OHC contractions. Therefore, in more apical regions, the OHCs would not rotate toward the basal end of the cochlea as much as they do in more basal regions (Fig. 16 B).

Other structures that also showed longitudinal displacements (besides the OHCs and DCs) were the HCs and, to a smaller extent, the RL and the TM. We believe that these structures are just passively following the displacements imposed by the OHCs.

The radial motion of the OC at low frequencies is complex

OHC and DC motion

We present the first systematic study of the radial micromechanical motion of the OHCs as a function of focal depth. Previous investigators have presented measurements of OHCs at a single focal depth (usually at the focal level of the RL). Vujanovic et al. (65,66) measured the motion toward the apical and basal end of the OHCs in a gerbil hemicochlea preparation, but only report the transverse component of motion. Clearly, for such a complex structure as the OC, we expect that the vibration pattern of the organ in any direction cannot be resolved by measurements at one location. Our data show that the vibration of the OHC in the radial dimension is complex and depends on focal level.

All magnitudes of radial displacement of all rows of OHCs at the level of the RL was hundreds of times smaller compared to the magnitude of the corresponding radial displacements for focal levels close to the basal end of the OHCs. This increase in the radial displacement of the OHCs, as we focused from their apical to their basal end, appeared to be gradual. During OHC contraction, the OHC1 and OHC2 were displaced toward the spiral lamina, whereas the OHC3 were displaced toward the spiral ligament. Using our data and simple anatomic models of the OHCs, we concluded that the radial motion of the OHCs was a combination of contraction and pivoting (see above, Anatomical measurements). This complex motion of the OHCs seems to be the direct consequence of their anatomical location in the OC. Our data suggest that when the cells contract, they also pivot toward more compliant regions. For OHC1 and OHC2, this direction was toward the inner tunnel, and for OHC3 it was toward the outer tunnel of the OC (Fig. 17). Recently, Scherer and Gummer (28) and Chan and Hudspeth (22), using electrical stimulation, reported phase reversals between different rows of OHC at the level of the RL.

FIGURE 17.

Schematic drawing showing the radial view of the OC. The OC is shown in two states: at rest (gray lines) and at maximum contraction (black lines). The cartoon summarizes our findings of how the OC moves at low frequencies (∼2–6 octaves below CF; details in text). All motions have been exaggerated for visualization purposes.

Previous studies (23,57), using low-frequency electric stimulation in immobilized guinea pig cochlear explants, reported that the displacement of the IHC and pillar cell region was ∼40% of the displacements measured in the OHC region. The authors proposed a model in which the contractions of OHC result in a radial shear of the RL (e.g., see Fig. 8 in Reuter and Zenner (57)). As a consequence, the apical end of the OHC shows larger radial displacement than the basal end. These data at first appear to contradict our measurements; we showed that the radial motion of the OHC increases toward its basal end. We believe that the RL motion observed in the above-mentioned studies is a consequence of their methodology. Specifically, in both studies, the BM was immobilized; therefore, during OHC contractions, only the RL was allowed to move. Nevertheless, our data is consistent with their finding of small radial displacements in the IHC and PC region.

As we focused deeper into the OC, away from the basal end of the OHCs, the contrast of the structures decreased and we were not able to visualize the entire length of the DC. Therefore, most of our measurements are made from the apical half of the DC that surrounds the OHCs. DC motion decreased as we focused from the apical end toward the basal end of the cell. The direction of motion of the apical end of the DC was that of the corresponding OHCs. Vujanovic et al. (65) reported that in the hemicochlea preparation, at low frequencies, the movement of the DC was similar to that of the basal end of the OHC. This is consistent with our findings. In Fig. 17, we illustrate the apical ends of DC2 and DC3 moving apart, but the basal ends moving together. The existence of gap junctions (49) between the lateral sides of the DC leads us to believe that DC from all rows would move together toward their basal end.

OPC and HC motion

Small (∼100 nm) radial motions were sometimes seen in the OPC region near the basal end of the OHC. This motion could be bending of the middle of the OPCs due to the OHC1/DC complex pushing toward the spiral lamina.

The HC region adjacent to the OHC3 follows the amplitude and direction of motion of OHC3. At focal levels close to the BM, the amplitude of radial HC motion decreases and the direction shifts toward the spiral lamina (Fig. 17, arrows). This was particularly evident in our middle-turn experiments, where we could clearly see the edge of the HCs (Fig. 3 D) at focal levels close to the BM. We do not have a good explanation for the antiphasic motion between the upper half of the HCs and the edge of the HCs. In general, the radial motion of the HCs seems to be the direct consequence of their location with respect to the OHC3. We are not aware of any quantitative studies on the radial motion of HCs as a function of focal level.

TM and hair bundle motion

The motion of the TM depended on radial position and was generally hundreds of times smaller than the motion of the basal end of the OHC. The magnitude of TM motion was in the noise of our measurements (which ranged from 10 nm to 100 nm peak-to-peak) at radial locations close to the IHC and the IPC and increased above the OHCs. The direction of TM motion during OHC contraction was toward the spiral lamina. Our data (Figs. 12 and 13) suggest that the magnitude of TM motion was approximately three times larger in the apical turn compared to the middle turn. This difference could be due to the different orientations of the cochlea in the two experiments.

In some middle-turn experiments, we were able to measure the motion of the TM_edge. The magnitude of motion of this structure increased as we focused closer to the RL and (during OHC contraction) the direction of motion was toward the spiral ligament. This is the same direction of motion seen for the OHC3 and HC. In the apical turn, the TM_edge extended more toward the spiral ligament, i.e., it appeared to be wider in the radial dimension. Therefore, measurements of the TM_edge were not possible in the apex, because the view of TM_edge was obstructed by the overlying stria vascularis. Other studies (58,67) have also reported that the distance from the spiral limbus attachment of the TM to the edge of the TM was larger in the cochlear apex than in the base.

Our anatomical observations (i.e., Fig. 3, A and B) show that in our preparations the TM overlies the OC in a manner similar to the way it overlies the OC in vivo, and that the TM has not suffered major shape changes due to our fluid composition (for more details, see Karavitaki (37)). The structural composition and mechanical properties of the TM (for a review, see Freeman and co-workers (68,69); also, see Shoelson et al. (70)) and the anatomical relation of the TM to the RL, coupled with our measurements, make plausible the possibility of the TM rotating about the limbal zone and stretching at the marginal band (Fig. 17). More experiments need to be done to substantiate this hypothesis.

Gummer et al. (71) have used an excised guinea pig cochlea preparation and recorded the motion of the TM in both the radial and transverse directions. At low frequencies (∼1–1.8 octaves below the CF), the major component of motion of the TM was in the transverse direction, i.e., perpendicular to the RL, and smaller motions were seen in the radial direction (22). The radial component of motion was toward the spiral lamina when the BM was displaced toward the SV (see Gummer et al. (71), Figs. 2 B and 3 B). Their data were collected in the apical turn and appear to be consistent with our findings regarding the radial component of TM motion.

The investigation of the motion of the TM has been of great interest due to its influence on the motion of the IHC and OHC hair bundles. We have attempted to measure the motion of the hair bundles. In most of our experiments, motion of both the IHC and OHC hair bundles was very small and in the noise of our measurements. For most experiments, we could not resolve whether the motion was due to hair-bundle rotation or translation (due to the motion of the OC). Therefore, we will not be discussing these results any further.

BM motion

The radial motion of the BM was hundreds of times smaller than the motion recorded at the base of the OHCs, and usually in the noise of our measurements. This was partly due to the low contrast of our images at the BM level. Motion in the transverse direction cannot be ruled out. In fact, in Fig. 17, we have included the transverse motion observed by other investigators using electric stimulation. We view those studies as complementary to ours, and therefore we incorporate their results to present a more complete picture of the OC motion under low-frequency (several octaves below the CF) electric stimulation.

Mammano and Ashmore (17) measured the transverse motion of Claudius's cells (CC, next to the outermost row of HC), and the HC (at the level of the RL) in response to electric current, in the apical turn of excised guinea pig cochleae. The motion of the CC was taken to represent the motion of the BM at that region, and was found to be ∼5.4 times less than the motion of the HC. In addition, during OHC contraction the BM moved toward the scala vestibule, whereas the RL moved toward the scala tympani. No measurements were made at other BM or RL locations. In Fig. 17, we have included this antiphasic motion between the BM and RL. We feel that the relative magnitude between the BM and RL motion will depend on radial location and that more experiments are needed to determine this relative motion.

Xue et al. (16,72) and Nuttall et al. (18,73) measured the transverse motion of several radial locations across the BM. These studies were performed in the basal end of gerbil (16,72) or guinea pig (18,73) cochleae. Electrical stimulation revealed phase differences between the arcuate zone (AZ) and the pectinate zone (PZ) of the BM. During OHC contraction, the AZ moved toward the scala tympani while the PZ moved toward the SV (Fig. 17). Nuttall et al. (18) made measurements at several radial locations and found that the motion of the PZ was largest (∼1.5 nm) close to the foot of the OPC and OHC1 and decreased gradually from the region of OHC2 to CC (∼0.6 nm). In our illustration (Fig. 17), we have included this antiphasic motion between the AZ and PZ. Recently, Chan and Hudspeth (22) also reported that in response to electrical stimulation the transverse motion of the BM was small (∼1 nm) and showed phase variations with radial location.

Karavitaki and Mountain (74) have shown that the efferent medial olivocochlear (MOC) fibers that cross the tunnel of Corti (ToC) to innervate the OHCs exhibit longitudinal displacement during OHC contractions, with magnitude similar to or larger than OHC displacements. MOC fiber displacements were shown to be due to fluid flow in the ToC. Fluid flow into the ToC could be the cause of the antiphasic motion between the AZ and PZ. Specifically, during OHC contraction, the BM would move toward the SV, whereas the RL would move toward the scala tympani (17). This would decrease the cross-sectional area of the OC and cause fluid to be pushed into the ToC. Some of that fluid would flow longitudinally, displacing the MOC fibers, and the rest could cause the relatively compliant AZ (12–14) to be displaced toward the scala tympani.

Predicted OC vibration pattern and relation to intact preparations

We predict that for stimulus frequencies ∼2–6 octaves lower than the CF, the OC vibration pattern is as shown in Fig. 17. We and others believe that in the intact cochlea the vibration of the OC will be the superposition of two components, the pressure-driven component and the OHC-driven component (30,37,48). Depending on the stimulus type (electrical versus acoustical), stimulus frequency (relative to CF), and level of excitation, the relative contribution in magnitude and phase of each of these components will change. Consequently, any factor that affects OHC contractions, i.e., the frequency and the level of the input, will also have an effect in the vibration of the OC. In this study, we emphasized the OHC-driven component and found that it would give rise to a complex vibration pattern at low frequencies (∼2–6 octaves below the CF). In vivo, for low-level stimuli that mainly evoke the OHC-driven component, our proposed vibration pattern (Fig. 17) would be plausible.

The motion of the OC at low frequencies (several octaves below the CF) is important in shaping the tail region of the auditory nerve fiber (ANF) tuning curves. Stanković and Guinan (75) reported that the responses of ANF at tail frequencies ∼3–4 octaves below the CF showed phase changes with level and were not the result of a simple coupling between the motion of the BM and the bending of the IHC hair bundles. They hypothesized that this phase change was affected by cochlear mechanics beyond the level of the BM and before the level of the synapse and could be the result of multiple modes of OC vibrations. Recently, Guinan et al. (76) observed in vivo MOC-induced inhibition of the first peak of the ANF response that could not be explained using the traditional traveling-wave-induced BM motion. They hypothesized that the motion that might explain this inhibition comes before the first peak of the traveling wave. Radial fluid motion in the subtectorial space (30) has been reported as a result of OHC contractions and could provide a mechanical correlate for this observed inhibition. Because the inhibition comes before the first peak of the traveling wave, there should be a low-frequency (at least 3–4 octaves below the CF) motion that shapes the first peak of the ANF response. Our interpretation of the low-frequency motion of the OC supports such complex vibration and the possibility of mode shifts, depending on the level of excitation, due to the level dependence of OHC contractions.

CONCLUSIONS

1. We present the first systematic study on the internal micromechanical motion of the OC due to electrically evoked OHC contractions at frequencies 2–6 octaves below the CF.

2. Our anatomical measurements show that the OHCs in the gerbil cochlea are oriented perpendicular to the RL in both the radial and longitudinal directions in the apical turn and in the longitudinal direction in the middle turn. In the middle turn, OHCs are oriented at ∼70° below the RL with their basal ends facing toward the spiral ligament.

3. The longitudinal motion of the OC is simple: all structures move in phase and toward the basal end of the cochlea, although by different amounts.

4. The radial motion of the OC is complex. During OHC contractions,

   • the motion of the TM, RL, OPC, and BM is small;
   • the motion of OHC/DC complex is large at the basal end of the OHCs and decreases toward the RL and BM;
   • OHC1 and OHC2 pivot about the RL toward the spiral lamina;
   • OHC3 pivots about the RL toward the spiral ligament;
   • HCs follow the motion of OHC3.

5. The estimated OHC percent length change is in the range 0.7–3.6%, which is the same order of magnitude as in the isolated OHC studies. Our finding supports the idea that OHC motility in an intact cochlea can significantly affect OC motion.

6. During OHC contractions, fluid flows into the tunnel of Corti (74). This flow could be the cause of the previously observed antiphasic transverse motion between the AZ and the PZ of the BM.

7. The complex micromechanical motion of the OC may explain the phase changes observed in ANF responses to tail frequencies and the MOC-induced inhibition of the first peak of the ANF response (76).

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

APPENDIX A: THE EFFECT OF COCHLEAR ORIENTATION ON MOTION ESTIMATES

The orientation of the I_p with respect to the long axis of the OHCs could affect our estimates of motion in the radial and longitudinal directions. To illustrate this, consider the OHC geometry shown in Fig. 18. Here, the OHC is treated as a cylinder in two states: 1), at rest (thin line) and 2), at maximum contraction (thick line). The axis running along the long axis of the cell is the vertical dimension and the axis perpendicular to the long axis can be either the radial or the longitudinal dimension (due to the radial symmetry of the cylinder). Assuming that the volume of the cell remains constant, OHC contraction will result in shortening in the vertical dimension and expansion in the radial or longitudinal dimension. This expansion translates into an increase in the radius of the cell, marked as R_a (actual change of radius). If our imaging plane is perpendicular to the long axis of the cell (i.e., γ_R = 90°), then the observed change in radius R_o = R_a. If our imaging plane is as shown in Fig. 18 A, i.e., γ_R > 90°, then R_o > R_a. Specifically, R_o = R_a/cos(π(γ_R − 90)/180). Similar arguments hold for the longitudinal dimension. In Fig. 18 B, we show the surface view of an OHC at rest (inner circle) and at maximum contraction (outer circle). The orientation is such that γ_R > 90° while γ_L = 90°. In this case, L_o = L_a, but R_o > R_a. Therefore, we would be overestimating the radial component of motion. In our experiments, γ_R (γ_L) were between 80° and 90° (−95° and −84°); therefore, at the most we would be overestimating the motions by ∼1.5%.

FIGURE 18.

(A) Schematic drawing of an OHC's radial cross section. The cell is shown at rest (thin lines) and at maximum contraction (thick lines). H, vertical axis, in this case parallel to the long axis of the cell, generally considered to be the axis parallel to the optical axis; r, radial axis; R_a, actual radial displacement; R_o, observed radial displacement; all other acronyms as defined in Fig. 6 B. Surface view of the OHC at rest (thin lines) and at maximum contraction (thick lines).

APPENDIX B: COCHLEAR ELECTROANATOMICAL MODEL

To relate our electrical stimuli to those used with isolated OHCs, a simple electroanatomical cochlear model was used to estimate intracochlear and intracellular potentials. The electroanatomical model is a simplified one-dimensional finite-difference model based on physiologically derived parameters. We used this model to predict the spatial distribution of the voltage in SM. The model was also used to predict the spatial distribution of the voltage across the basolateral membrane (R_b) of the OHC.

Model description

Fig. 19 shows the first, second, and last sections of the model. The input to each section is the voltage in SV that results from our current stimulation (Fig. 7, curve fit). The lumped resistance R_rm represents the resistance of the Reissner's membrane per unit section. The lumped elements R_sv and C_sv represent the resistance and capacitance, respectively, of the stria vascularis per unit section. The lumped elements R_a, C_a and R_b, C_b represent the apical and basal resistance and capacitance of all the OHCs per unit section. The sections are coupled by the axial resistance of the SM per unit section, R_sm. The model is short-circuited at both ends, since in our preparation the two ends are open fluid spaces.

FIGURE 19.

One-dimensional cochlear electroanatomical model. Three sections of the model are shown. All parameters are as explained in text.

Parameter estimation

All parameters were scaled according to the length of each model section. The length of each section was equal to Δx = X/N, where X is the total length of the cochlea and N is the total number of model sections. We assumed the cochlea length to be X = 11.1 mm (38), and we set the number of sections at N = 100. Furthermore, there was no spatial variation in the parameters of the model, except for the input voltage.

To get an estimate of the resistance per unit section, we used the Johnstone et al. (77) estimate of the resistivity of Reissner's membrane (ρ_rm = 36.8 kΩ mm²) and divided it by the Reissner's membrane area (A_rm = Δx × 0.4 mm) of each section. The final value was R_rm = 829 kΩ/section. We have not been able to estimate a value for the capacitance of Reissner's membrane, and thus have not included it in the model.

To estimate the impedance per unit section, we first estimated the input impedance of SM to be 10 kΩ/mm (77–79) and then multiplied it by the length of each section, Δx. The final value was R_sm = 1.1 kΩ/section.

To get an estimate of the resistance per unit section we used the Johnstone et al. (77) estimate of the resistivity of stria vascularis (ρ_sv = 4.8 kΩ mm²) and divided it by the stria vascularis area (A_sv = Δx × 0.2 mm) of each section. The final value was R_sv = 216 kΩ/section. Nakajima and Mountain (80) and Nakajima (81) have estimated the time constant of the stria vascularis from their cochlear microphonic frequency response data to be τ_sv ≈ 0.22 ms. Using this value, we calculated the capacitance of the stria vascularis to be C_sv = τ_sv/R_sv = 1.05 nF/section.

We used the same values as in Nakajima and Mountain (80) and Nakajima (81) for most of the OHC membrane parameters. The apical and basal OHC capacitance were estimated by combining data from Santos-Sacchi (82) for the total capacitance of the cell and data from Dallos (83) for the ratio of C_a/C_b. For OHCs from the middle turn of the gerbil cochlea, C_a = 2 pF/OHC and C_b = 21 pF/OHC. To get the capacitance per unit section, we multiplied the capacitance of an individual OHC by (Δx/d), where d is the diameter of an OHC plus the space between adjacent OHCs of the same row. We used d = 10 μm and multiplied each capacitance by 3, since there are three rows of OHC per section. The final values were C_a = 66 pF/section and C_b = 699 pF/section.

To calculate the values for the apical resistance of the OHC, we considered the OHC at rest. We estimated that at rest, the percentage of open transduction channels could range from 10% (84, in vitro data) to 50% (85, in vivo data). Nakajima and Mountain (80) and Nakajima (81) have estimated the maximum apical conductance of the OHCs to be G_max = 11 nS/OHC. Therefore, G_rest ranged from 1.1 to 5.5 nS/OHC. To calculate the conductance per section, we multiplied the conductance of an individual OHC by (3Δx/d). The apical resistance per unit section was then calculated by taking the inverse of the conductance. The final value, R_a, ranged from 5.5 to 27.3 MΩ/section.

Finally, R_b was calculated based on the assumptions that R_a ≫ R_b at rest and that the total OHC input resistance is 12 MΩ (86). Therefore, R_b = 12 MΩ/OHC. The basal resistance per unit section was calculated by dividing the basal resistance per OHC by (3Δx/d). The final value was R_b = 0.36 MΩ/section.

Model predictions

In Fig. 20, A and B, we plot the input voltage (V_sv), the SM voltage (V_sm), and the OHC basolateral membrane voltage (V_b) as a function of longitudinal position, for a low-frequency (10 Hz) stimulus. We show V_b for two different values for the R_a, corresponding to 10% and 50% of the transduction channels being open. All output voltages are scaled versions of the input voltage. As the number of open channels increased, the V_b increased. Fig. 20, C and D, shows the same voltages for a high-frequency (2000 Hz) stimulus. All voltages are smaller compared to their low-frequency values. In addition, V_b is independent of the number of open transduction channels.

FIGURE 20.

Model results of the voltage in SM (V_sm) and the voltage across the basolateral membrane of the OHCs (V_b) as a function of longitudinal position relative to the input-current electrode. V_b is shown for two cases: 1), when the open probability of the transduction channels is 10% (V_b _10%) and 2), when the open probability is 50% (V_b _50%). Also shown is the input voltage (V_sv) resulting from 1 mA of input current. All voltages are shown for a 10-Hz stimulus (A and B) and a 2000-Hz stimulus (C and D).

The modeling results shown in Fig. 20 may offer an explanation as to why we had to use such large currents (compared to isolated OHC studies) to stimulate the OHC in our excised cochlea preparation. Due to the shunting effect of the capacitance in stria vascularis (87), the voltage across the basolateral membrane of the OHCs is smaller by ∼2–3 orders of magnitude compared to the input voltage and it depends on the open probability of the transduction channels as well as the spatial location of the measurement location relative to the stimulating electrode. As a consequence, the amount of current needed to stimulate the OHCs will vary (and did vary) between experiments and will depend on the physiological state of the transduction channels and the measurement location. In most of our experiments, the imaging location (and therefore the cochlear location of our data collection) was ∼300 nm away from the stimulating electrode. From Fig. 20, we can see that at that location and at low stimulus frequencies, V_b is ∼0.8 mV/mA or 4 mV/mA when the open probability of the transduction channels is 10% or 50%, respectively. At the same location but at higher frequencies, V_b is ∼2 mV/mA and is independent of the open probability of the transduction channels.