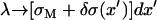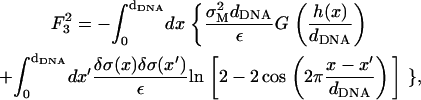Abstract
We present a theoretical study of the physical properties of cationic lipid-DNA (CL-DNA) complexes—a promising synthetically based nonviral carrier of DNA for gene therapy. The study is based on a coarse-grained molecular model, which is used in Monte Carlo simulations of mesoscopically large systems over timescales long enough to address experimental reality. In the present work, we focus on the statistical-mechanical behavior of lamellar complexes, which in Monte Carlo simulations self-assemble spontaneously from a disordered random initial state. We measure the DNA-interaxial spacing, dDNA, and the local cationic area charge density, σM, for a wide range of values of the parameter φc representing the fraction of cationic lipids. For weakly charged complexes (low values of φc), we find that dDNA has a linear dependence on 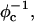 which is in excellent agreement with x-ray diffraction experimental data. We also observe, in qualitative agreement with previous Poisson-Boltzmann calculations of the system, large fluctuations in the local area charge density with a pronounced minimum of σM halfway between adjacent DNA molecules. For highly-charged complexes (large φc), we find moderate charge density fluctuations and observe deviations from linear dependence of dDNA on
which is in excellent agreement with x-ray diffraction experimental data. We also observe, in qualitative agreement with previous Poisson-Boltzmann calculations of the system, large fluctuations in the local area charge density with a pronounced minimum of σM halfway between adjacent DNA molecules. For highly-charged complexes (large φc), we find moderate charge density fluctuations and observe deviations from linear dependence of dDNA on 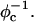 This last result, together with other findings such as the decrease in the effective stretching modulus of the complex and the increased rate at which pores are formed in the complex membranes, are indicative of the gradual loss of mechanical stability of the complex, which occurs when φc becomes large. We suggest that this may be the origin of the recently observed enhanced transfection efficiency of lamellar CL-DNA complexes at high charge densities, because the completion of the transfection process requires the disassembly of the complex and the release of the DNA into the cytoplasm. Some of the structural properties of the system are also predicted by a continuum free energy minimization. The analysis, which semiquantitatively agrees with the computational results, shows that that mesoscale physical behavior of CL-DNA complexes is governed by interplay among electrostatic, elastic, and mixing free energies.
This last result, together with other findings such as the decrease in the effective stretching modulus of the complex and the increased rate at which pores are formed in the complex membranes, are indicative of the gradual loss of mechanical stability of the complex, which occurs when φc becomes large. We suggest that this may be the origin of the recently observed enhanced transfection efficiency of lamellar CL-DNA complexes at high charge densities, because the completion of the transfection process requires the disassembly of the complex and the release of the DNA into the cytoplasm. Some of the structural properties of the system are also predicted by a continuum free energy minimization. The analysis, which semiquantitatively agrees with the computational results, shows that that mesoscale physical behavior of CL-DNA complexes is governed by interplay among electrostatic, elastic, and mixing free energies.
INTRODUCTION
Somatic gene therapy holds great promise for future medical applications, for example, as new treatment for various inherited diseases and cancers (1,2). Viral vectors have been the most widely used systems for this purpose (3,4), but synthetic nonviral vectors are emerging as an attractive alternative because of their inherent advantages (5–7). These advantages include ease and variable preparation, unlimited length of the transported DNA, and lack of specific immune response due to the absence of viral peptide and proteins (7–9). Complexes consisting of cationic lipids (CLs) and DNA comprise one of the most promising classes of nonviral vectors. They are already used widely for in vitro transfection of mammalian cells in research applications, and have even reached the stage of empirical clinical trials (10). Currently, their efficiency of gene transfer is considerably lower than that of viral vectors (11,12). Substantial improvement of their efficiency is required before cationic lipid-DNA (CL-DNA) complexes become available for therapeutic purposes.
CL-DNA complexes are formed spontaneously when DNA is mixed with cationic and natural lipids in an aqueous environment (13,14). Their formation is driven by the electrostatic attraction between negatively charged DNA and cationic lipid headgroups, and through the entropic gain associated with the concurrent release of the tightly bounded counterions from the CL and DNA (13–16). X-ray diffraction experiments have revealed that CL-DNA complexes exist in a variety of mesoscopic structures (17,18). These structures include a multilamellar phase where DNA monolayers are intercalated between lipid bilayers ( ) (13), and an inverted hexagonal phase with DNA encapsulated within cationic lipid monolayers tubes and arranged on a two-dimensional hexagonal lattice (
) (13), and an inverted hexagonal phase with DNA encapsulated within cationic lipid monolayers tubes and arranged on a two-dimensional hexagonal lattice ( ) (14). In the more commonly observed
) (14). In the more commonly observed  phase, the DNA chains form a one-dimensional lattice, where the interaxial spacing dDNA decreases with the charge density of the membrane. Isoelectric complexes, where the charges on the DNA exactly match those on the CL, are the most stable ones since they enable nearly complete counterion release (15). For transfection, positively charged complexes are used, which can adhere to the negatively charged cell plasma membrane (12).
phase, the DNA chains form a one-dimensional lattice, where the interaxial spacing dDNA decreases with the charge density of the membrane. Isoelectric complexes, where the charges on the DNA exactly match those on the CL, are the most stable ones since they enable nearly complete counterion release (15). For transfection, positively charged complexes are used, which can adhere to the negatively charged cell plasma membrane (12).
Despite all the promise of CL-DNA complexes as gene vectors, their transfection efficiency (TE; the ability to transfer DNA into cells followed by expression) remains substantially lower than that of viral vectors (11,12). This has spurred an intense research activity aimed at enhancing TE (11,12,19–22). Recent tragic events associated with the use of engineered adenovirus vectors have further stimulated the search for efficient synthetic DNA carriers (23,24). Recognizing that the structure of CL-DNA complexes may strongly influence their function and TE, much of the effort in theoretical and experimental studies has been devoted to understanding the mechanisms governing complex formation, structure, and phase behavior (18,25). The most widely used approach to describe the free energy of the complexes is the mean-field Poisson-Boltzmann equation, which takes into account the electrostatic interactions of a charged continuum and the mixing entropy of the lipids and counterions (15,26). The bending energy of the lipid layer is introduced by means of the effective Helfrich energy (16,27). Thus, the preferred structure is determined by a delicate interplay between electrostatic interactions and bending elasticity, both depending on the molecular nature and composition of the lipids. The vast majority of neutral lipids, when complexed with CLs, lead to the  phase. Addition of the neutral lipid DOPE (or other PE-based lipids) drives the spontaneous curvature negatively, thereby inducing the transition to the
phase. Addition of the neutral lipid DOPE (or other PE-based lipids) drives the spontaneous curvature negatively, thereby inducing the transition to the  phase (14). This transition is also promoted by addition of the cosurfactant hexanol, which lowers the bilayer bending rigidity.
phase (14). This transition is also promoted by addition of the cosurfactant hexanol, which lowers the bilayer bending rigidity.
The relationship between the physical properties and TE of CL-DNA complexes has been studied in a recent set of experiments utilizing a combination of several techniques (synchrotron x-ray diffraction for structure determination, laser scanning confocal microscopy to probe the interactions of complexes with cells, and luciferase reporter-gene expression assays to measure TE) (12). The most notable result of these experiments is the identification of the membrane charge density, σM, as a key universal parameter that governs TE of  complexes (28). The highest transfection rate has been observed at intermediate σM, reaching values that are comparable to the high, σM-independent, TE of DOPE-containing
complexes (28). The highest transfection rate has been observed at intermediate σM, reaching values that are comparable to the high, σM-independent, TE of DOPE-containing  complexes (29). That lamellar complexes complete the high TE of hexagonal complexes is of prime importance because, as mentioned above, most commonly used lipids prefer the
complexes (29). That lamellar complexes complete the high TE of hexagonal complexes is of prime importance because, as mentioned above, most commonly used lipids prefer the  over the
over the  phase. Moreover, with newly synthesized multivalent lipids with headgroups whose charge is as large as Z = 5, it is possible to reach the optimal TE with a smaller number of CLs. This is a desirable feature, which reduces the cost and, more importantly, the toxic effects of the CLs. It also means a smaller metabolic effort for the elimination of the lipids from the cell.
phase. Moreover, with newly synthesized multivalent lipids with headgroups whose charge is as large as Z = 5, it is possible to reach the optimal TE with a smaller number of CLs. This is a desirable feature, which reduces the cost and, more importantly, the toxic effects of the CLs. It also means a smaller metabolic effort for the elimination of the lipids from the cell.
Based on the above TE data as well as x-ray diffraction and laser scanning confocal microscopy imaging, a model of cellular entry of  complexes has been proposed, which suggests that the process of transfection involves two stages (12): Stage 1, cellular uptake via endocytosis; and Stage 2, escape of the complex from the endosome, presumably through the fusion of the complex with the endosomal membrane and release of the DNA into the cytoplasm. The adhesion of the complex to the cell is mediated by electrostatic attraction between the positively charged complex and the negatively charged cell's plasma membrane. The transfection process is limited by the rate of the second step, which increases exponentially with σM. The independence of
complexes has been proposed, which suggests that the process of transfection involves two stages (12): Stage 1, cellular uptake via endocytosis; and Stage 2, escape of the complex from the endosome, presumably through the fusion of the complex with the endosomal membrane and release of the DNA into the cytoplasm. The adhesion of the complex to the cell is mediated by electrostatic attraction between the positively charged complex and the negatively charged cell's plasma membrane. The transfection process is limited by the rate of the second step, which increases exponentially with σM. The independence of  complexes TE on σM (in the low σM regime) has been attributed to the mismatch between the positive curvature of the outermost lipid monolayer (which provides the complex with hydrophobic shielding) and the complex negative spontaneous curvature. This elastically frustrated state drives, independently of σM, the rapid fusion of the
complexes TE on σM (in the low σM regime) has been attributed to the mismatch between the positive curvature of the outermost lipid monolayer (which provides the complex with hydrophobic shielding) and the complex negative spontaneous curvature. This elastically frustrated state drives, independently of σM, the rapid fusion of the  complex with the plasma or endosomal membrane. Lamellar complexes with very high σM also exhibit reduced TE, which should be attributed to the inability of the DNA to dissociate from the highly charged membranes (of the free complex) and to become available for expression (29).
complex with the plasma or endosomal membrane. Lamellar complexes with very high σM also exhibit reduced TE, which should be attributed to the inability of the DNA to dissociate from the highly charged membranes (of the free complex) and to become available for expression (29).
Theoretical modeling of large molecular assemblies pose significant challenges due to the spatial complexity of such systems and by the range of temporal scales involved. In the case of CL-DNA complexes, the size of the complex may be as large as 1 μm, while the basic unit cell of the 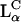 complex is in the nanometer range (the DNA spacing is typically dDNA ∼20–70 Å, and the interlayer spacing d ≃ 65 Å). Since both short- (steric, hydrophobic), and long-range (electrostatic) interactions determine the physical and biomedical properties of CL-DNA complexes, it is essential that these systems will be studied at all possible levels of detail. Moreover, phase transitions of CL-DNA complexes as well as other topological changes (e.g., membrane fusion which occurs during transfection) involves the collective motion of many lipid molecules and, therefore, inherently take place on a variety of spatial and temporal scales.
complex is in the nanometer range (the DNA spacing is typically dDNA ∼20–70 Å, and the interlayer spacing d ≃ 65 Å). Since both short- (steric, hydrophobic), and long-range (electrostatic) interactions determine the physical and biomedical properties of CL-DNA complexes, it is essential that these systems will be studied at all possible levels of detail. Moreover, phase transitions of CL-DNA complexes as well as other topological changes (e.g., membrane fusion which occurs during transfection) involves the collective motion of many lipid molecules and, therefore, inherently take place on a variety of spatial and temporal scales.
To address the multiscale nature of CL-DNA complexes, a variety of models, differing in the length and the timescales of the phenomena of interest have been devised. At the microscopic molecular level, we have atomistic molecular dynamics simulations in which the lipids, DNA, and the embedding solvent are modeled explicitly in full (classical) atomic detail (30). These simulations provide valuable information regarding the molecular structure of the complexes, such as the role played by the neutral PC headgroups (more specifically, the N+ end of the P−–N+ dipole) in the screening of the electrostatic repulsion between the DNA chains. The length and timescales of atomistic simulations are limited by memory and CPU requirement to several nanometers and nanoseconds, which is far below the macroscopic regime encompassing the statistics and evolution of large molecular ensembles. At the macroscopic level, only the continuum behavior of existing CL-DNA structures can be addressed based on free energy functionals, which are insensitive to the fine details of the lipids and DNA (15,25,26). Electrostatic screening effects between the DNA chains resulting from nonspecific interactions between the lipids and DNA have been reported in these studies. This observation is complementary to the specific mechanisms observed in detailed atomistic computer models.
In this article, we present an “intermediate” molecular modeling approach that retains the most essential components of self-assembly and molecular statistics, but avoids the computational overhead of a full atomistic model. The model (31) extends an existing coarse-grained (CG) molecular bilayer model (32,33) by including both charged and neutral lipids, as well as charged DNA molecules. The intermolecular potentials between different molecular species are designed to mimic the hydrophobic effect without the explicit presence of solvent. Thus, the approach carefully balances the need for molecular detail with computational practicality in a manner that allows for solvent-free simulations of complex self-assembly over long enough timescales to address experimental reality. In addition to showing spontaneous self-assembly of CL-DNA complexes, we also investigate the structural properties of lamellar complexes and measure a number of important quantities such as the dependence of the interaxial distance between DNA chains on the fraction of charged lipids, the polarization of the cationic charge distribution, local area density fluctuations, and the effective two-dimensional stretching elastic modulus, 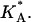 Some of these quantities are not easily accessible to theoretical continuum models and may require further approximations. One of the more interesting results is the decrease in
Some of these quantities are not easily accessible to theoretical continuum models and may require further approximations. One of the more interesting results is the decrease in 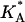 upon increasing the membrane charge density σM, which reflects reduced mechanical stability and a higher probability of structural defects, such as membrane pores. The observations of such pores is consistent with the experimental findings of enhanced transfection efficiencies at high concentration of CLs, because pores must be formed to enable the escape of the DNA from the complex (see discussion above). It demonstrates the utility of CG modeling in addressing some key features of complex biological systems in general, and lipid-DNA assemblies in particular.
upon increasing the membrane charge density σM, which reflects reduced mechanical stability and a higher probability of structural defects, such as membrane pores. The observations of such pores is consistent with the experimental findings of enhanced transfection efficiencies at high concentration of CLs, because pores must be formed to enable the escape of the DNA from the complex (see discussion above). It demonstrates the utility of CG modeling in addressing some key features of complex biological systems in general, and lipid-DNA assemblies in particular.
We focus on isoelectric lamellar complexes in which the total charges carried by the CLs and DNA are equal. The mechanism of counterion release is most effective at this point, making the free energy of the complex minimal (15). The counterions concentrations inside the complex depend on their bulk concentrations. Here, we study the very low bulk concentration limit in which the counterions are (almost) completely depleted from the complex. This regime has been previously addressed in atomistic computer simulations of CL-DNA complexes (30). Counterions effects have been dealt with in the framework of continuum Poisson-Boltzmann (PB) theory (15,25,26). While this approach captures certain features of the charge distribution and the electric fields in the complex, it neglects several important factors such as the discrete nature of the ions and their finite sizes, which may govern their distribution in the gaps of (sub)nanometer dimensions that exist between the membranes and the DNA. Treating the water in these tiny voids as a bulk medium of effective dielectric constant ε = 78 and neglecting dehydration effects are other gross approximations made by most current modeling techniques.
We use a continuum model to analyze some of the simulation results. Our analytical study is based on the minimization of a phenomenological free energy functional with respect to the profile of the membrane and the cationic charge distribution. This free energy includes contributions from all the electrostatic interactions existing between the lipids and the (infinite array of) DNA molecules, as well as terms associated with the mixing entropy and (small length scale) protrusion modes (34) of lipids. We show, both computationally and analytically, that the cationic charge distribution is polarized. The minimum of the charge density is obtained halfway between adjacent DNA molecules while the maximum is not reached right above the DNA, but is slightly shifted. The origin of this shift is the ability of the lipids not located right above the DNA to protrude and thus position their charged headgroups in regions of the complex where the electrostatic potential created by the DNA array is lower. Interestingly, we find that the charge density in the immediate vicinity of the DNA tends to match effective area charge density of the DNA rod. Charge matching between narrowly separated surfaces has been observed in previous studies of CL-DNA complexes (15,27), as well as in studies of other molecular assemblies (35). It has been attributed to the increased concentration of ions, which are bound to remain in the confined volume between surfaces to neutralize the system. Charge matching is favorable because it enables the release of these strongly confined ions. Our study, which is based on an ion-free model, suggests that charge matching can be also driven by other mechanisms.
The article is organized as follows: In the next section, we present our CG model of CL-DNA complexes and provide most of the details of the simulations (except for the details of a new Monte Carlo (MC) scheme that we use to sample the constant tension ensemble, which we introduce in Appendix 1). The results of our simulations are described in the two following sections dealing, respectively, with the dependence of the DNA spacing and the complex stability on the charge density, and the charge density fluctuations. The computational results are compared to the predictions of a analytical continuum model in Appendix 2. We close the article with a brief discussion of the main results and an outline of some future prospects.
COMPUTER MODEL
The computer model of CL-DNA complex is based on a bilayer CG model presented elsewhere (32,33). The lipids are modeled as short trimer molecules consisting of one “hydrophilic” and two “hydrophobic” beads, which are connected to each other by stiff linear springs (33). The model does not include explicit solvent. Rather, a set of short-range attractive intermolecular potentials is used, which effectively mimic hydrophobicity and allow self-assembly of bilayer from molecular disorder (31). Depending on the area density of the lipids, the bilayer is found in either a solid or a fluid phase (32), where the latter is characterized by an in-plane lipid diffusion and out-of-plane fluctuations whose spectrum is well depicted by Helfrich-effective Hamiltonian (36). The model of the CL-DNA complex is obtained by:
Choosing a fraction φc of the lipids and placing a unit (point) charge + e at the centers of their hydrophilic bead.
Introducing DNA molecules, each of which is modeled as a rigid rod with a uniform axial charge density λDNA = − e/1.7 Å and radius RDNA = 10 Å. The diameter of the spherical particles constituting the lipids is set to σ≃6.3Å (see definition of σ in Farago (32)), which yields an area per lipid alipid ≃ 70 Å2 for uncharged bilayers. Excluded volume interactions between rods (R) and spheres (S) are introduced via a truncated (at
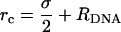 ) and shifted potential of the form:
) and shifted potential of the form: 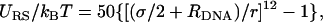 where r is the distance between the center of the sphere and the axis of symmetry of the rod. The distance between nearest-neighbor rods is restricted to dDNA ≥ 2RDNA.
where r is the distance between the center of the sphere and the axis of symmetry of the rod. The distance between nearest-neighbor rods is restricted to dDNA ≥ 2RDNA.
Modeling the DNA strands as infinite rods carrying uniform charge density λ is consistent with the CG approach of the model, where only electrostatics, noise, and simple geometric features are retained. In this representation of DNA molecules, we ignore the effects associated with 1), their flexibility; and 2), the discrete nature of their charge distribution. The first approximation is justified in view of the fact that the DNA persistence length (ξp ∼ 500 Å) is an order-of-magnitude larger than all the other relevant length scales in the problem. Curvature fluctuations involve free energy penalty of ∼1 kBT per ξp of DNA length, which is negligible compared to the complex stabilization free energy of ∼102–103 kBT per persistence length (15). The second approximation is supported by numerical studies revealing that the electrostatic potential around the DNA surface is not much different from that produced by the continuous charge density, except for a narrow regime in its immediate vicinity (37).
We study isoelectric complexes where the total charges of the DNA and the CLs neutralize each other, with no added counterions. Simulations of the quasi two-dimensional complex are conducted in a rectangular system of size Lx × Ly × Lz, with full periodic boundaries along the x and y directions, and periodicity with respect to only lipid mobility and short-range interactions in the z direction. The simulations were performed at room temperature and with a bulk water uniform dielectric constant ε = 78. The rods are arranged in a one-dimensional array, parallel to the y axis and with equal spacing along the x-direction. Long-range electrostatic interactions between the charged spheres, infinite rods, and their periodic images were accounted for using the Lekner summation method (38). The electrostatic potential energy, per simulation cell, between a CL whose charged headgroup is located at 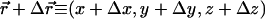 and another CL and its replicas located at (x + mLx, y + nLy, z), where m, n are integers, is given by the exponentially convergent summation of, e.g., the form
and another CL and its replicas located at (x + mLx, y + nLy, z), where m, n are integers, is given by the exponentially convergent summation of, e.g., the form
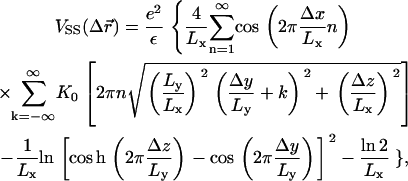 |
(1) |
where K0 is the modified Bessel function of order 0. The self-energy 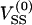 that arises from a charged sphere with its own periodic images is found by evaluating the expression
that arises from a charged sphere with its own periodic images is found by evaluating the expression
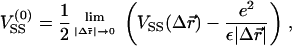 |
(2) |
and is given in Grønbech-Jensen et al. (38). The sphere-rod electrostatic energy per simulation cell is the combined logarithmic interactions between a point charge and a one-dimensional array of line charges. It is given by (39)
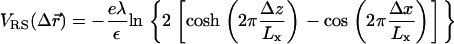 |
(3) |
The rod-rod electrostatic self-energy is (39)
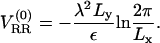 |
(4) |
Simulations of electrostatics in water-free models are usually conducted with a uniform dielectric constant due to the complexity of including mirror charges in a disordered molecular ensemble. In PB theories (15,35), a different type of boundary condition (BC) is usually assumed, namely that the dielectric constant vanishes in the interior of the DNA and the lipid membrane. This latter approximation is justified by the fact that the (bulk) water dielectric constant, ε = 78, is much larger than all the other relevant dielectric constants. The electric field lines prefer to stay in high dielectric media and the limit ε = 0 corresponds to systems in which the electric field is entirely contained within the aqueous part. Fortunately, the exclusion of electric fields from the DNA and the membranes is not solely related to their low dielectric constants. In our simulations, it is mainly a matter of the geometry and the charge distribution in the system. Therefore, the electrostatic forces, through which the charges in water interact with each other, are expected to be insensitive to the dielectric constants of the DNA and the membranes. Computational studies (39) of electrostatics near similar simple geometric interfaces indicate that the net effect of mirror images is, indeed, minor. This observation also serves as a justification for our choice of BCs. Rather than using full periodic BCs in all three directions, we study an infinite “slab” consisting of a single array of charged DNA molecules and two bilayers (Fig. 1), in which only the inner monolayers (facing the DNA rods) are charged while the outer monolayers consist of neutral lipids only. The interaction between different slabs (whose overall net charge is neutral) is well screened and is significantly weaker than the Coulomb interactions between the charged components within each slab.
FIGURE 1.
Equilibrium configuration of a complex consisting of two bilayer membranes, each with 390 lipids and five DNA strands. The lipids are modeled as trimers with hydrophilic (black) and hydrophobic (gray) particles. The DNA (red) are modeled as rigid rods with a uniform negative axial charge density. The complex is isoelectric, i.e., the negative charge of the DNA is neutralized by the charge of the cationic lipids with no added salt. Thus, each bilayer in the shown complex includes 150 monovalent lipids, all of which reside in the inner layers facing the DNA array. Each DNA rod carries a total charge of −60 e.
In a preceding publication (31), we have shown that complexes such as the one appearing in Fig. 1 are formed spontaneously in simulations starting from a disordered initial state where the lipids are randomly distributed within the simulation cell. This demonstrates that the complex represents a stable equilibrium phase of the system. In this work, we focus on structural properties of CL-DNA complexes and use preassembled complexes for this purpose. The simulations were performed at constant surface tension γ = 0 by employing a new sampling scheme to generate area-changing trial moves. The sampling scheme, which is different from the commonly used method of sampling the (N, γ, T) ensemble (40), is described in detail in Appendix 1. The rest of the details of the simulations appear in Farago et al. (31).
DNA spacing and mechanical stability
Measuring the DNA interaxial spacing, dDNA, serves as a critical test to our model's ability to mimic the mesoscale behavior of CL-DNA complexes, because dDNA can be measured in x-ray diffraction experiments. The experimental data of Safinya et al. (13,18) shows that for isoelectric complexes, the dependence of dDNA on the membrane charge density σM = 2eφc/alipid is governed by the relationship (41)
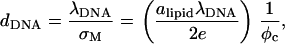 |
(5) |
which results from simple mass conservation in the lamellar geometry.
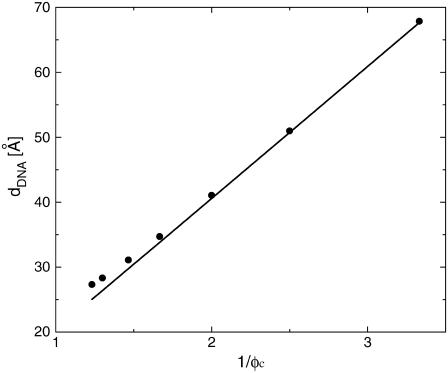
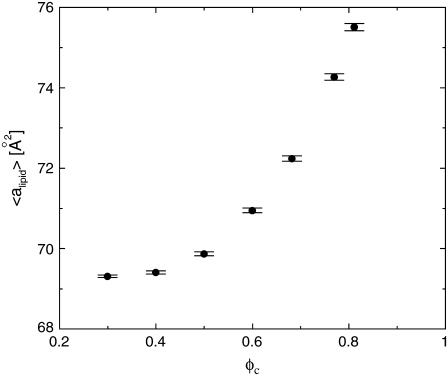
The computational results for the average spacing between adjacent DNA rods, dDNA, are plotted in Fig. 2 as a function of the inverse of the fraction of charged lipids, 1/φc. The solid line is a fit to Eq. 5 with alipid = 69 Å2 which is the area per lipid in uncharged membranes. The deviation from linear behavior at high charge densities arises from the increase in alipid with φc (Fig. 3). The numerical data is in excellent agreement with the experimental results reported in Koltover et al. (13). Specifically, the experimental dDNA versus φc data (see Fig. 4 B in (13)) show agreement with Eq. 5 at low charge densities (with a value of alipid, which is slightly different than the one defined here) and a similar deviation trend at high charge densities (note that our Eq. 5 and the comparable one in (13) express the same relationship in different forms; see Discussion in (41).) The assumption underlying Eq. 5 is that the effective interactions between the DNA are repulsive and balanced by the elastic membrane forces. Linear elastic stress acting on a membrane is related to alipid and its equilibrium value 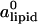 by
by 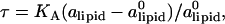 where KA is the two-dimensional stretching modulus, which for lipid bilayers is typically in the range
where KA is the two-dimensional stretching modulus, which for lipid bilayers is typically in the range 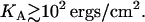 At high charge densities, the electrostatic stress is sufficiently large to eliminate the membrane thermal undulations and increase alipid (42). In this study, we find for complexes with φc ∼ 0.85 that the strain
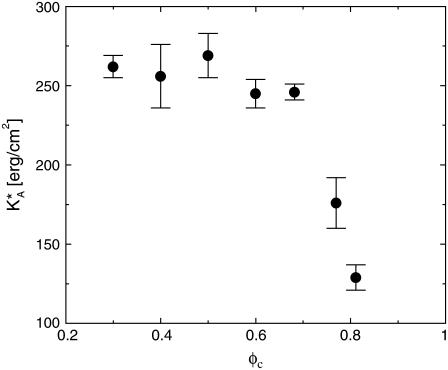
At high charge densities, the electrostatic stress is sufficiently large to eliminate the membrane thermal undulations and increase alipid (42). In this study, we find for complexes with φc ∼ 0.85 that the strain 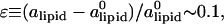 which is somewhat larger than the typical strain lipid bilayers withstand before rupture (ɛ ∼ 0.02–0.05, (43)). Membranes with higher φc have indeed been found to be susceptible to pore formation, as illustrated by the configuration in Fig. 4 of a complex with φc ∼ 0.9. The discrepancy between experimentally observed rupture strains and the strain found in our model is not surprising, given the coarse-grained lipid-model of simple three-point objects. It may also be partially attributed to the system-size dependence of the rupture strain (44). The loss of mechanical stability is also evident from the rapid decrease in the effective stretching modulus of the complex
which is somewhat larger than the typical strain lipid bilayers withstand before rupture (ɛ ∼ 0.02–0.05, (43)). Membranes with higher φc have indeed been found to be susceptible to pore formation, as illustrated by the configuration in Fig. 4 of a complex with φc ∼ 0.9. The discrepancy between experimentally observed rupture strains and the strain found in our model is not surprising, given the coarse-grained lipid-model of simple three-point objects. It may also be partially attributed to the system-size dependence of the rupture strain (44). The loss of mechanical stability is also evident from the rapid decrease in the effective stretching modulus of the complex 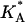 for
for 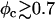 (Fig. 5), which has been extracted from the mean-square of fluctuations in alipid:
(Fig. 5), which has been extracted from the mean-square of fluctuations in alipid: 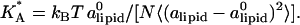 The larger area fluctuations at high φc increase the probability of pore opening which, in turn, may lead to disassociation of the complex.
The larger area fluctuations at high φc increase the probability of pore opening which, in turn, may lead to disassociation of the complex.
FIGURE 2.
Average DNA spacing, dDNA, as a function of the inverse of the fraction of charged lipids 1/φc. Markers, numerical results (uncertainties are smaller than symbols); solid line, fit to Eq. 5 with alipid = 69 Å2.
FIGURE 3.
The average area per lipid, alipid, as a function of the fraction of charged lipids φc.
FIGURE 4.
Equilibrium configuration of a complex with φc ∼ 0.9 whose membranes develop pores.
FIGURE 5.
The effective stretching modulus, 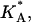 of the complex as a function of φc.
of the complex as a function of φc.
It is interesting to compare the inter-DNA electrostatic interactions in the complex with the same interactions in bulk in the presence of monovalent counterions (45). In both cases, the bare electrostatic repulsion is screened by the distribution of microions and CLs around the DNA. In the complex, the distribution of the cationic charge is limited by a geometric constraint, namely the residence of the CLs on the membrane surface, which maintains a finite separation from the inter-DNA plane. Therefore, we expect such screening to be less efficient than in bulk solutions. It is also reasonable to expect that, compared to three-dimensional systems, the confinement to a surface increases the repulsive electrostatic interactions between the cationic charges, which further increases the magnitude of the effective inter-DNA repulsive force.
Since our model does not include water explicitly, the hydration forces, which may be significant at small dDNA, are missing from the picture (46). This can be corrected either by introducing an additional short-range DNA-DNA potential that explicitly account for the hydration free energy or assuming that RDNA represents the hydrated rather than the bare DNA radius. Since the hydration forces decay on DNA-DNA surface separations of ≳1 nm, their introduction into the model will only modify the results at small dDNA (large φc). Specifically, this will increase the effective DNA-DNA repulsion and, therefore, will strengthen the trend observed in Fig. 2 that at high charge densities Eq. 5 underestimates dDNA. It will also shift the limit of mechanical stability to slightly lower charge densities. Another feature missing in our model is the contribution of DNA bending fluctuations to the inter-DNA interaction. The effect of these fluctuations in bulk is to increase the decay length of both hydration and electrostatic forces (47). One may expect a similar contribution to inter-DNA interactions in CL-DNA complexes, although we are unaware of any systematic study of this effect in two dimensions. X-ray studies find weak positional disorder in CL-DNA complexes. The typical correlated domain size of the one-dimensional lattice of DNA extends to nearly 10 unit cells (13), which is twice as large as the size of the complex in our simulations.
Our computational results explain well the recently observed enhanced TE of lamellar CL-DNA complexes at high charge densities (12,28). The limiting stage of the transfection process is the escape of the complex from the endosome in which it is initially trapped after entering the cell. Escape from the endosome occurs through activated fusion of the complex and endosomal membranes, during which both must be perforated. Having a complex with poor mechanical stability is an advantage at this stage, since such a complex will tend to open pores more easily, and through these pores the DNA may be released to the cytoplasm. We suggest that the loss of mechanical stability results from the cationic charge of the lipids and the pressure that it exerts on the complex membrane. At high charge densities this pressure exceeds the rupture tension of the membrane and, thus, leads to mechanical failure of the complex.
Charge density modulations
The quantity defined as φc represents the mean number fraction of charge lipids. However, the lateral distribution of cationic charge on the membranes need not be uniform. One may expect the CLs to accumulate above and below the negatively charged DNA rods. This tendency to minimize the electrostatic energy of the CLs-DNA interactions is competed by the thermally induced mixing entropy and the repulsive electrostatic interactions between the CLs, which favor homogeneous composition of the cationic and neutral lipids. Furthermore, charge density modulations may be coupled to membrane undulations (27,48), and both can contribute to lowering the free energy of the complex. As discussed above, the stability of the complex is directly related to its TE and, therefore, it is important to study the effect of these “degrees of freedom” of the lipids.
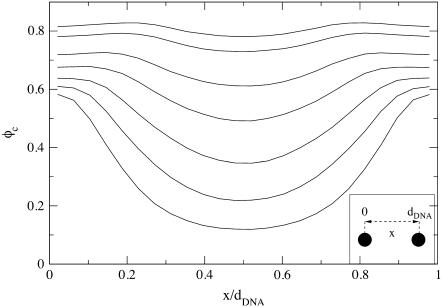
The dependence of φc on x, the position within a unit cell of the complex (i.e., the interval between adjacent DNA rods), is depicted in Fig. 6, where x = 0 and x = dDNA correspond to lipids located right above or below the DNA (see inset of Fig. 6). The curves, from bottom to top, are for the following values of the mean number fraction: φc = 150/500 = 0.3; 150/375 = 0.4; 150/300 = 0.5; 150/250 = 0.6; 150/220 ∼ 0.68; 150/195 ∼ 0.77; and 150/185 ∼ 0.81. As expected, we find that for all values of φc, the minimum of φc(x) is achieved for x = dDNA/2, i.e., in the middle of the unit cell. The minimum is more pronounced for low values of φc, in which case the maximum of φc(x) is at x = 0 and x = dDNA. At the higher values of φc, the maximum shifts from the edge of the unit cell toward the center and, in general, the fluctuations in φc(x) become quite small.
FIGURE 6.
Local fraction of charged lipids φc as a function of x, the position within a unit cell of the complex. Curves, from bottom to top, correspond to mean fraction of 0.3, 0.4, 0.5, 0.6, 0.68, 0.77, and 0.81.
The shift in the maximum of φc(x) from the immediate vicinity of the DNA toward the center of the cell has been previously reported in theoretical studies of the system based on PB theory (15,27). It has been attributed to the tendency of the system to match the areal charge density of the membrane with the effective areal charge density of the DNA, σDNA ≡ −λDNA/(2πRDNA) ∼ 9.4 × 10−3 e/Å2. This involves attraction of CLs toward the DNA at low values of φc and significant charge modulation over the relatively large distance between the DNA rods. On the other hand, when φc is large and dDNA is small, the charge density fluctuations are weak and CLs must be depleted from above/below the DNA to match the local charge density of the DNA.
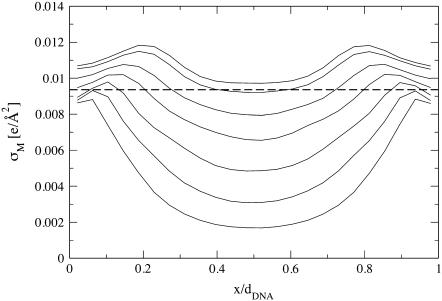
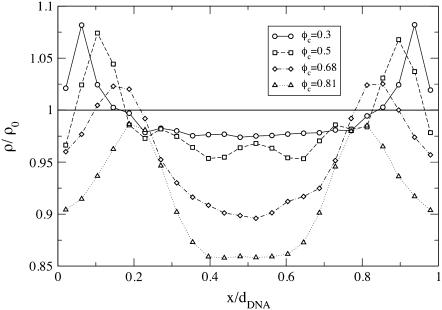
The tendency to match the local charge densities of the membranes with σDNA is seen more clearly in Fig. 7. Here, the charge density σM(x) rather than φc(x) is plotted as a function of x. The dashed horizontal line corresponds to the effective charge density of the DNA σDNA ∼ 9.4 × 10−3 e/Å2. The graphs show that for all values of φc, the local charge density at the edge of the unit cell remains within 15% of σDNA. More interestingly, the graphs show that in contrast to φc(x), the maximum of σ(x) is always shifted from the DNA toward the center of the unit cell. This observation deserves some special comment: In most analytical studies of membranes, area density fluctuations are neglected (or, rather, it is assumed that the local area per lipid alipid(x) is constant) and, therefore, φc(x) and σM(x) = 2eφc(x)/alipid(x) are proportional to each other. Our computational results indicate that area density fluctuations (see Fig. 8) may be quite important and serve as an additional degree of freedom that further reduces the free energy of the system. In Fig. 8, 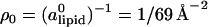 denotes the area density of uncharged membranes. For large φc, ρ < ρ0 for all values of x, reflecting the fact the mean area per lipid increases at high charge densities (see Fig. 3 and discussion above). More noticeable are the area density fluctuations within the unit cell, which can be observed for all values of φc. The location of the maximum area density coincides with that of the maximum charge density and, therefore, can be attributed to the accumulation of charged lipids. Had the area density been constant, this would mean depletion of the neutral lipids from the same region in the unit cell. Area density fluctuations represent an additional degree of freedom of the system, which permit a more uniform distribution of the neutral lipids, and, thus, pays off in terms of lower mixing entropy. The magnitude of the area density fluctuations is roughly given by
denotes the area density of uncharged membranes. For large φc, ρ < ρ0 for all values of x, reflecting the fact the mean area per lipid increases at high charge densities (see Fig. 3 and discussion above). More noticeable are the area density fluctuations within the unit cell, which can be observed for all values of φc. The location of the maximum area density coincides with that of the maximum charge density and, therefore, can be attributed to the accumulation of charged lipids. Had the area density been constant, this would mean depletion of the neutral lipids from the same region in the unit cell. Area density fluctuations represent an additional degree of freedom of the system, which permit a more uniform distribution of the neutral lipids, and, thus, pays off in terms of lower mixing entropy. The magnitude of the area density fluctuations is roughly given by 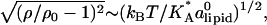 which for typical values of the parameters (
which for typical values of the parameters (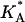 ∼ 250 ergs/cm2,
∼ 250 ergs/cm2, 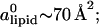 see Figs. 3 and 5) yields
see Figs. 3 and 5) yields 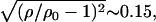 in reasonable agreement with our results in Fig. 8.
in reasonable agreement with our results in Fig. 8.
FIGURE 7.
Local charge density of the membranes σM as a function of x. Curves, from bottom to top, correspond to φc = 0.3, 0.4, 0.5, 0.6, 0.68, 0.77, and 0.81. Dashed horizontal line corresponds to the effective charge density of the DNA σDNA ∼ 9.4 × 10−3 e/Å2.
FIGURE 8.
Total area density of the lipids ρ as a function of x for different values of φc. The expression ρ0 = (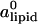 )−1 = 1/69 Å−2 is the area density of uncharged membranes. Lines are guide to the eyes.
)−1 = 1/69 Å−2 is the area density of uncharged membranes. Lines are guide to the eyes.
As mentioned above, local charge density matching is the origin of the CLs tendency to migrate toward the middle of the unit cell. Solutions of the PB equation (15,35) show that the concentration of counterions, which will be bound in the narrow water gap that exists between the DNA and the membrane, increase with the charge density mismatch. An accumulation of counterions in such a small volume is energetically unfavorable and will lead to a very large osmotic pressure. Two comments should be made regarding the solution of the PB equation: First, the screening of the electrostatic interactions by the highly confined counterions is probably overestimated by continuum PB theory because the slithering of counterions into the small gaps will be hindered both dynamically (excluded volume) and thermodynamically (dehydration). Second, our simulations of isoelectric complexes with no counterions apply to the no-screening limit where this effect is not expected to occur. We therefore conclude that local charge density matching may be also driven by other factors. Indeed, in the absence of screening one must consider the interactions of the CLs with the periodic array of line charges rather than with the closest DNA rod. The Coulomb energy due to the interaction of a charge + e with an infinite periodic array of rods of charge density per unit length λ < 0 is given by Eq. 3, with Lx = dDNA. For a charge residing on a perfectly flat surface located a distance Δz = D ≡ RDNA + σ/2 ∼ 13 Å above the midplane of the DNA array, Eq. 3 simplifies to 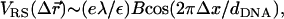 with
with 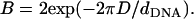 This expression is valid as long as B < 1, which is indeed the case for the above value of D and the range of values of the DNA interaxial spacing dDNA ∼ 25–50 Å considered in this work. For a nearly flat surface with Δz = D − h (0 ≤ h ≪ D), the sphere-rod electrostatic energy reads
This expression is valid as long as B < 1, which is indeed the case for the above value of D and the range of values of the DNA interaxial spacing dDNA ∼ 25–50 Å considered in this work. For a nearly flat surface with Δz = D − h (0 ≤ h ≪ D), the sphere-rod electrostatic energy reads
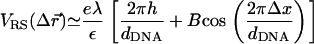 |
(6) |
The first term in this equation reflects the long-range nature of unscreened electrostatic interactions which makes the potential of the infinite array of line charges look similar to the potential of a uniformly charged surface with areal charge density σM = λ/dDNA. The second term is due to the periodicity of the system and represents the tendency of cationic lipids to favor the proximity of the anionic DNA rods (Δx = 0). The attraction of the CLs to the DNA rods, located at the edge of the unit cell, will be offset by their attraction toward the midplane of the DNA array (first terms in Eq. 6). This attraction draws the CLs toward the center of the unit cell because, right above the DNA rod, the vertical separation between the surface and the DNA array is restricted to Δz = D (h = 0) by excluded volume interactions. Away from the DNA and close to the center of the unit cell, the elastic deformation of the surface permits Δz < D (h > 0), which is energetically favorable. The highest cationic charge density will be obtained at the minimum value of the sphere-rod electrostatic energy VRS. A detailed calculation based on a continuum expression for the free energy, which includes contributions of the electrostatic and elastic energies and of mixing entropy, is presented in Appendix 2. We show that only for infinitely rigid surfaces the maximum of charge density is observed at the edge of the unit cell. In all other cases, the membrane tends to deform toward the midplane of the DNA array, which leads to shifting of the maximum of σM(x) toward the center of the cell. This is in agreement with our results in Fig. 7, although the deformation of the membrane is unnoticeable in snapshots of the system (e.g., Fig. 1). Our calculation shows that the typical amplitude of the deformation is extremely small, of the order of 1–2 Å. This estimate is model-dependent, but in agreement with previous studies of the system (27,48), and explains the apparent flatness of the membrane observed in our simulations.
DISCUSSION
We have presented a molecular simulation method that captures the self-assembly of cationic liposomes complexed with DNA—a promising synthetically based nonviral carrier of DNA for gene therapy. The method is an intermediate modeling approach between atomistic computer simulations and continuum phenomenological theories. Like the former, it utilizes a molecular description of the system; but similarly to the latter, it employs a coarse-grained (CG) representation of the intramolecular atomic details. The reduced number of degrees of freedom, as well as the fact that the model does not require explicit representation of the embedding solvent, lead to a significant improvement in computational efficiency. Thus, the approach carefully balances the need for molecular detail with computational practicality in a manner that allows for solvent-free simulations of complex self-assembly over long enough timescales to address experimental reality.
In addition to showing spontaneous self-assembly of cationic lipid-DNA complexes, the broad utility of the model is illustrated by demonstrating excellent agreement with x-ray diffraction experimental data for the dependence of the interaxial distance between DNA chains, dDNA, on the fraction of charged lipids φc. Specifically, we find that dDNA is inversely proportional to φc—a relationship that can be also derived by a simple packing argument where the DNA rods form a space-filling one-dimensional lattice. This result is indicative of a repulsive long-range inter-DNA interaction. The predominant contribution to this interaction is due to nonspecific electrostatic repulsion between the negatively charged DNA rods, which is only partially screened by the cationic charge on the membranes. We note that the magnitude of the repulsive interaction plays no role in the packing argument. Therefore, a linear relationship between dDNA and 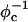 is predicted by both our CG simulations and the PB theory, despite the fact that, in the PB treatment, the screening of inter-DNA repulsion is also due to the counterions presented in the complex.
is predicted by both our CG simulations and the PB theory, despite the fact that, in the PB treatment, the screening of inter-DNA repulsion is also due to the counterions presented in the complex.
Certain features of CL-DNA complexes, for instance the process of self-assembly and structural defects (Fig. 4), can be addressed more effectively through CG simulations rather than by continuum theories of existing structures. This point is nicely demonstrated by our simulations of highly-charged complexes. Upon increasing the fraction of the CLs, we find that: 1), the area per lipid increases; 2), the effective stretching modulus of the complex decreases; and 3), the rate of pore formation increases, which eventually leads to the disintegration of the complex. All together, these results indicate that the higher the charge density of the membranes, the lower the mechanical stability of the system. This is a key observation that may explain the recently observed enhanced transfection efficiency (TE) of lamellar CL-DNA complexes at high charge densities. Transfection is viewed as a two-stage process: 1), cellular uptake via endocytosis; and 2), escape of the complex from the endosome, presumably through fusion of the lipids with the endosomal membrane and release of the DNA into the cytoplasm. TE of lamellar complexes is limited by the rate of the second stage and, hence, increases with the decrease of mechanical stability, i.e., with increase of charge density.
Given the consistency of agreement between our CG molecular approach and observed experimental features, we suggest that the presented model is an appropriate and promising tool for investigating the statistics and dynamics of lipid-DNA complexes on spatial and temporal scales relevant for biological and biomedical applications. In future work, we plan to develop models that would mimic CL-DNA complexes with improved gene delivery performance, such as complexes containing multivalent lipids and lipids attached to short polymer chains. A special effort will be made to develop a model for the inverted hexagonal ( ) structure, and to examine the mechanical behavior of this phase, which appears to be experimentally quite distinct from the behavior of the lamellar phase. We will also investigate the effect of counterions that must be presented in the positively charged complexes that adhere to the negatively charged cell membrane (at the initial stage of the transfection process). The model may be also extended to include some features of the DNA helical structure. These more advanced models may lead to a better understanding of the principles governing the statistical-mechanical behavior of CL-DNA complexes, which is crucial for systematic and successful design of efficient synthetic vectors for gene therapy.
) structure, and to examine the mechanical behavior of this phase, which appears to be experimentally quite distinct from the behavior of the lamellar phase. We will also investigate the effect of counterions that must be presented in the positively charged complexes that adhere to the negatively charged cell membrane (at the initial stage of the transfection process). The model may be also extended to include some features of the DNA helical structure. These more advanced models may lead to a better understanding of the principles governing the statistical-mechanical behavior of CL-DNA complexes, which is crucial for systematic and successful design of efficient synthetic vectors for gene therapy.
APPENDIX 1: SIMULATIONS AT CONSTANT SURFACE TENSION
Bilayer membranes may be considered as narrow interfaces consisting of lipids and the hydration layers that separate two aqueous bulk phases. Simulations of liquid/liquid interfaces can be performed in a variety of statistical ensembles. Assuming that the temperature T and number of particles N are fixed, one may use the (N, T, V, Ap) ensemble, in which the total volume of the system, V, and the projected area of the interface, Ap, are held constant. Alternatively, the normal and transverse components of the pressure tensor, Pn and Pt may be fixed, letting V and Ap fluctuate. Another common choice is the constant surface tension ensemble (N, T, V, γ), which mimics the experimental conditions more closely than the (N, T, V, Ap) ensemble. The (N, T, V, γ) is of particular importance for simulations of membranes, which can exhibit large undulations at vanishing surface tension. Accessing the γ = 0 regime is crucial to modeling such systems.
There has been an ongoing theoretical debate concerning the statistical thermodynamic definition of γ. In analytical studies, the surface tension is usually regarded as the thermodynamic variable conjugate to the total interface area A, which is the sum of the projected area Ap, and the area stored in the thermal undulations ΔA. Because of the relatively high value of their stretching modulus, bilayer membranes are often assumed to have a fixed total area, and γ is used as a Lagrange multiplier fixing the value of A. However, in computer simulations it is difficult to sample an ensemble where A is constant since ΔA cannot be easily controlled and, moreover, its value is not well defined (in contrast to continuum models). It is, therefore, more common in computer simulations that the surface tension is treated as conjugate to Ap, which is the cross-sectional area of the simulation cell. With this convention, one readily derives the following relationship between γ and the pressure tensor (49)
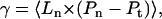 |
(7) |
where Ln is the size of the system in the direction perpendicular to the interface, and 〈…〉 denotes thermal average. This quantity coincides with yet another quantity commonly referred to as the “surface tension”, namely the q2 coefficient in the expression describing the dependence of the mean thermal fluctuations on the wave vector (the “spectral intensity”) (33):
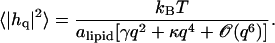 |
(8) |
To simulate the (N, T, V, γ) ensemble, one needs to sample configurations, in which the total volume of the system is conserved while the area is allowed to fluctuate. The common method to generate such an ensemble is to consider a rectangular simulation box of volume V = Lx × Ly × Lz and projected area Ap = Lx × Ly and, occasionally, rescale the dimensions of the box and the molecular coordinates 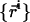 in the following manner (40):
in the following manner (40):
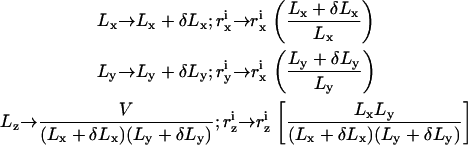 |
(9) |
In scaled coordinates, 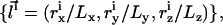 the partition function is given by
the partition function is given by
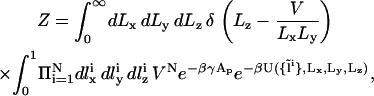 |
(10) |
where δ is the Dirac delta function, U is the energy of the configuration, and β = 1/kBT. Since the volume V and number of particles N are both fixed, the acceptance criterion is given by
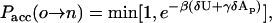 |
(11) |
where δU and δAp denote, respectively, the difference in the energy and projected area between the new (n) and old (o) configurations.
Equation 9 defines a one-to-one, locally volume preserving, transformation of the molecular coordinates between rectangular simulation boxes of slightly different dimensions. In principle, however, only the total volume of the simulation cell must be conserved and, therefore, other one-to-one transformation may be proposed. One such transformation, which is particularly suitable for solvent-free interfacial systems, is
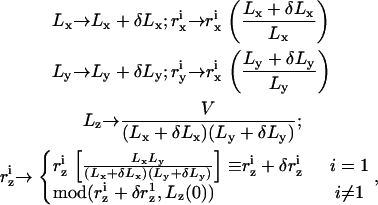 |
(12) |
where Lz(0) is the initial (at t = 0) height of the simulation box, and “mod” is the modulus operator. Unlike transformation (9), only the coordinates of one particle (labeled “1”) are rescaled proportionally to the size of the box in (Eq. 12). Therefore, a priori, only this particle is guaranteed to remain within the rescaled simulation box, while all the others may be displaced beyond the boundaries of the system in the z direction (0 ≤ z < Lz). Detailed balance requires that in the case of such an event, the move attempt will be rejected, i.e., the energy of the new configuration is defined U = ∞. Let us consider an interface located close to the center of the box (z ∼ Lz/2), separating two dense bulk liquid phases. Let us also assume that the particle with index “1” resides on the interface. For such a solvent-containing system, rescaling the dimensions of the simulation box and the molecular coordinates according to transformation (12) will usually fail. Decreasing Lz (Lz < Lz(0)) will lead to ejection of some solvent particles from the system, while increasing Lz (Lz > Lz(0)) will lead to the formation of an empty stripe and changing the bulk densities, which is energetically very costly. In solvent-free models, on the other hand, the bulk phases are “empty” and such a problem will arise only if the interface is located close to one of the z boundaries. For infinitely long runs, the fraction of time that the interface spends near the boundaries scales like w/Lz (where w is the physical width of the interface), which can be made arbitrarily small by increasing Lz (i.e., by changing the “volumes” of the empty bulk phases). In practice, Lz need not be very large since the diffusion of the interface is so vanishingly slow that it will never reach one of the boundaries within conceivable simulation time. With function (12) defining the transformation between simulation boxes of different shapes, and in terms of the scaled coordinates 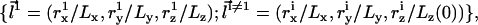 the partition function in Eq. 10 is rewritten as
the partition function in Eq. 10 is rewritten as
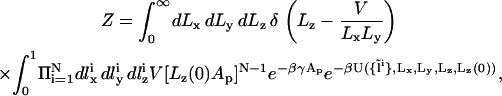 |
(13) |
from which we readily conclude that the acceptance criterion should be
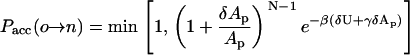 |
(14) |
This criterion resembles the acceptance criterion for simulations of the two-dimensional isobaric-isothermal ensemble, accept for the exponent of the term (1 + δAp/Ap) being N − 1 rather than N. This could be interpreted in the following way: Simulating a thin interface of width w at constant γ is similar to simulating a two-dimensional system at constant pressure. The center of mass of the interface can be found with equal probability at any position along the z direction of the simulation box. However, because of the total volume conservation, the height of the (mostly empty) simulation box scales with the inverse of the area Ap. The contribution of this degree of freedom is expressed by the additional factor (1 + δAp/Ap)−1.
We have performed simulations of identical systems (both neutral membranes and CL-DNA complexes) using sampling methods defined by Eqs. 9 and 12, and measured the probability distributions of the energy and the area of the system. Both methods produced identical distribution functions, but the time it took to obtain reasonably accurate results was considerably shorter with the new sampling scheme (Eq. 12) (∼2 × 106 MC time units) than with the conventional one (Eq. 9) (∼107 MC time units). The superior effectiveness of the new scheme should be attributed to larger area changes per reshaping attempt, δAp, that the new scheme permits, which were typically half an order-of-magnitude larger than in the old scheme. We believe that the origin of this is the fact that the membranes in our simulations are “softer” with respect to area changes than they are with respect to the variations of their width. In the conventional sampling scheme, area and width fluctuations are coupled by local volume conservation, which greatly reduces the magnitude of acceptable reshaping moves. In the new scheme this coupling is removed, enabling area variations that do not simultaneously squeeze the layers against each other or pull them apart.
APPENDIX 2: ANALYTICAL MODELING
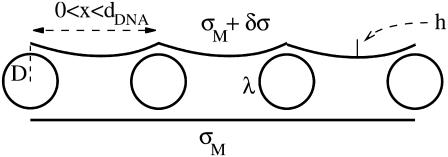
To estimate the deformation of the membranes and the charge density fluctuations within a unit cell of the complex, we consider the system shown schematically in Fig. 9. This system consists of three charge distributions: an infinite array of equally spaced rods with density per unit length λ < 0, and two surfaces with mean charge density σM > 0 per unit area (representing the monolayers facing the DNA array on each side). The vertical distance Δz(x) of the surfaces from the midplane of the DNA is Δz = D ≡ RDNA + σ/2 ∼ 13 Å at the edge of the unit cell (x = 0, dDNA), and may be smaller (Δz = D − h < D ; h(x) > 0) for 0 < x < dDNA due to the electrostatically induced deformation of the surfaces. We denote the charge density fluctuations by δσ(x), and consider the limit of small fluctuations |δσ|≪ σM, as well as the limit of small membrane deformation |h|/dDNA ≪ 1. As a reference state for energy calculations, we take a complex with perfectly flat surfaces and no charge density fluctuations. Since the complex is isoelectric, the mean charge density of the surfaces is related to the DNA linear charge density by
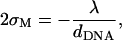 |
(15) |
while
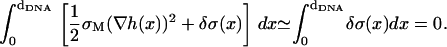 |
(16) |
FIGURE 9.
Schematic picture of the complex consisting of an array of equally spaced DNA rods with nearest-neighbor spacing dDNA and two surfaces separated a distance D from the midplane of the DNA array. The DNA rods are uniformly charged with charge density λ < 0 per unit length. Surfaces have a mean charge density σM > 0 per unit area and local charge density σM + δσ(x). Their local height above/below the DNA midplane is denoted by D − h(x). Lower surface is drawn in the reference state, where δσ = 0 and h = 0.
For a fixed value of dDNA, the free energy of a unit cell of the complex per unit length in the y direction (parallel to the DNA rods) consists of the following contributions:
- The Coulomb energy of the interaction between the DNA rods and the charged surfaces is given by (see Eq. 6)
The prefactor 2 in this expression is due to the two surfaces interacting with the DNA rods. Treating B in Eq. 17 as a small parameter (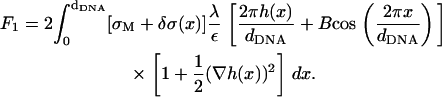
(17) 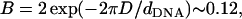 for D ∼ 13 Å and dDNA ∼30 Å, which is of the same order of magnitude as (δσ/σ) and (h/dDNA)), we see that the leading term in the above expression is
for D ∼ 13 Å and dDNA ∼30 Å, which is of the same order of magnitude as (δσ/σ) and (h/dDNA)), we see that the leading term in the above expression is
The superscript in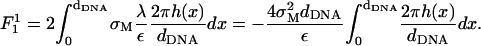
(18) 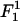 (as well as in the other terms of the free energy appearing below) denotes the order of the term in the small parameters of the expansion. The next (second-order) term is given by
(as well as in the other terms of the free energy appearing below) denotes the order of the term in the small parameters of the expansion. The next (second-order) term is given by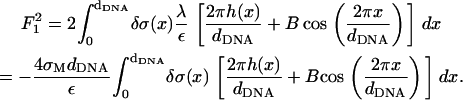
(19) - The Coulomb energy of the interaction between the two charged surfaces, which is in leading order, is given by
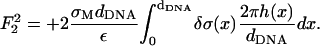
(20) - The mixing entropy of the charged and neutral lipids in each surface which, ignoring the variations in the area per lipid (see Fig. 8), is given by
where e/alipid is the maximum possible charge density (obtained when all the lipids are charged) and, obviously, σM ≤ e/alipid.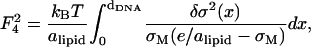
(22) - Concerning the elastic energy of the deformation of the surfaces, in previous theoretical studies of CL-DNA complexes (27,48), this energy has been associated with the bending of the surfaces and has been expressed in terms of Helfrich effective Hamiltonian (36). However, Helfrich effective Hamiltonian captures the elasticity of surfaces only on length scale, which are typically larger than the length of the unit cell dDNA ∼ 25–50 Å. At smaller scales, the elastic behavior of membranes is dominated by individual or collective lipid protrusions. Protrusion modes tend to increase the local surface area and the restoring force acting against these protrusions can, therefore, be characterized by an effective local surface tension γp. The corresponding elastic energy (per unit length in the y direction) is given (for two surfaces of length dDNA in the x direction) by (34)
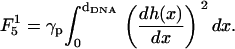
(23)
The crossover from long-scale bending dominated to short-scale surface tension-dominated elasticity occurs on length scale l, which is of the order of 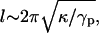 where κ is the bending modulus. Our previous measurements (32) give κ ∼ 40 kBT and l ∼ 50 Å, which yields γp ∼ 25 × 10−2 J/m2. Values of γp measured for other computer models of bilayer membranes (50,51) have been found to be of the same order of magnitude—which happens to be comparable to the surface tension of water-oil interfaces. Notice that the superscript “1” rather than “2” is used in Eq. 23, i.e., we consider this term as linear in the expansion parameters despite the fact that the elastic energy appears as a second-order term in (h/dDNA). This is because the surface tension γp is an order-of-magnitude larger than the energy per unit area
where κ is the bending modulus. Our previous measurements (32) give κ ∼ 40 kBT and l ∼ 50 Å, which yields γp ∼ 25 × 10−2 J/m2. Values of γp measured for other computer models of bilayer membranes (50,51) have been found to be of the same order of magnitude—which happens to be comparable to the surface tension of water-oil interfaces. Notice that the superscript “1” rather than “2” is used in Eq. 23, i.e., we consider this term as linear in the expansion parameters despite the fact that the elastic energy appears as a second-order term in (h/dDNA). This is because the surface tension γp is an order-of-magnitude larger than the energy per unit area 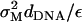 appearing in
appearing in 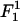 (18) and, therefore, these two terms are comparable to each other. The surface tension γp is also an order-of-magnitude larger than the thermal energy per lipid area kBT/alipid, appearing in the second-order term
(18) and, therefore, these two terms are comparable to each other. The surface tension γp is also an order-of-magnitude larger than the thermal energy per lipid area kBT/alipid, appearing in the second-order term 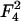 (22), which is associated with the mixing entropy.
(22), which is associated with the mixing entropy.
With the above expressions for the various terms in the free energy of the system, the equilibrium profile 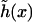 of the surfaces is found by minimizing the leading first-order contribution
of the surfaces is found by minimizing the leading first-order contribution 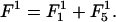 The function
The function 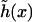 is determined by the Euler-Lagrange equation
is determined by the Euler-Lagrange equation
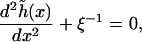 |
(24) |
where the length scale is 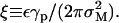 The solution to Eq. 24, with boundary conditions
The solution to Eq. 24, with boundary conditions 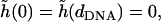 is
is
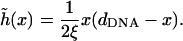 |
(25) |
The maximum deformation of the surfaces is obtained at the center of the unit cell (x = dDNA/2). For typical values of the physical parameters in the system,
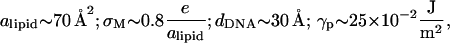 |
(26) |
we find 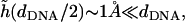 which justifies treating (h/dDNA) as a small parameter and explains the apparent flatness of the surfaces observed in the simulations (e.g., Fig. 1). It should be noted that our analysis ignores the very small overlap that exists between the surface
which justifies treating (h/dDNA) as a small parameter and explains the apparent flatness of the surfaces observed in the simulations (e.g., Fig. 1). It should be noted that our analysis ignores the very small overlap that exists between the surface 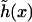 and the excluded volume of the DNA rods near the edges of the unit cell.
and the excluded volume of the DNA rods near the edges of the unit cell.
The charge density fluctuations δσ(x) will be determined by minimizing the free energy given by the sum of second order terms 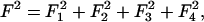 under the total charge conservation constraint (16) and with
under the total charge conservation constraint (16) and with  Expressing δσ(x) as a Fourier series
Expressing δσ(x) as a Fourier series
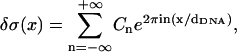 |
(27) |
we find, after some algebra, that the optimal charge distribution is obtained for the Fourier series
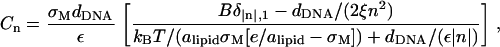 |
(28) |
where δ in the numerator denotes Krönecker delta. An approximate, but more useful, form for δσ(x) can be obtained by noting that typical values of the physical parameters (see Eq. 26) lead to the first term in the denominator being larger than the second term for all values of n. Thus, a reasonable approximation may be obtained by dropping the smaller term, which effectively means neglecting the term 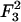 (Eq. 21) in the second-order free energy. Without this term, the real space form of δσ is given by
(Eq. 21) in the second-order free energy. Without this term, the real space form of δσ is given by
 |
(29) |
where lB = e2/(ε kBT) ∼ 7.1 Å is the Bjerrum length, and A = B−1(π/2) × (dDNA/ξ). From this expression we readily conclude that 1), only for A = 0, which corresponds to the limit of infinitely rigid surfaces (γp → ∞), is the peak of the charge distribution at the edge of the unit cell; 2), upon increasing A, the maximum of δσ(x) shifts gradually toward the center of the unit cell; and 3), it stays in the center, x = dDNA/2, for all values A ≥ 2π2.
One can easily verify that for the range of parameters in our simulations, 0 < A < 2π2—which explains our observation of the maximum of δσ(x) somewhere between the edge and the center of the unit cell (see Fig. 7). We can also use Eq. 29 to estimate the amplitude of the charge fluctuations. For the physical parameters given in Eq. 26, we have B ∼ 0.12. The maximum of δσ(x) is obtained for x ∼ 0.1dDNA (which should be compared to x ∼ 0.2dDNA in the simulations), where δσ/σM ∼ 0.07 (compare to δσ/σM ∼ 0.1 in the simulations). We consider this semiquantitative agreement with the numerical results as reasonable, given the approximate nature of our analytical model.
References
- 1.Felgner, P. L., and G. Rhodes. 1991. Gene therapeutics. Nature. 349:351–352. [DOI] [PubMed] [Google Scholar]
- 2.Smyth-Templeton, N., and D. D. Lasic, editors. 2000. Gene Therapy. Therapeutic Mechanisms and Strategies. Marcel Dekker, New York.
- 3.Smith, A. E. 1995. Viral vectors in gene therapy. Annu. Rev. Microbiol. 49:807–838. [DOI] [PubMed] [Google Scholar]
- 4.Kay, M. A., J. C. Glorioso, and L. Naldini. 2001. Viral vectors for gene therapy: the art of turning infectious agents into vehicles of therapeutics. Nat. Med. 7:33–40. [DOI] [PubMed] [Google Scholar]
- 5.Felgner, P. L., M. J. Heller, P. Lehn, J.-P. Behr, and F. C. Szoka, editors. 1996. Artificial self-assembling systems for gene delivery. American Chemical Society, Washington DC.
- 6.Huang, L., M. C. Hung, and E. Wagner, editors. 1999. Non-Viral Vectors for Gene Therapy. Academic Press, San Diego, CA.
- 7.Mahato, R. I., and S. W. Kim, editors. 2002. Pharmaceutical Perspectives of Nucleic Acid-Based Therapeutics. Taylor and Francis, London and New York.
- 8.Felgner, P. L. 1997. Nonviral strategies for gene therapy. Sci. Am. 276:102–106. [DOI] [PubMed] [Google Scholar]
- 9.Kamiya, H., H. Tsuchiya, J. Yamazaki, and H. Harashima. 2001. Intracellular trafficking and transgene expression of viral and non-viral gene vectors. Adv. Drug Deliv. Rev. 52:153–164. [DOI] [PubMed] [Google Scholar]
- 10.Edelstein, M. L., M. R. Abedi, J. Wixon, and R. M. Edelstein. 2004. Gene therapy clinical trials worldwide 1989–2004—an overview. J. Gene Med. 6:597–602. [DOI] [PubMed] [Google Scholar]
- 11.Willard, H. F. 2000. Genomics and gene therapy—artificial chromosomes coming to life. Science. 290:1308–1309. [DOI] [PubMed] [Google Scholar]
- 12.Ewert, K., N. L. Slack, A. Ahmad, H. M. Evans, A. J. Lin, C. E. Samuel, and C. R. Safinya. 2004. Cationic lipid-DNA complexes for gene therapy: understanding the relationship between complex structure and gene delivery pathways at the molecular level. Curr. Med. Chem. 11:133–149. [DOI] [PubMed] [Google Scholar]
- 13.Koltover, I., T. Salditt, J. O. Rädler, and C. R. Safinya. 1997. Structure of DNA-cationic liposome complexes: DNA intercalation in multilamellar membranes in distinct interhelical packing regimes. Science. 275:810–814. [DOI] [PubMed] [Google Scholar]
- 14.Rädler, J. O., I. Koltover, T. Salditt, and C. R. Safinya. 1998. An inverted hexagonal phase of cationic liposome-DNA complexes related to DNA release and delivery. Science. 281:78–81. [DOI] [PubMed] [Google Scholar]
- 15.Harries, D., S. May, W. M. Gelbart, and A. Ben-Shaul. 1998. Structure, stability, and thermodynamics of lamellar DNA-lipid complexes. Biophys. J. 75:159–173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.May, S., D. Harries, and A. Ben-Shaul. 2000. The phase behavior of cationic lipid-DNA complexes. Biophys. J. 78:1681–1697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lasic, D. D., H. Strey, M. C. A. Stuart, R. Podgornik, and P. M. D. Frederik. 1997. The structure of DNA-liposome complexes. J. Am. Chem. Soc. 119:832–833. [Google Scholar]
- 18.Safinya, C. R. 2001. Structures of lipid-DNA complexes: supramolecular assembly and gene delivery. Curr. Opin. Struct. Biol. 11:440–448. [DOI] [PubMed] [Google Scholar]
- 19.Clark, P. R., and E. M. Hersh. 1999. Cationic lipid-mediated gene transfer: current concepts. Curr. Opin. Mol. Ther. 1:158–176. [PubMed] [Google Scholar]
- 20.Chesnoy, S., and L. Huang. 2000. Structure and function of lipid-DNA complexes for gene delivery. Annu. Rev. Biophys. Biomol. Struct. 29:27–47. [DOI] [PubMed] [Google Scholar]
- 21.Ferber, D. 2001. Gene therapy: safer and virus-free? Science. 294:1638–1642. [DOI] [PubMed] [Google Scholar]
- 22.Alper, J. 2002. Drug delivery—breaching the membrane. Science. 296:838–839. [DOI] [PubMed] [Google Scholar]
- 23.Marshall, E. 2000. Biomedicine—gene therapy on trial. Science. 288:951–957. [PubMed] [Google Scholar]
- 24.Marshall, E. 2002. Gene therapy—what to do when clear success comes with an unclear risk? Science. 298:510–511. [DOI] [PubMed] [Google Scholar]
- 25.May, S., and A. Ben-Shaul. 2004. Modeling of cationic lipid-DNA complexes. Curr. Med. Chem. 11:151–167. [DOI] [PubMed] [Google Scholar]
- 26.Bruinsma, R. 1998. Electrostatics of DNA cationic lipid complexes: isoelectric instability. Eur. Phys. J. B. 4:75–88. [Google Scholar]
- 27.Harries, D., S. May, and A. Ben-Shaul. 2003. Curvature and charge modulations in lamellar DNA-lipid complexes. J. Phys. Chem. B. 107:3624–3630. [Google Scholar]
- 28.Lin, A. J., N. L. Slack, A. Ahmad, C. X. George, C. E. Samuel, and C. R. Safinya. 2003. Three-dimensional imaging of lipid gene-carriers: membrane charge density controls universal transfection behavior in lamellar cationic liposome-DNA complexes. Biophys. J. 84:3307–3316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ahmad, A., H. M. Evans, K. Ewert, C. X. George, C. E. Samuel, and C. R. Safinya. 2005. New multivalent cationic lipids reveal bell curve for transfection efficiency versus membrane charge density: lipid-DNA complexes for gene delivery. J. Gene Med. 7:739–748. [DOI] [PubMed] [Google Scholar]
- 30.Bandyopadhyay, S., M. Tarek, and M. L. Klein. 1999. Molecular dynamics study of a lipid-DNA complex. J. Phys. Chem. B. 103:10075–10080. [Google Scholar]
- 31.Farago, O., N. Grønbech-Jensen, and P. Pincus. 2006. Mesoscale computer modeling of lipid-DNA complexes for gene therapy. Phys. Rev. Lett. 96:018102. [DOI] [PubMed] [Google Scholar]
- 32.Farago, O. 2003. “Water-free” computer model for fluid bilayer membranes. J. Chem. Phys. 119:596–605. [Google Scholar]
- 33.Farago, O., and P. Pincus. 2004. Statistical mechanics of bilayer membrane with a fixed projected area. J. Chem. Phys. 120:2934–2950. [DOI] [PubMed] [Google Scholar]
- 34.Lipowsky, R., and S. Grotehans. 1993. Hydration vs. protrusion forces between lipid bilayers. Europhys. Lett. 23:599–604. [Google Scholar]
- 35.Haleva, E., N. Ben-Tal, and H. Diamant. 2004. Increased concentration of polyvalent phospholipids in the adsorption domain of a charged protein. Biophys. J. 86:2165–2178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Helfrich, W. 1973. Elastic properties of lipid bilayers—theory and possible experiments. Z. Naturforsch. 28C:693–703. [DOI] [PubMed] [Google Scholar]
- 37.Wagner, K., E. Keyes, T. W. Kephart, and G. Edwards. 1997. Analytical Debye-Hückel model for electrostatic potentials around dissolved DNA. Biophys. J. 73:21–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Grønbech-Jensen, N., G. Hummer, and K. M. Beardmore. 1997. Lekner summation of Coulomb interactions in partially periodic systems. Mol. Phys. 92:941–945. [Google Scholar]
- 39.Mashl, R. J., and N. Grønbech-Jensen. 1998. Effective interactions between rigid polyelectrolytes and like-charged planar surfaces. J. Chem. Phys. 109:4617–4623. [Google Scholar]
- 40.Groot, R. D., and K. L. Rabone. 2001. Mesoscopic simulation of cell membrane damage, morphology change and rupture by nonionic surfactants. Biophys. J. 81:725–736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Koltover, I., T. Salditt, and C. R. Safinya. 1999. Phase diagram, stability, and overcharging of lamellar cationic lipid-DNA self-assembled complexes. Biophys. J. 77:915–924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Lau, A. W. C., and P. Pincus. 1999. Binding of oppositely charged membranes and membrane reorganization. Eur. Phys. J. B. 10:175–180. [Google Scholar]
- 43.Boal, D. 2002. Mechanics of the Cell. Cambridge University Press, Cambridge, UK.
- 44.Tolpekina, T. V., W. K. den Otter, and W. J. Briels. 2004. Simulations of stable pores in membranes: system size dependence and line tension. J. Chem. Phys. 121:8014–8020. [DOI] [PubMed] [Google Scholar]
- 45.Strey, H. H., R. Podgornik, D. C. Rau, and V. A. Persegian. 1998. DNA-DNA interactions. Curr. Opin. Struct. Biol. 8:309–313. [DOI] [PubMed] [Google Scholar]
- 46.Rau, D. C., B. K. Lee, and V. A. Persegian. 1984. Measurement of the repulsive force between poly-electrolyte molecules in ionic solution: hydration forces between parallel DNA double helices. Proc. Natl. Acad. Sci. USA. 81:2621–2625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Podgornik, R., D. C. Rau, and V. A. Parsegian. 1989. The action of intermolecular forces on the organization of DNA double helices: fluctuation-enhanced decay of electrostatic double-layer and hydration forces. Macromolecules. 22:1780–1786. [Google Scholar]
- 48.Schiessel, H., and H. Aranda-Espinoza. 2001. Electrostatically induced undulations of lamellar DNA-lipid complexes. Eur. Phys. J. E. 5:499–506. [Google Scholar]
- 49.Rowlinson, J. S., and B. Widom. 1982. Molecular Theory of Capillarity. Oxford University Press, Oxford, UK.
- 50.Lindahl, E., and O. Edholm. 2000. Mesoscopic undulations and thickness fluctuations in lipid bilayers from molecular dynamics simulations. Biophys. J. 79:426–433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Marrink, S. J., and A. E. Mark. 2001. Effect of undulations on surface tension in simulated bilayers. J. Phys. Chem. B. 105:6122–6127. [Google Scholar]