Abstract
Genomewide association studies are now a widely used approach in the search for loci that affect complex traits. After detection of significant association, estimates of penetrance and allele-frequency parameters for the associated variant indicate the importance of that variant and facilitate the planning of replication studies. However, when these estimates are based on the original data used to detect the variant, the results are affected by an ascertainment bias known as the “winner’s curse.” The actual genetic effect is typically smaller than its estimate. This overestimation of the genetic effect may cause replication studies to fail because the necessary sample size is underestimated. Here, we present an approach that corrects for the ascertainment bias and generates an estimate of the frequency of a variant and its penetrance parameters. The method produces a point estimate and confidence region for the parameter estimates. We study the performance of this method using simulated data sets and show that it is possible to greatly reduce the bias in the parameter estimates, even when the original association study had low power. The uncertainty of the estimate decreases with increasing sample size, independent of the power of the original test for association. Finally, we show that application of the method to case-control data can improve the design of replication studies considerably.
Identification of the genetic variants that contribute to complex traits is an important current challenge in the field of human genetics. Although there is a steady stream of reported associations, replication of findings is often inconsistent, even for those associations that do ultimately turn out to be genuine.1,2 In large part, the difficulties of replication occur because most genuine associations have modest effects; hence, there is generally incomplete power to detect associations in any given study. These challenges will undoubtedly continue as we move into the era of affordable whole-genome association studies, through which it is possible to detect variants of small effect anywhere in the genome.3,4
When a study identifies a marker that shows evidence of association with a disease, it is common to estimate the impact of this variant on the phenotype of interest. This impact is often expressed as an odds ratio—that is, the ratio of the odds of manifesting the disease in carriers of the risk allele to the odds of manifesting the disease in noncarriers. A complete description of the impact of a variant affecting a binary phenotype includes two sets of parameters: the frequencies of the genotypes and the penetrances of the genotypes. These parameters can be used to assess the impact of the detected variant, as measured, for example, by the attributable risk. Estimation of the strength of the effect of a genetic variant on the phenotype is also helpful for planning successful replication studies.
Unfortunately, estimation of these parameters with the same data set that was used to identify the variant of interest is not straightforward, since the data set does not constitute a random population sample for two reasons. First, samples that are used for association mapping are usually collected to oversample affected individuals relative to their frequency in the population (e.g., the sample might include equal numbers of cases and controls). Second, and more seriously, there is a major ascertainment effect that occurs when a variant is of interest specifically because it was significant for association. For a variant that is genuinely—but weakly—associated with disease, there may be only low or moderate power to detect association. Hence, when there is a significant result, it may imply that the genotype counts of cases and controls are more different from each other than expected. Consequently, the estimates of effect size are biased upward. This effect, which is an example of the “winner’s curse” from economics,5 depends strongly on the power of the initial test for association.6 If the power is high, most random draws from the distribution of genotype counts will result in a significant test for association; thus, the ascertainment effect is small. On the other hand, if the power is low, conditioning on a successful association scan will result in a big ascertainment effect.
This problem is well appreciated in the field. It has been observed that the odds ratio of a disease variant is usually overestimated in the study that first describes the variant. In a meta-analysis of 301 association studies of 25 putative disease loci, Lohmueller et al.2 concluded that, even though the replication studies indicated that 11 of the loci were genuinely associated with disease, a striking 24 of the 25 loci were reported in the initial study to have an odds ratio higher than the estimates based on subsequent replication studies. One important implication of the winner’s curse is that it makes it hard to design appropriately powered replication studies. If the sample size of a replication study is chosen on the basis of the odds ratio observed in the initial study, then the replication will almost certainly be underpowered.1
Göring et al.6 were the first to highlight the challenges of the winner’s curse for genome scans. Studying the problem for variance-components linkage scans of QTLs, they showed that, for low-powered studies, the naive estimate of the genetic effect at a significant locus is almost uncorrelated with the true underlying genetic effect; this results in a significant overestimation. They concluded that the only method for generating a useful estimate is to collect a large, independent, population-based sample of individuals, without regard to phenotype, and then to phenotype and genotype each individual. Although such a sample would provide unbiased estimates of allele frequencies and penetrance parameters with properly calibrated confidence regions, this may be a prohibitively expensive solution to the problem. Thus, it is of interest to develop methods that generate unbiased estimates of the parameters of interest from the same data set used to detect the variant.
Several authors have since described methods that correct for the ascertainment bias when estimating genetic effects after a whole-genome scan for linkage. Allison et al.7 noted that, for a specified genetic model, the distribution of the effect, constrained by ascertainment bias, can be analyzed. Using a method-of-moments approach, they calculated an estimate of the genetic effect. Siegmund8 proposed lowering the confidence limit in the initial test, thus accepting a large number of false-positive results. As indicated above, this leads to a high power for each individual test and only a small ascertainment effect. Siegmund8 then suggested calculating CIs and accounting for the high number of tests by increasing the stringency of the CIs. To correct for ascertainment, this method also requires specifying the genetic model. Sun and Bull9 suggested multiple methods based on randomly splitting the sample into a detection sample and an estimation sample. By comparing the estimate generated from the detection sample and the estimate from the estimation sample, they were able to calculate a correction factor for the ascertainment effect. However, the resulting estimator is still somewhat biased, and the SE of the corrected estimate is actually higher than the SE of the naive estimator.9 In a somewhat analogous setting, one study of family-based association tests proposed that the available information be split into two orthogonal components.10 Then, one component of the information is used to validate promising signals from the other component. However, that study focused primarily on testing rather than estimation.
Although some of the methods for correcting for the winner’s curse in linkage studies could be extended to association studies, association studies differ from linkage studies in several respects. The sample collected for an association study is more similar to a random population sample, which allows a more precise calculation of the sampling probabilities. Furthermore, the power of an association study should be much higher than the power of a linkage study of the same trait,11 so it is not clear how well the conclusions of Göring et al.6 apply to whole-genome scans for complex diseases.
The goal of the present study was to develop a method for generating corrected estimates of genetic-effect size for a locus that was identified in a significant test for association. Instead of calculating an odds ratio or relative-risk parameter, we use information about the population prevalence of the disease to estimate directly the penetrance parameters of the variants of interest. This allows us to perform the estimation for any specific genetic model (e.g., additive or dominant) or for a completely general genetic model. We describe an algorithm for calculating the approximate maximum-likelihood estimates (MLEs) of the frequencies and the penetrance parameters of the genotypes and associated confidence regions. We find that, for a variety of genetic models, our estimator corrects the ascertainment effect and provides reasonably accurate estimates and well-calibrated CIs while slightly underestimating the genetic effect. We show that these corrected estimates provide a far better basis for designing replication studies than do the naive uncorrected estimates. Last, we show an application of the method to the association of the Pro12Ala polymorphism in PPARγ with type 2 diabetes.12
Methods
Model
We developed a fairly general model for calculating the likelihood of a set of penetrance parameters and genotype frequencies conditional on having observed a “significant” signal for association at a certain biallelic marker. It is assumed that significance is determined according to a prespecified test and type 1 error rate (α). In a data set of na affected individuals and nu unaffected individuals, we consider the three genotypes g1, g2, and g3 indicating, respectively, the minor-allele homozygote, the heterozygote, and the major-allele homozygote. Let the data D=(a1,…,a3,u1…,u3) be the counts of these genotypes in affected and unaffected individuals that constitute the significant signal for association. Furthermore, let φ=(φ1,…,φ3) be the population frequencies of the genotypes, let θ=(θ1,…,θ3) be the penetrances, and let F be the population prevalence of the disease phenotype. F, which is assumed to be known from independent data, will be used to constrain the sample space for the other parameters as follows:
 |
We split the ascertainment into two parts. Let B indicate that, as required, the marker of interest shows significant association at level α, and let S be the experimental design of sampling na affected individuals and nu unaffected individuals, regardless of the prevalence F. We use 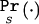 as a shorthand for Pr(·|S). We calculate the likelihood L(θ,φ) and obtain an MLE for θ and φ, using the equation
as a shorthand for Pr(·|S). We calculate the likelihood L(θ,φ) and obtain an MLE for θ and φ, using the equation
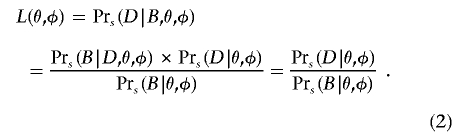 |
This result is obtained using the fact that the data D constitute, by definition, a significant result, so D implies B; hence, 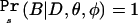 . The numerator on the right side of equation (2) is the likelihood of the observed genotype counts, and the denominator is the power of the test used in the initial genome scan. The numerator is maximized at the naive penetrance estimates. Meanwhile, the denominator (power) is made smaller as the penetrance values move closer together. This has the effect of tilting the maximum likelihood toward smaller differences among the penetrances. Notice that equation (2) is undefined when the power is 0 (e.g., if all the φi=0); however, power=0 implies that observing a significant result is impossible. Since we condition our estimation on observing a significant result, this case can be ignored.
. The numerator on the right side of equation (2) is the likelihood of the observed genotype counts, and the denominator is the power of the test used in the initial genome scan. The numerator is maximized at the naive penetrance estimates. Meanwhile, the denominator (power) is made smaller as the penetrance values move closer together. This has the effect of tilting the maximum likelihood toward smaller differences among the penetrances. Notice that equation (2) is undefined when the power is 0 (e.g., if all the φi=0); however, power=0 implies that observing a significant result is impossible. Since we condition our estimation on observing a significant result, this case can be ignored.
Under the assumption that the samples of affected and unaffected individuals are only a small proportion of the affected and unaffected individuals in the population, 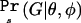 is the product of two multinomial distributions
is the product of two multinomial distributions
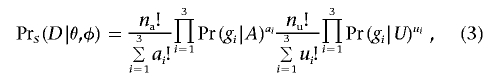 |
where A indicates the affected phenotype and U the unaffected phenotype. Pr(gi|A) is the probability that a randomly selected affected individual carries genotype gi and can be calculated
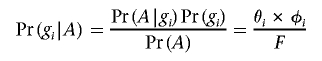 |
and
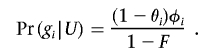 |
A general expression for the denominator of equation (2) is
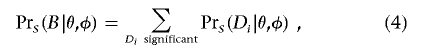 |
where the Di represent all significant realizations of the data vector D.
For many designs of tests for association, it is possible to calculate the power of the initial test exactly (see appendix A). To apply this algorithm to tests that do not have a simple method of power calculation, equation (4) can be evaluated by sampling Di conditional on θ and φ and approximating Pr(B|θ,φ) by Monte Carlo integration. These calculations assume that controls are selected to not show the phenotype of interest. If random (unphenotyped) controls are used, equation (3) is modified by replacing Pr(gi|U) with Pr(gi). Note that, although, in the initial scan for association, several tests can be performed at each of many markers, the multiple testing affects the estimates only indirectly through the choice of the level of significance, α.
The equations can be extended to estimate gene-gene interaction parameters. To assess the interaction of m loci in the genome, all possible combinations of genotypes have to be considered, so there are k=3m states. Enumerating these states 1,…,k, the set of genotype counts can then be expressed as D={u1,…,uk,a1,…,ak}, and the goal is to estimate the vector of population genotype frequencies φ=(φ1,…,φk) and the vector of penetrances θ=(θ1,…,θk) by extending equations (1)–(4).
The Algorithm
We designed a two-stage algorithm to estimate the population frequencies of the underlying genotypes and their penetrance parameters conditional on a known disease prevalence F, by maximizing L(θ,φ). In the first step, we generated an approximate likelihood surface by sampling m=30,000 independent sets of parameters conditional on F (i.e., that satisfy eq. [1]). The three genotypes were assumed to be in Hardy-Weinberg proportions in the overall population. We then calculated the likelihood L(D|φ1,…,φ3, θ1,…,θ3) for each parameter set and selected the set with the highest likelihood as a first approximation of the point estimate of the parameters. In the second step, we improved this estimate by perturbing each parameter value by a small value ε and accepting the new parameter values if the likelihood is higher than the likelihood of the old maximum. By repeating this procedure 3,000 times, reducing ε with every repetition, we generated highly stable estimates. We assessed the fidelity of this algorithm by analyzing a set of data sets multiple times, and we observed that the parameter estimates differed by a magnitude of only 10-5. To generate estimates for a known genetic model, we repeated the analysis in parameter spaces that are constrained accordingly.
We generated 95% confidence regions by comparing the likelihood of all initial m parameter points with the likelihood of the point estimate. We included all points for which twice the difference of log-likelihoods was <95th percentile of a χ2 distribution with 3 df. (The model contains three free parameters: an allele frequency and three penetrances that are jointly constrained to produce the overall disease prevalence F.) For simpler genetic models, we used fewer degrees of freedom as appropriate.
Analysis of the Algorithm
We tested our algorithm by simulating association scan data and then estimating the true underlying parameters according to the following scheme:
-
1.
Simulate genotype counts D on the basis of minor-allele frequency f and penetrances θ1, θ2, and θ3 for a sample of n cases and n controls, according to equation (3), under the assumption of Hardy-Weinberg equilibrium in the general population.
-
2.
Perform χ2 test of significance for the simulated data, comparing allele counts in cases and controls at significance level α=10-6. If significant, move to step 3; otherwise, return to step 1.
-
3. Generate three estimates (
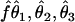 ) on the basis of D:
) on the basis of D:-
a. without correcting for the ascertainment effect (naive estimator),
-
b. with use of the correction for ascertainment described here, and
-
c. simulating a second, independent sample and generating the estimates on the basis of the second sample.
-
a.
Using this procedure, we performed two simulation studies: (1) a simple example to explore the basic properties of the winner’s curse and the proposed correction and (2) a set of studies simulated under a large number of penetrance models, to assess the effect of genetic model, sample size, and power of the initial study.
Simulation study 1
We set the minor-allele frequency f=0.2 and considered three additive combinations for the penetrance parameters (θ1,θ2,θ3): (0.18, 0.14, 0.1), (0.25, 0.175, 0.1), and (0.32, 0.21, 0.1). At a sample size of n=400 and α=10-6, these three parameter sets yielded power of 0.03, 0.54, and 0.97, respectively. We assumed that the underlying model was known to be additive, and we constrained the parameter space accordingly. For each estimate, we calculated the estimated additive component 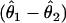 and compared the resulting distributions.
and compared the resulting distributions.
Simulation study 2
We sampled random data sets of 1,000 parameter combinations for each n∈{100,200,400,800}, generating the minor-allele frequency f from a uniform distribution on (0.05,0.5), drawing θ1 and θ3 independently from a uniform distribution on (0,1), and setting
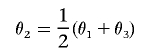 |
(additive model). We sampled from such data sets to have approximately uniformly distributed power in the initial test for association, by evaluating 100 parameter sets with a power between 0.005 and 0.1, 100 sets with a power between 0.1 and 0.2, and so on; the last category was 100 parameter sets with a power between 0.9 and 0.995. All other parameter sets were rejected. For each parameter set, we generated one set of genotype counts D. On the basis of D, we obtained one estimate under the assumption that the underlying genetic model was known to be additive, constraining the parameter space accordingly, and a second estimate under the assumption that the model was unknown.
We summarized the difference between the estimated penetrances 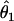 ,
, 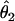 , and
, and 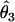 and the true values θ1, θ2, and θ3 as the sum of squared deviations (ssq)
and the true values θ1, θ2, and θ3 as the sum of squared deviations (ssq)
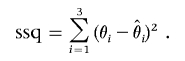 |
To evaluate the bias of the different estimation methods, we calculated the true additive effect θ2-θ1 and compared it with the estimates of the same effect, calculating
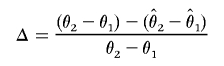 |
for corrected estimates and uncorrected estimates. Our results indicate that the winner’s curse has only a small effect on estimates of the allele frequency f (data not shown).
Furthermore, we evaluated whether the true underlying parameters lie within the confidence region by comparing the likelihoods L(θ,f) and 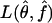 . We calculated the relative size of the confidence region, dividing the number of sampled parameter points that were in the confidence region by 30,000, the total number of parameter points sampled during step 1 of the estimation procedure.
. We calculated the relative size of the confidence region, dividing the number of sampled parameter points that were in the confidence region by 30,000, the total number of parameter points sampled during step 1 of the estimation procedure.
We repeated the analysis by simulating data under four genetic models: dominant (θ1=θ2), recessive (θ2=θ3), multiplicative (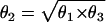 ), and a general three-parameter model (θ2 sampled independently). When we performed the same analysis, we found no qualitative differences among models (data not shown).
), and a general three-parameter model (θ2 sampled independently). When we performed the same analysis, we found no qualitative differences among models (data not shown).
To assess the effect of misspecifying the disease prevalence, we simulated 1,000 association studies of 400 cases and 400 controls in which the specified prevalence was 20%, 40%, or 60% of the true prevalence parameter. We observed that the estimates of the penetrance parameters were affected by this change, in the sense that the mean square error increased with increasing misspecification. However, the median odds ratio of the minor allele compared with that of the major allele was unaffected. Furthermore, when sample sizes were calculated for a replication study with an allele-based test, sample sizes predicted under a misspecified prevalence were as precise as sample sizes predicted under the correct prevalence.
To estimate the sample size necessary for a replication study, we calculated the minimum sample size (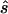 ) necessary to achieve a power of 0.80 at a significance level of 10-6 under the assumption of a test that compared allele frequencies on the basis of
) necessary to achieve a power of 0.80 at a significance level of 10-6 under the assumption of a test that compared allele frequencies on the basis of 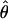 and
and 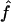 generated with the unconstrained model (see appendix A). We performed the same computation for each point in the confidence region, considering the maximum of the results as the upper bound of sample sizes necessary to replicate the association (
generated with the unconstrained model (see appendix A). We performed the same computation for each point in the confidence region, considering the maximum of the results as the upper bound of sample sizes necessary to replicate the association (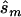 ). We repeated this calculation for three additional tests of association, comparing (1) the number of homozygotes for the minor allele, (2) the number of homozygotes of the major allele, and (3) the number of heterozygotes in a χ2 test. We selected the test that required the smallest of those four sample sizes as the best test for a replication study and recorded the sample size required under this best test.
). We repeated this calculation for three additional tests of association, comparing (1) the number of homozygotes for the minor allele, (2) the number of homozygotes of the major allele, and (3) the number of heterozygotes in a χ2 test. We selected the test that required the smallest of those four sample sizes as the best test for a replication study and recorded the sample size required under this best test.
Results
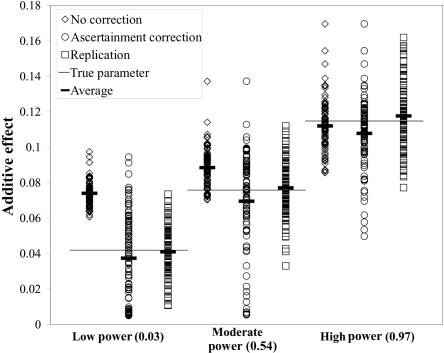
For a qualitative assessment of the algorithm, we selected three parameter sets with additive penetrance representing a low-powered study (0.03), a moderately powered study (0.54), and a high-powered study (0.97). For each parameter set, we simulated 100 significant association studies of 400 affected and 400 unaffected individuals and obtained three estimates of the penetrance parameters: (1) without correcting for the ascertainment effect, (2) with application of the algorithm described earlier to correct for ascertainment, and (3) with an independent sample that was not conditioned to show a significant association result. For the low-powered parameter set, the uncorrected estimate for each of the 100 simulated studies is considerably higher than the true underlying value, clearly demonstrating the effect of the winner’s curse (fig. 1). In moderately powered studies, the uncorrected estimate is still clearly biased toward overestimation of the genetic effect: in 93 of the 100 studies, the estimated effect of the variant is higher than the true underlying effect size. Only in the high-powered study are the estimates centered on the true underlying value.
Figure 1. .
Estimates of the genetic effect generated for three parameter sets with low, intermediate, and high power. For each parameter set, 100 significant association studies were generated, and the underlying parameters were estimated by three different methods: (1) not correcting for ascertainment (diamonds), (2) correcting for ascertainment (circles), and (3) collecting a second unascertained sample and basing the estimate on that sample (squares). The vertical axis shows the estimated genetic effect; the horizontal axis groups the estimates by the power of the initial study. The horizontal line in each power category indicates the true underlying genetic effect, and the short horizontal bar indicates the average of each distribution of 100 data sets.
In contrast, the estimate that is corrected for ascertainment yields a distribution of estimates that is centered on the true value in all three cases. The average of the estimated effect is close to the true value, regardless of the underlying power, although the estimates are biased slightly downward. However, in every set of simulated data sets analyzed with ascertainment correction, we observe a cluster of simulated data sets in which the estimated genetic effect is far below the true effect. These points represent case-control studies in which the test statistic is only slightly larger than the critical value C. The probability of observing such a test statistic near C conditional on observing a test statistic >C is large for genetic models with small effect sizes, but it is not very large for models with moderate or large effect sizes. In the models we considered, whenever the test statistic was close to C, a model of low genetic effect had the highest likelihood. Furthermore, under most genetic models, some data sets generated a test statistic near C. In these data sets, the effect size was underestimated after correction for ascertainment. Thus, the corrected estimate has a bias toward underestimating the effect size.
We can also observe differences in the variances of the estimates. In general, figure 1 reveals that estimates of genetic effect can vary widely, even if no ascertainment bias is introduced. In comparison with the distribution of estimates generated from the unascertained sample, the uncorrected estimates for low- and moderately powered studies are more tightly clustered around the biased average, whereas estimates generated with the corrected method are more widely dispersed. These results illustrate the problems of the winner’s curse in low-powered association studies and show that our algorithm generates nearly unbiased estimates of the penetrance parameters.
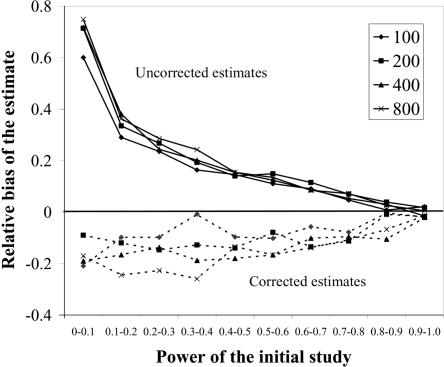
To assess the bias of our method in a more systematic fashion, we calculated the relative difference between the estimated and true underlying genetic effect, Δ, for each data set generated in simulation study 2 (see the “Simulation study 2” section) that was simulated with an additive model. Without correction for ascertainment, the genetic effect is overestimated by 20%, on average, over all parameter sets, independent of sample size. After applying the correction for ascertainment, we underestimate the additive effect of the causative allele by 12% of the true additive effect. To assess the effect of the power of the initial test for association on these biases, we stratified the simulated association scans by the power of each scan and averaged the bias over all parameter sets in power intervals of 0.10, starting in a bin of 0.05–0.10 power.
Figure 2 shows the average bias for case and control sample sizes between 100 and 800. Figure 2 indicates that the bias of the uncorrected estimate is strongly dependent on the power of the underlying test for association (solid lines). If the power of the initial scan is low (<10%), then the additive effect is overestimated by 70%, on average, when the ascertainment effect is not taken into account. In contrast, if the power of the initial test is >0.90, then the uncorrected estimate has almost no bias. By comparison, figure 2 illustrates that the corrected estimate is biased toward underestimating the genetic effect but that the power of the initial study has only limited effect on the bias of the corrected estimate (dashed lines). The average bias for parameter sets with power <0.10 (−17%) is only slightly more pronounced than the average bias of data sets for which the power is between 0.60 and 0.70 (−11%). Only if the power of the initial scan is >0.90 is the bias of the corrected estimate negligible.
Figure 2. .
Bias of the uncorrected and corrected estimates of the additive genetic effect. For each of the sample sizes, the data set has been stratified into 10 categories of power indicated on the horizontal axis. The vertical axis indicates the average relative bias observed in each power category. We performed simulations with four sample sizes, as indicated by the legend. The solid lines show the bias of estimates of penetrance parameters that were generated without correction for ascertainment, whereas the dashed lines show the bias of estimates generated while correcting for ascertainment.
We analyzed the impact of sample size on the precision of the corrected estimate, using data sets generated with simulation scheme 2 (see the “Simulation study 2” section). Since the winner’s curse effect is dependent on the power of the initial test for association, it can be expected that, for a given set of parameters, the precision of an estimate will increase with sample size, since the power rises with sample size. To determine whether sample size would also have a direct effect on the precision of the estimate beyond the effect of increased power, we conditioned each data set of 1,000 simulated scans to have a uniform distribution of power in the initial test for association. Here, we present data simulated with the additive model. Generating data with other genetic models yielded similar results.
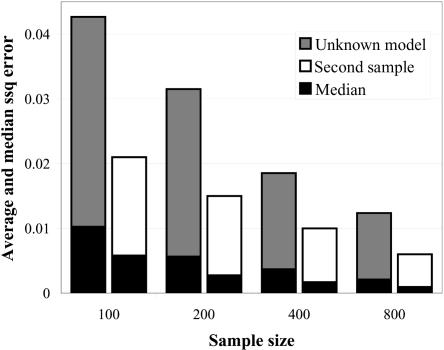
Figure 3 displays the difference between the estimated and the true parameters as a function of sample size. The dark gray bars show the average ssq error for estimates generated with our method, under the assumption that the true underlying model is unknown.
Figure 3. .
Accuracy of point estimates for penetrance parameters dependent on sample size (horizontal axis). All estimates were corrected for ascertainment. The height of each bar indicates the average difference between the true and inferred parameters measured as ssq (see the “Methods” section), and the black portion of the bar displays the median ssq statistic. The dark gray bars show the ssq error of estimates generated without conditioning on a genetic model. The white bars show the ssq error of an estimate generated from an unascertained sample of the same size without knowing the underlying model.
The results indicate that the accuracy of the estimated penetrances strongly depend on sample size. Analysis of association studies with 800 cases and controls resulted, on average, in roughly a quarter of the ssq error of the same analysis of studies with 100 cases and controls. Figure 3 also shows that the medians of the error scores (black part of each bar) was considerably lower than the average, indicating that the distribution of the relative error and ssq over 1,000 simulated data sets consists of mostly estimates with a small error and a few estimates with a high error. These statistics can be appreciated by comparing them with an estimate generated from an independent sample of equal size with the assumption of unknown penetrance parameters (fig. 3, white bars). Unsurprisingly, the unascertained sample generated more-precise estimates (smaller ssq values) than did the ascertained sample. Nevertheless, comparison of the values between the sample sizes revealed that the median ssq of an independent sample was roughly the same as the median ssq of an ascertained sample with twice the sample size.
We can quantify the uncertainty of the point estimate as a four-dimensional confidence region corresponding to the three penetrance parameters and the allele frequency. Assessing whether the confidence regions were well calibrated, we observed the true value falling in the constructed 95% confidence regions in 94.7% of all simulated data sets. Thus, our statistic yields appropriate confidence regions.
The volume of this confidence region summarizes the extent of uncertainty as a single statistic. We estimated this volume for each simulated data set relative to the size of the underlying parameter space and observed a strong effect of sample size on the size of the confidence region. For each doubling of the sample size, the average volume of the confidence region was approximately halved. Furthermore, the results indicate that estimates generated from a second independent sample have only slightly smaller confidence regions than do the bias-corrected estimates obtained from the original association sample.
Replication Studies
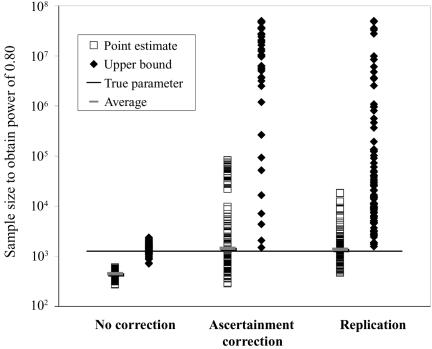
Using the MLEs of minor-allele frequency and penetrance parameters, we calculated the sample size (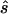 ) required to achieve power of ⩾0.80 at a significance level of α=10-6 in a replication study with an allele-based test for association. First, we applied this analysis to estimates from 100 simulated association studies, shown in the “Low power” section of figure 1, generated in simulation study 1. For each estimated set of parameters, we calculated the replication sample size
) required to achieve power of ⩾0.80 at a significance level of α=10-6 in a replication study with an allele-based test for association. First, we applied this analysis to estimates from 100 simulated association studies, shown in the “Low power” section of figure 1, generated in simulation study 1. For each estimated set of parameters, we calculated the replication sample size 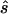 and the upper bound
and the upper bound 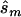 (see the “Methods” section). We compared these estimated sample sizes with the true sample size required to replicate the association with power of 0.80 and observed that none of the sample sizes based on uncorrected estimates was sufficient (fig. 4); none generated a power >0.04. For 27% of all simulated data sets, even the upper bound of this sample size
(see the “Methods” section). We compared these estimated sample sizes with the true sample size required to replicate the association with power of 0.80 and observed that none of the sample sizes based on uncorrected estimates was sufficient (fig. 4); none generated a power >0.04. For 27% of all simulated data sets, even the upper bound of this sample size 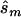 is too small to generate sufficient power.
is too small to generate sufficient power.
Figure 4. .
Estimated sample size for a replication study. We used the 100 parameter estimates for the low-powered study described in figure 1 to calculate the sample size required to achieve 0.80 power for α=10-6 in a replication study. The vertical axis indicates the calculated sample size, and the horizontal axis shows the method used to estimate the sample size; the squares represent results based on point estimates; the diamonds show results based on upper 95% bounds. The horizontal line shows the actual required sample size (1,261), and the short horizontal bars display the average of each set of point estimates.
In contrast, the sample sizes calculated using the corrected estimates are centered on the true required sample size. Nevertheless, the distribution of sample sizes is quite broad. For many simulated data sets, the calculated replication sample size is quite different from the truth. Since the effect size is low, penetrance estimates that differ by 0.02 result in very different replication sample sizes. The uncertainty in estimates of small effect size is reflected in the large upper bound of each estimate; only 4 of the 100 data sets resulted in an 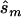 <10,000. A similar level of uncertainty can be observed in estimates generated from unascertained samples; here, we observe that only 35 unascertained samples resulted in
<10,000. A similar level of uncertainty can be observed in estimates generated from unascertained samples; here, we observe that only 35 unascertained samples resulted in 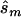 <10,000.
<10,000.
However, this analysis assumes that the test for the replication study is chosen independent of the estimated penetrance parameter. Instead, we can select the test that is most powerful for the estimated parameters. To evaluate this approach, we compared two strategies for planning replication studies: (1) select a test for association independent of the estimated parameters and then estimate the necessary sample size and (2) select the test statistic that is most powerful for the estimated penetrance parameters and estimate the sample size required for a replication study with that test. We applied both strategies to data sets simulated with simulation study 2, using three-parameter models, recessive models, and multiplicative models for various different sample sizes (table 1). All data were analyzed using the three-parameter model; thus, no knowledge about the underlying genetic model was assumed.
Table 1. .
Design of Replication Studies Based on the Estimated Penetrance Parameters[Note]
| Replication Test |
|||||
| Allele Based |
Best Model |
||||
| Sample Size and Genetic Model |
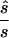 |
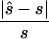 |
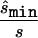 |
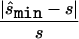 |
Ratio |
| 100/100: | |||||
| Multiplicative | 1.09 | .37 | 1.00 | .34 | .87 |
| Three parameter | 1.10 | .39 | .96 | .24 | .59 |
| Recessive | 1.03 | .39 | .87 | .28 | .42 |
| 200/200: | |||||
| Multiplicative | 1.07 | .40 | .99 | .38 | .88 |
| Three parameter | 1.06 | .40 | .97 | .22 | .55 |
| Recessive | 1.07 | .38 | .91 | .25 | .41 |
| 400/400: | |||||
| Multiplicative | 1.13 | .41 | 1.04 | .38 | .87 |
| Three parameter | 1.13 | .41 | .98 | .20 | .44 |
| Recessive | 1.03 | .38 | .95 | .22 | .41 |
| 800/800: | |||||
| Multiplicative | 1.12 | .44 | 1.03 | .42 | .87 |
| Three parameter | 1.10 | .41 | .98 | .17 | .38 |
| Recessive | 1.11 | .39 | .99 | .21 | .37 |
Note.— Designing samples of the indicated sizes (number of cases/number of controls) were simulated assuming a multiplicative model, a three-parameter model, or a recessive model. For each replicate simulation, the sample size 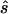 to obtain 80% power in a replication study was estimated. Here,
to obtain 80% power in a replication study was estimated. Here, 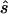 is compared with the true required sample size s for two test strategies: with use of the allele-based test or with choice of the best of several test statistics. Columns 2 and 4 show the median ratio, and columns 3 and 5 display the median relative difference. The final column shows the ratio between the estimated sample sizes for the first and the second strategy.
is compared with the true required sample size s for two test strategies: with use of the allele-based test or with choice of the best of several test statistics. Columns 2 and 4 show the median ratio, and columns 3 and 5 display the median relative difference. The final column shows the ratio between the estimated sample sizes for the first and the second strategy.
First strategy
For each data set, we calculated the sample size 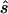 required to replicate the association with an allele-based test. The median ratio between
required to replicate the association with an allele-based test. The median ratio between 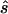 and the true sample size is slightly >1.0 (table 1, column 2). The median deviation between the true and the estimated necessary sample size relative to the true necessary sample size is ∼0.4, indicating that, in ∼50% of all simulated cases, the predicted necessary sample size is over- or underestimated by ⩾40%. Both the median ratio and the median deviation seem to be unaffected by the underlying genetic model or the sample size.
and the true sample size is slightly >1.0 (table 1, column 2). The median deviation between the true and the estimated necessary sample size relative to the true necessary sample size is ∼0.4, indicating that, in ∼50% of all simulated cases, the predicted necessary sample size is over- or underestimated by ⩾40%. Both the median ratio and the median deviation seem to be unaffected by the underlying genetic model or the sample size.
Second strategy
To design the replication study on the basis of the estimated penetrance parameters, we calculated the replication sample size 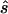 for four different tests of association, selecting the one that required the smallest
for four different tests of association, selecting the one that required the smallest 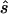 (i.e.,
(i.e., 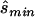 ). The four tests assessed the difference between affected and unaffected individuals in (1) the homozygotes for the minor allele, (2) the homozygotes for the major allele, (3) heterozygotes, and (4) allele count. We then calculated the true sample size necessary for the selected optimal test and the ratio between the estimated sample size and the necessary true sample size; see appendix A for details about these calculations. The results for these comparisons are seen in columns 3 and 5 of table 1, which displays the same statistics as described above, whereas the last column shows the ratio of
). The four tests assessed the difference between affected and unaffected individuals in (1) the homozygotes for the minor allele, (2) the homozygotes for the major allele, (3) heterozygotes, and (4) allele count. We then calculated the true sample size necessary for the selected optimal test and the ratio between the estimated sample size and the necessary true sample size; see appendix A for details about these calculations. The results for these comparisons are seen in columns 3 and 5 of table 1, which displays the same statistics as described above, whereas the last column shows the ratio of 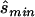 generated with strategy 2 to
generated with strategy 2 to 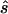 generated with strategy 1. Other than for the first strategy, the summary statistics depend on sample size and on the underlying genetic model. If the optimal test is the allele-based test employed in the first strategy, we expect no improvement from applying the second strategy. This can be observed for data generated with the multiplicative model in which the allele-based test was almost always the most powerful test.
generated with strategy 1. Other than for the first strategy, the summary statistics depend on sample size and on the underlying genetic model. If the optimal test is the allele-based test employed in the first strategy, we expect no improvement from applying the second strategy. This can be observed for data generated with the multiplicative model in which the allele-based test was almost always the most powerful test.
In contrast, for parameter sets generated with the three-parameter model, the allele-based test is only sometimes optimal. Thus, the required sample size for replication studies designed with the second strategy is about half (38%–59%) of the sample size required under the first strategy. We also observe that the median ratio 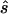 :s is close to 1, and the median normalized difference between the estimated value and the true value is ∼0.2 (0.17–0.24), indicating that sample sizes calculated here are centered on the true required sample size and are reasonably accurate.
:s is close to 1, and the median normalized difference between the estimated value and the true value is ∼0.2 (0.17–0.24), indicating that sample sizes calculated here are centered on the true required sample size and are reasonably accurate.
Finally, for data simulated with the recessive model, the allele-based test is never the best test to use. Thus, use of the second strategy generates replication sample sizes that are lower than the sample sizes generated with the first strategy; in our analysis, we observed that the second strategy required ∼40% of the sample required under the first strategy. However, for penetrance estimates based on small initial sample sizes, the sample size required in the replication study is somewhat underestimated. For sample sizes that are more appropriate for whole-genome association studies, this ratio is close to 1. The median relative difference between the necessary sample size and the estimated sample size is ∼0.24.
Thus, the results suggest that use of the data to inform the design of the replication study is an advantageous strategy. It provides a smaller relative error and a bigger proportion of tests for which we can provide an upper bound for the necessary sample size. Most importantly, it reduces the required number of samples that need to be typed for the replication study while retaining the targeted power.
Data Example
A well-known example of the winner’s curse in practice is the Pro12Ala substitution in PPARγ and its association with type 2 diabetes.12 The first published report of this association was based on a comparison of the frequency of the PPARγ proline homozygote in 91 Japanese Americans affected with type 2 diabetes and 54 healthy controls. The study observed a significantly smaller proportion of proline homozygotes in unaffected individuals (45) than in affected individuals (87). From these data, the authors estimated a 4.35-fold risk that carriers of the Pro/Pro genotype will develop type 2 diabetes. However, among five follow-up studies with sample sizes of 450–1,200 probands, only one study found a significant replication of the result.14–18 A larger follow-up study combined with a meta-analysis of all the previous studies, excluding the initial report, included >3,000 individuals.19 The study did find a significant association of the Pro/Ala polymorphism with type 2 diabetes. However, the meta-analysis estimated the odds ratio of the Pro allele to be 1.25, much lower than the original estimate of 4.35.
We applied the methods described in the present study to the initial PPARγ data,12 to estimate the allele frequency and penetrance parameters and to calculate from those values the odds ratio for the Pro/Pro genotype. We assumed that the association had been found with a test comparing the number of observed Pro/Pro genotypes at a significance level of .05. Furthermore, we set the prevalence of type 2 diabetes in Japanese Americans to the worldwide prevalence of 0.028 (see the work of Wild et al.20). Variation of the disease prevalence between 0.015 and 0.04 changed the estimated penetrance parameters without affecting the odds ratios. Thus, moderate changes in the assumed prevalence do not affect our conclusions.
Without constraining the genetic model, we generated an MLE of 0.049 for the allele frequency and penetrances of 0.0 for Ala/Ala, 0.0265 for Ala/Pro, and 0.0282 for Pro/Pro. From these estimates, we calculated the odds ratio of the Pro/Pro genotype and the odds ratio of the Pro allele (table 2). Furthermore, we calculated the odds ratios for every point in the 95% confidence region to generate CIs. The resulting CIs clearly exclude the naive estimate of 4.35 but are consistent with the odds ratio estimated by Altshuler et al.19 Because of the low counts of heterozygotes and Ala/Ala homozygotes in the sample, the penetrance estimates for those two genotypes were quite variable, and underdominant models, in which the penetrance of Ala/Pro is smaller than the penetrance of Ala/Ala, were included in the confidence region. Thus, the 95% CI of the odds ratios includes values <1. Constraining the penetrance parameters to Pro-recessive models did not affect our conclusions.
Table 2. .
Estimated Odds Ratios of the Pro12Ala Mutation in the PPARγ Gene[Note]
| Data Source | Pro/Pro Odds Ratio (CI) | Pro Odds Ratio (CI) |
| Deeb et al.,12 uncorrected estimate | 4.35 (1.27–14.91) | 4.54 (1.39–14.86) |
| Deeb et al.,12 corrected estimate | 1.09 (.47–2.63) | 1.12 (.39–2.09) |
| Altshuler et al.19 | … | 1.25 (1.11–1.43) |
Note.— The case-control data collected by Deeb et al.12 showed a significant association between the Pro/Pro genotype and type 2 diabetes. From their data, we estimated the odds ratios for both the Pro/Pro genotype and for the proline allele. The first row shows the results without correction for the ascertainment effect, and the second row shows the results obtained for these data with use of our method. The third row provides an estimate of the odds ratio of the proline allele generated from a large meta-analysis.19
On the basis of these estimates, we calculated that a minimum sample size of 2,100 is required to replicate the association, with the assumption of a population frequency of 0.15 of the Ala allele. This is considerably larger than the sample size used by the early and inconsistent replication attempts14–18 but smaller than the sample used in the eventual study and meta-analysis that ultimately provided strong support for the association. Thus, this analysis would have predicted that the initial replication attempts were underpowered.
Discussion
Estimates of the genetic effect of a newly detected variant are confounded by ascertainment. It has been argued that the only way to obtain an unbiased estimate is to generate a second independent sample.6 However, this view is overly pessimistic. As we show here, we can, in fact, obtain corrected estimates that are far less biased than the naive estimates. We have performed extensive testing of the algorithm, conditioning on a uniform distribution of test power to allow us to draw inferences about the impact of sample size without being confounded by the power of the initial study. The results indicate that our algorithm generates an accurate estimate of the penetrance parameters of a disease allele. An independent sample of at least half the size of the initial case-control sample is required to obtain an estimate that is more accurate than the corrected estimate based on the initial sample. The algorithm also provides well-calibrated confidence regions for the penetrance parameters, thus quantifying the uncertainty of each estimate. We have shown that the sample size of the association scan strongly influences the precision of the estimate and the size of the confidence region, independent of the underlying genetic model. Nevertheless, we observed a small bias toward underestimation of the genetic effect that is independent of the sample size. The power of the initial association scan also has a major impact on the size of the confidence region but has only little influence on the precision of the point estimate or on the extent of the negative bias. Thus, we concluded that the sample sizes used in whole-genome association studies will provide sufficient data to generate useful estimates of the penetrance parameters of an allele.
For simplicity, we assumed that the initial test for association is a simple comparison of allele frequencies between cases and controls. Application of the algorithm to any other testing method is generally straightforward, requiring only an efficient way to calculate the power of the initial scan for association conditional on the penetrance and frequency parameters. Although these calculations are usually simple for single-point methods, they may be more complicated for multipoint methods, necessitating the estimation of power by computer simulation.
Furthermore, the estimation procedure also requires a good understanding of the sampling scheme that was used to collect cases and controls. In the results we presented, it was assumed that cases and controls were randomly drawn from affected and unaffected people in a population. In real association studies, this may not be the case; for example, samples are often drawn from patients at one or more medical facilities. However, a model of random sampling serves as a good approximation of this opportunistic ascertainment.21 Extending the algorithm to other sampling designs is possible, although some care should be taken in interpreting the results, as illustrated by the following example. In a commonly used study design, particularly for diseases with late onset age, random members of the population, rather than unaffected individuals, are sampled as the control group. For this type of sample, modification of equation (3) will take into account the fact that the control group provides no information about the penetrance parameters; the rest of the algorithm is unchanged. In general, the algorithm in this work can be applied to any sampling scheme that can be described in a simple statistical model. Problems will arise if the ascertainment strategy is not clearly documented. Especially in meta-analyses, this is likely to be the case. For such data, it may be more fruitful to assess the error in the estimation procedure by simulating different ascertainment strategies or to adopt bootstrap algorithms similar to the ones presented by Sun and Bull.9
A more general problem for estimating genetic risk of association data is that, in practice, the manifestation of a complex disease not only will be governed by the alleles at one locus but will also depend on environmental and genetic covariates. If these covariates are unknown, they cannot be accounted for by the estimation procedure. Thus, we are estimating marginal penetrances, summarizing the effects of other genomic loci and environmental factors on the disease as the penetrance parameters of one allele. If studies are performed in different populations, the frequency of genetic covariates might vary significantly across samples, resulting in very different marginal penetrances. However, this problem is not specific to the described algorithm; as long as we are aware of only a subset of all covariates, we are confined to calculating marginal risks of these known covariates.
This problem can be somewhat alleviated by extending the scheme presented here to estimation of genotype-environmental interaction or the effect of multiple loci at once. By estimating the penetrance of combinations of genotypes, it is possible to calculate an MLE for models of gene-gene or gene-environment interaction. Thus, it is possible to compare the resulting likelihood with the likelihood generated under a model of no interaction. Since the two models are nested, the support for an interaction parameter can be tested by a likelihood-ratio test. Thus, the interaction between an allele and a covariate can be identified and quantified, and the covariate can be controlled for in further studies.
We have also shown that the corrected estimates can be used to calculate the sample size required to replicate a new finding. Although the estimates are biased toward weaker genetic effects, this results in overestimating the required sample size by only 10%. Furthermore, it is possible to quantify the uncertainty in that estimate of the sample size, allowing the researcher to plan the study accordingly. Moreover, we have demonstrated that estimating the set of penetrance parameters provides another major advantage for planning replication studies: based on the three parameters, it is possible to predict what kind of test would be most powerful in the replication study and to design the study accordingly. We have demonstrated that even a rough comparison between simple tests was sufficient to reduce the required sample size significantly.
In summary, we have provided an algorithm that generates estimates of the frequency and penetrances of a variant while correcting for the winner’s curse. Providing these estimates in future publications of association-mapping results should facilitate evaluation of the genetic effect of a variant, the planning of replication studies, and comparison of the results of multiple signals observed in the same region.
Acknowledgments
We thank Graham Coop, Michael Boehnke, Laura Scott, Richard Spielman, and two anonymous reviewers for helpful comments. This work was supported in part by National Institutes of Health grants HG002772 and HL084729. The C program used for the method and simulation studies is available from S.Z. (S.Z.'s Web site).
Appendix A : Power Calculation
Multiple methods exist to calculate the power of a test for association. The most commonly used algorithm uses a normal approximation of the χ2 test statistic (e.g., the work of Pritchard and Przeworski13). This approximation can be imprecise, especially if the resulting power is small (<0.01). Since calculating the likelihood of each parameter point requires a precise calculation of the power, we instead use equation (4), summing over all realizations of the 2×2 table that result in a significant test for association. To speed up computation, we calculate in advance all critical values—cv1(ca) and cv2(ca)—of allele-counts of allele 0 in the unaffected sample (cu) conditional on the allele counts in the affected sample (ca) that result in a significant Pearson's χ2 test, by solving the quadratic equation
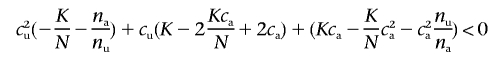 |
for cu, where na is the affected sample size, nu is the unaffected sample size, N=na+nu, and K is the critical value of a χ21 distribution at the appropriate significance level. Using those critical values, we can then calculate the power of the association scan with
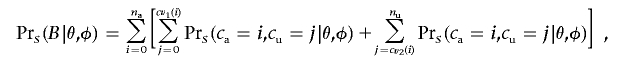 |
where the summed probabilities are calculated using equation (3).
To calculate the sample sizes for replication studies, we used the normal approximation mentioned in the work of Pritchard and Przeworski.13 Under the null hypothesis, the difference
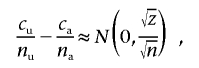 |
with 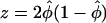 if n=na=nu and
if n=na=nu and 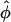 is the frequency of allele 0 in the sample. With qu=Pr(0|U) and qa=Pr(0|A) as the frequency of allele 0 in the unaffected and affected individuals, respectively, the alternative is approximately normally distributed, with expectation μ=qu-qa and variance
is the frequency of allele 0 in the sample. With qu=Pr(0|U) and qa=Pr(0|A) as the frequency of allele 0 in the unaffected and affected individuals, respectively, the alternative is approximately normally distributed, with expectation μ=qu-qa and variance
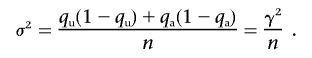 |
With α as the critical value of a standard normal distribution at an appropriate significance level and β as its 20th percentile, we can then calculate the sample size necessary to obtain 0.80 power as
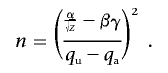 |
Web Resource
The URL for data presented herein is as follows:
- S.Z.'s Web site, http://www.sph.umich.edu/csg/zollner (for supplementary material containing results for additional genetic models, the size of the 95% confidence region for different sample sizes, and results for misspecified disease prevalence)
References
- 1.Hirschhorn JN, Lohmueller K, Byrne E, Hirschhorn K (2002) A comprehensive review of genetic association studies. Genet Med 4:45–61 [DOI] [PubMed] [Google Scholar]
- 2.Lohmueller KE, Pearce CL, Pike M, Lander ES, Hirschhorn JN (2003) Meta-analysis of genetic association studies supports a contribution of common variants to susceptibility to common disease. Nat Genet 33:177–182 10.1038/ng1071 [DOI] [PubMed] [Google Scholar]
- 3.Herbert A, Gerry NP, McQueen MB, Heid IM, Pfeufer A, Illig T, Wichmann HE, Meitinger T, Hunter D, Hu FB, et al (2006) A common genetic variant is associated with adult and childhood obesity. Science 312:279–283 10.1126/science.1124779 [DOI] [PubMed] [Google Scholar]
- 4.Edwards AO, Ritter R, Abel JK, Manning A, Panhuysen C, Farrer LA (2005) Complement factor H polymorphism and age-related macular degeneration. Science 308:421–424 10.1126/science.1110189 [DOI] [PubMed] [Google Scholar]
- 5.Capen EC, Clapp RV, Campbell WM (1971) Competitive bidding in high-risk situations. J Petrol Technol 23:641–653 [Google Scholar]
- 6.Göring HHH, Terwilliger JD, Blangero J (2001) Large upward bias in estimation of locus-specific effects from genomewide scans. Am J Hum Genet 69:1357–1369 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Allison DB, Fernandez JR, Heo M, Zhu S, Etzel C, Beasley TM, Amos CI (2002) Bias in estimates of quantitative-trait–locus effect in genome scans: demonstration of the phenomenon and a method-of-moments procedure for reducing bias. Am J Hum Genet 70:575–585 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Siegmund D (2002) Upward bias in estimation of genetic effects. Am J Hum Genet 71:1183–1188 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sun L, Bull SB (2005) Reduction of selection bias in genomewide studies by resampling. Genet Epidemiol 28:352–367 10.1002/gepi.20068 [DOI] [PubMed] [Google Scholar]
- 10.Van Steen K, McQueen MB, Herbert A, Raby B, Lyon H, DeMeo DL, Murphy A, Su J, Datta S, Rosenow C, et al (2005) Genomic screening and replication using the same data set in family-based association testing. Nat Genet 37:683–691 10.1038/ng1582 [DOI] [PubMed] [Google Scholar]
- 11.Risch N, Merikangas K (1996) The future of genetic studies of complex human diseases. Science 273:1516–1517 10.1126/science.273.5281.1516 [DOI] [PubMed] [Google Scholar]
- 12.Deeb SS, Fajas L, Nemoto M, Pihlajamäki J, Mykkänen L, Kuusisto J, Laakso M, Fujimoto W, Auwerx J (1998) A Pro12Ala substitution in PPARγ2 associated with decreased receptor activity, lower body mass index and improved insulin sensitivity. Nat Genet 20:284–287 10.1038/3099 [DOI] [PubMed] [Google Scholar]
- 13.Pritchard JK, Przeworski M (2001) Linkage disequilibrium in humans: models and data. Am J Hum Genet 69:1–14 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Clement K, Hercberg S, Passinge B, Galan P, Varroud-Vial M, Shuldiner AR, Beamer BA, Charpentier G, Guy-Grand B, Froguel P, et al (2000) The Pro112Gln and Pro12Ala PPARγ mutations in obesity and type 2 diabetes. Int J Obes Relat Metab Disord 24:391–393 10.1038/sj.ijo.0801191 [DOI] [PubMed] [Google Scholar]
- 15.Hara K, Okada T, Tobe K, Yasuda K, Mori Y, Kadowaki H, Hagura R, Akanuma Y, Kimura S, Ito C, et al (2000) The Pro12Ala polymorphism in PPARγ2 may confer resistance to type 2 diabetes. Biochem Biophys Res Commun 271:212–216 10.1006/bbrc.2000.2605 [DOI] [PubMed] [Google Scholar]
- 16.Mancini FP, Vaccaro O, Sabatino L, Tufano A, Rivellese AA, Riccardi G, Colantuoni V (1999) Pro12Ala substitution in the peroxisome profilerator activated receptor-γ2 is not associated with type 2 diabetes. Diabetes 48:1466–1468 10.2337/diabetes.48.7.1466 [DOI] [PubMed] [Google Scholar]
- 17.Meirhaeghe A, Fajas L, Helbecque N, Cottel D, Auwerx J, Deeb SS, Amouyel P (2000) Impact of the peroxisome profilerator activated receptor γ2 Pro12Ala polymorphism on adiposity, lipids and non-insulin-dependent diabetes mellitus. Int J Obes Relat Metab Disord 24:195–199 10.1038/sj.ijo.0801112 [DOI] [PubMed] [Google Scholar]
- 18.Ringel J, Engli S, Distler A, Sharma AM (1999) Pro12Ala missense mutation of the peroxisome profilerator activated receptor γ and diabetes mellitus. Biochem Biophys Res Commun 254:450–453 10.1006/bbrc.1998.9962 [DOI] [PubMed] [Google Scholar]
- 19.Altshuler D, Hirschhorn JN, Klannemark M, Lindgren CM, Vohl CM, Nemesh J, Lane CR, Schaffner SF, Bolk S, Brewer C et al (2000) The common PPARγPro12Ala12 polymorphism is associated with decreased risk of type 2 diabetes. Nat Genet 26:76–80 10.1038/79839 [DOI] [PubMed] [Google Scholar]
- 20.Wild S, Roglic G, Green A, Sicree R, King H (2004) Global prevalence of diabetes: estimates for the year 2000 and projections for 2030. Diabetes Care 27:1047–1053 10.2337/diacare.27.5.1047 [DOI] [PubMed] [Google Scholar]
- 21.Voight B, Pritchard JK (2005) Confounding from cryptic relatedness in case-control association studies. PLoS Genet 1:e32 10.1371/journal.pgen.0010032 [DOI] [PMC free article] [PubMed] [Google Scholar]