Abstract
The parameters of the immune response dynamics are usually estimated by the use of deterministic ordinary differential equations that relate data trends to parameter values. Since the physical basis of the response is stochastic, we are investigating the intensity of the data fluctuations resulting from the intrinsic response stochasticity, the so-called process noise. Dealing with the CD8+ T-cell responses of virus-infected mice, we find that the process noise influence cannot be neglected and we propose a parameter estimation approach that includes the process noise stochastic fluctuations. We show that the variations in data can be explained completely by the process noise. This explanation is an alternative to the one resulting from standard modeling approaches which say that the difference among individual immune responses is the consequence of the difference in parameter values.
INTRODUCTION
Mathematical modeling of immunological data is a very powerful tool for understanding the immune system dynamics. In this article we discuss attempts to understand immune response dynamics based on deterministic ordinary differential equation (ODE) models that are widely used in literature (1–4). The immune response is the result of a large amount of interactions among individual cells. Therefore, there exists a structural similarity of the immune response models to the mass-action law model of chemical reactions (5).
The physical basis of chemical reactions is stochastic. The reaction takes place when randomly moving particles are in such a close distance that interparticle forces become dominant. It seems reasonable to say that intercellular interactions have the same stochastic nature. In the limiting case of a large volume containing a large amount of chemical molecules involved in the interactions, the concentration fluctuations due to the process stochasticity, so-called process noise (6), can be neglected (7,8). Taking into account the usual setup for chemical reactions, and the fact that the amounts have the order of 1023 molecules, the good agreement of ODE models with experiment outcomes is to be expected. However, molecular amounts are a lot larger than the amounts of cells observed in immunological data. Hence, we can expect that the process noise of immunological reactions is more important (9). This is also the reason for an increasing number of efforts similar to the stochastic simulation of the immune response presented in Chao et al. (10).
The parameter estimation of stochastic immunological processes is usually based on ODE models that are fitted to the data. The stochastic fluctuations of the observed data are treated as the result of measurement errors. The relation of the fluctuation intensity, and the course of its intensity change with the process parameters is beyond the scope of these ODE-based treatments. In other words, the intrinsic fluctuation due to the process noise, resulting from the stochastic nature of intercellular interactions, is neglected when deterministic ODE models are fitted to data.
In this article we investigate the influence of the process noise on data. In the case that the process noise intensity cannot be neglected, there are at least two important consequences. First, commonly used parameter estimation procedures, based on ODE models relating only trends to the parameter estimation, fail to process the information about observed stochastic data variations, and also fail to incorporate them into the parameter estimation. Second, the process noise can be one explanation for the variations in cell amounts, or viral loads, among infected individuals. This explanation is an alternative to the explanation originating from ODE modeling approaches where the difference among immune responses is explained by differences in the parameters (3).
Here, we deal with the CD8+ T-cell response to the lymphocytic choriomeningitis virus (LCMV) infection, in sequel text, the LCMV data. In our analysis, we consider a model in which the expected amount of cells is assumed to be large and, in which important spatial components of the cell movement and the cell-cell interaction via chemical signals (11,12) are neglected. The same simplifications are used to justify deterministic ODE models. However, the type of modeling regime (13) we consider here is continuous and stochastic. From the available data, we intentionally select the data that seem particularly well fitted by a deterministic ODE-based model. Regardless of that, our analysis shows not only that the process noise should not be neglected, but that it may be considered as the dominant source of stochastic data variations. A detailed discussion about different types of modeling regimes for understanding biochemical reactions is provided in Turner et al.(13).
The “Dynamical hypothesis of the LCMV CD8+ response” section explains, in short, the source of the data, the biphasic hypothesis of the CD8+ T-cell response after LCMV infection, its parameters, and the ODE description. In the “Measurement Noise” section, we discuss the data-fitting procedure based on the assumption of measurement error models. We find that the fluctuations in the LCMV data can be described only if the intensity of the measurement error is large. Using stochastic simulations, in the “Process noise” section, we show that the fluctuation intensity can be partly ascribed to the process noise. The section entitled “Probability density functions of the cell amounts” deals with an analytical approach to modeling the stochasticity in the LCMV data. We use the maximum likelihood method to fit the stochastic biphasic model of the LCMV data in the section “Parameter estimation based on measurement and process noise models”, and the final section provides the conclusions.
DYNAMICAL HYPOTHESIS OF THE LCMV CD8+ RESPONSE
In the experiments (14) a group of mice is simultaneously infected by the LCMV. In the subsequent time intervals, the spleens of three to four mice are removed, and the amounts of different types of CD4+ and CD8+ cells, specific for the particular epitopes of the virus, are counted. The averages of these three to four mice are the data points we are dealing with. For each data point three to four new mice are used. In this article, we have decided to model gp33 CD8+ data, because it seems that they are already well described by the deterministic biphasic ODE model (1). Due to the absence of an exact number of mice used for each data point, that is three or four, in the rest of the article we assume that all the data points are obtained from three mice.
The hypothesis that is explored in this article is the one proposed for the T-cell dynamics of LCMV-infected mice (1). Under this hypothesis, there are two types of T cells, so-called effector and memory cells. In sequel text, the amount of effector and memory cells will be denoted by A and M, respectively. Moreover, this model proposes that the T-cell exponential proliferation starts with the delay Ton after the infection (1). Then, the change of T-cell amount can be divided into two phases.
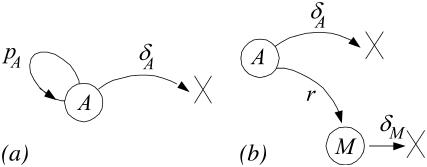
The first phase is the expansion phase that starts at the time Ton, during which T-cells proliferate at a rate pA starting from a small amount of precursor cells A(Ton), and simultaneously die at a rate δA. This phase is depicted in Fig. 1 a. If the length of this phase is T − Ton, the corresponding ODE of this phase is:
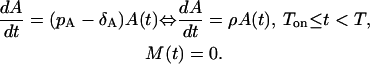 |
(1) |
FIGURE 1.
Hypothesis of CD8+ T-cell response. (a) The expansion phase and (b) the contraction phase. A, effector cells; M, memory cells; pA, proliferation rate of effector cells; δA, death rate of effector cells; r, recruitment rate of effector to memory cells; δM, death rate of memory cells.
Obviously, the model assumes that there are no memory cells in the expansion phase. In these equations, we introduce the parameter ρ for the net proliferation rate that is used in the previous work (1). The net proliferation rate is the difference between the proliferation pA and the death rate δA, i.e.,
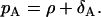 |
(2) |
The equivalence introduced in Eq. 1 says that the stochastic process of the simultaneous proliferation (pA) and death (δA) of the cells has the same ODE description as the stochastic proliferation process with the net rate ρ. This does not mean that these two stochastic processes are equivalent. For example, it can be shown that they have different variances (see Appendix I). However, if the proliferation rate pA is much higher than δA, then pA ≈ ρ, and in this extreme case, the two stochastic processes may be considered equivalent.
The second phase is the contraction phase, during which the pool of memory cells M is recruited from the pool of effector cells A at the rate r. During this phase, the effector and memory cells die at rates δA and δM, respectively. The stochastic process of the second phase is described in Fig. 1 b, and the corresponding ODE model is:
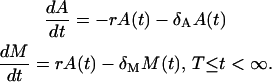 |
(3) |
Both of the phases are described by the linear differential equations, i.e., the presented model has a piecewise linear structure. To obtain the model parameters, the model has to be fitted to the data. Since in the experiment the amount of the effector and memory cells cannot be distinguished, the data fit is based on the total cell amount
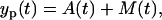 |
(4) |
where the index p stands for the ODE model prediction given the parameters.
Due to the deterministic nature of the model in Eqs. 1–3, it is possible to estimate the proliferation and death rates without estimating the delay Ton and the cell amount A(Ton). In the previous work (1), these parameters are incorporated into a single parameter A(0) assuming that the proliferation starts without any delay at t = 0. This possibility is welcome, because the first data point is obtained at t1 = 4 days; i.e., the T-cell amount dynamics before t1 is not observed. The parameter A(0) is the result of the mathematical simplification and it is interpreted as a generalized recruitment parameter (1). The estimated A(0) values (1) are smaller than directly estimated precursor T-cell amount (15). This indicates that the T-cell amount dynamics between the antigen injection t = 0 and the first data point collection t = t1 is more complex than the one described by Eq. 1 and Ton = 0.
Measurement noise
It is a common practice in immunology that the model parameters are obtained from the successful least-square fit of the model to the data (LSLIN) or to the log-transformed data (LSLOG). Here, we discuss widely accepted opinion that LSLOG data fit is more appropriate for the immunological data collected from an exponentially proliferating cell population, such as the one we are dealing with in this article. However, we will show that the assumption of the optimality of the LSLOG data fit leads to a large measurement error estimation.
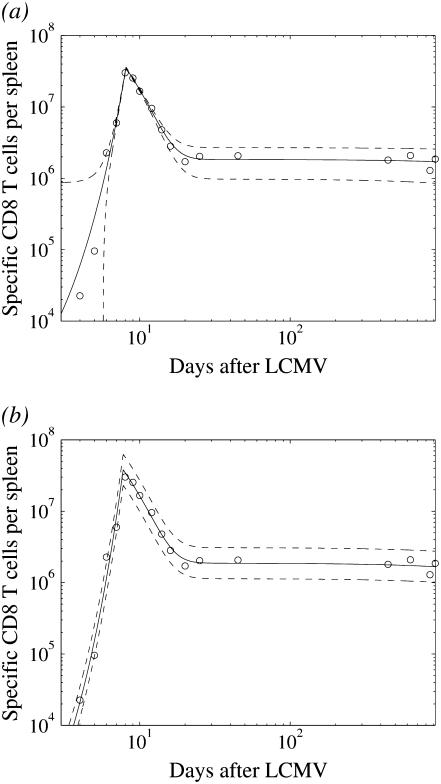
Fig. 2 shows the LSLIN and the LSLOG fit of the data using the same deterministic biphasic model given by Eqs. 1 and 3. In both cases, the model prediction (solid line) is close to the data points after the time T. It seems that the LSLIN data fit is less precise because of the large residuals for small values of the cell amount. However, these residuals are a few orders of magnitude smaller in comparison to the residuals of the LSLOG fit for large values around the time T. The quality difference of the two fits is not clear, unless the model for measurement errors is considered.
FIGURE 2.
The least-square (LS) data fit of the ODE biphasic model. (a) LS fit of data (LSLIN), two standand deviation band for Θa = 1.8 × 1011 (dashed). (b) LS fit of log-transformed data (LSLOG), two standand deviation band for Θm = 0.064 (dashed).
Unfortunately, the model for measurement errors is not provided, and we start our analysis with the hypothesis that the parameter estimation based on the LSLIN data fit is optimal in least-square (LS) and maximum-likelihood (ML) sense. This hypothesis means that the measurement error model is:
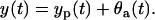 |
(5) |
In this model y(t) is the measurement, yp(t) is the ODE model prediction, which is equal to the expected measurement value 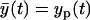 , and θa(t) is the error. This error is a zero-mean, Gaussian random variable with the constant variance Θa and uncorrelated in time (white random sequence). In sequel, due to its form, we will name this measurement error model “additive”.
, and θa(t) is the error. This error is a zero-mean, Gaussian random variable with the constant variance Θa and uncorrelated in time (white random sequence). In sequel, due to its form, we will name this measurement error model “additive”.
The variance Θa can be estimated from the LSLIN data fit as the mean of the square of residuals
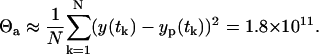 |
(6) |
Based on the measurement error assumption, 95% of the data must be in the two standand deviation band of the error around the model prediction yp(t). The lower 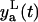 and the upper
and the upper 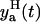 limits of this band are
limits of this band are
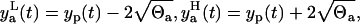 |
(7) |
and this band is plotted in Fig. 2 a. Because we have 17 data points, we expect one data point outside the band (17 × 0.95 ≈ 16). Indeed, by careful inspection, we find one point, the third from the left, outside the band. This indicates that our data can be explained by the deterministic model, Eqs. 1–3, and the additive measurement error model, Eq. 5. However, the standard deviation of the error is 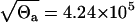 , and we can see from Fig. 2 a that large errors may be expected even though the expected amount of cells yp(t) is of one order of magnitude smaller. Thus, unrealistically, the measurement y(t) given by Eq. 5 may be negative. This is the reason to discard the LSLIN data fit from our further consideration, although most of the estimated parameter values (A(0) = 119.5, ρ = 1.55, r = 0.021, δA = 0.38, δM = 0.1 × 10−3, T = 8.1) are similar to the previous parameter estimates (1). Naturally, one can propose the additive error model where the variance of the error scales with yp(t), but then the LSLIN data fit would not be optimal in LS and ML sense.
, and we can see from Fig. 2 a that large errors may be expected even though the expected amount of cells yp(t) is of one order of magnitude smaller. Thus, unrealistically, the measurement y(t) given by Eq. 5 may be negative. This is the reason to discard the LSLIN data fit from our further consideration, although most of the estimated parameter values (A(0) = 119.5, ρ = 1.55, r = 0.021, δA = 0.38, δM = 0.1 × 10−3, T = 8.1) are similar to the previous parameter estimates (1). Naturally, one can propose the additive error model where the variance of the error scales with yp(t), but then the LSLIN data fit would not be optimal in LS and ML sense.
Now, we will assume the hypothesis that the LSLOG data fit parameter estimation is optimal in LS and ML sense. This hypothesis means that the measurement error model is:
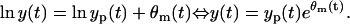 |
(8) |
The error θm(t) is again a zero-mean, Gaussian variable with the constant variance Θm(t) and uncorrelated in the time. The parameters obtained from the LSLOG data fit are listed in Table 1 together with the 95% confidence intervals (C.I.) computed by the bootstrap method (16). The values for the bootstrap method are generated using the model in Eq. 8; yp(t) is computed for the estimated parameters (Table 1) and θm(t) is generated from the Gaussian random number generator with the variance Θm estimated from the data fit as
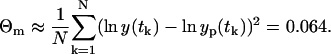 |
(9) |
TABLE 1.
The parameter estimations: LSLOG, from the LS data fit of the log-transformed data; ML, from the maximum-likelihood data fit that includes the process noise and the measurement error model; Lit, from the literature (1)
| LSLOG
|
ML
|
Lit
|
||||
|---|---|---|---|---|---|---|
| Value | 95% C.I. | Value | 95% C.I. | Value | 95% C.I. | |
| A(0) | 7.31 | 4.9–12.7 | – | – | 12.1 | 3.3–32.5 |
| pA | 2.38* | 2.29*–2.46* | 2.53 | 2.23–2.70 | 2.29* | – |
| ρ | 1.99 | 1.91–2.06 | 2.14* | 1.96*–2.28* | 1.89 | 1.73–2.08 |
| δA | 0.39 | 0.35–0.43 | 0.39 | 0.31–0.49 | 0.40 | 0.34–0.47 |
| r | 0.020 | 0.018–0.023 | 0.018 | 0.014–0.026 | 0.018 | 0.015–0.022 |
| δM(10−3) | 0.13 | 0–0.28 | 0.09 | 0–0.53 | 0 | – |
| T0 | 7.77 | 7.69–7.86 | 7.51 | 7.32–7.68 | 7.9 | 7.8–8.1 |
The parameters marked with * are computed based on the relation pA = ρ + δA. The 95% confidence intervals (C.I.) are computed using 500 runs for the bootstrap method (16).
Under hypothesis of Eq. 8, 95% of the data will be in the band, around the model prediction yp(t), that corresponds to the two standard deviation range of the error θm(t). The lower 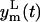 and the upper
and the upper 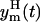 limits of this band are
limits of this band are
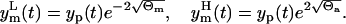 |
(10) |
This band is plotted in Fig. 2 b and we can discover again the same point, the third from the left, outside the band. This agrees with our expectation and indicates that the observation model in Eq. 8 and the LSLOG data fit might be appropriate for our data. Considering a small value for Θm, such as one estimated in Eq. 9, and applying the Taylor expansion, we can find from Eq. 8
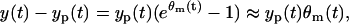 |
(11) |
or, in other words, the observation model in Eq. 8 is equivalent to the following observation model
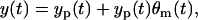 |
(12) |
in which the intensity of the measurement error scales with yp(t), and the error variance is 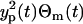 . Due to the scaling form, this measurement error model is, so-called, “multiplicative”. Moreover, the error θm(t) can be considered as the relative measurement error since
. Due to the scaling form, this measurement error model is, so-called, “multiplicative”. Moreover, the error θm(t) can be considered as the relative measurement error since
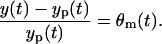 |
(13) |
The estimated variance Θm = 0.064 corresponds to the relative standard error of 25% (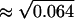 ). This level of the error seems acceptable and we confirm that the measurement model in Eq. 8, i.e., multiplicative model, and the LSLOG data fit are more adequate to our data than the additive model of Eq. 5 and the LSLIN data fit.
). This level of the error seems acceptable and we confirm that the measurement model in Eq. 8, i.e., multiplicative model, and the LSLOG data fit are more adequate to our data than the additive model of Eq. 5 and the LSLIN data fit.
However, we should bear in mind that the estimated standard error relates to the error intensity in the measurements that are the averages of three measurements. To estimate the variance of the cell amount of an individual measurement, the variance Θm = 0.064 must be multiplied by three. Then, the standard error of one measurement is 44% (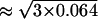 ). Now, is it possible that during one experiment we lose or gain nearly half of the cells? The arguments for supporting this large error lie in the fact that the cells are counted after an extensive mouse surgery. On the other hand, the organs are taken from the mouse completely and it is not clear how nearly 50% of the cells can be gained or lost.
). Now, is it possible that during one experiment we lose or gain nearly half of the cells? The arguments for supporting this large error lie in the fact that the cells are counted after an extensive mouse surgery. On the other hand, the organs are taken from the mouse completely and it is not clear how nearly 50% of the cells can be gained or lost.
Based on the large intensity of the estimated measurement errors, we conclude that none of the two presented fits can be appropriate. The reason for that can be found in the incorrect error model, as well as in an incorrect biphasic ODE model. Instead of trying to find and justify refined models, we will estimate the intensity of the other source of stochastic fluctuations that interferes with measurement errors in producing an erratic behavior of experimental data.
Process noise
Having in mind the stochastic nature of the immune response, the underlying assumption of the presented data fits is that the outcome of the stochastic process can be approximated by ODEs, and that all stochastic fluctuations can be assigned to measurement errors. However, the ODE approximation for the cell amount may be valid only for a cell amount large enough so that the intensity of intrinsic process fluctuations, i.e., the process noise, can be neglected. In this section, we use the stochastic simulations to illustrate the intensity of the fluctuations, which might be expected due to the process noise. It is worth mentioning that the process noise would be responsible for the stochastic outcome of experimental measurements even if we make error-free measurements.
The stochastic nature of the biphasic hypothesis for the CD8+ T-cell response can be precisely described using the master equation (5). In our case, the master equation describes the time increase of the probability of A number of effector cells and M number of memory cells, where A and M are integers.
The master equation for the expansion phase is
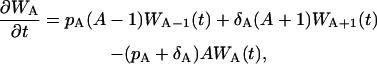 |
(14) |
where WA(t) is the probability of A effector cells at time t, and the rates pA and δA are the same as in the ODE description, Eq. 1. This master equation does not include the probability of memory cell amount M, because it is a constant value, i.e., M = 0.
At the time T, the second phase takes place and the master equation for this phase is
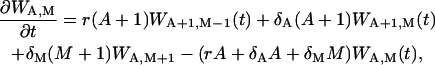 |
(15) |
where WA,M(t) is the probability of A effector cells and M memory cells at the time t; the rates of recruitment r, the death rate of effector cells δA, and the death rate of memory cells δM are the same as in ODE description, Eq. 3. As we can see, the master equation describes the changes of the joint probability WA,M because A and M change simultaneously.
To illustrate the process noise influence on the LCMV data, we use Gillespie's (17) simulation that produces a result equivalent to the stochastic processes described by Eqs. 14 and 15. Each run of the simulation predicts the cell amount in one mouse. These values would be measured in the mouse in the absence of measurement errors.
Ideally, the simulations should start at the time Ton ≠ 0, with the initial value A(Ton) and the corresponding initial variance of the T-cell amount. However, all these parameters are unknown. As we use simulations only as an illustration, we run the simulations with Ton = 0 and use the parameters and the initial condition A(0) estimated by the LSLOG data fit (Table 1). We also do not assume any uncertainty in the initial condition A(0). Moreover, in the expansion phase, we considered pA = ρ (Table 1) and δA = 0. This process has a smaller variance of the realization than the one resulting from the assumption of Eq. 2, where δA ≠ 0, and provides us the minimal process noise intensity estimation based on the LSLOG data fit estimated parameters (Table 1).
We find that the original Gillespie's algorithm appears to be very slow when the amount of cells reaches the order of 107. Therefore, we use the faster modification of this algorithm, so-called τ-leap (18), with the fixed time step τ. We take the time step τ = 0.01 so that the following condition (18) is satisfied (see Appendix II)
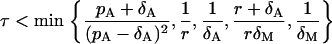 |
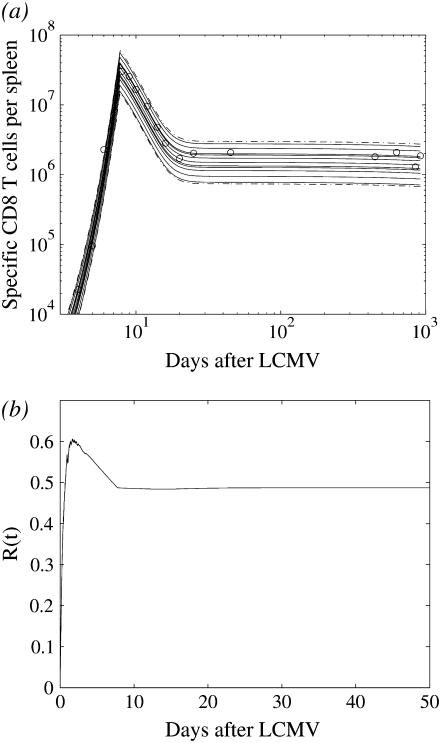
The result of 500 runs of the simulation is summarized in Fig. 3 a. This figure shows that even though the same initial value and parameters are used, the cell amount is different over the different runs. We can also notice that the trajectories look as if they were the solutions of the deterministic ODE model with the different parameters or initial conditions. The variance of trajectories ΞG(t), computed at each time instant t, is the variance resulting from the process noise. The LCMV data are the averages of the T-cell amount observed in the spleen of three mice. Hence, the fluctuations in the data originating from the process noise will have the variance Ξ(t), given by
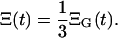 |
(16) |
FIGURE 3.
Stochastic simulations of the acute response. (a) Ten simulation runs, each corresponding to the amount of CD8+ T cells in the spleen of one mouse (solid), 95% interval for the cell amount resulting from the 500 simulation runs (dashed). (b) R(t) is the ratio between the variance estimated from the 500 simulation runs and the variance estimated from the data.
Finally, we can compute the ratio R(t)
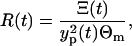 |
(17) |
that is the ratio between the estimated variance resulting from the process noise and the total variance of the data fluctuations, estimated as the variance of the measurement errors as 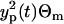 , with Θm = 0.064. The ratio is plotted in Fig. 3 b and changes in the range between 0 and 0.6. We can say that, in average, 0.5 of the total variance originates from the process noise. The variance resulting from the process noise is not a negligible part of the variance of the data estimated from the data fit.
, with Θm = 0.064. The ratio is plotted in Fig. 3 b and changes in the range between 0 and 0.6. We can say that, in average, 0.5 of the total variance originates from the process noise. The variance resulting from the process noise is not a negligible part of the variance of the data estimated from the data fit.
The simulation runs with Ton = 0 possibly lead to overestimated influence of the process noise on the data. However, despite this possibility, the results of this section illustrate that the variance resulting from the process noise cannot be a priori neglected. In other words, the process noise intensity analysis must be included in data-based parameter estimation.
Probability density functions of the cell amounts
When including the process noise into data fitting, we face the problem of estimating the distribution of effector and memory cell amounts in the absence of the measurement errors. A large number of the Gillespie's simulations, explained in the previous section, is certainly one way to do that, but the number of runs and the amount of computations for estimating the distributions make this approach unfeasible for the use in iterative optimization numerical schemes for optimal data fits, i.e., parameter estimations. In this section, we will show approximations that can be used to estimate the distribution of the data resulting exclusively from the process noise of the biphasic immune response hypothesis.
We already explain in the previous section that the beginning of the proliferation phase is possibly governed by a more complex mechanism than the one described by Eq. 14. We include this in our analysis assuming that the proliferation phase is described by Eq. 14, but only after the time point when the first data point is sampled (t1 = 4 days). As a result, we will estimate from the data both the expected cell amount and its variance at the time t1. Naturally, in any further attempt to reveal the complex dynamics of the early moments of the proliferation phase before t1, the result of that dynamics must agree with the estimates of the cell amount and the corresponding variance at the time t1.
The starting point for the approximation are the master equations, Eqs. 14 and 15. In the rest of this article, A(t) and M(t) will be reserved for the cell amounts resulting from stochastic processes. Using the system size expansion (8) (see Appendix I), we can derive the following Langevin equation for the first phase:
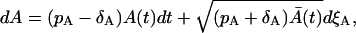 |
(18) |
where 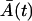 is the solution of the deterministic ODE, Eq. 1, given the initial condition
is the solution of the deterministic ODE, Eq. 1, given the initial condition 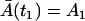 , and ξA is the Wiener process. Similarly, the Langevin equation for the second phase is given by
, and ξA is the Wiener process. Similarly, the Langevin equation for the second phase is given by
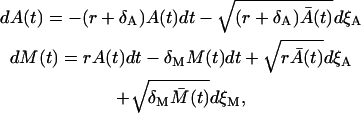 |
(19) |
where 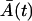 and
and 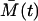 are the solutions of deterministic ODEs in Eq. 3 for the initial conditions
are the solutions of deterministic ODEs in Eq. 3 for the initial conditions 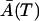 , computed at the last point of the first phase, and
, computed at the last point of the first phase, and 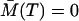 . The ξA and ξM are the independent Wiener processes. Equations 18 and 19 are, so-called, linear Îto stochastic differential equations and their solutions are Gaussian random variables (6). The distribution of the cell amounts in the first phase is
. The ξA and ξM are the independent Wiener processes. Equations 18 and 19 are, so-called, linear Îto stochastic differential equations and their solutions are Gaussian random variables (6). The distribution of the cell amounts in the first phase is
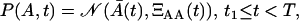 |
(20) |
where ΞAA(t) is the variance of A(t). Naturally, in the expansion phase, the cell distribution is given only by P(A, t), since M = 0. In the contraction phase, the cell distribution is given by Gaussian joint probability density function of A and M
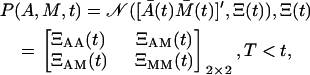 |
(21) |
where ′ denotes the vector transposition, and Ξ(t) is the 2 × 2 covariance matrix.
We should notice that the second-order moments in the probability density functions P(A, t) and P(A, M, t) are dependent on time. The application of the Îto calculus (6) to Eqs. 18 and 19 leads to the following set of ordinary differential equations for t1 ≤ t < T
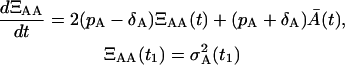 |
(22) |
and for T < t, using ΞMM(T) = ΞAM(T) = 0,
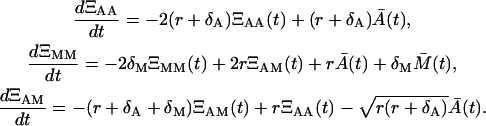 |
(23) |
Naturally, the initial condition ΞAA(t1) has to be specified and it is the variance of the initial condition A(t1) denoted as 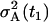 . There is no need to specify the initial condition ΞAA(T), since it results from the solution of Eq. 22. Similarly, due to the zero memory cells all along the time from 0 until T, we have ΞMM(T) = ΞAM(T) = 0.
. There is no need to specify the initial condition ΞAA(T), since it results from the solution of Eq. 22. Similarly, due to the zero memory cells all along the time from 0 until T, we have ΞMM(T) = ΞAM(T) = 0.
The Langevin Eqs. 18 and 19 have the same structure as would be obtained in the corresponding chemical Langevin equation (19) resulting from the second-order truncated Kramer-Moyal equation (5). The only difference is that the random process intensities depend on the expected values 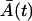 and
and 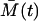 , whereas in the chemical Langevin equation they would depend on the stochastically fluctuating A(t) and M(t).
, whereas in the chemical Langevin equation they would depend on the stochastically fluctuating A(t) and M(t).
The validity and the precision of the approximation types, Eqs. 18 and 19, are limited and their comparison with the chemical Langevin equation is discussed in Gillespie (19). Some of the basic requirements are that the expected amount of cells has to be large, and multiple steady states are not allowed. In our case, the first requirement is fulfilled only approximately, whereas the second is fulfilled completely. This is because immediately after the time T, the expected amount of the memory cells 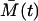 is small. However, the small value of M(t) can hardly influence the Gaussian distribution of the total cell amount A(t) + M(t), since A(t) is large. Moreover, due to the large A(T), shortly after the time T, the amount of the memory cells M(t) quickly increases and has a Gaussian distribution. Similarly, all the effector cells are ultimately recruited to the memory stage, or they die, and just before this happens to the last cells, the expected amount
is small. However, the small value of M(t) can hardly influence the Gaussian distribution of the total cell amount A(t) + M(t), since A(t) is large. Moreover, due to the large A(T), shortly after the time T, the amount of the memory cells M(t) quickly increases and has a Gaussian distribution. Similarly, all the effector cells are ultimately recruited to the memory stage, or they die, and just before this happens to the last cells, the expected amount 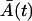 is small. Simultaneously,
is small. Simultaneously, 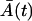 is small in comparison to the amount of the memory cells M(t), hence A(t) can hardly influence the Gaussian distribution of the total cell amount. Based on this reasoning, the previous LSLOG fit and Gillespie's simulation, we are expecting Gaussian distribution of the total cell amount. Thus, in our case, we consider the Langevin equation approximations, introduced in this section, as acceptable for computing the mean value and the variance of the total cell amount.
is small in comparison to the amount of the memory cells M(t), hence A(t) can hardly influence the Gaussian distribution of the total cell amount. Based on this reasoning, the previous LSLOG fit and Gillespie's simulation, we are expecting Gaussian distribution of the total cell amount. Thus, in our case, we consider the Langevin equation approximations, introduced in this section, as acceptable for computing the mean value and the variance of the total cell amount.
Parameter estimation based on measurement and process noise models
In this section, we will exploit the ability to predict the probability density functions (PDFs) of effector and memory cells to estimate the parameters of the model introduced in Section 2. Of course, to do the parameter estimation we should also have a model of the measurement error. Only in that case, can we match the predicted PDFs resulting from the process noise to the measured data.
Let us assume that the measurement error is also Gaussian. Because the predicted PDFs from the previous section are Gaussian, the PDF of a single measurement will also be Gaussian. In the LCMV infection data each data point is an average of three individual independent samples. Therefore, the probability, or likelihood, of observing the sequence of {y(t1), y(t2), …y(tK)} data is
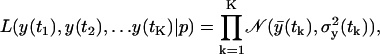 |
(24) |
where p denotes the vector of the parameters that appear in the expressions for expected value of the measurement at the time tk, 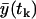 , and for the variance at the same time
, and for the variance at the same time 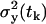 .
.
For the lack of the measurement error model, we consider the multiplicative measurement error model with the constant variance Θm, as it is described in the section “Measurement noise”, Eq. 12. However, here we consider the stochastic model prediction yp(t) = A(t) + M(t), where A(t) and M(t) are described by the master equations (Eqs. 14 and 15) and are approximated by the Langevin equations (Eqs. 18 and 19). In this way, the variance Θm corresponds to a single measurement error. Due to the Gaussian assumption, the expected value of the measurement at the time tk is
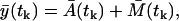 |
(25) |
and the variance is 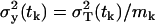 . The factor 1/mk results from the fact that we are predicting the variance of the data samples, which are the averages of mk independent measurements, in our case, mk = 3. The total variance of a measurement from a single mouse
. The factor 1/mk results from the fact that we are predicting the variance of the data samples, which are the averages of mk independent measurements, in our case, mk = 3. The total variance of a measurement from a single mouse 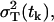 based on Eqs. 22 and 23 and the multiplicative measurement error model, is
based on Eqs. 22 and 23 and the multiplicative measurement error model, is
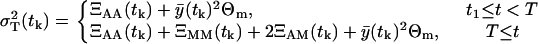 |
(26) |
We should notice that the expected values 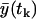 and the variances
and the variances 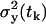 depend on the rates and T introduced in the section entitled “Dynamical hypothesis of the LCMV CD8+ response”, as well as on the initial condition for the expected cell amount
depend on the rates and T introduced in the section entitled “Dynamical hypothesis of the LCMV CD8+ response”, as well as on the initial condition for the expected cell amount 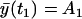 , the variance of the cell amount
, the variance of the cell amount 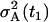 , and the measurement noise variance Θm. In the absence of any other constraints, all these values must be estimated from the data.
, and the measurement noise variance Θm. In the absence of any other constraints, all these values must be estimated from the data.
We perform a maximum-likelihood parameter estimation, after applying the logarithm to Eq. 24 and under the Gaussian measurement error assumption, equivalent to
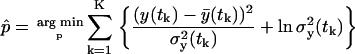 |
(27) |
In all the parameter estimations discussed below, we exploit the parameter values obtained from the LSLOG data fit (see Table 1) to set the initial values for the cost function minimization of Eq. 27. The initial values of the parameters r, δA, δM, T are the same as those obtained from the LSLOG data fit. The initial value for the parameter pA is pA = ρ − δA, where ρ is also the result of the estimation based on the LSLOG data fit. Moreover, we assume that the relative error of a single measurement with the variance 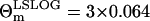 , estimated from the LSLOG data fit, is a good initial estimation for the total variance observed in the data. Along this reasoning, instead of having to deal with
, estimated from the LSLOG data fit, is a good initial estimation for the total variance observed in the data. Along this reasoning, instead of having to deal with 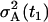 and Θm, we use R(t1) and RT resulting from the parameterization
and Θm, we use R(t1) and RT resulting from the parameterization
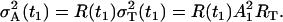 |
(28) |
The parameter R(t1) denotes the fraction of the total variance 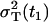 at the time t1, and the parameter RT defines the intensity of the total variance
at the time t1, and the parameter RT defines the intensity of the total variance 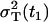 relative to
relative to 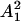 , square of the expected amount of the cells at t1. Naturally, the rest of the total variance is assigned to the multiplicative measurement error, i.e.,
, square of the expected amount of the cells at t1. Naturally, the rest of the total variance is assigned to the multiplicative measurement error, i.e.,
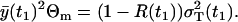 |
(29) |
In the case of the negligible process noise R(t1) = 0, it is obvious that RT = Θm. This parameterization is useful, because it provides the initial guess 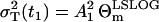 in the minimization of Eq. 27. Consequently, the values we estimate are R(t1) (0 ≤ R(t1) ≤ 1) and the total variance parameter RT. Thus, the parameter vector in Eq. 27 is p = [pA rδA δM T A1 R(t1) RT].
in the minimization of Eq. 27. Consequently, the values we estimate are R(t1) (0 ≤ R(t1) ≤ 1) and the total variance parameter RT. Thus, the parameter vector in Eq. 27 is p = [pA rδA δM T A1 R(t1) RT].
In this work we use the MATLAB function fmincon and ode45 (MathWorks, Natick, MA) for the minimization in Eq. 27 and for carrying out the solutions of ODEs, respectively. The parameters A1 and R(t1) are the only parameters for which we do not use the results of the previous LSLOG data fit to set initial guesses. We try the different values and find that the optimal parameter vector 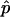 always has A1 and R(t1) close to the values initially guessed. Therefore, we search for the global minimum using the initial guesses in which A1 and R(t1) are gradually changing in the range [15 × 103, 30 × 103] and [0, 1], respectively. Based on this, we can identify the series of local minimums with
always has A1 and R(t1) close to the values initially guessed. Therefore, we search for the global minimum using the initial guesses in which A1 and R(t1) are gradually changing in the range [15 × 103, 30 × 103] and [0, 1], respectively. Based on this, we can identify the series of local minimums with 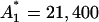 ,
, 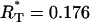 , and R(t1) ∈ [0, 1]. The values of R(t1) resulting from the optimization are always close to the initial guess of this parameter. The results for all other parameters are always quite the same and they are listed in Table 1. Among the minimums, we find one global minimum with R*(t1) = 0.45. The ratio between the variance resulting from the process noise and the total variance
, and R(t1) ∈ [0, 1]. The values of R(t1) resulting from the optimization are always close to the initial guess of this parameter. The results for all other parameters are always quite the same and they are listed in Table 1. Among the minimums, we find one global minimum with R*(t1) = 0.45. The ratio between the variance resulting from the process noise and the total variance 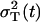 is
is
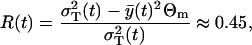 |
(30) |
where the process noise variance is expressed as the difference of the total variance 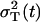 and the multiplicative measurement error variance,
and the multiplicative measurement error variance, 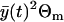 . The ratio R(t) remains quite constant for all t ∈ [0, T]. Therefore, we find that the standard deviation of the relative error of a single measurement is approximately
. The ratio R(t) remains quite constant for all t ∈ [0, T]. Therefore, we find that the standard deviation of the relative error of a single measurement is approximately
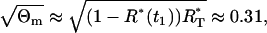 |
(31) |
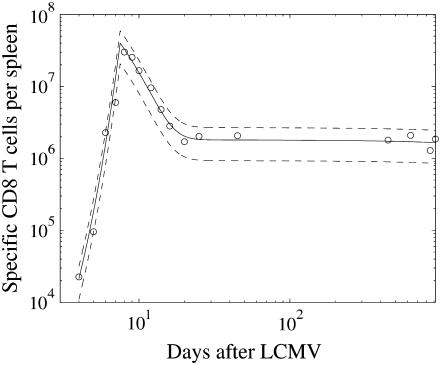
that is ∼31%. The mean values and two standard deviation band, resulting from the parameter estimation (Table 1), are presented in Fig. 4. By careful inspection, we can conclude that, like in the previous LSLIN and LSLOG cases, one point is outside the two standard deviation band. Because 95% of the data is inside the band, we can confirm that the data fit and the parameter estimates are consistent with the experimental data. The confidence intervals presented in Table 1 are in this case (ML) also computed by the bootstrap method (16). However, the data for the bootstrap are generated based on Gillespie's simulations, Eqs. 14 and 15, and the multiplicative measurement error assumption. The Gillespies simulations are started at the time t1, with the initial value 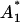 and the corresponding variance
and the corresponding variance 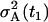 .
.
FIGURE 4.
The maximum-likelihood (ML) data fit of the stochastic Langevin approximations: ML expected values of data, two standard deviation band resulting from the process noise (dashed), the experimental data (circles).
To test the robustness of the measurement error intensity estimation, we compare the value of the cost function in the global minimum with the values obtained for the minimums with R(t1) ∈ [0, 1]. The difference is in the range of 10−4 order of magnitude, which results in the ratio of likelihood approximately equal to 1. This suggests that our data can be equally well described with the parameters obtained in the global minimum independently of the measurement error intensity. In other words, our parameter estimation is robust to a different assumption of the measurement error intensity.
This also suggests that the data can be explained solely by the process noise, R(t1) = 1, which means that the influence of measurement noise on our data can be neglected and that the observation model for the cell amount in one mouse is
 |
(32) |
We should underline that this possibility is based exclusively on the consistent treatment of the underlying stochastic processes. In this treatment we do not neglect the intensity of measurement error. The zero intensity of measurement error is a possibility resulting from the data-based parameter estimation.
CONCLUSION
This study presents an effort to understand better the stochastic fluctuations of the immune response data. In parameter estimations these fluctuations are usually considered as a result of measurement errors or parameter variations among the individuals. Interestingly enough, the process noise, which is actually an intrinsic property of the immune response, has not been considered at all in parameter estimation.
The process noise is tightly connected with the immune response dynamics. Consequently, it should be taken into account before any parameter variation is considered. In our study, we try to understand how much of the data fluctuations result from the process noise and how much from the measurement errors. First, using Gillespie's simulations, we show that the intensity of the process noise should not be a priori neglected. Second, we propose a maximum-likelihood parameter estimation based on data PDF predictions. These PDFs include the process noise, as well as the measurement error model.
Using the data from the LCMV-infected mice experiment, we find that the parameter estimations are robust to the intensity of the relative measurement error. This opens the possibility, contrary to the usual assumption, that stochastic data fluctuations are completely explained by the process noise. The estimated intensity of measurement error would be negligible, and no further parameter variations would be necessary to explain stochastic data fluctuations. It is worth mentioning that in our experiment the order of magnitude for the cell amount is 107. This amount of cells is considered to be large for immunological data. In experiments with smaller amount of cells, the process noise will have even larger influence.
Our point is that the parameter estimation should be based on the solid measurement error model. Observed trends and fluctuations in the immune response data can be explained by the stochastic dynamical model. But only if we take into account the measurement error model, do we know how much of the data trends and data fluctuations must be explained by the stochastic dynamical model and its parameters. Parameter variations should be included in the analysis only after the measurement error and process noise intensities are constrained.
Most of the theoretical immunology developments and discussions are related to dynamical hypotheses that can be different with a reason from experiment to experiment. Simultaneously, the limited set of measurement methods is in use, even in different experiments. Therefore, we believe that enough data can be provided and that there should be given more attention to the calibration of measurement methods, i.e., to the modeling of measurement errors of each particular method. The solid measurement error model will not only define the limitation for dynamical hypothesis, but also should be an essential part of the parameter estimation and hypothesis test procedures.
Acknowledgments
This work was supported by Netherlands Organization for Scientific Research (Vici grant No. 016.048.603 to R.J.D.B.).
APPENDIX I: THE PROLIFERATION PHASE
First, we will consider the process with the simultaneous proliferation (pA) and the death (δA). The master equation for this process is given by Eq. 14. According to the van Kampen system size expansion (8)
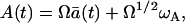 |
(33) |
where 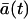 is expected value of a(t) = A(t)/Ω and Ω is so-called system size. When a(t) has a dimension of concentration, as in chemistry, Ω is the volume that is large enough and contains enough molecules, so that the variation of ±1 molecule can be considered as a continuous change. Consequently, a(t) and A(t) can take all values on the real axis and not just specific values and integers, respectively. Because we are not dealing with the concentrations, we define the system size Ω as the maximal expected amount of cells. From the system size expansion we obtain an ODE for the expected value
is expected value of a(t) = A(t)/Ω and Ω is so-called system size. When a(t) has a dimension of concentration, as in chemistry, Ω is the volume that is large enough and contains enough molecules, so that the variation of ±1 molecule can be considered as a continuous change. Consequently, a(t) and A(t) can take all values on the real axis and not just specific values and integers, respectively. Because we are not dealing with the concentrations, we define the system size Ω as the maximal expected amount of cells. From the system size expansion we obtain an ODE for the expected value
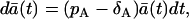 |
(34) |
and the second-order PDE for 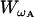 , which is the PDF of ωA, is
, which is the PDF of ωA, is
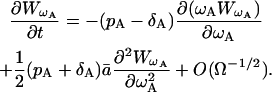 |
(35) |
Neglecting the terms of the order Ω−1/2, we can conclude that ωA(t) is described by the following Langevin equation
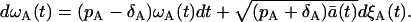 |
(36) |
The cancellation of O(Ω−1/2) is justified if Ω is large.
Going back to Eq. 33, we find that
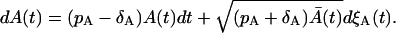 |
(37) |
If we consider the proliferation process with the rate ρ, using the similar derivation as above, we obtain
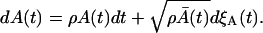 |
(38) |
When ρ = pA − δA, the expected values of Eq. 37 and 38 are equal. However, the variances are different because of the difference in the Wiener process terms. Consequently, the process with the proliferation (pA) and the death (δA) simultaneously present is not equivalent to the process with the proliferation rate ρ = pA − δA.
APPENDIX II: THE TIME STEP τ-SELECTION
Using the expression (Eq. 26a) from Gillespie (18), the time step τ for the first phase should satisfy
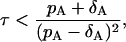 |
(39) |
and in the second phase should satisfy
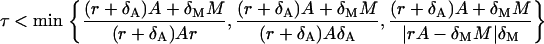 |
(40) |
The condition of the second phase depends on A and M. However, we can find that the first two expressions are bounded from below, i.e.,
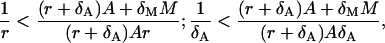 |
that is obtained by the substitution M = 0. Moreover, for the third expression we can consider the equivalent one, which results from the division of nominator and dominator by A, and its limits 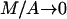 and
and 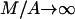 that are
that are
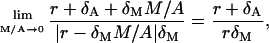 |
and
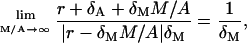 |
respectively. Actually, they are the candidates for the lower bounds of the third expression in Eq. 40. Because we do not know which the lower one is, we can say that the condition Eq. 40 is satisfied if
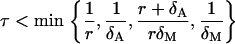 |
Finally, the single τ-value that will simultaneously satisfy the conditions Eqs. 39 and 40 can be chosen using the following criterion
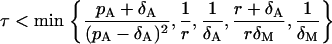 |
D. Milutinović's present address is Duke University Laboratory of Computational Immunology, Durham, NC, USA. E-mail: dejan.m@duke.edu.
References
- 1.De Boer, R., D. Homann, and A. Perelson. 2003. Different dynamics of CD4+ and CD8+ T cell responses during and after acute lymphocytic choriomeningitis virus infection. J. Immunol. 171:3928–3935. [DOI] [PubMed] [Google Scholar]
- 2.Perelson, A., D. Kirschner, and R. De Boer. 1993. Dynamics of HIV infection of CD4+ T cells. Math. Biosci. 114:81–125. [DOI] [PubMed] [Google Scholar]
- 3.Bonhoeffer, S., G. Funk, H. Gunthard, M. Fischer, and V. Muller. 2003. Glancing behind virus load variation in HIV-1 infection. Trends Microbiol. 11:499–504. [DOI] [PubMed] [Google Scholar]
- 4.Nowak, M., and R. May. 2000. Virus Dynamics Mathematical Principles of Immunology and Virology. Oxford University Press, Oxford, UK.
- 5.Gardiner, C. W. 1985. Handbook of Stochastic Methods for Physics, Chemistry and the Natural Sciences, 2nd Ed. Springer-Verlag, New York.
- 6.Jazwinsky, A. 1970. Stochastic Processes and Filtering Theory. Academic Press, London, UK.
- 7.Kurtz, T. 1970. Solutions of ordinary differential equations as limits of pure jump Markov processes. J. Appl. Prob. 7:49–58. [Google Scholar]
- 8.van Kampen, N. G. 1992. Stochastic Processes in Physics and Chemistry. North-Holland Publishing, Amsterdam, The Netherlands.
- 9.Gillespie, D. 2002. The chemical Langevin and Fokker-Planck equations for the reversible isomerization reaction. J. Phys. Chem. A. 106:5063–5071. [Google Scholar]
- 10.Chao, D., M. Davenport, S. Forrest, and A. Perelson. 2004. A stochastic model of cytotoxic T cell responses. J. Theor. Biol. 228:227–240. [DOI] [PubMed] [Google Scholar]
- 11.McKane, A., and T. Newman. 2004. Stochastic models in population biology and their deterministic analogs. Phys. Review E. 70:041902. [DOI] [PubMed] [Google Scholar]
- 12.Newman, T., and R. Grima. 2004. Many-body theory of chemotactic cell-cell interactions. Phys. Review E 70, Art. No. 051916. [DOI] [PubMed]
- 13.Turner, T., S. Schnell, and K. Burrage. 2004. Stochastic approaches for modelling in vivo reactions. Comput. Biol. Chem. 28:165–178. [DOI] [PubMed] [Google Scholar]
- 14.Homann, D., L. Teyton, and M. Oldstone. 2001. Differential regulation of antiviral T-cell immunity results in stable CD8+ but declining CD4+ T-cell memory. Nat. Med. 7:913–919. [DOI] [PubMed] [Google Scholar]
- 15.Blattman, J., R. Antia, D. Sourdive, X. Wang, S. Kaech, K. Murali-Krishna, J. Altman, and R. Ahmed. 2002. Estimating the precursor frequency of naive antigen-specific CD8 T cells. J. Exp. Med. 195:657–664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Efron, B., and R. Tibshirani. 1986. Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy. Stat. Sci. 1:54–77. [Google Scholar]
- 17.Gillespie, D. 1977. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 81:2340–2361. [Google Scholar]
- 18.Gillespie, D. 2001. Approximate accelerated stochastic simulation of chemically reacting systems. J. Chem. Phys. 115:1716–1733. [Google Scholar]
- 19.Gillespie, D. 2000. The chemical Langevin equation. J. Chem. Phys. 113:297–306. [Google Scholar]