Abstract
The free [Ca2+] in endoplasmic/sarcoplasmic reticulum Ca2+ stores regulates excitability of Ca2+ release by stimulating the Ca2+ release channels. Just how the stored Ca2+ regulates activation of these channels is still disputed. One proposal attributes luminal Ca2+-activation to luminal facing regulatory sites, whereas another envisages Ca2+ permeation to cytoplasmic sites. This study develops a unified model for luminal Ca2+ activation for single cardiac ryanodine receptors (RyR2) and RyRs in coupled clusters in artificial lipid bilayers. It is shown that luminal regulation of RyR2 involves three modes of action associated with Ca2+ sensors in different parts of the molecule; a luminal activation site (L-site, 60 μM affinity), a cytoplasmic activation site (A-site, 0.9 μM affinity), and a novel cytoplasmic inactivation site (I2-site, 1.2 μM affinity). RyR activation by luminal Ca2+ is demonstrated to occur by a multistep process dubbed luminal-triggered Ca2+ feedthrough. Ca2+ binding to the L-site initiates brief openings (1 ms duration at 1–10 s−1) allowing luminal Ca2+ to access the A-site, producing up to 30-fold prolongation of openings. The model explains a broad data set, reconciles previous conflicting observations and provides a foundation for understanding the action of pharmacological agents, RyR-associated proteins, and RyR2 mutations on a range of Ca2+-mediated physiological and pathological processes.
INTRODUCTION
In cardiac muscle, contraction is mediated by depolarization and subsequent opening of voltage-dependent, L-type Ca2+ channels in the cell membrane (sarcolemma). Opening of these channels allows Ca2+ influx into the cell, which in turn opens Ca2+ release channels in the sarcoplasmic reticulum (SR) membrane. SR Ca2+ release can be a small highly localized increase in Ca2+ concentration called a spark, or can propagate along the cell in a Ca2+ wave, or can occur simultaneously along the length of the cell resulting in a global increase of Ca2+ called a transient (1). Ca2+ sparks are believed to be the elementary SR Ca2+ release event and Ca2+ waves and transients are thought to be the summation of spark events (2).
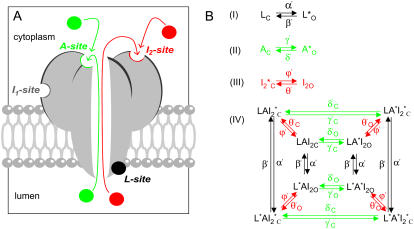
It has long been known that the excitability of Ca2+ release from muscle SR is substantially increased by its luminal Ca2+ load ([Ca2+]L) (3,4). More recently, it has been shown that the excitability of neuronal endoplasmic reticulum (ER) is regulated in the same way, suggesting that modulation of Ca2+ signaling by [Ca2+]L is a general phenomenon (5). However, the basis for load-dependent excitability remains controversial. Experiments on muscle cells and isolated SR vesicles have found that the effect of [Ca2+]L on Ca2+ release could not be explained entirely by the associated Ca2+ gradient across the SR and that [Ca2+]L must somehow control the Ca2+ permeability of the membrane (6,7). This was confirmed when activity of isolated RyRs in artificial bilayers was found to be modulated by [Ca2+]L (8). At issue is the mechanism underlying the activation of RyRs by luminal Ca2+ being attributed to two quite different processes. The true-luminal hypothesis attributes luminal Ca2+-activation and inhibition to Ca2+ regulatory sites on the luminal side of the RyR (9). The feedthrough hypothesis proposes that luminal Ca2+ permeates the pore and binds to cytoplasmic activation and inhibition sites (10–12). The latter is supported by the close correlation between the effect of [Ca2+]L and Ca2+ flux (lumen to cytoplasm), and by the observation that luminal regulation is dependent on Ca2+ buffering on the cytoplasmic side of the membrane (11). However, there is an increasing body of evidence suggesting that there are sensing sites for Ca2+ regulation on the luminal side of the protein. For example, it has been shown that luminal Ca2+-activation is abolished by tryptic digestion of the luminal side of cardiac ryanodine receptors (RyR2) (13). Although a recent bilayer study has presented evidence that both mechanisms somehow control skeletal ryanodine receptors (RyR1) (14), it is not understood how cytoplasmic and luminal Ca2+ sites explain current observations or reconcile conflicting interpretations in the literature. In this study, measurements of the gating kinetics of isolated RyR2 in lipid bilayers underlie the proposal of a novel mechanism for activation of RyRs by luminal-triggered Ca2+ feedthrough. This model predicts that in addition to cytoplasmic sites for Ca2+-activation and low affinity Ca2+/Mg2+-inhibition, RyRs possess a luminal Ca2+ binding site and a high affinity cytoplasmic Ca2+ inactivation site (Fig. 1). Ca2+ binding at the luminal site is sufficient to activate channel openings whereupon Ca2+ flows from lumen to cytoplasm (feedthrough) either enhances activation or causes inactivation.
FIGURE 1.
The luminal-triggered Ca2+ feedthrough model for [Ca2+]L regulation of RyRs. (A) Schematic of luminal-triggered Ca2+ feedthrough. Ca2+ binding to the L-site causes channel opening whereupon luminal Ca2+ has access to the cytoplasmic Ca2+ activation (A-site) and inactivation sites (I2-site). The I1-site that mediates the low affinity Ca2+/Mg2+ is not included in the model (see text for details). (B) Kinetic schemes for Ca2+ binding at the L-, A-, and I2-sites (Schemes I–III) and the overall scheme (Scheme IV) resulting from the combined action of Ca2+ at all three sites. Schemes I–III are representations of multistep processes. Hence some reaction rates have complex dependencies on [Ca2+] and these are given in the equations listed in Table 1. Asterisks indicate sites occupied with Ca2+. Reaction rates that depend on the Ca2+ current have subscripts o and c to indicate rates associated with open and closed channels, respectively. The open and closed status of the channel associated with each kinetic state is indicated by the subscripts O and C, respectively.
Little is known about the mechanisms underlying the activation and termination of Ca2+ sparks in muscle. The quantal nature of Ca2+ spark intensities suggests that they are produced by the concerted opening of up to 10 RyRs (15). Recent studies of the coupled gating of RyRs in artificial lipid bilayers may provide new insight into the triggering mechanisms for Ca2+ sparks (14,16,17). These investigations showed that Ca2+ feedthrough not only regulates the host RyR but also activates adjacent RyRs in a cluster. This study examines the roles of the luminal and cytoplasmic Ca2+ sites in generating this phenomenon in bilayers and how they might contribute to spark generation in muscle.
MATERIALS AND METHODS
SR vesicles (containing RyR2) were obtained from sheep hearts and were reconstituted into artificial lipid bilayers as previously described (18). Lipid bilayers were formed from phosphatidylethanolamine and phosphatidylcholine (8:2 wt/wt) in n-decane (50 mg/ml). During experiments, the cis (cytoplasmic) and trans (luminal) solutions contained 250 mM Cs+ (230 mM CsCH3O3S, 20 mM CsCl) and various concentrations of CaCl2. The trans solution was altered by addition of aliquots of stock solutions and the cis solution by local perfusion which allowed solution exchange within ∼1 s (19).
Solutions were pH-buffered with 10 mM n-tris[Hydroxymethyl]methyl-2-aminoethanesulfonic acid and solutions were titrated to pH 7.4 using CsOH. Free [Ca2+] up to 100 nM was estimated using published association constants (20) and the program Bound and Determined (21) and concentrations higher than this were measured using a Ca2+ electrode (Radiometer, Copenhagen, Denmark). [Ca2+] below 10 μM was buffered with 4.5 mM 1,2-bis(o-aminophenoxy)ethane-n,n,n′,n′-tetraacetic acid (4K+) (BAPTA) and titrated with CaCl2. [Ca2+] in the range 10–50 μM was buffered with either sodium citrate (up to 6 mM) or dibromo BAPTA (up to 2 mM).
Acquisition and analysis of ion channel recordings
Bilayer apparatus and data recording methods have been described previously (14). Electrical potentials are expressed using standard physiological convention (i.e., cytoplasmic side relative to the luminal side at virtual ground). Measurements were carried out at 23 ± 2°C. Before analysis, the current signal was digitally filtered at 1 kHz with a Gaussian filter and sampled at 5 kHz. Single channel properties were measured using Channel2 software (P. W. Gage and M. Smith, Australian National University, Canberra). Open probability (Po) and open and closed durations were calculated from single channel records using a threshold discriminator at 50% of channel amplitude. For experiments in which bilayers contained several RyRs, Po was calculated from the time-averaged current divided by the unitary current and the number of channels (n). Both methods of calculating Po gave similar results. The mean channel open and closed durations (τo and τc) could also be calculated from mean open and closed durations in multichannel recordings (τo(n) and τc(n)), provided that multiple openings were rare: τo = τo(n) and τc = τc(n) × n. The number of channels in each experiment was determined during periods of strong activation, which were usually achieved by turning off the local perfusion and exposing the RyRs to the cis bath. The values τo and τc were calculated mainly from the recording of 100–1000 opening events. However, under conditions that produced extremely low channel activity, the mean durations were obtained from as few as 40 events covering >400 s of recording (sampling error <40−½, i.e., <16%). Dwell-time frequency histograms of channel open and closed events were obtained exclusively from single channel recordings and were displayed as probabilities (counts/total number of events). These were plotted using the log-bin method suggested by Sigworth and Sine (22), which displays exponentials as peaked distributions centered at their exponential time constant. Sampling bins were equally spaced on a log scale with 3.5 or 7 bins per decade.
On rare occasions (<5% of experiments), RyRs appeared to form coupled clusters in the bilayer, similar to that seen for RyR1 (14). The experiments on coupled and uncoupled RyRs were analyzed and presented separately. Channel gating in coupled clusters was analyzed using the Hidden Markov Model (23), as described previously (14). The algorithm calculated the transition probability matrix of the underlying Markov process from the raw signal using maximum likelihood criteria. The mean channel opening and closing rates were calculated from the transition probability matrix.
Ca2+-dependencies of Po, τo, and opening rate were characterized by fitting these data with Hill curves using the following equations for activation and inactivation (shown here for the case of Po, similar equations apply to τo and opening rate):
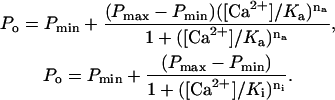 |
The expressions Pmin and Pmax are the activities of the minimally and maximally activated channel, Ka and Ki are the [Ca2+] for half-activation and inhibition, and na and ni are the corresponding Hill coefficients. The theory was fitted with the data using the method of least-squares.
The luminal-triggered Ca2+ feedthrough model: Kinetic schemes and equations
RyRs are known to possess cytoplasmic sites for Ca2+-activation (A-sites ∼1 μM affinity) and low-affinity Ca2+/Mg2+-inhibition (I1-site, ∼10 mM affinity, previously named the I-site). Based on novel data presented below, the model includes a cytoplasmic Ca2+-inactivation site (the I2-site, which causes partial inactivation with ∼1 μM affinity) and a luminal activation site (L-site, ∼60 μM affinity). Fig. 1 A shows a schematic representation of the locations of these sites on the RyR protein. It is envisaged that the channel can open if Ca2+ is bound to either the A- or L-sites. Thus luminal Ca2+ can open the channel by binding to the L-site, whereupon the flow of Ca2+ through the pore can increase the cytoplasmic [Ca2+] in the vicinity of the pore mouth ([Ca2+]P) and reinforce channel activation (increasing τo) by binding to the A-site or inactivate the channel by binding to the I2-site (decreasing τo).
Kinetic schemes for Ca2+ binding at the L-, A-, and I2-sites are shown in Fig. 1 B (I–III) and the overall regulation of RyRs by the three Ca2+ sites is described by an eight-state model (Scheme IV) presenting the amalgamation of Schemes I–III. The equations describing the action of luminal and cytoplasmic Ca2+ on channel activity and the model parameters are listed in Table 1. The I1-site was not considered in the model calculations because Ca2+ feedthrough is unlikely to increase [Ca2+]P to levels where significant Ca2+ binding will occur at this site.
TABLE 1.
Equations and parameters of the luminal-triggered Ca2+ feedthrough model
| Eq. | Eq. | |||||||
|---|---|---|---|---|---|---|---|---|
| L-site | ||||||||
| 2 | 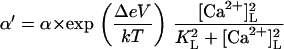 |
3 | β′=β | Affinity | Opening (0V) | V-dependence | Closing | |
| +ATP | KL = 60 μM | α = 2.7 s−1 | Δ = 0.4 | β = 1000 s−1 | ||||
| −ATP | KL = 45 μM | α = 0.6 s−1 | Δ = 0.4 | β = 1000 s−1 | ||||
| A-site | ||||||||
| 4 | 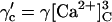 |
5 | 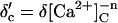 |
Affinity | Opening | Feedthrough | Closing | |
| +ATP | KA = 1 μM | γ = 43 s−1μM−3 | X = 15 μM/pA | δ = 220 s−1μM (n = 1) | ||||
| 6 | 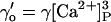 |
7a, | 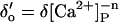 |
−ATP | KA = 6 μM | γ = 1.0 s−1μM−3 | X = 15 μM/pA | δ = 700 s−1 (n = 0) |
| 7b | 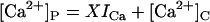 |
|||||||
| I2-site | ||||||||
| 8 | 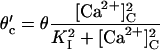 |
9 | ϕ′=ϕ | Affinity | Closing | Feedthrough | Opening | |
| +ATP | KI = 1.2 μM | θ = 250 s−1 | Y = 0.35 μM/pA | ϕ = 300 s−1 | ||||
| 10a | 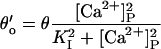 |
10b | 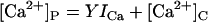 |
−ATP | KI = 1.2 μM | θ = 800 s−1 | Y = 0.35 μM/pA | ϕ = 400 s−1 |
Equations describe the [Ca2+]-dependencies of opening and closing rates associated with each site (refer to Scheme IV in Fig. 1 B). KA was derived from the theoretical half-maximal [Ca2+]C-activation of Po and was not used in the fitting of the model. The reaction rates are distinguished from model parameters with an apostrophe (e.g., α′). γ′, δ′, and θ′ depend on the Ca2+ current through the pore and therefore take on different values for the open and closed states (indicated by subscripts, o and c). In Eq. 2, T is the temperature in degrees K, k is the Boltzmann constant and V is bilayer voltage.
The first step in developing the luminal-triggered Ca2+ feedthrough model was to formulate a phenomenological description of RyR2 regulation by cytoplasmic Ca2+. The kinetic schemes used previously to describe cytoplasmic Ca2+-activation of RyRs are complex and involve many closed and open states (24,25). To avoid this level of complexity the whole cytoplasmic Ca2+-activation process was lumped into two single-step Ca2+ binding schemes associated with the A- and I2-sites (Schemes II and III in Fig. 1 B). Thus, the parameters γ, δ, θ, ϕ, Δ, and KI in Eqs. 4–10 were adjusted until the model fitted the cytoplasmic Ca2+ concentration ([Ca2+]C)-dependencies of τo and τc (Figs. 5 and 10). The second step was to ascertain the gating properties associated with the L-site (Scheme I). This was done by fitting the voltage/luminal Ca2+ concentration ([Ca2+]L)-dependence of τc (Fig. 6) using the parameters α, β, KL in Eqs. 2 and 3. The final step was to calculate the effects of Ca2+ feedthrough on the voltage/[Ca2+]L-dependencies of τo, τc, and their associated dwell-time distributions from theoretical estimates of [Ca2+]P and compare these estimates with the data.
FIGURE 5.
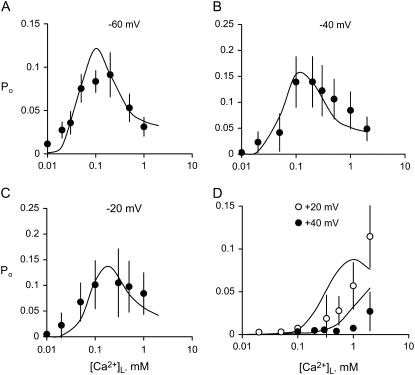
The [Ca2+]L-dependence of RyR2 Po. (A–D) RyRs were activated at the voltage indicated, by 2 mM ATP and 100 nM [Ca2+]C. Data points show the mean ± SE of 3–18 measurements. Solid curves show the fit to the data of the luminal-triggered Ca2+ feedthrough model using the parameters listed in Table 1.
FIGURE 10.
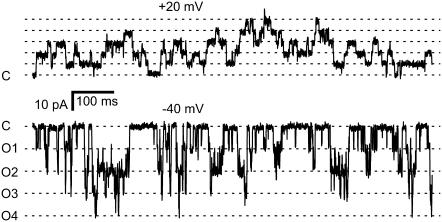
Recordings from an experiment with six RyRs in the bilayer showing coupled gating. At +20 mV (top trace), the channels appeared to gate independently. The dashed lines indicated the current levels associated with various numbers of open channels. The closed current level is labeled C. At −40 mV (bottom trace), the opening of a single channel (transitions from C to O1) was followed closely by openings to higher levels. Only four levels are apparent in this section (labeled O1–O4). The baths contained symmetric 250 mM Cs+ solutions with 2 mM ATP, [Ca2+]C = 100 nM, and [Ca2+]L = 1 mM.
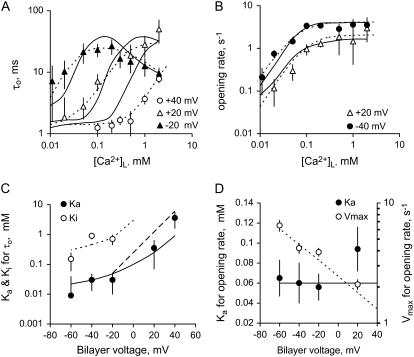
FIGURE 6.
The effects of membrane potential on the [Ca2+]L-dependent gating of RyR2. (A) Mean channel open times at three membrane voltages and (B) channel opening rates at two voltages. Rates were calculated from the inverse of the mean of closed times. The data points show mean ± SE of 3–14 measurements. In panels A and B, the dashed curves show Hill fits to the data (parameter values plotted in C and D) and the solid curves show the fits of the luminal-triggered Ca2+ feedthrough model using the parameters listed in Table 1. (C) Half-activating and inactivating [Ca2+]L, Ka (•), and Ki (○) for τo. (D) The Ka for RyR opening rate (•) and maximum opening rate (Vmax ○). The Hill coefficient for opening rate was 1.6 ± 0.3. In panels C and D, the solid and dashed curves show the fit to the data of the luminal-triggered Ca2+ feedthrough model. The line (long dashes) shows the voltage-dependence in Ka expected from translocation of Ca2+ through the membrane voltage (i.e., where 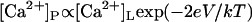 ).
).
Ion diffusion theory (26) was used to calculate [Ca2+]P and its dependence on ICa (pA) and distance from the pore (r, nm) under the buffering conditions used here.
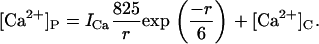 |
(1) |
For a given distance from the pore, [Ca2+]P has a linear dependence on ICa, which is encapsulated in the parameters X in Eq. 7b and Y in Eq. 10b (see Table 1). ICa was calculated using a rate theory model of RyR conductance (27). This part of the model has only two adjustable parameters, X and Y.
Model predictions were made by simulating the time series of channel gating events and using these to generate theoretical open and closed dwell time distributions, τo, τc, and Po. For each set of experimental conditions, the model reaction rates were calculated using the equations in Table 1. The sojourn of the simulated channel through its various states was driven by a random number generator in conjunction with the transition probability matrix that was derived from the model reaction rates. Sequential open and closed events were marked by transitions between open and closed states in the model. The effects of limited time resolution in the data were accommodated by amalgamating simulated events shorter than <200 μs.
RESULTS
The effects of cytoplasmic and luminal Ca2+ on RyR2 in the presence of ATP are presented here first because 1), it is recognized that the effects of luminal Ca2+ require the presence of cytoplasmic agonists such as ATP, caffeine, or sulmazole (8,28,29); and 2), ATP is the physiological coagonist. Data are presented that define the affinity and gating properties of one luminal and two cytoplasmic Ca2+ sites on RyR2. These properties were used to construct the luminal-triggered Ca2+ feedthrough model. The results were then fitted by adjusting the model parameters associated with the proximity of the two cytoplasmic Ca2+ binding sites to the pore mouth. The model is then applied to elucidating the effects of ATP and ion channel coupling on RyR regulation by Ca2+.
Activation of RyR2 by cytoplasmic Ca2+ in the presence of ATP
It is shown that the activity of RyR2 was dependent on both [Ca2+]C (Fig. 2 A) and [Ca2+]L (Fig. 2 B). The experiments in this section focus on the properties of the A- and I2-sites as revealed by the effects of [Ca2+]C on RyR2 activity. Fig. 2 A highlights the gradual transition in the gating properties that occurs as the dominant cytoplasmic agonist switches from ATP to Ca2+. RyRs activated by ATP (100 nM [Ca2+]C, Fig. 2 A, top three traces) had relatively long open and closed events compared to RyRs activated by high [Ca2+]C (with 2 mM ATP, Fig. 2 A, bottom two traces). To probe the gating mechanisms for this behavior, RyR gating was analyzed by compiling frequency histograms of open and closed times. These could be described by the sum of two exponential decays (these appear as peaked distributions when using the log-bin method in Fig. 3). The time-constants and relative weighting of the exponential components depended on [Ca2+]C and [Ca2+]L. Time-constants within each open time distribution had a 3–10-fold separation and lay within the range 1–50 ms (e.g., dashed lines in Fig. 3 A). The closed time distributions varied considerably with [Ca2+]C. In the presence of 0.1 μM [Ca2+]C, two widely separated exponentials were clearly resolved (open arrows in Fig. 3 B) in which >80% of the events were associated with the longer time-constant. Raising [Ca2+]C progressively reduced the longer time constant until both were quite similar at 10 μM (solid arrows in Fig. 3 B). The dwell-time distributions are frequently represented here by their means. The value τo gave a good representation of the average time-constant of the open time distribution and the value for τc lay within 20% of the longer closed time constant.
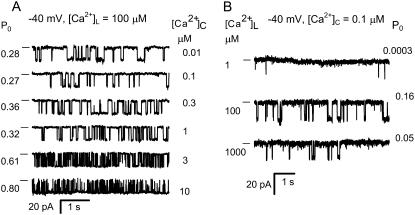
FIGURE 2.
The effects of [Ca2+]L and [Ca2+]C on the activity of RyR2 (−40 mV). (A) The effect of [Ca2+]C on the activity of a RyR in the presence of 100 μM [Ca2+]L. Increasing [Ca2+]C increases Po in association with a decrease in duration of mean open and closed events. Channel openings are downward current jumps from the baseline (indicated with a dash). (B) The effect of [Ca2+]L on RyR activity in the presence of 0.1 μM [Ca2+]C and 2 mM ATP.
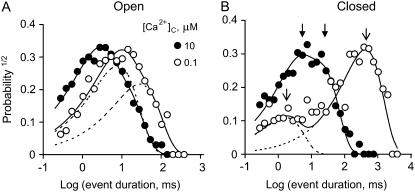
FIGURE 3.
Dwell-time probability distributions of channel open (A) and closed (B) events. The data are plotted using the log-bin method of Sigworth and Sine (22). Event duration distributions were compiled from a single RyR, which was activated by 2 mM ATP and the indicated [Ca2+]C in the presence of 100 μM [Ca2+]L (−40 mV). An increase in [Ca2+]C from 0.1 to 10 μM shifted both the open and closed distributions to shorter times. Solid curves show double-exponential fits to the data and dashed curves show individual exponential components for the fits to the open circles. When using the log-bin method the exponential components within these distributions appear as peaks centered at their respective time-constants. The arrows in panel B show the time constants associated with the data at 0.1 μM [Ca2+]C (○, open arrows) and 10 μM [Ca2+]C (•, solid arrows).
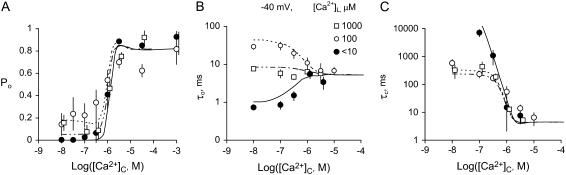
The effects of [Ca2+]C on the RyR2 gating properties, Po, τo, and τc, are shown in Fig. 4. Cytoplasmic Ca2+ activated RyR2 at μM levels (Fig. 4 A). Luminal Ca2+ had a marked effect on Pmin at −40 mV (Hill parameters are listed in Table 2), whereas it had a relatively small effect on Pmax. The values for Ka and hence A-site affinity, showed no significant dependence on [Ca2+]L or membrane potential (P > 0.06, see Table 2). The [Ca2+]C-dependencies of τo shown in Fig. 4 B reveal activation and inactivation processes associated with μM [Ca2+]C. In the virtual absence of luminal Ca2+ ([Ca2+]L < 10 μM), τo increased with [Ca2+]C (channel activation, Fig. 4 B, solid circle), whereas 100 μM [Ca2+]L unmasked a previously unidentified [Ca2+]C-dependent inactivation that decreased τo (Fig. 4 B, open circle). Despite this inactivation, raised [Ca2+]C caused an increase in Po via a decrease in τc that overwhelmed the effect of inactivation (Po = τo/(τc + τo) with 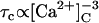 in Fig. 4 C and
in Fig. 4 C and 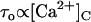 in Fig. 4 B). The value τo at 1000 μM [Ca2+]L had values between those at <10 and 100 μM [Ca2+]L and did not show a significant dependence on [Ca2+]C. The value τc at 1000 μM [Ca2+]L was very similar to that seen at 100 μM. The underlying mechanism for the complex effects of [Ca2+]C and [Ca2+]L on τo and τc are explained with the description of the model characteristics (see below).
in Fig. 4 B). The value τo at 1000 μM [Ca2+]L had values between those at <10 and 100 μM [Ca2+]L and did not show a significant dependence on [Ca2+]C. The value τc at 1000 μM [Ca2+]L was very similar to that seen at 100 μM. The underlying mechanism for the complex effects of [Ca2+]C and [Ca2+]L on τo and τc are explained with the description of the model characteristics (see below).
FIGURE 4.
The effect of [Ca2+]C on the activity of RyR2 at −40 mV. The values Po, τo, and τc were measured in the presence of 2 mM ATP at [Ca2+]L <10 μM (•), 100 μM (○), or 1000 μM (□). (A) Mean open probability Po mean ± SE. The numbers of experiments and the Hill parameters are listed in Table 2 (Hill fits to the data are not shown). (B, C) The mean ± SE of three-to-eight measurements of τo and τc. The curves [Ca2+]L <10 μM (solid), 100 μM (short dashes), and 100 μM (short/long dashes) show the fit to the data of the luminal-triggered Ca2+ feedthrough model using the parameters in Table 1.
TABLE 2.
Hill parameters for cytoplasmic Ca2+-activation of RyR2 Po
| No. | Voltage mV | [Ca2+]LμM | N | Pmax | Pmin | KaμM | na |
|---|---|---|---|---|---|---|---|
| 2 mM ATP | |||||||
| 1 | −40 | <10 | 11 | 0.9 ± 0.04 | 0.003 ± 0.04 | 0.9 ± 0.14 | 2 ± 1.3 |
| 2 | −40 | 100 | 16 | 0.66 ± 0.18 | 0.20 ± 0.07 | 0.5 ± 0.17 | 2 ± 2 |
| 3 | −40 | 1000 | 7 | 0.65 ± 0.06 | 0.07 ± 0.03 | 1.1 ± 0.16 | 2.4 ± 2 |
| 4 | 40 | <10 | 11 | 0.8 ± 0.03 | 0.01± 0.04 | 0.7 ± 0.12 | 3.0 ± 2.4 |
| 5 | 40 | 100 | 15 | 0.65 ± 0.05 | 0.01 ± 0.05 | 0.6 ± 0.16 | 1.5 ± 1.0 |
| 6 | 40 | 1000 | 7 | 0.85 ± 0.03 | 0.02 ± 0.02 | 1.5 ± 0.25 | 2.2 ± 0.8 |
| 0 mM ATP | |||||||
| 7 | −40 | 100 | 13 | 0.54 ± 0.13 | 0 ± 0.03 | 5.4 ± 2.0 | 2 ± 1.9 |
| 8 | 40 | 100 | 13 | 0.50 ± 0.06 | 0 ± 0.03 | 7.6 ± 1.7 | 2 ± 1.8 |
In the model, the activation and inactivation phenomena are attributed to the A- and I2-sites, respectively. The properties of these sites are derived from the data in Fig. 4 as follows: RyR gating due to the A- site is described by Scheme II (Fig. 1 B). In the absence of luminal Ca2+, the opening and closing rates associated with the A-site are reflected in the channel open and closed times (γ′ ≈ 1/τc and δ′ ≈ 1/τo). To account for the [Ca2+]C-dependencies of τo and τc in Fig. 4, δ′ ∝[Ca2+]C (Fig. 4 B, solid circle, Eqs. 5 and 7) and 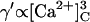 (Fig. 4 C, solid circle; Eqs. 4 and 6). RyR gating due to the I2 inactivation site is described by Scheme III (Fig. 1 B) where the equivalent opening and closing rates (ϕ′ and θ′) are given by Eqs. 8–10a. Inactivation in response to [Ca2+]C appears to be only partial (i.e., <40%), because even at 10 μM Ca2+ where the I2-site is saturated, Po > 0.6. To account for this the closing rate, θ′, is given a sublinear dependence on [Ca2+]P with an upper limit.
(Fig. 4 C, solid circle; Eqs. 4 and 6). RyR gating due to the I2 inactivation site is described by Scheme III (Fig. 1 B) where the equivalent opening and closing rates (ϕ′ and θ′) are given by Eqs. 8–10a. Inactivation in response to [Ca2+]C appears to be only partial (i.e., <40%), because even at 10 μM Ca2+ where the I2-site is saturated, Po > 0.6. To account for this the closing rate, θ′, is given a sublinear dependence on [Ca2+]P with an upper limit.
Bell-shaped dependence of RyR2 activity on [Ca2+]L in the presence of ATP
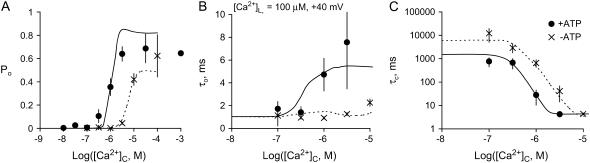
Although several studies have reported a bell-shaped [Ca2+]L-dependence of RyR1 Po in the presence of ATP, there has been no equivalent demonstration of this in RyR2. In the absence of luminal Ca2+ the activity of RyR2 was virtually zero (Po = (8 ± 4) × 10−4 at [Ca2+]L ∼0.1 μM, n = 6) indicating a near-absolute requirement for luminal Ca2+. Increasing [Ca2+]L (from 1 to 100 μM at −40 mV) substantially increased the activity of the RyRs, whereas a further increase to 1 mM decreased channel activity (Fig. 2 B). At −60 mV and −40 mV, voltages favoring the flow of Ca2+ from luminal to cytoplasmic baths, the [Ca2+]L for half-activation of Po, was 50 μM (Ka for the left side of the bell) and [Ca2+]L for half-inactivation was 1 mM (Ki for the right side of the bell, Fig. 5, A and B). Both Ka and Ki increased as the bilayer voltage became more positive (Fig. 5, C and D), and at positive voltages the decline in Po was beyond the experimental range of [Ca2+]L (Ki could no longer be monitored).
Luminal Ca2+ would not be expected to influence the channel-opening rate (1/τc) other than by affecting a luminal site because cytoplasmic sites are inaccessible to luminal ions when the channel is closed. Therefore, analysis of τo and τc should provide valuable information of the effect of Ca2+ feedthrough in channel activation. The results show that [Ca2+]L had very different effects on τo and channel opening rate (Fig. 6). The value τo had a bell-shaped dependence on [Ca2+]L, which is shown at several voltages in Fig. 6 A (the bell is most clearly seen at −20 mV). The Ka and Ki values for the [Ca2+]L-dependence of τo over the entire experimental voltage range is shown in Fig. 6 C. The values Ka and Ki increased with voltage in a way expected for Ca2+ ions, which must cross the membrane to reach their effector site (long-dashed line, Fig. 6 C). These results indicate that luminal Ca2+ activation and inactivation of τo are mediated by cytoplasmic facing sites. Moreover, the nonadditive effects of luminal and cytoplasmic Ca2+ on channel activation and inhibition indicate that the luminal and cytoplasmic actions are meditated by common binding sites.
Luminal Ca2+ activated RyR2 by increasing their opening rate and approached a maximum (Vmax) at high concentrations (Fig. 6 B). The voltage-dependence of Ka and Vmax are shown in Fig. 6 D. The Ka indicates the involvement of a Ca2+ binding site with an affinity (KL) ∼60 μM and the Vmax indicates that the Ca2+-bound site can trigger channel openings at a rate of 1–10 s−1. The Ka for opening rate did not show a significant voltage-dependence (P > 0.15, t-test) indicating that luminal Ca2+ ions do not move through the trans-membrane electric field to reach the site. Vmax varied threefold over the experimental voltage range and this could reflect an intrinsic voltage-dependence of the RyR opening mechanism. Taken together, these results indicate that [Ca2+]L-activation of opening rate is mediated by luminal facing sites of action.
The properties of the L-site are derived from the data in Fig. 6, B and D, as follows: RyR2 opening rate associated with the L-site (α′ in Scheme I) has an asymptotic dependence on [Ca2+]L (Fig. 6 B) that is characteristic of a two-step mechanism [(LC + 2Ca2+) ↔ L*C ↔ L*O] in which Ca2+ binding (which is relatively fast) leads to channel opening. In the absence of Ca2+ feedthrough, the mean duration of these openings (∼1 ms) is determined by the closing rate, β′. The Hill coefficient for the [Ca2+]L-dependence of opening rate was 1.6, suggesting a second-order dependence of α′ on [Ca2+]L in Eq. 2. The voltage-dependence of Vmax is accommodated by imposing a voltage-dependence on α′.
Characteristics of the luminal-triggered Ca2+ feedthrough model
The model accounts for the [Ca2+]L-, [Ca2+]C-, and voltage-dependencies of τo and τc over the range −60 mV to +20 mV (Figs. 4–6, curves, the model discrepancy at +40 mV is discussed in the section on model limitations). The model predictions of the [Ca2+]C-dependencies of τo and τc, shown in Fig. 4, B and C, can be understood in terms of the various reaction steps in Scheme IV. In the absence of luminal Ca2+, τo is primarily determined by the rates 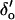 and
and 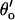 of the steps LAI2C ← LA*I2O → LA*I*2C. These rates have opposite [Ca2+]C-dependencies and their effects on the [Ca2+]C-dependence of τo tend to cancel, leaving a small increase in τo with increasing [Ca2+]C (Fig. 4 B, solid curve). When [Ca2+]L = 100 μM the L-site is mostly bound to Ca2+ so that τo is primarily determined by the inactivation transitions in L*AI*2C ← L*AI2O ↔ L*A*I2O → L*A*I*2C. Under these conditions the [Ca2+]C-dependent decrease in τo (Fig. 4 B, short dashes) reflects the Ca2+-inactivation rate,
of the steps LAI2C ← LA*I2O → LA*I*2C. These rates have opposite [Ca2+]C-dependencies and their effects on the [Ca2+]C-dependence of τo tend to cancel, leaving a small increase in τo with increasing [Ca2+]C (Fig. 4 B, solid curve). When [Ca2+]L = 100 μM the L-site is mostly bound to Ca2+ so that τo is primarily determined by the inactivation transitions in L*AI*2C ← L*AI2O ↔ L*A*I2O → L*A*I*2C. Under these conditions the [Ca2+]C-dependent decrease in τo (Fig. 4 B, short dashes) reflects the Ca2+-inactivation rate, 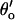 . Fig. 4 C shows the model predictions of the [Ca2+]C-dependence of τc. At low [Ca2+]C τc is primarily determined by α′ in the reaction step LAI2C→L*AI2O so that τc depends on [Ca2+]L (compare curves at 10 μM and 100 μM [Ca2+]L in Fig. 4 C). Increasing [Ca2+]C decreases τc as γ′c increasingly determines the channel opening rate via the reaction step LAI2C →LA*I2O. When [Ca2+]C ≥ 3 μM, γ′c becomes very large, then ϕ′ in the reactivation step LA*I*2C →LA*I2O determines the lower limit for τc at high [Ca2+]C. When [Ca2+]L = 1000 μM the Ca2+ feedthrough is large enough to cause saturation of the I2-site so that [Ca2+]C is unable to modulate inactivation (Fig. 4 B, long/short dashes).
. Fig. 4 C shows the model predictions of the [Ca2+]C-dependence of τc. At low [Ca2+]C τc is primarily determined by α′ in the reaction step LAI2C→L*AI2O so that τc depends on [Ca2+]L (compare curves at 10 μM and 100 μM [Ca2+]L in Fig. 4 C). Increasing [Ca2+]C decreases τc as γ′c increasingly determines the channel opening rate via the reaction step LAI2C →LA*I2O. When [Ca2+]C ≥ 3 μM, γ′c becomes very large, then ϕ′ in the reactivation step LA*I*2C →LA*I2O determines the lower limit for τc at high [Ca2+]C. When [Ca2+]L = 1000 μM the Ca2+ feedthrough is large enough to cause saturation of the I2-site so that [Ca2+]C is unable to modulate inactivation (Fig. 4 B, long/short dashes).
The effects of [Ca2+]L and voltage on τo and τc are compared with the model in Fig. 6, A and B, respectively. In the absence of Ca2+ feedthrough (low [Ca2+]L or large positive voltage), τo is determined by β′ in the reaction LAI2C ← L*AI2O. The contribution of Ca2+ feedthrough is modeled by an extension of the former scheme: LAI2C ← L*AI2O ↔ L*A*I2O → L*A*I*2C. Increasing Ca2+ feedthrough biases the state occupancies to the right so that the closing step on the left becomes less frequent. Hence, τo increases with [Ca2+]L until the Ca2+-dependent closing step on the right becomes fast enough to decrease τo. According to the conductance model, the curvature in the voltage-dependencies in the log-plots in Fig. 6 C comes from saturation of ICa as the driving force on Ca2+ becomes large. Fig. 6 B shows the corresponding model predictions of channel opening rate at 100 nM [Ca2+]C. At these low [Ca2+]C, the channel opening rate reflects α′ in the luminal activation step LAI2C→L*AI2O. The luminal site affinity (KL) determines the [Ca2+]L range for the rising phase in the opening rate.
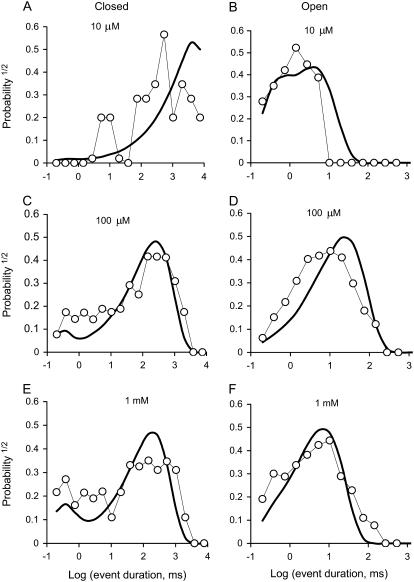
In addition to τo and τc, it was found that the model could also account for the effect of [Ca2+]L on the shape of the dwell-time distributions in the presence of low [Ca2+]C. Fig. 7 shows the distribution of channel open and closed times at three [Ca2+]L representing the subactivating (10 μM), maximal-activating (100 μM), and inactivating regions (1 mM) of the bell-shaped dependence of RyR2 activity on [Ca2+]L (−40 mV, [Ca2+]C = 100 nM). The shape of the closed time distributions varied considerably with [Ca2+]L (Fig. 7, A, C, and E). As [Ca2+]L increased, the time-constant of the main exponential component decreased from 10 s to 200 ms and the distribution changed from unimodal to bimodal with the appearance of another time constant of ∼1 ms. Open time distributions (Fig. 7 B, D, and F) were double exponentials as described in Fig. 3. Although the peak of the log-binned open distributions depended on [Ca2+]L, the shape of the distributions was similar over the experimental range. The model faithfully reproduced the effect of [Ca2+]L on these dwell time distributions (Fig. 7, curves). According to the model, closure of the channel causes termination of Ca2+ feedthrough which, at low [Ca2+]C, leads to deactivation of the RyR via Ca2+ dissociation from the A-site, underlying the long closed events. By the same process, channel closures allow Ca2+ dissociation from the I2-site, which permits reopening of the channel. The 1-ms time constant in the closed dwell-time distributions is associated with instances of recovery from I2-site inactivation that occurred before the channel had time to deactivate.
FIGURE 7.
The effect of [Ca2+]L on closed (A, C, and E) and open (B, D, and F) dwell-time distributions. The data are plotted using the log-bin method of Sigworth and Sine (22). Event duration distributions were compiled from a single RyR, which was activated by cytoplasmic 2 mM ATP (100 nM [Ca2+]C and voltage = −40 mV) and the indicated [Ca2+]L. The data are plotted using log-bins with 3.5 per decade. Solid curves show simulated distributions generated from the luminal-triggered Ca2+ feedthrough model using the parameters listed in Table 1.
The effect of ATP on activation by [Ca2+]C and [Ca2+]L
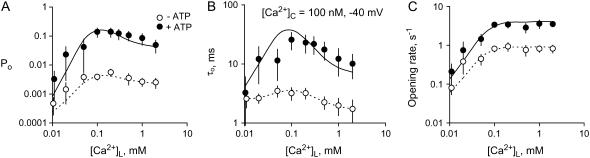
The effects of ATP are reexamined here in the light of the new Ca2+ regulation model. Fig. 8 compares the [Ca2+]C-dependent properties of RyR2 in the presence and absence of ATP. ATP increased Po over the entire experimental range of [Ca2+]C (Fig. 8 A). It increased the maximal activation at high [Ca2+]C (Pmax), decreased the [Ca2+]C for half-activation (Ka), and altered Po at subactivating [Ca2+]C (Pmin) depending on [Ca2+]L and voltage (Table 2). In accord with previous findings (30), ATP activated RyRs through an increase in τo and a decrease in τc (Fig. 8, B and C). In the virtual absence of Ca2+ feedthrough (+40 mV), [Ca2+]C caused a much bigger increase in τo and Po in the presence of ATP than in its absence.
FIGURE 8.
The effect of ATP and [Ca2+]C on the activity of RyR2 at +40 mV. The values Po, τo, and τc were measured in the presence of 2 mM ATP (•) and in its absence (×). (A) Mean open probability Po mean ± SE. The numbers of experiments and the Hill parameters are listed in Table 2 (Hill fits to the data are not shown). (B, C) The mean ± SE of 3–9 measurements of τo and τc. The curves (2 mM ATP, solid; and absence of ATP, dashed) show the fits of the luminal-triggered Ca2+ feedthrough model using the parameters in Table 1.
Fig. 9 compares the [Ca2+]L-dependent properties of RyR2 in the presence and absence of ATP. Also, as previously reported, ATP markedly amplified the effects of [Ca2+]L on Po (at low [Ca2+]C, Fig. 9 A). In the presence of ATP (−40 mV), τo showed a bell-shaped dependence on [Ca2+]L whereas in the absence of ATP, τo remained relatively constant (Fig. 9 B). It is interesting to note that ATP had similar effects on the [Ca2+]L- and [Ca2+]C-dependencies of τo in that, in both cases, an increase in Ca2+ could only increase τo when ATP was present. This is consistent with common sites of action for cytoplasmic and luminal Ca2+. Ka for opening rate was not significantly affected by ATP (Fig. 9 B), indicating that ATP did not modify the affinity of the L-site. Rather, ATP appeared to stabilize the open state of the channel and destabilize the closed state.
FIGURE 9.
The effects of ATP on the [Ca2+]L-dependent gating of RyR2. (A) The open probability of RyRs (100 nM [Ca2+]C and voltage = −40 mV) in the presence of 2 mM ATP (•) and in its absence (○). Also shown are the corresponding τo (B) and opening rates (C). Solid and dashed curves show the fit to the data of the luminal-triggered Ca2+ feedthrough model using the parameters listed in Table 1. The data points show mean ± SE of 3–18 measurements. Hill fits (not shown) to the opening rate reveal that 2 mM ATP increases Vmax from 0.8 ± 0.1 to 4.0 ± 0.4 without significantly changing Ka (Ka = 45 ± 8 μM and 60 ± 20 μM in the absence and presence of ATP, respectively).
In the model, the ability of ATP to increase τo in response to Ca2+ binding at the A-site is encapsulated in the parameter n in Eqs. 5 and 7a. In the presence of ATP, τo ∝ [Ca2+]C (Fig. 8 B, solid circle), which is indicative of the channel closing rate, 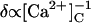 (i.e., n = 1). In the absence of ATP, τo is nearly independent of [Ca2+]C (Fig. 8 B, ×) so that n = 0. The larger τc in the absence of ATP (Fig. 8 C, ×) is accommodated in the model by a 13-fold decrease in the opening rate constant associated with the A-site, γ (see Table 1).
(i.e., n = 1). In the absence of ATP, τo is nearly independent of [Ca2+]C (Fig. 8 B, ×) so that n = 0. The larger τc in the absence of ATP (Fig. 8 C, ×) is accommodated in the model by a 13-fold decrease in the opening rate constant associated with the A-site, γ (see Table 1).
The model predictions for the [Ca2+]L-dependencies of τo and τc in the absence of ATP can be explained along similar lines to those presented above for ATP-activated RyRs. The contribution of Ca2+ feedthrough to τo depends on the steps LAI2C ← L*AI2O ↔ L*A*I2O → L*A*I*2C. However, in the absence of ATP the states L*A*I2O and L*AI2O have approximately the same average duration. Therefore, although Ca2+ feedthrough biases the state occupancies to the right, in the absence of ATP this causes no significant increase in τo. Fig. 9 B shows the corresponding model predictions of channel opening rate. The decreased [Ca2+]L-dependent opening rate in the absence of ATP was accommodated by a decrease in α′ in the luminal activation step LAI2C→L*AI2O.
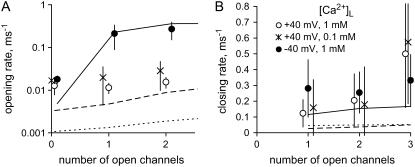
Ca2+ feedthrough couples RyR2 in lipid bilayers
In six instances, vesicle fusion events incorporated clusters of 3–6 RyR2 into the bilayer. At subactivating [Ca2+]C (100 nM Ca2+ and 2 mM ATP) and when conditions favored Ca2+ feedthrough, the opening of one RyR tended to promote the opening of other RyRs (i.e., channels displayed coupled gating). Fig. 10 shows a recording of six RyRs at positive and negative bilayer potentials. The current trace shows transitions between the current baseline (labeled C for closed) and equally spaced levels corresponding to 1–6 open channels. At −40 mV, channel openings were clearly grouped into bursts and the weighting of current levels in these records markedly deviated from a binomial distribution (not shown). Hidden Markov Model analysis of these records (see Materials and Methods) showed that the mean RyR opening rate associated with transitions between the current baseline and level O1 was ∼10× slower than opening rates associated with transitions between higher levels (Fig. 11 A, solid circle). Channel closing rates did not depend on the number of open RyRs (Fig. 11 B). Thus, RyR coupling appeared to be mediated by the opening rates. The degree of channel coupling was substantially reduced by decreasing [Ca2+]L from 1 mM to 0.1 mM or by application of positive bilayer potentials (Fig. 11 A), conditions that oppose Ca2+ feedthrough. These results are consistent with the notion that the opening of one channel in the bilayer permits Ca2+ feedthrough that can trigger the opening of neighboring RyRs via their A-sites. The luminal-triggered Ca2+ feedthrough model was extended to include this possibility by introducing another parameter, Z, which describes the proportionality between ICa and its effect on [Ca2+]P at a neighboring channel. The predicted opening and closing rates for the first opening in a cluster were calculated the same way as for single RyRs. The rates associated with the nth channel opening were calculated using a value for [Ca2+]P in Eqs. 7b and 10b that incorporated the additional term, 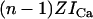 .
.
FIGURE 11.
The dependence of mean channel opening rate (A) and closing rate (B) on the number of open channels. Rates were measured in the presence of 2 mM ATP and 100 nM [Ca2+]C. Opening rates were significantly increased (P < 0.05, t-test) by the presence of other open channels under conditions that favored Ca2+ feedthrough (•, −40 mV [Ca2+]L = 1 mM, six measurements). When Ca2+ feedthrough was relatively low, this did not occur (○, +40 mV [Ca2+]L = 1 mM; ×, −40 mV [Ca2+]L = 0.1 mM, three measurements each). Closing rates did not significantly depend on the presence of other open channels in the bilayer. The data are compared with predictions of the luminal-triggered Ca2+ feedthrough model: •, solid line; ×, long dashes; and ○, dashed line.
The model predictions are compared with the data using a Z value of 0.3. Given the experimental buffering conditions, this corresponds to an interpore separation of ∼3 nm, which corresponds to the separation of neighboring RyR pores in the triad junction (31). Although the model tends to underestimate the gating rates, it does give a qualitative account of voltage- and [Ca2+]L-dependent coupling via channel opening rates. In the model, the first channel opening in the cluster is controlled as described for single RyRs (see above). Thus, at 100 nM [Ca2+]C, 1 mM [Ca2+]L, and −40 mV, luminal Ca2+ binding to the L-site is the primary trigger for channel opening whereas Ca2+ feedthrough serves to reinforce the stability of channel opening. However, the primary trigger for subsequent channel openings is the A-site because feedthrough from the first open channel elevates [Ca2+]P to 1–3 μM. At these [Ca2+]C, channel opening rates via the A-site are more than 10-fold higher than those attainable via the luminal L-site. In the model, the channel closing rates are slightly increased by the opening of neighboring channels because Ca2+ feedthrough also contributes to inactivation of neighboring RyRs via I2-sites.
Model limitations
The luminal-triggered Ca2+ feedthrough model accounts for the Ca2+ regulation of RyR2 by the actions of three Ca2+ binding sites that are linked by Ca2+ flowing through the pore. However, other Ca2+ regulation mechanisms could also play a role in controlling Ca2+ release from the SR. For example, the model does not include the low affinity Ca2+/Mg2+ inhibition mechanism (18). In addition, the [Ca2+]C-activation mechanism is known to be complex and involves several Ca2+-dependent steps (24,25). Simplification of this into A- and I2-site gating mechanisms should make the model unsuitable for predicting the complex shape of the dwell-time distributions. With this in mind, it is surprising that the model accounts so well for the [Ca2+]L-dependent dwell-time distributions at subactivating [Ca2+]C (Fig. 7). There is also the possibility that the L-site modulates the RyR in other ways than merely causing channel opening. An example of this has recently been reported in RyR1 (14) where a luminal Ca2+ binding site was shown to modulate the A-site affinity for Mg2+ (preliminary data indicates that this phenomenon does not occur in RyR2).
As yet, there has been no direct measure of the Ca2+ current under experimental conditions. Therefore, ICa is estimated from rate theory calculations based on an energy barrier model of the RyR pore (27). A possible failure of the energy barrier model to accurately predict ICa under some conditions could underlie the deviation of the model from the data (see the voltage-dependence in τo that occurred between +20 mV and +40 mV in Fig. 6, A and C). The rate theory model provided a good prediction of the total current in the channel (Cs+ plus Ca2+ in this instance, not shown). However, at +40 mV, ICa is relatively small and only represents ∼1% of the total current. Therefore, it is possible for the model to accurately predict the total current and yet be an order-of-magnitude out in estimating ICa. Just a twofold error in ICa would account for the deviations between the model and the data at +40 mV. Interestingly, τo at positive voltages could be better explained by a voltage-dependent equilibrium between Ca2+ on either end of the pore in which 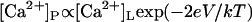 (Fig. 6 C, long dashes). In any case, the luminal-triggered Ca2+ feedthrough model provides a good fit to the data between −60 mV and +20 mV, which encompasses the membrane potential of the SR (0 mV, (32)).
(Fig. 6 C, long dashes). In any case, the luminal-triggered Ca2+ feedthrough model provides a good fit to the data between −60 mV and +20 mV, which encompasses the membrane potential of the SR (0 mV, (32)).
The extension of the luminal-triggered Ca2+ feedthrough model to coupled RyR clusters involved a number of assumptions that are yet to be validated. In the model, coupling occurs between nearest neighbors, although it could also occur between more remote pores. It is not clear that, in the bilayer, RyRs do form the same arrays as they do in muscle. The model assumes that the action of Ca2+ feedthrough on neighboring channels can be predicted by the steady-state action of raised [Ca2+]C. However, neighboring RyRs would be stimulated by a rapid stepwise increase in [Ca2+]C and it is known that RyRs can exhibit gating properties that are peculiar to non-steady-state situations (33,34).
DISCUSSION
The results obtained here support the proposition that RyR activation by Ca2+ stores is due to Ca2+ binding sites on both the luminal and cytoplasmic sides of the channel. This study shows that store regulation of RyRs and ER/SR excitability involves three modes of action associated with different parts of the RyR molecule; the L-site, A-site, and I2-site (Fig. 1). The L- and I2-sites have not been previously identified and this study makes the first measurement of their properties. The effects of [Ca2+]L on opening rate in Fig. 6, B and C, highlight the existence of a luminal-facing Ca2+ activation site (L-site) with an affinity of 60 μM. The binding of Ca2+ to the L-site on its own can activate channel openings of ∼1 ms duration at rates of ∼1–10 s−1. Once the channel is open, the flux of Ca2+ from the luminal to cytoplasmic sides of the channel increases the cytoplasmic [Ca2+] near the A-site and produces up to 30-fold prolongation of channel openings. Thus, a large component of the RyR activation by luminal Ca2+ (up to 97%) is due to the effects of Ca2+ feedthrough. However, without the luminal site to trigger the initial channel openings, activation by [Ca2+]L would not occur. Therefore, the proposed mechanism for store activation of RyRs is luminal-triggered Ca2+ feedthrough, incorporating both the true luminal and feedthrough hypothesis. This hybrid mechanism would explain the apparently contradictory findings whereby enzyme digestion of luminal RyR domains abolishes luminal Ca2+ activation (13), but there is a close correlation between RyR activity and Ca2+ flux through the pore (10).
Ca2+-inactivation
This study makes the first demonstration in single channel recording of a high affinity, [Ca2+]C-dependent inactivation in RyRs. It is manifest as a Ca2+-dependent reduction in channel τo (Figs. 2 A and 4 B). The affinity of the I2-site is ∼1.2 μM, which is similar to that of the A-site (0.9 μM) so that both activation and inactivation occur over the same range of [Ca2+]C. [Ca2+]C-activation overrides the effects of the I2-site, which causes ≤20% reduction in Po in response to cytoplasmic Ca2+. However, the I2-site causes up to 98% reduction in Po in response to feedthrough of luminal Ca2+ in the presence of physiological (100 nM) [Ca2+]C. This is because channel closures block Ca2+ feedthrough, leading to deactivation via the A-site and substantial lengthening of closed events.
It is well known that cytoplasmic Ca2+ and Mg2+ cause identical inhibition of RyRs at high concentrations (∼1 mM for RyR1 and ∼10 mM for RyR2 (35)). This inhibitory action is mediated by a low affinity nonspecific cation site (I1-site, previously named the I-site). It was thought that inactivation by high [Ca2+]L was mediated by Ca2+ feedthrough to the I1-site (11) because until now, the I1-site was the only Ca2+-dependent inhibition mechanism that had been clearly identified in RyRs. It is unlikely that the I1-site causes inactivation by high [Ca2+]L because inactivation has a similar [Ca2+]L sensitivity in RyR1 and RyR2 (see (11) and (10)) whereas the Ca2+ sensitivity of the I1-site differs 10-fold between the two isoforms. Moreover, the I1-site shows no specificity between Ca2+ and Mg2+, whereas the luminal inhibition via the I2-site is ∼100-fold less sensitive to Mg2+ than to Ca2+ (unpublished data).
Accessibility of A- and I2-sites to luminal Ca2+
It is noteworthy that even though the A- and I2-sites have similar affinity for cytoplasmic Ca2+, the effects of luminal Ca2+ on these sites occur over quite different ranges of [Ca2+]L. The model indicates that the feedthrough effects of Ca2+ are ∼40-fold larger for the A-site than for the I2-site (see X and Y in Table 1), which suggests a marked difference in the accessibility of these sites to luminal Ca2+. This difference is readily explained by the relative proximity of these sites to the Ca2+ pore (10). Ca2+ emanating from the pore will diffuse into the cytoplasm and be sequestered by buffering molecules (4.5 mM BAPTA). This leads to a decline in [Ca2+] with distance from the pore (see Eq. 1). The luminal-triggered Ca2+ feedthrough model predicts that each pA of Ca2+ current through the channel causes a 15 μM increase in [Ca2+] at the A-site and a 0.35 μM increase at the I2-site (e.g., ICa = 4.9 pA at −40 mV when [Ca2+]L = 1 mM hence [Ca2+]P = 73 μM at the A-site and 1.7 μM at the I2-site). This places the A- and I2-sites at 11 nm and 26 nm from the pore, respectively. Given that the furthest point on the RyR from the pore is ∼20 nm (36), it would seem that the I2-sites are located at the periphery of the protein or perhaps on an adjacent inhibitory protein. The relative proximity of the A- and I2-sites to the pore is in accord with the observation that Ca2+ buffering of the cytoplasmic bath affects inactivation much more strongly than activation (10).
Cytoplasmic agonists and luminal Ca2+ activation
Several studies have shown that [Ca2+]L-dependent activation of RyRs is mainly seen in the presence of agonists such as ATP, caffeine, or sulmazole (8,28,29). Previously it was proposed that these agonists unmask a luminal Ca2+ sensing site (6). The luminal-triggered Ca2+ feedthrough model points to a different mechanism in which the L-site affinity is not altered by agonists. Rather, they stabilize the channel open conformation, destabilize the closed conformation, and, in conjunction with Ca2+ feedthrough, markedly increase channel activation in response to [Ca2+]L.
One of these agonists, ATP, is shown here to enhance [Ca2+]L-activation of RyR2 by three modes of action. Firstly, ATP increases the rate of opening of RyRs that occurs in response to Ca2+ binding at the L-site (Fig. 9 C). Secondly, in accord with previous findings (37), ATP is a cofactor that causes τo to increase in response to Ca2+ binding at the A-site. Therefore, Ca2+ feedthrough should increase τo in the presence of ATP, whereas in the absence of ATP, τo should not be altered. The results show this to be the case (Fig. 9 B). Thirdly, ATP decreases the rate of inactivation via the I2-site. In regard to the last two actions, the effects of ATP on the [Ca2+]L-dependence of τo were entirely consistent with Ca2+ feedthrough and the observed effects of ATP on the [Ca2+]C-dependence of τo (Fig. 9, dashed and solid curves).
Previous studies (30,38–40) have shown that cytoplasmic agonists such as caffeine and ATP have quite different effects on RyR gating than Ca2+. Caffeine and ATP produce a much lower Po and they generate much longer channel openings and closures than Ca2+ (Fig. 2 A, see top trace showing an RyR activated by ATP with bottom trace of an RyR activated by Ca2+ and ATP). The different forms of activation by Ca2+ and ATP can be understood in terms of the luminal-triggered Ca2+ feedthrough model. Firstly, cytoplasmic Ca2+ activation via the A-site can cause much faster activation rates than ATP, which is limited by the triggering of openings by the L-site (hence the longer τc and the lower Pmax with ATP relative to Ca2+). Secondly, channels activated by cytoplasmic Ca2+ are more affected by I2-site mediated inactivation than ATP-activated RyRs (hence τo is longer ATP than with Ca2+).
Another prediction of the model is that cardiac and skeletal RyR isoforms are differently regulated by luminal Ca2+. It is known that there are marked differences in the ways that RyR1 and RyR2 are regulated by the cytoplasmic milieu (41). Of particular relevance is that RyR1 and RyR2 are differently regulated by cytoplasmic ATP. RyR1 can be activated by ATP in the absence of cytoplasmic and luminal Ca2+ (10,14). However, as shown here and elsewhere (28,42), ATP acts as a cofactor on RyR2, which increases its activation in response to Ca2+ but does not in itself trigger channel openings. This difference in ATP regulation underlies important differences in the way that RyR1 and RyR2 respond to luminal Ca2+ (see Scheme V). It is proposed here that opening of RyR2 at 100 nM [Ca2+]C is primarily triggered by Ca2+ binding to the L-site whereas Ca2+ feedthrough serves to reinforce stability of channel opening. However, in RyR1, cytoplasmic ATP will trigger channel openings so that the L-site is bypassed, resulting in a mechanism that is identical to that previously proposed for RyR1 (10). It is possible that in the absence of ATP, RyR1 would default to the RyR2 mechanism for luminal Ca2+ regulation provided that RyR1 also has an L-site.
 |
Scheme V |
More generally, this model predicts that any cofactor that prolongs channel openings triggered by cytoplasmic Ca2+ will promote RyR activation by luminal Ca2+ (the converse will be true for cytoplasmic antagonists). This might be highly relevant to the effects of RyR2 mutations associated with Sudden Cardiac Death, which are known to enhance activation by luminal Ca2+ (43) and the ability of polyunsaturated fatty acids, which are RyR antagonists, to protect myocardium against store-overload-induced arrhythmias (44,45). A number of RyR2 co-proteins have been found to modify [Ca2+]L-regulation of RyRs. The luminal Ca2+ buffering protein, calsequestrin (CSQ), along with triadin and junctin, are known to bind to RyR2 and confer luminal Ca2+ activation, thus being considered as the luminal Ca2+ sensor (46). However, it is not yet clear if these proteins constitute the L-site itself or whether they merely act as a cofactor that prolongs the channel openings triggered by [Ca2+]C. In addition, CSQ dissociation from RyR2 could be a sensor for Ca2+ overload of the SR. Exposure of RyR2 in bilayers to 5 mM [Ca2+]L caused a substantial increase in their activity via CSQ dissociation (46). Earlier studies by the same authors found the same treatment caused an increase in the Ca2+ affinity of the A-site (29). In this study [Ca2+]L was kept below 2 mM to minimize the possibility of CSQ dissociation from the RyR. Another cytoplasmic protein, calmodulin (CAM), decreases RyR2 sensitivity to [Ca2+]C via the A-site and appears to modify the action of Ca2+ feedthrough on RyR2 activity (47). It is unlikely that CAM contains the A- or I2-sites since CAM was not present in this study. CAM is rapidly dissociated from RyRs by the mM [Ca2+] used to promote SR vesicle fusion with the bilayer.
Coupled gating of RyR2 in muscle
The coupled opening of RyRs observed here is very similar to the phenomenon reported previously in RyR1 and RyR2 (14,16,17), where it was proposed that coupling occurred when Ca2+ flow through one channel raised the local [Ca2+]C sufficiently to activate neighboring RyRs. This was based on the findings that 1), the coupling only occurred under conditions favoring Ca2+ feedthrough; 2), coupling did not occur in the presence of a strong cytoplasmic triggering stimulus ([Ca2+]C = 100 μM); and 3) the opening of one channel caused an approximately fivefold reduction in Mg2+-inhibition of the other RyRs, suggesting that local [Ca2+]C is indeed increased and is competing with Mg2+ for the A-sites. In this study, RyR2 coupling was also promoted under conditions favorable to Ca2+ feedthrough. The coupling of RyR2 seen here differed slightly from those reported in RyR1. There was a much larger relative difference between the first and second opening rates in RyR2 than RyR1 (compare 10× for RyR2 versus 2× for RyR1). This probably reflects the different ligand sensitivities of the two isoforms. RyR1 is more strongly stimulated by ATP than RyR2 so that the initial opening rate for RyR1 in a cluster is much higher. However, the rate of subsequent channel openings for RyR1 and RyR2 are similar because both isoforms have similar sensitivity to cytoplasmic Ca2+.
Ca2+ sparks are believed to arise from the coupled activation of up to 10 RyRs in the triad junction (15). Freeze fracture electron micrographs show that RyRs within the triad junction are organized into square, two-dimensional arrays (31). The coupling between RyR openings in lipid bilayer experiments suggests that during SR vesicle isolation and reconstitution, fragments of these RyR arrays are retained. The model for luminal-triggered Ca2+ feedthrough highlights the different mechanisms that might underlie the frequency and morphology of Ca2+ sparks. Spark frequency is likely to be governed by the opening rate of RyRs in the absence of any open channels, whereas spark morphology would depend on coupling between RyRs. The precise role of the L-, A-, and I2-sites in regulating RyR2 in the cell is likely to depend on how intracellular Mg2+ interacts with these sites. The free [Mg2+] in the cytoplasm and lumen is ∼1 mM and this level of Mg2+ has been shown to lower the apparent Ca2+ affinity of the A-site to ∼10 μM (11) and the L-site to 500 μM (unpublished observations). In the case of the L-site, this places the affinity right in the middle of the physiological range of luminal Ca2+.
In vivo, a Ca2+ spark can occur spontaneously or be initiated by the opening of a single L-type Ca2+ channel in the sarcolemma (induced sparks) (1). The results here suggest that sparks can be triggered by either binding of luminal Ca2+ to the L-site (spontaneous sparks) or binding of cytoplasmic Ca2+ to the A-site (induced and spontaneous sparks). According to the model, spark frequency is governed by the sum of the opening rates associated with L-site and A-sites. Hence spark frequency should increase with SR Ca2+ load or with increased cytoplasmic Ca2+ activation. This is consistent with the finding that spark frequency increases with increasing luminal and cytoplasmic stimuli (48,49). In permeabilized cardiac cells, ATP depletion in the presence of 200 nM [Ca2+]C was shown to decrease the frequency of spontaneous sparks by >90% even though the Ca2+ load of the SR was increased (49). This is consistent with bilayer experiments showing that removal of ATP results in a fivefold decrease in RyR opening rate via the L-site (compare α ± ATP in Table 1; at 200 nM [Ca2+]C the L-site is the main trigger for RyR openings). Interestingly, some RyR activators and inhibitors have only transient effects on spark frequency because any initial change in RyR2 activity results in an opposing change in SR Ca2+ load, a process dubbed autoregulation. Why this happens for caffeine and tetracaine (48) and not for ATP (49) is still a mystery. The answer might be found in knowledge of the relative effects of these substances on the L- and A-sites.
According to the model, sparks triggered by either the L- site or A-site should have the same morphology because in either case the subsequent activity of RyRs is governed by the binding of feedthrough Ca2+ to the A-site and I2-sites. The A-sites mediate the coordinated opening of RyRs in a spark and the I2-sites govern their termination. Model calculations (not shown) indicate that an I2-site inactivation rate of 1000 s−1 (fourfold higher than measured here) would explain the amplitude distribution and duration of sparks reported by Wang et al. (15). Whether these mechanisms indeed control spark morphology is yet to be determined.
In conclusion, RyRs possess a luminal site for Ca2+-activation with an affinity of 60 μM (L-site) and cytoplasmic sites for Ca2+-activation and Ca2+-inactivation that have ∼1 μM affinity (A- and I2-sites). Store Ca2+ regulates RyR activity by binding to the A-, L-, and I2-sites and substances that alter channel gating associated with any of these sites will alter the regulation of RyRs by luminal Ca2+. A unifying kinetic model is developed that makes the first quantitative predictions of Ca2+ permeability of the ER/SR. This model provides a framework for understanding the mode of action of pharmacological agents (e.g., ATP and caffeine), RyR-associated proteins (e.g., calsequestrin), and RyR2 mutations (e.g., those associated with sudden cardiac death) on a whole range of Ca2+ mediated physiological and pathological processes.
Acknowledgments
Sheep hearts were provided by Dr. Tony Quail. Thanks to Drs. Graham Lamb, Dirk vanHelden, and Liz Milward for critically reading the article and to Paul Johnson, Melissa Dafo, Bronwyn Hiles, and Katherine Bradley for assisting with the experiments.
D.R.L. was supported by a Senior Brawn Fellowship from the University of Newcastle. This work was supported by the Australian Research Council (grant No. DP0557780) and by an infrastructure grant from NSW Health through Hunter Medical Research Institute.
References
- 1.Stern, M. D., and H. Cheng. 2004. Putting out the fire: what terminates calcium-induced calcium release in cardiac muscle? Cell Calcium. 35:591–601. [DOI] [PubMed] [Google Scholar]
- 2.Coombes, S., R. Hinch, and Y. Timofeeva. 2004. Receptors, sparks and waves in a fire-diffuse-fire framework for calcium release. Prog. Biophys. Mol. Biol. 85:197–216. [DOI] [PubMed] [Google Scholar]
- 3.Fabiato, A., and F. Fabiato. 1977. Calcium release from the sarcoplasmic reticulum. Circ. Res. 40:119–129. [DOI] [PubMed] [Google Scholar]
- 4.Ford, L. E., and R. J. Podolsky. 1972. Calcium uptake and force development by skinned muscle fibers in EGTA buffered solutions. J. Physiol. (Lond.). 223:1–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Verkhratsky, A. 2005. Physiology and pathophysiology of the calcium store in the endoplasmic reticulum of neurons. Physiol. Rev. 85:201–279. [DOI] [PubMed] [Google Scholar]
- 6.Sitsapesan, R., and A. J. Williams. 1997. Regulation of current flow through ryanodine receptors by luminal Ca2+. J. Membr. Biol. 159:179–185. [DOI] [PubMed] [Google Scholar]
- 7.Györke, S., I. Györke, V. Lukyanenko, D. Terentyev, S. Viatchenko-Karpinski, and T. F. Wiesner. 2002. Regulation of sarcoplasmic reticulum calcium release by luminal calcium in cardiac muscle. Front. Biosci. 7:d1454–d1463. [DOI] [PubMed] [Google Scholar]
- 8.Sitsapesan, R., and A. J. Williams. 1994. Regulation of the gating of the sheep cardiac sarcoplasmic reticulum Ca2+-release channel by luminal Ca2+. J. Membr. Biol. 137:215–226. [DOI] [PubMed] [Google Scholar]
- 9.Sitsapesan, R., and A. J. Williams. 1995. The gating of the sheep skeletal sarcoplasmic reticulum Ca2+-release channel is regulated by luminal Ca2+. J. Membr. Biol. 146:133–144. [DOI] [PubMed] [Google Scholar]
- 10.Tripathy, A., and G. Meissner. 1996. Sarcoplasmic reticulum lumenal Ca2+ has access to cytosolic activation and inactivation sites of skeletal muscle Ca2+ release channel. Biophys. J. 70:2600–2615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Xu, L., and G. Meissner. 1998. Regulation of cardiac muscle Ca2+ release channel by sarcoplasmic reticulum lumenal Ca2+. Biophys. J. 75:2302–2312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Herrmann-Frank, A., and F. Lehmann-Horn. 1996. Regulation of the purified Ca2+-release channel/ryanodine receptor complex of skeletal muscle sarcoplasmic reticulum by luminal calcium. Pflugers Arch. 432:155–157. [DOI] [PubMed] [Google Scholar]
- 13.Ching, L. L., A. J. Williams, and R. Sitsapesan. 2000. Evidence for Ca2+ activation and inactivation sites on the luminal side of the cardiac ryanodine receptor complex. Circ. Res. 87:201–206. [DOI] [PubMed] [Google Scholar]
- 14.Laver, D. R., E. R. O'Neill, and G. D. Lamb. 2004. Luminal Ca2+-regulated Mg2+ inhibition of skeletal RyRs reconstituted as isolated channels or coupled clusters. J. Gen. Physiol. 124:741–758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wang, S. Q., M. D. Stern, E. Rios, and H. Cheng. 2004. The quantal nature of Ca2+ sparks and in situ operation of the ryanodine receptor array in cardiac cells. Proc. Natl. Acad. Sci. USA. 101:3979–3984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Laver, D. R. 2006. Regulation of ryanodine receptors from skeletal and cardiac muscle during rest and excitation. Clin. Exp. Pharmacol. Physiol. 33:1107–1113. [DOI] [PubMed] [Google Scholar]
- 17.Laver, D. R. 2005. Coupled calcium release channels and their regulation by luminal and cytosolic ions. Eur. Biophys. J. 34:359–368. [DOI] [PubMed] [Google Scholar]
- 18.Laver, D. R., L. D. Roden, G. P. Ahern, K. R. Eager, P. R. Junankar, and A. F. Dalhunty. 1995. Cytoplasmic Ca2+ inhibits the ryanodine receptor from cardiac muscle. J. Membr. Biol. 147:7–22. [DOI] [PubMed] [Google Scholar]
- 19.O'Neill, E. R., M. M. Sakowska, and D. R. Laver. 2003. Regulation of the calcium release channel from skeletal muscle by suramin and the disulfonated stilbene derivatives DIDS, DBDS, and DNDS. Biophys. J. 84:1674–1689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Marks, P. W., and F. R. Maxfield. 1991. Preparation of solutions with free calcium concentration in the nanomolar range using 1,2-bis(o-aminophenoxy)ethane-n,n,n′,n′-tetraacetic acid. Anal. Biochem. 193:61–71. [DOI] [PubMed] [Google Scholar]
- 21.Brooks, S. P., and K. B. Storey. 1992. Bound and determined: a computer program for making buffers of defined ion concentrations. Anal. Biochem. 201:119–126. [DOI] [PubMed] [Google Scholar]
- 22.Sigworth, F. J., and S. M. Sine. 1987. Data transformations for improved display and fitting of single- channel dwell time histograms. Biophys. J. 52:1047–1054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Chung, S. H., J. B. Moore, L. G. Xia, L. S. Premkumar, and P. W. Gage. 1990. Characterization of single channel currents using digital signal processing techniques based on Hidden Markov Models. Philos. Trans. R. Soc. Lond. Biol. 329:265–285. [DOI] [PubMed] [Google Scholar]
- 24.Zahradnikova, A., and I. Zahradnik. 1996. A minimal gating model for the cardiac calcium release channel. Biophys. J. 71:2996–3012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zahradnik, I., S. Gyorke, and A. Zahradnikova. 2005. Calcium activation of ryanodine receptor channels—reconciling RyR gating models with tetrameric channel structure. J. Gen. Physiol. 126:515–527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Stern, M. D. 1992. Buffering of calcium in the vicinity of a channel pore. Cell Calcium. 13:183–192. [DOI] [PubMed] [Google Scholar]
- 27.Tinker, A., A. R. Lindsay, and A. J. Williams. 1992. A model for ionic conduction in the ryanodine receptor channel of sheep cardiac muscle sarcoplasmic reticulum. J. Gen. Physiol. 100:495–517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lukyanenko, V., I. Gyorke, and S. Gyorke. 1996. Regulation of calcium release by calcium inside the sarcoplasmic reticulum in ventricular myocytes. Pflugers Arch. 432:1047–1054. [DOI] [PubMed] [Google Scholar]
- 29.Gyorke, I., and S. Gyorke. 1998. Regulation of the cardiac ryanodine receptor channel by luminal Ca2+ involves luminal Ca2+ sensing sites. Biophys. J. 75:2801–2810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.McGarry, S. J., and A. J. Williams. 1994. Adenosine discriminates between the caffeine and adenine nucleotide sites on the sheep cardiac sarcoplasmic reticulum calcium-release channel. J. Membr. Biol. 137:169–177. [DOI] [PubMed] [Google Scholar]
- 31.Protasi, F., C. Franzini-Armstrong, and B. E. Flucher. 1997. Coordinated incorporation of skeletal muscle dihydropyridine receptors and ryanodine receptors in peripheral couplings of BC3H1 cells. J. Cell Biol. 137:859–870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Somlyo, A. V., H. G. Gonzalez-Serratos, H. Shuman, G. McClellan, and A. P. Somlyo. 1981. Calcium release and ionic changes in the sarcoplasmic reticulum of tetanized muscle: an electron-probe study. J. Cell Biol. 90:577–594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Gyorke, S., and M. Fill. 1993. Ryanodine receptor adaptation: control mechanism of Ca2+- induced Ca2+ release in heart. Science. 260:807–809. [DOI] [PubMed] [Google Scholar]
- 34.Schiefer, A., G. Meissner, and G. Isenberg. 1995. Ca2+ activation and Ca2+ inactivation of canine reconstituted cardiac sarcoplasmic reticulum Ca2+-release channels. J. Physiol. (Lond.). 289:337–348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Laver, D. R., T. M. Baynes, and A. F. Dulhunty. 1997. Magnesium inhibition of ryanodine-receptor calcium channels: evidence for two independent mechanisms. J. Membr. Biol. 156:213–229. [DOI] [PubMed] [Google Scholar]
- 36.Samso, M., T. Wagenknecht, and P. D. Allen. 2005. Internal structure and visualization of transmembrane domains of the RyR1 calcium release channel by cryo-EM. Nat. Struct. Mol. Biol. 12:539–544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Sitsapesan, R., and A. J. Williams. 1994. Gating of the native and purified cardiac SR Ca2+-release channels with monovalent cations as permeant species. Biophys. J. 67:1484–1494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Sitsapesan, R., and A. J. Williams. 1990. Mechanisms of caffeine activation of single calcium-release channels of sheep cardiac sarcoplasmic reticulum. J. Physiol. (Lond.). 423:425–439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Williams, A. J., and S. R. Holmberg. 1990. Sulmazole (AR-L 115BS) activates the sheep cardiac muscle sarcoplasmic reticulum calcium-release channel in the presence and absence of calcium. J. Membr. Biol. 115:167–178. [DOI] [PubMed] [Google Scholar]
- 40.Smith, J. S., R. Coronado, and G. Meissner. 1986. Single channel measurements of the calcium release channel from skeletal muscle sarcoplasmic reticulum. Activation by Ca2+ and ATP and modulation by Mg2+. J. Gen. Physiol. 88:573–588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Meissner, G. 1994. Ryanodine receptor/Ca2+ release channels and their regulation by endogenous effectors. Annu. Rev. Physiol. 56:485–508. [DOI] [PubMed] [Google Scholar]
- 42.Meissner, G., and J. S. Henderson. 1987. Rapid calcium release from cardiac sarcoplasmic reticulum vesicles is dependent on Ca2+ and is modulated by Mg2+, adenine nucleotide, and calmodulin. J. Biol. Chem. 262:3065–3073. [PubMed] [Google Scholar]
- 43.Jiang, D., R. Wang, B. Xiao, H. Kong, D. J. Hunt, P. Choi, L. Zhang, and S. R. W. Chen. 2005. Enhanced store overload-induced Ca2+ release and channel sensitivity to luminal Ca2+ activation are common defects of RyR2 mutations linked to ventricular tachycardia and sudden death. Circ. Res. 97:1173–1181. [DOI] [PubMed] [Google Scholar]
- 44.Honen, B. N., D. A. Saint, and D. R. Laver. 2003. Suppression of calcium sparks in rat ventricular myocytes and direct inhibition of sheep cardiac RyR channels by EPA, DHA and oleic acid. J. Membr. Biol. 196:95–103. [DOI] [PubMed] [Google Scholar]
- 45.Swan, J. S., K. Dibb, N. Negretti, S. C. O'Neill, and R. Sitsapesan. 2003. Effects of eicosapentaenoic acid on cardiac SR Ca2+-release and ryanodine receptor function. Cardiovasc. Res. 60:337–346. [DOI] [PubMed] [Google Scholar]
- 46.Gyorke, I., N. Hester, L. R. Jones, and S. Gyorke. 2004. The role of calsequestrin, triadin, and junctin in conferring cardiac ryanodine receptor responsiveness to luminal calcium. Biophys. J. 86:2121–2128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Xu, L., and G. Meissner. 2004. Mechanism of calmodulin inhibition of cardiac sarcoplasmic reticulum Ca2+ release channel (ryanodine receptor). Biophys. J. 86:797–804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Lukyanenko, V., S. Viatchenko-Karpinski, A. Smirnov, T. F. Wiesner, and S. Gyorke. 2001. Dynamic regulation of sarcoplasmic reticulum Ca2+ content and release by luminal Ca2+-sensitive leak in rat ventricular myocytes. Biophys. J. 81:785–798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Yang, Z., and D. S. Steele. 2001. Effects of cytosolic ATP on Ca2+ sparks and SR Ca2+ content in permeabilized cardiac myocytes. Circ. Res. 89:526–533. [DOI] [PubMed] [Google Scholar]