Multiple Association States between Glycine Receptors and Gephyrin Identified by SPT Analysis

Abstract

The scaffolding protein gephyrin is known to anchor glycine receptors (GlyR) at synapses and to participate in the dynamic equilibrium between synaptic and extrasynaptic GlyR in the neuronal membrane. Here we investigated the properties of this interaction in cells cotransfected with YFP-tagged gephyrin and GlyR subunits possessing an extracellular myc-tag. In HeLa cells and young neurons, single particle tracking was used to follow in real time individual GlyR, labeled with quantum dots, traveling into and out of gephyrin clusters. Analysis of the diffusion properties of two GlyR subunit types—able or unable to bind gephyrin—gave access to the association states of GlyR with its scaffolding protein. Our results indicated that an important portion of GlyR could be linked to a few molecules of gephyrin outside gephyrin clusters. This emphasizes the role of scaffolding proteins in the extrasynaptic membrane and supports the implication of gephyrin-gephyrin interactions in the stabilization of GlyR at synapses. The kinetic parameters controlling the equilibrium between GlyR inside and outside clusters were also characterized. Within clusters, we identified two subpopulations of GlyR with distinct degrees of stabilization between receptors and scaffolding proteins.

INTRODUCTION

Changes in the number of postsynaptic receptors are essential to the regulation of numerous neuronal processes such as the construction and the plasticity of synapses (1–3). Cycling between surface and intracellular compartments is no longer considered the only way of modulating the number of receptors at synapses. Strong evidence, revealed in imaging and electrophysiological studies, now supports the implication of surface trafficking (4). Observation of receptor movements in the plasma membrane of live cells, in real time and at the single molecule level, has been a decisive experimental advance that definitely favors the idea that lateral diffusion is an important parameter. More precisely, single particle imaging techniques have enabled the direct observation of i) receptors' exchanges between the extrasynaptic and the synaptic compartments (5,6); ii) transient stabilization by scaffolding proteins (7,8); and iii) changes in lateral dynamics induced by pharmacological treatment affecting neuronal activity (9), calcium influx (10), and cytoskeleton elements (11). In light of these results, the control of the receptor amount at synapses is now thought of in terms of regulation of the equilibrium between synaptic and extrasynaptic pools of receptors through lateral diffusion in the membrane and transient anchoring by scaffolding molecules.

Glycine is the predominant inhibitory neurotransmitter in the spinal cord. Mature glycine receptors (GlyR) are composed of two α-and three β-subunits (12). At inhibitory synapses, the cytoplasmic protein gephyrin, which binds to the β-subunit (13) and to microtubules (14), is a key partner of GlyR. Its role has been attested to by several experimental findings: gephyrin is required for the clustering of GlyR in front of glycine releasing sites (15), GlyR confinement is favored when the receptor is associated with gephyrin clusters (7), and intracellular GlyR-gephyrin association increases the accumulation rate of GlyR in the plasma membrane (16). Thus receptor-scaffold protein interactions are likely to tune the dynamic equilibrium between synaptic and extrasynaptic GlyR. Two, nonexclusive, levels of interaction could be implicated. First, receptors could diffuse in the extrasynaptic membrane and then be trapped at postsynaptic gephyrin clusters containing free binding sites. Second, receptors diffusing in the extrasynaptic membrane could already be associated with gephyrin, and “stabilization” at synapse would result from gephyrin-gephyrin interactions.

In mature neuronal networks, a large number of factors could take part in the modulation of the equilibrium between GlyR inside and outside gephyrin clusters. First, the lateral dynamics of GlyR might be hindered by molecular crowding within the membrane or by the presence of adhesion molecules at the edge of synapses. Second, the synaptic cleft might induce steric constraints on the diffusion of receptors labeled with an extracellular probe (5,10). These factors may complicate the analysis of the diffusion dynamics of GlyR and its regulation by gephyrin. Experiments were performed both in neurons cultured 3–4 days in vitro (DIV), a developmental stage at which only a few synaptic buttons are formed (17), and in HeLa cells. Cells were cotransfected with gephyrin and subunits of GlyR, as previously done to study the formation of GlyR-gephyrin clusters (16,18). We used a Venus (a yellow fluorescent protein (YFP)) (19) tagged gephyrin (VeGe) and myc-tagged GlyR α₁ (GlyR α₁) or α₁βgb subunits (GlyR α₁βgb). The GlyR α₁ subunit is the predominant adult GlyR α-subunit isoform (20) and GlyR α₁βgb is a chimeric GlyRα₁ containing the gephyrin binding sequence (βgb, which is sufficient to enable the receptor to interact with gephyrin (13).

We have compared the GlyR diffusion in neuronal and nonneuronal (HeLa) cells because the cell types differ in their membrane composition and cytoskeleton organization, two factors known to affect the lateral dynamics of transmembrane proteins. In particular, HeLa cells do not contain other GlyR α-or β-subunits that could interact with the studied transfected subunit and neurons may contain additional molecules (21) specifically controlling the lateral diffusion of neuroreceptors.

In cotransfected cells, single particle tracking techniques (22) were used to investigate the properties of tagged GlyR traveling in and out gephyrin clusters. Quantum dots (QDots) were chosen as fluorescent probes to label GlyR because i) compared to fluorophores, they can be detected at the single nanoparticle level with high signal/noise ratio for longer durations; and ii) compared to beads (∼500 nm in diameter, manipulated with an optical trap) used in other studies (7), QDots (∼15 nm in diameter) are closer to molecular sizes and they allow multiple receptors to be simultaneously tracked.

The combination of QD labeling with cotransfection led to new findings on the interactions controlling the stabilization of GlyR at gephyrin clusters. In particular, it enabled us to overcome many limitations encountered in previous work, due either to the size of the probe (7) or to the complex synaptic environment, which rendered the analysis of the receptor-scaffold interactions more difficult in mature neurons (5). We primarily took advantage of the ability of single molecule experiments to differentiate between subpopulations and to quantitatively analyze the dynamics of stochastic processes. First, we separately analyzed GlyR lateral dynamics inside and outside gephyrin clusters. We found significant differences in the diffusion properties of GlyR outside gephyrin clusters depending on their ability to bind gephyrin. This led to the identification of two subpopulations of GlyR outside gephyrin clusters. Using pharmacological treatments and gephyrin variants, respectively, we investigated the influence of the cytoskeleton elements and of gephyrin oligomerization abilities on GlyR diffusion. Together with previous findings on the endogenous receptors (11), our results allowed us to draw conclusions on the influence of gephyrin on synaptic and extrasynaptic GlyR dynamics. Second, for GlyR able to bind gephyrin, we determined the kinetic parameters of the dynamic equilibrium of GlyR traveling into and out of gephyrin clusters. Two subpopulations of receptors inside gephyrin clusters were characterized, corresponding to different degrees of stabilization. Altogether, our results led us to propose a new kinetic model accounting for the receptor-scaffold interaction and stabilization at synapses.

MATERIALS AND METHODS

Cell cultures and transient transfections

HeLa cells were cultured in Dulbecco's Modified Eagle's Medium (DMEM) (Invitrogen, Cergy Pontoise, France) containing 10% fetal calf serum (Invitrogen) at 36°C in a 5% CO₂ atmosphere. Transfection experiments were performed on subconfluent cultures (60% confluency) plated on glass coverslips (Assistant, Winigor, Germany) using the FuGENE 6 (Roche Diagnostics, Meylan, France) method according to the manufacturer's protocol. Cells were usually transfected with 2 μg of plasmid DNA in 60-mm dishes.

Primary cultures of spinal cord neurons were prepared from embryonic Sprague Dawley rats at day 14 as described previously (23). Cells were plated at a density of 5.10⁴ cells/cm² onto 18-mm diameter glass coverslips coated with 70 μg/mL poly-D,L-ornithine (Sigma, St Louis, MO) and then with 5% fetal calf serum. Cultures were maintained in serum-free Neurobasal medium supplemented with B27 (1X), 2 mM glutamine, and antibiotics (Invitrogen) at 36°C in a 5% CO₂ atmosphere. Neurons were transfected 2 or 3 days after plating using the Lipofectamine2000 method (Invitrogen) according to the manufacturer's protocol with 2 μg of plasmid DNA in 20-mm wells.

The construction of myc-tagged GlyR α₁ and α₁βgb subunit cDNA used in this study has been previously described (18). The Venus∷gephyrin chimera (VeGe, (19)) used in most of the experiments corresponds either to gephyrin Ge(2) (clone p1 (24)) or to Ge(2,4,5) (25) harboring a YFP at their N-termini. Untagged Ge(2) was used in some experiments. Ge(2,4,5) is a gephyrin variant unable to form trimers (26). A plasmid equimolar GlyR subunits/gephyrin ratio was used in all cotransfection experiments. Cells were imaged 24 h after transfection.

Drug treatments

Actin filaments and microtubules were depolymerized using latrunculin-A (3 μM, Sigma) and nocodazole (10 μM, Sigma), respectively. For single particle tracking (SPT) experiments, cells were preincubated with drugs added to the culture medium, then stained for GlyRs (see below) and imaged in the recording medium containing the appropriate drug. For each pharmacological treatment, immunofluorescence experiments were used to determine the incubation time (preincubation time + staining time). The shortest time leading to efficient depolymerization and ensuring the reversibility of the drug effect was chosen. Finally, before live imaging, neurons were incubated with latrunculin-A or nocodazole for 50 min.

Live cell GlyR staining and single particle imaging

We prepared an anti-myc antibody (mouse anti-myc, clone 9E10; Roche) covalently coupled to QDots (emitting at 655 nm) according to the protocol defined by Quantum Dot Corporation. In brief, amino-coated QDots activated with SMCC (Succinimidyl 4-[N-maleimidomethyl]cyclohexane-1-carboxylate) reacted with anti-myc antibodies reduced with dithiothreitol. Reagent concentrations were adjusted to optimize the control of the stoichiometry of the labeling of myc-tagged GlyRs by QDots. To increase the probability that no more than one antibody is present at the nanoparticle surface, we mixed antibodies and Qdots in a 1.5:1 ratio. After reaction, the constructs were purified by size-exclusion chromatography.

To label cell surface myc-tagged GlyR, cells were incubated for 10 min in anti-myc antibodies coupled to QDots. The concentration (∼0.3 nM) was adjusted to have 10–20 labeled GlyR per field of view (size 20 μm × 20 μm). Cells were then extensively washed. All washes and incubation steps were performed in fresh “air-MEM” medium supplemented with either fetal calf serum (10%) in the case of HeLa cells or B27 (1X) and Na-pyruvate (1 mM), both from Invitrogen, in the case of neurons. “Air-MEM” medium consisted of phenol-red-free minimal essential medium supplemented with glucose (33 mM, Sigma), HEPES (20 mM), and glutamine (2 mM) from Invitrogen.

Cells were imaged in this supplemented “air-MEM” medium at room temperature (HeLa cells) or at 37°C (neurons) in an open chamber mounted onto an inverted microscope (Olympus, Tokyo, Japan, IX70) equipped with a 60× objective (numerical aperture = 1.45, Olympus). QDots and Venus-YFP were detected using an Hg⁺ lamp and appropriate filter sets (525AF65/560DRLP/655WB20 and 470DF35/505DRLP/525AF45 for QDots and Venus, respectively; Omega Filters, Brattleboro, VT). For the Qdots, the excitation intensity was ∼150–500 W/cm². QDot recordings consisted of 512 consecutive frames acquired with an integration time of 75 ms with a charge-coupled device camera (Micromax 512EBFT, Roper Scientific, Tucson, AZ) using Metaview (Universal Imaging, West Chester, PA). For each recorded cell that was cotransfected with a Venus-tagged gephyrin, one image of VeGe clusters was taken with an integration time of 1 s as well as a brightfield image. All recordings were performed within 30 min after GlyR staining to avoid GlyR internalization (checked previously by acid wash assay (11) and immunoelectron microscopy (5)).

Single particle tracking and data analysis

Analysis of the trajectories was done using MATLAB (The MathWorks, Natick, MA). Single QDots were identified by their fluorescence intermittency, i.e., the alternation of periods when the QDot emitted fluorescence photons (“on” time) and periods when it was dark (“off” time) (27).

Tracking of single QDots

Single molecule tracking was performed with homemade software accounting for blinking in the fluorescence signal (28). In brief, the method consisted of two main steps applied on each frame successively. First, fluorescent spots were detected by cross correlating the image with a Gaussian model of the point spread function. Around the local maxima above a threshold, a least squares Gaussian fit was applied to determine the spot center with a spatial accuracy of 5–10 nm (depending on the signal/noise ratio). Second, the spots in a given frame were associated to the most likelihood trajectories estimated on previous frames of the image sequence. The criterion of association was based on the assumption of free Brownian diffusion of receptors. Only trajectories interrupted for no longer than 10 consecutive frames were considered. The set of trajectories was thus updated frame by frame, taking into account “off” events between 1 and 10 frames. After completion of the process, a manual association step was performed to obtain trajectories as long as possible and to check for possible error of the automatic program. The mean duration (averaged over all tracked QDots) of a trajectory was 36.2 s. Throughout the text, n corresponds to the number of individual trajectories considered in the analysis.

Values of the mean square displacement (MSD) were calculated from whole or parts of trajectories. This function enables the analysis of the lateral dynamics on short (initial diffusion coefficient) and long (types of motion) timescales.

Initial diffusion coefficient

Initial diffusion coefficients (D_2-5) were calculated with a fit between data points 2 and 5 of MSD curves versus time with the equation is the spot localization accuracy in one direction defined as the standard deviation of the difference between the actual and the estimated position determined by a Gaussian fit (29). To account for the statistical fluctuations in the calculation of the MSD of a finite trajectory, the fit was done by assigning a different weight to each point (30,31). Given the typical length of individual trajectories, the relative error bar in the diffusion coefficient due to statistical effects was ∼20%. Because of the large dispersal of values (over four orders of magnitude), the distributions of diffusion coefficient and the median values were compared rather than the mean values. Moreover, we plotted the cumulative probability C(d) of the diffusion coefficient D, defined as the probability that D is inferior to d. The use of C was preferred to the histogram (even in a semilogarithmic scale) because it allowed the direct reading of the median values and did not require an arbitrary binning of the data points.

Types of motion

All trajectories showing D_2-5 < 10⁻⁴ μm² s⁻¹ (i.e., showing a flat MSD) were classified as immobile. To sort the other trajectories according to their type of motion, a parameter for the relative deviation RD adapted from Kusumi et al. (32) was computed:

where MSD_N(t) is the value of the MSD at time t from a sequence of N frames and is the expected value of the MSD for a particle undergoing a Brownian diffusion with coefficient D_2-5. We chose to look at time t = 1.5 s because, by eye, the negative deviation of the MSD curve, characteristic of a restricted motion, occurred mostly around t = 1 s.

Trajectories undergoing simple Brownian diffusion with a coefficient D = 0.1, 0.01, and 0.001 μm² s⁻¹ and for N = 50, 100, 300, and 500 steps were generated (500 trajectories for each (D,N) combination). Moreover, the intermittent emission of the QDots used in the experiments was taken into account by using the phenomenological distributions of “on” and “off” times. We determined RD_min(D,N,1.5 s) (resp. RD_max(D,N,1.5 s)) the limit for which only 2.5% of trajectories had a lower (resp. larger) RD(D,N,1.5 s) value. The simulations indicated that RD_min and RD_max did not change much with D but varied a lot with N. So, for each trajectory i of length N⁽ⁱ⁾, RDmin⁽ⁱ⁾ and were extrapolated from the curves of RD_min and RD_max as a function of N determined by the simulations. All nonimmobile trajectories were then classified into three categories of motions: simple Brownian motion (RD_min < RD < RD_max), restricted (RD < RD_min), and directed (RD > RD_max). This classification is dependent on the observation rate (camera frame rate and exposure time) of our experiment. Indeed, because of the time averaging occurring over the frame time, hop diffusion and confined diffusion can be mistaken as slow simple Brownian diffusion and immobile motion, respectively (33).

Confinement diameter

To avoid points too tainted with statistical variations, we cut off the MSD at a maximum lag time of one-quarter of the total number of time steps (31). The MSD of the trajectories showing a restricted motion were then fitted by the expression for a confined diffusion added to a random walk on a longer timescale (hop diffusion is one of the mechanisms leading to this kind of MSD):

where L is the side of a square domain in which diffusion is confined and D_2-5 and D_mac the diffusion coefficients on short and longer timescales. We considered that receptors were confined in circular areas of diameter Moreover, we checked that the influence of time averaging (T = 75 ms) was weak in the case of the trajectories classified as restricted: as recommended in Destainville and Salomé (34), 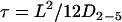was calculated and we found T ≪ τ in most cases.

Dwell time measurement

For cells cotransfected with VeGe and GlyR α₁βgb, the receptor dwell times inside and outside gephyrin clusters were measured. VeGe images were filtered using a multidimensional image analysis interface running in MetaMorph (V. Racine, J. Salamero, and J. B. Sibarita, unpublished work). Briefly, fluorescent clusters were detected with a procedure based on wavelet decomposition, allowing the selection of small structures with low intensities and large structures with high intensities at the same time. We checked that the VeGe clusters were stable entities and did not move significantly on the timescale of one recording (∼40 s). Once identified, VeGe clusters defined the inside and the outside VeGe cluster compartments. Because of their blinking property, QDot-tagged GlyR (GlyR-QDot) could be detected in three states: inside VeGe clusters (state 1), outside VeGe clusters (state 0), and nonemitting (state −1).

GlyR-QDot location during nonemitting events was approximated as follows (see Charrier et al. (11) for detailed illustration). When a GlyR-QDot was detected in the same compartment before and after the nonemitting event, it was considered to be remaining in the same compartment, and the duration of the nonemitting event was added to the time spent in this compartment. When GlyR-QDot was not detected in the same compartment before and after the nonemitting event, the duration of the nonemitting event was equally shared between the two compartments, to not favor any of them. After this time reallocation, the signal of single GlyR-QDots as a function of time (state 0 or 1) was averaged on a sliding window. More precisely, the lower resolution of VeGe cluster detection (pixel edges) compared to the pointing accuracy of QDots (<10% pixel size) could lead to an overestimation of dwell times of one frame. So the smoothing was used to counterbalance the artificial pixelization of the detected VeGe clusters.

After these data treatments, dwell times inside (t_IN) and outside (t_OUT) VeGe clusters were extracted from the state of GlyR-QDot as a function of time (see Fig. 5 B). The data analysis described above introduces uncertainty in the quantitative estimate of the dwell times. Since the duration of the nonemitting event is equally shared, this uncertainty is on the order of t/2, where t is the typical duration of nonemitting events. Since t is on average ∼0.3 s (four frames) and the duration of the nonemitting events represents <20%, the error on the dwell times does not affect the significance of our results (see Results). To ensure the validity of the procedure, it is also important to set antibody concentration so that the typical distance r between Qdots is sufficiently large to allow reliable identification of individual trajectories despite the nonemitting events. More precisely, r must be > ∼1 μm (using the value of D obtained for the fast diffusing extracluster GlyR), a condition which was always fulfilled in our experiments.

FIGURE 5.

Properties of the equilibrium between GlyR inside and outside clusters. (A) Simple scheme of the dynamic equilibrium (top panel). (Bottom panel) Example of a trajectory (in neurons) alternating between the inside (gray) and the outside (black) gephyrin clusters (dark gray) compartments. Scale bar: 5 μm. (B) Examples of localization (IN and OUT) as a function of time. The upper plot corresponds to the trajectory in (A). (C) Comparison between the cumulative probability of in (gray circle) and out (black square) dwell times in HeLa cells (left panel) and neurons (right panel). (Full lines) Biexponential fit of the data. Mean dwell times inside (〈t_IN〉) and outside (〈t_OUT〉) VeGe(2) clusters. (D) Proportion of QDots within gephyrin clusters as a function of time, averaged over all films (n =39, 46 for HeLa cells (left panel) and neurons (right panel), respectively, computed for “swapping” GlyR.

Statistical analysis and image preparation

Statistical analyses were done using MATLAB and StatView (Abacus Concepts, Berkeley, CA) on data compiled using Microsoft Excel (Microsoft France, Les Ulis, France). Images were prepared for printing using Illustrator (Adobe Systems, San Jose, CA).

RESULTS

We verified, carrying out immunohistochemistry experiments with a cell surface labeling of GlyR, in both HeLa cells and neurons, that GlyR-gephyrin interaction modified the distribution pattern of the two molecules as previously described (7,16). More specifically, on cells cotransfected with VeGe(2) and GlyR α₁βgb, as illustrated in Fig. 1 A, gephyrin and receptor clusters colocalize at the cell surface and large intracellular gephyrin aggregates not associated to surface GlyRs are present. Only the latter gephyrin aggregates exist when cotransfecting VeGe(2) with GlyR α₁. HeLa cells were preferred because they offer large flat and thin areas at their border, a situation convenient for videomicroscopy. To access GlyR lateral dynamics, we carried out experiments on HeLa cells and 3–4 DIV neurons where the GlyRs were labeled with QDots (previously described in Dahan et al. (5) and see Materials and Methods).

FIGURE 1.

Examples of VeGe(2) and GlyR α₁βgb distribution patterns and trajectories in cotransfected HeLa cells and 3–4 DIV neurons. (A) Gephyrin clusters (YFP fluorescence, green) and GlyR α1βgb immunopositive clusters (red, cell surface labeling: labeling at 4°C before fixation) colocalize at the cell surface (yellow puncta) in HeLa cells (A1–4) and in 3 DIV neurons (A5–8). A2 is a zoom of a characteristic large flat area of HeLa cells (white box in A1). Ve∷Ge and GlyR α₁βgb channels are shown separately (A3–4) and superimposed (A2). (A6–8) zooms of areas on a distal and on a proximal part of dendrite and on the soma, respectively (white boxes in A5). (B) Examples of MSD as a function of time for a simple Brownian diffusion (blue dots) and a restricted diffusion (green dots). (Inset) The corresponding trajectories are outside (blue) or inside (green) gephyrin clusters (red), respectively. Scale bar: 1 μm. (full lines) theoretical curves for the type of motion on a long timescale. (Green dotted line) linear fit on a short timescale for the MSD corresponding to a restricted diffusion.

Lateral dynamics and confinement of GlyR α₁βgb inside and outside gephyrin clusters

The MSD function was used to characterize the lateral dynamics of GlyR α₁βgb inside and outside gephyrin clusters on cells cotransfected with GlyR α₁βgb and VeGe(2). The thresholded VeGe image defined the inside and the outside VeGe cluster compartments (see Materials and Methods). Examples of trajectories and MSD are shown in Fig. 1 B. If a receptor was detected at least 90% of the time in the same compartment, its whole trajectory was used to characterize its movement in this particular compartment. For receptors that changed compartment during at least 10% of the recording, the physical characteristics of the trajectory in each compartment were considered separately.

The initial diffusion coefficient (D_2-5), calculated on the first 2–5 points of the MSD, informed us of the lateral diffusion on a short timescale. Because of the large dispersal of the D_2-5 values, the cumulative probability and the median values were used for comparison. Given the pointing accuracy (5–10 nm) and the sampling rate (13 Hz), the trajectories with D_2-5 < 10⁻⁴ μm² s⁻¹ could not be analyzed and were considered to belong to immobile objects. As expected, the median diffusion coefficient derived on a short timescale of GlyR α₁βgb outside gephyrin clusters was 12 and 10 times higher than the diffusion coefficient of GlyR α₁βgb inside gephyrin clusters, in HeLa cells, and in neurons, respectively (Fig. 2 A, Table 1). A further analysis on a longer timescale (≥1.5 s) was based on the relative deviation (32) of the experimental MSD compared to the MSD of a simple Brownian motion. This ensured the distinction between simple Brownian and restricted motions (see Materials and Methods). For the latter, we estimated the size of confinement (d_conf) of the trajectories by fitting the MSD with the expected generic expression for a restricted diffusion (see Materials and Methods). The confinement zones inside and outside VeGe(2) clusters were significantly different. Within clusters, d_conf was reduced by a factor of 1.7 and 3 in HeLa cells and neurons, respectively (Fig. 2 B, Table 1).

FIGURE 2.

Comparison of GlyR α₁ and α₁βgb dynamics. (A) Cumulative distribution of the initial diffusion coefficients. (B) Confinement diameter calculated on trajectories showing a restricted motion (mean ± SE). Experiments were performed in HeLa cells (A1, B1) and neurons (A2, B2). Comparison of the values obtained with GlyR α₁ (dark gray, n = 313, 213, 85, and 76 for A1, A2, B1, and B2, respectively), GlyR α₁βgb inside (gray, n = 59, 91, 33, and 55 for A1, A2, B1, and B2, respectively) and outside (black, n = 279, 332, 125, and 156 for A1, A2, B1, and B2, respectively) gephyrin clusters. Kolmogorov-Smirnov test (A) or Mann Whitney test (B) between indicated distribution and the values obtains for GlyR α1βgb outside gephyrin clusters: **p < 10⁻², ***p < 10⁻³, ****p < 10⁻⁴. (C) In neurons, cumulative distribution of the initial diffusion coefficients for all GlyR α₁βgb outside VeGe(2) clusters (dark diamond, n = 332), for GlyR α₁βgb not cotransfected with gephyrin (dark square) and for GlyR α₁βgb inside gephyrin clusters (gray circle). Estimation of the cumulative distribution of GlyR α1βgb outside VeGe(2) clusters affected by the presence of gephyrin (N1 values) for different value of N1/N: 0.1–0.4 (gray curves) and 0.5–0.9 (black curves). The calculated curves are bounded by 1 only when N1/N > 0.4.

TABLE 1.

Comparison of diffusion coefficients and confinement for all types of GlyR in HeLa cells and 3 DIV and 10 DIV neurons

Cell type	GlyR type	n	Median D (μm2 s−1)	Restricted (%)*	dconf† (nm)
HeLa cells	α1βgb inside	59	6.0 10−4	56	101 ± 13
	α1βgb outside	279	7.6 10−3	45	175 ± 14
	α1	313	2.7 10−2	27	275 ± 22
3 DIV neurons	α1βgb inside	91	6.0 10−4	62	126 ± 16
	α1βgb outside	332	6.1 10−3	47	388 ± 42
	α1	213	1.2 10−1	36	747 ± 85
10 DIV neurons‡	synaptic	90	1.0 10−3	51	166 ± 19
	extrasynaptic	231	7.0 10−3	–	–

^*Apart from immobile trajectories.

^†Mean ± SE on restricted trajectories.

^‡Data from Charrier et al. (11).

In both HeLa cells and neurons, GlyR at gephyrin clusters diffused more slowly, with a smaller confinement area than outside VeGe(2) clusters. These results confirmed that the interaction between GlyR α₁βgb and Venus-tagged gephyrin regulates GlyR lateral dynamics inside gephyrin clusters as it does at postsynaptic differentiation (5).

Comparison between GlyR α₁βgb inside/outside gephyrin clusters and endogenous GlyR synaptic/extrasynaptic

In previous SPT experiments (5,11), the lateral dynamics of the endogenous GlyR has been studied in 10–12 DIV spinal cord neurons where the synaptic contacts are biochemically “mature” (35). As seen in Table 1, the median diffusion coefficient was 10 times higher outside than inside VeGe(2) clusters and 7 times higher outside than inside synapses. Moreover the values outside VeGe(2) clusters and outside synapses were very close. d_conf at synapses did not significantly differ from the values inside VeGe(2) clusters (see Fig. 2 B, Table 1). These results indicated that the dynamic behavior of the endogenous synaptic and extrasynaptic receptors is mimicked by the behavior of GlyR α₁βgb inside and outside the gephyrin cluster in our model system. Thus, the equilibrium GlyR inside/GlyR outside (with regard to gephyrin clusters) strongly participates in the equilibrium GlyR synaptic/GlyR extrasynaptic.

Using the definitions of the number of transitions of GlyR between compartments and the residence time at synapses introduced in Charrier et al. (11), we found a small increase (1.5-fold) in the number of transitions associated with a decrease in residence time when comparing transfected and endogenous receptors (0.71 ± 0.11 (44 recordings, mean ± SE) and 0.45 ± 0.08 (12 recordings) transitions/QDot/minute, respectively; and mean residence time: 13 ± 4 s at synapses and 16 ± 6 s at VeGe(2) clusters, respectively).

Gephyrin-receptor interactions also regulate the diffusion of GlyR α₁βgb outside gephyrin clusters

HeLa cells and neurons were cotransfected with VeGe(2) and either GlyR α₁ or GlyR α₁βgb. In both cell types, GlyR α₁ moved, respectively, 4 and 20 times faster and was less confined than GlyR α₁βgb outside VeGe(2) clusters (Fig. 2, A and B, Table 1). The difference between the two cases was that the GlyR α₁ intracellular loop does not contain the βgb sequence of interaction with gephyrin. The βgb sequence is small (18 amino acids) compared to the size of the whole intracellular loop (106 amino acids). It is therefore probably not the reason for the dramatic reduction of dynamics. The observed change in lateral diffusion is, rather, due to an interaction with a molecule directly or indirectly linked to this βgb sequence. We suggest that a small amount of gephyrin is linked to GlyR α₁βgb even outside gephyrin clusters. Gephyrin attached intracellularly to GlyR may i), generate a steric hindrance effect in the cytoplasm, slowing down the receptor diffusion; or ii), allow indirect interactions with subscaffold elements, such as the cytoskeleton, and increase the confinement effects.

GlyR α₁βgb could interact either with endogenous gephyrin or with a small amount of VeGe(2), too small to be detected with our setup. Putative endogenous gephyrin is not implicated since GlyR α₁βgb transfected alone had the same distribution of diffusion coefficient as GlyR α₁ (Supplemental Materials Fig. 1S A). Therefore, the diffusion of GlyR α₁βgb outside VeGe(2) clusters is slowed down by interaction with VeGe. The difference in diffusion coefficient could also be due to the presence of the 28-kDa Venus tag, a molecule that can form dimers. The results of experiments in which cells were cotransfected with both GlyR α₁ or GlyR α₁βgb and untagged gephryrin led us to reject that possibility. Indeed, in the presence of untagged gephyrin, GlyR α₁ still diffused faster than GlyR α₁βgb (Supplemental Materials Fig. 1S B), as in experiments with VeGe.

Gephyrin can form trimers via its N-terminal G-domain and it is believed that dimer formation results from its C-terminal E-domain (36). We performed experiments cotransfecting GlyR with a Venus-tagged gephyrin variant, referred to as VeGe(2,4,5), which cannot trimerize and behaves essentially as a monomer in vitro (26). When coexpressed with GlyR α₁βgb, VeGe(2,4,5) formed clusters although smaller than VeGe(2) ones, in agreement with recent data (26). We propose that these VeGe(2,4,5) clusters were formed as a result of both the five gephyrin binding sites on pentameric GlyR and the potential ability of gephyrin to dimerize. In VeGe(2,4,5) cotransfection experiments, GlyR α₁βgb outside VeGe(2,4,5) clusters had slower diffusion coefficients than GlyR α₁ (Supplemental Materials Fig. 1S C). Since a decrease in diffusion coefficient was found independently of trimerization, we assume that the amount of gephyrin linked to the receptor outside clusters is small. This is consistent with its nondetection with our setup.

We then tried to estimate a lower limit for the proportion of GlyR α₁βgb outside VeGe(2) whose dynamics was affected by the presence of gephyrin (see Fig. 2 C and Supplemental Materials for details). We made the assumption that the population P of GlyR α1βgb outside gephyrin clusters could be divided into two subpopulations: i), a population P1 of receptors linked to a few molecules of gephyrin slowing down their diffusion; and ii), a population P2 corresponding to GlyR α₁βgb not interacting with gephyrin. We supposed that the cumulative distribution, C_P2, of diffusion coefficients for P2 followed the cumulative probability of GlyR α₁βgb transfected alone. The cumulative probability, C_P, of the diffusion coefficient of the population, P (determined in the experiments), can be written C_P = a × C_P1 + (1 − a) × C_P2, with a the proportion of P1 elements in the population P. We calculated C_P1 for different a values, from 0.1 to 1 with a step of 0.1 (Fig. 2 C, gray and black curves). Given that a cumulative probability is comprised between 0 and 1, curves with values superior to 1 (a = 0.1–0.4, gray curves) were excluded. As a result, P1 appeared to constitute at least 40% of the total population. Although qualitative, this estimate indicates that the influence of gephyrin-receptor interactions on the dynamics of GlyR α₁βgb outside gephyrin clusters is not a minor effect.

Distinct effects of F-actin and microtubule disruption on GlyR lateral diffusion in neurons

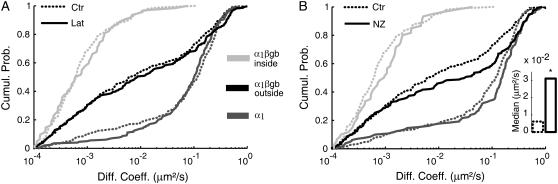
Cytoskeleton elements are implicated in the regulation of GlyR lateral diffusion in 10 DIV neurons (11). In 3 DIV neurons, we depolymerized actin filaments and microtubules with Latrunculin A and nocodazole, respectively (see Materials and Methods). Latrunculin treatment did not modify the lateral diffusion coefficients of any type of GlyR (see Fig. 3 A). In contrast, nocodazole treatment accelerated the diffusion of GlyR α₁βgb outside VeGe(2) clusters (see Fig. 3 B). However, receptors diffusing slowly (D < 10⁻³ μm² s⁻¹) were not affected. This result is consistent with those obtained for native receptors in more mature 10 DIV neurons (11).

FIGURE 3.

Effects of latrunculin and nocodazole on the initial diffusion coefficient of GlyR in 3–4 DIV neurons. Comparison of the cumulative distributions obtained in control conditions (Ctr, full lines) and (A) after latrunculin treatment (lat, dotted lines), (B) after nocodazole treatment (NZ, dotted lines). Values obtained for GlyR α₁ (dark gray, n = 213, 198, and 130 for Ctr, Lat, and NZ, respectively), GlyR α₁βgb inside (gray, n = 91, 62, and 60 for Ctr, Lat, and NZ, respectively) and outside (black, n = 332, 218, and 209 for Ctr, Lat, and NZ, respectively) gephyrin clusters. All cells were cotransfected with VeGe(2). Kolmogorov-Smirnov test p-values are >0.05 except for the comparison of the distributions of GlyR α₁βgb outside VeGe(2) clusters in Ctr and NZ conditions (p-value < 0.01). (B, inset) Highlighting of the median values for GlyR α₁βgb outside VeGe(2) clusters. Wilcoxon rank sum test for equal medians, *p-value < 0.05.

Identification of two GlyR subpopulations inside gephyrin clusters

Two types of receptors inside VeGe(2) clusters were distinguished (see Fig. 4 A), namely, the “stable” GlyR, which remains in the clusters during the recording duration of ∼40 s and the “swapping” of GlyR, which switches between compartments. The fraction of “stable” GlyR was ≈60% of the total number of receptors inside clusters. To characterize the lateral diffusion within VeGe(2) clusters, we considered the whole trajectory for “stable” GlyR and the portions of trajectory inside clusters for “swapping” ones (see Fig. 4 A, green). In both HeLa cells (see Fig. 4 B) and neurons (see Fig. 4 C), the two subpopulations had different dynamics properties: i) “swapping” GlyR diffused significantly faster than “stable” GlyR; ii) the proportion of “swapping” receptors showing a restricted diffusion (27% (n = 22), 39% (n = 38) in HeLa cells and neurons, respectively) was lower than the proportion of “stable” GlyR with a restricted diffusion (72% (n = 37), 75% (n = 53) in HeLa cells and neurons, respectively); and iii) the confinement area of these restricted trajectories was higher in the case of “swapping” GlyR. Thus “stable” GlyRs diffused slower and were more confined than the “swapping” ones. The different dynamic properties of these two types of receptors suggest that several stabilization degrees exist within gephyrin clusters.

FIGURE 4.

Identification of two GlyR subpopulations within a gephyrin cluster. (A) Examples of trajectories for a “stable” (upper trajectory, circle) and a “swapping” GlyR (bottom trajectory, triangle); (gray) parts inside VeGe(2) clusters (dark gray). (B, C) Cumulative probability of diffusion coefficients inside VeGe(2) clusters for “stable” (circle) and “swapping” (triangle) GlyR in HeLa cells (B) and neurons (C). “Swapping” GlyRs diffuse faster than “stable” GlyRs (Kolmogorov-Smirnov test: HeLa cells, p-value < 0.01; neurons, p-value < 0.05). (inset) Vertical bars give the confinement diameter (d_conf, mean ± SE) for trajectories showing a restricted motion.

Kinetic properties of the dynamic equilibrium for “swapping” GlyR

For each “swapping” GlyR (see an example in Fig. 5 A), we extracted the times spent inside (t_IN) and outside (t_OUT) VeGe(2) clusters (see Materials and Methods). Trajectories can be represented as IN and OUT states as a function of time (see Fig. 5 B). The cumulative probability of in and out dwell times were better adjusted by a biexponential function (Fig. 5 C) than by a single exponential one (not shown). Their comparison (see Fig. 5 C) indicated that the probability of getting out of a cluster for a receptor inside was higher than the probability of getting inside for a receptor outside a cluster. The computation of the dwell times yielded mean values 〈t_IN〉 = 2.2 s (2.3 s) and 〈t_OUT〉 = 5.1 s (4.3 s) (see Fig. 5 C) with standard deviation 4.3 s (4.6 s) and 8.2 s (7.2 s) in HeLa cells (neurons). Dwell times of “stable” receptors are by definition necessarily superior to the recording duration. Because its value (38.4 s) represents more than 8 times the standard deviation of 〈t_IN〉 for “swapping” receptors, this further supports the notion that “stable” and “swapping” GlyRs are two distinct populations. The mean dwell times allowed us to evaluate the fraction of time spent inside the VeGe compartment (F_IN), namely We found that “swapping” receptors spent on average 30% and 35% of their time inside VeGe(2) clusters for HeLa cells and neurons, respectively.

We next checked whether the IN and OUT populations of receptors had reached a stationary value. To this aim, the proportion P_IN(t) of QDots inside VeGe clusters was calculated at each time, t, and averaged over N recordings, considering only the “swapping” receptors (see Fig. 5 D). This proportion was stable (mean ± SD; HeLa cells: P_IN = 29.1% ± 2.8%; neurons: P_IN = 33.4% ± 2.2%, N = 39 and 46 for HeLa cells and neurons, respectively). Values of F_IN are in remarkable agreement with P_IN values. This indicates that the approach based on time averaging is fully consistent with that based on ensemble averaging. Furthermore, the values found in HeLa cells and in neurons are close, suggesting that the equilibrium characteristics are independent of the cell type.

DISCUSSION

Stabilization of GlyR within synapses is mainly provided by scaffolding clusters

Diffusion properties for GlyR α₁βgb in the presence of VeGe(2) have been characterized using diffusion coefficients and confinement area. This α₁βgb subunit forms homomeric receptors able to bind gephyrin (13), in this case VeGe(2). The values measured for exogenous GlyR inside and outside gephyrin clusters in 3 DIV neurons, where synapses have not yet been formed (37), were close to the ones found in 10 DIV neurons (5,11) for the endogenous GlyR in the synaptic and extrasynaptic compartments. The size of VeGe(2) clusters is comparable in young neurons (3 DIV, i.e., without synapses, ≈0.16 μm² (7)) and in older ones (9–12 DIV, i.e., when synapses are formed, ≈0.3 μm² (19)). This indicates that the GlyR-gephyrin interaction is sufficient to form clusters of appropriate size. This also suggests that the prepostsynaptic interaction does not regulate this size. Furthermore, comparison of GlyR-QD behavior at VeGe(2) nonsynaptic clusters and at synapses (5,11) allows us to conclude that the physical properties of GlyR lateral diffusion was comparable at nonsynaptic VeGe(2) clusters (i.e., in young neurons) and at synapses. Therefore, given that synaptic diffusion and confinement are controlled by gephyrin clusters, we hypothesize that physical diffusive properties set the size of GlyR-gephyrin coclusters.

QDots do not seem to induce important steric constraints on GlyR dynamics inside synapses. This is consistent with previous experiments (5) that have shown that similar synaptic diffusion characteristics were measured when labeling GlyR with either QDots or a much smaller probe (Cy3). However, Groc et al. (9) reported that α-amino-3-hydroxy-5-methyl-isoxazole receptors (AMPAR) diffusion was slowed down within synapses when using QDots as probes. The difference in steric hindrance effects due to QDots within excitatory (9) and inhibitory synapses possibly results from the differences in the molecular organization of the synapses.

Although the diffusion properties were very similar, we observed a small increase in the number of transitions and a decrease in the residence time when comparing the results obtained in VeGe(2) clusters in 3 DIV neurons with those at synapses (in 10 DIV neurons (11)). This could result from the presence of transmembrane proteins (38), such as adhesion molecules, at the border of the synapse. By creating obstacles, they might act as molecular barriers limiting the entry and exit of receptors (4,39).

Receptors may diffuse bound to gephyrin molecules even outside gephyrin clusters

The lateral dynamics of GlyR α₁βgb outside gephyrin clusters and of GlyR α₁ were remarkably different. This is likely due to an interaction of GlyR α₁βgb with gephyrin. Indeed, the βgb sequence is too small to slow down GlyR α₁βgb diffusion, and the decrease of coefficient diffusions was only observed when VeGe was present. Moreover, the formation of gephyrin clusters is believed to depend on dimerization and trimerization (36). The similarity between GlyR diffusion properties measured with both variants of gephyrin able or unable to trimerize means that the number of the gephyrin molecules diffusing jointly with GlyR α₁βgb is likely to be small. This is consistent with the fact that the associated fluorescence could not be detected with our setup. We estimated that at least 40% of GlyR α₁βgb outside gephyrin clusters was associated with gephyrin molecules (see Results and Fig. 2 C). This suggests that gephyrin affects the diffusion of a significant portion of GlyR. The comparison of the cumulative probability of diffusion coefficients (Supplemental Materials, Fig. 3 S) of GlyR α₁βgb outside VeGe(2) clusters and of the endogenous extrasynaptic GlyR (11) indicates that some endogenous extrasynaptic GlyRs are also likely to diffuse in a gephyrin-bound form.

Previous data, showing that gephyrin binds to components of motor protein complexes (40) and that some GlyR clusters are associated with gephyrin on their way to the cell surface (16,41), emphasized the role of gephyrin in GlyR intracellular transport toward the membrane. Since GlyRs are delivered at an extrasynaptic location (42) before being selectively retained at synaptic sites (18), our results are compatible with the persistence of gephyrin-GlyR interaction during the process of surface insertion and subsequent lateral diffusion.

If receptors diffuse together with scaffolding proteins, then scaffold-scaffold interactions can also account for GlyR interactions with postsynaptic domains. Consequently, from now on, both gephyrin-receptor interactions and gephyrin-gephyrin interactions have to be considered in the regulation of the dynamic equilibrium of GlyR traveling into and out of gephyrin clusters.

Effects of cytoskeleton disruption on lateral dynamics

In 3 DIV neurons, destabilization of microtubules increased GlyR α₁βgb diffusion coefficients outside VeGe(2) clusters. This is consistent with previous results (11) showing that the microtubules regulate the lateral diffusion of endogenous GlyR in the extrasynaptic compartment at 10 DIV. In contrast, the diffusion of GlyR α₁ was not modified by microtubule depolymerization. Since a significant portion of GlyR diffuses together with gephyrin in the extrasynaptic membrane, our results indicate that the influence of microtubules on GlyR diffusion results from direct or indirect gephyrin-microtubule interaction.

Although F-actin controls the diffusion of synaptic receptors (11), we found no effect of any cytoskeleton element disruption on GlyR α₁βgb inside VeGe(2) clusters. Actually, in 10 DIV neurons, actin microfilaments belong to a large cortical meshwork and are concentrated beneath postsynaptic membranes (43). Our results suggest that microfilaments might not contribute to the size and shape of the VeGe(2) clusters.

Several degrees of GlyR stabilization exist within gephyrin clusters

On the timescale of our experiments (∼40 s), “swapping” GlyR may enter gephyrin clusters, be stabilized, and then be released outside. The “stable” GlyRs had previously entered a gephyrin cluster and then were stabilized enough to stay inside during more than these 40 s. At VeGe(2) clusters, “stable” receptors diffused slower and were more confined than “swapping” ones. Altogether, these results suggest that several degrees of stabilization by gephyrin may coexist within clusters and operate on different timescales.

The existence of several pools of receptors within the same compartment, more particularly at synapses, seems to be a general feature for inhibitory and excitatory receptors. Previous studies based on SPT experiments have led to the distinction between slow and rapid receptors: ∼80% of synaptic GlyR has a diffusion coefficient below 0.01 μm² s⁻¹ (5) and half of synaptic AMPAR below 0.007 μm² s⁻¹ (6). The notion of distinct populations of given receptors at synapses was also established using other approaches. Fluorescent recovery after photobleaching experiments indicated that a large proportion (>50%) of GABA_A (44) and AMPAR (45) was immobile at synapses within at least 15 min. In electrophysiological studies combined with irreversible blocker agent (46) or photoinactivation (47), it was found that a significant portion of N-methyl-D-aspartate (up to 35% within 7 min) and AMPAR was also stable at synapses.

Properties of the equilibrium of GlyR traveling into and out of gephyrin clusters

The ratio between IN and OUT populations of “swapping” receptors are at a stationary value. Therefore, GlyR exchanges between inside and outside gephyrin clusters are likely to be at steady state on the timescale of our experiments. This supports a mesoscopic model (K. Sekimoto and A. Triller, unpublished) accounting for the regulation of the local density of receptors at steady states in which i), scaffold proteins and receptors are reciprocally stabilized; and ii), local exchanges of molecules and synapse stability occur in a state of quasiequilibrium.

To further estimate the binding energy of receptors with gephryin clusters, we assume that receptors diffuse in a potential U equal to 0 and U₀ (U₀ < 0) outside and inside gephyrin clusters, respectively. At thermal equilibrium, the proportion P_IN of receptors inside gephyrin cluster is given by

where α is the fraction of the total cell surface occupied by gephyrin clusters, T the temperature, and k the Boltzmann constant. In HeLa cells and neurons, respectively, a measurement of mean α ± SE gave 5.6% ± 0.6% (n = 20 cells) and 7.9% ± 0.5% (n = 20 cells). Using P_IN measured for “swapping” receptors, U₀ is found to be equal to ∼−2 kT and −1.8 kT in HeLa cells and in neurons, respectively. This suggests that, for “swapping” receptors, gephyrin clusters can be viewed as potential wells with a depth only slightly higher than the thermal energy.

When comparing P_IN with F_IN, the fraction of time spent inside gephyrin clusters by a single receptor along their trajectories, we found very similar results: P_IN ≈ F_IN ≈ 30% (35%) in HeLa cells (neurons). In other terms, the value obtained by time averaging (F_IN) coincides with the one determined by ensemble averaging (P_IN). Therefore, paradoxically, SPT experiments allow the characterization of populations. For instance, the ratio between the receptor densities in both compartments (d_IN and d_OUT) can be estimated as follows: d_IN/d_OUT = P_IN (1 − α)/(α(1 − P_IN)). The density of receptors inside gephyrin clusters was ∼7 and 6 times higher than the density in the extracluster membrane in HeLa cells and neurons, respectively. However, these values are only based on measurements on “swapping” receptors and do not take into account the fraction of stable receptors inside and outside gephyrin clusters. In general, the combination of SPT experiments with electrophysiological data (49) or mass measurement approach (50) will allow a quantitative and dynamic description of the postsynaptic membrane at steady state through the characterization of the kinetic parameters controlling the total dynamic equilibrium.

CONCLUSIONS

In this work, we showed that the tracking of Qdot-tagged receptors, combined with the transfections of different types of GlyR subunits, revealed multiple association states between GlyR and gephyrin that, to our knowledge, had not been identified in previous tracking experiments: i), a significant fraction (>40%) of extracluster receptors are bound to scaffolding gephyrin; and ii), two subpopulations of receptors coexist within gephyrin clusters, with different degrees of stabilization. The dependence of extracluster receptor diffusion on the cytoskeleton was related to the receptor binding to scaffold protein. Our findings strongly suggest that the regulation of GlyRs at synapses can occur not only through receptor-gephyrin interactions but also through gephyrin-gephyrin interactions. In the latter case, extrasynaptic diffusing GlyR-gephyrin complexes are likely to bind to already formed postsynaptic gephyrin clusters.

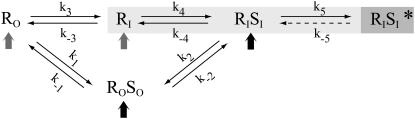
Overall, our data point to a kinetic scheme in which GlyR exchanges between the inside and the outside of gephyrin clusters result from different equilibria (Fig. 6). The association of GlyR with gephyrin even outside gephyrin clusters (see Results) may have several origins: i), they can be preassembled during their transport toward the plasma membrane (black arrow) (16); ii), they can reach the membrane separately (gray arrow) and become associated once in the extracluster membrane (reaction k₁); or iii), they can get outside a gephyrin cluster together (reaction k₂). Then GlyR can enter and exit a gephyrin cluster based either on a receptor-gephyrin interaction (reaction k₃, k₄) or on a gephyrin-gephyrin interaction (reaction k₋₂). Ultimately, once captured inside a gephyrin cluster, GlyR can reach a higher level of stabilization (reaction k₅), which might arise, for instance, from clustering with other trapped receptors. Importantly, this general scheme was observed both in nonneuronal (HeLa) cells and in young neurons, indicating that it is intrinsic to the GlyR-gephyrin interactions and not on molecular partners specifically expressed in neuronal cells. All the reactions of this dynamic equilibrium may be regulated, ultimately controlling the receptor number at synapses.

FIGURE 6.

Schematic view of the different paths leading to stabilization of GlyR by gephyrin clusters. Receptor (R) and its scaffolding protein gephyrin (S) may be preassembled before to be inserted in the cell membrane (black arrow) or they may reach the membrane separately (gray arrow). Receptor-scaffold complexes may be formed outside (equilibrium 1) or inside (equilibrium 4) gephyrin clusters. Both exchanges of receptors (equilibrium 3) and of receptor-scaffold assemblies (equilibrium 2) may occur between the inside (suffix I) and the outside (suffix O) gephyrin clusters' compartments. Once within clusters, receptor-scaffold complexes may reach a higher level of stabilization (equilibrium 5, *).

From a general viewpoint, probing molecular interactions directly in living cells is an important challenge (51). It is of particular interest to go beyond in vitro studies, which cannot take into account, for instance, biochemical and biophysical properties due to the two-dimensional nature of the membrane, inhomogeneities of protein concentrations, or interfering interactions with other molecules such as lipids. The advent of single molecule techniques in live cells now provides a way to study in situ biochemical reactions one molecule at a time. Our experiments show that it is a powerful tool to decipher the kinetic properties of biological assemblies.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.