Membrane Remodeling from N-BAR Domain Interactions: Insights from Multi-Scale Simulation

Abstract

Liposome remodeling processes (e.g., vesiculation and tubulation) due to N-BAR domain interactions with the lipid bilayer are explored with a multi-scale simulation approach. Results from atomistic-level molecular dynamics simulations of membrane binding to the concave face of N-BAR domains are used along with discretized mesoscopic field-theoretic simulations to examine how the spontaneous curvature fields generated by N-BAR domains result in membrane remodeling. It is found that tubulation can be generated by anisotropic N-BAR spontaneous curvature fields, whereas vesiculation is only observed with isotropic N-BAR spontaneous curvature fields at high density. The results of the multi-scale simulations provide insight into recent experimental observations.

INTRODUCTION

Proteins can play an integral role in determining the shapes of lipid bilayers by altering the local curvature (1–7). In particular, the crescent-shaped N-BAR (Bin/amphiphysin/Rvs) domain dimer protein module has been observed to induce curvature in liposomes in vitro, resulting in vesiculation at high concentrations and tubulation at intermediate concentrations (5). The N-BAR domain dimer contains both the BAR domain, as well as two N-terminal amphipathic helices. The crystal structure of the Drosophila amphiphysin BAR domain has recently been determined, revealing a crescent-shaped dimer with a high density of positively charged residues on its concave surface (5). The combination of both the charge distribution and the shape suggests that the induced curvature originates from the binding of negatively charged membranes to its positively charged concave surface. Recent experiments support this idea, and also suggest that the N-terminal helices contribute to curvature generation by embedding in the lipid bilayer (7,8). BAR domains without the N-terminal amphipathic helices have also been observed to induce tubulation (9). However, in general, the radius of curvature generated by BAR and N-BAR domains (radius of curvature ∼15–25 nm) does not match the intrinsic curvature of the BAR domain (radius of curvature ∼11 nm) (5,8). Similar results have been observed for various N-BAR-domain-containing proteins (3,5,10–13), including N-BAR domains with additional structural motifs.

Enhanced liposome tubulation has also been observed in vitro with N-BAR domains from human endophilin-A1 (7); the unique structure of this BAR domain contains two helix-loop appendages that were observed, via fluorescence resonance energy transfer, to penetrate into the lipid bilayer. Recent studies with endophilin N-BAR domains (8) support the notion that the N-terminal amphipathic helices indeed embed in the bilayer and have a large effect on the rate the N-BAR domains unbind from the membrane. These results support the notion that molecular-level details of the BAR domain can have an effect on much longer length- and timescale phenomena such as membrane remodeling (i.e., liposome vesiculation and tubulation).

Recent molecular dynamics (MD) simulations of the N-BAR domain dimer in our group (14) have observed membrane binding to the N-BAR concave face, resulting in the generation of a local membrane curvature that matches the curvature of the N-BAR domain. It was found that a range of induced local curvatures resulted from N-BAR domain binding at different orientations to the membrane; in the case that the N-BAR domain was oriented along the membrane normal vector, the maximum curvature was observed.

Our atomistic-level MD simulations have confirmed that membrane interactions with N-BAR domains can alter the bilayer curvature over atomistic-level length- and timescales. However, simulating the process of liposome vesiculation and tubulation with atomistic-level MD requires spanning length- and timescales ranging from the atomistic (nanometers, nanoseconds) all the way up to the mesoscopic or even semimacroscopic (micrometers, seconds). At the atomistic spatial and temporal scales, the mechanisms associated with the way in which a single N-BAR domain binds to a liposome can be explored (e.g., binding of positively charged residues and N-terminal helix insertion into the bilayer (8)). At mesoscopic length- and timescales, it is instead the collective effect of a time- and spatially-averaged N-BAR domain-containing protein density at the bilayer interface that should be considered. In other words, over large length- and timescales, it is the organization and averaged collective nature of a large number of N-BAR domain-containing proteins on the surface of the liposome that should drive the process of membrane remodeling. It is therefore essential to characterize these interactions at the proper length- and timescales to develop an overall understanding of N-BAR domain-induced membrane remodeling.

The problem described above cannot be addressed with current atomistic-level MD simulation, as the structural reorganization of the liposome occurs on timescales on the order of seconds (7). Alternatively, coarse-grained (CG) models might be applied to model lipid bilayers (15–23) and bilayers with nonlipid molecules (23). This approach might eventually provide an attractive route to model the vesiculation/tubulation of a liposome due to N-BAR domain binding. In principle, quantitatively accurate CG models of an N-BAR domain-containing protein, the surrounding bilayer, and solvent could be developed. Still, simulating a 200 nm, fully solvated liposome with many explicit CG N-BAR domain proteins bound to it would require a currently unprecedented computational effort, and the timescales associated with the vesiculation process (on the order of milliseconds to seconds (7)) would still not likely be obtainable.

Alternatively, a multi-scale theoretical and computational methodology can be employed, where a mesoscopic-scale model is formulated within a field-theoretic framework (24–35). (In Ayton et al. (27), the summation limits in the second summation appearing in Eqs. 9 and 10 should be 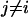to N_c,i). The two spatial/temporal scales (i.e., the atomistic and mesoscopic scales) are connected via material properties (e.g., bending and bulk moduli) and structural characteristics (e.g., spontaneous curvature, bilayer thickness) that are originally evaluated at the atomistic level (29,36,37) and then subsequently employed as key parameterizations at the mesoscopic level. The mesoscopic model describes free energy differences of the overall system in various perturbed and reference states (26–28). N-BAR domain binding can be incorporated into the mesoscopic model by including a local spontaneous curvature field that can be modeled at various degrees of complexity. In this scenario, the N-BAR domain proteins are not explicitly represented and, strictly speaking, the exact instantaneous location of any given N-BAR protein is not specified. This level of abstraction originates from the fact that the mesoscopic field theory-based model corresponds to an ensemble of atomistic-level systems and, as such, an averaged N-BAR domain protein density must be considered.

Importantly, within this multi-scale model, different types of N-BAR-induced spontaneous curvature fields can be explored. For example, two possible scenarios can be envisioned: In the first, the N-BAR domains at the atomistic level sample all possible locations/orientations on the liposome surface. Over time, this averaging results in an isotropic spontaneous curvature field at the mesoscopic level. The second scenario corresponds to the case of an anisotropic N-BAR domain density. Here, the spontaneous curvature has some preferred direction on the surface of the liposome that arises from the collective, averaged effects of the atomistic level N-BAR domains present on the liposome surface. The origin of this effect involves both the collective interaction between N-BAR domain proteins themselves, as well as an indirect collective interaction in which the local curvature generated by one N-BAR domain couples to the curvature generated by others in nearby regions.

The exact form of the mesoscopic model can be specified at various degrees of complexity, depending on the available underlying atomistic-level information. However, even for relatively simple field-theoretic representations, the complex functional integrals and boundary conditions can make a direct application of the approach quite challenging (28,31–34), even without membrane remodeling included in the problem (e.g., liposome vesiculation and tubulation). Rather than directly evaluate the field-theoretic model, an alternative is to discretize it into a set of interacting quasi-particles and to use its known solutions in certain limits to help define the quasi-particle interaction terms. This latter approach forms the basis of our second generation Elastic Membrane Model Version 2 (EM2) (25–29). The term “quasi-particle” is used here, as the particles have no direct correspondence to an atom or a molecule. Rather, they represent predefined fine-grained volumes of matter with length scales on the order of tens of nanometers. The quasi-particles are in essence free energy “particles”.

METHODS

Mesoscopic model

To model the large topological shape changes arising from the N-BAR domain-induced spontaneous curvature, the mesoscopic EM2 methodology must first be extended. In its original formulation, the EM2 quasi-particles were connected via a network of “material bonds” to give the mesoscopic membrane structural integrity, as well as to model the bulk elastic response of the bilayer (27). The extension here involves removing the restriction of the bond network, and thus it gives the mesoscopic model the all-important ability to deform and reassemble into a variety of distinct shapes as it seeks out the free-energy minima. The effect of an average N-BAR domain protein density on a liposome surface can then be incorporated into a modified version of the EM2 model. The atomistic-level MD results from our previous work (14) will also be bridged in a multi-scale fashion into this modified framework. This new feature of the EM2 model appears in the form of an additional spontaneous curvature field modeled at two levels of complexity, as described earlier. It should be noted that the resulting dynamics (and hence pathways/mechanisms) of the modified EM2 model are not related to the actual underlying atomistic-level dynamics and are more like, for example, Landau-Ginzburg composition dynamics (26,28). As such, the present EM2 methodology has the ability to predict new free-energy minima, and hence new structures, but the actual pathways that are involved in going from the initial to the final state can only be interpreted qualitatively at this level of the model formulation.

The modified EM2 model is based on a suitable field theoretic model. The case of a liposome interacting with an N-BAR domain protein concentration treats the bilayer as a thin two-dimensional surface embedded in a three-dimensional space (38,39). Following Helfrich (38), a local Cartesian reference frame is embedded at a point on the membrane surface such that the local z axis lies along the local bilayer normal vector, 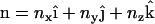. The direction of the local x and y axes then define the local tangential unit vectors 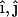. Two independent local principle curvatures, c₁ and c₂, can then be defined as 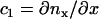and 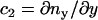. These two curvatures also define the local radii of curvature as 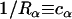, 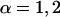. The mean curvature is thus given by 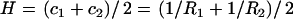. A quadratic form for the bending free energy (38,39) can then be given by the free-energy difference, F, expressed as

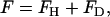(1)

where F_H is the mean curvature contribution,

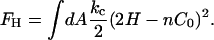(2)

In Eq. 2, C₀ is a spontaneous curvature, k_c is the bending modulus, and n is the number of degrees of freedom of the spontaneous curvature. Saddle curvature effects (38–41) are incorporated in F_D and can be expressed in terms of a deviatoric (saddle) curvature energy contribution (40). This point will be discussed in more detail in the Appendix and in the Supplementary Material. The area element dA in Eq. 1 corresponds to an area element on the surface of the membrane in the local membrane reference plane (39). The spontaneous curvature, C₀ (42), is this term that characterizes the average effect of the N-BAR domains on the bilayer. It should be noted that with 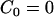, Eq. 1 gives the free-energy difference of the membrane relative to a locally flat membrane state.

Depending on the nature of the averaged spatial distribution of N-BAR domains on the bilayer surface, different types of spontaneous curvatures can be modeled in Eq. 1. An isotropic spontaneous curvature has n = 2 (i.e., two identical radii of spontaneous curvature) and C₀ is thus a nonzero constant over the membrane surface. An anisotropic spontaneous curvature has n = 1 (i.e., one radius of curvature component described by a specific direction), and this local directionality can be expressed with an in-plane unit vector, 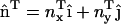. Furthermore, the direction of the local anisotropic spontaneous curvature can change over the membrane surface, which can be expressed as 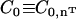. The additional subscript indicates that the spontaneous curvature only occurs along the direction specified by 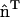; in other directions, there is no spontaneous curvature. In subsequent discussions, the additional subscript will be dropped for the sake of clarity; however, the directionality still holds. It should be noted that in the anisotropic case, if this continuum model was to be directly employed in a mesoscopic simulation, care must be taken in specifying the two radii of curvatures, c₁ and c₂. One of the curvatures should be evaluated along 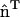, whereas the other is in the orthogonal direction. Only the curvature evaluated along 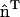should be associated with the anisotropic spontaneous curvature. In systems with complicated topologies, where the directionality of the anisotropic spontaneous curvature varies over the surface, this direct continuum approach could become quite complicated. However, as will be shown, a direct evaluation of Eqs. 1 and 2 is not necessary with the EM2 quasi-particle approach. In the context of N-BAR domain proteins, an anisotropic curvature scenario could be envisioned where a large collection of N-BAR domain proteins on the membrane surface align to some degree; this may result in a large C₀ in the direction of the N-BAR domain protein alignment. In subsequent discussions, the curvature degrees of freedom, i.e., n = 1,2, will be used to specify which spontaneous curvature model is used.

Importantly, the magnitude or strength of the spontaneous curvature, C₀, can be interpreted as the product of an averaged N-BAR domain density, ρ, an area element δA, and the intrinsic curvature of a single N-BAR domain, i.e., 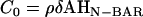, where 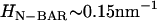(14), which is derived in a multi-scale fashion from the atomistic MD simulations (cf. Fig. 1). It should be noted that the curvature of the N-BAR domain can be characterized by a single principle curvature; the form of the spontaneous curvature in Eq. 1 reflects this aspect. The means by which the isotropic and anisotropic spontaneous curvature is incorporated into the EM2 model will be further discussed in the Appendix.

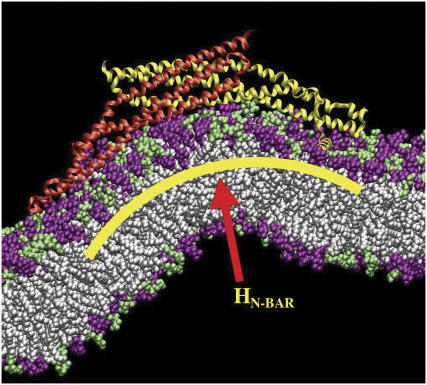
FIGURE 1.

Snapshot from an all-atom MD simulation of the Drosophila amphiphysin N-BAR domain-inducing curvature in a negatively charged lipid bilayer composed of 30% dioleoylphosphatidylserine (green headgroups) and 70% dioleoylphosphatidylcholine (purple headgroups). Over the course of this 27 ns MD simulation, the N-BAR domain bends the membrane to locally adopt the curvature of its concave surface. The yellow arc indicates the maximum curvature of the bilayer due to the N-BAR domain, H_N-BAR.

Mesoscopic N-BAR domain/liposome simulations

A series of EM2 liposome simulations were performed to examine the possible effects of N-BAR domain-induced spontaneous curvature. The goal was to interpret previous experiments (5) by effectively examining the concentration dependence of N-BAR domain-induced spontaneous curvature. This was accomplished by increasing the N-BAR domain density on the EM2 liposome surface. It should be noted that the concentration reported experimentally refers to the concentration of the N-BAR (or BAR) domain proteins in solution, and it is not necessarily equal to the concentration of the domains bound to the liposome surface. However, some direct correlation between the solvent and liposome surface concentrations seems reasonable. The N-BAR concentration on the liposome surface is therefore modeled here via the strength of the spontaneous curvature field in Eq. 1; a weak spontaneous curvature field thus corresponds to a low N-BAR concentration, whereas a high field, with a maximum possible value being equal to the local molecular-scale curvature of the N-BAR domain (shown in Fig. 1), corresponds to a high concentration.

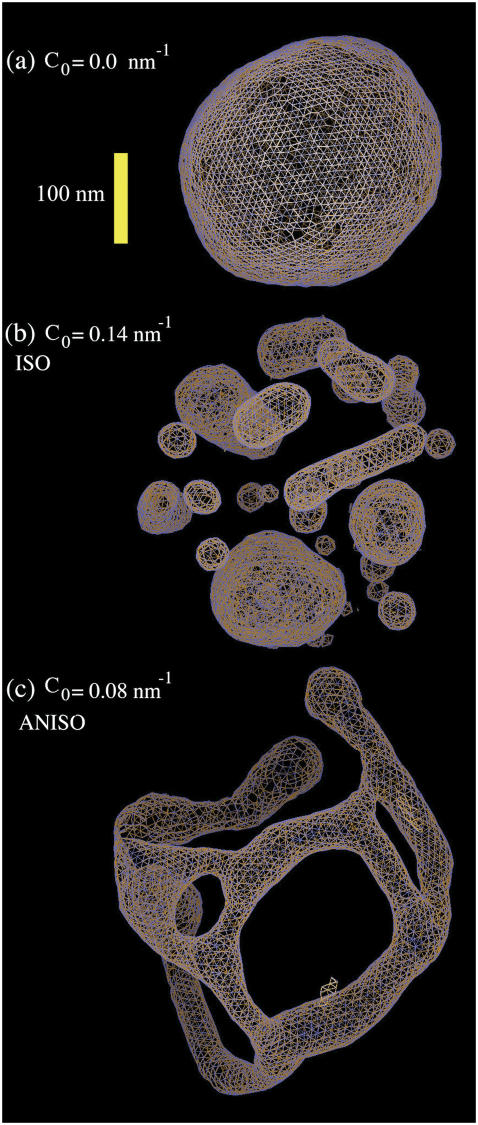
To provide a reference state, an initial EM2 simulation of a liposome was performed with no spontaneous curvature (no bound N-BAR domains) and with the parameters in Table 1. A snapshot of the final structure is shown in Fig. 2 a. The fact that the final simulation snapshot is not perfectly spherical reflects the presence of thermal fluctuation effects at this length scale (i.e., on the order of 100 nm) (24,27,29,31). The two different N-BAR domain spontaneous curvature fields (isotropic, (n = 2 in Eq. 1) and anisotropic (n = 1 in Eq. 1)) were then examined at various curvature field strengths corresponding to various possible N-BAR concentrations on the membrane surface. The maximum spontaneous curvature obtainable was assumed to be that observed from the original atomistic-level MD simulation (14), 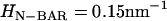(cf. Fig. 1). With 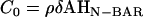, possible values of C₀ then ranged from 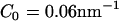(low concentration) to 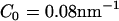(medium concentration), to 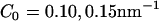(high concentration).

TABLE 1.

Key parameters

Parameter	Symbol	Value
Liposome radius	rL	136 ± 7 nm
Temperature	T	308 K
EM2 length scale	σ	6.8 nm
Time step	δt	0.02 ps
EM2 energy	ɛ	5.5–6.5 amu (nm/ps)2
Bending modulus	kc	27 amu (nm/ps)2
Spontaneous curvature	C0	0.05–0.2 nm−1
Number of EM2 particles	N	4000
Bilayer thickness	h	3.4 nm
Number of time steps	τ	2 × 106
Tubule radius	rT	44.6 ± 0.2 nm

FIGURE 2.

(a) An EM2 liposome with an initial radius as in Table 1 and no N-BAR spontaneous curvature, i.e., C₀ = 0 nm⁻¹. (b) The liposome as in a subjected to an isotropic (n = 2 in Eq. 1) spontaneous curvature field with a value of C₀ = 0.14 nm⁻¹. (c) The liposome as in a subjected to an anisotropic (n = 1 in Eq. 1) spontaneous curvature field with a value of C₀ = 0.08 nm⁻¹. The yellow scale bar corresponds to 100 nm.

RESULTS AND DISCUSSION

As previously noted, the design of the mesoscopic EM2 liposome simulations was motivated by some specific experimental observations (5). As such, before discussing the current simulation results, a brief summary of previous experimental work will be given. After that, the EM2 results, at various increasing N-BAR domain density strengths, will be presented.

Summary of experimental results

In Peter et al. (5), liposomes were examined for N-BAR (BAR domain plus the amphipathic helix at the N-terminus, see Fig. 1), as well as BAR domains at various concentrations (5−40 μm) using electron microscopy. For the N-BAR case relevant to the present multi-scale simulations, it was observed that liposome tubulation occurred at intermediate concentrations (20 μM), whereas liposome vesiculation occurred at high concentration (40 μM). Tubulation resulted in tubules with an outer diameter of ∼46 nm, whereas vesiculation of the liposome resulted in an array of smaller liposomes with a range of shapes and sizes.

Low to medium N-BAR concentrations

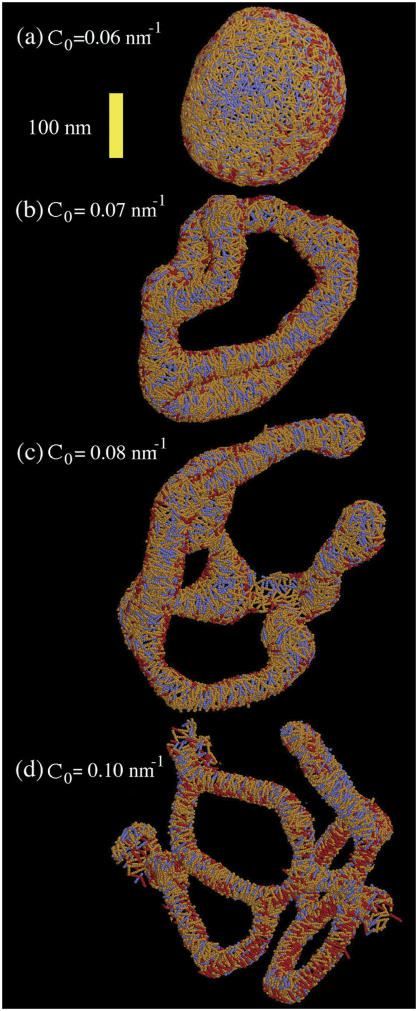
For the isotropic spontaneous curvature field scenario (n = 2 in Eq. 1), and for the low and medium values of C₀, the liposome exhibited a distorted structure with irregular dints. However, a very different picture was found when the anisotropic curvature field was used (n = 1 in Eq. 1). At low concentrations, the liposome remained intact (as shown in Fig. 3 a), whereas at intermediate concentrations () the liposome was tubulated into a complicated structure as shown in Figs. 2 c and 3 c. Note that the colors of the EM2 particles in Fig. 3 are represented by their curvature field vectors, 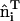, so that the orientational correlations in the local curvature fields can be identified. In this case, a close inspection of Fig. 3 a reveals an almost isotropic distribution of curvature fields. The cross-sectional diameter of the tubulated structure was in the range of ∼40–50 nm. It is possible, however, that this structure could, over very long simulations, anneal into a single tubule. The local spontaneous curvature fields interact to “wrap” around the emergent tubule structures. This effect is shown in Fig. 3, b–d, where the 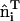vectors lie roughly perpendicular to the vector describing the local symmetry axis of the tubulated structures.

FIGURE 3.

Liposome as in Fig. 1 a subjected to various anisotropic spontaneous curvature fields. The specific field value is shown in the figure. The yellow scale bar is corresponds to 100 nm. The orientational structure of the single radius of spontaneous curvature is shown via the stick-representation of the EM2 quasi-particles. The different colors indicate correlations in the local orientation: blue regions have a radius of curvature direction orthogonal to red regions. Orange regions are intermediate.

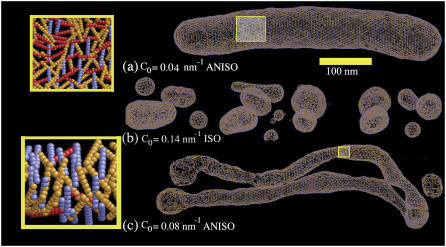
To determine whether the original starting structure of the liposome had any persistent effect on the resulting structures, a macro-tubule system was also examined. The initial radius of the macro-tubule was 44 nm; this system mimics a tubulated “neck” between two large vesicles, for example. In Fig. 4, the macro-tubule is shown under conditions similar to that used in the previous liposome simulation, except that it was found that the macro-tubule was not stable when no spontaneous curvature field was present. Rather, the macro-tubule “split” over time into two separate membrane sheets. In contrast, the macro-tubule structure remained stable when a weak anisotropic curvature field was used, as shown in Fig. 4 a. This result mirrors that observed in the liposome case; the inset shows that the orientational distribution of the spontaneous curvature field is very close to isotropic over the macro-tubule surface. At moderate anisotropic curvature field strengths, a pronounced tubulation results (Fig. 4 c); the tubulated shape is “held intact” by the anisotropic curvature field density, as shown in the inset.

FIGURE 4.

(a) An EM2 tubule with an initial radius as in Table 1 and with N-BAR anisotropic spontaneous curvature of C₀ = 0.04 nm⁻¹. (b) The tubule as in a subjected to an isotropic (n = 2) spontaneous curvature field with a value of C₀ = 0.14 nm⁻¹. (c) The tubule as in a subjected to an anisotropic (n = 1) spontaneous curvature field with a value of C₀ = 0.08 nm⁻¹. The close-up images in the yellow boxes show the orientational dependence of the spontaneous curvature field. In a, very little correlation is observed; in c the spontaneous curvature field “wraps” around the tubulated structure. The yellow scale bar is corresponds to 100 nm.

With the above results in hand, it is possible to relate the multi-scale EM2 simulations back to the medium concentration N-BAR experiments, where liposomes were observed to undergo tubulation. From the simulation results, tubulated liposomes were only observed with an anisotropic N-BAR curvature field. This leads us to conclude that some degree of collective orientational order of the N-BAR domains is required experimentally to facilitate tubulation, and that some degree of spatial ordering of the N-BAR domains on the real liposome surface exists.

High N-BAR concentration

With the isotropic curvature field (n = 2 in Eq. 1) at around the maximum possible curvature 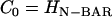, a pronounced vesiculation was observed. In Fig. 2 b, a snapshot of an isotropic EM2 simulation with 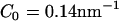is shown. An array of different sized and shaped vesicles emerged from the original single liposome. Some of the vesicles were elongated, some were quite small (with diameters around 30 nm), whereas others were larger with diameters around 100 nm. Interestingly, the elongated structures had cross-sectional diameters similar to those observed in experiment (5) at ∼40 nm. These results indicate that a uniform and isotropic N-BAR domain spontaneous curvature field can indeed result in vesiculation at high N-BAR densities.

In contrast, simulations with the high density anisotropic N-BAR curvature field resulted in tubulated structures as shown in Fig. 3 d. As the field strength is increased, the cross-sectional diameter of the tubules decreased to the point that by 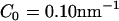, the cross-sectional diameter was ∼30 nm. The anisotropic N-BAR curvature field at high concentration simulations never resulted in vesiculated structures similar to those observed experimentally.

In the case of the initial macro-tubule, the strong isotropic curvature field with 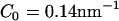(Fig. 4 b) again yielded vesiculation into a variety of vesicle shapes and sizes. The strong anisotropic field, however, tubulated the macro-tubule in a similar manner as was observed with the original liposome (image not shown).

As in the low/medium N-BAR concentration case, the present EM2 simulation results can be compared with the experimental observations where vesiculation was observed at high N-BAR concentrations. From the high density N-BAR domain density EM2 simulations, vesiculated structures were only observed with the isotropic spontaneous curvature field. High density anisotropic N-BAR curvature fields generated tubulated structures. Combining these results, it is suggested here that the experimental high concentration N-BAR domain system likely has an isotropic spatial distribution of N-BAR domains on the liposome surface.

There are three possible explanations for why high density liposome-bound N-BAR domains could have an isotropic (as opposed to anisotropic) spatial/orientational distribution and therefore result in liposome vesiculation. The first explanation is that the embedded N-terminal helices could result in an additional radius of curvature in a direction not along the N-BAR domain arc (9) (cf. Fig. 1). The second is that the embedded N-terminal helices could disrupt N-BAR domain alignment such that at high densities a more isotropic distribution is favored. The third possible explanation is that the initial interaction of the N-terminal helices with the liposome surface is quite strong and occurs over a short timescale. In the latter, one can envision a scenario where the N-terminal helices very quickly “grab hold” of the membrane; if this process happens so that many N-BAR domains bind to the membrane over a short time window and in random directions (i.e., high concentrations), then an initial isotropic spatial distribution of N-BAR domains on the liposome surface could result. This initial N-BAR distribution, once formed, also might not anneal very much over time into any more correlated structures, and vesiculation therefore results.

SUMMARY AND CONCLUSIONS

In light of the EM2 simulation results presented here, it will be important to examine with higher resolution, both experimentally and computationally, the spatial and orientational distribution of a collection of N-BAR domains on the surface of a liposome as it undergoes either vesiculation and/or tubulation. Given the very long time- and length scales involved, the current theoretical “field-based” analysis suggests that the features of the collective spatial and orientational correlations of the averaged N-BAR domain-induced spontaneous curvature field should be very important for the membrane remodeling process. Future work in our group will explore this issue through coarse-grained molecular simulation and, hopefully, additional experimental results will become available as at the same time.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

APPENDIX: EXTENSION TO THE EM2 MESOSCOPIC MEMBRANE MODEL

A detailed discussion of how Eq. 1 is discretized into a set of interacting EM2 quasi-particles can be found elsewhere (27); here, only a few key features are presented. The first step in arriving at the EM2 model involves bending a perfectly flat membrane whose energy is given by Eq. 1 into a perfect spherical cup with an isotropic spontaneous curvature. This deformation is used to initially parameterize the discretized EM2 model. Under this specific deformation, Eq. 1 is approximated by a new discretized mesoscopic energy, F^eff, which is expressed as (27)

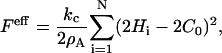(3)

where 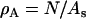and A_s is the initial surface area of the liposome, and N is the number of EM2 quasi-particles. The mean curvature at the ith EM2 quasi-particle is given by H_i.

The next step involves taking Eq. 3 and then expressing it as a pairwise sum of interacting EM2 quasi-particles as

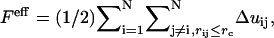(4)

where

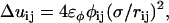(5)

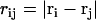, σ is the fundamental discretization length scale, and r_c is a preset cutoff radius. The term 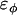is the fundamental energy and can be related to the original bending modulus, k_c (27) as , where 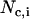is the number of j EM2 quasi-particles that are found about the ith EM2 quasi-particle. As the EM2 quasi-particles are not bonded together, different pairs of interacting particles will occur during the course of the simulation; the summation in F^eff reflects this new aspect. The term 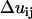contains the spontaneous bending contribution via the orientationally dependent φ_ij term (27). Other variations for the functional form of φ_ij term could be devised; however, mirroring that which was previously done (27), φ_ij is chosen to be

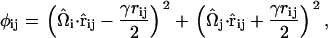(6)

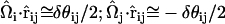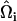where it can be shown that . Here, is the angle between and 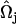, where 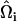and 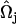are EM2 quasi-particle orientation unit vectors that represent the local membrane normal. It can be shown that under this specific deformation, F^eff gives a discretized solution to F in Eq. 1 to second order in an expansion in 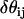. It can also be shown that 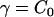. When the model is allowed to dynamically evolve at finite temperature, thermal undulations emerge. Since EM2 originates with Eq. 1, which is a free-energy difference relative to a perfectly curved state, deviations from this (arbitrary) ideal starting point occur.

The deviatoric contribution to the energy can be examined by deforming a perfectly flat EM2 membrane into a saddle point where 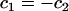at the location of the ith EM2 quasi-particle. In this case, the deviatoric energy contribution, 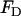, as appearing in Eq. 1, is that proposed in Fischer (40) and is given by

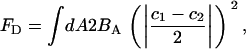(7)

where B_A is the deviatoric modulus and can be related to the more familiar Gaussian bending modulus (see Supplementary Material). In this perfect saddle deformation, the energy of the membrane as given by Eq. 1 can now be transformed into the discrete EM2 form. It can be shown that the ith EM2 quasi-particle's contribution to the energy is given by

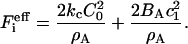(8)

If Eq. 4 is then used, noting that 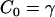, then is it found that the deviatoric modulus B_A is related to the bending modulus via 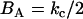. As such, for this saddle deformation, the EM2 model gives a discretized representation of Eq. 1, where 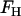is originally given by Eq. 2 and 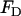is given by Eq. 7.

In the original EM2 formulation (27), the EM2 quasi-particles were connected via a network of “material bonds”. The modification here removes this restriction; rather, a spherically symmetric inverse power interaction is employed. As such, the EM2 particles are not “bonded” together, but can adjust to various topologies due to the soft nature of the interaction.

Modeling an anisotropic spontaneous curvature within EM2 requires incorporating an in-plane local directionality to the spontaneous curvature. The pairwise quasi-particle nature of the EM2 approach allows for a number of possible schemes to model an anisotropic curvature; one possible scheme is proposed here. In this case, the anisotropic form of Eqs. 1 and 2 act as a guide to design a quasi-particle model that can capture the essential physics associated with anisotropic spontaneous curvatures. An anisotropic spontaneous curvature field (i.e., with n = 1) can be modeled/approximated by generalizing Eq. 6 to include an orientationally dependent γ as 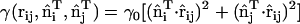, where 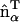gives the in-plane local orientation for the α-EM2 quasi-particle and 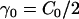. This model results in a spontaneous curvature that incorporates a degree of local directionality. For example, consider when two EM2 quasi-particles have a relative location/orientation such that they are located end-to-end and their 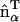vectors are parallel; the resulting spontaneous curvature then occurs along r_ij. Conversely, when two EM2 quasi-particles have their 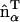vectors perpendicular to r_ij, no spontaneous curvature is generated. If a small domain of EM2 particles with similar 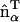in-plane orientation vectors is considered, then the directionality of resulting curvature for this domain will be strongly correlated with orientation vectors. From a physical viewpoint, this scenario corresponds to a large array of N-BAR domains that have aligned to some degree; the resulting curvature of the membrane follows from the intrinsic curvature of the N-BAR domains themselves. It should be noted that this interaction is not directly related to an expansion in ; other forms could also be constructed.