Lactose Permease H⁺-Lactose Symporter: Mechanical Switch or Brownian Ratchet?

Abstract

Lactose permease structure is deemed consistent with a mechanical switch device for H⁺-coupled symport. Because the crystallography-assigned docking position of thiodigalactoside (TDG) does not make close contact with several amino acids essential for symport; the switch model requires allosteric interactions between the proton and sugar binding sites. The docking program, Autodock 3 reveals other lactose-docking sites. An alternative cotransport mechanism is proposed where His-322 imidazolium, positioned in the central pore equidistant (5–7 Å) between six charged amino acids, Arg-302 and Lys-319 opposing Glu-269, Glu-325, Asp-237, and Asp-240, transfers a proton transiently to an H-bonded lactose hydroxyl group. Protonated lactose and its dissociation product H₃O⁺ are repelled by reprotonated His-322 and drift in the electrostatic field toward the cytosol. This Brownian ratchet model, unlike the conventional carrier model, accounts for diminished symport by H322N mutant; how H322 mutants become uniporters; why exchanging Lys-319 with Asp-240 paradoxically inactivates symport; how some multiple mutants become revertant transporters; the raised export rate and affinity toward lactose of uncoupled mutants; the altered specificity toward lactose, melibiose, and galactose of some mutants, and the proton dissociation rate of H322 being 100-fold faster than the symport turnover rate.

INTRODUCTION

The crystallographic description of Escherichia coli lactose permease, a member of the major facilitator superfamily of membrane transport proteins, has added significantly to our understanding of the structure of membrane transporters (1–5). Nevertheless, the mechanism of lactose-proton cotransport remains ambiguous. Although arguments supporting an alternating mechanical “rocker switch” mechanism have been deduced from various kinds of mutation study, other findings are inconsistent with this mechanically coupled device, but more in harmony with an alternative stochastic model, to be discussed here.

The rocker switch model of symport

A mechanical rocker switch mechanism for the Escherichia coli lactose permease (LacY) cotransport cycle has been inferred from kinetic, mutation, cross-linking, and, most recently, x-ray studies of the crystallized transporter protein (2,6,7). The model proposes that inward- and outward-facing conformations alternately expose the centrally bound disaccharide and proton to the adjacent cytosolic and external (periplasmic) solutions. This requires large-scale, precise, cyclic, coordinated conformational changes in transmembrane helices II, IV, and V in the N-terminal domain and VII, X, and XI in the C- terminal domain.

Recent x-ray comparisons of the crystallized LacY permease structure liganded to the high-affinity disaccharide β-D-galactopyranosyl-1-thio−β-galactopyranoside (TDG) with the unliganded LacY permease show small conformational differences resulting from TDG binding around Arg-144, Glu-126, and Glu-269 (7) . The TDG-induced disruption of a salt bridge between Arg-144 and Glu-126 is thought to promote movement of Glu-269 from a shielded hydrophobic environment into an exposed hydrophilic region, thereby altering its pK_a and hypothetically permitting proton transference via a bridging water molecule to the imidazole group of H322 (7). This is believed to activate large-scale conformational changes leading to inversion of the locations of lactose and H-ligand binding sites to the trans side.

The position of TDG, the high-affinity disaccharide ligand, localized by x-ray crystallography within the central pore, is taken to be consistent with the rocker mechanism (4,7,8). However, this singular positioning of the ligand within the central pore does not readily explain how it is transported along the length of the pore, or how mutation of a single residue, e.g., H322 to F322 converts the H⁺-lactose (D-galactose-β1-4-D-glucose) symporter to a lactose/melibiose uniporter (9–12). Similar models in which a proton transfer reaction is activated by lactose have been proposed (13,14). As will be seen, none account for the finding that when the charged amino acids surrounding H322 are substituted by neutral replacements, downhill flow of lactose, or melibiose (D-galactopyranosyl-α1-6-D-glucose), and protons is recovered after mutation at any of five other “suppressor” sites with charged or uncharged amino acids (15).

The salt bridge problem

Salt bridges provide a more energetically favorable environment to accommodate charged residues, particularly where the dielectric constant is low (16). It is proposed additionally that the oppositely charged amino acid pairs, Lys-319 with Asp-240 and Asp-237 with Lys-358, form salt bridges that “stabilize the H-bond network” (16–19). A problem with this scheme is that interchange of Lys-319 with Asp-240 with the double mutant K319D, D240K, although preserving the salt bridge, abolishes transport activity. However, this is not considered sufficient grounds for rejecting the view that both salt bridges are required to maintain the transport cycle, although the role of the K319/D240 salt bridge in proton translocation remains equivocal (18,20).

The relationship of proton motive force with symport

Another shortcoming of the mechanical rocker model of LacY permease activity is its lack of specific guidance regarding the relationship between the combined pH and electrical potential gradients, the proton motive force (PMF) across the symporter, and the kinetics of lactose transport in wild-type and uncoupled transporter mutants.

Loss of PMF, or uncoupling of the H⁺ gradient from lactose flow decreases lactose accumulation and increases both lactose efflux and its apparent affinity, as measured kinetically, for the export site (21–27). However, the affinities of right-side-out, or inside-out membrane vesicles containing LacY to lactose or TDG, measured by ligand binding, are symmetrical in the presence or absence of a PMF (28). This suggests that the apparent difference in affinity between inside and outside sites, like that with the GLUT1 transporter in human erythrocytes, is only observed when net ligand transport occurs, but not when measured by direct binding assays (29–32).

The role of Histidine 322 in LacY symport

The necessity for histidine H322 participation in the LacY symport pump cycle has been questioned (11,33). Mutation of H322 to asparagine, H322N, permits a low level of H⁺-gradient-induced uphill lactose transport to ∼5% of wild-type accumulation and passive downhill lactose movement with accompanying proton movements (downhill symport). However, when H322 is replaced by arginine or phenylalanine (H322R or H322F), only downhill lactose flow without protons (uniport) is observed (21,34). Since the conversion of the symporter to a uniporter can occur by substituting a nonionizing benzyl for an imidazole group, loss of symporter function may be considered to be due to loss of an essential intermediate site in the proton transport chain without concurrent loss of the lactose-binding site. Nevertheless, as protonation of H322 imidazole is thought to induce inversion of the symporter (7,19), it is surprising that the F322 mutant lacks a strong inhibitory effect on either the net or exchange lactose/melibiose uniport process (6,10,33,35). Moreover, the observation that symport process is partially retained when asparagine is substituted for H322, even though its amide residue is not protonatable, suggests that an alternative mechanism to the rocker model for H⁺-lactose symport may exist. It is evident that proton transfer at H322, or its substitute cannot be the trigger for inversion of the ligand-binding site of LacY. As the uniport mechanism is also considered to be an alternating carrier process lacking H⁺ coupling, the conformational changes determining the inversion process at the central sugar binding site in the uniporter mode should be similar, or identical, to those of the symporter (36).

Another problem in reconciling H322 with its assigned role in the cyclic process leading to H⁺-lactose symport is that its proton turnover rate should match the turnover rate of the symporter, i.e., 20–50 Hz (37,38). Nachliel and Gutman (39,40) have shown that protons diffuse rapidly within the large, water-filled central cavity of LacY, and protonation rates of H322, over a wide pH range, are two orders of magnitude faster than the turnover rate of the symporter in the presence or absence of lactose. This is discordant with a symport model, which requires synchronized mechanical linkages between the various stages of proton-lactose transit and the conformational changes they evoke. It would seem that the rapid rate of Brownian motion within the central cavity militates against such a precise clockwork model.

Electrostatic basis for asymmetry of the alternating carrier model of LacY

The inwardly directed PMF across the LacY symporter is thought to hasten return of the negatively charged empty carrier to the exofacial side of the transporter, thereby reducing the rate of ligand export while reciprocally increasing the ligand import rate (22,23,25). Two negatively charged amino acids might fulfill the role of PMF responsive elements. However, replacement of any five of the six charged amino acids most associated with symport—D240, E269, and E325, along with R302, K319, and H322—by nonionizable amino acids still permits downhill proton and lactose flow. Replacement of all six amino acids with nonionizable substitutes permits a limited degree of lactose uniport (15,41). These findings indicate that no amino acid can be individually assigned to the role of a proton conductor, or be responsible for PMF-evoked acceleration of the empty carrier. However, it is evident that K319, H322, and E325 all play important roles in H⁺-coupled lactose flow.

Some mutations alter LacY specificity for lactose, melibiose, and galactose

An additional problem is that the specificity of LacY toward various transported sugar ligands varies with different mutations or inhibitors (5,33,35,41–46). This is difficult to reconcile with a single site for sugar ligand binding as envisaged by the carrier model for symport (20,41,43).

To rationalize some of these problems we have applied the molecular docking program Autodock 3 to TDG-liganded LacY (Protein Data Bank (PDB) entry, 1PV7) and its unliganded forms at pH 6.5 and 5.5 (2CFP and 2CFQ). Many available mutation studies give valuable qualitative information about the effects of electrostatic potential changes within the central cavity. When combined with the three-dimensional (3D) crystal structure of LacY, these can now be accommodated with an alternative model for lactose symport.

METHODS

Docking studies have been performed using Autodock 3 (http://autodock.scripps.edu) (47) on the published crystal structure of the mutant lactose symporter LacY (PDB entry, 1PV7) and the unliganded forms of the transporter (2CFP and 2CFQ). The 3-D structures of TDG, β-D lactose, melibiose, maltose, β-D-glucose, α- and β-D-galactose, and several other oligosaccharides, among which is the tetrasaccharide stachyose α−D-Gal-[1-6]-α−D-Gal-[1-6]-α−D-Glc-[1-2]-β-D-Fru, known to have minimal cotransport activity in LacY(48,49), were obtained from Sweet II (The German Cancer research Centre DFKZ, http://www.dkfz.de/spec/sweet/) and used as docking ligands. Docking utilized a 3D grid with a spacing of 0.375 Å, centered on the LacY molecule, with 100 points in each dimension.

DeepView/Swiss-PDBViewer (http://www.expasy.ord/spdbv) was used both to construct the 3D mutant protein forms of LacY (1PV7) and to view the mutant proteins and the ligands. After mutation in silico, the altered structures were subjected to an energy minimization routine using the GROMOS96 implementation within Deepview, before observing the effects of lactose-docking with Autodock (47).

The electrostatic potential maps were prepared using the routines for the solution of the Coulomb equation in Swiss PDB Viewer, or using the routines in the Voidoo software package (University of Uppsala Software Factory http://alpha2.bmc.uu.se/usf/voidoo.html). The Nottingham Algorithms Group (NAG) routine, E01TGF, was used to derive 2D grids of interpolated electrostatic values at 1-Å intervals (http://www.nag.com/numeric/fl/manual20/pdf/E01/e01tgf) within selected planes. The electrostatic potential gradients in the x and y directions within each plane were estimated using vector addition of the local potential differences of the eight nearest neighbor cells surrounding each cell. The gradients of the differences in the computed electrostatic potential distributions in the region around H322 in the control and some multiple mutants were also obtained by vector addition.

Hydration of both unliganded and docked-lactose forms of LacY was simulated using “Flood”, part of the Voidoo package. This necessitated constructing a cage around the protein structure so that the software “sees” “cavities” rather than “invaginations”.

RESULTS

In silico saccharide docking to LacY

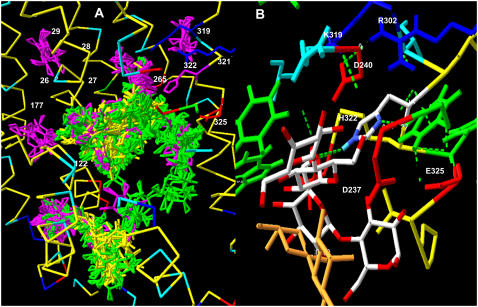
Unlike glucose docking on GLUT1 (30,50), neither lactose, TDG, nor melibiose dock at clearly defined cluster sites on LacY; instead, the docking sites cover the walls of the endofacial and central cavity regions. The docked positions of disaccharides TDG and β-D-lactose on LacY have affinities in the range 0.02–0.5 mM, as determined by Autodock 3 (average for lactose = 0.4 mM) (Table 1). Also, in contrast to the docking studies on GLUT1 (30,50), there is no evidence of a continuous pathway for sugar movement across LacY, as no lactose, melibiose, or TDG (not shown) docking is observed in the exofacial vestibule (Fig. 1 A). This absence probably results from a narrowing of the exofacial vestibule in the crystallized form of LacY (PDB 1PV7), which is a thermostable LacY mutant, C154G lacking any transport activity. This distortion of the basic major facilitator superfamily structure has been removed in the templated form of GLUT1 (PDB 1SUK) (50), and thereby permits four clusters of glucose docking sites in the exofacial vestibule of GLUT1 (30). However, even in the C154G LacY mutant, there are isolated clusters docking sites of D-galactose in the exofacial vestibule (Fig. 1 A).

TABLE 1.

Sugars docking to H322

	Number of molecules docked to H322	Average affinity of molecules docked to H322 (mM)	Average affinity (mM) of molecules docked to LacY (n = 80–90)	Docking groups
Lactose	6	0.65	0.4 ± 0.034	O1=3, O4=1, O6=1, ring O= 1
Melibiose	6	0.25	0.24 ± 0.023	O2=3, O4=2, ring O=4
Galactose	7	0.08	0.16 ± 0.06	O2=2. O3=3, O4=3, O6=1, ring O=3

FIGURE 1.

(A) Slab view of LacY centered on the central pore, showing all the lactose (yellow), melibiose (green), and galactose (purple) docking sites on LacY. Superimposed numbers show the positions of mutations, which alter the sugar specificity of the transporter (Table 4). (B) The orange colored molecule shows TDG in the assigned position by crystallography (1) and two additional docked lactose molecules H-bonded to lactose H322 within the central cavity of LacY.

Surprisingly, none of the TDG molecules docked with Autodock 3 coincides exactly with the position of TDG assigned by crystallography (Fig. 1 B, orange molecule). The current version of the rocker mechanism requires that TDG should initially dock to Arg-144, Glu-269, and Trp-151 (7). Autodock assigns four possible TDG docking positions to within 3 Å of the OH group of W151, so these findings are consistent with the recent finding that TDG binds close to this central tryptophan residue (51). Nevertheless, none has the coordinates assigned by crystallography. The nearest docked TDG molecule, shown in the CPK color scheme, is within 1.5 Å of the galactopyranosyl ring, which crystallography indicates binds to W151, but deviates by >3 Å from the other galactose ring. The TDG molecule with the highest affinity assigned by Autodock docks >10 Å from the crystal-assigned TDG position (not shown).

The ligand binding site for TDG as identified by crystallography is absent from unliganded LacY (7). Nevertheless, around H322, there are no significant differences between lactose docking positions assigned by Autodock 3 in the liganded (PDB 1PV7) and unliganded form of LacY (PDB 2CFQ, at pH 5.5), although substantial differences are observed in lactose docking positions at other sites on the endofacial cavity walls (not shown). Similar lack of agreement with the crystal docking assignments for TDG has been reported using molecular dynamic simulation (14).

Computerized molecular docking studies on a crystal structure of a protein such as LacY have a clear advantage over such studies on a templated model structure, as with GLUT1, as the postulated templated structure may be less dependable and so must be “authenticated” in as many ways as possible (14,30,52,52,53). Nevertheless, such corroborating procedures should also be applied to any predicted conformational changes deviating from the existing x-ray structure.

Although the x-ray structure is taken as a benchmark of reliability, the prediction of mechanism based on results from x-ray data should not be viewed uncritically. According to Horsefield et al. (53), there are several possible reasons for differences between ligand docking positions in silico and crystallographic assignments. Some of the interactions could be affected by the crystallization process itself, or x-irradiation could shift the docking position of the ligand. Additionally, ligand binding to low-affinity sites is not stable enough to give satisfactory x-ray diffraction images, and thus is not revealed by crystallography. These explanations are used to account for the 2.8-Å root mean-square deviations between the positions of ubiquinone in the native structure of succinate/ubiquinone oxidoreductase (Q₁-site) assigned by x-ray crystallography and the position of ubiquinone when docked by the molecular recognition program GOLD (Q₂ site). Similar arguments hold for the lack of conjunction between lactose binding to LacY assigned by crystallography—by the same laboratory—and those predicted with Autodock, as observed here.

Another possibility is that Autodock incorrectly assigns TDG and lactose docking positions. However, this is an unlikely explanation for the many observed differences between in silico and crystal docking of TDG on lactose permease. Autodock examines an extremely large number of potential docking sites on the basis of the van der Waals, electrostatic, and ligand torsional forces (47), and generates similar docking positions for a number of different sugar ligands for lactose permease. The following sugars generated similar docking patterns: lactose, melibiose (Fig. 1 A), maltose, TDG, and stachyose (Fig. 2 C) in that there was no evident clustering of the docked sugars. Nevertheless, both melibiose and maltose have similar docking patterns within the central cavity of LacY and both dock at separate sites from lactose in the region between Asp-240 and Asp-237 and Glu-325 (average K_i of 27 docked melibiose molecules in this region, as obtained by Autodock 3, 0.29 ± 0.05 mM) (Figs. 1 A and 3 B).

FIGURE 2.

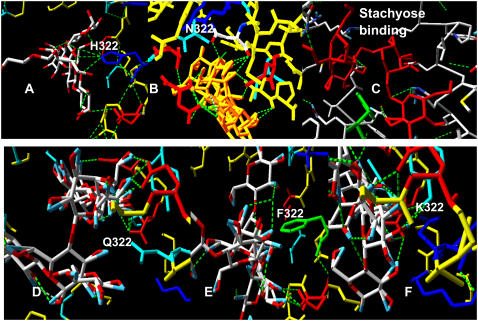
Slab view showing the central pore of LacY with the docked positions of lactose close to position 322. (A) Lactose H-bonds to H322 and B) N322 not at Q, F or K 322. (C) Stachyose also H-bonds between a glycosidic oxygen and H322. (D–F) Positions of lactose docked to glutamine, phenylalanine, and lysine mutations of H322. None of these has any lactose H-bonded at position 322.

FIGURE 3.

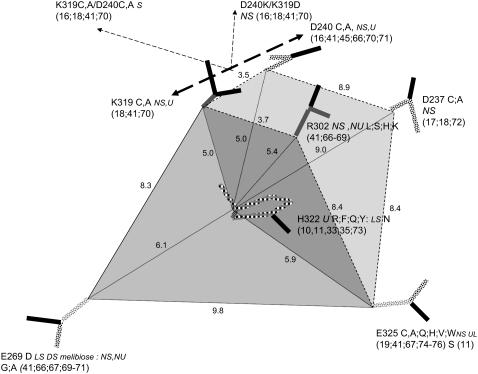
Scale diagram showing the relationship of the six fixed-charge amino acids close to H322 within the central cavity of LacY. Also shown are the single mutations at each of these positions and their effects on LacY transport function. NS, no symport; U, uniport; NU, no uniport; UL, lactose uniport; DS, downhill H⁺ -lactose symport. The shaded areas delineate the planar trapezoids between K319/R302/E325/E269 KREE en face and K319/D240/D237/E325 KDDE perpendicular.

Role of His-322 in active transport of lactose

When Arg, Phe, Gln, or Tyr is substituted for H322 in LacY, LacY H⁺-lactose symporter becomes a uniporter (Table 2) (33,34). However, when asparagine replaces histidine 322 (H322N), uphill H-lactose symport is still observed, albeit at only a twentieth of the rate and extent of lactose accumulation seen in the wild-type (11,33,34). On this basis, it has been argued that H322 is inessential for symporter function.

TABLE 2.

Single mutations

Position on LacY	Mutant	LacY function	References
237	D237(A,C,N)	NS	(17,18,72)
240	D240(C,A)	NSL	(16,41,45,66,70,71)
269	E269D	SL; low UL	(41,66,67,69–71)
269	E269(A,G)	NSL,DSM	(41,66,67,69–71)
302	R302(L,S,H,K)	No activity	(41,66–69)
319	K319(C,A)	NSL,	(18,41,70)
322	H322(R,F,Q,Y)	Low UL; raised UM	(10,35,73)
322	H322N	Low SL	(11,33)
325	E325D	SL	(19,41,67,74–76)
325	E325(A,C,D)	UL	(19,41,67,74–76)
325	E325S	No activity	(11)

NS, no symport; NSL, no symport of lactose; UL, lactose uniport; DSM, downhill melibiose symport; SL, symport of lactose; UM, melibiose uniport.

The lactose transport system of Streptococcus thermophilus Lac S permease has structural similarity around H376 to the sequence adjacent to H322 in E. Coli LacY. Lac S E379 is an analog of LacY E325 in E. coli. In Lac S permease the mutant H376Q has reduced lactose symporter activity and zero melibiose and methyl-D-thiogalactopyranoside symport activity (27,33).

Our docking studies show that only histidine or asparagine in LacY at position 322 can H-bond to an oxygen atom of closely docked lactose. Lactose H-bonds to H322, only at its Nɛ4 position (Fig. 2, A–C, and Table 1).

H322 imidazole also H-bonds between its Nδ1 position and Tyr-236 OH, which retards rotation of the imidazole ring and raises the pK_a of the imidazole base. Lactose can H-bond to both oxy residues of the asparagine mutation, H322N (Fig. 2 B). However, no H-bonding to lactose is observed with R322, Q322, Y322, or F322 mutants (Fig. 2, D–F). A possible inference is that amino acids at position 322 permitting H-bonding to sugar oxygen electrons are required for H-lactose symport activity.

Electrostatic forces within the hydrated central pore

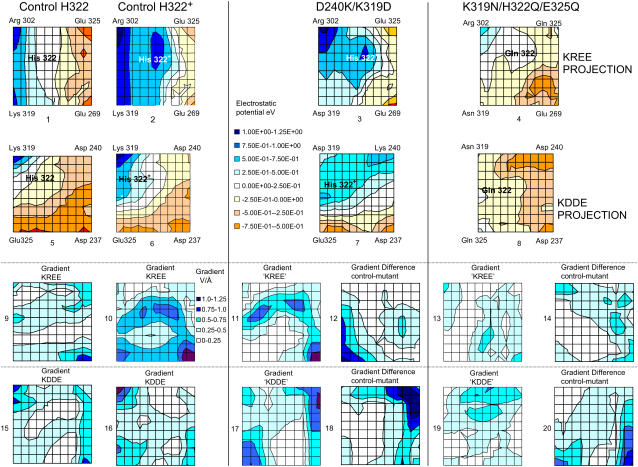
Six charged amino acid side chains at the vertices of two intersecting planar trapezoids, positioned edge to face, are equidistant (4.8–6.25 Å) to H322 (Figs. 3 and 4 A). H322 imidazole lies at the centroid of the Lys-319/Arg-302/Glu-325/Glu-269 plane (KREE) and the Lys-319/Asp-237/Asp-240/Glu-325 plane (KDDE), which is normal and on the diagonal joining Glu-325 and Lys-319 of the KREE plane (Figs. 3 and 4 A). Evidently, the charge state of H322 has a pivotal role in electrostatic charge balance within the space between the other six local charged groups close to the roof of the central cavity. The central cavity is open to the cytoplasmic solution and can be filled with several hundred water molecules (14), as we confirmed using Flood (University of Uppsala Software Factory http://alpha2.bmc.uu.se/usf/voidoo.html) (not shown). It is therefore likely that the local dielectric constant surrounding H322 is closer to that of the external solution than it would be in the center of a nonpolar globular protein (∼20–80 vs. 4) (39,40). Electrostatic potential maps of the central docking zone within the hydrated endofacial cavity (see Methods) disclose a uniform charge distribution in a band between Arg-302 and Lys-319 of ∼1.0 eV on the KREE plane when H322 is protonated (Fig. 5, panel 2). This electropositive region projects toward H322 in the KDDE plane (Fig. 5, panel 6) and decreases sharply in a band between Glu-269 and Glu-325 (KREE), extending in the KDDE plane toward Asp-237. Protonation of H322 imidazole generates an increase in local potential difference of 0.5–1.0 eV/Å in a 2- to 3-Å-wide band stretching between H322 and Glu-269 and Glu-325 in the KREE plane (Fig. 5, panels 1 and 2). The region most affected by protonation of H322 imidazole coincides with where docked lactose H-bonds to H322 (Figs. 2 A and 4, A and B). The electrostatic potential gradients of Lac Y in KREE and KDDE planes with protonated H322 are illustrated in Fig. 5, panels 10 and 16, respectively. Twin parallel tracks with a continuous gradient of 0.5–1.0 eV/Å cross the field (Fig. 5, panel 10). The upper track lies between Arg-302 and Glu-325 and the lower between Lys-319 and Glu-269. There is a shallow gradient (0.25–0.5 eV/Å) between Lys-319, Glu-325, and Asp-237 in the KDDE plane (Fig. 5, panel 16).

FIGURE 4.

Two views of the quadrilateral planes centered on H322. (A) The KREE plane is facing and the KDDE plane is seen on edge; the positions of two lactose molecules H-bonded to H322 are shown. (B) Docking positions of galactose (purple), melibiose (green), and lactose (yellow) within 3 Å of H322.

FIGURE 5.

Effects of protonation of H322 on the electrostatic charge distribution on the KREE and KDDE planes. A comparison of panels 2 and 6 with panels 1 and 5 shows the effects of protonation of His-322 in the KREE and KDDE planes, respectively. The color chart shows the potential scale: highest potential, 1.25 eV, lowest potential, 0.5 eV. Comparison of the electrostatic potential maps of control (protonated His-322) (panels 2 and 6), double mutant D240K/K319D (panels 3 and 7), and treble mutant K319N/H322/E325Q (panels 4 and 8). (Panels 1–4) KREE plane or equivalent. (Panels 5–8) KDDE or equivalent plane. (Panels 9–11, 13, 14–17, and 19) The electrostatic potential gradient maps are derived from the contour maps in panels 1–8, respectively, i.e., the potentials in the KREE and KDDE planes of the control and D240K/K319D double mutant and K319N/H322Q/E325Q triple mutant. (Panels 12 and 18) Differences obtained by subtraction of electrostatic potential gradient between control and D240K/K319D double mutant in the KREE and KDDE planes, respectively. (Panels 14 and 18) Difference maps between control gradients and triple mutant K319N/H322′/E325Q gradients in the KREE and KDDE planes, respectively, i.e., the gradient of the difference between panels 2 and 4 shown in panel 14 and the gradient of the difference between panels 5 and 8 shown in panel 20. The areas of white space in these difference maps indicate that there is no difference in the electrostatic potential gradients between control and mutant gradients.

Proton transfer between H322, water, and lactose

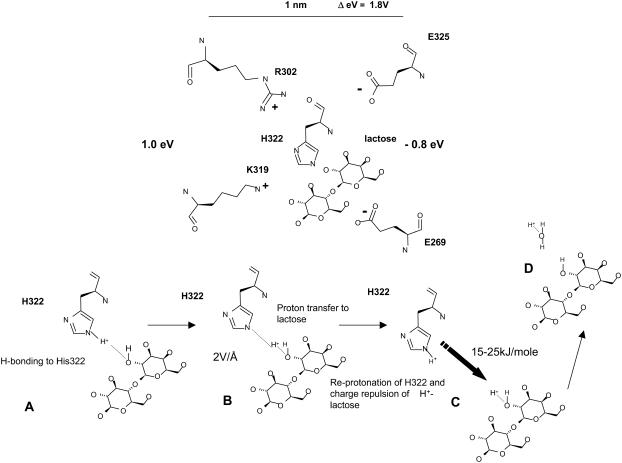
An alternative symport mechanism to the mechanical rocker model is one in which a proton is transferred from H322 imidazole Nɛ4 via the N-H⁺-OH H-bond to lactose (Table 1) to form a short-lived protonated alcohol hydroxonium group H⁺OH on lactose (Fig. 6). Hydroxonium ions are short lived (t_½ ≈ 2.0 ns) and have a very low pKa of∼−2.0 (54–56). Consequently, lactose alcohol hydroxonium forms in significant amounts only when the lactose acceptor and imidazolium proton donor make close contact, by H-bonding. However, among many disaccharides, lactose has been shown to be particularly amenable to complex formation with proton donating amino acids in vacuo (70). Sugar hydroxyl groups also make good proton donors for imidazole pK_a ∼12.0 and the proton transfer rate is relatively fast in solution (10,000 s⁻¹) (57–59). The lactose hydroxonium proton will dissociate to either form a hydroxonium ion on one of the adjacent caging water molecules or restore the imidazolium by geminate recombination.

FIGURE 6.

Mechanism of proton transfer between His-322 and lactose by (a) H-bonding between NH and OH followed by (b) proton transference between imidazolium and OH, and (c) reprotonation of imidazolium with protonated lactose adjacent.

After H322 imidazolium proton transference to lactose, the imidazole base is free to reassociate with another proton (Fig. 6 c). If this event occurs during the ∼2.0-ns interval when protonated lactose is present in the primary water shell surrounding the lactose-histidine complex, it will increase the overall energy of charge repulsion between the electropositive charges emanating from Arg-302 and Lys-319 and the still-protonated lactose, raising the net repulsive energy from 5 to ∼25 kJ mole⁻¹. This repulsive force prevents geminate recombination of the lactose proton with H322 (with a dielectric constant of 20, the recombination rate is typically reduced by a factor of 10⁵) and greatly increases the probability that lactose and its associated proton will be expelled from the primary hydration shell of polarized water surrounding the lactose-histidine complex. During the time the sugar remains charged and thereafter, its dissociation product, protonated water (H₃O⁺) drifts in a direction controlled by the anisotropic electrostatic charge distribution on the pore wall toward the electronegative endofacial surface. This process is analogous to the way an electrospray ionizer first ionizes then drives the ionized products in a mass spectrometer (60). A similar principle is adopted to activate movement in several Brownian synthetic machines (61–63).

Kinetics of proton movement within the central cavity of LacY

The kinetics of proton movements within the central cavity of LacY are critically important to this model of H⁺-lactose symport. In free solution the rate coefficient for imidazole protonation is 1.5 × 10¹⁰ M⁻¹ s⁻¹, and the rate coefficient for imidazolium dissociation is 1700 s⁻¹. Hence, the pK_a for imidazolium is 6.94 (57,58).

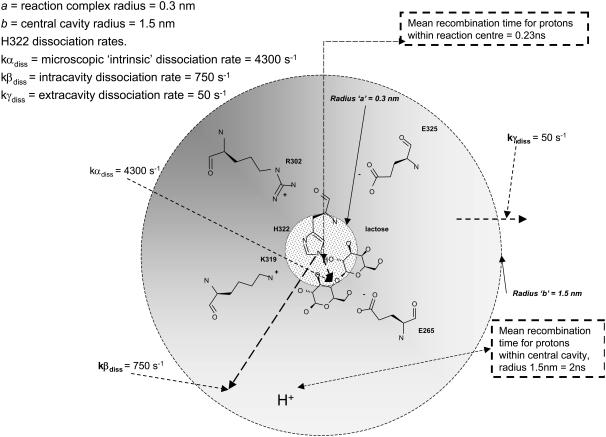
The pK_a of LacY H322 in situ is 7.3, a factor of 2 less than that of imidazolium in water (39,40). This increased basicity is probably a consequence of its H-bonding interaction with neighboring Tyr-236 (Fig. 1 B). As the protonation rate of imidazole within the cavity remains close to the diffusion control rate k_ass = 1.5 × 10¹⁰ M⁻¹ s⁻¹, the proton dissociation rate k_βdiss = 750 s⁻¹ is evidently reduced (Fig. 6).

Given that k_D = 2.5 × 10¹⁰ M⁻¹ s⁻¹, then inversion of formulas 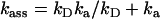and 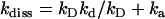yields the microscopic boundary rate constants in the radiation boundary condition k_a = 3.8 × 10¹⁰ M⁻¹ s⁻¹ and k_diss = 4300 s⁻¹ (Fig. 7).

FIGURE 7.

Diagram showing the relationships between the rate constants for proton dissociation within the central cavity of LacY.

However, the rate coefficient of protonation of LacY H322 measured directly is much smaller, k_ass = 1 × 10⁹ M⁻¹ s⁻¹ than the free solution value (39,40). With the pK_a of His-322 at 7.3, the corresponding dissociation rate coefficient k_γdiss = 50 s⁻¹ (Fig. 6). Assuming that the real microscopic dissociation rate of the histidine is the same as in free solution, then only 1.2% of its dissociations result in net loss of protons from the central cavity; the remainder recombine with H322 imidazole.

The average rate for proton recombination with H322 can be estimated as follows. First, let us assume that the central cavity of LacY is a closed sphere of radius b with a H322 imidazole-H-bonded lactose reactive site at its center. If the imidazole-lactose complex has a radius a, then the mean reaction time, 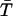, of a reactive particle generated at some point in the sphere b, a distance r from the center, can be obtained. This is achieved by solution of the backward diffusion equation using a reflecting boundary at the surface of the cavity and a radiation boundary condition at the reactive site. The boundary rate constant for reassociation k_a = 3.8 × 10¹⁰ M⁻¹ s⁻¹. The equation used to solve for the mean reaction time is:

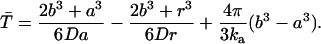(A10)

The first two terms in the right-hand side of the above equation represent the mean time to hit the reactive site for the first time, and the final term is the mean time to react once the sphere has been hit. The final term is the volume of the cavity V (minus excluded volume of the reaction site) divided by the boundary rate constant. In an isotropic electrostatic field, the rate constant for proton recombination at the reactive site for a particle distributed with uniform concentration in the cavity = k_a/V (Fig. 7).

Taking the radius of the central cavity of LacY to be 1.5 nm and that of the imidazole-lactose reaction center to be 3 Å gives a mean recombination time of 0.23 ns. Because of their similar pK_a values, the recombination rates for protonated lactose and hydroxonium ions will be similar. If the H322 imidazole is protonated from a source other than protonated lactose, then recombination with the protonated lactose is blocked by strong Coulombic repulsion until either the imidazole deprotonates again (average time ∼240 ns), or until the protonated lactose deprotonates (∼2 ns).

A key question is whether there is a significant probability of reprotonating H322 imidazole with another proton before recombination with the geminate proton in lactose hydroxonium. These other protons must arise either from a source outside the central cavity, i.e., periplasm, possibly by traversing a proton wire to the central cavity through the protein (39,64), or from additional protons in the cavity.

Once both lactose and imidazolium protonations occur, the mean time for protonated lactose to reach the surface of the cavity, including the effects of both diffusion and Coulombic repulsion, can be calculated by solving the appropriate backward Debye-Smoluchowski equation using the Green's function method, which is given by

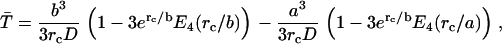(A16)

where r_c is the Onsager distance, at which the Coulomb interaction energy between the two ions is equal to thermal energy, kT, and E₄(x) is an exponential integral function (65). The first term in each bracket corresponds to the simple deterministic solution allowing for the repulsive force and frictional drag. The terms with the exponential integrals are the corrections to allow for random diffusive motion (see Appendix).

If the lifetime of the imidazole with respect to reprotonation is1 ns, then the probability of its reprotonation before geminate recombination with the proton from protonated lactose is 0.18.

Given that the proton ionic diffusion coefficient is 1 × 10⁻⁹ m² s⁻¹ (ionic mobility ∼4 × 10⁻⁸ m² s⁻¹ V⁻¹) (39), and a local dielectric constant of 20, the initial electrostatic repulsion of protonated lactose at the point of contact with imidazolium generates a drift velocity out of the cavity of ∼30 m s⁻¹. This reduces to ∼1 m s⁻¹ at the edge of the cavity. A very crude estimate of the average exit time is 0.4 ns. This is ∼50 times faster than the random diffusive escape rate. Thus, the escape time, assisted by the Coulombic repulsion, is substantially less than the time for either the histidine or the lactose to deprotonate. This shows that the suggested mechanism for cotransport of lactose is a possible option.

The relatively slow rate of proton pumping of LacY permease (turnover rate ∼20–50 s⁻¹) (37,38) is consistent with the low probability of proton escape from the central cavity. However, as seen above, this does not correlate with the microscopic rates of deprotonation of H322 within the central cavity.

Rationalization of the electrostatic model of LacY with mutation studies

Assuming that the electrostatic fields generated by the charged amino acids within 5–7 Å of H322 are the most proximal force determinants of symport, then mutations of these amino acids affecting any charge sign or position will influence the force vectors within the enclosed space. A number of mutation studies can be reinterpreted in terms of the above mechanism.

Single amino acid replacements

Replacement of either of the two basic amino acids close to H322 inhibits symport activity. Replacement of Arg-302 by either Leu, Ser, His, or Lys inhibits both symport and uniport activity (Figs. 3 and 4 and Table 2), (41,66–69). Replacement of Lys-319 with either electroneutral Cys or Ala also leads to inactivation of symport (18,41,70). Similarly, replacement of acid residue Asp-240 with neutral residues Cys or Ala inactivates the symport (16,41,45,66,70,71). Replacement of Glu-269 with Asp, E269D, permits both limited uphill H⁺-symport of lactose and lactose uniport, however replacements with neutral Gly or Ala, E269G or E269A, respectively, are devoid of both H⁺-lactose symport or uniport. However, surprisingly, TDG and other galactosides, e.g., melibiose, can induce downhill H⁺-symport in these mutants.

The importance of Glu-325 and its relationship with H322 was demonstrated by Carrasco et al. (77). The E325A mutant has no symport activity, but is as effective at uniport as Gln, His, Val, Cys, or Trp substitutions at position 325 (77).

Thus, it is evident that replacement of any single charged residue within the near vicinity of H322 with a neutral residue abolishes symport and often uniport also, whereas mutations conserving charge tend to conserve some residual transport function.

Although single charge replacements can only cause distortions of the electrostatic fields, multiple replacements either exaggerate, or sometimes may induce, compensatory changes, which reduce the net deformation. Such revertant mutants can produce some recovery of the transport function.

The effects of the D240K/K319D double mutant on electrostatic potential

Double replacement of both Lys-319 and Asp-240 by Ala or Cys leaves symport activity unchanged, as it conserves the electrostatic potential gradients across the KREE plane between Arg-302 and Glu-269 and Glu-325 (16,78). Similarly, when Asp-237 and Lys-358 are both replaced with the neutral amino acids cysteine or alanine, symporter activity remains intact. However, when only one of these amino acids is replaced, symport activity is lost. Switching of Asp for Lys between positions 237 and 358 with the double mutant D237K/K358D also preserves full transport activity and contrasts with the effects of double mutant D240K/K319D, where symport activity remains at zero. As K358 is almost twice as far from H322 as K319 (13.8 Å vs. 7.5 Å) and its electrostatic potential vector does not intersect with either the KREE or KDDE planes (Figs. 3 and 4 A), transposition of the ion pair K358/D237 has a negligible effect on the charge distribution close to H322. It is therefore unsurprising that this double mutation is without effect on symport and contrasts with the large effect of transposition of the K319/D240 pair on the potential field around H322 (Table 3) (16,18,20,78).

TABLE 3.

Multiple mutants

Positions on LacY	Mutant	LacY function	References
177/322	V177/N322	DS	(9)
237/358	D237K/K358D	SL	(17,18,70–72)
237/358	D237(A,C)/K358(A,C)	SL	(17,18,70–72)
240/319	D240(A,C)/K319(A,C)	SL	(16,18,41;70)
240/319	D240K/K319D	No activity	(16,18,41,70)
269/302/322/325	E269Q/R302L/H322Q/E325Q	No activity	(15)
269/302/322/319/325	E269Q/R302L/H322Q/K319N/E325Q	LU/DSM	(15)
319/325	K319N/E325Q	DSL	(13,66)
319/322/325	K319N/H322Q/E325Q	DSL/STDG	(79)
319/322/325	K319N/H322(R,Y)/E325Q	LU	(79)
322/325	H322E/E325H	No activity	(11,75)
322/325	H322N/E325S	DLS/SM	(11)

DS, downhill symport only; SL, lactose symport; LU, lactose uniport; DSM, downhill symport of melibiose; DLS, downhill lactose symport; STDG, symport TDG.

The lack of transport function of the double mutant D240K/K319D is discordant with the view that these amino acids behave as a reversible salt bridge. Reversal of the positions of residues K319/D240 causes large alterations in the electrostatic potential field around H322. The predicted electrostatic potential and potential gradient maps of the double mutant D240K/K319D shown in Fig. 5 (panels 3 and 7) and the electrostatic gradients in the equivalent KREE and KDDE planes of the D240K/K319D double mutant are shown in Fig. 5, panels 11 and 17. As expected, large decreases in the electrostatic potential gradients occur near positions 319 and 240 when Lys and Asp at positions 319 and 240 are exchanged. Comparison of the mutant gradient in the KREE plane with control (Fig. 5, panels 11 and 12, and 17 and 18) shows that the continuous positive potential gradient between 319 and 269 is abolished in the mutant (cf. Fig. 5, panels 10 and 11). This is apparent as a loss of electropositive gradient around position 325, seen in the lower left corner of Fig. 5, panel 11, and in the difference map between control and mutant potentials (Fig. 5, panel 12).

The loss of the electrostatic potential gradient between Lys-319, His-322, and Glu-269 elucidates why this double mutant disrupts symporter activity so effectively. The proton drift rate within the central cavity driven by the normal fixed potential is abrogated despite conservation of net charge and the potential for salt bridge formation.

Rescuing downhill symport by the triple mutant K319N/H322Q/E325Q

It is evident that rescue of poorly functioning uniport mutants can be attained by multiple selective neutral substitutions at positions 319, 322, and 325. None of these single mutants permits H⁺-lactose symport, and they have only low rates of lactose uniport (Table 2). However, the double mutant K319N/E325Q permits more rapid downhill coupled proton and lactose flow (13,66) and the triple mutant K319N/H322Q/E325Q allows downhill H⁺-TDG symport, but not H⁺-lactose symport (Table 3) (79).

Examination of the electrostatic map of the triple mutant K319N/H322Q/E325Q around H322 shows that despite loss of three charged groups (Fig. 5, panels 4 and 8), the electrostatic potential gradients in both the KREE and KDDE planes are similar to those of the wild-type LacY. This is shown quantatively in Fig. 5, panels 13, 14, 19, and 20). The positive potential gradient between the central region and Glu-269 is conserved, as demonstrated by the large area of white space in the central region of the KREE plane, Fig. 5, panel 14). White space in the difference maps signifies an absence of difference in the potential gradients between the triple mutant and control. A similar lack of gradient difference between the triple mutant and control exists in the KDDE plane in the sector bounded by Gln-322, Gln-325, and Asp-237 (Fig. 5, panel 20).

Mimicry by the triple mutant of the wild-type electrostatic gradients could be an explanation for the preservation of the capacity to transport lactose, albeit only in the uniport mode. The mutant suppressor, by restoring the electrostatic potential gradients within the field that are introduced by single mutations, could reduce major residue displacements and thereby rehabilitate the transport function along the pathway.

LacY specificity toward lactose, melibiose and galactose

Several LacY mutations lose their capacity for growth on lactose media, without concurrent loss of their capacity to grow on melibiose, or galactose-enriched media. The position numbers in Fig. 1 A signify the mutation sites that alter LacY specificity. Two are in the outer vestibule (29 and 33); four in the central cavity close to H322 (265, 321, 322, and 325), and another in a side pocket (177). Lactose, melibiose, and galactose all dock close to H322, although melibiose, unlike lactose, docks close to E325. Positions 177 and 319 are close to galactose clusters and not near either lactose or melibiose sites. Mutations (Table 4) causing major selectivity changes are localized at three main loci, A122, C148, and H322. When the mutation A122C is alkylated with N-ethylmaleimide (NEM), active lactose symport is abolished. Lactose, melibiose, and TDG protect against inactivation of C122 by NEM, but galactose does not protect against NEM inactivation. Galactose transport is also unaffected by NEM reaction with C122 (5,79). Mutations at 122 with large side chains, e.g., F122 or Y122, also inhibit lactose, but not galactose transport (Table 4).

TABLE 4.

Mutations altering sugar specificity on LacY

Mutation position	Mutation	Action	Docking on LacY	Reference
26,27,29	Y26D,F2; F29L	No uphill symport, or downhill lactose uniport, but downhill melibiose uniport	27 and 29 closer to lactose and melibiose (3–4 Å) than galactose (5 Å)	(45)
33	W33(S,Q,Y,A,H,F)	Altered sugar specificity	In outer vestibule (no docking near crystal LacY mutant)	(43)
122	A122C(F,Y)	Alkylation at C122 or bulky sidechains at 122 inhibit lactose, melibiose symport but not galactose symport.	Lactose and melibiose dock within 5 Å of A122, but not galactose	(5)
148	C148	Lactose protects against alkylation better than galactose	4 Å from lactose docking, not close to galactose docking	(46)
177/319	V177/N319	Induces maltose transport	Close to galactose, melibiose, and lactose docking	(42)
240,321,322	D240Y, L321Q, H322Y	No uphill or downhill lactose symport, but downhill melibiose uniport.	240 close to melibiose and lactose docking but not to galactose	(45)
269, 302, 319, 322, 325	E269Q/R302L/H322Q/E325Q	Downhill lactose uniport, downhill melibiose H+ symport	Close docking of melibiose, lactose, and galactose to D240	(41,42)
306	S306L	Increases melibiose transport, not lactose	In external vestibule	(42,44,46)
322	H322(F,Y)	No lactose symport; slow lactose uniport; no lactose accelerated exchange, melibiose exchange exit present	In central cavity	(35)
322 177/322	H322N, V177N/H322N	Loss of lactose symport, low-affinity melibiose, transports maltose.	Galactose docks close in a pocket outside central cavity near 177, not close to either lactose or melibiose docking.	(33)

See Fig. 1 for the crystallographic structure of LacY.

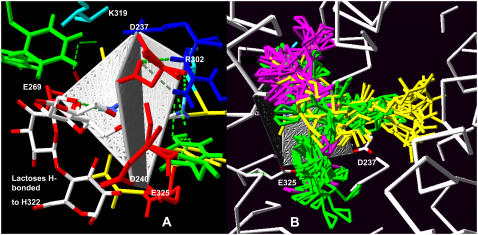
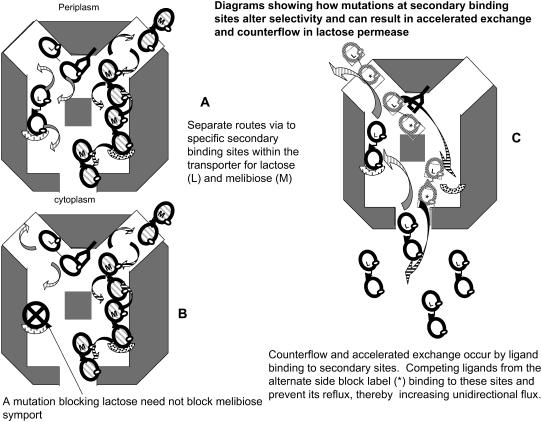
Consistent with altered relative capacities for transport of lactose, melibiose, and galactose by single or multiple mutations is the finding that the docking profiles of these sugars differs substantially on LacY (Figs. 1 A and 4 B). It seems likely that there are several possible tracks for passive sugar permeation across the LacY. Selective blockade will alter the relative capacity to transport these sugars (Fig. 8, A and B). Similar multiple tracks discriminating between quercetin and D-glucose have been previously inferred from kinetic and docking studies using transport in human erythrocyte GLUT1 (30) and for Cl⁻ and H⁺ in CIC channels (80).

FIGURE 8.

(A and B) Diagram showing how mutations can alter LacY selectivity for lactose and melibiose transport by preventing lactose binding to secondary sites within the transporter, thereby affecting lactose but not melibiose transit. (C) Diagram showing the condition for accelerated exchange or counterflow. Labeled lactose enters the LacY from the outside (periplasmic side). In contrast to the situation in A, it is prevented from binding to secondary binding sites within the central cavity by unlabeled lactose entering from the cytoplasmic side. This prevents labeled lactose reflux to the periplasmic side and consequently increases the apparent rate of labeled uptake. This will result in countertransport if the cytoplasmic lactose concentration is higher than the periplasmic concentration.

DISCUSSION

A seemingly compelling reason for accepting a unique sugar-binding site within LacY is the corroborating evidence advanced from mutation studies (20). Only a few amino acids are absolutely required for active transport. However, indispensability for symport implies only that the particular amino acid is an essential component in the matrix of interactions necessary for ligand binding and/or transport. Cysteine mutagenesis and site-directed labeling studies have shown that ∼70 of the total 417 amino acids in LacY have their reactivity to alkylating agents either activated or inhibited by ligand (TDG) binding (81–86). Nearly all of the TDG-sensitive sites on the periplasmic side have increased reactivity, whereas 16 of the 24 sites on the cytoplasmic side have decreased reactivity. This pattern of reactivity is consistent with the separate inward and outward facing conformations of the rocker model (84). However, another interpretation is that the reactivity of most groups lining the pore cavity is reduced by the high TDG concentrations accumulated within the cavity, whereas the exofacial sites are exposed only to dilute ligand concentrations.

Rationalization of asymmetric cotransport kinetics with LacY structure

Explanation of flux asymmetry in the context of this new cotransport model is relatively straightforward. The electrostatic potential across the polarized KREE plane between the positively charged band between R302 and K315 and the negatively charged belt between E325 and E269 supplies a steady-state driving force (Fig. 5, panels 1, 2, 9, and 10, and Fig. 6). This can be exploited by injection of mobile protonated species, e.g., protonated lactose and protons, into the field after H322 imidazolium dissociation. The steady-state electrostatic potential gradients within the LacY cavity are maintained by the transmembrane potential in the living cell, which is regulated at ∼80–120 mV over pH range 5–8 by independent ion pumps (38,85). The anisotropic electrostatic field across H322 determines the probability that protonated lactose and dissociated protons will drift toward the endofacial pole of the transporter rather than the periplasmic pole. The limiting accumulation ratio, C_in/C_out, by this mechanism, as with the carrier mechanism, is controlled by the energy transduced from the membrane potential in pH range 5–8, ∼80–120 mV (23,85).

Thus, at 310°K, C_in/C_out = exp(zFΔPD/RT) = 90; where z is the charge, F the Faraday constant, ΔPD the membrane potential (V), R the gas constant, and T the temperature (°K).

As mentioned in the Introduction, the apparent difference in affinity between inside and outside sites, like that with the GLUT1 transporter in human erythrocytes, is only observed when net ligand transport occurs, but not when measured by direct binding assays (29–32).

As with GLUT1(30), asymmetry between influx and efflux can be ascribed to the imported labeled (cis) ligand binding to sites within the central cavity, with partially occluded access to the trans surface of the transporter. Reflux of labeled ligand from this cavity reduces net “unidirectional” flow (Fig. 8 C). However, when a competing unlabeled ligand is present in the trans solution, as in the exchange condition, it prevents labeled ligand binding from the cis solution to the low-affinity binding sites in the central cavity. The resulting retardation of reflux of labeled ligand generates an apparent acceleration of unidirectional influx of labeled ligand. Uphill counterflow into the cytosol can also be induced by this mechanism.

Additionally, during net exit of lactose across the LacY symporter from a high intracellular concentration (zero trans efflux), lactose has to diffuse upstream against the inward drift of lactose and water hydroxonium ions induced by the electrostatic gradients in the center of the protein. This upstream movement may retard uncharged lactose efflux and further reduce the apparent affinity for export (21,25,26,36).

LacY has a similar large endofacial vestibule to GLUT1, into which lactose or melibiose from the periplasmic solution will accumulate and bind (Fig. 1 A). Furthermore, disaccharide accumulation here will be exaggerated by symport. It is proposed that ligand accumulation within this internal cavity is the precondition for generation of both accelerated exchange and counterflow in LacY as in GLUT1. Any mutation that substantially alters the fixed or fluctuating potential close to H322 will both slow symport and simultaneously increase the apparent affinity and rate of lactose export, because competition for export “sites” will be reduced by lack of accumulation of ligand from the external solution within the central cavity.

Similar principles have been demonstrated experimentally by spectroscopy of photolytic dissociation of carbon monoxide from myoglobin. At 250°K, CO binds in microcavities within myoglobin after photodissociation from heme at low temperatures (86). Geminate recombination of this bound CO slows the net rate of CO dissociation from the protein. Xenon, which can also fill the microcavities, competes with CO binding here, but not on heme. Xenon, by preventing local accumulation of CO, prevents its geminate recombination with heme and thereby increases the net dissociation rate of CO by 50% at this temperature.

Similarity between the proposed model of H⁺-lactose symport driven by electrostatic potential and Brownian ratchet molecular motors and pumps

This new model for H⁺-lactose symport has several features in common with Brownian motors (62,87,88), namely, a source of randomly fluctuating kT energy emanating from a stabilized molecule that is transferable to a contiguous mobile molecule. Brownian models of active transport and motility apply potential energy to the transported molecule, which is guided thereafter via a route statistically favoring either forward or backward escape. In this case, the energy comes from electrostatic repulsion between imidazolium anchored within a protein chain conjoined via an H-bond and mobile protonated lactose. Similar force is used to motivate translation in molecular shuttles (61,62). The scalar force generated by electrostatic repulsion is channelled by the anisotropic electrostatic field and thereby converted to a vector force. This is a necessary condition for any form of chemically induced active transport (89).

By definition, a ratchet prevents reversal of positional displacement. The low probability of protonated lactose reentering the water cage surrounding His-322, after ejection by electrostatic repulsion, accounts for the molecular ratcheting effect here. “Resetting” of the “imidazolium pump” has to come from a fresh proton, possibly supplied via a proton-wire connecting the central cavity with the periplasmic solution, similar to that proposed for cytochrome c oxidase (39,40,64,90). The electrostatic potential within the protein cavity is maintained by independent pumps in the bacterial membranes requiring an exogenous energy source (85). These essential processes for maintenance and resetting of the symporter pump are otherwise described as “escapement”, “balance”, and “linkage” processes (62,91). In the absence of these energy-requiring housekeeping processes, protons and other counterions will accumulate within the central cavity and neutralize the driving force for polarized flow.

Thus reversal of the proton gradient or PMF will generate proton leaks from the cavity to the periplasmic solution, with resulting loss of the strict 1:1 lactose: proton “stoichiometry” (22,23,36,85). This mode of proton leakage, viewed as an aberration of the mechanical symporter, is intrinsic to the electrostatic potential ratchet pump mechanism.

The explicit example of a Brownian ratchet model described here has both practical and theoretical advantages over the conventional rocker model of symport. The practical advantages are that it rationalizes how several single mutations can alter the symport to a uniport. It also provides a framework for testing how multiple mutations can lead to revertant forms and an explanation for why no single amino acid can be identified with the role of charge carrier either for return of the empty carrier or for proton conduction. It also proffers a straightforward explanation for the fast rates of proton diffusion, association with, and dissociation from H322 (∼10 kHz) within the central cavity of LacY, although the turnover rate of the symporter is ∼50 Hz (37–40). The mechanical rocker model requires that proton dissociation rate from H322 should be similar to the turnover rate of the permease, ∼50 Hz (19,37). Additionally, the asymmetry of the transport system is viewed as a structural feature of electrostatic charge distribution within the conducting cavity, supported by pumps maintaining the electrochemical potential gradients across the bacterial membrane (85).

Conventional mechanical models of biological pumps and motility make the common assumption that the mobile ligand species can be levered from their primary to secondary positions by force generated by cyclic protein conformational changes. An advantage of Brownian ratchet models is that they do not require extrapolation of macroscopic mechanics, invoking levers, pivots, springs, pulleys, and gears to the microscopic domain. A number of artificial macromolecular chemical motor devices have been synthesized that generate switchable ligand motion simply via reversible H-bonding and charge interactions between the stabilized and the mobile components when coupled to Brownian motion and an anisotropic escapement (61,62,88,92).

The Na⁺/K⁺ ATPase has been proposed as a Brownian motor device on the basis of the stimulating effects of external oscillating currents on ouabain-sensitive and ATP-dependent Rb⁺ and Na⁺ fluxes, respectively (93,94). A recent model for serotonin symport based on the “long-pore effect” has similarities to the current model, in relation to the view that the motive force for symport results from collisional interactions between the transported molecules, rather than by mechanical leverage exerted by protein conformational change (95,96). Thus, the alternating carrier model is not the only option for description of biological transport.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

APPENDIX

The backward diffusion equation for the probability density of diffusing from initial position r₀ to position r in time t is

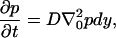(A1)

where the differentiation in the Laplacian operator is with respect to the initial coordinates r₀ (as opposed to the more usual forward diffusion equation where the differentiation is with respect to r). For a lucid discussion of forward and backward equations, see Karlin and Taylor (97). Modifications can be made to include an external force if desired.

Assuming spherical symmetry for the cavity only, the radial diffusion is relevant:

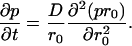(A2)

If the particle is reflected at the surface of the cavity (r = b), then the appropriate boundary condition is

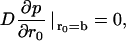(A3)

and if the particle reacts at a sphere of radius a in the center of the cavity, with a microscopic rate coefficient k_a, then the appropriate (radiation) boundary condition is

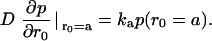(A4)

The advantage of the backward equation is that a number of other important functions are governed by it; for example, the probability that the particle has not yet reacted (survival probability) is defined by

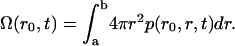(A5)

Because the integration only removes the dependence on r, the survival probability obeys the same backward equation as p:

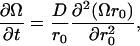(A6)

and the same boundary conditions, with the initial condition 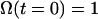, signifying that the particle has not reacted at time zero.

The mean reaction time may be calculated from the survival probability by

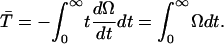(A7)

The first equality follows because minus the time derivative represents the probability density of the reaction time; the second equality follows from integration by parts.

Integrating the backward equation over time gives the backward equation for the mean reaction time:

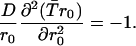(A8)

The general solution to this equation is

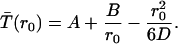(A9)

Moreover, applying the reflecting outer boundary condition and the inner radiation boundary condition, the solution for the mean reaction time for a particle initially at separation r₀ is found to be

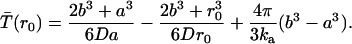(A10)

The first two terms represent the mean time to hit a for the first time (first-passage time); this can be seen by taking the limit 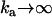. The third term represents the mean time to react for a pair in contact; this can be seen by taking the limit 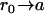. This solution can also be obtained by the Green's function method.

The Green's function method is also a convenient method for finding the mean time to hit the surface of the sphere with a repulsive Coulomb force. The backward equation for the mean time is modified to include the repulsion, and becomes (98)

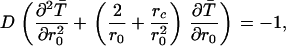(A11)

where r_c (the Onsager distance) is the distance at which the coulomb interaction energy becomes equal to the thermal energy kT. The inner boundary condition is reflecting,

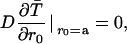(A12)

and the outer boundary condition absorbing,

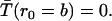(A13)

Linearly independent solutions of the equations obeying each boundary condition are 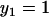for the inner boundary and 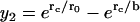for the outer boundary. The Wronskian is 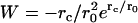. Applying the Green's function method, the mean exit time is given by the integral

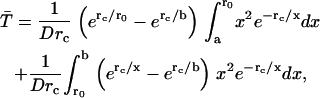(A14)

which can be evaluated after some algebra:

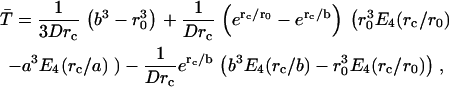(A15)

where E₄(x) represents an exponential integral function (99). Taking the limit where the particle starts at the reflecting inner boundary, this equation simplifies to

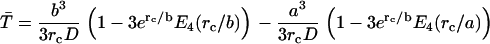(A16)

The exponential integral may be calculated numerically using, for example, the algorithm of Gautschi (100).