Modeling of Spatial Metabolite Distributions in the Cardiac Sarcomere

Abstract

Although a high ATP diffusion rate implies homogeneous distribution of the principal energetic currency in the cytosol, local diffusion barriers represented by macromolecular structures can render ATP concentrations to be inhomogeneous. A method is presented here that provides apparent diffusion coefficient values in local intracellular regions and allows the estimation of spatial metabolite distribution. The apparent local diffusion coefficient for ATP in cardiac myofibrils was determined from the analysis of diffusion-dependent rightward shift of the substrate dependence for actomyosin ATPase activity using the reaction-diffusion model, which accounted for the properties of phosphotransfer reactions. This functional analysis, which took into account the local diffusional ATP delivery to the active sites, provided an apparent value that was three orders of magnitude lower than that defined by direct methods for the cytosol. The low value of the diffusion coefficient was shown to define unusual properties of the intracellular space in working heart, where small reductions in ATP levels in the surrounding cytosol result in a large drop in [ATP] inside myofibrils. This drop is critical for vital cellular functions, and the analysis presented here defines its physical basis. The diffusion barriers thus defined explain the coexistence of pathological energy deficit with almost normal average ATP levels.

INTRODUCTION

Current progress in biological sciences in a great part could be characterized by a switch from biochemical analysis of separated reactions in vitro to the in situ analysis of whole biosystems. It requires implementation of novel experimental techniques and bioinformatic tools for analysis, which can tackle the complexity of systems biology. An example could be stable isotope tracer data analysis, where the noninvasive methods of tracing the in situ bioprocesses are supplemented by complex analytical software, which automatically constructs and solves thousands of equations for all isotopic isomers. Until recently, this kind of analysis was only available for steady-state conditions (1); now it allows for the evaluation of the parameters of system regulation and metabolic fluxes using nonsteady-state data (2–4). The correct description of spatial metabolite distribution, which is defined by local structures such as “fuzzy spaces” (5) would advance the understanding of cell operations one more step. Fuzzy spaces could create huge metabolite gradients by hampering diffusion, so that it appears to be much slower than expected based on the general cytosolic diffusion coefficient. Currently, the analysis of intracellular processes in situ, even those not restricted by steady state, in general does not take into account spatial metabolite distribution, thus averaging their distribution in the intracellular space. Averaging the metabolite concentrations could essentially misrepresent the real picture of metabolic regulation and thus restrict the understanding of life processes, as shown in the example presented below. This article is an attempt to overcome this restriction in the specific case of cardiac cells by evaluating the local diffusion restrictions and related ATP distribution in myofibrils.

Cardiac cells are high consumers of ATP energy, and imbalance between ATP requirement, production, and delivery is an indicator of a number of diseases such as dilated cardiomyopathy or cardiac allograft vasculopathy (6,7). The high value of ATP diffusion coefficient, as determined using the nuclear magnetic resonance technique (8), implies that ATP is distributed homogeneously. In this case, its concentration remains sufficient to maintain the maximal activation of all possible energy-consuming processes in any part of, and under any conditions in, living cells. In this case, when average [ATP] remains high, the existence of energy deficit seems paradoxical (9). However, strong energy deficit can coexist with high ATP levels; in the absence of phosphocreatine (PCr), an 18% reduction of ATP is incompatible with life (10). According to the biochemical properties of practically all ATP-sensitive processes, changes in [ATP] must be more profound to affect them; therefore, the coexistence of energy-deficient states with high average ATP levels seems incomprehensible. A possible explanation could be that ATP is distributed inhomogeneously, so that a large decrease in local areas could be manifested as a small decline at average levels. This explanation is in line with the well-known fact that if ATP diffusion is facilitated by parallel diffusion of PCr and active creatine kinase, which catalyzes phosphotransfer or high-energy phosphate exchange, the range of viable ATP concentrations could be higher (11). Several experimental studies in vitro have very elegantly demonstrated restricted diffusion of ATP in myofibrils (12,13).

Various functional tests could be used for diffusion coefficient determination. An extremely low diffusion coefficient, as a physical basis for inhomogeneous ATP distribution, was defined in the subsarcolemmal compartment based on the analysis of ATP-sensitive K⁺ (K_ATP) channel activity, which can sense the local [ATP] set by adjacent ATPases at levels different from the average value (14,15). Slow diffusion and high ATP consumption set local [ATP] in the high-sensitivity range of the channel, so that minor changes in its primary structure, insignificant for permeability, could contribute to heart disease (16). A similarly low diffusion coefficient in the submembrane microcompartment, was obtained earlier for cyclic AMP diffusion (17,18). Nonequivalence of different ATP sources for supply of the energy-consuming processes (19–21) assumes that the ATP pool is not well-mixed. The different pools of pyruvate found in neurons and astrocytes (22–24) also support the hypothesis that nonmembrane-separated compartments with highly different metabolite concentrations can exist. The physical basis for such compartmentalization is the low value of the diffusion coefficient, the estimation of which would provide an understanding of the spatial and temporal organization of intracellular processes.

The anomalously slow diffusion, estimated for some compartments where macromolecular obstacles can dramatically restrict diffusion (25,26), does not conflict with the high average value of the diffusion coefficient for ATP in the cytosol (27). Although the latter value characterizes displacement in the cytosol, the functional estimation of the diffusion coefficient accounts for local diffusion barriers as they appear in a particular process.

In this study, we developed a method to estimate the apparent ATP diffusion coefficient in isolated myofibrils, using a specific computational method applied to the analysis of their ATPase activity (28). In the absence of phosphocreatine, the myofibrillar ATPase expressed as a function of [ATP] in the medium seemed to be less active than in the presence of phosphocreatine. Restrictions in diffusional delivery of ATP as it was consumed internally resulted in lower [ATP] in the myofibrils than in the medium. The decreased activity, which in fact corresponds to low internal [ATP], is attributed to the external ATP levels, and this appears as a rightward shift of the ATPase activity. Therefore, the change of concentration dependence in the dense structure and its restoration after diffusion facilitation is an indicator of diffusion limitations, and the value of respective shift can be used to define the diffusion coefficient, as described below in the first part of the Results section.

The diffusion coefficient, revealed from experimental data analysis, and the known spatial distribution and phosphotransfer enzyme properties were used to calculate the spatiotemporal ATP distribution in working myofibrils in situ. This calculation, described in the second part of the Results section, revealed that in the working heart, a small decrease in average [ATP] is coupled with a greater local drop in the ATP-consuming compartments, which could explain the coexistence of pathological energy deficit with high average ATP levels.

METHODS

One-dimensional diffusion along the radius in isolated myofibrils

The model, schematized in Fig. 1 a, considers myosin ATPase, which creates the ATP gradient, diffusion of external ATP, and produced ADP. Actomyosin ATPase activity (J_ATP) was described by the following equation (29):

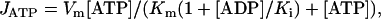(1)

where V_m was taken to be 0.22 mM/s observed in the experiment analyzed (28), K_m was 10 μM, and K_i was 200 μM (29).

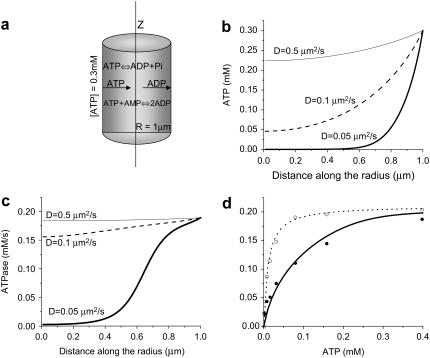
FIGURE 1.

Estimation of the ATP diffusion coefficient from the diffusion-dependent rightward shift of actomyosin ATPase activity. (a) Schematized model considers myosin ATPase, which creates an ATP gradient, and its diffusion from the external medium and reverse diffusion of ADP. (b and c) Distribution of, respectively, ATP and ATPase activity along the radius of a cylindrical myofibril computed as a steady-state solution of the system of partial differential equations, which accounts for ATP diffusion, its consumption by actomyosin complex, and adenylate kinase activity (described in the text). (d) Average ATPase activity of myofibrils as a function of external ATP concentration, showing experimental data obtained in the absence of phosphocreatine (solid circles); with the respective model simulation (solid line), which describes the experimental data at diffusion coefficient D = 0.1 μm²/s and AK reaction under the steady-state conditions. ATPase activity measured in the presence of phosphocreatine (12 mM, open circles) is also shown with its respective model simulation (dotted line).

Adenylate kinase (AK) activity was not inhibited under the experimental conditions. J_AK was described by the following equation:

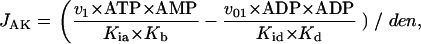(2)

where 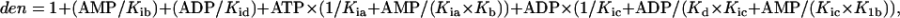v₁ = 300., v₀₁ = 300, K_ia = 0.1, K_ib = 0.1, K_b = 0.1, K_d = 0.1, K_1b = 34.9, K_id = 0.1, and K_ic = 0.1.

ADP concentration was determined according to the mass conservation equation:

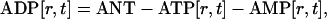where ANT is the total adenine nucleotide concentration equal to the external ATP added into the suspension.

With the given parameters, Eq. 2 describes the known properties of the AK reaction: equilibrium constant (ATP × AMP/ADP²) is ∼1 (30–32), and the K_m for the substrates (0.25 mM for ATP, 0.01 mM for ADP, and 0.06 mM for AMP (33–35)).

Distribution of ATP and ATPase activity along the radius of a cylindrical myofibril was obtained as a steady-state solution of the following system of partial differential equations:

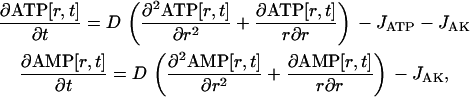(3)

with boundary conditions ATP[R,t] = ANT, ATP[−R,t] = ANT, AMP[R,t] = 0, and AMP[−R,t]= 0.

Mean ATPase activity

The particular curves were obtained by assigning the diffusion coefficient D to the values shown in Fig. 1. External [ATP] = ANT was 0.3 mM, the maximal value used in the experiment analyzed. ATPase activity shown in Fig. 1 c was reconstructed according to the known nucleotide concentrations shown in Fig. 1 b.

To compare the computed values with experimental ATPase activity of myofibrils, the calculated nonhomogenous in-space ATPase activity (in fact, distributed along the radius, as shown in Fig. 1 c) has to be presented as an average value. For such a comparison, the average in-space activity was calculated for each external ATP concentration used in the experiment:

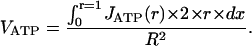(4)

Spatial distribution of enzyme activities used in the model of two-dimensional diffusion in myofibrils

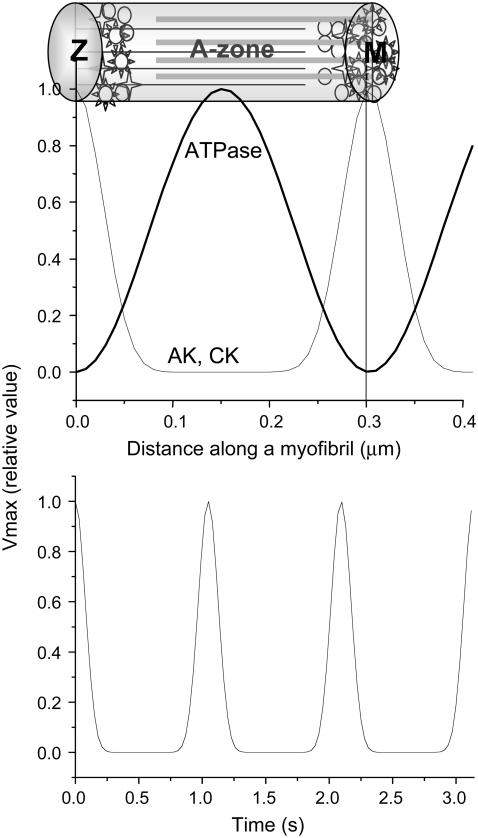
According to the electron microscopic data (36), peaks in creatine kinase (CK) or AK density correspond to M- and Z-lines, where ATPase activity is minimal. Maxima of ATPase activity correspond to the center of actin and myosin overlapping the A-zone. This distribution of enzyme activity along the z axis of a myofibril was described as follows:

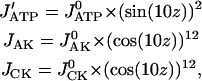(5)

Here, 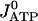is described according to Eq. 1, 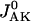is in accord with Eq. 2, and 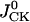is described by the similar equation

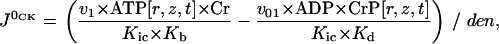(6)

where

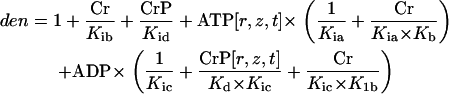Equation 6, with the parameters, v₁ = 6.886, v₀₁ = 29.333, K_ia = 0.9, K_ib = 34.9, K_b = 15.5, K_d = 4.73, K_1b = 34.9, K_id = 4.73, and K_ic = 0.2224 taken from Lawson and Veech (37), describe the known equilibrium and K_m for all the substrates (38).

Oscillatory behavior of ATPase activity in time, with maximum at systole and minimum at diastole, is described using the function J_ATP = J′_ATP × (cos(3t)¹⁸, which assumes the duration of systole to be ∼0.2 of the total cardiac cycle. J′_ATP is described by Eq. 5.

The reaction-diffusion model describing two-dimensional diffusion was expressed by the system of partial differential equations

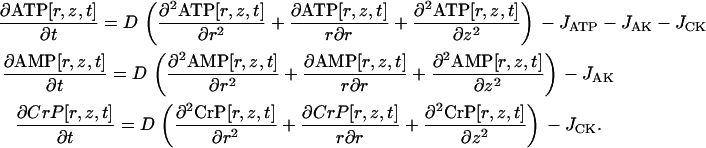(7)

Here, r is a direction along the radius of a cylindrical myofibril, which varies from −R to R = 1.0 μm, and z (from −L to L = 1.0 μm) is a direction along the longitude of the myofibril. The distance between the Z- and M-lines was taken to be ∼0.3 μm. D was determined according to the estimation for an isolated myofibril with a radius of 1.0 μm performed in the previous step of the analysis.

For the boundary conditions of CK and AK, equilibrium was assumed in external cytosol. In this case, for the total nucleotide concentration [ANP] = 7 mM, total creatine [CrT] = 40 mM, and given that ATP[R,z,t] = ATP[−R,z,t] = ATP[r,0,t] = ATP[r,L,t] = t₀, where t₀ is [ATP] in cytosol. The boundary concentrations of other variables were described as follows:

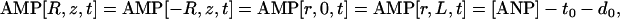where d₀ is [ADP] in cytosol, and

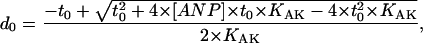(8)

as follows from AK equilibrium in surrounding cytosol; and

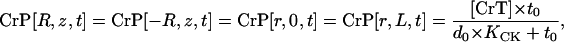(9)

as follows from CK equilibrium in surrounding cytosol.

Initial concentrations of all the variables inside a myofibril were taken as equal to their boundary values.

The systems of partial differential equations corresponding to one- and two-dimensional reaction-diffusion models were solved using “Mathematica” software (Wolfram Research, Champaign, IL). The models are described in more detail in Supplementary Materials.

RESULTS

Fig. 1 illustrates the ATP diffusion coefficient determination based on the analysis of ATPase activity in isolated myofibrils, specifically the rightward shift of reaction-rate substrate dependence, which was reversed by the phosphocreatine-facilitated diffusion (28), i.e., parallel diffusion of ATP and phosphocreatine and exchange of high-energy phosphate in creatine kinase reaction. The experimental data used for the analysis are as follows.

The substrate concentration, which corresponds to a half-maximal reaction rate (K_m), for actomyosin complex was reported to be 10 μM (29). In isolated myofibrils, where the native structure and diffusion barriers, respectively, are preserved, K_m shifted to ∼80 μM (28). The diffusion facilitation by addition of phosphocreatine restored the normal K_m value of 10 μM, thus validating that the rightward shift was induced by diffusion limitations. To analyze this experimental observation to define the diffusion coefficient for ATP as it appears locally in myofibrils, the reaction-diffusion model described above was used.

The reaction-diffusion model used for the analysis of myosin ATPase activity considered a myofibril to be a homogenous cylinder with a radius R = 1 μm (Fig. 1 a), in accord with Smith and White (39), who measured the dimensions of isolated myofibrils using phase contrast microscopy. The model accounted for the measured ATPase activity (J_ATP) and adenylate kinase activity (J_AK), maintaining equilibrium concentrations of ATP, ADP, and AMP, and assumed that the substrate and product diffusion proceeded according to Fick's law. Thus, the distribution of adenine nucleotides along the radius of a cylindrical myofibril was obtained as a steady-state solution of the system of partial differential equations (Eq. 3).

The steady-state distribution of ATP along the radius (Fig. 1 b) was calculated at the different values of diffusion coefficient D. For a low value of D, the [ATP] inside a myofibril is much less than the external concentration. Accordingly, D also defines the reaction rate at each point of the cylinder cross-section along the radius J_ATP(r) (Fig. 1 c). The value corresponding to the experimental data is the average ATPase activity calculated from J_ATP(r). A decrease of D markedly affects local ATPase activity inside the myofibril (Fig. 1 c), which results in an apparent rightward shift of the average ATPase activity.

The dotted curve in Fig. 1 d shows the ATP dependence of actomyosin ATPase activity in the absence of diffusion limitations (29). Only one parameter in the model was unknown (D), and when D = 0.1 μm²/s, the rightward shift in apparent ATPase activity coincides with the experimental value (Fig. 1 d, thick curve). Phosphotransfer from creatine phospate shunted the diffusion barriers, and its presence (28) restored the normal ATP dependence of actomyosin ATPase (Fig. 1 d, dashed curve).

The diffusion coefficient, defined above, allows computing the spatial distribution of ATP as is described next.

If the diffusion coefficient is known, the values of high-energy phosphate concentration in cytosol, actomyosin ATPase activity, and the spatial distribution of the ATP consumption sites and phosphotransfer enzymes define the energetic status at each point inside the myofibril. These parameters are, in general, known (40,41); therefore, the value of D defined as described above allows us to predict the energetic state inside myofibrils in living cardiomyocytes. To make such a prediction, the reaction-diffusion model was modified, so that to account for the spatial distribution of high-energy phosphates not only along the radius but also along the central axis of the myofibril, where the enzyme activities were distributed inhomogenously.

Fig. 2 illustrates the spatial setting of the enzyme activities in the model, taken according to the available structural data (36), and the oscillations in time during cycles of cardiac contractions. These settings, along with the diffusion coefficient and the global energetic state of the cell, expressed as surrounding ATP levels, define the spatiotemporal distribution of ATP inside myofibrils. ATPase activity, measured experimentally as an average value for low and moderate work states in vivo (40,41), in fact is maximal in the A-zones, where actin and myosin filaments overlap. Therefore, in the model, the ATPase activity, which on average corresponded to the measured values, was assumed to be distributed inhomogeneously, as is shown in Fig. 2 a. According to the electron microscopic data, the distribution of creatine kinase and adenylate kinase along a myofibril is also inhomogeneous (36); the model assumed the corresponding distribution as shown in Fig. 2 a. Total creatine, (Cr +PCr), 40 mM (42), as well as the total adenine nucleotide amount (ATP +ADP +AMP), 7 mM (43), were constant, whereas the concentration of components varied in space and time. Variation of the actomyosin ATPase activity over time was simulated as shown in Fig. 2 b, which assumes that the period of contraction accounts for 20% of the total cycle. The details of the settings for spatial distribution of enzyme activities could be found in the figure legend.

FIGURE 2.

Enzyme spatial distribution, as set for the two-dimensional reaction-diffusion model of ATP consumption in myofibrils. Distribution of ATPase, CK, and AK activity along a myofibril (a) and time course of ATPase activity (b) during cardiac contraction cycles, as assumed in the model.

The reaction-diffusion model, which accounted for the inhomogeneity along the longitude of the myofibril, in this case was expressed by the system of two-dimensional diffusion equations (Eq. 9).

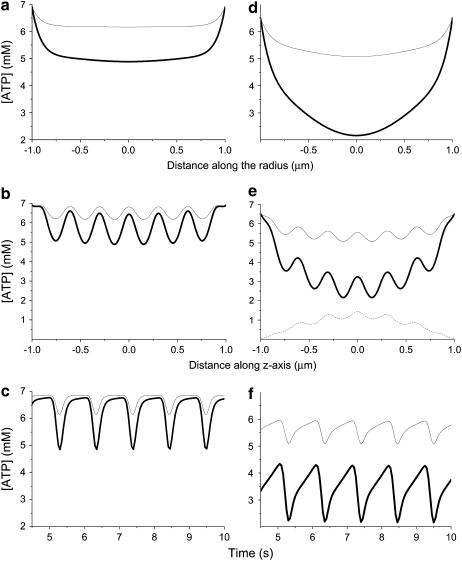
Fig. 3 shows the results of simulation of spatial and temporal distribution of ATP in myofibrils given the activities shown in Fig. 2 and the diffusion coefficient determined, as illustrated in Fig. 1. Fig. 3, a, b, d, and e, shows the spatial distribution of ATP concentration in the moment of highest ATP consumption (peak in Fig. 2 b) along the radius of cross-section in the middle of the A-zone (a and d) and along the central axis (b and e). In e, the respective distributions of AMP are also shown, as are the temporal oscillations of [ATP] in the central point of cross-section in the middle of the A-zone (c and f).

FIGURE 3.

Expected intramyofibrillar ATP levels computed for diffusion coefficient D = 0.1 μm²/s, defined as illustrated in Fig. 1 d. The calculations were made for two different ATPase activity levels: 1.4 mM/s (thin lines), which corresponded to rest, and 3.4 mM/s (thick lines), which corresponded to moderate workloads. The reaction-diffusion model accounted for inhomogenous distribution of the enzyme activity in space and time, as is shown in Fig. 2. (a, b, d, and e) Spatial distribution of ATP concentration in the moment of highest ATP consumption (peaks in Fig. 2 b) along the radius of cross-section in the middle of the A-zone (a and d) and along the central axis (b and e); and also the temporal oscillations of [ATP] in the central point of cross-section in the middle of the A-zone (c and f). For a–c, the surrounding [ATP] was set to 6.9 mM, and for d–f, it was 6.5 mM. (e) Dotted line shows the respective spatial distribution of AMP.

The left panels (a–c) refer to normal conditions (surrounding ATP = 6.9 mM and ADP = 0.1 mM), whereas the right panels (d–f) correspond to physiological conditions of severe stress or disease (44) (surrounding ATP = 6.5 mM and ADP = 0.5 mM). The only difference in the surrounding [ATP] results in the sharp distinctions in the local ATP distribution.

Even at 6.9 mM surrounding [ATP], in the center of a myofibril in the middle of the A-zone, [ATP] declines to 5 mM at high workload. The difference disappears in the regions of Z- and M-lines where ATPase activity is insignificant and ATP delivery through the external surface facilitated by creatine kinase is sufficient to shunt the ATP gradients. However, the gradients exist in the A-zone, where ATPase activity reaches its maximum and phosphotransfer activities are low. The time course shows that [ATP], decreased during systole, returns to the surrounding value by the end of diastole.

When the ATP levels in the surrounding cytosol drop from 6.9 to 6.5 mM (Fig. 3, d–f) during systole, ATP in the A-zone declines to 2 mM and does not recover during diastole. ATP concentration remains low not only in the A-zone but also in the M-line. Thus, a decrease in surrounding [ATP] from 6.9 to 6.5 mM under the diffusion restriction is translated into a sharp local drop, which could limit the function of myofibrils.

DISCUSSION

Currently, the generally accepted concept, based on a high ATP diffusion coefficient, which was defined using the NMR method, cannot explain numerous observations coming from studies of various cellular functions, e.g., showing ATP compartmentalization in myofibrils (12,13), which could result in paradoxical energy deficits in cardiac cells under conditions of high average [ATP]. Therefore, we defined diffusion coefficients independently, from a functional study: ATPase activity of actomyosin in myofibrils, which was different in the presence and absence of PCr. Assuming that the difference depended on the diffusion restrictions, we defined the diffusion coefficient, which allowed us to describe the experimental situation. This analytical approach revealed anomalously slow diffusion, which, due to the barriers represented by macromolecular obstacles, appeared to be three orders less than that defined using nuclear magnetic resonance (8). Then, using the diffusion coefficient thereby defined, we described the spatial and temporal metabolite distribution that could be expected in a working myofibril in situ and found that it could affect the energy delivery to working myofibrils even under conditions of high levels of ATP in the surrounding cytosol. Fig. 3 shows that even under a moderate workload, the ATP concentration can drop from 6.5 mM in surrounding cytosol to 2 mM in the regions of cross-section of central myofibril axis with the A-zone of actomyosin overlapping. The models allowed us to calculate the average expected ATP concentration under this condition. Cardiac cells consist mainly of myofibrils and mitochondria, so that there is practically no “free” cytosol. Integrating the ATP concentration throughout the volume of myofibril, we found that the average concentration was 5 mM. If the mitochondrial compartments were taken into account, the average ATP would have been even higher, so that the difference between average and minimal local ATP concentration in the described situation surpasses 3 mM. If, under the same conditions of 6.5 mM extramyofibrillar ATP, the workload increases from 3.4 (see Fig.3) to 5.2 mM/s (not shown), which is still within the physiological range, the ATP level drops in the center of the A-zone to 0.1 mM, which can create an energy-deficient state, whereas the average intramyofibrillar ATP is 4.3 mM. This value (or an even higher one, if one also considers the mitochondrial compartment) would represent the minimal possible ATP levels; further drops in ATP would result in damage to cardiac cells.

The method of indirect determination of the diffusion constant based on cell function studies provides a value that allows an explanation of cell physiology data, but at first glance it seems to be inconsistent with the direct measurement of diffusion coefficient, e.g., that provided by the NMR method (8). Also, diffusion constants of molecules in the filament lattice have been experimentally determined by the photobleaching recovery technique (45). Both the radial and longitudinal diffusion constants of myoglobin, a molecule with molecular mass 17 kDa that is much larger than ATP, has been found to be 1.1–1.3 μm² s⁻¹ in skeletal muscle cells as well as in cardiomyocytes. In general, direct methods show that diffusion is fast, whereas indirect cell physiology data indicate that diffusion is slow. Probably the existence of physical barriers created by macromolecular crowding in some areas of the cytosol could impede diffusion, so that the metabolites diffuse quickly in the absence, but apparently slowly in the presence, of such barriers. Therefore the use of a directly defined diffusion constant without consideration of diffusional barriers could result in extremely incorrect conclusions.

This study uses the indirectly defined diffusional constant as a homogeneous characteristic of diffusion throughout myofibrils, and this may represent another extreme and evidently is a great simplification taken in the model. If direct methods characterize the fastest diffusion in the “highways” of the myofibrillar compartment, the method presented here gives the average value for the diffusion from periphery to the catalytic sites of actomyosin complexes. Presumably, the A-zone could be characterized by slower diffusion than other regions, for which direct methods give correct values. The average value could be composed of fast components, measured by direct methods, and also extremely slow components present possibly in restricted areas. In fact, the value present here is much higher than that found in another studies. An example of slow apparent diffusion coefficient could be the value for cyclo-AMP diffusion coefficient of 10⁻⁵ μm² s⁻¹ found in Rich et al. (18) in the subsarcolemmal layer.

Since this study considers average diffusion characteristics inside myofibrils, we admit that real metabolite distribution could differ from the presented picture. However, it shows that apparent diffusion could be slow in some regions, and the real differences in ATP levels therefore could be extremely high. Therefore, although it is a simplification, this study makes a step forward from the basically homogeneous characterization currently prevalent to a real heterogeneous description of spatiotemporal organization of intracellular metabolites. It should stimulate more detailed studies of the geometrical structure of diffusion barriers, which will allow a better description of local metabolite distribution.

Fig. 3 shows that the difference between surrounding and intramyofibrillar levels depends not only on diffusion coefficient, but also on ATP consumption. The slower the consumption rate, the less the ATP gradient. This could be a reason why another study performed on isolated myofibrils did not reveal the difference between outside and intramyofibrillar concentration. In fast skeletal myofibrils the K_m for ATP of myofibrillar ATPase measured at 4°C in the absence of creatine phosphate was found to be 6 μM (46).

The ATP gradient depends also on the surrounding ATP levels. As our calculations show, the difference between local and surrounding [ATP] increases when the surrounding [ATP] decreases. This translation of small changes in surrounding ATP levels into a large local ATP drop is based on the properties of creatine kinase reaction, which transfers the high-energy phosphate between ATP and creatine. According to the equilibrium constant of this reaction, when surrounding [ATP] is 6.9 mM (out of 7.0 mM total adenine nucleotides), the phosphocreatine level is 12 mM (out of 40 mM total creatine) and its diffusion is sufficient to maintain high local ATP levels. A decrease of ATP to 6.5 mM leads to a fivefold increase of [ADP] (from 0.1 to 0.5 mM), and as creatine kinase equilibrium is still maintained, this shift results in a drop of phosphocreatine to 3 mM. Thus, when [ATP] is 6.9 mM the total phosphocreatine and ATP levels (18.9 mM) are sufficient to provide normal diffusional delivery of this energetic currency. When [ATP] drops to 6.5 mM, the total phosphocreatine and ATP levels drop drastically (to 9.5 mM) and this impairs local energy supply. Thus, the highly limited diffusion creatine kinase reaction translates small reductions of surrounding ATP into high ATP declines in the local ATP-consuming regions with high diffusion restrictions. This is an example of an unusual property of the intracellular space created by highly restricted diffusion. Thus, diffusion limitations could define new functionality for the well-known components, such that the creatine kinase functions as an amplifier of cytosolic ATP oscillations (15).

Also, some data interpreted in terms of channeling may be better explained in terms of slow diffusion. Diffusion limitations slow down the exchange between distinct metabolite pools, an effect that could be erroneously interpreted as channeling. The existence of such distinct pools with slow exchange has been documented, for instance, for glycolytic metabolites (23).

Diffusion restrictions, which define unexpected properties of the intracellular space, are a fascinating subject for future study, which may improve our understanding of intracellular spatiotemporal organization. With many of the necessary tools at hand, the time is right to expand our focus beyond the bounds of one- or even zero-dimensional mixed cytosol to three-dimensional structures organized in time.