Theoretical Characterization of Carbon Monoxide Vibrational Spectrum in Sperm Whale Myoglobin Distal Pocket

Abstract

In this article we use the perturbed matrix method and an extended molecular dynamics sampling of the carbon monoxide (CO) in the myoglobin distal pocket to characterize the CO vibrational spectrum and hence to relate its spectroscopic features with the atomic-molecular behavior. Results show the accuracy of the method employed and confirm the assignment of the spectroscopic B₁ and B₂ states proposed by Lim et al.

INTRODUCTION

Myoglobin (Mb), one of the most studied proteins so far, has been characterized by a great variety of techniques ranging from x-ray crystallography to molecular simulation (1–21). Myoglobin's small size, relative structural stability, and yet complex functional behavior (involving relevant conformational fluctuations as well as covalent binding of ligands) make this protein a virtually perfect model system to investigate, at the atomistic level, protein biochemical activity. Carbon monoxide (CO), one of the possible myoglobin ligands, has been used as a probe for the kinetics of the covalent binding process (2,22) (heme-CO binding) as well as for characterizing the Mb-ligand interaction during ligand diffusion in the protein matrix (23,24). In particular, CO (time-resolved) vibrational spectra have been extensively used in the last decade to determine CO behavior just after photolysis of its covalent bond to heme (14,19,25,26), characterizing the presence of two distinct spectroscopic states (B₁, B₂) probably corresponding to two different CO-heme relative orientations and still not uniquely assigned (27–33). Recent attempts to obtain vibrational (IR) spectra of CO in myoglobin by molecular dynamics (MD) simulations (34,35), providing a reasonable qualitative reproduction of experimental data, were based on a purely classical CO model, treating its intramolecular (quantum) vibrational mode as a classical degree of freedom and hence evaluating the IR spectrum via the CO dipole autocorrelation function. Such an approach is heavily dependent on the details of the semiempirical CO model used and may provide artifacts caused by the classical approximation of vibrational excitation.

Recently (36,37) we extended the perturbed matrix method (PMM), introduced previously (38,39), to model quantum-mechanically vibrational excitations of molecules in complex systems (i.e., including the effects of the atomic-molecular environment on IR spectra). In those articles we applied our method to CO in solution (water and chloroform), showing its efficiency and reliability. In this article we apply the same methodology to determine the CO IR spectrum in the Mb distal pocket, as obtained by PMM and MD simulations using the three-site “quadrupolar” CO model (40) employed in previous articles.

METHODS

Initial coordinates for the simulation of Mb with photodissociated CO were taken from the 1.15 Å resolution crystal structure of CO-bound sperm whale Mb (PDB entry 1BZR) (41), in which we cut the CO-Fe bond. Thus, from the beginning of the simulation the system was modeled as an unliganded state of Mb with CO. According to recently published articles (33,42), His(E7)64 was modeled as the neutral tautomer, with hydrogen at the ɛ position. The protein was solvated in a box with explicit SPC water molecules (43), large enough to contain the protein and 0.8 nm of solvent on all sides. The total number of atoms for the system was ∼21,000.

MD simulations were performed with the Gromacs software package (44) using the GROMOS96 force field (45). The CO molecule was modeled with the three-site “quadrupolar” CO model (40). Simulations were carried out at constant temperature (300 K) using the isothermal temperature coupling (46) within a fixed-volume rectangular box and using periodic boundary conditions. The Lincs algorithm (47), to constrain bond lengths, and the rototranslational constraint algorithm (48), to stop protein rototranslational motions, were used. The initial velocities were taken randomly from a Maxwellian distribution at 300 K, and a time step of 2 fs was used in all simulations.

The particle mesh Ewald (PME) method (49) was used for the calculation of the long-range interactions with a grid spacing of 0.12 nm combined with a fourth-order B-spline interpolation to compute the potential and forces between grid points. A nonbond pair list cutoff of 9.0 Å was used for short-range interactions, and the pair list was updated every five time steps.

After thermalization and equilibration, we perform an initial 1-ns simulation to obtain a relaxed structure of the system with the ligand in the principal docking site of the distal pocket. Starting from this structure, we have performed five MD simulations using different initial velocities, given by 300 K Maxwellian distributions, each stopped at the first carbon monoxide escape from the distal pocket for a total of 21 ns of MD simulation of the photodissociated CO in the distal pocket.

Carbon monoxide vibrational states were obtained using the method described in detail in a previous article (36). In brief, the ground-state electronic energy along the internuclear distance of an isolated CO molecule was obtained by density functional theory (DFT) calculations. Note that, as described in a previous article (36), the internuclear distance range we utilized is about ± 0.15 Å around the equilibrium distance (∼1.1 Å), which is, for a stiff vibrational mode as in CO, a proper fluctuation range for estimating the vibrational frequency within the harmonic approximation (36). Becke's three parameters exchange (50) and Lee, Yang, Parr correlation (51) function (B3LYP) were used for DFT calculations in conjunction with triple-ζ atomic basis set with polarization and diffuse functions, i.e., aug-cc-pv-tz (52). Configuration interactions (53) including single, double, and triple excitations (CISDT) calculations, using the above B3LYP/ aug-cc-pv-tz orbitals, were then carried out at each internuclear distance using an active space as large as 10 electrons in 35 orbitals for evaluating the unperturbed electronic states considered for PMM calculations. As shown in the previous article (36), such a computational procedure provides a very accurate description of vibrational and electronic states of the isolated CO molecule. All our quantum chemical calculations on isolated carbon monoxide were performed using the Gamess US package (54).

The essence of PMM is to use high-quality unperturbed electronic states as a basis set to express the Hamiltonian matrix of the quantum center (CO molecule) including the electric field perturbation resulting from the atomic environment (36–39), which is approximately equivalent to CI calculations including the perturbing electric field in the Hamiltonian operator.

Therefore, at each MD frame we obtained, by means of PMM, the corresponding perturbed electronic states providing the corresponding perturbed energy and dipole moment along the intramolecular coordinate (internuclear distance), hence allowing the evaluation of perturbed CO harmonic vibrational states (φ_v) by solving (36)

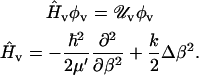In the previous equations, the vibrational Hamiltonian operator Ĥ_v is defined by the reduced mass μ′, the intramolecular coordinate β, and the harmonic force constant k obtained via quadratic fit of the perturbed electronic ground state energy in β. Once the perturbed vibrational eigenstates and eigenvalues (φ_v, U_v) were evaluated along the MD trajectory, we easily obtained the vibrational spectrum I(λ) (considering a unitary radiation density per unit frequency) via (36)

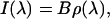where B is the Einstein coefficient for the first perturbed vibrational excitation and ρ(λ) is the corresponding probability density of excitation in the frequency-wavelength space. Note that I(λ), as expressed by the last equation, is not equivalent to the frequency probability density (in our case ρ(λ)) typically reported in other articles, as it involves the transition dipole effect.

RESULTS

To evaluate the equilibrium IR spectrum of CO within the distal pocket, we used the MD configurations as obtained by five independent MD trajectories all starting from the principal docking site (the most probable CO site just after photolysis) and interrupted at the first CO escape from distal pocket. Interestingly, no CO escaped outside the protein within the MD sampling achieved and the total 21 ns corresponding to CO within the distal pocket as obtained by the five MD trajectories, provide a distal pocket escape mean life of ∼4–5 ns. Note that the configuration storing frequency (a configuration every 1 ps) guaranteed no time correlation and a good convergence for the excitation properties provided by PMM (55).

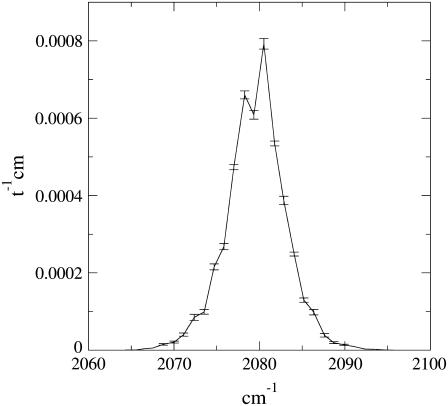
In Fig. 1 we show the IR spectrum and also report the noise (one standard deviation of the signal) for each bin used along the frequency axes (the bin size, defining our spectrum resolution, is 1 cm⁻¹). Note that the calculated IR spectrum is ∼60 cm⁻¹ red-shifted with respect to the experimental one as a result of the ∼60 cm⁻¹ red shift provided by quantum chemical calculations used for the isolated CO (36) and in line with the accuracy limit of sophisticated quantum chemical calculations in determining the vibrational frequency. The figure clearly indicates the presence of two well-separated peaks, whose signal difference is far beyond the noise, corresponding to the experimentally observed B₁ and B₂ peaks, although with a lower frequency separation: ∼2 cm⁻¹ (our calculations) versus ∼10 cm⁻¹ (experimental) (24). Although it reproduces the experimental spectrum shape and width reasonably closely (within the noise) (32), the theoretical IR spectrum in Fig. 1 underestimates the peak shift as well as the absorption full range (∼30 cm⁻¹ versus ∼60 cm⁻¹). It is worth noting that for a molecule like CO, the IR spectrum broadening we compute can be ascribed only to the perturbing field fluctuations as provided by the environment atomic motions.

FIGURE 1.

Carbon monoxide vibrational spectrum in myoglobin distal pocket as obtained by PMM and MD simulations. The error bars shown correspond to a standard deviation of the property, and time is expressed in atomic units.

Interestingly, evaluations of the vibrational frequency distribution in the myoglobin distal pocket, as obtained by completely classical models (10,34), provided an absorption full range between ∼20 cm⁻¹ and ∼60 cm⁻¹, indeed showing that for such classical methods the model details and/or the actual strategy employed to evaluate the vibrational frequencies (estimating the classical perturbed stretching constant or via the time autocorrelation function of the classically fluctuating dipole) may cause significant variations. The same methods also show discrepancies concerning the shape of the frequency distribution: one (10), as the authors correctly state, does not provide two clear peaks; the other (34) provides two main peaks (shifted by ∼8 cm⁻¹), but other relevant peaks are also present, thus raising serious doubts about the quantitative reliability of such evaluations. In fact, in both articles the frequency distribution shown is rather noisy, as expected by the limited sampling used, and no error bars are reported, making it impossible to judge the significance of the various peaks and hence very difficult to do a quantitative comparison with our results. Moreover, our quantum mechanically based calculations showed that the perturbed transition dipole for the vibrational excitation considered is not constant in the absorption frequency range, and the use of the frequency distribution alone provides a larger peak separation (4–5 cm⁻¹), implying that disregarding the transition dipole is not really appropriate to describe spectroscopic features.

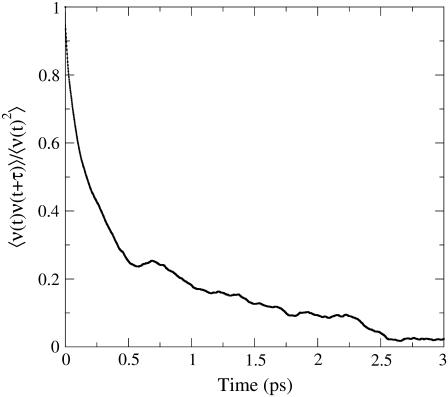
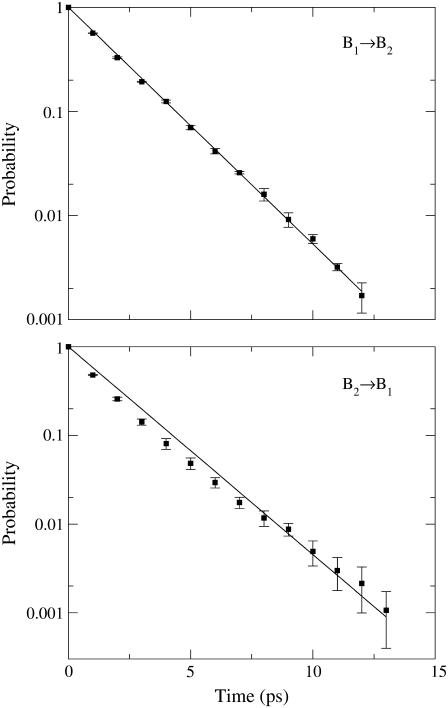
In recent literature on condensed phase spectroscopy (56) the relevance of the dynamic correlation of the excitation frequency has been pointed out. Analysis of time autocorrelation function of the excitation frequency as obtained from our MD simulations and shown in Fig. 2 provides a mean correlation time of ∼200 fs, well matching a similar evaluation performed on the electronic excitation of solvated acetone (55). Such a short correlation time results from the fast relaxation of the perturbing electric field associated to the motions of the environment atoms. To quantitatively evaluate the B₁ and B₂ interconversion rates, we calculated the transition time distribution for crossing the ∼2079 cm⁻¹ border frequency (see Fig. 1) corresponding to the IR spectrum minimum between the B₁ and B₂ peaks. Fig. 3 shows, on a logarithmic scale, such distributions indicating that both B₁→B₂ and B₂→B₁ transitions may be well described by an exponential decay, with time constants of ∼2 ps, well matching the experimental observations (32). These results demonstrate the PMM accuracy, the good quality of the GROMOS and quadrupolar three sites, CO force fields, and the importance of using a quantum mechanically based method for evaluating the excitation spectra.

FIGURE 2.

Time autocorrelation function of the excitation frequency as provided by PMM and MD simulations.

FIGURE 3.

Transition time distributions for the B₁ and B₂ interconversion (see text).

The B₁ and B₂ spectroscopic states have been extensively studied in recent years (23,24,27,29–31,33), leading to the widely accepted idea that such states correspond to the opposite orientations, in the principal docking site, of the CO molecule with respect to the iron atom. However, the assignment of the B₁ and B₂ states to CO orientations is still controversial. In fact, Lim et al. (28,29,31) proposed the B₂ (low-frequency) state to be defined by the CO orientation with the carbon atom pointing toward the iron, whereas Nienhaus et al. (30,33) made the opposite assignment, and theoretical computational attempts, largely based on classical approximations in modeling vibrational excitation, did not provide conclusive quantitative results, although they showed qualitative agreement (10) with the Lim et al. assignment. To address this problem in detail, we first analyzed the CO behavior in the distal pocket in terms of its orientations with respect to the heme plane as defined by the corresponding CO polar angles (the out-of-plane angle θ and the in plane rotation angle φ) (34).

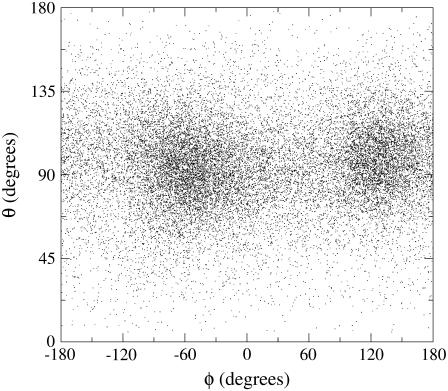
In Fig. 4 we show the distribution of the MD configurations on the θ-φ plane, clearly indicating the presence of two stable angular conformations both centered at θ ≈ 90° (i.e., CO parallel to the heme plane). These two angular states correspond, in the principal docking site, to the two opposite CO orientations toward the iron, with the state centered at θ ≈ 90°, φ ≈ −60° associated to the CO orientation with the carbon atom pointing toward the iron. Interestingly, within the 21 ns considered, the CO molecule mostly resided in the principal docking site as expected from previous computational and experimental data (5,6,9,10,13,57,58).

FIGURE 4.

Projection of the MD sampling over polar angles plane defining the carbon monoxide orientation with respect to the heme plane. Note that the out-of-plane angle θ is zero when the CO molecule is perpendicular to the heme plane.

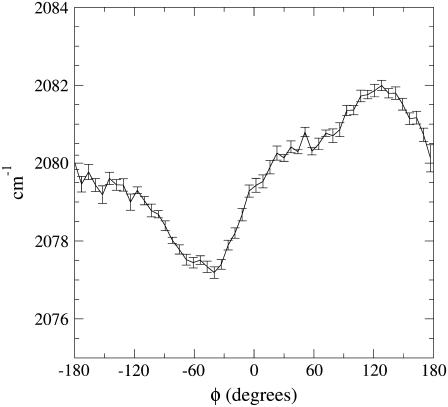
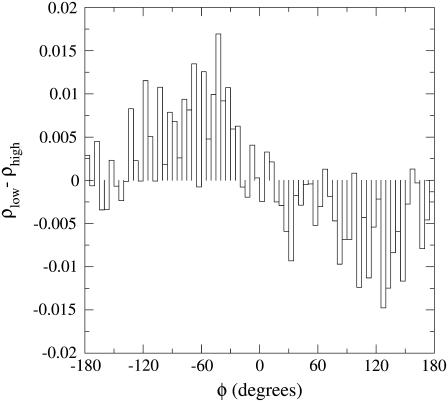
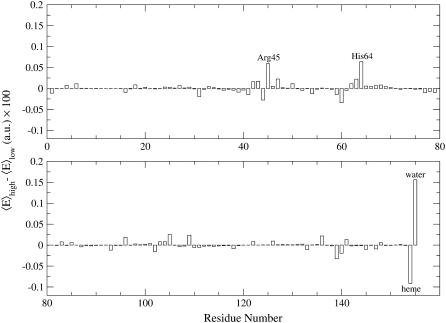
In Fig. 5 we show the IR mean excitation frequency as a function of the rotation angle φ along with the corresponding noise. It is evident that the largest frequency shift is for the two CO rotational orientations corresponding to φ ≈ −60° and φ ≈ 120°, indicating that the B₁ and B₂ peaks found in our spectrum are mainly caused by such rotational CO states as indeed clearly shown by Fig. 6, where we report the difference of the probability distributions in φ for the low- and high-frequency IR peaks (such distributions are obtained by the subpopulations belonging to the bins corresponding to the maxima, and the use of the distributions difference filters out the noise present in both subpopulations). These two CO rotational states defined by the φ angle do not exactly correspond to the CO orientations with the carbon or oxygen toward the iron but rather to the opposite CO dipole orientations in the heme plane, equivalent to the Lim et al. assignment when the CO molecule is located in the principal docking site. Such results clearly show that at physiological conditions the Lim et al. B₁ and B₂ states assignment is likely to be the correct one, although the B states should be properly described in terms of CO dipole orientations in the heme plane rather than orientations with either carbon or oxygen pointing toward the iron. Finally, in Fig. 7 we show the difference between the mean electric field component parallel to the carbon monoxide bond caused by each protein residue, the heme, and solvent, as provided by the two subpopulations corresponding to the B₁ and B₂ absorption maxima. It can be noted that the infrared absorption split between the B states, mainly a result of the CO dipole rotation with respect to the (perturbing) electric field, is largely determined by some key residues (in particular residues in the distal pocket), the heme group, and the solvent. Interestingly, the latter generates the largest electric field variation, hence showing the solvent relevance in the CO spectroscopic behavior in myoglobin.

FIGURE 5.

Mean excitation frequency as a function of the rotational angle φ. The error bars shown correspond to a standard deviation of the property.

FIGURE 6.

Difference of the probability distributions as a function of the polar angle φ, as obtained subtracting the high-frequency peak probability from that of the low-frequency peak (see text).

FIGURE 7.

Difference between the mean electric field component parallel to the carbon monoxide bond attributable to each protein residue, the Heme, and solvent, as obtained by the two subpopulations corresponding to the B₁ and B₂ absorption maxima.

CONCLUSIONS

The combined use of PMM with an extended MD sampling of the CO in the myoglobin distal pocket provided a clear assignment of the experimentally observed B states to the opposite CO rotational orientations in the heme plane, fully confirming the Lim et al. assignment based on spectroscopic data and in line with previous computational studies (10,34,35) that, although employing a purely classical approach, reproduced qualitatively the main experimental observations. Interestingly, such rotational states correspond to the opposite CO dipole orientations with respect to the perturbing electric field, hence suggesting the possibility of similar IR splitting in other myoglobin cavities.

Moreover, it emerged that such B-state splitting is largely determined by specific interactions including the CO-solvent one, which exerts the largest contribution.