Abstract
The extracellular space of the brain is the heterogeneous porous medium formed by the spaces between the brain cells. Diffusion in this interstitial space is the mechanism by which glucose and oxygen are delivered to the brain cells from the vascular system. It is also a medium for the transport of certain informational substances between the cells (called volume transmission), and for drug delivery. This work involves three-dimensional modeling of the extracellular space as void space in close-packed arrays of fluid membrane vesicles. These packings are generated by minimizing the configurational energy using a Monte Carlo procedure. Both regular and random packs of vesicles are considered. A random walk algorithm is then used to compute the geometric tortuosities, and the results are compared with published experimental data. For the random packings, it is found that although the absolute values for the tortuosities differ, the dependence of the tortuosity on pore volume fraction is very similar to that observed in experiment. The tortuosities we measure are larger than those computed in previous studies of packings of convex polytopes, and modeling improvements, which require higher resolution studies and an improved modeling of brain cell shapes and mechanical properties, could help resolve remaining discrepancies between model simulations and experiment. It is also shown that the specular reflection scheme is the appropriate technique for implementing zero-flux boundary conditions in random walk simulations commonly encountered in diffusion problems.
INTRODUCTION
The interstitial space between cells in the brain is called the extracellular space (ECS) (1). Diffusion in the ECS is an essential component in many processes ranging from the delivery of glucose to cells to novel intracellular communication; it is also the primary mechanism for drug delivery to the brain and is important for measurements such as diffusion-weighted magnetic resonance imaging.
The brain is composed of a heterogeneous packing of a large number of different cell types. While the cell bodies of brain cells typically have a diameter in the range of 5–50 μm, many of the cellular elements in the central nervous system are smaller. A typical brain cell is enclosed in a lipid bilayer membrane containing various receptors and protein channels, and there are numerous extensions from the cell body—called processes—which play a fundamental role in intercellular communications (2). Although these cells are densely packed, there is a small ECS between each cell. The cells do not appear to be in direct contact, except at gap junctions, and it is generally estimated that the width of the gap between the cells is on the order of 200 Å (3). There is a large amount of experimental data that clearly shows that the ECS comprises ∼20% of the total volume of the brain (1). The ECS is filled with an electrolyte containing various ions and a small number of larger organic molecules. The collection of long-chain molecules in the ECS forms what is called extracellular matrix (4). Many of these molecules are tethered to the cell membranes, but others float freely in the ECS. Although there is considerable interest in the extracellular matrix, its density and composition, as well as its influence on the diffusive processes in the ECS, are not well known.
Most of what is known about the structure of the ECS comes from measuring the diffusion constants of various molecules. This data can be summarized in terms of the behavior of the tortuosity, λ, defined here as the square-root of the ratio of the diffusion constant of the molecule in a free medium (water or dilute gel), D, over the value in the ECS (D*), i.e., 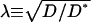 . In healthy brain tissue, λ is typically ∼1.6, but can be as large as 1.9–2 when there are pathologies that involve cellular swelling.
. In healthy brain tissue, λ is typically ∼1.6, but can be as large as 1.9–2 when there are pathologies that involve cellular swelling.
The extra cellular space has a very complex structure, since the shapes of the constitutive cells are complex and the connecting passages are tortuous and have a random connectivity. There are two distinct factors contributing to the measured tortuosity. The first is purely geometrical: in the ECS, the diffusing particle has only a limited number of tortuous paths to follow, requiring a longer time to diffuse a given distance (5). This contribution to the tortuosity is called the geometric tortuosity. Another possible contribution comes from an enhanced viscosity in the ECS (called constitutive effects) caused by the impeded movement of the diffusing molecule by the extracellular matrix (6,7). Only the geometric dependence of tortuosity will be considered in this article.
There are also a considerable amount of experimental data on the behavior of the volume fraction of the ECS, α, and the tortuosity, λ, in osmotically stressed brain tissue. In recent experiments, the size of the ECS was controlled by varying the osmotic pressure of media bathing isolated brain tissue (8,9). Measurements on rat cortex have shown (10) that while α decreases under hypo-osmolarity and increases with hyperosmolarity, λ increases in hypotonic media, but reaches a plateau after first decreasing slightly in hypertonic media, in contradiction to the usual expectation that λ should monotonously decrease with increasing α.
There have been a large number of attempts to compute the tortuosity from models representing the brain structure. Rusakov and Kullmann (6) constructed a computational model based on differential geometry to determine the tortuosity of brain tissue. Their model involved representing the ECS as a three-dimensional random porous structure and computing the increase in the mean local path length of the diffusing molecule in the tissue as compared to the free medium. However, as Nicholson (1) pointed out, such geometric approaches suffer from the drawback that it is hard to correctly weight the contributions of different paths.
Chen and Nicholson (11) used the area outside regular arrays of convex impermeable surfaces with rounded corners to model the ECS in two dimensions. The tortuosity for these models was computed by transforming the problem into one that involved solving a simple Laplace equation in the interstitial region, by applying principles of homogenization theory (12). Using these models, they studied the dependence of the tortuosity on the separation 2h between the planar surfaces in the arrays and the radius of curvature a of the corners (see Fig. 1). They also considered random arrangements of cells of random shape in two dimensions. On the basis of their results, they argued that the behavior of λ as the brain underwent osmotic stress could be due to fact that the brain cells change their shape with changes in osmolarity. They argued that it is possible that λ can remain constant with increasing α if there are “lakes” at the junctions between the cells, which locally trap diffusing molecules, thereby offsetting the increased diffusion in the expanding free space.
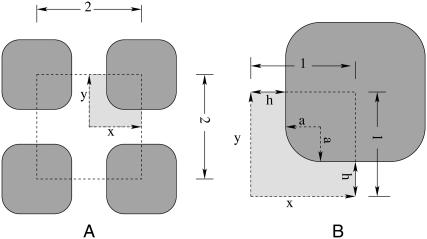
FIGURE 1.
(A) Two-dimensional regular arrangement of square cells with rounded corners. (B) Detail of the periodic repeat unit used for testing the random walk algorithm and various implementations of zero flux boundary conditions. The figure has been redrawn from Chen and Nicholson (11).
More recently, Tao and Nicholson (13) considered several model geometries of periodic arrays of convex polytopes in three dimensions. In these models, the ECS was an interconnected planar array of uniform thickness. For these geometries, they obtained the simple relationship 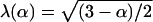 , which is the same as a result Maxwell derived for a dilute suspensions of spheres (14), and argued that three-dimensional models constructed from convex polytopes do not capture the critical structural features of the brain's ECS. In subsequent work, which incorporated concave elements into the model (15–18), it was found that geometrical tortuosities very similar to those measured in experiments were obtained if the “dead space” created by the concave invaginations were sufficiently large. Hrabětová et al. (19) presents some experimental justification for dead-space microdomains, as well as some suggestions about how they may form.
, which is the same as a result Maxwell derived for a dilute suspensions of spheres (14), and argued that three-dimensional models constructed from convex polytopes do not capture the critical structural features of the brain's ECS. In subsequent work, which incorporated concave elements into the model (15–18), it was found that geometrical tortuosities very similar to those measured in experiments were obtained if the “dead space” created by the concave invaginations were sufficiently large. Hrabětová et al. (19) presents some experimental justification for dead-space microdomains, as well as some suggestions about how they may form.
In this article, we model the ECS network in three dimensions by relaxing an array of fluid membrane vesicles. While this first-principles approach yields only a crude approximation of the ECS of brain tissue, two-dimensional cross-sections of the resulting networks look very similar to the random networks studied in Chen and Nicholson (11), and it is likely that shape changes at ECS network junctions induced by osmotic challenge can be modeled reasonably accurately. Since the initial arrays of spherical vesicles have porosities in the range 32–40%, depending on the degree of polydispersity (20), we expect—and do find—that the void space at junctions in the resulting ECS networks is relatively large. The ECS networks we generate consist of curved passages along multicell contact lines connecting these junctions. Diffusivities in this network are measured using the particle tracking algorithm developed to study dispersion in beadpacks (21,22). The influence of osmotic stress is studied by imposing a pressure difference between the interior and exterior regions of the vesicles.
MODELING
The brain is composed of a complex array of cells with a wide range of size, structure, and function. As a result, the connecting passages in the ECS are tortuous, the connectivity is random, and there are many relevant length scales. Furthermore, many of the cellular elements are not spherical, but have a tubular or sheetlike structure. A first-principles modeling of diffusion in the brain's ECS is therefore extremely difficult, and the complexity of the problem is the primary reason that most efforts to model the ECS have utilized regular arrays of convex polytopes.
Cells are bounded by a lipid bilayer membrane, and the interior of the cell contains the cytoskeleton, a complex filamentous network comprised of microtubules, actin filaments, and intermediate filaments. Together, these structures provide shape and mechanical integrity for the cell. While the elastic properties of individual cells are not well understood, the mechanical properties of lipid-bilayer membranes have been studied intensively recently, and it has been shown that their elastic and thermal properties can be well described using a theory based on the curvature elasticity of thin shells. For example, the characteristic discocyte shape of a red blood cell can be obtained by minimizing the curvature energy with the constraints of fixed membrane area and a particular fixed enclosed volume.
Ideally, if we knew how to model the mechanical properties of these cells, we could relax random arrays of the cells to form structurally representative examples of the brain and its extracellular space. Various techniques such as homogenization theory or random walk algorithms could then be used to determine the tortuosity as a function of the porosity. However, as noted above, the structure and elastic behavior of cells is quite complicated, and it is not clear how it should be modeled. What we have done, therefore, is to use a simple model of the curvature elasticity of thin shells to describe the mechanical properties of the cells. While this is, at best, only a very crude approximation to the elastic properties of real cells, it enables us to study the dependence of the tortuosity on pore volume fraction and osmotic stress in both regular and random arrays of vesicles with well-defined elastic properties. In this article, we do not consider the influence of the extracellular matrix. Although measurements of the molecular weight dependence of the tortuosity indicate that the extracellular matrix may significantly affect the values of the tortuosity in certain cases, due to the limited understanding of viscous effects on tortuosity, we do not consider them here. We hope that the current approach will provide insight into the influence of various structural factors on the geometric tortuosity, and serve as a guide for more detailed future studies.
Fluid membranes and vesicles
In the current approximation, the shape of the cell is determined by the curvature elasticity of the lipid bilayer surrounding the cell; the molecular properties, architecture, and the interactions of the membrane constituents enter only through the functional form of the elastic energy and the values of the elastic moduli.
A lipid membrane is free to adjust its surface area so as to minimize the free energy of the amphiphiles. On the timescale of a typical experiment, the number of lipids in a membrane does not change, so that the area of the membrane is constant and the interfacial tension is zero in the unstressed state. The shape and fluctuation spectra of lipid membranes are determined by its curvature elasticity.
Spontaneous curvature model of fluid membrane elasticity
As already noted, the Hamiltonian of fluid membranes is not only invariant under rotations and translations, but also under reparameterizations. This additional invariance is due to the fluid structure, which does not allow a preferred coordinate system, and therefore cannot support shear stress. Fluid membranes are compressible, but the compressibility modulus is usually rather large, so that they are often studied in the incompressible limit, where the membrane area is fixed. In this case, the only contribution to the configurational energy is the bending energy (23–25)
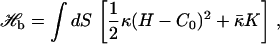 |
(1) |
where κ is the bending rigidity, 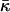 the saddle-splay modulus, and C0 the spontaneous curvature; H = C1 + C2 and K = C1C2 are the trace and determinant of the curvature tensor, respectively. For fixed topology, the second term in Eq. 1 is a constant, by the Gauss-Bonnet theorem. Morse et al. (26) have shown that a finite compressibility does not change the scaling behavior; we therefore ignore compressibility effects in the following.
the saddle-splay modulus, and C0 the spontaneous curvature; H = C1 + C2 and K = C1C2 are the trace and determinant of the curvature tensor, respectively. For fixed topology, the second term in Eq. 1 is a constant, by the Gauss-Bonnet theorem. Morse et al. (26) have shown that a finite compressibility does not change the scaling behavior; we therefore ignore compressibility effects in the following.
Randomly-triangulated surface models for fluid membranes
We model a membrane as a triangulated network of particles that form a regular two-dimensional array embedded in d = 3 spatial dimensions. Vesicles are closed sheets with the topology of a sphere.
We employ a simple string-and-bead model (27) in which the particles or vertices of the triangular network interact via the tethering potential
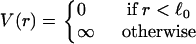 |
(2) |
The potential V(r) acts only between tethered nearest neighbors; it ensures that the distance between nearest neighbors is <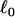 . In simulations, self-avoidance can be guaranteed by placing a particle at each vertex that is sufficiently large that it cannot pass through the network mesh. Because of the large values for the bending rigidity we employ, self-intersection of individual vesicles does not occur, and this was not necessary. Nevertheless, it is convenient to include the hard sphere potential
. In simulations, self-avoidance can be guaranteed by placing a particle at each vertex that is sufficiently large that it cannot pass through the network mesh. Because of the large values for the bending rigidity we employ, self-intersection of individual vesicles does not occur, and this was not necessary. Nevertheless, it is convenient to include the hard sphere potential
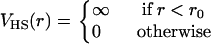 |
(3) |
between all particles in the same vesicle. We use r0 = 1 and  in our simulations.
in our simulations.
To model fluid membranes, this network model has to be modified to allow for the diffusion of vertices in the membrane. This is done by making the connectivity of the network a dynamic variable. The simplest way to do so is to cut and reattach tethers between the four beads of two neighboring triangles (28–33). To maintain the triangular nature of the network, a bond-flip is only allowed if the initially connected vertices have at least four neighbors each. Also, a bond-flip is only possible if the distance of the two initially disconnected vertices falls within the tether length. The bond-flip algorithm has the advantage that it preserves both the two-dimensional connectivity and the topology of the network (27).
We assume that the spontaneous curvature of the membrane is zero, and use a discretization of the squared Laplacian form of the bending energy
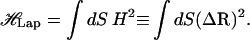 |
(4) |
A general introduction to methods for discretizing operators on triangulated random surfaces is given by Itzykson (34). On a triangulated surface, the mean curvature at node i is
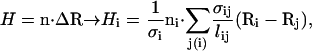 |
(5) |
where ni is the surface normal at node i and the sum is over the neighbors of site i. The value lij is the distance between the two nodes i and j, σij is the length of a bond in the dual lattice (34), and
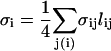 |
(6) |
is the area of the virtual dual cell of vertex i. The length σij in Eqs. 5 and 6 is given by σij = lij[cot(θ1) + cot(θ2)]/2, where θ1 and θ2 are the two angles opposite link ij in the triangles (ijk) and (ijk′), respectively.
Since n‖ΔR for surfaces embedded in three dimensions, Eq. 5 implies that the Laplacian squared bending energy can be written as (34,35)
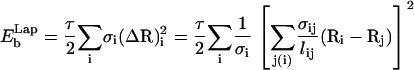 |
(7) |
with τ = κ.
Porous network generation
Using the discrete free energy Eq. 7, we have generated various three-dimensional arrays of nonintersecting vesicles by minimizing the configurational free energy. A general introduction to the Monte Carlo procedure we employed can be found in Gompper and Kroll (27). Both regular and random networks have been generated. In the first case, a Monte Carlo simulation of a single vesicle was performed in a cubic box. The size of the box was periodically allowed to shrink, while making sure that the vesicle does not intersect the box surface. This was done by checking that none of the tethers intersect the box surfaces. The value κ/kBT = 30 was used for the bending rigidity, ensuring that that vesicle surface is smooth. This procedure was continued until a porosity of 20% was attained. Simulations performed using larger values of the bending rigidity yielded configurations consistent with those obtained for this value of κ. A simple cubic periodic array was then obtained by replicating this elementary cell. Osmotically stressed periodic arrays of various porosities were generated in the same way while applying a pressure difference between the vesicle interior and exterior, keeping the box size fixed.
Random networks were generated using a similar procedure after starting with a random close-packed array of spherical vesicles in a simulation cell with periodic boundary conditions. As the size of the simulation cell was decreased, the vesicles deformed, creating a tightly packed random array of highly deformed vesicles. During this procedure, self-avoidance was ensured by making sure that a vesicle's tethers do not intersect the surface triangles of adjacent vesicles. Arrays with a wide range of porosities were generated in this way. We did not consider osmotically stressed random arrays.
The interstitial spaces separating the vesicles were then used to model the ECS.
RANDOM WALK SIMULATION
Lagrangian particle tracking methods are more efficient than finite element methods for solving the convection-diffusion equation in problems where Peclet numbers are very large and/or the geometries are complex (36). Particle tracking methods are more stable, easy to implement, and free from numerical dispersion and mesh generation problems. In the current application, the Peclet number is zero. However, the three-dimensional geometries we consider are very complex, and mesh generation and refinement problems prevented us from using finite element methods in three dimensions. We therefore used a random walk method, which is the most straightforward implementation of the Lagrangian particle tracking method. In the random walk model we use, the position of a tracer particle is determined by the following stochastic differential equation (21),
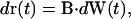 |
(8) |
where B · dW is a random displacement vector. B is a constant diagonal matrix whose components are proportional to the diffusion coefficients in the respective directions, and dW is an increment of a continuous Gaussian process. An Euler approximation for Eq. 8 can be written as
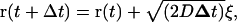 |
(9) |
where ξ is a vector of length 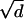 with random direction; d is the spatial dimension.
with random direction; d is the spatial dimension.
It is well known that random walk algorithms describe a diffusion process. However, there is no consensus regarding the correct implementation of certain boundary conditions for particle-based methods. In this work, we use both periodic and zero-flux boundary conditions. Although the implementation of periodic boundary conditions is straightforward, several procedures have been used in the literature to describe zero-flux boundary conditions (21). The appropriate choice is analyzed in the following.
Proposed implementations of the zero-flux boundary condition are
- Specular reflection. The trajectory, r(t) of a tracer particle undergoing specular reflection at the x = 0 plane is given by
where R is the mirror reflection operator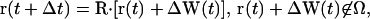
(10) 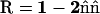 ,
, 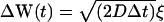 , and Ω is the diffusion domain. The value
, and Ω is the diffusion domain. The value 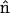 is the unit vector normal to the x = 0 plane (36).
is the unit vector normal to the x = 0 plane (36). Rejection. The move is rejected if r(t) + ΔW(t)∉Ω, i.e., for that time step Δt the particle remains at its previous position (37,38).
Multiple rejection. The increment ΔW(t) is rejected and a new increment is found until r(t) + ΔW(t) ∈ Ω (39).
Interruption. The particle stops at the boundary and its clock is incremented by γΔt with γ given by
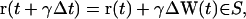 |
(11) |
where ∑ is the boundary of Ω. For the remainder of the time step, Δt′ = (1 − γ)Δt, the particle moves away from the boundary in a new randomly chosen direction, ΔW(t + γΔt)) (21,40).
It is shown in Szymczak and Ladd (36) that some of these schemes (multiple rejection and interruption) fail to impose the zero-flux boundary condition correctly. For the current application, we determine the most accurate procedure by performing random walk simulations in a well-defined two-dimensional geometry whose tortuosity can be accurately determined by an alternate method. The procedure that yields the most accurate results will be used in subsequent three-dimensional simulations.
Implementation in two dimensions
We have chosen to use the two-dimensional geometry shown in Fig. 1, which is one of the lattice arrangements of cells studied by Chen et al. (11). Accurate estimates for the tortuosity have been determined by applying the homogenization method discussed in detail in Chen and Nicholson (11). Since the geometry is simpler in this case, mesh generation problems did not occur. The construction of the two-dimensional geometry and the mesh generation is done in GAMBIT (Fluent Inc., Lebanon, NH), and the tortuosity is computed by numerically solving the final Laplace equation using FLUENT (Fluent, Inc.) software. FLUENT's user-defined scalar feature has been used for defining the variable ω of Chen and Nicholson (11), and the default parameters in FLUENT—velocity, viscosity, etc.—are set to zero. Also, the default criterion for convergence in FLUENT has been used.
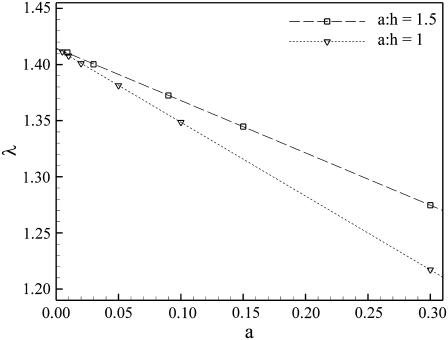
Results for the tortuosity as a function of a, the radius of curvature of the corners, for fixed a/h = 1 and 1.5, are shown in Fig. 2. For fixed a/h, it can be seen that λ(a) is linear in a. Although the slope of the straight line depends on the value of the ratio a/h, the intercept with λ-axis is the same, e.g., 1.414, in both cases. For fixed a/h, the limit a → 0 results in a network of tubes, which is known to have the tortuosity 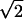 (43).
(43).
FIGURE 2.
Plots of λ vs. a for a/h = 1.5 and a/h = 1. The value a is the curvature radius of the cell corners in the two-dimensional array shown in Fig. 1. Tortuosities were computed using the approach based on homogenization theory.
Four sets of random walk simulations were performed using the same geometry, with each set corresponding to one of the four implementations of the zero flux boundary conditions discussed above. The region lying within the unit square and outside the shaded region is the interstitial domain occupied by the diffusing particles. Periodic boundary conditions are imposed at the edges of the unit cell (to model an infinite periodic system), and no-flux boundary conditions were implemented on the solid boundaries. At the start of the simulation, the domain is uniformly filled with large number of tracer particles. At each time step, the coordinates of the tracer particles are updated according to
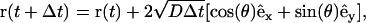 |
(12) |
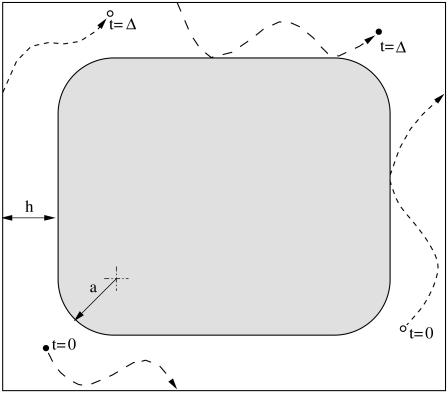
where θ is a random angle uniformly distributed in the interval [0, 2π]. When a tracer particle crosses one of the sides of the unit square, periodic boundary conditions are applied, and it reenters the diffusion domain at the opposite side, as illustrated in Fig. 3. If the potential move intersects a solid surface, appropriate boundary conditions for the various discrete versions of the no-flux boundary conditions described above are applied. For the rejection and multiple rejection versions of the boundary condition, multiple surface intersections during one time step cannot occur. However, for the specular reflection and interruption algorithms, multiple intersections are possible. In these cases, if the potential move intersects a solid surface, the time step is reduced from Δt to λΔt so that r(t + λΔt) lies on the boundary. The particle's angle of departure from the surface is then chosen by either the specular-reflection or interruption scheme, and the particle completes the move in the appropriate direction for the remainder of the time step. In cases where two or more surfaces are very close to each other, a particle lying between them might undergo multiple deflections between the surfaces until it completes the move, and the procedure needs to be repeated until the full time step Δt is elapsed. Tracer particles are tracked in both reduced and global coordinates; the reduced coordinates are the local coordinates within the square unit, and the global coordinates are the particles' positions in an infinite medium.
FIGURE 3.
Repeat unit used in the random walk simulations of diffusion in the regular array shown in Fig. 1. The figure also illustrates the implementation of periodic boundary conditions for two hypothetical tracer particles.
The second moment of the relative global displacement of the particles, which is needed to determine the effective diffusion constant, is given by
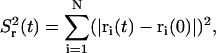 |
(13) |
where N is the number of tracer particles. The apparent diffusion coefficient is then given by the long time limit of
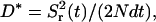 |
(14) |
where d is the spatial dimension; the tortuosity is 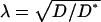 .
.
Results for the tortuosities for a/h = 1 are plotted in Fig. 4, where it can be seen that only the specular reflection implementation of the zero-flux boundary condition yields the correct results for the tortuosities for all values of a. The expected linear relation between λ and a is only observed for this case. Table 1 contains a comparison of results for λ(a) obtained using the homogenization method and the random walk algorithm using specular reflection boundary conditions.
FIGURE 4.
Plots of λ vs. a. Values of the tortuosity were obtained by performing random walk simulations of diffusion in the two-dimensional lattice arrangement of Fig. 1 for various implementations of the zero-flux boundary condition at the cell surface. The value a/h = 1, where a is the radius of curvature of the cell corners and h is half the gap width between the cells.
TABLE 1.
Comparison of results for λ(a) obtained in random walk simulations using specular-reflection boundary conditions with those obtained using the homogenization method described by Chen and Nicholson (11)
| a | λ Using random walk method with specular-reflection boundary condition | λ Using homogenization method |
|---|---|---|
| 0.005 | 1.4120 | 1.4114 |
| 0.01 | 1.4044 | 1.4077 |
| 0.02 | 1.4002 | 1.4009 |
| 0.05 | 1.3814 | 1.3813 |
| 0.1 | 1.3484 | 1.3485 |
| 0.2 | 1.2841 | 1.2836 |
| 0.3 | 1.2172 | 1.2172 |
As can be seen in Fig. 4, for other implementations of the no-flux boundary condition, results for the tortuosity begin to deviate from the correct result as a approaches zero, i.e., as the tubes become narrower. For the rejection boundary condition, the move is rejected when a particle hits the solid surface. Particles near solid surfaces therefore move slower than those in the bulk, and the tortuosity is somewhat larger for all tube diameters. As the tubes become narrower and narrower, more and more of the particles hit a solid boundary during an update, and an ever increasing number of moves are rejected. Consequently, particles in these regions tend to remain there, and the tortuosity increases. In the case of the multiple rejection boundary condition, new increments are attempted until one is found that does not intersect the surface. In the narrow tubular regions, this means that the diffusion becomes one-dimensional as h goes to zero. In addition, since the particles cannot be deflected by the walls, they tend to continue to move along their line of motion at the junctions in this limit. The diffusion process therefore becomes one-dimensional as h → 0, and the tortuosity approaches 1 (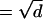 , since d = 1 here). Finally, for the interruption boundary condition, the overall move is a combination of two or more random variables; the variance of the particle's displacement (and hence overall displacement of the particles) is therefore increased, and the computed tortuosity is smaller than the correct value.
, since d = 1 here). Finally, for the interruption boundary condition, the overall move is a combination of two or more random variables; the variance of the particle's displacement (and hence overall displacement of the particles) is therefore increased, and the computed tortuosity is smaller than the correct value.
The convergence properties of the Euler approximation for linear stochastic equations depend on whether one seeks to approximate the moments of the particle distribution, or to satisfy an error criterion for particle position (44). The former requirement is known as weak convergence, and the rate is linear, both in the number of particles, N, and in the time step, Δt; the latter is known as strong convergence, and the rate is 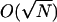 (21). In the present work, since we are interested in finding tortuosities in different porous media, which would require computing the second moment of the particle displacements, the weak convergence criterion is used.
(21). In the present work, since we are interested in finding tortuosities in different porous media, which would require computing the second moment of the particle displacements, the weak convergence criterion is used.
The simulations in two dimensions were performed using between 104 and 2 × 104 tracer particles. Generally, it was found that 10,000 particles was sufficient. The size of time step (Δt) was chosen so that a further reduction in Δt resulted in no changes in the measured tortuosity. The size of the time step size depended on the value of a. The appropriate choice of Δt decreased from 4 × 10−4 to 5 × 10−5 as a was reduced from 0.3 to 0.005. Because of the initial uniform distribution of tracer particles, converged results were obtained using no more than 1000 time steps. This was sufficient to produce results for 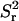 , which scaled linearly in time.
, which scaled linearly in time.
Implementation in three dimensions
Three-dimensional simulations were performed in the void spaces of both the regular and random vesicle packs generated using the procedure described above. Figs. 5 and 6 show the elementary repeat unit for the cubic array and the random network. In both cases, the unit cell is a cube with edges of length 1. At each time step, the coordinates of the tracer particles are updated according to
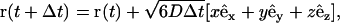 |
(15) |
where (x, y, z) is a random point on a unit sphere determined by Marsaglia's algorithm (45). As in two dimensions, periodic boundary conditions were imposed on the faces of the unit cube, and zero-flux boundary conditions on the cell surfaces. The generalization of the random walk-specular reflection algorithm to three dimensions is straightforward.
FIGURE 5.
Single relaxed vesicle in a periodic unit cube. The unit cube is replicated periodically to form the network. Neighboring cells are in contact along their flat surfaces. Diffusion occurs in the void space external to the cubes.
FIGURE 6.
A random array of 18 highly deformed vesicles forming a random porous network. The unit cell is the unit cube, which is replicated periodically to form the network. Diffusion occurs in the void space between the vesicles. (The number of vesicles in the figure is >18 because periodic images of some of the vesicles were included to avoid cuts through the vesicles.)
At the start of the simulations, the pore space was populated with a random uniform distribution of tracer particles. The number of tracer particles was typically on the order of 50,000. At each time step, the coordinates of the tracer particles were updated according to Eq. 15 and specular reflection boundary conditions were used if the particle intersected a solid surface.
To improve the efficiency of the algorithm when determining whether a particle's trajectory intersects a vesicle surface during a time step, the unit simulation cell is divided into several subcells. Each subcell has a linked list of all surface triangles located in the subcell (46). When a particle's coordinates are updated, it is then only necessary to check for intersections with surface triangles in the same and nearest-neighbor subcells. This reduces the computational time by a factor proportional to the number of subunit cubes.
The number of time steps in the simulation is chosen sufficiently large that the slope of a plot of 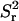 vs. t reaches its asymptotic value. For the configurations considered in this article, it was found that 1000 time steps were sufficient for simulations involving 50,000 tracer particles. The time increment, Δt, was initially taken to be 4 × 10−5, so that the particle's displacement during a time step was ∼5% of the size of the unit simulation cell. In a given simulation, Δt was gradually reduced until the asymptotic slope of a plot of
vs. t reaches its asymptotic value. For the configurations considered in this article, it was found that 1000 time steps were sufficient for simulations involving 50,000 tracer particles. The time increment, Δt, was initially taken to be 4 × 10−5, so that the particle's displacement during a time step was ∼5% of the size of the unit simulation cell. In a given simulation, Δt was gradually reduced until the asymptotic slope of a plot of 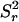 vs. t did not change if the time step is further reduced.
vs. t did not change if the time step is further reduced.
PORE-SIZE DISTRIBUTION
The pore volume fraction, α, does not characterize the structure of the porous domain. Additional information is contained in the pore-size distribution, P(s), which is the probability that a small volume element of pore space is located a (nearest) distance s from a pore surface (47). To determine P(s), a large number (∼100,000) of uniformly distributed points are randomly chosen in the void space and the closest distance s of each point to any pore surface is measured. P(s) is the normalized sum of the number of points, which lie at a distance s ± ds from the solid surface. Since the normalized distribution satisfies 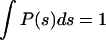 , P(s) has the dimension of inverse length. P(0) is the ratio of the pore surface area to the pore volume, S/Vp ≡ 1/Rh, where Rh is called the mean hydraulic radius, a quantity that can be measured in diffusion nuclear magnetic resonance experiments (48).
, P(s) has the dimension of inverse length. P(0) is the ratio of the pore surface area to the pore volume, S/Vp ≡ 1/Rh, where Rh is called the mean hydraulic radius, a quantity that can be measured in diffusion nuclear magnetic resonance experiments (48).
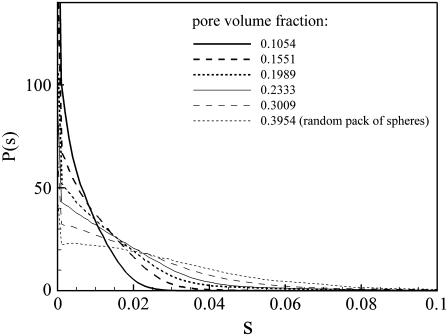
Results for the pore-size distribution in both the periodic and random porous networks we generated are shown in Figs. 7 and 8, respectively. When comparing the results, it is important to remember that in both cases, the periodic simulation cell has a linear dimension of 1, and s is measured in these units. The sharp peak of P(s) at s very close to 0, indicates that the cells are in very close contact with each other. This remains true even as the pore volume is increased; however, the area of contact is significantly reduced in this case, implying a nonuniform shrinkage of cells—as proposed in Chen and Nicholson (11) during osmotic stress.
FIGURE 7.
Pore-size distributions of the regular porous network for a range of pore volume fractions. P(s) is the fraction of the porous region that is distance s from the nearest cell wall.
FIGURE 8.
Pore-size distributions of the random porous network for a range of pore volume fractions. P(s) is the fraction of the porous region that is distance s from the nearest cell wall.
RESULTS AND DISCUSSION
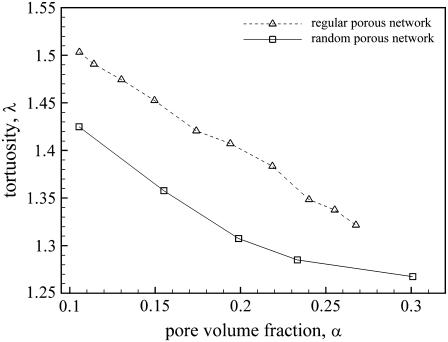
Our results for the geometric tortuosities as a function of the pore volume fraction for both the regular and random packings are shown in Fig. 9. The range of pore volume fractions we considered is 0.11–0.27 for regular networks and 0.10–0.30 for the random packing. First, note that the tortuosities we calculate for the cubic array are significantly larger than those obtained by Tao and Nicholson (13) in their study of uniformly spaced convex cells. The reason for this is that the networks considered in Tao and Nicholson (13) consisted of polytopes with sharp corners. In contrast, the configurations we obtain by minimizing the curvature energy (see Fig. 5) have rounded vertices. In fact, inspection of Fig. 5 shows that the curvature at the cube vertices is smaller than along the edges; as a consequence, the pore space at the junctions is comparatively large.
FIGURE 9.
Tortuosities obtained from random walk simulations in the regular and random porous networks as a function of the pore volume fractions.
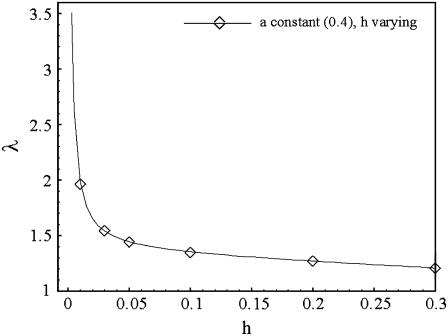
The effect of having junctions with a larger radius of curvature than the typical dimension of the connecting tubular regions can be seen in Fig. 10, which contains a plot of the tortuosity of the two-dimensional network shown in Fig. 1 as a function of h, for fixed a = 0.4. For h > 0.1, the tortuosities plotted in Fig. 10 are slightly smaller than those shown in Fig. 2 for h = a. For smaller h, however, the tortuosities increase dramatically, since diffusing particles spend an ever-increasing amount of time trapped at the junctions as h → 0. The ratio of the characteristic size of junctions to the connecting tubular regions is therefore a primary factor that determines the tortuosity, and explains the differences between our results and those of Tao and Nicholson (13).
FIGURE 10.
Plot of λ as a function of h for fixed a = 0.4. a is the radius of curvature of the cell corners in the regular two-dimensional array shown in Fig. 1, and h is half the gap width between the cells. Tortuosities were computed using the approach based on homogenization theory.
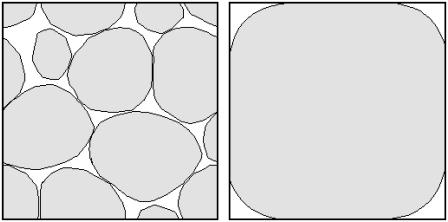
The results presented in Fig. 9 also show that the random network has tortuosities that are smaller than those for the regular array. This is probably due to the fact (see Fig. 11) that while the cubic array has an organized structure consisting of narrow channels and junctions, the random array does not (at least at the current resolution). Indeed, several regions of the void space in the random pack are surprisingly large; higher resolution studies (in which the number of surface triangles in a vesicle is increased) will be required to determine whether this remains true in the continuum limit. Insufficient resolution could also be a reason that the measured tortuosities for the random pack are lower than observed in experiment. The size of a typical surface triangle is 0.05 for cubic regular array (Fig. 5), and 0.1 for random pack (Fig. 6). This means that length scales smaller than this size are not resolved correctly. While this does not seem to be a problem for the cubic array, it is probable that higher resolution studies would show that the channels connecting the larger junctions in the random pack are much smaller than predicted here. On the other hand, the larger junctions are reasonably well resolved. Since an overestimation of the size of small channels reduces the tortuosity, we expect the tortuosity to increase for higher resolutions.
FIGURE 11.
Comparison of sample cross-sections of the random porous network (left) and regular network (right). In both cases, the pore volume fraction is ∼0.2.
It can also be seen that for the random network, the magnitude of the slope of the tortuosity versus pore volume fraction plot decreases with increasing α. This is what is observed in experiment. In fact, an overlay of the tortuosities of the random network with the experimental data (plotted in Fig. 12) shows that the random network does indeed provide a reasonably accurate representation of the pore volume fraction dependence of the tortuosity. It is important to note, however, that for pore volume fractions larger than the values studied, the vesicles are essentially spherical, and there is no plateau. For the plateau to extend to much larger values of porosity—as observed in experiment—it would probably be necessary to consider packings of polydisperse vesicles with nonspherical rest shapes.
FIGURE 12.
A comparison of simulation and experimental results for the tortuosity as a function of the pore volume fraction, α. The simulation results (right vertical axis) are those obtained for the random pack shown in Fig. 6. Experimental results (left vertical axis) were obtained from Chen and Nicholson (11). Although the absolute values of the tortuosities differ, the figure shows that the functional dependence of λ on α are very similar.
Finally, the pore-size distributions of both the regular cubic network (Fig. 7) and random network (Fig. 8) exhibit dramatic changes as a function of the porosity, indicating that there is a nonuniform shrinkage of the vesicle shapes as the porosity is decreased. This is consistent with the behavior proposed by Chen and Nicholson (11) to explain the experimentally observed dependence of the tortuosity on pore volume fraction. In addition, the two-dimensional cross section of the random network shown in Fig. 11 confirms the existence of “lakes” connected, for the most part, by narrow channels.
First-principles modeling studies of the type described in this article provide valuable insight into the geometric properties of the brain's ECS. The networks we considered are constructed by minimizing the configurational energy of the constituent vesicles. We used a simple model free energy, Eq. 1, which is known to provide a good description of the configurational energy of fluid membranes. This is certainly an oversimplification, since it ignores elastic contributions from the cytoskeleton, structural heterogeneities, etc. Nevertheless, we believe that the general features we observe, such as increased tortuosity due to the comparatively large size of the pore void space at network junctions, will remain valid when more sophisticated models for the cells' mechanical and elastic properties become available. Indeed, our results lend credence to the suggestion by Chen and Nicholson (11) that localized residual space at network junctions, the “lakes,” can help explain both the large tortuosities observed in experiment as well as the characteristic behavior of the tortuosity under osmotic stress. Our results for the random vesicle packs are clearly resolution-limited, and higher resolution studies are required to determine the extent to which models of this type can explain the observed behavior, and resolve remaining questions regarding the importance of viscous or constitutive contributions to the measured tortuosity.
Acknowledgments
Support from the National Science Foundation under grant No. DMR-0513393 is gratefully acknowledged.
References
- 1.Nicholson, C. 2001. Diffusion and related transport mechanisms in brain tissue. Rep. Prog. Phys. 64:815–884. [Google Scholar]
- 2.Nicholls, J. G., A. R. Martin, and B. G. Wallace. 1992. From Neuron to Brain: A Cellular Approach To The Function of The Nervous System, 3rd Ed. Sinauer Associates, Sunderland, MA.
- 3.Villegas, G. M., and J. Fernández. 1966. Permeability to thorium dioxide of the intercellular space of frog cerebral hemisphere. Exp. Neurol. 15:18–36. [DOI] [PubMed] [Google Scholar]
- 4.Ruoslahti, E. 1996. Brain extracellular matrix. Glycobiology. 6:489–492. [DOI] [PubMed] [Google Scholar]
- 5.Harris, E. J., and G. P. Burn. 1949. The transfer of sodium and potassium ions between muscle and the surrounding medium. Trans. Faraday Soc. 45:508–528. [Google Scholar]
- 6.Rusakov, D. A., and D. M. Kullmann. 1998. Geometric and viscous components of the tortuosity of the extracellular space in the brain. Proc. Natl. Acad. Sci. USA. 95:8975–8980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.El-Kareh, A. W., S. L. Braunstein, and T. W. Secomb. 1993. Effect of cell arrangement and interstitial volume fraction on the diffusivity of monoclonal antibodies in tissue. Biophys. J. 64:1638–1646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tao, L. 1999. Effects of osmotic stress on dextran diffusion in rat neocortex studied with integrative optical imaging. J. Neurophysiol. 81:2501–2507. [DOI] [PubMed] [Google Scholar]
- 9.Krizaj, D., M. E. Rice, R. A. Wardle, and C. Nicholson. 1996. Water compartmentalization and extracellular tortuosity after osmotic challenge in cerebellum of Trachemys scripta. J. Physiol. 492:887–896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kume-Kick, J., T. Mazel, I. Voříšek, S. H. L. Tao, and C. Nicholson. 2002. Independence of extracellular tortuosity and volume fraction during osmotic challenge in rat neocortex. J. Physiol. 542:515–527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Chen, K. C., and C. Nicholson. 2000. Changes in brain cell shape create residual extracellular space volume and explain tortuosity behavior during osmotic challenge. Proc. Natl. Acad. Sci. USA. 97:8306–8311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bensoussan, A., J. L. Lions, and G. Papanicolaou. 1978. Asymptotic Analysis for Periodic Structures. North Holland Science Publishers, New York.
- 13.Tao, L., and C. Nicholson. 2004. Maximum geometrical hindrance to Diffusion in brain extracellular space surrounding uniformly spaced convex cells. J. Theor. Biol. 229:59–68. [DOI] [PubMed] [Google Scholar]
- 14.Crank, J. 1975. The Mathematics of Diffusion, 2nd Ed. Clarendon Press, Oxford, UK.
- 15.Tao, A., L. Tao, and C. Nicholson. 2005. Cell cavities increase tortuosity in brain extracellular space. J. Theor. Biol. 234:525–536. [DOI] [PubMed] [Google Scholar]
- 16.Hrabe, J., S. Hrabětová, and K. Segeth. 2004. A model of effective diffusion and tortuosity in the extracellular space of the brain. Biophys. J. 87:1606–1617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hrabětová, S., and C. Nicholson. 2004. Contribution of dead-space microdomains to tortuosity of brain extracellular space. Neurochem. Int. 45:467–477. [DOI] [PubMed] [Google Scholar]
- 18.Nicholson, C. 2005. Factors governing diffusing molecular signals in brain extracellular space. J. Neural Transm. 112:29–44. [DOI] [PubMed] [Google Scholar]
- 19.Hrabětová, S., J. Hrabe, and C. Nicholson. 2003. Dead-space microdomains hinder extracellular diffusion in rat neocortex during ischemia. J. Neurosci. 23:8351–8359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Maier, R. S., D. M. Kroll, H. T. Davis, and R. S. Bernard. 1999. Simulation of flow in bidisperse sphere packings. J. Colloid Interface Sci. 217:341–347. [DOI] [PubMed] [Google Scholar]
- 21.Maier, R. S., D. M. Kroll, R. S. Bernard, S. E. Howington, J. F. Peters, and H. T. Davis. 2000. Pore-scale simulation of dispersion. Phys. Fluids. 12:2065–2079. [Google Scholar]
- 22.Maier, R. S., D. M. Kroll, R. S. Bernard, S. E. Howington, J. F. Peters, and H. T. Davis. 2003. Hydrodynamic dispersion in confined packed beds. Phys. Fluids. 15:3795–3815. [Google Scholar]
- 23.Canham, P. B. 1970. The minimum energy of bending as a possible explanation of the biconcave shape of the human red blood cell. J. Theor. Biol. 26:61–81. [DOI] [PubMed] [Google Scholar]
- 24.Helfrich, W. 1973. Elastic properties of lipid bilayers: theory and possible experiments. Z. Naturforsch. 28c:693–703. [DOI] [PubMed] [Google Scholar]
- 25.Evans, E. A. 1974. Bending resistance and chemically induced moments in membranes bilayers. Biophys. J. 14:923–931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Morse, D. C., and S. T. Milner. 1995. Statistical mechanics of closed fluid membranes. Phys. Rev. E. 52:5918–5945. [DOI] [PubMed] [Google Scholar]
- 27.Gompper, G., and D. Kroll. 2004. Triangulated-surface models of fluctuating membranes. In Statistical Mechanics of Membranes and Surfaces. D. Nelson, T. Piram, and S. Weinberg, editors. World Scientific, Singapore.
- 28.Kazakov, V. A., I. K. Kostov, and A. A. Migdal. 1985. Critical properties of randomly triangulated planar random surfaces. Phys. Lett. B. 157:295–300. [Google Scholar]
- 29.Boulatov, D. V., V. A. Kazakov, I. K. Kostov, and A. A. Migdal. 1986. Analytical and numerical study of a model of dynamically triangulated random surfaces. Nucl. Phys. B. 275:641–686. [Google Scholar]
- 30.Billoire, A., and F. David. 1986. Scaling properties of randomly triangulated planar random surfaces: a numerical study. Nucl. Phys. B. 275:617–640. [Google Scholar]
- 31.Ho, J. S., and A. Baumgärtner. 1990. Simulations of fluid self-avoiding membranes. Europhys. Lett. 12:295–300. [Google Scholar]
- 32.Kroll, D. M., and G. Gompper. 1992. The conformation of fluid membranes: Monte Carlo simulations. Science. 255:968–971. [DOI] [PubMed] [Google Scholar]
- 33.Boal, D. H., and M. Rao. 1992. Scaling behavior of fluid membranes in three dimensions. Phys. Rev. A. 45:R6947–R6950. [DOI] [PubMed] [Google Scholar]
- 34.Itzykson, C. 1986.Proceedings of the GIFT Seminar, Jaca 85. J. Abad, M. Asorey, and A. Cruz, editors. World Scientific, Singapore.
- 35.Espriu, D. 1987. Triangulated random surfaces. Phys. Lett. B. 194:271–276. [Google Scholar]
- 36.Szymczak, P., and A. J. C. Ladd. 2003. Boundary conditions for stochastic solutions of the convection-diffusion equation. Phys. Rev. E. 68:036704–1–036704–12. [DOI] [PubMed] [Google Scholar]
- 37.Drazer, G., and J. Koplik. 2001. Tracer dispersion in two-dimensional rough fractures. Phys. Rev. E. 63:056104. [DOI] [PubMed] [Google Scholar]
- 38.Kurowski, P., I. Ippolito, J. P. Hulin, J. Koplik, and E. J. Hinch. 1994. Anomalous dispersion in a dipole flow geometry. Phys. Fluids. 6:108–117. [Google Scholar]
- 39.Rage, T. 1996. Studies of Tracer Dispersion and Fluid Flow in Porous Media. PhD thesis, University of Oslo, Oslo, Norway.
- 40.Salles, J., J. F. Thovert, R. Delannay, L. Prevors, J. L. Auriault, and P. M. Adler. 1993. Taylor dispersion in porous media. Determination of the dispersion tensor. Phys. Fluids A. 5:2348–2376. [Google Scholar]
- 41.Reference deleted in proof.
- 42.Reference deleted in proof.
- 43.Mathias, R. T. 1983. Effect of tortuous extracellular pathways on resistance measurements. Biophys. J. 42:55–59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Kloeden, P. E., and E. Platen. 1992. Numerical solution of stochastic differential equations. In Applications of Mathematics Series, Vol. 23. Springer-Verlag, Heidelberg.
- 45.Marsaglia, G. 1972. Choosing a point from the surface of a sphere. Ann. Math. Stat. 43:645–646. [Google Scholar]
- 46.Allen, M., and D. Tildesley. 1987. Computer Simulation of Fluids. Clarendon Press, Oxford, UK.
- 47.Maier, R. S., D. M. Kroll, Y. E. Kutsovsky, H. T. Davis, and R. S. Bernard. 1998. Simulation of flow through bead packs using lattice Boltzmann method. Phys. Fluids. 10:60–74. [Google Scholar]
- 48.Mair, R., G. Wong, D. Hoffmann, M. Hürlimann, S. Patz, L. Schwartz, and R. Walsworth. 1999. Probing porous media with gas diffusion NMR. Phys. Rev. Lett. 83:3324–3327. [DOI] [PubMed] [Google Scholar]