Investigating the neural basis for functional and effective connectivity. Application to fMRI

Abstract

Viewing cognitive functions as mediated by networks has begun to play a central role in interpreting neuroscientific data, and studies evaluating interregional functional and effective connectivity have become staples of the neuroimaging literature. The neurobiological substrates of functional and effective connectivity are, however, uncertain. We have constructed neurobiologically realistic models for visual and auditory object processing with multiple interconnected brain regions that perform delayed match-to-sample (DMS) tasks. We used these models to investigate how neurobiological parameters affect the interregional functional connectivity between functional magnetic resonance imaging (fMRI) time-series. Variability is included in the models as subject-to-subject differences in the strengths of anatomical connections, scan-to-scan changes in the level of attention, and trial-to-trial interactions with non-specific neurons processing noise stimuli. We find that time-series correlations between integrated synaptic activities between the anterior temporal and the prefrontal cortex were larger during the DMS task than during a control task. These results were less clear when the integrated synaptic activity was haemodynamically convolved to generate simulated fMRI activity. As the strength of the model anatomical connectivity between temporal and frontal cortex was weakened, so too was the strength of the corresponding functional connectivity. These results provide a partial validation for using fMRI functional connectivity to assess brain interregional relations.

1. Introduction

In the past few years, as the use of functional brain imaging techniques, such as functional magnetic resonance imaging (fMRI), positron emission tomography (PET), and electro- and magnetoencephalography (EEG and MEG), have come more and more to dominate investigations of the neural substrates of human cognition, the conceptual importance of viewing cognitive functions as mediated by networks of interacting brain regions has started to play a central role in the interpretation of neuroscientific data (Mesulam 1990; Horwitz et al. 1992; Friston 1994; Fuster 2000; McIntosh 2000). Unlike investigations of brain lesions or of neuronal electrophysiological recordings, many functional brain imaging techniques provide data simultaneously from most cortical areas and thus are ideal for investigating how different brain regions interact during behavioural tasks (Horwitz et al. 1999). It is no surprise, therefore, that there have been a large number of studies of interregional neural interactions utilizing fMRI, PET or EEG/MEG data (e.g. Gevins et al. 1989; Horwitz et al. 1992a; Bullmore et al. 1996), and determinations of functional and effective connectivity (Friston 1994; Horwitz 1994; McIntosh & Gonzalez-Lima 1994) have become staples of the neuroimaging literature. Moreover, these connectivity notions also are utilized by neuroscientists who work at the neuronal and ensemble levels of analysis (e.g. Ts'o et al. 1986; Aertsen et al. 1989; Wilson & McNaughton 1994; Nicolelis et al. 1995). How all these notions of connectivity are related to each other and to anatomical connectivity, is far from obvious (Horwitz 2003).

In a series of articles, we will attempt to clarify how some aspects of the concepts of functional and effective connectivity, as applied to functional brain imaging data, are to be understood in terms of neuroanatomy and neurophysiology. In this first paper, we will focus primarily on one of the haemodynamic methods (fMRI; however, because many of the issues discussed here apply as well to PET, we will also include some discussion applicable to this technique); subsequent papers will address other aspects of functional/effective connectivity, as well as other methods for assessing neural interactions. As is well known, the limited spatial and temporal resolution of the haemodynamic functional imaging techniques results in a significant loss of information as one goes from the microscopic level of dynamic neuronal activity to the macroscopic level changes in regional cerebral blood flow (rCBF), metabolism and blood oxygenation (BOLD) measured by PET/fMRI (a brief overview of PET and fMRI methodology can be found in Horwitz et al. (2000); for more information about fMRI, see Bandettini (2003)). Of the factors that result in this loss of information, the following are particularly important: (i) multiple neuronal populations are present in any resolvable PET or fMRI region of interest (including a single voxel), and local and afferent neuronal activities are combined into a single signal; (ii) the disparity between the temporal dimension appropriate for neurons (on the order of milliseconds) and that available from haemodynamic data (about a minute for PET, at best a few seconds for fMRI owing to the haemodynamic delay) is such that transient components of activity are undetectable by the haemodynamic methods; (iii) electrophysiological studies at the neuronal level generally record the spiking activity of neurons, whereas the evidence is now fairly substantial that the haemodynamic methods are indicative of synaptic and postsynaptic activity (e.g. Jueptner & Weiller 1995; Lauritzen 2001; Logothetis et al. 2001); one consequence of this is that increases in excitatory and inhibitory synaptic activity can lead to increased metabolic activity (Logothetis 2003).

The presence of these factors means that it is very difficult, if not impossible, experimentally to measure all the neuronal activities, both spiking and synaptic, at multiple locations, and at the same time measure the corresponding haemodynamic activities, from which functional connectivities can be computed at multiple levels and related across levels and modalities. An alternative approach, which we employ, is to use computational neural modelling (for a review of the use of computational modelling and functional neuroimaging, see Horwitz et al. (2000)). In a computational model, one can keep track of all the neuronal activities, all the synaptic activities, and the associated haemodynamic changes, and thus can relate the macroscopic to the microscopic. In essence, unlike the actual brain, in a model we know the ‘answer’—the full pattern of time-varying changes in interregional relationships.

Therefore, we employ a large-scale, neurobiologically plausible computational model that can generate both simulated neuronal activities, and simulated PET and fMRI data (Tagamets & Horwitz 1998; Horwitz & Tagamets 1999; Husain et al. 2002, 2004). The model performs a delayed matched-to-sample (DMS) task. Two forms of this model exist—one for visual object processing (Tagamets & Horwitz 1998), the second for auditory object processing (Husain et al. 2004). Furthermore, the visual model was extended so that combined transcranial magnetic stimulation (TMS) and PET studies could be simulated (Husain et al. 2002). TMS has been used in conjunction with PET as a tool for investigating functional connectivity (Fox et al. 1997; Paus et al. 1998; Mottaghy et al. 2000). Recently, studies combining TMS and fMRI have been reported (Bohning et al. 2000; Siebner et al. 2003; Li et al. 2004). The model, whose construction was based on experimental neuroanatomical and neurophysiological measurements, generates simulated neuronal data that agree with experimental data obtained from mammalian studies, and also generates simulated PET/fMRI data that are in accord with experimental findings from human studies. Unlike some simulations that have been employed to examine the ‘neural’ substrate of a functional neuroimaging result (e.g. Anderson et al. 2003; Gitelman et al. 2003), our model has the advantage that it is neurally plausible, complex, contains both excitatory and inhibitory neurons, has feed-forward and feedback connections and includes a diversity of regions containing neurons that possess different response properties (e.g. some regions have neurons that fire only when external stimuli are present; others have neurons that are active when no external stimuli are present). This type of model provides a useful testing ground for investigating both experimental paradigms and data analysis methods (Horwitz 2004).

A useful way to think about the issues involved in relating neural activity to neuroimaging functional connectivity data is the following. We have a system (the neural network under study) whose constituent interrelationships we want to assess; these relationships can be a function of the intrinsic dynamics of the network (for example, in our case the neurons comprising the auditory network have better responses to more transient stimuli than the neurons that are part of the visual network). The dynamics of the network interrelationships can also be influenced by the experimental paradigm: if the stimuli presented are appropriate for the network, there should be greater processing than if the stimuli are not appropriate. Other characteristics of the experimental parameters such as the duration of stimuli and the rate of stimuli presentation can also affect the strength of the network interrelationships. The fMRI results that one obtains to evaluate the functional interrelationships using a particular experimental design will also depend on the particular choices made for the scanning parameters, and on the intrinsic haemodynamic response properties of the brain. Finally, the specific feature of the BOLD signal one chooses to employ to evaluate the functional connectivity can potentially affect the measured value of the functional connectivity (see §2 for examples). All these issues can be individually explored and controlled using our computational modelling approach.

In this paper we will use the large-scale computational model outlined above to examine the relationship between the macroscopic measures of functional and effective connectivity (as obtained from functional neuroimaging data) and their neural substrates. We will begin with a concise overview of the concepts of functional and effective connectivity, as applied by various neuroscientific methods of investigation. We shall then briefly review the large-scale network model. This will be followed by a discussion of the sources of variability that are used in functional (and effective) connectivity analysis, and a description of how these variability sources will be simulated in our model. Our main results will ensue, followed by some comments about how these concepts can be interpreted. Our focus in this paper will be on functional connectivity as used in fMRI and PET (and also deoxyglucose autoradiographic studies). In subsequent papers, we will address some of the relatively newer notions related to effective connectivity (e.g. structural equation modelling (McIntosh et al. 1994); Granger causality (Goebel et al. 2003; Roebroeck et al. 2005); dynamic causal modelling (Friston et al. 2003)) that have recently emerged, as well as examining measures of functional connectivity used with EEG/MEG data.

2. Functional and effective connectivity

For decades investigators have attempted to use neurophysiological data obtained simultaneously from two or more neural elements to compute a measure of the functional interaction between these elements. The neural elements could be neurons, small ensembles of neurons, or entire brain regions, and the data could be obtained using electrical, magnetic or haemodynamic techniques. In all cases, the central idea is that activities that covary together suggest that the neurons generating the activities may be interacting. Two aspects of functional interactivity need to be distinguished; they are called functional and effective connectivity (Friston 1994). Two neural entities are said to be functionally connected if their activities are correlated; effective connectivity refers to the direct influence of one neural entity on a second. Thus, functional connectivity does not necessarily imply a causal link, whereas effective connectivity does. As pointed out by Friston (see Lee et al. 2003), effective connectivity is model dependent, whereas functional connectivity is not (at least not explicitly; note, however, that in the evaluation of functional connectivity as a simple correlation coefficient, it is implicitly assumed that the interactions are linear and instantaneous; see Lahaye et al. (2003) and Roebroeck et al. (2005) for approaches that avoid these assumptions). It should be noted that different investigators have, over the years, used different terms to represent these two notions, but the functional neuroimaging community seems to have settled on these general designations (Horwitz 2003).

A variety of measures and algorithms are used to compute quantities that embody the concept of functional connectivity (and likewise for effective connectivity). However, there are conceptual difficulties associated with these efforts, as has been discussed recently (see Horwitz (2003) for an overview; the reader is also referred to a report on a recently held workshop on functional connectivity (Lee et al. 2003), in which there was extensive discussion of many of the themes and current controversies in the field). Specifically, multiple measures of what constitutes functional connectivity have been employed, each relatively specific for the particular type of data under study. Although much effort has gone into making these measures statistically and computationally sound, very little effort has been spent making them neurobiologically meaningful. Moreover, very little work has been undertaken to establish how (or if) these variously defined notions of functional connectivity are related to one another. Adding to this complexity is the fact that one can extend the notion of interregional functional connectivity from being a relationship between just two regions to one involving large numbers of brain regions by utilizing methods such as principal components analysis (Friston et al. 1993), partial least-squares (McIntosh, Bookstein et al. 1996) and other such multivariate methods.

To illustrate this diversity, a set of measures for PET/fMRI functional connectivity, taken from the published literature, is provided. It should be noted that the measures (and importantly, the associated computational algorithms) below are by no means complete (especially for fMRI, where new measures seem to appear daily), but are only a representative sample of what is currently being used.

(a) Positron emission tomography and autoradiography

For rCBF PET activation data, some investigators calculate functional connectivity by correlating rCBF data within a task condition and across subjects (e.g. Horwitz et al. 1992a, 1998; McIntosh et al. 1994; Jennings et al. 1998), whereas others perform correlations across tasks (e.g. Friston et al. 1993). The first approach was also used in studies that looked at interregional correlations (mostly obtained from subjects at rest), using PET to measure glucose metabolism (e.g. Horwitz et al. 1984, 1986; Bartlett et al. 1987), and in non-human mammals (often rats; e.g. McIntosh & Gonzalez-Lima 1991) using autoradiographic data (usually ¹⁴C-deoxyglucose). The reasoning behind the first method starts with the fact that subjects perform tasks with different abilities, as shown by differences in accuracy, reaction time and other measures of performance. This subject-to-subject variability suggests that the activity of the brain network mediating a task also varies from subject to subject. So, for example, if one subject, for whatever reason, uses one of the brain regions comprising the network less than a second subject to perform the task of interest, a second region of the network, functionally linked to the first, will also be used less in the first, relative to the second individual. The result is a large covariance (i.e. functional connectivity) in the activities between the two regions across subjects. This method of evaluating functional connectivity depends on the assumption that there is sufficient spontaneous variability across subjects to yield neurobiologically meaningful interregional covariation. It may fail if the task of interest is (i) too variable, so that multiple strategies are possible (presumably each being mediated by a different neural network; a good example is found in Glabus et al. (2003)); or (ii) so automatic that the subject-to-subject variability is swamped by non-neurobiologcal variability from the scanning system.

The other approach to calculating functional connectivity mentioned above attempts to measure the interregional covariance from an experimentally imposed task variability. The idea here is that there are multiple scans of each subject, and the scans correspond to a task that varies in some way from scan to scan. For example, in Friston et al. (1993), there were 12 PET scans in which the subject heard a letter (once every 2 s). In six of the scans, the subject repeated the letter heard, and in the other six which alternated with the first six, the subject was required to generate a word beginning with the letter heard (each scan lasted about 2 min). In other cases, one might have some parametric modulation in the conditions during each scan (e.g. the amount of time a visual stimulus needed to be held in short-term memory; McIntosh et al. (1996b)), or over the entire course of the PET session, there may be a learning effect, or else attention may wane, so that scans performed later in the scanning session are different from those performed earlier. The critical assumption here is that the functional network mediating the task is the same for all the conditions; that is, the changing conditions do not lead to the use of a different functional network.

(b) Functional magnetic resonance imaging

The advent of fMRI has resulted in a dramatic increase in the number of ways in which interregional functional connectivity has been computed. Because of the higher temporal resolution (compared with PET), there are numerous features of the fMRI signal that can be used as the data that enter into the evaluation of the covariance or correlation matrix, as we have discussed previously (Horwitz 2003). Among the distinctions that have led to different ways to evaluate fMRI-based interregional functional connectivity are the following: (i) linear (e.g. Bokde et al. 2001) versus nonlinear (e.g. Buechel & Friston 1997); (ii) instantaneous (e.g. Hampson et al. 2002) versus time-shifted (e.g. Lahaye et al. 2003); (iii) resting state (e.g. Biswal et al. 1995) versus an active experimental condition (e.g. Toni et al. 2002); (iv) within-condition (e.g. Hampson et al. 2002) versus across-conditions (e.g. Bullmore et al. 2000); (v) within-subject (e.g. Goncalves et al. 2001) versus data averaged across subjects (e.g. Bokde et al. 2001); (vi) correlating time courses (e.g. Buechel & Friston 1997; Bullmore et al. 2000) versus correlating a measure of block or subject activity (e.g. Pugh et al. 2000). Note that several of the studies cited appear more than once, demonstrating that there are many choices that an investigator needs to make in deciding how to compute fMRI-based functional connectivity. Some of these distinctions apply to PET data as well as to fMRI, but because the use of fMRI has become so prevalent in the last few years, the number and diversity in fMRI-based functional connectivity analyses dominate the literature.

This brief overview of some of the diverse measures of PET and fMRI functional connectivity reinforces the points made earlier: (i) there are multiple measures in use, and there is no guarantee that the conclusions drawn using one measure will be the same as using another; (ii) very little work has been done to relate the various measures to each other; and (iii) the neural substrates of each measure are unknown.

3. Large-scale neural network model

This section provides a brief overview of our large-scale neural network model (Tagamets & Horwitz 1998; Husain et al. 2004). The two versions of the model perform either a visual or an auditory DMS task for shape (two-dimensional object shape for the visual task, tonal pattern shape for the auditory task). The DMS task involves the presentation of a shape, a delay, and the presentation of a second shape; the model determines if the second stimulus is the same as the first. Multiple trials (e.g. 10) are used to simulate a PET or fMRI study.

Each model incorporates four major brain regions representing the ventral object processing stream (Ungerleider & Mishkin 1982) for the visual task, and an analogous stream for the auditory task (Rauschecker & Tian 2000): (i) primary sensory cortex (V1/V2 for the visual model; primary auditory cortex for the auditory model); (ii) secondary sensory cortex (V4 for vision, belt and parabelt areas for audition); (iii) a perceptual integration region (inferior temporal (IT) cortex for vision, superior temporal gyrus/sulcus (STG/STS, henceforth called ST) for audition); and (iv) prefrontal cortex (PFC) which incorporates short-term working memory. Every region is composed of multiple basic units, each of which represents a simplified cortical column; the basic unit comprises an interacting pair of excitatory–inhibitory neurons (modified Wilson–Cowan units; Wilson & Cowan 1972). Regions are linked by both feed-forward and feedback connections. There are different scales of spatial integration in the visual model in the first three stages, with the primary sensory region having the smallest receptive field, and IT the largest. Likewise, in the auditory model, there are different scales of spectrotemporal integration in the first three stages, with the smallest spectrotemporal window of integration occurring in the first stage (A1/A2), and the largest in ST.

Each region (except IT and ST) in our models contains subpopulations whose excitatory neuronal units possess different response properties. For example, for the visual model in V1/V2 and V4, neuronal units have different orientation selectivities; in the auditory model, the analogous regions are selective for the direction of frequency change. The PFC for both the auditory and visual versions of the model has four different types of neuronal units whose response properties are based on the findings of Funahashi et al. (1993): units that respond when a stimulus is present, two kinds of units that show activity during the delay interval and units whose activities increase when a match between the second and first stimuli occurs. Feed-forward and feedback connections between regions were based on primate neuroanatomical data. Parameters were chosen so that the excitatory elements have simulated neuronal activities resembling those found in electrophysiological recordings from monkeys performing similar tasks (e.g. Funahashi et al. 1993; Bodner et al. 1996; Kikuchi-Yorioka & Sawaguchi 2000). For the visual model, tables detailing the values of the parameters used, and a thorough discussion of all the assumptions employed, are given in Tagamets & Horwitz (1998); analogous details concerning the auditory model are presented in Husain et al. (2004).

An important feature of the model concerns how the ‘task instructions’ are handled so that the model knows which task (DMS or a control task in which noise patterns are presented) has to be performed. This was accomplished by means of a continuous biasing (e.g. attention) variable that modulates a subset of prefrontal units by diffuse synaptic inputs, the functional strength of which controls whether the stimuli are to be retained in working memory (for the DMS task) or not (during the control task). Activity in each brain area, therefore, is a combination of feed-forward activity determined in part by the presence of an input stimulus, feedback activity determined in part by the strength of the modulatory biasing signal and local activity within each region.

An fMRI or PET study is simulated by presenting stimuli to an area of the model that represents either the lateral geniculate nucleus (LGN) or the medial geniculate nucleus (MGN). The fMRI/PET response is simulated by temporally and spatially integrating the absolute value of the synaptic activity in each region over an appropriate time course and for simulating fMRI, convolving these values with a function representing haemodynamic delay (Horwitz & Tagamets 1999).

4. Simulating functional connectivity—types of variability

There are multiple sources of the variability found in functional neuroimaging data. Some of these originate from the scanning technique, some are non-neural (e.g. changes in the vasculature may lead to changes in the fMRI haemodynamic response function; changes in brain CO₂ concentration can alter cerebral blood flow), and some are neural, but are not related to the experimental condition under study (e.g. intrinsic neural noise; inputs from neurons not participating in the task). However, some of the variability observed in the functional neuroimaging signal can be utilized to provide the covariance needed to evaluate functional connectivity (see Horwitz et al. (1992b) for an early discussion of this; although aimed towards covariation of PET data, many of the points are applicable to fMRI data). The main idea is that variability in the activity in one node of the neural network mediating the task under study is propagated to other nodes, resulting in a larger covariance between the nodes than would be the case if the nodes were not interacting with one another. The various methods of evaluating functional connectivity attempt to tap one or more of these neurally based sources of covariation.

For fMRI, there are three main sources of variation that can be utilized to assess functional connectivity. I will call them (i) subject-to-subject, (ii) block-to-block and (iii) item-to-item (or MR volume-to-volume); the first two can be used as well for PET. The idea behind using subject-to-subject variability to evaluate interregional functional connectivity was discussed above in the section on PET. Likewise, the equivalent of block-to-block variability was also mentioned in the PET section, where it was pointed out that the variability can be either experimentally induced (e.g. parametrically varying some aspect of the task) or uncontrolled (e.g. a subject is more attentive during one experimental block than during another). Finally, the central notion for all methods that examine the interregional correlation between fMRI time-series is that there is a kind of trial-to-trial variability within the neural network used to perform a task that presents as volume-to-volume variability (e.g. one item is harder than another; neural noise gets propagated to some other nodes in the network mediating the task; different volumes may correspond to different tasks or conditions, which would be the case for event-related designs). The key to using our simulation model to examine interregional functional connectivity rests on developing reasonably realistic ways to generate the three different types of variability that the various measures of functional connectivity attempt to access.

The original formulation of our model conceived of the model as representing a single subject. Several sources of variability were included in the original model (for details, see Husain et al. (2004) and Tagamets & Horwitz (1998)), although the amount of variability they generated was fairly small: the electrical activity of each neural element contains a noise term; the weights between the regions comprising the model, which represent the strengths of the anatomical linkages, possess some variability that changed every time a new network was generated. To produce the kinds of variability that lend themselves to functional connectivity analysis in a somewhat non-arbitrary and realistic way, the model has been extended in three ways.1

(a) Variable anatomical connectivity

To simulate subject-to-subject variability, we altered the strengths of the anatomical connections between regions in a pseudo-random fashion. Thus, the strengths of the interregional connections in the ideal network were multiplied by some percentage (range, 65–98%) that is different for each individual network (in our simulations, we use 10 individual networks representing 10 subjects). This range of alterations enabled each network to still perform the DMS task, although with more variable accuracy2 (see table 1 for the percentages used for each of the 10 networks, and for the simulated behavioural response expressed as percentage of correct trials). This method of simulating subject-to-subject variability can be thought of as representing the kind of variability that could arise in real subjects owing to neural developmental differences.

Table 1.

Values of anatomical connection weights for the visual model for each ‘subject’ simulated.

connection	subj1	subj2	subj3	subj4	subj5	subj6	subj7	subj8	subj9	subj10
ev1v→ev4c	81	95	65	79	88	77	87	78	83	77
ev1v→ev4v	83	94	83	75	92	88	71	74	76	70
ev1h→ev4c	84	93	84	77	72	84	84	88	85	93
ev1h→ev4h	81	91	85	78	81	93	95	80	82	94
ev4c→eit	82	94	70	76	72	73	84	86	71	91
ev4v→eit	84	95	84	74	91	81	76	94	89	95
ev4h→eit	80	92	90	76	90	83	80	83	92	98
efd1→efd2	85	95	85	75	80	70	94	79	90	71
efd1→efr	85	92	85	77	75	79	73	76	82	89
efd2→efd1	94	93	94	92	91	95	95	97	91	95
eit→efs	83	91	83	77	70	85	82	75	82	97
efs→efd2	81	93	81	79	74	90	79	91	73	98
efs→efr	82	95	82	78	74	72	90	77	76	95
% correct	78	72	89	44	61	72	72	67	61	67

The values are the percentages of the connection weights used in the Tagamets–Horwitz model (Tagamets & Horwitz 1998). Shown in the bottom row is the percentage of correct responses of each subject for the DMS task; a correct response for a match was increased activity in five or more units in the FR module. Abbreviations: ev1v (h), excitatory V1/V2 vertically (horizontally) selective; ev4v(h,c), excitatory V4 vertically (horizontally, corner) selective; eit, excitatory IT; efd1(2), excitatory frontal D1(2); efs(r), excitatory FS(R) modules. Any connections (such as feedback connections) not listed were not modified.

(b) Variable top-down bias effects (e.g. attention)

To simulate the block-to-block variability in an individual subject, we used different values of the biasing parameter that controls how well the model maintains prefrontal activity during the delay component of each task. In the original versions of the model (Tagamets & Horwitz 1998; Husain et al. 2004), this parameter had a value of 0.3 during the DMS task and 0.05 during the control task. Here, we varied the bias parameter from 0.20 to 0.30 in steps of 0.02, thus resulting in six blocks for the DMS task. One can think of this approach as representing a waxing or waning, or fluctuation of attention during a scanning session.

(c) Inclusion of non-specific neurons

To simulate what we have called the trial-to-trial variability within an experimental condition, we doubled the number of units in each module, with the added units representing non-specific neurons that are not part of the network mediating the task (cf. Deco et al. 2004). The non-specific elements of each module are connected to each other in the same way as are the task-specific neurons. However, the non-specific modules are connected in a random way to the task-specific regions, and this pattern of connections changes on each trial. Moreover, the input to the non-specific neurons consists of random noise patterns that are presented asynchronously and randomly relative to the presentation times of the stimuli to the task-specific elements. The net effect of this arrangement is that the task-specific neurons in each module receive random neural activity from the non-specific neurons that varies for each trial. The result is that this adds trial-to-trial variability to the responses of each task-specific neuron, allowing us to model the interactions between the network mediating the task of interest and brain regions not specifically involved in the task that are likely to occur in real subjects (e.g. seeing a particular visual stimulus may lead an individual subject to recall some object from her past).

5. Simulation results

To use our simulations as a way to help understand the neural bases of functional connectivity, we first have to demonstrate that our simulation model possesses a sufficient degree of realism to be useful for exploring some of the definitional complexities associated with the concepts of functional and effective connectivity. To do this, we must show that, with appropriate parameter choices, evaluation of the simulated functional connectivity reflects the neuronal interrelationships that are actually present. To this end, we performed two simulation studies. The first addressed the following question: are the functional connectivities between elements of the model neural network larger when the network is engaged in task performance than when it is not? A positive answer would indicate that fMRI-measured functional connectivity can, in principle, be used as an indicator of functional interrelationships in the brain. The second study addressed the following question: if two regions are anatomically connected, and if the network within which these regions are embedded is active, is the value of the functional connectivity a function of the strength of the anatomical connectivity between these two elements of the network? A positive answer would suggest that fMRI-measured functional connectivity can depend on the interregional anatomical connectivity.3 Obtaining positive answers to both questions would also imply that our simulation model can be useful for exploring the neural bases of functional and effective connectivity.

(a) Neural activity

To be able to assess the functional connectivity results, we first need to present the neuronal results. Figure 1 shows a diagram of the visual network model, focusing on the anatomical relationships between the modules comprising the network. In figure 2, we present a diagram of a single trial of the DMS task that is used for the visual model (the task parameters are given in the legend to figure 2). A visual shape is presented, there is a delay period, and then a second shape is presented; the model must determine if the second object is the same as the first. The attention parameter is set at a high level so that these neurons can perform the DMS task. At the same time, ‘scrambled’ shapes are being presented (asynchronously relative to the task objects) to the non-specific neurons (for these neurons, the biasing signal is set at a low value so that only ‘passive viewing’ is engaged). There is also a control task where scrambled shapes are presented to the task-specific neurons, and the biasing signal is set at a low value so that only passive viewing is performed by the network.

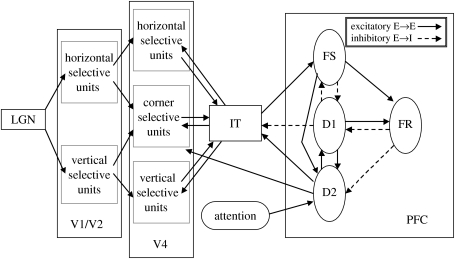
Figure 1.

Network diagram of the visual object processing model (Tagamets & Horwitz 1998). The regions of the model (V1/V2, V4, IT, PFC) form a complex network of feed-forward and feedback connections; these interregional connections can be either excitatory (excitatory-to-excitatory elements, shown as solid lines) or inhibitory (excitatory-to-inhibitory elements, shown as dashed lines). In the PFC region, FS contains stimulus-sensitive units, D1 and D2 contain units active during the delay part of a delayed match-to-sample task, and FR contains units whose activity increases if there is a match between the first and second stimuli of a trial. See text for details.

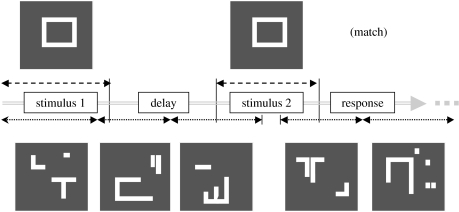
Figure 2.

Diagram of the delayed match-to-sample task. The top of the diagram shows examples of the shape stimuli presented to the specific neurons in the model that are engaged in the task; the bottom shows the degraded shape stimuli presented (asynchronously, relative to the shape stimuli) to the non-specific neurons. Each shape is presented for 1 s, the delay period is 1.5 s, the response period (which includes the intertrial interval) is 1 s.

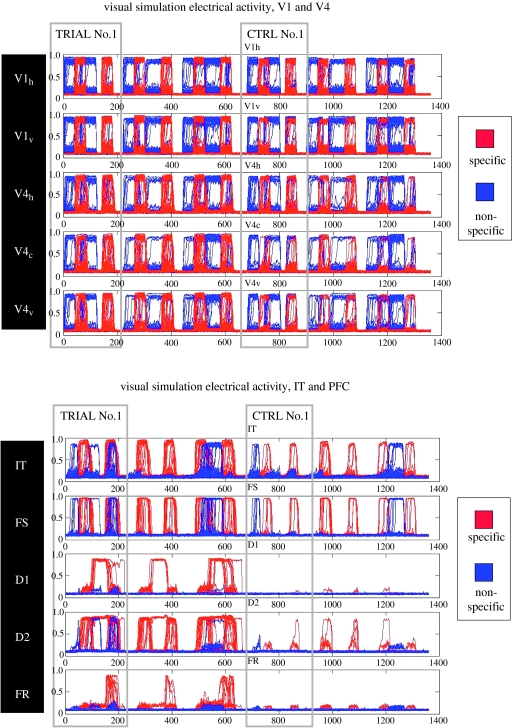
Figure 3 shows the neural activity (i.e. the equivalent of the neuronal spiking activity) of all the neurons in all the modules of the model for three trials of the DMS task and for three trials of the control task in a ‘typical’ subject (subject 1). The first and third trials were ‘match’ trials where the second stimulus was identical to the first; the second trial was a ‘non-match’ case. The neural activities of the task-specific neurons are shown in red, those of the non-specific neurons are shown in blue. Several important points are demonstrated in figure 3. First, in the primary visual cortex there is little difference in the amount of neural activity between the task-specific and the non-specific neurons, and between task and control trials. Second, such differences increase as one goes along the ventral visual processing stream from occipital to temporal to frontal cortex; the task-specific (‘red’) neurons show greater neural activity than the ‘blue’ (non-specific) neurons, and there is more activity during the task trials than during the control trials. The FR module, whose neurons increase their activity if there is a match between first and second stimuli, show these behaviours most clearly, and demonstrate that our model can perform the DMS task.

Figure 3.

Simulated neuronal activity in all the neurons in all the brain regions of figure 1 for one block of the DMS condition and one block of the control condition. Each panel shows the neural activity for six trials. The first three trials correspond to the DMS task, with the first and third trials constituting ‘match’ conditions (where the second stimulus is the same as the first) and the second trial constituting a non-match condition. The next three trials are for the control task, where degraded shapes were used. The activity of the specific neurons is shown in red, whereas the activity of the non-specific neurons is in blue (note that the specific activity was plotted after the non-specific activity; thus, in many cases the red graphs are drawn in front of the blue graphs). The x-axis is expressed in time-steps, with each time-step corresponding to 5 ms. V1h stands for the horizontally selective units of V1/V2, V1v for the vertically selective units of V1/V2, V4c,h,v for the corner- (horizontal-, vertical-) selective units of V4.

Perhaps the best module on which to focus our attention is IT because it receives feed-forward inputs from the visual processing area V4 (and from V1/V2 via V4), and in turn, projects to the FS module in the frontal lobe (it also receives a diffuse feedback anatomical connection from the FD1 and FD2 modules). If one thinks about the relationship between this module's activity and that in other modules, one could propose that based on the neural data, IT's functional connectivity with more posterior modules should be relatively unchanged whether the network is engaged in the DMS task or in the control task. Conversely, IT's functional connectivity with the frontal modules should appear stronger during the DMS task condition than during the control condition.

(b) fMRI functional connectivity

(i) Simulating an fMRI time-series

As mentioned in §1, strong evidence has accumulated suggesting that it is the input activity to neurons that best correlates with the BOLD signal (i.e. the local field potentials (LFPs); see Logothetis et al. (2001) and Logothetis (2003)). Our method for transforming simulated neuronal activity into simulated fMRI (or PET) data explicitly assumes that this is the case (Horwitz & Tagamets 1999). Specifically, we take the absolute value of the synaptic activity, integrated over a relevant time-period and over all the neural elements in a module (which means that we combine the data from each module's subpopulations, since at the spatial resolution of fMRI, the neurons from all the subpopulations would be in the same brain location), as the quantity that will be transformed into the simulated fMRI or PET signal. For PET, the time-period corresponds to approximately 30–60 s, because that is the time needed to acquire a volume of PET regional cerebral blood flow data. For fMRI, the transformation process is somewhat more complicated. First, for a typical MR scanner, one can acquire a slice of data in about 50 ms. So, we integrate the absolute value of the synaptic activity in a module over the slice acquisition time (in our simulations we use 50 ms). The resulting time-series for each region can be thought of as the ‘gold standard’—what a noiseless, fast MRI scanner would show if there were no haemodynamic delay or other possible confounds, such as nonlinearities, affecting the relationship between neural activity and the blood oxygenation dependent signal. Each regional time-series is then convolved with a haemodynamic response function to produce a temporally smoothed time-series. For simplicity, we use a Poisson function, which is characterized by a single parameter λ (its mean and standard deviation; units are in s). More complicated functions representing the haemodynamic response could, of course, be employed (e.g. Buxton et al. 1998; Friston et al. 2000). This smoothed time-series is sampled every Tr second (Tr is the repetition time—the time needed to acquire an entire volume's worth of data; in most fMRI studies, data from each slice are collected sequentially, either directly or in an interleaved fashion). The resulting function is the simulated fMRI time-series. It is these simulated time-series that we use to compute the interregional functional connectivity.

In our previous papers, we have spatially integrated the activity over all the submodules of the PFC when simulating PET or fMRI data. For connectivity analysis, because the anatomical connections between the PFC submodules are complex, we will treat the PFC submodules as if they are spatially separated from each other, thus allowing us to investigate their individual functional connections.

(ii) Computing functional connectivity

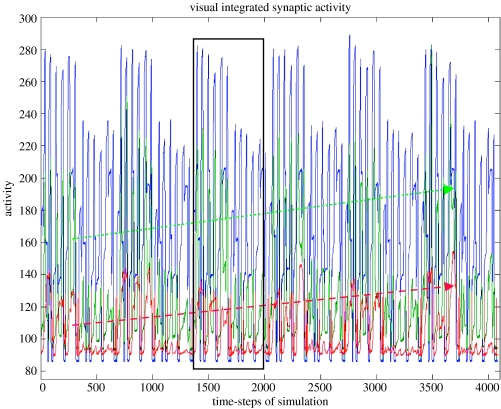
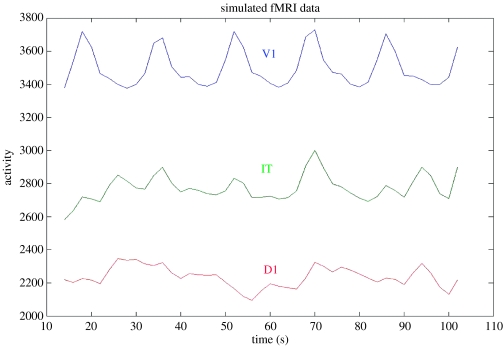
To see if the functional connectivity obtained using our model reflects the underlying pattern of neural relationships, we shall use one of the simplest definitions of the fMRI functional connectivity, namely, the correlation between the within-task time-series (e.g. Hampson et al. 2002). For our simulation, we had three trials of the DMS task, and three trials of the control task. Figure 4 shows the time course of the integrated synaptic activity (ISA) in three of the regions of the visual model (V1/V2, IT and D1), and figure 5 shows the corresponding simulated fMRI signal in subject 1 (our typical subject). Each visual stimulus had a 1 s duration, the delay period was 1.5 s in length and the inter-trial interval was 1 s. We assumed a slice acquisition time of 50 ms and a Tr of 2 s; the haemodynamic response function was characterized by a delay parameter of length 6 s.

Figure 4.

Graphs of the integrated synaptic activity in the V1/V2 (blue), IT (green) and D1(red) modules. As seen in the V1/V2 graph, there were three DMS trials and three control trials for each of six levels of attention (lowest on the left, highest on the right). The activity in the IT and D1 modules increases with attention, as indicated by the dashed lines. One block, with three DMS and three control trials, is shown in the box. The temporal integration interval was 50 ms; see text for details. The values of the activity (y-axis) are in arbitrary units.

Figure 5.

Graphs of the simulated fMRI signal corresponding to the data shown in figure 4. The integrated synaptic activity was convolved with a Poisson function (delay parameter=6 s) and sampled with a Tr=2 s. A portion of the time course for the last block has been removed to eliminate edge effects from the convolution computation. The values along the vertical axis are in arbitrary units.

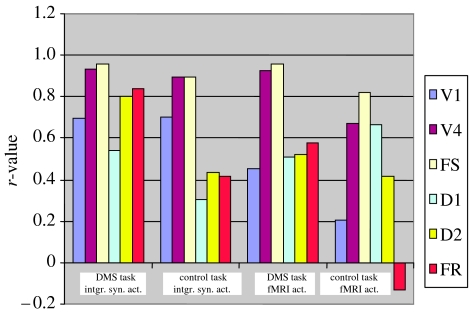
Figure 6 shows bar graphs of the within-task functional connectivity (expressed as a correlation coefficient) between IT and all the other modules in the model in subject 1. The plots on the left correspond to the functional connectivity of the time-series derived from the ISA, whereas those on the right were obtained using the fMRI time-series.4 Several features of these graphs are notable: (i) in terms of the ISA time-series, IT has strong functional connectivity with posterior areas during both the DMS and control tasks; (ii) for the ISA time-series, there is also strong functional connectivity with frontal areas D2 and FR during the DMS task, but not during the control task; (iii) the fMRI time-series show somewhat similar results, although the IT-D2 functional connectivities are not as distinctly different as they were using the ISA.

Figure 6.

Functional connectivity of IT with all the other brain regions in a ‘typical’ subject (subject 1—see tables 1 and 2) in the visual tasks. The strength of the functional connectivity is expressed as a correlation coefficient evaluated between time-series within each condition (see text). Shown on the left are the functional connectivities of the integrated synaptic activity for the DMS task and for the control task; on the right are the corresponding quantities for the fMRI signal.

Table 2 presents functional connectivity values between IT and all other brain regions for all 10 simulated subjects, and the mean and standard deviation of the individual subject correlation coefficients.5 Also shown in the table are the values of the differences between the correlation coefficients during the DMS and control tasks. These latter values demonstrate that the results discussed for subject 1 are present in most of the other subjects (and in the mean correlation coefficient). Note that except for the IT-v1 correlations, the functional connectivity values obtained using the ISA are always larger for the DMS task than they are for the control task. The correlations based on the fMRI time-series show a similar behaviour, but with several exceptions.

Table 2.

Values of the simulated functional connectivity (expressed as a correlation coefficient) between IT and the other brain regions for each subject for the DMS task and for the control task.

correlations between IT and all other brain regions
	subj1	subj2	subj3	subj4	subj5	subj6	subj7	subj8	subj9	subj10	mean	s.d.
r(task)
v1	0.6945	0.3091	0.6875	0.6807	0.7171	0.6832	0.7376	0.6935	0.7053	0.5894	0.6498	0.1258
v4	0.9335	0.9493	0.9296	0.9151	0.9323	0.937	0.9371	0.9368	0.9279	0.9161	0.9315	0.0102
fs	0.9576	0.9854	0.9571	0.9554	0.9496	0.9651	0.9570	0.9556	0.9554	0.9727	0.9611	0.0106
d1	0.5431	0.9289	0.5452	0.6915	0.6293	0.6659	0.4351	0.4401	0.5931	0.8416	0.6314	0.1596
d2	0.7991	0.9635	0.7947	0.8264	0.7691	0.8467	0.7512	0.7411	0.7800	0.9111	0.8183	0.0714
fr	0.8415	0.9176	0.8204	0.7927	0.7923	0.8481	0.8200	0.7702	0.7958	0.8661	0.8265	0.0435
r(ctrl)
v1	0.6993	0.6108	0.7113	0.7283	0.7350	0.6730	0.7140	0.6635	0.7202	0.6065	0.6862	0.0467
v4	0.8940	0.9014	0.8941	0.8772	0.9052	0.8922	0.9009	0.9025	0.8974	0.8932	0.8958	0.0079
fs	0.8971	0.9605	0.891	0.8605	0.8627	0.9243	0.9003	0.8934	0.8844	0.9480	0.9022	0.0330
d1	0.3028	0.7651	0.2736	0.1889	0.2384	0.5223	0.3147	0.3588	0.2202	0.6570	0.3842	0.1970
d2	0.4337	0.7944	0.4093	0.3198	0.3247	0.5966	0.4066	0.5001	0.3011	0.7390	0.4825	0.1746
fr	0.4191	0.8292	0.3805	0.2631	0.3518	0.5222	0.4723	0.4122	0.3388	0.7149	0.4704	0.1763
r(taskfmri)
v1	0.4538	0.3446	0.4333	0.5369	0.5309	0.6661	0.6226	0.6741	0.3432	0.4000	0.5005	0.1250
v4	0.9257	0.9932	0.8488	0.9162	0.9271	0.9805	0.9590	0.9740	0.8083	0.9830	0.9316	0.0612
fs	0.9557	0.9982	0.9857	0.9876	0.9559	0.9910	0.9592	0.9849	0.9625	0.9975	0.9778	0.0175
d1	0.5111	0.9506	0.7910	0.8146	0.6509	0.8129	0.4397	0.6250	0.5939	0.9371	0.7127	0.1746
d2	0.5213	0.9884	0.8011	0.8427	0.6522	0.8614	0.5266	0.7598	0.5631	0.9700	0.7487	0.1750
fr	0.5770	0.9889	0.8070	0.8879	0.6055	0.9180	0.7465	0.7610	0.5773	0.9723	0.7841	0.1585
r(ctrlfmri)
v1	0.2050	0.7026	0.2802	0.3829	0.4144	0.3383	0.4850	0.1008	0.5264	0.5422	0.3978	0.1767
v4	0.6729	0.9509	0.6669	0.6433	0.8473	0.7617	0.8966	0.8059	0.8570	0.9496	0.8052	0.1153
fs	0.8219	0.9891	0.7908	0.6335	0.7256	0.9303	0.8074	0.9272	0.8571	0.9908	0.8474	0.1155
d1	0.6654	0.8608	0.3891	0.3213	0.3955	0.7175	0.4429	0.6395	0.2327	0.9139	0.5579	0.2338
d2	0.4178	0.7541	0.1868	0.0056	−0.0338	0.3519	0.1708	0.5276	0.0404	0.7769	0.3198	0.2969
fr	−0.1344	0.8949	0.6396	−0.1975	0.6355	0.5541	0.4646	0.6459	0.5301	0.9096	0.4943	0.3766
Δr(task−ctrl)
v1	−0.0048	−0.3017	−0.0238	−0.0476	−0.0179	0.0102	0.0236	0.0300	−0.0149	−0.0171	−0.0364	0.0960
v4	0.0395	0.0479	0.0355	0.0379	0.0271	0.0448	0.0362	0.0343	0.0305	0.0229	0.0357	0.0076
fs	0.0605	0.0249	0.0661	0.0949	0.0869	0.0408	0.0567	0.0622	0.0710	0.0247	0.0589	0.0235
d1	0.2403	0.1638	0.2716	0.5026	0.3909	0.1436	0.1204	0.0813	0.3729	0.1846	0.2472	0.1364
d2	0.3654	0.1691	0.3854	0.5066	0.4444	0.2501	0.3446	0.2410	0.4789	0.1721	0.3358	0.1228
fr	0.4224	0.0884	0.4399	0.5296	0.4405	0.3259	0.3477	0.3580	0.4570	0.1512	0.3561	0.1338
Δr(taskfmri−ctrlfmri)
v1	0.2488	−0.3580	0.1531	0.1540	0.1165	0.3278	0.1376	0.5733	−0.1832	−0.1422	0.1028	0.2696
v4	0.2528	0.0423	0.1819	0.2729	0.0798	0.2188	0.0624	0.1681	−0.0487	0.0334	0.1264	0.1072
fs	0.1338	0.0091	0.1949	0.3541	0.2303	0.0607	0.1518	0.0577	0.1054	0.0067	0.1304	0.1082
d1	−0.1543	0.0898	0.4019	0.4933	0.2554	0.0954	−0.0032	−0.0145	0.3612	0.0232	0.1548	0.2115
d2	0.1035	0.2343	0.6143	0.8371	0.6860	0.5095	0.3558	0.2322	0.5227	0.1931	0.4289	0.2417
fr	0.7114	0.0940	0.1674	1.0854	−0.0300	0.3639	0.2819	0.1151	0.0472	0.0627	0.2899	0.3516

Also shown are the means (and s.d.) across the 10 subjects. r(task) are the functional connectivity values obtained from time-series of the integrated synaptic activity during the DMS task; r(ctrl) is the same quantity for the control task; r(taskfmri) is the same quantity evaluated using the time-series of the simulated fMRI activity during the DMS task and r(ctrlfmri) is the fMRI functional connectivity during the control task; Δr(task−ctrl) is the difference between r(task) and r(ctrl); Δr(taskfmri−ctrlfmri) is the difference between r(taskfmri) and r(ctrlfmri).

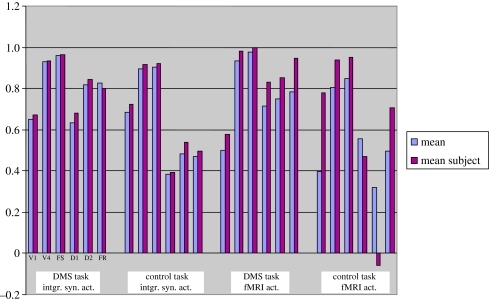
Several studies have averaged the fMRI time-series from the different subjects (or some such procedure) to produce a ‘mean subject’ (e.g. Bullmore et al. 2000; Bokde et al. 2001) upon which to perform functional or effective connectivity analysis. We took our 10 subjects and averaged together the ISA for the DMS task and separately for the control task. The resulting time-series were then convolved with the haemodynamic response function and sampled at the Tr value used for the previous analysis. The correlations between the IT time-series and that in the other brain regions are shown in figure 7 (which also shows the corresponding functional connectivity values for the mean correlation coefficients of the 10 subjects from table 2). For ISA-based functional connectivity, it is seen that the values for the mean-subject and for the mean across subjects are quite similar to one another and demonstrate the findings reported above. The fMRI-based functional connectivity shows more divergence between the mean across subjects and the mean-subject, especially during the control task (see figure 7).

Figure 7.

Mean functional connectivity of IT with all the other brain regions. Shown are the mean correlation coefficient across all the subjects (blue) and the corresponding quantities from the ‘mean’ subject, obtained by averaging the integrated synaptic activity time-series across all the subjects (burgundy).

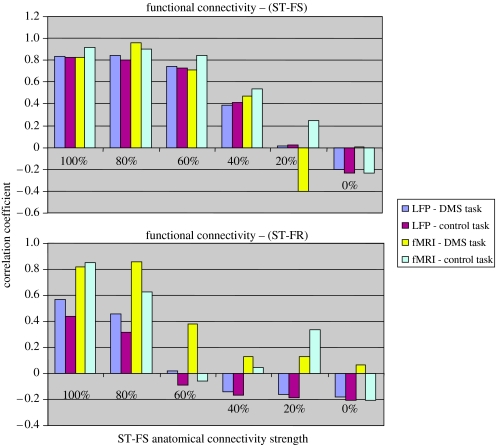
In our next simulation, we investigated how the interregional functional connectivity depends on the underlying anatomical connectivity. We used the auditory model (task and scanning parameters are specified in the caption to figure 8), and reduced the value of the anatomical connection weight from ST to FS to 80, 60, 40, 20 and 0% of the original value (note that the connection weights from frontal areas to ST were not modified). This situation is of some interest for its relevance to functional connectivity analyses of neurodegenerative diseases, such as Alzheimer's disease (Horwitz et al. 1995). Figure 8 shows the values of the correlations between ST and FS (top panel) and between ST and FR (which is not directly connected to ST). The ST–FS functional connectivity shows a nonlinear reduction that is similar for the time-series obtained from the ISA and from the fMRI activity, and additionally, does not depend on the task being performed. The latter result is not surprising since these two regions are connected. The ST–FR functional connectivity evaluated from the ISA shows a somewhat similar behaviour, as does that obtained using the fMRI time-series. These results demonstrate that brain regions not directly linked anatomically can be functionally connected if they are part of the network mediating the task of interest, but that the strength of the functional connectivity can depend on the integrity of network anatomy.

Figure 8.

Functional connectivity versus anatomic connectivity for the auditory model (Husain et al. 2004). Shown are the correlations between the activity in ST and FS (which is directly connected anatomically to ST; top graph) and FR (which is not directly connected to ST; bottom graph) for the integrated synaptic activity and for the fMRI activity for both the DMS task and for the control task. In the bar graphs, the strengths of the functional connectivity (correlation coefficient) is plotted for each anatomical connection strength (expressed as a percentage of the connection strength used in the original model).

6. Discussion

In this paper, we have used biologically realistic large-scale neural models of the visual and auditory object-processing cortical pathways to simulate DMS tasks. Examining the neuronal activities of the different regions in the models suggested that one of the regions (IT/ST) should possess strong functional interactions with posterior areas during both the DMS task and control task (where random noise stimuli are presented). However, the functional interactions with frontal areas should be stronger for the DMS task than for the control task. Our simulated functional connectivity results were in agreement with these expectations. We found that the IT/ST functional connectivity with PFC areas, evaluated using the within-task time-series of the integrated synaptic activities, was generally smaller during the control condition than during the DMS task, whereas the functional connectivity values with posterior areas were similar for the two conditions. As the strength of the feed-forward anatomic connection from IT/ST to PFC was weakened, so too were the strengths of the evaluated functional connectivity between IT/ST and PFC areas, although in a nonlinear manner. We also found somewhat similar results for the functional connectivity evaluated using the fMRI time-series (given the choices of the scanning and task parameters we used), although these results were perhaps not as clear as those for the functional connectivity based on the ISA time-series. Some differences in the values of the calculated functional connectivity occurred, depending on how it was calculated. In particular, the mean-subject fMRI correlations during the control task differed from those obtained evaluating the mean over the 10 subjects. Taken together, these simulated results indicate that our large-scale neural model can provide a useful and powerful means to investigate the neural basis of functional and effective connectivity.

As mentioned earlier, this is the first in a series of studies that will use these biologically realistic models to explore the neural substrates of many of the different types of functional and effective connectivity that have been proposed and used by functional brain imagers. In the current paper, which focuses on fMRI, we provided an overview of the issues involved and a brief history of some of the different definitions that have been employed. Our simulated results emphasized one of the simplest definitions of functional connectivity in the fMRI literature: the within-subject, within-condition, correlation between two region-of-interest time-series (e.g. Hampson et al. 2002). There were two sources of variability that our calculation of functional connectivity depended on: block-to-block and trial-to-trial. For the cases we presented, it is likely that the block-to-block variability had a greater effect on the value of the functional connectivity than did the trial-to-trial variability. In our simulations, the major source of the block-to-block variability was the strength of ‘attention’ parameter. Our simulated results thus speak to the importance of top-down effects such as attention as a modulator of functional connectivity and, consequently, of network performance (Horwitz et al. 1992b; Buechel and Friston 1997; McIntosh et al. 1999; Grady et al. 2001; Rowe et al. 2005).

The results of our simulations demonstrate that within-task analyses of functional and effective connectivity, as have been used with PET (e.g. McIntosh et al. 1999; Glabus et al. 2003) and fMRI (e.g. Bokde et al. 2001; Hampson et al. 2002) can, in principle, reflect some aspects of the underlying neuronal interactions. As illustrated in figure 8, when these interactions are being mediated along a direct anatomical link between two regions, the strength of the fMRI functional connectivity can be related to the strength of the anatomical link. A similar result was shown for PET data in a prior publication (Horwitz 2004). The simulations whose results were presented in figure 8 also indicate that PET or fMRI-measured functional and effective connectivity can be useful for investigating neurodegenerative diseases (e.g. Grafton et al. 1994; Horwitz et al. 1995; Grady et al. 2001; Rowe et al. 2002).

Table 2 presents the functional connectivity values between IT and the other brain regions in all 10 simulated subjects. As can be seen, the values differed across the subjects. As indicated in table 1, these subjects had different anatomical connection weights. For example, subject 1 represented a ‘typical’ subject and subject 2 had stronger anatomical weights between most brain areas than did subject 1. The differences in IT-ISA functional connectivity between the DMS and control tasks in subject 2 are relatively small (owing to the fact that the within-condition correlations are quite large for both conditions); a similar conclusion applies to the fMRI-derived functional connectivity values. In spite of the differences between subjects, the mean values of the correlation coefficients representing the functional connectivity between IT and the other brain regions showed the relevant pattern, as did the values for the typical subject (subject 1; a reduction in value for the IT-frontal functional connections between the DMS and control tasks), particularly for the ISA functional connections, but also for those based on fMRI data. A similar result was found using the mean-subject data. Both Goncalves et al. (2001), using fMRI, and Glabus et al. (2003), using PET, have reported large between-subject differences in effective connectivities. However, in both studies, the overall pattern of effective connections for the group model provided a reasonable representation of the tasks under study. Our simulated results, and these experimental findings, thus suggest that in normal subjects, there can be substantial subject-to-subject differences in the values of the interregional functional or effective connectivity for a task (more if the task permits multiple strategies to be employed; see Glabus et al. (2003) for a compelling example), and lead us to recommend that within-subject connectivity analysis be carried out. However, group results can still provide useful information as to how tasks are being mediated in normal individuals.

There are many other questions that our simulations could address, but space limitations prevent us from pursuing them here. Several of these questions are worth mentioning, however, to give a feeling for how computational neural modelling can add insight to functional neuroimaging. First, comparing and contrasting how the various sources of variability affect the calculated functional connectivity is a topic that our modelling formalism can investigate, especially when done in conjunction with appropriately designed experiments in which the different sources of variance can be estimated. Another important issue that will be explored concerns the role of neural inhibition in affecting functional connectivity values. We have previously published a study based on the visual model that suggests that the influence of synaptic inhibition on fMRI/PET activations is likely to be determined by both task context and local circuitry (Tagamets & Horwitz 2001). Another question concerns the contribution of feedback connections in determining the strength of the functional connectivity. These types of issues will be particularly critical as powerful new methods (e.g. Granger causality (Goebel et al. 2003); dynamic causal modelling (Friston et al. 2003); ‘dynamic’ connectivity (Breakspear 2004)) become widely used. Most importantly, being able to simulate functional (or effective) connectivity with a particular model, and comparing the simulated values against experimentally calculated ones, will be another test of the ability of the model to account for observed data. If successful, this will add support to the validity of the hypothesized neural mechanisms in the model that are attempting to account for the cognitive phenomena under study.