Prospects for Association Mapping in Classical Inbred Mouse Strains

Abstract

The collection of classical inbred mouse strains displays heritable variation in a large number of complex traits. Many generations of historical recombination have contributed to the panel of classical strain genomes, raising the possibility that quantitative trait loci could be located with high resolution by correlating strain genotypes and phenotypes. Although this association mapping framework has been successful in several empirical applications, its expected performance remains unclear. We used computer simulations based on a publicly available, dense single-nucleotide polymorphism (SNP) map to measure the power and false-positive rate of association mapping on a genomic scale across 30 commonly used classical inbred strains. Expected power is (i) often low for phenotypic effect sizes that are realistic for complex traits, (ii) highly variable across the genome, and (iii) correlated with linkage disequilibrium, aspects of the allele frequency distribution, and haplotype characteristics, as predicted by theory. Simulations also demonstrate clear potential for spurious associations to be generated by unequal relatedness among the strains. These findings suggest that association mapping in the classical strains is best applied in combination with other procedures, such as QTL mapping.

CLASSICAL inbred mouse strains provide powerful model systems for dissecting the genetic basis of complex phenotypes. The collection of widely available strains displays dramatic genetic variation in many quantitative traits, and the association of phenotypes with molecular markers in controlled crosses can reveal chromosomal regions that contain the causal loci. This strategy, quantitative trait locus (QTL) mapping, provides essential information about the genetic basis of complex phenotypes, including locus positions, effect sizes, and modes of action. However, standard QTL designs involve only one generation of recombination, so that phenotypic variation is typically associated with large genomic regions. This low level of mapping resolution has left the genes underlying most mouse QTL unidentified (Flint et al. 2005). Populations of lines formed by additional generations of recombination, including recombinant inbred lines, advanced intercross lines, and heterogeneous stocks, allow finer mapping resolution (Mott et al. 2000; Williams et al. 2001; Churchill et al. 2004; Yalcin et al. 2005; Valdar et al. 2006), but narrowing the resulting genomic intervals to small numbers of contributing genes still constitutes a formidable challenge.

The recent ability to genotype strains at markers from across the genome and the low resolution of most crossing studies has led some investigators to pursue an alternative approach to mapping complex trait variation. In this method (originally referred to as “in silico mapping”), genotypes and phenotypes from groups of classical inbred strains are compared to identify genomic regions that correlate with phenotypic variation (Grupe et al. 2001; Pletcher et al. 2004). Because the collective genomes of classical strains have experienced many generations of recombination during their histories, loci can be located with higher precision than in typical crossing designs. Additionally, in contrast to F₂ or backcross experiments, where each mouse has a unique genome, large numbers of animals with the same genotype can be measured, increasing the precision and accuracy of phenotypic estimates. Finally, the classical strains need be genotyped only once, accelerating the identification of genotype–phenotype associations.

Researchers have successfully applied this approach to fine map loci underlying complex trait variation in the classical strains. Some studies have used association mapping to narrow genomic intervals previously determined to contribute to phenotypic variation (through crosses), including metastasis (Park et al. 2003), blood pressure (DiPetrillo et al. 2004), and plasma cholesterol (Wang et al. 2004; Cervino et al. 2005). Other studies have conducted association mapping on a genomewide scale and recovered associations that overlap with strong candidate genes (Grupe et al. 2001; Liao et al. 2004; Pletcher et al. 2004; Wang et al. 2005; Liu et al. 2006).

Despite these successful applications, serious concerns about the validity of this method as a general approach for dissecting the genetic basis of complex traits have been raised (Chesler et al. 2001; Darvasi 2001; Cuppen 2005). The number of available strains is small, suggesting that the ability to detect contributions from loci with small to moderate effects might be compromised. Additionally, the classical strains have a complex history that includes several forms of nonrandom mating: admixture between divergent natural populations, inbreeding, and other biases (Silver 1995; Beck et al. 2000; Wade and Daly 2005). This history has led to unequal relatedness among the strains, a phenomenon with the potential to produce correlations between genotype and phenotype in the absence of QTL (Lander and Schork 1994; Ewens and Spielman 1995; Pritchard and Rosenberg 1999; Risch 2000; Cervino et al. 2005; Mhyre et al. 2005). The history of the strains also affects allele frequency spectra, patterns of linkage disequilibrium, and the distribution of haplotypes across the genome. The contributions of these variables to the performance of association mapping in the classical strains have not been examined. Here, we use computer simulations based on publicly available SNP genotypes to quantify the expected performance of this approach across classical strain genomes.

MATERIALS AND METHODS

Strain and marker selection:

We selected genotypes for all single-nucleotide polymorphisms (SNPs) (n = 70,656) that had complete data for and were variable across 30 classical strains (Table 1) from the Inbred Laboratory Mouse Haplotype Map (“HapMap”) (http://www.broad.mit.edu/personal/claire/MouseHapMap/Inbred.htm; February 2006 version; Wade and Daly 2005), which features the most dense genotype information currently available. These strains were selected on the basis of two criteria: (i) inclusion in the HapMap and (ii) designation as priority strains by the Mouse Phenome Project (Bogue and Grubb 2004; Grubb et al. 2004; http://aretha.jax.org/pub-cgi/phenome/mpdcgi?rtn=docs/home), a large-scale effort to collect and collate phenotypic information for the classical strains. Although the strain sets examined in empirical studies might vary on the basis of the phenotype of interest, we reasoned that the availability of genotypic and phenotypic information for this strain collection makes it a likely focus for association mapping studies. We did not consider wild-derived strains because their divergent evolutionary histories have strong potential to generate spurious associations between genotype and phenotype (Mhyre et al. 2005).

TABLE 1.

Classical inbred mouse strains used for simulations of association mapping

Strain	Classification
A/J	Castle
AKR/J	Castle
BALB/cByJ	Castle
BTBR T +tf/tf	Castle
BUB/BnJ	Other
CBA/J	Castle
CE/J	Castle
C3H/HeJ	Castle
C57BL/6J	C57 related
C57BLKS/J	C57 related
C57L/J	C57 related
C57BR/cdJ	C57 related
C58/J	C57 related
DBA/2J	Castle
FVB/NJ	Swiss
I/LnJ	Castle
KK/HIJ	Japanese
LP/J	Castle
MA/MyJ	C57 related
NOD/LtJ	Swiss
NON/LtJ	Swiss
NZB/B1NJ	New Zealand
NZW/LacJ	New Zealand
PL/J	Other
RIIIS/J	Other
SEA/GnJ	Castle
SJL/J	Swiss
SM/J	Castle
SWR/J	Swiss
129S1/SvImJ	Castle

Classification is based on Beck et al. (2000).

Power simulations:

Phenotypes for individual strains were created from SNP genotypes. To simulate an additive QTL mapping to a particular genomic region, one SNP was designated as the causal locus. Genotypes at this SNP were recoded as 0 or 1 (the additive effect, a), and the variance across this set of recoded genotypes was assumed to be the additive genetic variance (V_a). Strain phenotypes determined by particular fractions of variance at this locus (proportion of variance explained, PVE, analogous to a locus-specific heritability) were generated by calculating the variance contributed by effects outside this locus, which could include those from the environment or loci mapping elsewhere in the genome, as

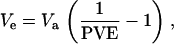drawing a random effect from a normal distribution (mean = 0; variance = V_e), and adding this effect to a for each strain. In separate simulations, we considered the following PVE values: 0.05, 0.10, 0.15, 0.20, 0.25, 0.30, 0.35, 0.40, 0.45, and 0.50.

We assigned marker haplotypes in a genomic window by removing the causal SNP and concatenating contiguous sets of SNPs flanking the causal SNP. In separate tests, we considered haplotypes composed of two, three, four, five, six, and seven marker SNPs. Tests of association were performed by comparing phenotypes across haplotypic classes using a one-way ANOVA. P-values were estimated by comparison of the observed F-test to a distribution of 1000 (chosen to allow exploration of many parameter values across the genome) F-tests obtained by randomly permuting phenotypes across strains. For each genomic window, 1000 separate phenotypic simulations were performed. Power was estimated as the fraction of simulations with P < 0.05. We followed this procedure for each window in the genome (allowing each SNP to act as the causal SNP). Pseudocode for the power simulation procedure could be written as:

•  For each window size (number of SNPs in haplotype)

•   For each SNP in the genome

•    For each PVE

•     For 1000 replicates

•      Remove causal SNP

•      Obtain P-value for ANOVA association test

•     Loop

•    Loop

•   Loop

•  Loop

By calculating power separately for each genomic window, our approach did not directly simulate genomic scans for genotype–phenotype associations. Several factors motivated this decision. First, performing full genomic scans and accounting for these tests in each simulation replicate would be computationally demanding and would drastically reduce the number of genomic regions and parameter combinations (PVE and number of markers) that could be explored. Second, the power of genomic scans depends critically on the manner in which corrections for multiple testing are performed. The best method for adjusting for the very large number of tests performed in genomic association testing is not currently obvious and is an active area of research (Pletcher et al. 2004; Hirschhorn and Daly 2005; Balding 2006; McClurg et al. 2006). Third, our power estimates describe important variation among genomic regions and should be directly relevant to the increasingly common approach of finely localizing associations in the classical strains that were first identified with another method, such as QTL mapping. Finally, our general conclusion that association mapping in the classical strains is underpowered is conservative: accounting for multiple tests would only further reduce power.

False-positive simulations:

The false-positive rate of association mapping could be estimated by setting phenotypic effects to zero and performing association tests. Instead, we sought to model the more realistic scenario of a phenotype that does not map to the genomic region being tested, but still displays heritable variation across the classical strains in a manner that reflects their unequal relatedness.

To accomplish this goal, we used genomic similarity between strains to create phenotypes. Our measure of similarity was the fraction of SNPs from across the genome at which each of the 30 strains differed from a common strain, WSB/EiJ. We selected this strain because (i) it was included in the Inbred Strain HapMap, (ii) it is fairly closely related to the tested classical strains (which are predominantly descended from Mus domesticus; Wade and Daly 2005), and (iii) it was not included in the strain set used for the power simulations. This simplified approach assumes that two very closely related strains will show more similar genomic SNP distances from WSB/EiJ than will two strains with longer divergence times.

To simulate phenotypes, the variance in this distance was treated as the total additive genetic variance, V_a. For each simulation, phenotypes with particular heritabilities—but no locus-specific effects—were generated from this (constant) V_a using the approach described above. Association testing was then conducted separately for each genomic window. Phenotypes with total heritabilities of 0.4, 0.6, and 0.8 (assumed to come from loci outside the window under consideration) were considered in separate simulations. We selected these heritabilities to span a realistic range for complex phenotypes likely to be subject to association mapping in the classical strains. We considered haplotypes composed of two, three, and four neighboring SNPs in separate simulations. This approach recognizes that the potential for unequal relatedness among strains to produce spurious genotype–phenotype associations varies among genomic regions and allows this potential to be quantitatively measured.

Measuring marker characteristics:

We examined correlations between power and several measures of genotypic variation, including linkage disequilibria, allele frequencies, haplotype number, and haplotype diversity. Linkage disequilibrium was estimated as the average value of R² (Hill and Robertson 1968) or D′ (Lewontin 1964) among all pairs of marker SNPs in a genomic window. Haplotype diversity across the k observed haplotypes was measured as

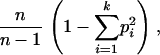where p_i is the frequency of the ith haplotype (Nei 1987). The size of each genomic interval was calculated as the difference between the physical positions of the first and last markers in a window.

RESULTS

Power:

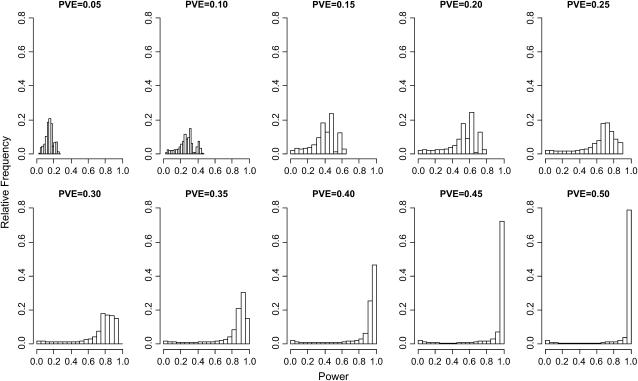
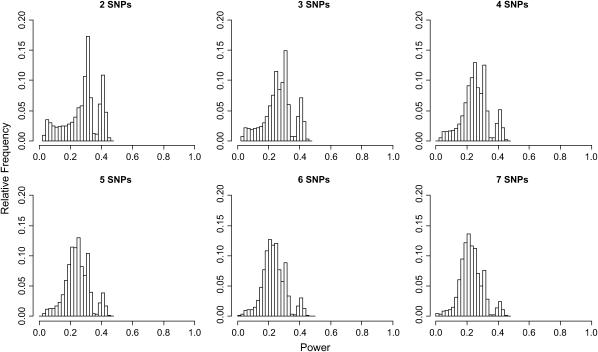
Genomic distributions of power to detect genotype–phenotype associations across the classical strains show several patterns (Table 2). First, as expected, average power increases steadily with increasing PVE (Figure 1). Second, power is generally low for PVE values < ∼0.25 (Figure 1). For example, assuming a PVE of 0.10, the average power across the genome using 3-SNP haplotypes is only 0.266 and the maximum is just 0.464. Third, similar power distributions are observed when haplotypes are composed of different numbers of marker SNPs (within a given PVE level; Figure 2). This pattern indicates that haplotype block sizes generally exceed the window sizes considered here, suggesting that the inbred strain HapMap has sufficient SNP density to capture most common haplotypic variation among the classical strains. Finally, power varies substantially among genomic locations (Figure 1). Some genomic windows retain little power to detect associations, even when PVE is large, while other regions display consistently higher power.

TABLE 2.

Summary statistics of power to associate genotypes with complex trait variation in classical inbred strains

		Power
Parameters		Standard deviation	Range (minimum, maximum)
PVE	Marker SNPs			Average
0.05	2	0.155	0.051	0.025, 0.272
	3	0.148	0.045	0.024, 0.276
	4	0.142	0.041	0, 0.269
	5	0.137	0.039	0, 0.275
	6	0.132	0.037	0, 0.277
	7	0.128	0.036	0, 0.269
0.10	2	0.278	0.106	0.024, 0.472
	3	0.266	0.092	0.021, 0.464
	4	0.255	0.083	0, 0.469
	5	0.245	0.079	0, 0.465
	6	0.236	0.075	0, 0.486
	7	0.228	0.073	0, 0.464
0.15	2	0.406	0.158	0.019, 0.650
	3	0.393	0.137	0.014, 0.642
	4	0.380	0.124	0, 0.642
	5	0.366	0.116	0, 0.643
	6	0.354	0.111	0, 0.652
	7	0.343	0.108	0, 0.642
0.20	2	0.528	0.203	0.009, 0.790
	3	0.518	0.175	0.012, 0.791
	4	0.506	0.157	0, 0.782
	5	0.491	0.147	0, 0.781
	6	0.477	0.141	0, 0.783
	7	0.464	0.138	0, 0.785
0.25	2	0.634	0.237	0.005, 0.892
	3	0.632	0.204	0.006, 0.888
	4	0.623	0.182	0, 0.885
	5	0.610	0.170	0, 0.889
	6	0.596	0.162	0, 0.886
	7	0.582	0.160	0, 0.884
0.30	2	0.719	0.259	0.004, 0.957
	3	0.726	0.223	0.003, 0.954
	4	0.723	0.197	0.001, 0.956
	5	0.714	0.184	0, 0.957
	6	0.702	0.175	0, 0.950
	7	0.690	0.173	0, 0.954
0.35	2	0.782	0.270	0.001, 0.986
	3	0.799	0.232	0, 0.986
	4	0.803	0.205	0, 0.987
	5	0.798	0.190	0, 0.986
	6	0.790	0.181	0, 0.986
	7	0.780	0.179	0, 0.985
0.40	2	0.826	0.274	0, 0.998
	3	0.850	0.235	0, 0.998
	4	0.860	0.207	0, 0.999
	5	0.860	0.191	0, 0.999
	6	0.856	0.182	0, 0.999
	7	0.849	0.180	0, 0.998
0.45	2	0.854	0.272	0, 1
	3	0.882	0.234	0, 1
	4	0.897	0.205	0, 1
	5	0.901	0.189	0, 1
	6	0.901	0.180	0, 1
	7	0.897	0.178	0, 1
0.50	2	0.872	0.269	0, 1
	3	0.903	0.230	0, 1
	4	0.920	0.201	0, 1
	5	0.926	0.185	0, 1
	6	0.929	0.176	0, 1
	7	0.927	0.176	0, 1

Figure 1.—

Genomic distributions of power for association tests using 3-SNP haplotypes.

Figure 2.—

Genomic distributions of power for association tests when the causal variant has PVE = 0.10. The label above each histogram is the number of contiguous marker SNPs combined to construct haplotypes. Note that the scale of the y-axis differs from that in Figure 1.

To understand the determinants of variation in power across classical strain genomes, we compared power to several characteristics of the SNP markers. Here, we focus on results assuming PVE = 0.10, which is a reasonable effect size for QTL underlying many quantitative traits. Similar results were observed for other PVE values.

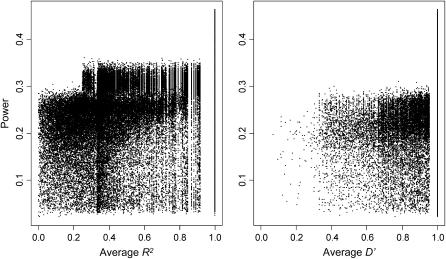
The power to associate marker genotypes with complex trait variation is expected to increase with linkage disequilibrium. Positive correlations between power and average pairwise linkage disequilibrium support this prediction for the classical strains (Figure 3; Table 3). R² shows stronger correlations with power than does D′; this difference is predicted by theory (Devlin and Risch 1995; Pritchard and Przeworski 2001).

Figure 3.—

Scatterplots of power vs. linkage disequilibrium. PVE = 0.10 and association tests were performed with 3-SNP haplotypes.

TABLE 3.

Spearman's correlations between power and genotypic characteristics

	Correlation with power
Marker SNPs	Average R2	Average D′	Difference between causal and marker frequencies	Haplotype no.	Haplotype diversity	Window size
2	0.483	0.301	−0.693	−0.541	−0.322	−0.239
3	0.556	0.418	−0.602	−0.661	−0.445	−0.260
4	0.614	0.515	−0.548	−0.741	−0.529	−0.277
5	0.643	0.572	−0.511	−0.785	−0.578	−0.287
6	0.665	0.615	−0.484	−0.817	−0.616	−0.299
7	0.680	0.644	−0.463	−0.840	−0.644	−0.304

Assumes PVE = 0.10. P < 10⁻¹⁵ for all tests.

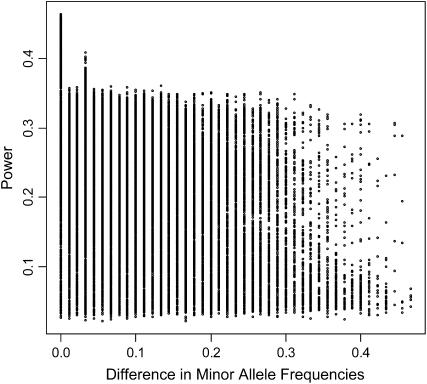
Increased power is also expected when allele frequencies at marker and causal SNPs are more similar (Zondervan and Cardon 2004). Accordingly, power is negatively correlated with the absolute value of the difference between the causal SNP minor allele frequency and the average minor allele frequency of the marker SNPs (Figure 4; Table 3). These correlations are similar in magnitude to observed correlations between power and linkage disequilibrium.

Figure 4.—

Scatterplot of power vs. the absolute value of the difference between causal SNP minor allele frequency and the average minor allele frequency of the marker SNPs. PVE = 0.10 and association tests were performed with 3-SNP haplotypes.

Additionally, power should depend on the distribution of marker haplotypes. As the number of haplotypes grows, phenotypes for each haplotypic class are estimated (less accurately) from fewer strains and the number of degrees of freedom for the between-class test in the ANOVA increases. As predicted, genomic regions with fewer haplotypes exhibit significantly greater power (Table 3). This pattern underlies the apparently bimodal power distributions observed for lower PVE values (Figure 1): genomic regions harboring only two haplotypes show clear increases in power relative to regions with higher haplotype numbers. Power is also negatively correlated with haplotype diversity (Table 3), suggesting effects of both haplotype number and frequency.

Finally, the amount of historical recombination in an interval will differ across the genome because of variation in recombination rate and SNP density. As a result, power should be related to the size of the genomic interval. This prediction is supported by the results: window size and power are negatively correlated (Table 3).

Linkage disequilibrium, the difference between causal and marker SNP frequencies, haplotype number, haplotype diversity, and window size all contribute to the power to detect genotype–phenotype associations. We used multiple regression to (i) determine whether each variable influences power when effects of the other variables have been taken into account and (ii) estimate how much of the variation in power can be explained by combining these measures of marker variation. To satisfy assumptions of linear regression, all proportions, including power, R², D′, differences in marker-causal SNP frequency, and haplotype diversity were arcsine-square-root transformed prior to analysis. We selected the set of variables that explain the most genomic variation in power using the step function in the R statistical software (Ihaka and Gentleman 1996), with default settings. We report the results of analyses using 3-SNP marker haplotypes (similar patterns were seen with alternative marker numbers). Both forward and backward stepwise procedures selected all variables (P < 0.05), indicating that each measure contributes independently to power (despite strong intercorrelations between variables). Although this pattern was consistent across PVE values, the relative contributions of each variable differed. Total adjusted R²-values decreased with increasing PVE, ranging from 0.562 (PVE = 0.05) to 0.215 (PVE = 0.5). Potential issues with stepwise multiple regression suggest that these estimates should be viewed with caution (McCullagh and Nelder 1989). Nevertheless, the conclusion that combinations of the measured genotypic variables provide predictive information about power seems warranted.

Because different groups of strains have different histories, strain choice is expected to affect the power of association mapping. As a preliminary investigation into the effects of strain choice on method performance, we measured power across all intervals of chromosome 1 using 10 randomly selected subsets of 20 strains (from the original 30). Power is reduced relative to the 30-strain set across all 20-strain subsets and parameter combinations (results not shown). Pairs of strain sets show correlations in power (Table 4), suggesting that haplotype structure is reasonably conserved. However, correlations are moderate in magnitude and vary among strain set pairs (Table 4), indicating that associations identified in one strain set are not necessarily expected to replicate in a different group of strains.

TABLE 4.

Pairwise Spearman's correlations between power estimates across chromosome 1 intervals for 10 randomly selected sets of 20 classical strains each

Strain sets	2	3	4	5	6	7	8	9	10
1	0.789	0.803	0.717	0.753	0.822	0.734	0.715	0.762	0.859
2		0.805	0.752	0.742	0.819	0.732	0.712	0.774	0.805
3			0.716	0.756	0.819	0.722	0.688	0.776	0.830
4				0.761	0.745	0.781	0.788	0.842	0.735
5					0.787	0.848	0.768	0.799	0.758
6						0.755	0.706	0.804	0.811
7							0.789	0.800	0.757
8								0.758	0.730
9									0.774

Assumes PVE = 0.10 and 3-SNP haplotypes. P < 10⁻¹⁵ for all correlations.

False-positive rates:

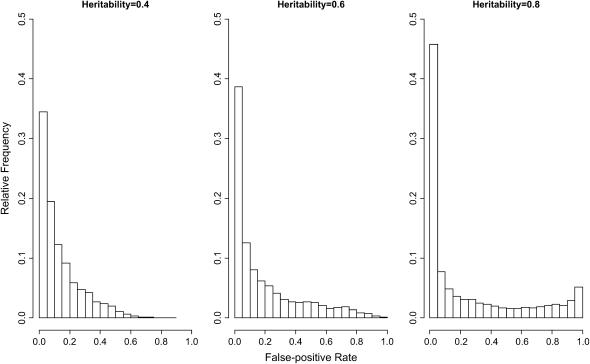
Results from simulations of phenotypes with heritable variation across the strains but without locus-specific effects reveal two key patterns (Figure 5). First, there is clear potential for the generation of spurious genotype–phenotype associations in the classical strains and this potential varies substantially across the genome. Although most genomic regions show acceptable false-positive rates of ≤0.05, many regions show higher rates, including false-positive frequencies of 1 when trait heritability is 0.8. For example, the mean false-positive rate assuming 3-SNP haplotypes and a heritability of 0.8 is 0.257. Second, the risk of false positives is higher for traits with higher heritabilities.

Figure 5.—

Genomic distributions of the false-positive rate for association tests using 3-SNP haplotypes. Heritability is the fraction of phenotypic variance due to additive genetic variance contributed by loci outside the tested window.

DISCUSSION

Reduced power:

Association mapping in classical strains of mice can localize QTL of large effect to narrow genomic intervals. Our estimates suggest that, on average, a locus with PVE of 0.35 can be detected with ∼80% power using available SNP maps. Therefore, association mapping in the classical strains will often be useful for dissecting phenotypes with simpler genetic bases. However, our results point to the generally low power of this approach for finding loci underlying complex traits. First, most loci that contribute to the genetic basis of complex traits are expected to explain <35% of the phenotypic variance and will therefore often go undetected. For example, recovering loci with PVE of 0.10, which could be interpreted as a relatively large effect size for some phenotypes, with an average power of ∼0.25 is simply not adequate for a general approach to mapping QTL. Second, these estimates have not been adjusted for multiple testing, suggesting that further reductions in power will accompany genomic scans for genotype–phenotype associations. Finally, our simulations assumed a simple additive model of quantitative variation. Although the inbred nature of the strains precludes dominance from contributing to phenotypic variance, associations generated by epistatic interactions will be even more challenging to find.

The low average power of association mapping in the classical strains is primarily attributable to the small number of strains (Darvasi 2001). In fact, empirical studies applying this approach have typically used fewer than the 30 strains assumed here. For comparison, standard QTL mapping usually employs hundreds of mice and association mapping in humans often involves thousands of individuals. Although estimates of genetic effects are improved by using inbred strains (in which measurement error and environmental contributions can be minimized), finding loci with small to moderate genetic effects on complex traits will generally require larger sample sizes using any strategy (Lynch and Walsh 1998; Darvasi 2001; Hirschhorn and Daly 2005). The PVE attributable to a detected association may also be overestimated as a consequence of the small number of strains (Beavis 1994).

Although average power is low, there is substantial variation across the genome, showing that the performance of association mapping crucially depends on factors other than the number of strains. The histories of the classical strains are responsible for this genomic variation in power. Evolutionary forces including mutation, recombination, selection, and drift have shaped genomic patterns of genotypic and phenotypic variation and affected the ability to correlate individual genomic regions with complex traits among the strains. Although the relative contributions of these and other processes to current diversity are unclear, combinations of genotypic characteristics provide information about the relative power across the genome. Genomic regions with high linkage disequilibrium and (accordingly) limited haplotype diversity offer higher power. Additionally, the emphasis of current SNP maps on common variation translates into a higher likelihood of detecting QTL with intermediate frequencies across the strains (such QTL are also easier to detect with small sample sizes). As a result, this approach focuses more attention on variation ultimately derived from the wild ancestors of the classical strains and less on mutations that have arisen since their founding.

Potential for spurious associations:

The potential for population structure to generate spurious associations between genotype and phenotype has long been recognized in human and plant genetics. The problem is especially important for the classical mouse strains, which have histories involving admixture between divergent populations and patently nonrandom mating (Silver 1995; Beck et al. 2000; Wade and Daly 2005). We illustrated this effect with a simple model assuming that closely related strains have more similar phenotypes and that the genetic variants responsible for phenotypic variation are not located in the genomic interval being tested. Although more elaborate models could be envisioned, this approach captures the primary cause of false-positive associations: unequal relatedness among the strains. Our results suggest a nontrivial risk of spurious associations across the classical strains.

Fortunately, several methods have been developed that adjust for the effects of population structure on association mapping using patterns of variation at unlinked markers (Devlin and Roeder 1999; Pritchard et al. 2000; Reich and Goldstein 2001; Yu et al. 2006). A particularly promising approach for the classical strains accounts for the effects of unequal relatedness on multiple levels (Yu et al. 2006). Now that genomewide SNP and microsatellite polymorphism data exist for the classical strains, these strategies can begin to be applied. Efforts to minimize spurious associations will also benefit from full resequencing surveys of the classical strains, which will produce patterns of variation that are free from ascertainment and that better reflect population structure and phylogenetic history among the strains.

Future prospects:

The recent accumulation of genomewide polymorphism data (Wiltshire et al. 2003; Cervino et al. 2005; Wade and Daly 2005) and phenotypic measurements (Bogue and Grubb 2004; Grubb et al. 2004) for the classical strains is an exciting development in mouse genetics. Although many loci underlying complex trait variation will be missed by association mapping with the current strain set, the higher mapping resolution of those loci that are found should continue to motivate the development and application of this approach.

In addition to accounting for the effects of population structure, several possibilities exist for improving the performance of association mapping across the classical strains. Haplotype delineation using diversity (Patil et al. 2001; Zhang et al. 2002), linkage disequilibrium (Gabriel et al. 2002), and information theoretic (Anderson and Novembre 2003) criteria should increase power. Detailed investigations of haplotype block structure in the classical strains will also be required to measure the expected level of mapping resolution. Useful information on genomic haplotype structure across the classical strains is rapidly accumulating (Wade et al. 2002; Wiltshire et al. 2003; Frazer et al. 2004; Ideraabdullah et al. 2004; Yalcin et al. 2004; Cuppen 2005; Wade and Daly 2005; Zhang et al. 2005). Because classical strain genomes are ultimately derived from wild representatives of M. domesticus, M. musculus, M. castaneus, and M. molossinus (Wade et al. 2002; Wade and Daly 2005), detailed comparisons to patterns of haplotype diversity in natural populations of house mice would enable association mapping in the classical strains. Additionally, the application of model-based association procedures that better incorporate information on strain history in each genomic region could improve power (Yalcin et al. 2005; Cervino et al. 2007) and continued examination of different statistical methods is warranted (McClurg et al. 2006).

Combining association mapping with other approaches, including QTL mapping, is also a fertile area for future research (Cervino et al. 2005, 2007; DiPetrillo et al. 2005). The ability of association mapping to refine genomic regions identified by QTL mapping will depend on the relationships of the crossed strains to the remaining strains; therefore, strain selection in QTL mapping could be influenced by patterns of haplotypic diversity across the larger strain set. The expected joint resolution and power of QTL mapping and association mapping deserves modeling attention. Method development might be informed by advances in combining linkage and association mapping in human genetics (Abecasis et al. 2000; Jung et al. 2005; Wang and Elston 2006).