Abstract
Density functional calculations with the B3PW91 functional have been carried out on the TpRh(CNMe) species [Tp = HB(pyrazolyl)3] as a model for Tp′Rh(CNCH2CMe3) [Tp′ = HB(3,5-dimethylpyrazolyl)3] in interaction with propane. Two σ complexes have been found as minima coordinated through either a methyl or a methylene C H bond, the former being more stable. The approach of the alkane to TpRh(CNMe) has been studied. Although no transition state could be located, study of this path reveals the key importance of the partial decoordination of one pyrazole ring. The full coordination of the alkane can only be achieved when the metal is essentially in a square pyramid coordination with one of the three pyrazole groups only weakly interacting with Rh. The main reaction of the methyl σ complex is oxidative addition, leading to the n-propyl hydride complex. In contrast, two reactions are found for the methylene σ complex: (i) oxidative addition to give the isopropyl complex and (ii) exchange between the secondary and primary C
H bond, the former being more stable. The approach of the alkane to TpRh(CNMe) has been studied. Although no transition state could be located, study of this path reveals the key importance of the partial decoordination of one pyrazole ring. The full coordination of the alkane can only be achieved when the metal is essentially in a square pyramid coordination with one of the three pyrazole groups only weakly interacting with Rh. The main reaction of the methyl σ complex is oxidative addition, leading to the n-propyl hydride complex. In contrast, two reactions are found for the methylene σ complex: (i) oxidative addition to give the isopropyl complex and (ii) exchange between the secondary and primary C H bonds to convert the methylene complex of propane into a methyl complex of propane. This latter reaction has a much lower barrier than the oxidative addition at the methylene C
H bonds to convert the methylene complex of propane into a methyl complex of propane. This latter reaction has a much lower barrier than the oxidative addition at the methylene C H bond. The results account well for most of the experimental results obtained from kinetic studies. Steric factors are found to control the energy barriers between these various processes, disfavoring any process that brings the central carbon into close proximity to Rh.
H bond. The results account well for most of the experimental results obtained from kinetic studies. Steric factors are found to control the energy barriers between these various processes, disfavoring any process that brings the central carbon into close proximity to Rh.
Keywords: density functional theory, hydrocarbon activation, rhodium, selectivity
The activation of hydrocarbon C H bonds by homogeneous transition metal complexes is an important and challenging prerequisite to the successful transformation of these raw resources into value-added products. In the past decade, useful processes have been developed that employ alkane activation via oxidative addition; significant examples include alkane dehydrogenation (1–4), alkane and arene borylation (5–9), and alkane metathesis (10). In all of these developments, selectivity in activation has been a critical issue, and rhodium and iridium transition metal complexes have been found to show a strong preference for the activation of the methyl C
H bonds by homogeneous transition metal complexes is an important and challenging prerequisite to the successful transformation of these raw resources into value-added products. In the past decade, useful processes have been developed that employ alkane activation via oxidative addition; significant examples include alkane dehydrogenation (1–4), alkane and arene borylation (5–9), and alkane metathesis (10). In all of these developments, selectivity in activation has been a critical issue, and rhodium and iridium transition metal complexes have been found to show a strong preference for the activation of the methyl C H bonds in alkanes, despite the presence of weaker methylene C
H bonds in alkanes, despite the presence of weaker methylene C H bonds. The intermediacy of σ-alkane complexes has been found to play a critical role in these activation reactions (11–14). Binding of alkanes has been studied experimentally by using time-resolved IR (15–17) and NMR spectroscopies (18).
H bonds. The intermediacy of σ-alkane complexes has been found to play a critical role in these activation reactions (11–14). Binding of alkanes has been studied experimentally by using time-resolved IR (15–17) and NMR spectroscopies (18).
One system in which the kinetic vs. thermodynamic preference for activation of various aromatic and aliphatic C H bonds has been investigated in detail is the trispyrazolylborate–rhodium complexes, Tp′Rh(CNR)(alkyl)H [Tp′ = Tris-(3,5-dimethylpyrazolyl)borate; R = neopentyl], in which the reactive 16-electron Rh(I) fragment [Tp′Rh(CNR)] undergoes oxidative addition to give stable 18-electron Rh(III) octahedral products. Experimental investigation of this system has established the thermodynamic preference for a wide variety of hydrocarbon substrates, as indicated in Table 1 (19–21). Of particular note is the comparison of the activation of a methyl C
H bonds has been investigated in detail is the trispyrazolylborate–rhodium complexes, Tp′Rh(CNR)(alkyl)H [Tp′ = Tris-(3,5-dimethylpyrazolyl)borate; R = neopentyl], in which the reactive 16-electron Rh(I) fragment [Tp′Rh(CNR)] undergoes oxidative addition to give stable 18-electron Rh(III) octahedral products. Experimental investigation of this system has established the thermodynamic preference for a wide variety of hydrocarbon substrates, as indicated in Table 1 (19–21). Of particular note is the comparison of the activation of a methyl C H bond in pentane vs. a methylene C
H bond in pentane vs. a methylene C H bond in cyclohexane. The thermodynamic preference for the former substrate was found to be 2.07 kcal·mol−1 (1 kcal·mol−1 = 4.18 kJ·mol−1), which, when corrected for statistical factors, corresponds to a 95:1 preference for activation of methyl over methylene C
H bond in cyclohexane. The thermodynamic preference for the former substrate was found to be 2.07 kcal·mol−1 (1 kcal·mol−1 = 4.18 kJ·mol−1), which, when corrected for statistical factors, corresponds to a 95:1 preference for activation of methyl over methylene C H bonds.§ Confirmation of this conclusion comes from the independent synthesis of the isopropyl complex Tp′Rh(CNR)(CHMe2)H, which rearranges in benzene solution to the more stable n-propyl isomer Tp′Rh(CNR)(CH2CH2CH3)H before loss of propane (22).
H bonds.§ Confirmation of this conclusion comes from the independent synthesis of the isopropyl complex Tp′Rh(CNR)(CHMe2)H, which rearranges in benzene solution to the more stable n-propyl isomer Tp′Rh(CNR)(CH2CH2CH3)H before loss of propane (22).
Table 1.
Relative experimental stabilities (kcal·mol−1) of hydrocarbon activation products in equilibria of the type Tp′Rh(L)(R)H + R′H ⇌ Tp′Rh(L)(R′)H + RH
| R | ΔG°* |
|---|---|
| Phenyl | 0 |
HC CHCMe3 CHCMe3
|
5.31 |
| Mesityl | 6.65 |
| Methallyl | 7.82 |
| Methyl | 7.90 |
| n-Pentyl | 9.35 |
| c-Hexyl | 11.42 |
| c-Pentyl | 11.46 |
*Relative to Tp′Rh(L)(Ph)H (L = CNR).
In addition to these experimental determinations of the thermodynamic stability of isomers resulting from alkane activation, it was also possible to determine the kinetic preference for C H activation. Photochemical generation of the fragment [Tp′Rh(CNR)] in pentane or propane gives exclusively the n-alkyl hydride product (19). Because independent synthesis of the isopropyl hydride isomer demonstrated that such a species should have been stable under the reaction conditions, the lack of observation of any methylene activation products indicates that the n-alkyl activation products are the kinetic products as well.
H activation. Photochemical generation of the fragment [Tp′Rh(CNR)] in pentane or propane gives exclusively the n-alkyl hydride product (19). Because independent synthesis of the isopropyl hydride isomer demonstrated that such a species should have been stable under the reaction conditions, the lack of observation of any methylene activation products indicates that the n-alkyl activation products are the kinetic products as well.
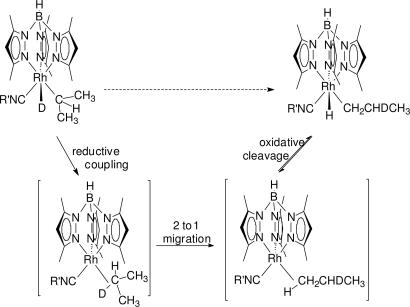
In the related [Tp′Rh(CO)] system, flash photolysis studies indicated that the unsaturated metal fragment first binds to the hydrocarbon to form a σ-alkane complex, which then undergoes C H oxidative cleavage in a second unimolecular reaction (23–25). Density functional theory calculations have confirmed the stability of an alkane complex of TpRh(CO) (26). The same type of σ-alkane complexes are involved in the [Tp′Rh(CNR)] system, as evidenced by the rearrangement of the deuterated compound Tp′Rh(CNR)(i-propyl)D to Tp′Rh(CNR)(CH2CHDCH3)H in benzene solvent (Fig. 1). If the reductive coupling to produce the C
H oxidative cleavage in a second unimolecular reaction (23–25). Density functional theory calculations have confirmed the stability of an alkane complex of TpRh(CO) (26). The same type of σ-alkane complexes are involved in the [Tp′Rh(CNR)] system, as evidenced by the rearrangement of the deuterated compound Tp′Rh(CNR)(i-propyl)D to Tp′Rh(CNR)(CH2CHDCH3)H in benzene solvent (Fig. 1). If the reductive coupling to produce the C D bond were to occur with liberation of propane-d1, the resulting unsaturated intermediate would have been trapped by irreversible reaction with the benzene solvent. Observation of the rearranged product indicates a unimolecular pathway that is consistent with σ-alkane complexes as intermediates (22).
D bond were to occur with liberation of propane-d1, the resulting unsaturated intermediate would have been trapped by irreversible reaction with the benzene solvent. Observation of the rearranged product indicates a unimolecular pathway that is consistent with σ-alkane complexes as intermediates (22).
Fig. 1.
Mechanism for intramolecular H/D exchange.
By studying the kinetics of rearrangements of a series of alkyl deuteride complexes, and by kinetic modeling of the rearrangements, including a determination of isotope effects (27), the relative barrier heights for C H oxidative cleavage, migration from one C
H oxidative cleavage, migration from one C H bond to an adjacent C
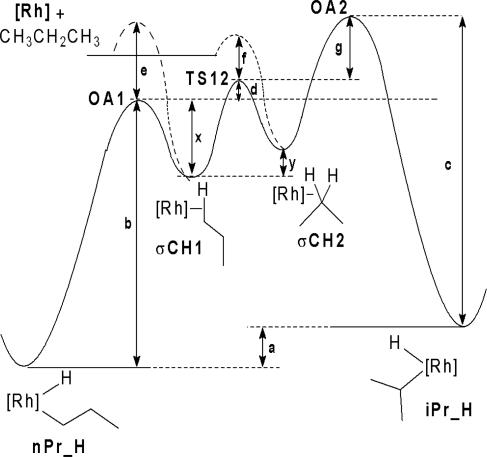
H bond to an adjacent C H bond, and dissociation of the alkane from the metal were determined (22). Although this study did not provide an indication of the energies of either the methyl or methylene σ-alkane complexes, it did provide energy differences between the various processes available to the σ-alkane complexes. The reaction coordinate for propane activation, with the experimentally determined values, is shown in Fig. 2. Because the energies of the σ-alkane complexes were undetermined, they were assumed to be equal in the experimental situation (this assumption has no effect on the selectivities). Also note that the reaction sequence nPrH → σCH1 → σCH2 → σCH1 → nPrH allows the metal to migrate from one end of the alkyl chain to the other.
H bond, and dissociation of the alkane from the metal were determined (22). Although this study did not provide an indication of the energies of either the methyl or methylene σ-alkane complexes, it did provide energy differences between the various processes available to the σ-alkane complexes. The reaction coordinate for propane activation, with the experimentally determined values, is shown in Fig. 2. Because the energies of the σ-alkane complexes were undetermined, they were assumed to be equal in the experimental situation (this assumption has no effect on the selectivities). Also note that the reaction sequence nPrH → σCH1 → σCH2 → σCH1 → nPrH allows the metal to migrate from one end of the alkyl chain to the other.
Fig. 2.
Free-energy diagram (kcal·mol−1) for the reaction of Tp′Rh(CNR) with propane at 298 K. From experiment, b = 21.6, e = 1.1, d = 0.4, f = 0.4, y is assumed to be 0, and c = 21.5. Values a, g, and x are undetermined, but g is too high to observe iPr_H.
In the work described here, density functional theory computational studies of the coordination of propane by its methyl and methylene groups to a model of the trispyrazolylborate–rhodium complex, and the reactions that can occur from these intermediates, were carried out. The energy profiles compared favorably with the experimental data. As will be shown, the theoretical treatment not only provides valuable insight into the selectivities indicated in Fig. 2, but also gives information about the stabilities of the σ-alkane complexes that experiment cannot provide. The calculations will also demonstrate the importance of the steric factors in the structural and dynamic properties of this propane complex.
Results and Discussion
Structures of Complexes, Intermediates, and Transition States (TSs).
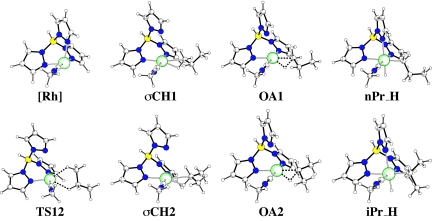
The geometries of all optimized structures and TSs are shown in Fig. 3. The TpRhI(CNMe) fragment, termed [Rh] in the following, is a d8 ML4 fragment. A planar coordination at the metal is expected when the metal fragment has no constraint, but Tp can only coordinate to the metal with the three N in a fac geometry. As a consequence, the d8 RhI fragment adopts a structure derived from a “trigonal bipyramid,” with one pyrazole and the isocyanide in the axial positions and one equatorial ligand missing. The axial–equatorial angles are 84° (to the axial pyrazole) and 97° (to the axial isocyanide); the angle between the two axial ligands is 177°. The pyrazole–pyrazole equatorial–equatorial angle is 107°. The equatorial bond lengths (Rh–N) are slightly longer (2.15 Å) than the axial Rh N bond length (2.08 Å).
N bond length (2.08 Å).
Fig. 3.
B3PW91-optimized geometries for the various extrema located along the reaction pathway shown in Fig. 2.
The propane coordinates to [Rh] through its methyl or methylene group, leading to two complexes with similar geometrical features. We first discuss the complex to the methyl group, σCH1. The σCH1 complex adopts a square planar structure, expected for a d8 RhI species, as a result of the almost total decoordination of one pyrazole ring. The propane C H bond to be activated is located trans to a normally bonded pyrazole ring and has the alkane chain and the weakly coordinated pyrazole (3.072 Å) on the same side of the square plane (Fig. 3). The propyl chain adopts a staggered conformation placing the distal methyl group in a space away from the pyrazole or isocyanide groups. The N–Rh–N angle of the two coordinated pyrazole ligands is 87°, which is significantly smaller than in free TpRh(CNMe). The alkane is η2-bonded to a single C
H bond to be activated is located trans to a normally bonded pyrazole ring and has the alkane chain and the weakly coordinated pyrazole (3.072 Å) on the same side of the square plane (Fig. 3). The propyl chain adopts a staggered conformation placing the distal methyl group in a space away from the pyrazole or isocyanide groups. The N–Rh–N angle of the two coordinated pyrazole ligands is 87°, which is significantly smaller than in free TpRh(CNMe). The alkane is η2-bonded to a single C H bond in the usual manner, i.e., H is closer to Rh than C is (1.843 Å vs. 2.427 Å), which leads to a Rh–H–C angle of 106°. This geometry forces another H to be close to the metal (2.26 Å), the third H being further away. The alkane chain and the weakly coordinated pyrazole are far from each other, and there is probably little or no interaction between these two fragments. In addition, the methyl group, which is present in the experimental Tp′ ligand, would not interfere with the alkane.
H bond in the usual manner, i.e., H is closer to Rh than C is (1.843 Å vs. 2.427 Å), which leads to a Rh–H–C angle of 106°. This geometry forces another H to be close to the metal (2.26 Å), the third H being further away. The alkane chain and the weakly coordinated pyrazole are far from each other, and there is probably little or no interaction between these two fragments. In addition, the methyl group, which is present in the experimental Tp′ ligand, would not interfere with the alkane.
The coordination through the methylene gives σCH2, which also has a d8 square planar rhodium with one weakly coordinated pyrazole ring (3.03 Å). The coordination features of the two coordinated pyrazoles are similar to those calculated in σCH1. The propane is coordinated in an η2-fashion through a single C H bond (Rh–H = 1.862 Å; Rh–H–C = 110°), and, as in σCH1, this coordination forces the other H to be relatively close to the metal (2.33 Å). This proximity sets the latter H at a distance of 2.8 Å from the N of the weakly coordinated pyrazole, which may induce an additional weak stabilizing interaction of the type CH···N (28, 29). As a consequence of the coordination mode of the methylene group, the two methyl groups of the propane lie in the square plane of the complex. Overall, the propane is slightly farther away from Rh when coordinated through the methylene group (dRh
H bond (Rh–H = 1.862 Å; Rh–H–C = 110°), and, as in σCH1, this coordination forces the other H to be relatively close to the metal (2.33 Å). This proximity sets the latter H at a distance of 2.8 Å from the N of the weakly coordinated pyrazole, which may induce an additional weak stabilizing interaction of the type CH···N (28, 29). As a consequence of the coordination mode of the methylene group, the two methyl groups of the propane lie in the square plane of the complex. Overall, the propane is slightly farther away from Rh when coordinated through the methylene group (dRh C = 2.508 Å) than when coordinated through the methyl group (dRh
C = 2.508 Å) than when coordinated through the methyl group (dRh C = 2.427 Å), which results in part from larger steric interaction. These geometrical features of these propane complexes are in agreement with those calculated for TpRh(CO)(CH4) (26).
C = 2.427 Å), which results in part from larger steric interaction. These geometrical features of these propane complexes are in agreement with those calculated for TpRh(CO)(CH4) (26).
The TS for the methylene–methyl [1,2] shift (or [2,1] shift), TS12, also has a d8 square planar rhodium with one weakly coordinated pyrazole ring (3.04 Å). The two H involved in the exchange are at similar distances from Rh, with the methyl hydrogen being slightly closer (2.285 Å) than the methylene hydrogen (2.320 Å). In addition, a methyl H is 2.88 Å from the weakly bonded pyrazole, inducing some possible weak stabilizing interaction. The C C bond associated with the exchange is perpendicular to the square plane. The alkane has a staggered conformation, and consequently the two C
C bond associated with the exchange is perpendicular to the square plane. The alkane has a staggered conformation, and consequently the two C H bonds involved in the exchange are not coplanar.
H bonds involved in the exchange are not coplanar.
The geometry of the TS for oxidative addition to the methyl C H bond, OA1, is intermediate between square planar RhI d8 and octahedral RhIII d6, with the two additional ligands coming from the weakly interacting pyrazole (now 2.566 Å from Rh) and the propane hydrogen (1.576 Å from Rh) approaching from opposite sides of the square plane. The carbon is 2.196 Å from Rh and 1.426 Å from H. The alkyl chain is staggered and extends away from the metal fragment.
H bond, OA1, is intermediate between square planar RhI d8 and octahedral RhIII d6, with the two additional ligands coming from the weakly interacting pyrazole (now 2.566 Å from Rh) and the propane hydrogen (1.576 Å from Rh) approaching from opposite sides of the square plane. The carbon is 2.196 Å from Rh and 1.426 Å from H. The alkyl chain is staggered and extends away from the metal fragment.
The TS for oxidative addition to the methylene C H bond, OA2, is very similar to OA1. The Rh–H distance is slightly shorter than in OA1 (1.569 Å), but the carbon is slightly further away (2.225 Å). The distance between C and H is 1.488 Å, which is greater than in OA1. The difference between OA1 and OA2 is associated with the remainder of the alkyl chain. In OA1, the alkyl chain can extend away from the metal fragment, whereas in OA2 the chain is forced to be in closer proximity. As a result, the carbon is further away from Rh in OA2 than in OA1.
H bond, OA2, is very similar to OA1. The Rh–H distance is slightly shorter than in OA1 (1.569 Å), but the carbon is slightly further away (2.225 Å). The distance between C and H is 1.488 Å, which is greater than in OA1. The difference between OA1 and OA2 is associated with the remainder of the alkyl chain. In OA1, the alkyl chain can extend away from the metal fragment, whereas in OA2 the chain is forced to be in closer proximity. As a result, the carbon is further away from Rh in OA2 than in OA1.
The n-propyl–hydride (nPr_H) and the isopropyl–hydride (iPr_H) complexes have the expected octahedral geometry with no remarkable features. In particular, the three pyrazole rings are coordinated to Rh in both systems. The two complexes differ essentially in the length of the Rh C bonds (2.073 and 2.105 Å, respectively), which is 0.03 Å longer in iPr_H.
C bonds (2.073 and 2.105 Å, respectively), which is 0.03 Å longer in iPr_H.
Coordination of the Alkane.
No TS (i.e., barrier) for the coordination could be located, despite numerous attempts. This finding does not agree with the experimental evidence. The latter suggests the presence of a TS for coordination because the fragment [Rh] does show kinetic selectivity favoring (1.5×) coordination to a methylene over a methyl group (30). It is well recognized within the computational community that the coordination between two molecules may occur without an activation barrier if the stabilization associated with the formation of the complex significantly overcomes the energy needed to set the two fragments in the proper geometry to interact.
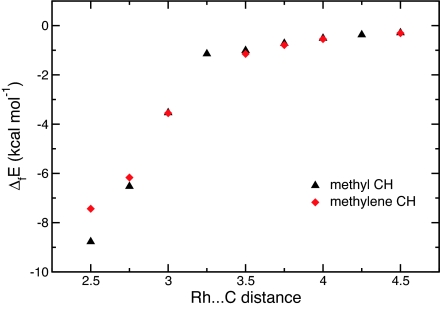
The coordination of the alkane at either the methyl or the methylene occurs with significant, but not total, decoordination of one pyrazole. The interaction of this third pyrazole is very weak in [Rh], which renders its decoordination and replacement by a σ-CH bond an exothermic process (vide infra). Therefore, we analyzed the manner in which the alkane approaches [Rh] and when the decoordination of the pyrazole occurs. The approach of the propane via either the methyl or the methylene was examined by using the associated Rh···C distance as a reaction coordinate and optimizing all other coordinates. The Rh···C distance was varied between 4.5 and 2.5 Å, which is close to the optimal distances in either σCH1 (2.427 Å) or σCH2 (2.505 Å). At 4.5 Å, the structure of the rhodium fragment is essentially that of free [Rh], and the energy is close to the sum of the energies of the isolated species. Selected points along the calculated reaction paths for alkane approach are shown in Fig. 4.
Fig. 4.
Evolution of the energy (kcal·mol−1) of the supersystem [Rh] + C3H8 along the pathway for coordination at the methyl and at the methylene carbons..
We first consider the coordination to the methyl group. The propane approaches [Rh] in the plane containing the axial pyrazole and the isocyanide, with the C H bond pointing toward Rh (the Rh–H–C angle is 180°). This approach is well documented for the approach of an alkane to a planar d8 complex (31). At this stage, the three pyrazole ligands are bonded to Rh. The C
H bond pointing toward Rh (the Rh–H–C angle is 180°). This approach is well documented for the approach of an alkane to a planar d8 complex (31). At this stage, the three pyrazole ligands are bonded to Rh. The C H bond begins to change its orientation when the Rh···C distance = 3.25 Å: the Rh–H–C angle is 167°, and the distances Rh–N (equatorial pyrazole), which are equivalent in free [Rh], already differ by 0.1 Å. When the Rh···C distance = 3 Å, the decoordination of the pyrazole is found to be almost as in σCH1. At this Rh···C distance, the H
H bond begins to change its orientation when the Rh···C distance = 3.25 Å: the Rh–H–C angle is 167°, and the distances Rh–N (equatorial pyrazole), which are equivalent in free [Rh], already differ by 0.1 Å. When the Rh···C distance = 3 Å, the decoordination of the pyrazole is found to be almost as in σCH1. At this Rh···C distance, the H C bond no longer points toward Rh and begins to acquire the geometry characteristic of the η2-bonded C
C bond no longer points toward Rh and begins to acquire the geometry characteristic of the η2-bonded C H, because the Rh–H–C angle = 136°. For Rh···C distances shorter than 3.0 Å, the main structural change is a further reduction of the Rh–H–C angle to 109° while the weakly bonded pyrazole moves marginally farther away from the metal (longer Rh–N distance = 3 Å). It is thus clear that decoordination of the pyrazole is needed for proper coordination of the alkane. The reorientation of the C
H, because the Rh–H–C angle = 136°. For Rh···C distances shorter than 3.0 Å, the main structural change is a further reduction of the Rh–H–C angle to 109° while the weakly bonded pyrazole moves marginally farther away from the metal (longer Rh–N distance = 3 Å). It is thus clear that decoordination of the pyrazole is needed for proper coordination of the alkane. The reorientation of the C H bond with respect to the metal–H direction is a well established phenomenon that has been shown by the calculations of Saillard and Hoffmann (31). Similar results are found for the approach to the methylene group of propane, although one sees that the isopropyl group rotates from being perpendicular to the developing square plane to being parallel to the plane as the Rh
H bond with respect to the metal–H direction is a well established phenomenon that has been shown by the calculations of Saillard and Hoffmann (31). Similar results are found for the approach to the methylene group of propane, although one sees that the isopropyl group rotates from being perpendicular to the developing square plane to being parallel to the plane as the Rh C bond forms. Significantly, the decoordination of the pyrazole occurs for the same range of Rh···C distances (3.5–3 Å).
C bond forms. Significantly, the decoordination of the pyrazole occurs for the same range of Rh···C distances (3.5–3 Å).
The total energy of the supersystem (propane and [Rh]) lowers as the distance Rh···C decreases (Table 2 and Fig. 4). At long Rh···C distances (≥3.25 Å), the stabilization energy is <1 kcal·mol−1 and is probably controlled by dipole–dipole interaction. It is remarkable that partial decoordination of the pyrazole is compensated by the coordination of the alkane, inasmuch as the energy of the supersystem is lowered by 2 kcal·mol−1. Further lowering of the energy by −9 kcal·mol−1 is reached at the σCH1 complex. Decomposing the binding energy, ΔfE, in terms of distortion energies, ΔdistE, of the metal and the alkane and interaction energy, ΔintE, between the two fragments, as in Eq. 1 (see Materials and Methods for details),
shows that the distortion of the propane is negligible during the approach and even small at σCH1 (Table 2). Likewise, the partial decoordination of one pyrazole ligand results in a distortion energy of the order of 3 kcal·mol−1. The small distortion energy is consistent with the ability of the Tp ligand to very easily change hapticity from κ3 to κ2, and even from κ3 to κ1 (32, 33). This ability to vary the Rh–N distance at low energy cost gives a flexibility to the metal fragment, which is key for its ability to coordinate weak Lewis bases such as alkanes. Finally, the change in the interaction energy shows how the reorientation of the alkane complex from a situation in which only H interacts with Rh to the sideways η2-coordination (even though the carbon remains further away from Rh than from H) stabilizes the alkane complex. It is rather surprising that the loss of a pyrazole ligand is more than compensated by the coordination of an alkane, because the bond-dissociation energy of an N-based ligand is expected to be higher than that of an alkane, which is an especially poor ligand. However, RhI has a strong propensity to be square planar, which clearly favors the κ3–κ2 isomerism (34–37). Analogous results have been obtained with a B H bond of the borate displacing a pyrazole of a bispyrazolyl borate (38). Time-resolved IR experiments on the intermediates involved in the reaction of Tp′Rh(CO)2 with alkanes are consistent with similar conclusions (23).
H bond of the borate displacing a pyrazole of a bispyrazolyl borate (38). Time-resolved IR experiments on the intermediates involved in the reaction of Tp′Rh(CO)2 with alkanes are consistent with similar conclusions (23).
Table 2.
Decomposition of the binding energy, ΔfE, between propane and [Rh] in terms of the distortion energy of [Rh], [ΔdistE(Rh)], the distortion energy of propane, [ΔdistE(Alk)], and interaction energy, (ΔintE), as a function of the Rh···C distance
| Rh···C distance, Å | Energy (kcal·mol−1) |
|||||||
|---|---|---|---|---|---|---|---|---|
| Primary carbon |
Secondary carbon |
|||||||
| ΔfE | ΔintE | ΔdistE(Rh) | ΔdistE(Alk) | ΔfE | ΔintE | ΔdistE(Rh) | ΔdistE(Alk) | |
| 2.50 | −8.8 | −13.8 | 3.2 | 1.8 | −7.4 | −12.6 | 3.2 | 2.0 |
| 2.75 | −6.5 | −10.5 | 2.9 | 1.0 | −6.2 | −10.4 | 3.0 | 1.1 |
| 3.00 | −3.5 | −6.9 | 2.8 | 0.6 | −3.6 | −7.1 | 2.9 | 0.7 |
| 3.25 | −1.1 | −2.0 | 0.7 | 0.2 | —* | —* | —* | —* |
| 3.50 | −1.0 | −1.4 | 0.3 | 0.1 | −1.1 | −1.6 | 0.4 | 0.1 |
| 3.75 | −0.7 | −1.0 | 0.3 | 0.0 | −0.8 | −1.1 | 0.3 | 0.0 |
| 4.00 | −0.5 | −0.8 | 0.2 | 0.0 | −0.5 | −0.8 | 0.2 | 0.0 |
| 4.25 | −0.4 | −0.6 | 0.2 | 0.0 | —† | —† | —† | —† |
| 4.5 | −0.3 | −0.5 | 0.2 | 0.0 | −0.3 | −0.6 | 0.2 | 0.0 |
Values are given for coordination to the methyl (primary) and methylene (secondary) groups.
*This point did not converge.
†This point was not calculated.
Comparing the same data for methyl and methylene coordination shows that the distortion energies of the two fragments are similar for both coordination approaches (Table 2), the less favorable coordination at the methylene C H bond being observed mainly in the smaller interaction energy. This finding additionally supports the importance of steric factors that prefer the coordination at primary over secondary carbon.
H bond being observed mainly in the smaller interaction energy. This finding additionally supports the importance of steric factors that prefer the coordination at primary over secondary carbon.
Energy Profiles for Reactions Involving the σ Propane Complexes.
The energy profile associated with the [1,2] shift and the oxidation addition at the primary and secondary carbon is given in Table 3 in terms of different types of energies (electronic energy, E, electronic energy corrected with zero-point energy, E + ZPE, and Gibbs free energy value, G). Whichever type of energy is considered, the trends are similar and in very good agreement with the experimental results, except for the dissociation process (vide infra), and we will only discuss E values here. The most stable situation corresponds to nPr_H, which is used as the energy reference. The isopropyl complex, iPr_H, is 4 kcal·mol−1 higher. The two σ complexes are <20 kcal·mol−1 higher, with σCH1 being preferred by 1.6 kcal·mol−1. The TSs for the oxidative addition to the methyl C H bond and the [1, 2] shift are very similar in energy, with the former being slightly more favorable. The TS for oxidative addition to the methylene C
H bond and the [1, 2] shift are very similar in energy, with the former being slightly more favorable. The TS for oxidative addition to the methylene C H bond is >4 kcal·mol−1 higher than that for the methyl C
H bond is >4 kcal·mol−1 higher than that for the methyl C H bond.
H bond.
Table 3.
Energy (E), energy with zero-point energy correction (E + ZPE), and Gibbs free energy (G), at 298 K, of extrema shown in Fig. 2, given relative to nPr_H
| Extreme | Energy, kcal·mol−1 |
|||
|---|---|---|---|---|
| Exp | ΔE | Δ(E + ZPE) | ΔG | |
| nPr_H | 0.0 | 0.0 | 0.0 | 0.0 |
| OA1 | 21.6 | 23.9 | 22.2 | 20.7 |
| σCH1 | n/a | 17.5 | 17.8 | 15.2 |
| TS12 | 22.0 | 25.9 | 25.6 | 23.0 |
| σCH2 | n/a | 19.1 | 19.3 | 16.7 |
| OA2 | n/a | 28.0 | 26.1 | 25.2 |
| iPr_H | n/a | 4.1 | 3.9 | 4.4 |
| [Rh] + C3H8 | 22.5 | 26.5 | 25.9 | 12.8 |
The available experimental values are given for comparison (7).
These results are in good agreement with a number of the experimental data obtained from the analysis of the kinetics of rearrangements of deuterium-labeled complexes nPr_D and iPr_D (Table 3). The reductive elimination of propane from either the n-propyl or the isopropyl hydride has an energetically accessible TS. It is most likely that this situation applies for all hydrocarbyls and thus accounts well for the facility of exchange of R H molecules, which is at the heart of the measurements. Coordination to the methyl C
H molecules, which is at the heart of the measurements. Coordination to the methyl C H bond is preferred, and although coordination to the methylene C
H bond is preferred, and although coordination to the methylene C H bond is less favored, the difference in energy between these two coordination sites is sufficiently small to account for the fact that coordination to the methylene carbon is an accessible process. When coordination at the methyl carbon occurs, the most likely process is the oxidative addition to give the propyl hydride. However the [1,2] shift has a similar energy barrier, but, the passage from methyl coordination to methylene coordination being endothermic, this equilibrium is strongly shifted toward coordination at the methyl group (14:1). The critical point is that coordination at the secondary carbon leads preferentially to the [2,1] shift and not to the oxidative addition at the methylene C
H bond is less favored, the difference in energy between these two coordination sites is sufficiently small to account for the fact that coordination to the methylene carbon is an accessible process. When coordination at the methyl carbon occurs, the most likely process is the oxidative addition to give the propyl hydride. However the [1,2] shift has a similar energy barrier, but, the passage from methyl coordination to methylene coordination being endothermic, this equilibrium is strongly shifted toward coordination at the methyl group (14:1). The critical point is that coordination at the secondary carbon leads preferentially to the [2,1] shift and not to the oxidative addition at the methylene C H bond to yield the isopropyl–hydride complex. One reason for this is that the oxidative addition to the methylene brings the central carbon into closer proximity to Rh, whereas the [2,1] shift moves this carbon away from the metal. The preference for the walking down the chain over the oxidative addition at the methylene carbon is fully supported by the experiments, which shows the absence of formation of isopropyl–hydride complex. These results also support the hypothesis that the metal fragment can migrate from one end of the alkane chain to the other.
H bond to yield the isopropyl–hydride complex. One reason for this is that the oxidative addition to the methylene brings the central carbon into closer proximity to Rh, whereas the [2,1] shift moves this carbon away from the metal. The preference for the walking down the chain over the oxidative addition at the methylene carbon is fully supported by the experiments, which shows the absence of formation of isopropyl–hydride complex. These results also support the hypothesis that the metal fragment can migrate from one end of the alkane chain to the other.
The experimental results demonstrate that the [2,1] shift occurs within the coordination sphere of the metal without full decoordination of the alkane. This aspect is more difficult to probe by the calculations. Although all intermolecular processes (oxidative addition and the C H exchange process within the coordination sphere) can be correctly analyzed by just considering the electronic energies (see Table 3), the comparison between inter- and intramolecular processes requires the explicit consideration of the change in entropy associated with the change in molecularity. The methodology currently used for calculation of the entropy contribution is not sufficiently accurate for carrying out a valid comparison between these processes, as illustrated by the value in Table 3 for ΔG of propane dissociation. The calculation of this process by using the harmonic approximation in the frequencies and neglecting the solvent is notably inappropriate. For instance, it has been shown that the entropy variation (still calculated as in a gas phase) may be exaggerated with the harmonic approximation (39). Furthermore, test calculations have shown that the solvent also greatly influences the variation in entropy (40–44).
H exchange process within the coordination sphere) can be correctly analyzed by just considering the electronic energies (see Table 3), the comparison between inter- and intramolecular processes requires the explicit consideration of the change in entropy associated with the change in molecularity. The methodology currently used for calculation of the entropy contribution is not sufficiently accurate for carrying out a valid comparison between these processes, as illustrated by the value in Table 3 for ΔG of propane dissociation. The calculation of this process by using the harmonic approximation in the frequencies and neglecting the solvent is notably inappropriate. For instance, it has been shown that the entropy variation (still calculated as in a gas phase) may be exaggerated with the harmonic approximation (39). Furthermore, test calculations have shown that the solvent also greatly influences the variation in entropy (40–44).
Materials and Methods
The experimental metal fragment Tp′Rh(CNCH2CMe3) [Tp′ = HB(3,5-dimethylpyrazolyl)3] was modeled by TpRh(CNCH3), where Tp is HB(pyrazolyl)3. This modeling was successful in reproducing quantitatively the relative bond-dissociative Rh C energy in Tp′Rh(CNCH2CMe3)(H)(R) (45). The calculations were performed with the Gaussian 03 package (46) at the B3PW91 level (47, 48). The Rh atom was represented by the pseudopotential of Dolg and coworkers (49), with the associated basis set augmented by an f polarization function (α = 1.35). The other atoms, C, N, H, and B, were represented with a 6–31G(d,p) basis set (50). The geometry optimizations were carried out without any symmetry constraint, and the nature of the extrema located were checked with analytical computation of the Hessian matrix. The connection between minima and TS was checked by geometry optimization from slightly altered TS geometries in both directions along the TS vector. The study of the coordination of methyl and the methylene carbon atom of propane to TpRh(CNMe) was performed through a succession of geometry optimizations under the constraint of fixed Rh···C bond distance. The formation energy, ΔfE, was calculated as the difference between the energy of the complexes and the sum of the energies of the two separated fragments in their optimized geometry. The energy of each fragment, TpRh(CNMe) and propane, in the geometry they have in the complex (for a given Rh···C distance) was used to estimate the deformation energies of the fragments, ΔdistE(Rh) and ΔdistE(Alk), and the interaction energy ΔintE.
C energy in Tp′Rh(CNCH2CMe3)(H)(R) (45). The calculations were performed with the Gaussian 03 package (46) at the B3PW91 level (47, 48). The Rh atom was represented by the pseudopotential of Dolg and coworkers (49), with the associated basis set augmented by an f polarization function (α = 1.35). The other atoms, C, N, H, and B, were represented with a 6–31G(d,p) basis set (50). The geometry optimizations were carried out without any symmetry constraint, and the nature of the extrema located were checked with analytical computation of the Hessian matrix. The connection between minima and TS was checked by geometry optimization from slightly altered TS geometries in both directions along the TS vector. The study of the coordination of methyl and the methylene carbon atom of propane to TpRh(CNMe) was performed through a succession of geometry optimizations under the constraint of fixed Rh···C bond distance. The formation energy, ΔfE, was calculated as the difference between the energy of the complexes and the sum of the energies of the two separated fragments in their optimized geometry. The energy of each fragment, TpRh(CNMe) and propane, in the geometry they have in the complex (for a given Rh···C distance) was used to estimate the deformation energies of the fragments, ΔdistE(Rh) and ΔdistE(Alk), and the interaction energy ΔintE.
Concluding Remarks
Density functional theory studies of the structure and dynamic behavior of propane coordinated to TpRh(CNMe) have shown that the coordination of the alkane is favorable because of the structural flexibility of the Tp ligand. Partial decoordination of one of the pyrazole ligands occurs without significant cost in energy, and this decoordination of the pyrazole is needed to allow the coordination of the alkane in an η2-manner with Rh closer to H than to C. Although only a single C H bond is really coordinated to Rh (η2), a geminal H is close enough to the metal to potentially induce additional stabilization with the metal. Coordination to methyl carbon is preferred over methylene, mostly for steric reasons. Steric factors also make the propyl–hydride complex more stable than the isopropyl–hydride complex, all the more so because the carbon is closer to the metal in the alkyl complexes than in the σ-alkane complexes. The TS for oxidative addition is also lower for the methyl C
H bond is really coordinated to Rh (η2), a geminal H is close enough to the metal to potentially induce additional stabilization with the metal. Coordination to methyl carbon is preferred over methylene, mostly for steric reasons. Steric factors also make the propyl–hydride complex more stable than the isopropyl–hydride complex, all the more so because the carbon is closer to the metal in the alkyl complexes than in the σ-alkane complexes. The TS for oxidative addition is also lower for the methyl C H bond. Activation at the methylene C
H bond. Activation at the methylene C H bond is not favored because the preferred reaction at the methylene C
H bond is not favored because the preferred reaction at the methylene C H bond is a [2,1] shift, which exchanges coordination from methylene to methyl C
H bond is a [2,1] shift, which exchanges coordination from methylene to methyl C H bonds. Thus, only the n-propyl hydride product is observed. Because the entropy changes of an intermolecular reaction cannot be calculated accurately, an exchange of σ complexes via an intramolecular route ([2,1] shift) vs. an intermolecular route (decoordination/coordination) could not be studied at a sufficient level of accuracy.
H bonds. Thus, only the n-propyl hydride product is observed. Because the entropy changes of an intermolecular reaction cannot be calculated accurately, an exchange of σ complexes via an intramolecular route ([2,1] shift) vs. an intermolecular route (decoordination/coordination) could not be studied at a sufficient level of accuracy.
The results obtained for the propane can apply, in part, to other alkanes. For instance, the preferable coordination to the terminal carbon of an alkane chain is clearly always going to be favored over coordination to internal carbons. It is also evident that oxidative addition to the methyl C H bond should be preferred over oxidative addition to a C
H bond should be preferred over oxidative addition to a C H bond of the internal part of the alkane. Walking of the alkane through successive [1,2] and [2,2] shifts can contribute to the transformation of a methylene-coordinated alkane to a methyl-coordinated alkane. This transformation could even occur at lower energy than the oxidative addition to a secondary (and a fortiori tertiary) carbon. However, it is probably unwise to transfer the values calculated in this work to other alkanes because the small energy differences between the reactions that are at the origin of the selectivity of the various processes are controlled by subtle steric facts. Examination of the coordination and reactivity of butane may provide a wider understanding of this chemistry.
H bond of the internal part of the alkane. Walking of the alkane through successive [1,2] and [2,2] shifts can contribute to the transformation of a methylene-coordinated alkane to a methyl-coordinated alkane. This transformation could even occur at lower energy than the oxidative addition to a secondary (and a fortiori tertiary) carbon. However, it is probably unwise to transfer the values calculated in this work to other alkanes because the small energy differences between the reactions that are at the origin of the selectivity of the various processes are controlled by subtle steric facts. Examination of the coordination and reactivity of butane may provide a wider understanding of this chemistry.
Acknowledgments
O.E. and E.C. thank the Centre National de la Recherche Scientifique and the French Ministère de l'Education Nationale, de l'Enseignement Supérieur et de la Recherche for financial support. This work was supported by U.S. Department of Energy Office of Basic Energy Sciences Grant FG02–86ER13569 (to W.D.J.).
Abbreviation
- TS
transition state.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. J.A.L. is a guest editor invited by the Editorial Board.
The statistical preference for a pentane methyl vs. a cyclohexane methylene C H bond is taken as 1:3 because there are two methyl groups vs. six methylene groups. We do not believe that a “per-hydrogen” basis is as useful, inasmuch as methyl groups will always have three hydrogens and methylenes will always have two hydrogens.
H bond is taken as 1:3 because there are two methyl groups vs. six methylene groups. We do not believe that a “per-hydrogen” basis is as useful, inasmuch as methyl groups will always have three hydrogens and methylenes will always have two hydrogens.
References
- 1.Zhang X, Kanzelberger M, Emge TJ, Goldman AS. J Am Chem Soc. 2004;126:13192–13193. doi: 10.1021/ja046476q. [DOI] [PubMed] [Google Scholar]
- 2.Liu F, Goldman AS. Chem Commun. 1999:655–656. [Google Scholar]
- 3.Jensen CM. Chem Commun. 1999:2443–2449. [Google Scholar]
- 4.Liu F, Pak EB, Singh B, Jensen CM, Goldman AS. J Am Chem Soc. 1999;121:4085–4087. [Google Scholar]
- 5.Chen H, Schlecht S, Semple TC, Hartwig JF. Science. 2000;287:1995–1997. doi: 10.1126/science.287.5460.1995. [DOI] [PubMed] [Google Scholar]
- 6.Ishiyama T, Nobuta Y, Hartwig JF, Miyaura N. Chem Commun. 2003:2924–2925. doi: 10.1039/b311103b. [DOI] [PubMed] [Google Scholar]
- 7.Cho J-Y, Iverson CN, Smith MR. J Am Chem Soc. 2000;122:12868–12869. [Google Scholar]
- 8.Cho J-Y, Tse MK, Holmes D, Maleczka RE, Smith MR. Science. 2002;295:305–308. doi: 10.1126/science.1067074. [DOI] [PubMed] [Google Scholar]
- 9.Maleczka RE, Shi F, Holmes D, Smith MR. J Am Chem Soc. 2003;125:7792–7793. doi: 10.1021/ja0349857. [DOI] [PubMed] [Google Scholar]
- 10.Goldman AS, Roy AH, Huang Z, Ahuja R, Schinski W, Brookhart M. Science. 2006;312:257–261. doi: 10.1126/science.1123787. [DOI] [PubMed] [Google Scholar]
- 11.Hall C, Perutz RN. Chem Rev. 1996;96:3125–3146. doi: 10.1021/cr9502615. [DOI] [PubMed] [Google Scholar]
- 12.Crabtree RH. Chem Rev. 1995;95:987–1007. [Google Scholar]
- 13.Crabtree RH. Angew Chem Int Ed Engl. 1993;32:789–805. [Google Scholar]
- 14.Labinger JA, Bercaw JE. Nature. 2002;417:507–514. doi: 10.1038/417507a. [DOI] [PubMed] [Google Scholar]
- 15.Wasserman EP, Moore CB, Bergman RG. Science. 1992;255:315–318. doi: 10.1126/science.255.5042.315. [DOI] [PubMed] [Google Scholar]
- 16.Bengali AA, Arndtsen BA, Burger PM, Schultz RH, Weiller BH, Kyle KR, Moore CB, Bergman RG. Pure Appl Chem. 1995;67:281–288. [Google Scholar]
- 17.Childs GI, Grills DC, Sun XZ, George MW. Pure Appl Chem. 2001;73:443–447. [Google Scholar]
- 18.Lawes DJ, Geftakis S, Ball GE. J Am Chem Soc. 2005;127:4134–4135. doi: 10.1021/ja044208m. [DOI] [PubMed] [Google Scholar]
- 19.Jones WD, Hessell ET. J Am Chem Soc. 1993;115:554–562. [Google Scholar]
- 20.Jones WD, Wick DD. Organometallics. 1999;18:495–505. [Google Scholar]
- 21.Lawes D, Geftakis S, Ball GE. J Am Chem Soc. 2005;127:4134–4135. doi: 10.1021/ja044208m. [DOI] [PubMed] [Google Scholar]
- 22.Northcutt TO, Wick DD, Vetter AJ, Jones WD. J Am Chem Soc. 2001;123:7257–7270. doi: 10.1021/ja003944x. [DOI] [PubMed] [Google Scholar]
- 23.Lian T, Bromberg SE, Yang H, Proulx G, Bergman RG, Harris CB. J Am Chem Soc. 1996;118:3769–3770. [Google Scholar]
- 24.Bromberg SE, Yang H, Asplund MC, Lian T, McNamara BK, Kotz KT, Yeston JS, Wilkens M, Frei H, Bergman RH, Harris CB. Science. 1997;278:260–263. [Google Scholar]
- 25.Asplund MC, Snee PT, Yeston JS, Wilkens MJ, Payne CK, Yang H, Kotz KT, Frei H, Bergman RG, Harris CB. J Am Chem Soc. 2002;124:10605–10612. doi: 10.1021/ja020418s. [DOI] [PubMed] [Google Scholar]
- 26.Zaric S, Hall MB. J Phys Chem A. 1998;102:1963–1964. [Google Scholar]
- 27.Jones WD. Acc Chem Res. 2003;36:140–146. doi: 10.1021/ar020148i. [DOI] [PubMed] [Google Scholar]
- 28.Calhorda MJ. Chem Commun. 2000:801–809. [Google Scholar]
- 29.Desiraju GR. Chem Commun. 2005:2995–3001. doi: 10.1039/b504372g. [DOI] [PubMed] [Google Scholar]
- 30.Vetter AJ, Flaschenriem C, Jones WD. J Am Chem Soc. 2005;127:12315–12322. doi: 10.1021/ja042152q. [DOI] [PubMed] [Google Scholar]
- 31.Saillard J-Y, Hoffmann R. J Am Chem Soc. 1984;106:2006–2026. [Google Scholar]
- 32.Slugovc C, Padilla-Martínez I, Sirol S, Carmona E. Coord Chem Rev. 2001;213:129–157. [Google Scholar]
- 33.Paneque M, Sirol S, Trujillo M, Carmona E, Gutiérrez-Puebla E, Angeles Monge M, Ruiz C, Malbosc F, Serra-le Berre C, Kalck P, et al. Chem Eur J. 2001;7:3869–3879. doi: 10.1002/1521-3765(20010917)7:18<3868::aid-chem3868>3.0.co;2-t. [DOI] [PubMed] [Google Scholar]
- 34.Akita M, Ohta K, Takahasi Y, Hikichi S, Moro-Oka Y. Organometallics. 1997;16:4121–4128. [Google Scholar]
- 35.Northcutt TO, Lachicotte RJ, Jones WD. Organometallics. 1998;17:5148–5152. [Google Scholar]
- 36.Bucher UE, Currao A, Nesper R, Rueegger H, Venanzi LM, Younger E. Inorg Chem. 1995;34:66–74. [Google Scholar]
- 37.Nicasio MC, Paneque M, Perez PJ, Pizzano A, Poveda ML, Rey L, Sirol S, Taboada S, Trujillo M, Monge A, et al. Inorg Chem. 2000;39:180–188. doi: 10.1021/ic990419u. [DOI] [PubMed] [Google Scholar]
- 38.Rodriguez V, Atheaux I, Donnadieu B, Sabo-Etienne S, Chaudret B. Organometallics. 2000;19:2916–2926. [Google Scholar]
- 39.Raynaud C, Daudey J-P, Jolibois F, Maron L. J Phys Chem A. 2006;110:101–105. doi: 10.1021/jp050771v. [DOI] [PubMed] [Google Scholar]
- 40.Cooper J, Ziegler T. Inorg Chem. 2002;41:6614–6622. doi: 10.1021/ic020294k. [DOI] [PubMed] [Google Scholar]
- 41.Sakaki S, Takayama T, Sumimoto M, Sugimoto M. J Am Chem Soc. 2004;126:3332–3348. doi: 10.1021/ja0304345. [DOI] [PubMed] [Google Scholar]
- 42.Rotzinger FP. Chem Rev. 2005;105:2003–2038. doi: 10.1021/cr030715v. [DOI] [PubMed] [Google Scholar]
- 43.Leung BO, Reidl DL, Armstrong DA, Rauk A. J Phys Chem A. 2004;108:2720–2725. [Google Scholar]
- 44.Ardura D, Lopez R, Sordo TL. J Phys Chem B. 2005;109:23618–23623. doi: 10.1021/jp0540499. [DOI] [PubMed] [Google Scholar]
- 45.Clot E, Mégret C, Eisenstein O, Perutz RN. J Am Chem Soc. 2006;128:8350–8357. doi: 10.1021/ja061803a. [DOI] [PubMed] [Google Scholar]
- 46.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Montgomery JA, Jr, Vreven T, Kudin KN, Burant JC, et al. Gaussian 03. Wallingford, CT: Gaussian, Inc.; 2004. Revision C.02. [Google Scholar]
- 47.Becke AD. J Chem Phys. 1993;98:5648–5652. [Google Scholar]
- 48.Perdew JP, Wang Y. Phys Rev B. 1992;45:13244–13249. doi: 10.1103/physrevb.45.13244. [DOI] [PubMed] [Google Scholar]
- 49.Andrae D, Häussermann U, Dolg M, Stoll H, Preuss H. Theor Chim Acta. 1990;77:123–141. [Google Scholar]
- 50.Hariharan PC, Pople JA. Theor Chim Acta. 1973;28:213–222. [Google Scholar]