Structures and spectral signatures of protonated water networks in bacteriorhodopsin

Abstract

Networks of internal water molecules are thought to provide proton transfer pathways in many enzymatic and photosynthetic reactions. Extremely broad absorption continua observed in recent IR spectroscopic measurements on the photodriven proton pump bacteriorhodopsin (BR) suggest such networks may also serve as proton storage and release sites for these reactions. By combining electronic structure calculations with molecular mechanical force fields, we examine the dynamics and the resulting IR spectra of two protonated water networks, H⁺·(H₂O)₃ and H⁺·(H₂O)₄, in the release pocket of the initial state of BR, which possibly serve as proton donors to the extracellular surface. For both network sizes, topologically similar structures are found, which are anchored at residues E194 and E204 and stabilized by additional hydrogen bonds from neighboring protein side chains. These protonated water networks assume neither the classic Zundel nor Eigen motives but prefer wire-like topologies. Upon gauging calculated IR spectra of finite clusters with experimental gas-phase data, it is possible to link spectral features computed for these chain-like structures in the initial state of the BR photocycle to the measured absorption continua, in particular for the larger H⁺·(H₂O)₄ network. Furthermore, the free energy of proton dislocation along these chains is found to be within the range that is easily accessible at room temperature because of fluctuations.

The light-driven proton pump bacteriorhodopsin (BR) converts light energy to chemical energy by a vectorial proton transport against a membrane potential (1). In addition to belonging to the best-studied proton-permeable ion channels (2) as such and being a natural host for studying proton conducting water wires (3), BR is an important representative of the G protein-coupled seven-α-helix receptor family (4). Thus, it comes as no surprise that this protein serves as a paradigmatic workhorse for both experiment and simulation. During its photocycle, protons are translocated to different positions within the transport channel, and a detailed dynamical picture is currently emerging for BR from the level of conformational changes to side-chain motion to individual atom displacements (5–9). In addition, biomolecular simulation strongly suggests the presence of locally mobile internal water molecules inside BR, which could easily serve as proton hosts and relays and thus establish a pathway from intracellular to extracellular space (10–12). A crucial step in this vectorial proton transfer is the actual release of a proton to the extracellular surface involving the so-called proton release group (XH). However, the very nature of XH is still a puzzling and disputed question.

Whereas other initial as well as transient proton positions in BR have been quite well characterized (9), the terminal release group has withdrawn itself from identification for a long time. Recent IR spectroscopic measurements (13–18) of wild-type BR and various mutants have provided strong evidence that the previously proposed glutamic acids E194 and E204 are not the proton donors in wild-type BR. Rather, these measurements relate the proton release to a bleaching of a broad continuum band that could be detected in an uncongested frequency window between ≈1,800 and 2,100 cm⁻¹ during the transition to the M intermediate. Such continua are well known from excess protons in aqueous systems (19) and are traditionally discussed in terms of the archetypal so-called Zundel and Eigen structures (20), i.e., the solvent-shared proton, [H₂O⋯H⋯OH₂]⁺ and the fully solvated hydronium, H₃O⁺·3(H₂O), respectively. Guided by these ideas, the continua have been interpreted as the spectral signature of the deprotonation of a water local area network (WLAN) (21) in the so-called release pocket close to the extracellular surface, which is known to be protonated in the initial state of the BR photocycle (bR). Initially, the bare Zundel cation, H₅O²⁺, has been considered as a minimal WLAN model (17, 22), whereas a more recent BR study (18) in conjunction with a gas-phase investigation of H⁺·(H₂O)_n clusters (23) suggests the situation is much more intricate, because larger WLANs, i.e., n > 2, might be involved.

Computer simulation (24–28), in principle, can link experimental spectroscopic data to underlying structures and even to the dynamics, if the spectra are time-resolved. Although normal-mode analysis of quasirigid molecules in the gas phase nowadays has become a standard tool, the computation of IR spectra in dynamically interacting environments, such as condensed phases or biomolecular matrices, is much more intricate, if based on electronic structure calculations (24, 29–34). Furthermore, a peculiar challenge is posed by the strongly anharmonic and flat potential energy surfaces as typically encountered by excess protons in hydrogen-bonded networks (20) such as WLANs, which challenges the harmonic approximation. The only practical solution is to compute the IR spectra by Fourier transforming the time autocorrelation function of the total dipole moment. Here, recent combinations (35, 36) of quantum mechanical (QM) density functional theory (applied in a small subsystem only) with molecular dynamics based on molecular mechanics (MM) force fields (for the large biomatrix) in the sense of hybrid (so-called QM/MM) methods suitable for Newtonian dynamics have proven to be the method of choice for theoretical IR spectroscopy in biophysics (32, 33). Still, it should be noted that this involves a significant computational effort, because rather long ab initio molecular dynamics trajectories of several tens of picoseconds are mandatory. Last but not least, the vibrational zero-point motion, which is neglected in the above approach, poses a more fundamental problem in view of the fact that a vibrational mode at 2,000 cm⁻¹ contributes a zero-point energy of ≈5 k_BT at ambient conditions, which “lifts” the protons above the underlying potential energy surface. Thus, in classical molecular dynamics where equipartition governs, a too-small region of configuration space is sampled and will, therefore, underestimate both local mobility and anharmonicity effects. However, it is possible to include very approximately the resulting effects by increasing the temperature, thus enhancing fluctuation effects, and applying suitable quantum corrections to spectra obtained from classical autocorrelations (37, 38). As a first step, Rousseau et al. (33, 39) computed IR spectra of protonated WLANs in the release pocket of the L state of BR embedded in a fully hydrated 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphatidylcholine (POPC) membrane. At this later stage in the photocycle, the release pocket is large enough to accommodate additional water molecules such that solvated Zundel and Eigen complexes, i.e., H₅O²⁺·4(H₂O) and H₃O⁺·3(H₂O), respectively, were investigated as sensible qualitative models in terms of an Ansatz. These hybrid Car–Parrinello molecular dynamics simulations have demonstrated that (i) the spectral features of protonated WLANs are mainly determined by the local protonation pattern and thus by their hydrogen-bonding topology, and (ii) the solvated Zundel and Eigen IR spectra are complementary in the regions below and above ≈2,000 cm^−1. However, Zundel-like topologies were found to desymmetrize spontaneously, such that the solvated Zundel complex had to be artificially stabilized by imposing external constraints on the four solvating water molecules to establish the proton-sharing Zundel symmetry (39).

In the present investigation, we will explore the structure and IR spectra of protonated WLANs in the ground state of BR being the initial bR state in the photocycle, which can be related most directly to the bleaching continuum band measured recently upon proton release (17, 18). For the proton solvation structure, the number of water molecules in the release pocket is crucial. X-ray crystallography clearly locates three water molecules in the release pocket carrying the labels W403, W404, and W405 in ref. 40. A fourth water may be present according to ref. 41, which will be denoted by W409*. These two most-probable possibilities are investigated separately, which yield H⁺·(H₂O)₃ and H⁺·(H₂O)₄ WLANs together with the excess proton. However, at variance with the well known Zundel and Eigen structures considered earlier (33, 39), the generated hydrogen-bonding topologies turn out to be much less symmetric, as observed for some H⁺·(H₂O)_n clusters in the gas phase (23), and lead to quasilinear protonated water wires in both cases.

Results and Discussion

Structures and Free Energy Surfaces.

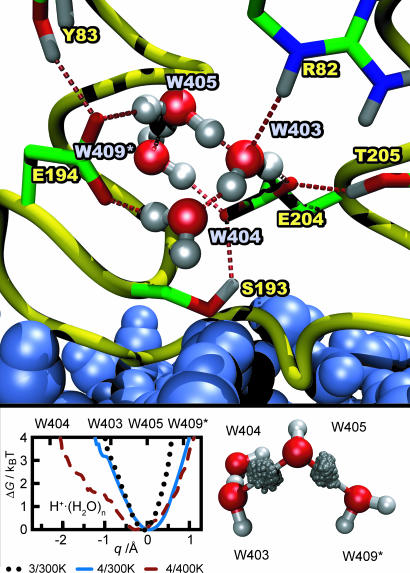
To set the stage, Fig. 1 depicts the location, hydrogen bonding to residues, and average structure of the H⁺·(H₂O)₄ WLAN in the release pocket. Interestingly, the four water molecules are found to form a protonated water wire, i.e., a hydrogen-bonded chain with the excess proton mainly residing on W405 but temporarily fluctuating to W403 and W409*. Different initial protonation patterns of the WLAN have been used, but the structure shown has been found to be independent of the particular water molecule on which the proton has been placed at startup. Water W409* is predominantly bound to W405, and the corresponding hydrogen bond breaks only a few times throughout all simulations performed.

Fig. 1.

Structural elements and proton distribution in the release pocket. (Upper) Average structure of the H⁺·(H₂O)₄ WLAN in the release pocket. Dashed lines symbolize hydrogen bonds to nearby sidegroups. Extracellular bulk water drawn in blue, which is separated by S193 from the release pocket. (Lower Left) Quantitative free-energy surface with respect to the relative location q (see Methods for definition) of the protonic defect in H⁺· (H₂O)_n, n = 3, 4, T = 300 and 400 K, marked as n/T in the legend. The q values that mark the different water positions have been determined from the average cluster structure. (Lower Right) Proton density distributions between the oxygens of H⁺· (H₂O)₄ in its average structure at 400 K. The WLAN has been rotated with respect to Upper to optimize visualization.

The hydrogen bonds of W403, W404, and W405 to the glutamic acids E194 and E204 are persistent in all simulations and are instrumental in stabilizing the structure of the release pocket. W404 occasionally hydrogen bonds to the NH group of Y79 and the CO group of P77 (not shown), whereas the free OH bond of W409* does not find any stable hydrogen-bonding partners in its vicinity. Here, the release pocket might accommodate one or more additional water molecules, although no intrusion of bulk water has been observed even throughout the long molecular mechanics simulations to prepare the systems. The hydroxyl groups of Y83, S193, and T205 stabilize furthermore the orientation of the glutamic acids. In particular, Y83 forms a stable hydrogen bond to E194, whereas the hydrogen bonds of S193 and T205 to E204 fluctuate throughout the simulation.

Turning our attention to the alternative number of water molecules in the pocket and thus to H⁺·(H₂O)₃, a quite similar internal structure for the release pocket, in particular the same wire-like topology, is found (not shown). In this case, the protonic defect also resides mainly on W405 but occasionally fluctuates to W403 as well. Because W409* is missing, W405 forms a hydrogen bond to the carboxyl group of E204, which is slightly tilted compared with the preferred situation for the H⁺·(H₂O)₄ WLAN.

It is reassuring to find that, with both numbers of water molecules in the release pocket, the excess proton is found mainly on W405 while fluctuating to the available nearby neighbors. Next, the free energy surface ΔG(q) along the collective variable q, which describes the relative position of the excess proton within the two water wires for n = 3 and 4 (see Methods for definition) is investigated in the Fig. 1 Lower Left. W404 features a fairly large oxygen–oxygen distance to W403 and is never reached by the excess proton. In stark contrast, for both the H⁺·(H₂O)₃ and H⁺·(H₂O)₄ WLAN at 300 K, the free energy barrier for the transition from W405 to W403 is very similar and, most importantly, in the range of only 2–3 k_BT and thus quite small. In the longer wire, proton migration to W409*, which is missing in H⁺·(H₂O)₃, has a comparable barrier. Such low barriers imply a high probability of a dynamical protonation of both W403 and W409* via W405 in the center. In other words, the protonic defect can be easily translocated along this hydrogen-bonded chain of water molecules within bR.

A missing ingredient in the present simulation is the quantum-mechanical effects on the nuclear motion. The only way to properly include them in the present realistic hybrid-density functional/force-field dynamics, i.e., without resorting to the harmonic approximation or restricting the dimensionality, which is hardly possible in view of the complexity of the q coordinate, would be to combine them with ab initio path integrals as used in much simpler cases (20, 42–45) within the ab initio centroid technique (46). Unfortunately, this is currently clearly beyond feasibility for biomolecular systems of the complexity of WLANs in BR. Still, such fluctuation effects can be mimicked in a crude way (38) by locally increasing the temperature of H⁺·(H₂O)₄ to 400 K, in addition to applying a suitable quantum correction when computing IR spectra (37), while keeping the protein at 300 K. Although this procedure does not provide a well defined ensemble considering the entire system, it is expected to nevertheless reveal the influence of fluctuations at a qualitative level. In this spirit, Fig. 1 Lower Left gives clear evidence that the global free energy minimum and thus the preferred location of the protonic defect are slightly shifted toward W403 but, most importantly, the well gets much more shallow and strongly anharmonic along q. This lowers the free energy cost to move the defect between W409* and W403 via W405 to only ≈1 k_BT and to ≈3 k_BT upon approaching even W404. As a result, quantum-mechanical fluctuations, in particular zero-point motion, are expected to considerably enhance the local mobility of the proton within this wire-like WLAN, thus strengthening the arguments obtained from the classical finite-temperature simulations. This is visualized by the corresponding proton distributions between W405 and its neighbors in the H⁺·(H₂O)₄ WLAN, as illustrated in Fig. 1 Lower Right. Whereas the proton in the hydrogen bond with W409* prefers to be closer to W405, its counterpart pointing to W403 is almost centered between the two water molecules and, in addition, its distribution is much broader, similar to what is observed in full ab initio path integral quantum simulations of protons in symmetrized hydrogen bonds (42).

IR Reference Spectra in the Gas Phase.

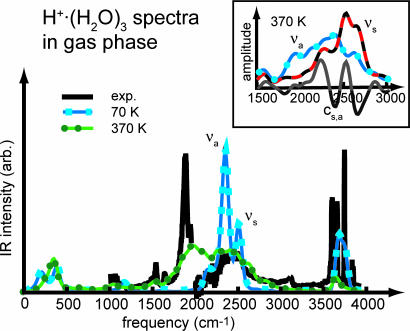
In addition to the proton dynamics as such, also the corresponding IR spectra critically depend on the zero-point energy (37). To gauge the approach to be used for BR, a closer look is first taken at temperature effects on IR spectra of protonated water clusters in the gas phase, available only recently (23). In particular, the partially and thus asymmetrically solvated hydronium core of H⁺·(H₂O)₃, i.e., H₃O⁺· 2(H₂O), resembles the binding motif as determined above for bR. In Fig. 2, the computed spectrum at ≈70 K nicely matches the broad band between 2,000 and 2,600 cm⁻¹ except for two overpronounced bands belonging to the symmetric and antisymmetric stretching modes ν_s ≈ 2,495 cm⁻¹ and ν_a ≈ 2,345 cm⁻¹ of the hydronium core. At this low temperature, these two modes are artificially decoupled, because only thermal fluctuations are present, but essentially reproduce the standard normal mode analysis (23). In the high-frequency region, this computed IR spectrum is again close to experiment concerning both the symmetric and antisymmetric stretches of the solvating H₂O molecules at ≈3,630 cm⁻¹ (vs. 3,639 cm⁻¹ in experiment) and ≈3,720 cm⁻¹ (vs. 3,720 cm⁻¹), respectively, and the free OH stretch at ≈3,650 cm⁻¹ (vs. 3,580 cm⁻¹) is only slightly shifted to the blue.

Fig. 2.

IR spectra of H⁺·(H₂O)₃ in the gas phase. The spectra obtained from two microcanonical Born–Oppenheimer NVE molecular dynamics runs with average temperatures of 72 and 372 K are compared with the experimental spectrum (23), which has a slight discontinuity at 2,000 cm⁻¹. (Inset) Power spectra (vibrational density of states) of the symmetric and antisymmetric stretch coordinates, ν_a and ν_s, defined in the text, and their frequency-dependent correlation c_s,a at 372 K.

Upon probing the effect of fluctuations by increasing the temperature to ≈370 K, two weak features at ≈1,050 and 1,530 cm⁻¹ appear in this region, which match nicely experimental bands on detailed inspection. In addition, the fluctuations broaden and red-shift the stretching modes of the hydronium core between 1,600 and 2,800 cm⁻¹. Most importantly, a broad resonance, absent at low temperature, appears at ≈1,970 cm⁻¹, which covers the experimental band of ν_a centered at 1,880 cm⁻¹ and is in accord with the calculated anharmonic frequency at 1,984 cm⁻¹ given in ref. 23. As can be seen by the decomposition of the power spectra in Fig. 2 Inset, this band is dominated by ν_a, because ν_s is weak here and does not couple to ν_a. This can be easily understood, because the transition dipole moment connected to the ν_a motion is much larger and thus carries much more IR intensity. Above 2,100 cm⁻¹, both modes are present and strongly coupled, yielding a broad IR peak in accord with experiment. Thus, probing the potential energy surface at a higher temperature leads to broadenings and significant red shifts of ν_a, while a coupling to ν_s in the blue part of its spectrum sets in. Compared with experiment, it is found that the computed ν_a band is too broad and slightly blue-shifted, which corroborates earlier findings (37) for anharmonic model potentials.

IR Spectra of Protonated WLANs in BR.

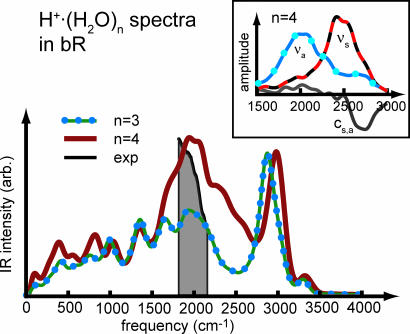
Having established both the merits and shortcomings of the computational approach for the specific case, attention is now turned on the spectra obtained from long ab initio hybrid-density functional/force field Car–Parrinello simulations of bR. The computed IR spectra of the H⁺·(H₂O)₃ and H⁺·(H₂O)₄ WLANs in bR are compared with each other in Fig. 3. Both topologies feature similar peak positions in the far-to-mid-infrared region up to 1,700 cm⁻¹, with slightly more intensity stemming from the longer chain of H⁺·(H₂O)₄. The corresponding IR bands can be assigned to librational and bending modes within the chains. In the region above 1,800 cm⁻¹, both spectra exhibit an extraordinarily broad band with a flat maximum at ≈1,940 cm⁻¹, followed by a slow but continuous drop at its high-frequency wing. At still higher frequencies, above 2,800 cm⁻¹, both spectra are almost identical, having intense peaks at ≈2,940 and 2,950 cm⁻¹, and much smaller ones at ≈3,350 cm⁻¹. These bands stem from stretching motions of strongly hydrogen-bonded, weakly hydrogen-bonded, and free OH bonds, the former with respect to the two glutamic acids E194 and E204 according to Fig. 1. When comparing frequencies to experiment, it should be kept in mind that these high-frequency motions are expected to be red-shifted by ≈100 cm⁻¹ because of the fictitious electron mass used in the Car–Parrinello dynamics (see Methods for a detailed assessment). This effect, however, is not significant for frequencies below 3,000 cm⁻¹, which will be compared subsequently to experiment, at the spectral resolution considered here.

Fig. 3.

IR spectra of the H⁺· (H₂O)₃ and H⁺· (H₂O)₄ WLANs in bR obtained from two isothermal Car–Parrinello molecular dynamics runs at 300 K. The gray-shaded area marks the range of the continuum band taken from ref. 16. (Inset) Power spectra of ν_s, ν_a, and their correlation c_s,a involving W405 in H⁺· (H₂O)₄.

Focusing now on the crucial regime between ≈1,800 cm⁻¹ and 2,800 cm⁻¹, where the continua have been measured, it is found that the peak of the H⁺·(H₂O)₄ wire is quite a bit broader and much more intense than its H⁺·(H₂O)₃ counterpart. Analogously to the H⁺·(H₂O)₃ cluster in the gas phase, this region is dominated by the ν_s and ν_a modes of those water molecules on which the excess proton is localized. This is revealed in Fig. 3 Inset decomposing the corresponding power spectra for ν_s and ν_a on W405 in the H⁺·(H₂O)₄ chain. The red part of the spectrum ≈1,900 cm⁻¹ is dominated by ν_a, whereas ν_s has its maximum close to 2,500 cm⁻¹. The separation of these two modes is much more pronounced in bR than in the gas phase (compare to Fig. 2 Inset), and their cross-correlations kick in only at ≈2,700 cm⁻¹.

Comparison with Experiment.

Finally, the computed spectra should be compared with experiment. Unfortunately, experimental data on the broad continua ascribed to protonated WLANs are available only in a rather small-frequency window, because protein bands congest even the time-resolved step-scan Fourier-transform IR spectra. Second, although the spectra due to the WLANs only are easily accessible in the simulation, they are obtained experimentally by measuring the difference of the bR to the M intermediate. This, on the other hand, is not accessible computationally, because it would require separate simulations with an absolute statistical accuracy far beyond current possibilities.

With these caveats in mind, the relative intensity of the continuum band taken from ref. 16 is compared with the two computed spectra in Fig. 3; the artificial absorbance changes due to photothermal heating of water uncovered in ref. 16 have been subtracted, as required. The peaks at 1,940 cm⁻¹ of both WLANs considered here fall well within the experimental continuum band but seem slightly blue-shifted with respect to the experimental maximum. The band shoulders toward higher frequencies are much broader than the experimental band. Carrying over the effects observed for the H⁺·(H₂O)₃ cluster in the gas phase according to Fig. 2, however, a systematic blue shift on the order of 100 cm⁻¹ is expected and an overestimated band width for the ν_a motion due to the classical dynamics. Upon carefully considering these two effects when comparing theory to experiment, in particular the spectrum of the longer protonated water wire, the H⁺·(H₂O)₄ WLAN is in astonishing agreement, because it carries more overall intensity than the H⁺·(H₂O)₃ wire.

Conclusions and Outlook

In an effort to understand the workings of vectorial proton transfer through BR, the proton release pocket close to the extracellular surface has been studied by hybrid molecular dynamics simulations, which combine density functional theory with empirical force fields. Two likely structures of a protonic defect in this water-filled cavity have been prepared, and the resulting free energy surfaces and, in particular, their IR spectra have been extracted. Both WLANs, H⁺·(H₂O)₃ and H⁺·(H₂O)₄, are similar in that they are characterized by a linear hydrogen-bonding topology, thus resulting in wire-like structures suspended by several surrounding side chains. Most importantly, the simulations confirm that the protonic defect seems to be stabilized by the two glutamic acids E194 and E204, as suggested earlier by experiments. Furthermore, the charge defect in the release pocket shows a high propensity to be delocalized along this quasi-one-dimensional network, which is traced back to local fluctuation effects. Thus, both classic Zundel- and Eigen-like complexes, i.e., [H₂O⋯H⋯OH₂]⁺ and H₃O⁺·3(H₂O), are inappropriate models or should be considered at best in the spirit of simplified limiting cases. Quantum effects are expected not only to increase the delocalization of the defects in the release pocket but also to render the free energy surface much smoother, which might explain the sizable isotope effects measured upon substituting D for H in BR (47, 48). Incidentally, the obtained picture of very dynamical WLANs, that is, fluxional protonic defects, is qualitatively similar to previous findings for isotropic proton migration in bulk water (20, 49). Transcending simulation, most direct comparison to experimental data lends substantial support to the claim that WLANs of the topology prepared in the present study, i.e., short one-dimensional water wires, should be the most relevant protonated networks of internal water molecules in the release pocket of BR. More generally, such WLANs are expected to serve as “proton sponges” in the workings of proteins, which recent findings for bacterial reaction centers seem to corroborate (50, 51).

Methods

The general approach, system setups, and simulation protocols follow previous work (33, 39) on the L-intermediate of BR.

Force-Field Model and Equilibration.

The protein model is based on the 1C3W crystal structure (40) of the bR state. Initial coordinates for hydrogens, the loop between the E and F helices, the N terminus, and a short part of the C terminus from E232 to A235 missing in the crystal structure have been generated by short annealing runs in vacuum with fixed-crystal coordinates. Standard protonation states at physiological conditions have been assumed for basic and acidic residues except for D96 and D115, which are protonated in bR. Buried water molecules according to the crystal structure have been retained, in particular W403, W404, and W405 in the release pocket, whereas surface water and lipid molecules have been discarded. An additional water molecule called W409*, which is labeled W409 in the 1QHJ crystal structure (41), has been added to the release pocket. Only in these initial force-field simulations, the excess proton has been modeled as a fixed hydronium ion replacing water molecule W403 from 1C3W. This protein model has been embedded in an equilibrated model of a fully solvated POPC lipid membrane. After deletion of overlapping molecules, 180 POPC and 8,175 water molecules remained in the system.

Protein interactions have been described by the Gromos 43a2 force field (52). Partial charges for the protonated retinal Schiff base from ref. 11 have been adapted to the united atom model of the Gromos force field. System setup and equilibration have been carried out with the Gromacs molecular dynamics suite (53). A careful stepwise decrease of positional restraints on the POPC membrane, the protein side chains, and finally the protein backbone has allowed a slow relaxation of the strained initial coordinates. During the following equilibration in the isothermal–isobaric ensemble, positional restraints of 1,000 kJ/(mol·nm²) were kept on some of the C_α atoms. Turning off the restraints completely for a 6-ns reference simulation led to an increase of the rmsd of the backbone atoms to the crystal structure from 0.5 to 1.1 Å but to much larger fluctuations of side-chain conformations. The system has been equilibrated for >10 ns to T = 300 K and P = 1 bar using Berendsen thermostats and anisotropic barostats. From this equilibration run, average length parameters of the orthorhombic periodic box of 78.7 Å × 78.7 Å × 80.0 Å have been determined, which were used for an additional 1-ns equilibration in the two isothermal Car–Parrinello molecular dynamics ensemble, the starting point for the hybrid simulations.

Hybrid Simulations of BR.

The hybrid-density functional/force-field simulations were conducted by using the interface (36) that couples the CPMD (54, 55) and Gromos (52) packages, as carefully assessed earlier for BR (39). In the first set of simulations, a H⁺·(H₂O)₄ WLAN spanned by the water molecules W403, W404, W405, and W409*, including the excess proton, comprised the fragment treated by density functional theory, whereas all remaining atoms of the environment were described by the force field as above. For a second set of simulations, additional water W409* has been moved from the release pocket into the bulk, thus reducing the density functional fragment to a H⁺·(H₂O)₃ WLAN.

For the density functional fragment, the Becke–Lee–Yang–Parr functional at a plane-wave cutoff of 70 Rydberg in a 30-a.u. cubic box and Troullier–Martins-type pseudopotentials for the ionic cores has been used. Car–Parrinello molecular dynamics were carried out by using a fictitious mass of 500 a.u. for the electron orbitals and the hydrogen mass for H. The temperatures of both electrons and ions were controlled by Nosé–Hoover chain thermostats. Equations of motion were integrated with a timestep of 4 a.u. (≈0.1 fs). Dipole moment and Wannier function centers, which were needed to compute the IR spectra, were sampled every fifth timestep.

Equilibration runs of ≈5 ps preceded any production. Placing the excess proton at different water molecules in the pocket upon initialization led to identical conformations within only 2 ps. For the computation of the IR spectra long ab initio trajectories of 32 and 51 ps for the H⁺·(H₂O)₄ and H⁺·(H₂O)₃ WLANs, respectively, were accumulated. Fluctuation effects, such as zero-point vibrational motion, have been probed by locally thermostating the H⁺·(H₂O)₄ cluster to 400 K, as has been motivated in the main text. In this additional simulation of 18-ps length, the immediate neighborhood and the rest of the system were kept at 300 K by using separate thermostat chains. Additional simulations of this kind with local temperatures of 450 and 500 K yielded similar results (not shown).

Reference Gas-Phase Simulations.

Microcanonical Born–Oppenheimer simulations of the H⁺·(H₂O)₃ cluster in the gas phase at an average temperature of 372 K were conducted to gauge the computational methods. Comparing these to Car–Parrinello simulations at 300 K analogous to those performed in bR showed an expected (55) red shift for the highest frequency (i.e., the stretch ≈3,600 cm⁻¹ of the two solvating water molecules) of ≈150 cm⁻¹ because of the fictitious orbital mass. The ν_a and ν_s region is slightly narrower in the Car–Parrinello case because of the somewhat lower temperature, but a red shift was no longer detected in this lower-frequency range. For the strongly red-shifted OH stretching modes in bR at ≈3,000 cm⁻¹, an upper limit of 100 cm⁻¹ is therefore estimated.

Data Analysis.

The collective variable (56) q = q_o + Σ_i (r_{Oi+1H i} − r_{O i Hi}) is obtained from OH distances, r_OH, involving consecutive oxygens O_i and O_i+1 and the hydrogen-bonded proton H_i between them along the hydrogen-bonded water wires H⁺·(H₂O)₃ and H⁺·(H₂O)₄. It locates the position of the excess proton therein and serves as a proton transfer coordinate. The offset q₀ has been determined such that q = 0 corresponds to the excess proton localized on W405 for both the H⁺·(H₂O)₃ and H⁺·(H₂O)₄ WLANs. Its suitably normalized canonical distribution function, ρ(q), allows to compute the free-energy surfaces from ΔG = −k_BT ln ρ(q), as plotted in Fig. 1 Lower Left; the marked oxygen positions along the q coordinate were determined from the average OO distances. For the computation of real-space proton-density distributions within the H⁺·(H₂O)₄ WLAN, see Fig. 1 Lower Left, relative proton positions had been transformed to the frame of reference defined by the average WLAN structure. The IR spectra in Figs. 2 and 3 were computed from Fourier transforms of the time autocorrelation functions of the total dipole moment determined by the electronic structure calculations of both H⁺·(H₂O)₃ and H⁺·(H₂O)₄ at a resolution of 10 cm⁻¹ and consecutive smoothing with Gaussians of 33 cm⁻¹ standard deviation. In addition, the so-called harmonic quantum correction factor has been applied, because it has been shown to work best for vibrational spectra of hydrogen-bonded systems (37). The power spectra of ν_s and ν_a shown in Figs. 2 and 3 Insets were obtained from the Fourier transforms of the autocorrelation functions of r_s = r_{Oi Hi} + r_{Oi Hi−1} and r_a = r_{Oi H i} − r_{Oi H i−1}, respectively. The correlation c_s,a was computed correspondingly from the cross-correlation function of r_s and r_a.

Abbreviations

BR

bacteriorhodopsin

bR

initial state of the BR photocycle

POPC

1-palmitoyl-2-oleoyl-sn-glycero-3-phosphatidylcholine

WLAN

water local area network.