Theoretical study of the rhenium–alkane interaction in transition metal–alkane σ-complexes

Abstract

Metal–alkane binding energies have been calculated for [CpRe(CO)₂](alkane) and [(CO)₂M(C₅H₄)CC(C₅H₄)M(CO)₂](alkane), where M = Re or Mn. Calculated binding energies were found to increase with the number of metal–alkane interaction sites. In all cases examined, the manganese–alkane binding energies were predicted to be significantly lower than those for the analogous rhenium–alkane complexes. The metal (Mn or Re)–alkane interaction was predicted to be primarily one of charge transfer, both from the alkane to the metal complex (70–80% of total charge transfer) and from the metal complex to the alkane (20–30% of the total charge transfer).

Carbon–hydrogen (CH) bond activation reactions are important from a fundamental point of view, as well as in more practical terms to medicine, academia, and industry, as they are being used for the conversion of common, inexpensive alkanes into reactive (and physiologically active) molecules (1, 2). Many transition metal complexes are now known that can be used to activate CH bonds in alkanes (3). With low-valent metal complexes, the first bond-breaking step involves oxidative addition of an alkane to an unsaturated metal center (Fig. 1). The goal of subsequent steps is to convert the alkyl group R into an alcohol ROH or other potentially useful functionalized organic molecule.

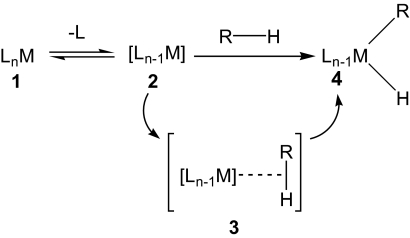
Fig. 1.

Oxidative addition of an alkane RH to an unsaturated metal complex, 2, which is typically generated by photolysis of a saturated metal complex, 1. The reaction is proposed to proceed via an alkane σ-complex intermediate, 3. Figure was adapted from ref. 4.

Many researchers today are focusing on the development of industrially practical organometallic oxidation catalysts (5–8), but there remain fundamental aspects of the CH activation process that are not fully understood. For instance, it is widely accepted that CH activation reactions proceed via alkane σ-complex intermediates (3) (Fig. 1, compound 3), and such species have recently been detected and studied in low-temperature NMR experiments (9–11). Although complexes with intramolecular CH/metal (so-called agostic) interactions have been isolated and crystallographically characterized (3), in systems where strong evidence has been provided for intermolecular metal–alkane coordination in solution (9–11), isolation and solid state structural characterization have not yet been accomplished.^†† Intermolecular metal–alkane complexes are therefore one of the most important targets in the study of CH activation; an understanding of the mechanisms of CH activation, which will allow researchers to better control and manipulate the outcome of the reactions, is crucial for the advancement of this area of chemistry.

Quantum chemical methods have become useful and practical tools in study of TM complexes (14–17). Particularly, advancements in density functional theory (DFT) (16) and the use of effective core potentials (14, 15) have made qualitatively accurate predictions of the structures and chemistry of TM complexes possible at a reasonable computational cost (17). The goals of the present work are twofold: to make computational predictions of the relative stabilities of a selection of alkane σ-complexes, which will aid synthetic chemists in their efforts toward isolating and fully characterizing such species, and to explain the nature of the alkane–metal interaction in such complexes.

Background

A σ-complex is a transition metal complex in which a σ-bond acts as a ligand. Intermolecular σ-complexes of borohydrides, silanes, and dihydrogen have all been isolated and characterized; as mentioned above, intermolecular alkane σ-complexes have proven to be much more elusive to isolation. The existence of isolable σ-complexes of any type is surprising, because σ bonds are far weaker electron donors than the lone pairs of more traditional ligands (e.g., amines, phosphines) or the π bonds of π-bonding ligands (e.g., alkenes, alkynes). The stability of σ-complexes is attributed in large part to the proposed occurrence of electron back-donation from a filled metal d orbital into the σ* orbital; such back-bonding is thought to be necessary for strong binding to occur (5).

Some of the earliest evidence for alkane σ-complexes came from studies of the Group 6 metal carbonyls. Photolysis of M(CO)₆ (M = Cr, Mo, W) produces M(CO)₅ fragments, which were shown, first by low-temperature UV/VIS (18, 19), and later by photoacoustic calorimetry (20–23) and gas-phase TRIR (24), to bind single alkane molecules as sixth ligands. The magnitude of the M(CO)₅(alkane) interaction is on the order of 10 kcal/mol (20–24).

As mentioned above, alkane σ-complexes are also believed to be intermediates in the activation of CH bonds by transition metal complexes. Early evidence for the presence of CH σ-complexes in CH activation reactions was provided by isotopic labeling NMR experiments on the reversible oxidative addition of cyclohexane to Cp*IrPMe₃ (25). In these experiments (25), and others similar to them (26–29), an inverse kinetic isotope effect and H/D exchange between the hydride and alkyl groups before elimination of the alkane indicated the presence of an alkane σ-complex intermediate. More recently, direct evidence for alkane σ-complex intermediates was obtained from TRIR flash kinetics studies on the photoinduced CH bond activation by Cp*Rh(CO)₂ in liquid rare gases (30–32). These experiments showed a reaction intermediate, assigned to be Cp*Rh(CO)(alkane), which became increasingly stable (relative to the reactants) with increasing alkane size, ranging from −0.9 kcal/mol for ethane to −2.3 kcal/mol for octane and from −2.4 kcal/mol for cyclopentane to −3.5 kcal/mol for cyclooctane (32). Also studied was the reaction profile of methane activation by CpRe(CO)₂ using computational methods, which predicted a methane σ-complex intermediate lying 8.7 kcal/mol below reactants in enthalpy, with an activation barrier to CH oxidative addition of 6.6 kcal/mol (33).

The present work focuses not on achieving CH activation, but on optimizing the stability of the proposed alkane σ-complex intermediate species. The goal in designing an isolable alkane σ-complex should be to choose the combination of metal, ligands, and alkane that is the most thermodynamically stable with respect to reactants and that has the highest barrier to oxidative addition. Inspection of existing experimental and theoretical evidence provides guidance in the design of such a complex. Using solution-phase TRIR spectroscopy, Childs et al. revealed a trend that is critical to the choice of metal center (34, 35). The group studied the reaction of complexes of the form CpM(CO)_x(n-heptane) with CO, and found that the rate of displacement of n-heptane by CO decreased with the identity of M both across and down Groups 5, 6, and 7 of the periodic table. The difference between the two extremes (top of Group 5 vs. bottom of Group 7) was remarkable; CpV(CO)₃(n-heptane) reacted 50,000 times more rapidly than CpRe(CO)₂(n-heptane). Also, for the choice of alkane, experiment indicates that large alkanes form more stable complexes than smaller alkanes, and that cyclic alkanes form more stable complexes than comparably sized linear alkanes (24, 32, 35). In agreement with the observed stability trends, several rhenium complexes with rather large alkanes, CpRe(CO)₂-(cyclopentane), -(cyclohexane), and -(n-pentane), have now been detected using low-temperature NMR (9–11).

The present study takes its lead from experimental evidence and investigates the stability of a series of CpRe(CO)₂(alkane) complexes, as well as that of several proposed but so far unknown binuclear analogs, [(CO)₂Re(C₅H₄)CC(C₅H₄)Re(CO)₂](alkane) (Fig. 2). Binding energies (BE) for selected examples of the manganese analogs of the complexes were also calculated to compare the alkane-binding capability of rhenium with that of a lighter Group 7 metal. The reported binding energies were calculated by using DFT with the Becke–Perdew 1986 (BP86) functional (36, 37).

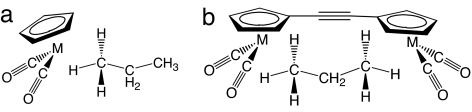
Fig. 2.

The mononuclear and binuclear alkane σ-complexes examined in this work, CpM(CO)₂(alkane) (a) and [(CO)₂M(C₅H₄)CC(C₅H₄)M(CO)₂] (b), M = Re or Mn.

Results and Discussion

Supporting Information.

For further details, see supporting informaiton (SI) Appendix, SI Tables 3–11, and SI Figs. 8–11.

Mononuclear Binding Energies.

For the mononuclear complexes, CpM(CO)₂(alkane), it was initially assumed that the binding in the n-alkane σ-complexes would occur at one of the terminal CH bonds; this is a reasonable assumption, because it is the terminal carbon that is activated in the CH activation reactions of related transition metal complexes. However, a recently published experiment brought the validity of that assumption into question. Ball et al. (10) found that in solution, (i-Pr(C₅H₄))Re(CO)₂(pentane) actually exists in three forms: (i-Pr(C₅H₄))Re(CO)₂(1-pentane), (i-Pr(C₅H₄))Re(CO)₂(2-pentane), and (i-Pr(C₅H₄))Re(CO)₂(3-pentane) in a ratio of 6:6.07:2.9. When compared with a statistical ratio of 6:4:2, this observed ratio corresponds to a thermodynamic preference of 0.13 kcal/mol for CH₂ binding over CH₃ binding. Also, Vetter et al. (38) observed a 1.5× kinetic preference for coordination at a secondary CH bond rather than at a primary CH bond for Tp′RhL(alkane) complexes (Tp′=Tris-(3,5-dimethylpyrazolyl)borate; L=CNCH₂CMe₃).

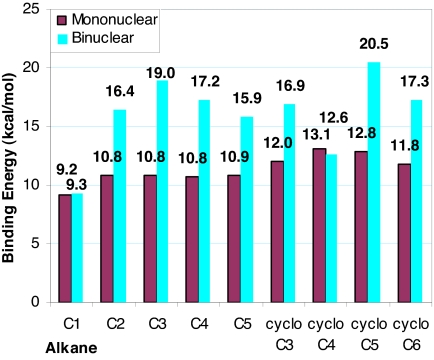
Binding energies at all possible interaction sites were calculated for the n-pentane and n-heptane CpRe(CO)₂ complexes (SI Table 3). The metal–alkane interaction strength was predicted to be larger by ≈1 kcal/mol when the interaction site was one of the terminal CH₃ groups (Fig. 2a) than when it was any of the secondary CH₂ groups (SI Table 3). This prediction is in disagreement with the slight thermodynamic preference (0.13 kcal/mol) for binding at secondary carbons observed by NMR (10). Differences between our calculations and solution-phase experimental results are to be expected because, in addition to their intrinsic errors, our calculations produce an estimate of gas-phase enthalpy, and do not account for changes in entropy or for the effects of solvation (which we expect to be small). There are also structural differences between the in silico and in situ experiments, which should be considered when comparing the two sets of results: the experimental structures contain i-Pr(C₅H₄) or Tp′ instead of Cp as a ligand. In any case, the linear alkane binding energies presented as final results in this work were calculated for the interaction of the metal center with the terminal CH₃ group (Fig. 3). Binding energies were also calculated for a series of cyclic alkanes (Fig. 3).

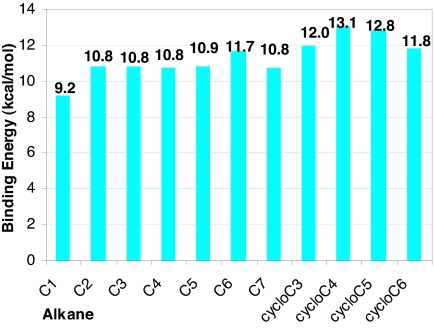
Fig. 3.

Mononuclear rhenium [[CpRe(CO)₂](alkane)] binding energies, calculated at the BP86/6–31G*, LANL2DZ level of theory. C1, C2, C3, C4, C5, C6, and C7 represent methane, ethane, n-propane, n-butane, n-pentane, n-hexane, and n-heptane, respectively. cycloC3, cycloC4, cycloC5, and cycloC6 represent cyclopropane, cyclobutane, cyclopentane, and cyclohexane, respectively.

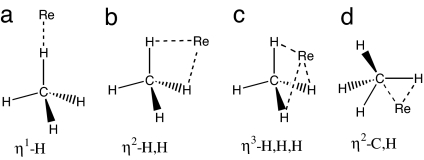
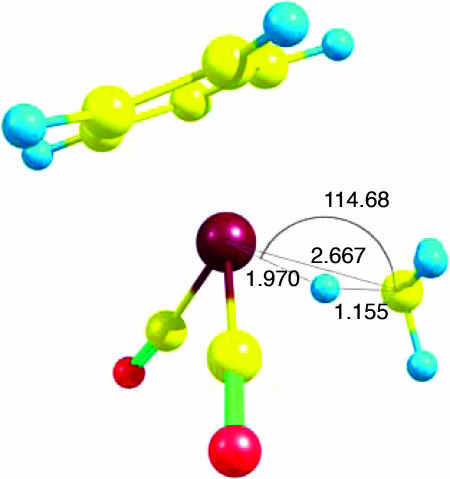
Several geometrical parameters were examined for each of the optimized mononuclear complexes (SI Table 5). For these complexes, only one CH bond of the interacting CH₂(cyclic alkanes)/CH₃(linear alkanes) group participates in the binding. The interaction is best described as an asymmetric η²-C, H type (Fig. 4d), in which the H atom lies closer to the metal atom M than does the C atom. An illustration of the optimized methane complex is provided as a representative example of the binding (Fig. 5). The MH–C angles range from 112° to 122° (SI Table 5), the MC distances from 2.58 Å to 2.72 Å, and the M-H distances from 1.91 Å to 1.97 Å (SI Table 5). The interacting CH bond is elongated by 0.06–0.07 Å relative to the free CH bonds on the same CH₂/CH₃ group (SI Table 5).

Fig. 4.

Four possible binding modes for alkane σ-complexes, shown here for methane.

Fig. 5.

Optimized [CpRe(CO)₂](methane) structure, calculated at the BP86/6-31G*, LANL2DZ level of theory. Bond lengths are provided in angstroms, bond angles are provided in degrees.

For the linear alkane complexes, the ethane to n-heptane (C2–C7) predicted binding energies are all fairly similar. The largest difference in binding energy is seen in comparing methane to ethane or any of the multicarbon alkanes. It appears that the presence of a CH₂/CH₃ group adjacent to the interacting CH₃ group significantly increases the metal–alkane interaction strength, but that further lengthening of the alkane chain has a much smaller effect.

The cyclopropane, cyclobutane, and cyclopentane binding energies are larger than those of their linear counterparts, and the cyclohexane value is roughly equal to that of n-hexane. The cyclobutane BE is the largest overall for the mononuclear complexes.

The reactivity of the mononuclear complexes [CpM(CO)₂](alkane), M = Mn or Re; alkane = n-heptane or cyclopentane have been investigated using infrared (IR) detection (39, 40). In the IR studies, the authors report enthalpies of activation (ΔH^‡) for the replacement of the coordinating alkane by a CO molecule. The ΔH^‡ values can be taken as lower limits of the strength of the metal complex–alkane interaction. They can serve as a rough check of the accuracy of the magnitudes of our computational values, and in this sense, they are in good agreement. The experimental values for ΔH^‡ are 13.6 kcal/mol (39) and 11.0 kcal/mol (40) for [CpRe(CO)₂](n-heptane) and 7.7 kcal/mol for [CpRe(CO)₂](cyclopentane); our respective calculated values are 10.8 kcal/mol and 12.8 kcal/mol.

The ultimate goal of our work is to find an alkane σ-complex that would be stable enough to isolate and fully characterize; we estimate that the binding enthalpy that this would require would be on the order of 30 kcal/mol. The mononuclear [[CpRe(CO)₂](alkane)] binding energies, whether predicted by computation or reported from experiment are too small to allow for isolation of these complexes at a reasonable temperature. For this reason, we chose to investigate their binuclear analogs, which could have significantly larger binding energies.

Binuclear Binding Energies.

The calculated binuclear rhenium binding energies are indeed significantly larger than those of their mononuclear counterparts (Fig. 6). The binuclear structures for ethane (Fig. 7), n-propane, n-butane (Fig. 7), n-pentane, cyclopropane, cyclopentane, and cyclohexane all show two alkane–metal interaction sites (SI Appendix), and it is the presence of this second metal–alkane interaction that increases the binding energies so significantly. This conclusion is further supported by the two exceptions to this trend, which do not show a significant increase in binding energy with the presence of a second metal center: methane and cyclobutane (Fig. 6). Methane and cyclobutane are predicted to interact significantly with only one rhenium atom of the binuclear complexes (SI Appendix).

Fig. 6.

Mononuclear rhenium ([CpRe(CO)₂](alkane)) binding energies and binuclear rhenium [[(CO)₂Re(C₅H₄)CC(C₅H₄)Re(CO)₂](alkane)] binding energies, all calculated at the BP86/6–31G*, LANL2DZ level of theory. C1, C2, C3, C4, C5, C6, and C7 represent methane, ethane, n-propane, n-butane, n-pentane, n-hexane, and n-heptane, respectively. cycloC3, cycloC4, cycloC5, and cycloC6 represent cyclopropane, cyclobutane, cyclopentane, and cyclohexane, respectively.

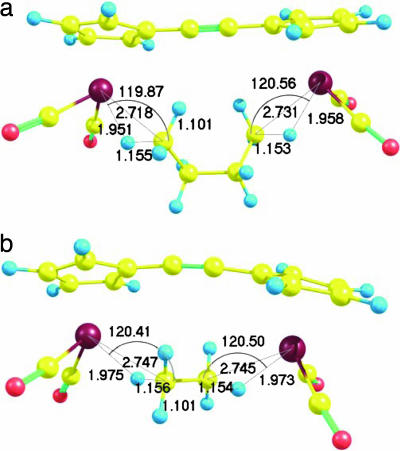
Fig. 7.

Optimized [(CO)₂Re(C₅H₄)CC(C₅H₄)Re(CO)₂](n-butane) (a) and [(CO)₂Re(C₅H₄)CC(C₅H₄)Re(CO)₂](ethane) (b) structures, calculated at the BP86/6-31G*, LANL2DZ level of theory. Bond lengths are provided in angstroms, bond angles are provided in degrees.

The binding observed at each of the two binding sites in the binuclear complexes is comparable to that observed at the mononuclear ([CpRe(CO)₂](alkane)) interaction sites; it is of the asymmetric η²-C, H type, and the MH and MC bond distances and MH–C angles are comparable to those seen in the optimized mononuclear complexes (SI Table 9).

For the mononuclear complexes, the binding energies were all fairly similar (Fig. 3). Lengthening of the alkane chain beyond two carbons had little effect on the magnitude of the binding energy. For the binuclear complexes, the length of the alkane chain is more important. The presence of one or two methylene spacers allows the terminal methyl groups of propane or butane to move freely, adopting a conformation in which their distances from the two metal centers are optimal for interaction (Fig. 7a). In the ethane complex, the two methyl groups have far less freedom, and to maximize their interaction with the two metal centers, the molecule can merely align itself between them (Fig. 7b). Accordingly, the binuclear ethane complex has both longer MH and MC distances (SI Table 9) and weaker binding than either the propane or butane complexes (Fig. 6).

Although it appears to be important for the terminal methyl groups of a linear alkane to have methylene spacers between them, too many methylene groups cause crowding, which limits the alkane's ability to adapt a favorable conformation for interaction with the metal complex. The pentane complex, for example, has larger MH and MC distances (SI Table 9) and a smaller binding energy than either the propane or butane complexes (Fig. 6). The n-propane molecule seems to strike a balance between flexibility and overall size, as it has the highest BE for the linear alkane complexes.

In the cyclic alkane complexes (excluding cyclobutane, which only interacts with one metal center), binding is predicted to occur with two adjacent carbons (SI Appendix). The calculated cyclopropane and cyclohexane structures both have larger M-H distances (SI Table 9) and smaller binding energies than the cyclopentane complex (Fig. 6). For cyclopropane, the reason for the difference may be that cyclopropane is limited in its ability to change conformation; the two interacting CH₂ groups are not able to rotate relative to each other, only to rigidly align themselves between the two metal centers. The cyclohexane molecule is more flexible than cyclopropane, but it appears to be simply too bulky to approach the metal centers as closely as cyclopentane is able to (SI Appendix).

As discussed above, the binuclear complexes display much geometrical flexibility. The CO and Cp groups on each metal center are able to rotate relative to the groups on the other metal center, and the alkane molecules have many possible conformations that allow them to interact with the metal centers. Complexes with such extensive flexibility are likely to have complicated potential energy surfaces with many local minima, some of which may be close in energy. The binuclear structures presented in this work are thus most likely only local minima on the potential energy surfaces of the complexes. The mononuclear structures are also likely to have many local minima, close in energy to each other. If the complexes reported in this work are indeed local minima, then the results presented here are slight underestimates of the maximum calculated interaction strengths, which would occur at the global minima. The regularity in trends of the predicted BEs for each series of complex–alkane combinations suggests that the structures presented in this work are reasonable representations, which are not likely to vary greatly from other favorable interaction modes that may exist. The geometry guesses that were used as the inputs for the initial optimizations of the mono- and binuclear complexes are shown in SI Appendix.

Several binuclear manganese complexes were also examined. The work of Childs et al. showed that manganese complex–alkane adducts are much less stable than their rhenium analogs (34, 35). In agreement with experiment, the calculated manganese binding energies are significantly lower than those of their rhenium analogs (Table 1).

Table 1.

Binuclear manganese and rhenium ([(CO)₂M(C₅H₄)CsC(C₅H₄)M(CO)₂](alkane)) binding energies (kcal/mol), calculated at the BP86/6–31G*, LANL2DZ level of theory

	Manganese	Rhenium
Ethane	8.0	16.4
n-Propane	12.7	19.0
n-Butane	12.1	17.2
n-Pentane	10.5	15.9

Nature of the Alkane–Metal Bond.

Absolutely localized molecular orbital (ALMO) energy decomposition analysis (EDA) calculations (41) were used to analyze the nature of the alkane–metal bond in the complexes presented in this work. The ALMO EDA separates the total interaction energy (ΔE_TOT) into four contributions: the geometric distortion energy needed to bring the fragments to their complex geometries (ΔE_GD), the frozen density interaction energy (ΔE_FRZ), the intramolecular orbital relaxation energy associated with the polarization of the metal complex and the alkane by each other (ΔE_POL), and the intermolecular orbital relaxation energy associated with the charge transfer between the metal complex and the alkane (ΔE_CT). The last term can be separated into two components: the energy lowering due to charge transfer from the metal complex to the alkane (ΔE_M→A), and the energy lowering due to the charge transfer from the alkane to the metal complex (ΔE_A→M). The ΔE_M→A term provides a qualitative measure of the backbonding contribution to the interaction energy. The ALMO EDA results for the mononuclear manganese and rhenium complexes with methane, n-heptane, and cyclobutane are presented in Table 2.

Table 2.

BP86/6-31G*, LANL2DZ EDA results for the mononuclear rhenium complexes of methane, n-heptane, and cyclobutane, optimized at the same level of theory

Energy term, kcal/mol	Re			Mn
	C1	C7	c-C4	C1	C7	c-C4
ΔEFRZ	−12.3	−13.1	−13.3	−7.8	−8.7	−9.4
ΔEPOL	4.4	5.2	5.7	2.4	3.0	3.6
ΔECT	21.7	23.3	25.5	15.2	16.8	18.7
ΔEM→A/ΔECT, %	26	24	25	30	28	27
ΔEA→M/ΔECT, %	74	76	75	70	72	73
ΔEGD	−3.4	−2.9	−4.1	−1.7	−1.5	−2.2
ΔETOT = ΔEFRZ + ΔEPOL + ΔECT + ΔEGD	10.4	12.5	13.8	8.1	9.6	10.7

The energies reported here are not directly comparable to the binding energies reported in Fig. 3 because they do not include zero-point vibration energies.

The analyses show that the major contribution to binding between the alkane and the metal center is charge transfer (≈80% of the total favorable binding contributions), whereas the polarization contribution is less significant (≈20%) and the frozen density interaction is repulsive (Table 2). Between 70 and 80% of the ΔE_CT is associated with charge transfer from the occupied orbitals of the alkane to the vacant orbitals of the metal complex (ΔE_A→M), and the remainder is due to backbonding (ΔE_M→A). The stronger binding observed for the rhenium complexes appears to be due to a higher total amount of charge transfer, and not to different relative amounts of forward- and back-donation (Table 2).

Conclusions

The main conclusions that should be drawn from this work are that the stability of an alkane σ-complex increases with the number of alkane–metal interaction sites, and that the binding interaction is primarily one of charge transfer, mostly from the alkane to the metal. Also, as expected, the manganese complex binding energies are significantly lower than those of their rhenium analogs; the lower BEs observed for the manganese complexes are due to lower amounts of total charge transfer, and not to different relative amounts of forward and back-donation, as compared with the rhenium complexes.

According to the calculations presented in this work, the binding energies for the binuclear complexes approach 20 kcal/mol; these complexes, once synthesized, are not likely to be stable at room temperature. Calculations are underway on a series of trinuclear complexes, which are expected to have higher BEs than the binuclear complexes, perhaps high enough to make them stable under ambient conditions. Also, there is some theoretical evidence that replacement of a π-accepting CO ligand, which is believed to compete with the alkane for the metal d electrons, by a pure σ-donor such as NH₃ increases the stability of alkane adducts (42). Calculations are in progress on a series of complexes with one or more of the CO ligands replaced by ammonia. Efforts are under way aimed at synthesizing some of the complexes examined in this paper. Future computational work will include further investigation of the effects of ligand identity on the strength of the metal–alkane interaction. The goal of such work will be to maximize the metal–alkane interaction, without actually causing activation of the CH bond, by adjusting the amount of metal-to-alkane back-bonding.

Methods

Each transition metal complex–alkane interaction energy was found by optimizing three structures, the entire alkane–transition metal complex, the transition-metal complex alone, and the alkane alone, and then subtracting the latter two energies from the first. In this work, favorable (negative) interaction energies are reported as positive binding energies.

The optimizations were performed first at the Hartree–Fock (HF) level (43), followed by a gradient-corrected DFT level optimization, using the exchange functional of Becke (36) and the correlation functional of Perdew (37), a combination known as BP86. The binding energies presented in this work are calculated at the BP86 level from the BP86-optimized structures. The BP86 functional combination is known for its consistently accurate predictions of the geometries, vibrational frequencies, and bond energies of transition metal complexes in general (44–47). It has also proven successful in the study of Group VI transition metal dihydrogen σ-complexes (48–50). For all calculations presented in this work, the 6–31G* basis set (51) was used for the non-metal atoms, and the LANL2DZ basis set and effective core potential (52) were used for rhenium and manganese.^§§ Vibrational frequencies and zero-point vibrational energies were calculated for the optimized structures. All optimized structures had zero imaginary frequencies^¶¶, indicating that they were minima on the potential energy surfaces. As recommended by Frenking et al. (14), the binding energies reported in this work have not been corrected for basis set superposition error (BSSE). However, the basis set superposition errors were estimated by using the standard counterpoise correction method (54), and are reported in SI Figs. 8 and 10. Cartesian coordinates, snapshots, and geometrical parameters of all complexes reported in this work are also provided in SI Appendix. Also, for the interested reader, structures and binding energies calculated at the Hartree–Fock (HF), DFT(B3LYP) (55), resolution-of-the-identity second-order Møller–Plesset perturbation theory (RIMP2) (56–61), and scaled opposite-spin MP2 (SOS-MP2) (62) levels of theory are also provided in SI Figs. 8–11.

ALMO EDA calculations were used to analyze the nature of the alkane–metal bond (41). The ALMO EDA calculations were performed without BSSE correction and without zero point vibrational energy corrections. The ALMO EDA calculations were performed using a developmental version of Q-CHEM; all other calculations reported in this work and in the SI were performed using either Q-CHEM 2.0 or Q-CHEM 3.0 (63, 64).

Abbreviations

TM

transition metal

DFT

density functional theory

BE

binding energy

ALMO

absolutely localized molecular orbital

EDA

energy decomposition analysis.

Note Added in Proof

For a review on the role of σ-complexes in σ-bond metathesis, see ref. 65.