Cyanobacterial clock, a stable phase oscillator with negligible intercellular coupling

Abstract

Accuracy in cellular function has to be achieved despite random fluctuations (noise) in the concentrations of different molecular constituents inside and outside the cell. The circadian oscillator in cyanobacteria is an example of resilience to noise. This resilience could be either the consequence of intercellular communication or the intrinsic property of the built-in biochemical network. Here we investigate the intercellular coupling hypothesis. A short theoretical depiction of interacting noisy phase oscillators, confirmed by numerical simulations, allows us to discriminate the effect of coupling from noise. Experimentally, by studying the phase of concurrent populations of different initial phases, we evaluate a very small upper limit of the intercellular coupling strength. In addition, in situ entrainment experiments confirm our ability to detect a coupling of the circadian oscillator to an external force and to describe explicitly the dynamic change of the mean phase. We demonstrate, therefore, that the cyanobacterial clock stability is a built-in property as the intercellular coupling effect is negligible.

The circadian clock is a self-sustaining biological oscillator that evolved in numerous organisms such as cyanobacteria, algae, fungi, plants, insects, and vertebrates to coordinate their metabolic and behavioral activities with the Earth's daily rotation (1). The free running period of the circadian clock is nearly, but not exactly, 24 h and is synchronized with the geophysical day by such periodic environmental cues as light, temperature, and nutrition. The molecular mechanism of the circadian rhythm production is generally described as a system of interlocked transcription/translation feedback loops (2).

Single cell in vivo monitoring revealed that individual cells generate autonomous circadian rhythms in protein abundance (3). In multicellular organisms, the individual cell rhythms appear to be noisy with drifting phases and frequencies (4, 5). Random fluctuations in the concentrations of different molecular constituents inside and outside the cell could be a cause of this noise (6). However, the whole organism is significantly more accurate, the temporal precision being achieved most probably through intercellular coupling of the individual noisy oscillators (7, 8).

In cyanobacteria, single cell oscillators are impressively stable, and a first estimation rules out strong intercellular coupling (9). Interestingly, these prokaryotes also have the simplest molecular mechanism at the heart of their circadian clock. In the absence of transcriptional activity in vivo (10), as well as alone in vitro (11), the three clock proteins KaiA, KaiB, and KaiC generate a self-sustained circadian oscillation of autophosphorylation and dephosphorylation. Recent chemical kinetics models (12, 13) provide a possible understanding of the three-protein oscillator, but the measured in vivo stability still remains unexplained. Do cyanobacteria possess not only the simplest circadian clock but also the most stable one? However, the same apparent stability could also be the result of weak intercellular coupling (14). The tendency for the individual phases of oscillation to drift away from each other could be overridden by an as-yet-unmeasured weak coupling. Is the clock stability a built-in property for each bacterium, or does a weak intercellular coupling make them appear like that?

Here we address this question by an accurate evaluation of the coupling constant. For that we first theoretically design our experiment to be able to distinguish coupling, even weak, from phase diffusion. As the precision of our evaluation increases with the length of the experiments, we continuously monitor, for a couple weeks, mixtures of cell populations with different initial phases. The inherent experimental noise contribution, initially dominant, is reduced by enhanced statistics. In the last section, we confirm our theoretical hypotheses and our experimental sensitivity by new experiments of in situ entrainment.

Model

The aim of this section is to show theoretically that when two populations with widely different abundances are mixed, the time evolution of the mean phase of the minority population will allow the coupling between bacteria to be measured directly.

Because single cell experiments (9) have previously ruled out a strong coupling between circadian clocks in cyanobacteria, we consider only the weak coupling limit. The cyanobacterial oscillators are taken to be phase oscillators (with constant amplitudes), and the interaction between two oscillators is described by the first Fourier term, i.e., the sine of the difference of the two oscillator phases (15). These assumptions will be experimentally confirmed afterward. Theoretical, numerical (15, 16) as well experimental (17) studies confirm that phase models can capture important synchronization properties of populations with weak interactions. This tremendous simplification of the oscillator complex dynamics exploits the fact that for a weak coupling, the amplitude variation or fluctuation can be separated from the slow phase change driven by the weak coupling and slight frequency differences among the oscillators (15).

The phase dynamics of two interacting oscillators is then given by

where φ_j(t) is the instantaneous phase of the oscillator, ω_j is its free-running frequency, and ε is the coupling constant.

Population of N Identical, Weakly Coupled, Noisy Oscillators.

The cyanobacterial oscillators are also submitted to noise. We discriminate here between two types of noise: the first, experimental, is generated by global environmental fluctuations or manual interventions such as addition of medium (see Materials and Methods). This affects all oscillators in roughly the same way and will not be taken into account in this section. A second type of noise, specific to each oscillator, comes from the stochastic nature of chemical reactions inside each cell. This can in principle affect the phase, as well as the free-running frequency or the shape of the oscillation. For a given experimental condition, single cell experiments showed a closely similar period of oscillation for all of the cells studied (standard deviation/mean < 0.5%). We therefore consider identical oscillators with the same free running frequency ω₀ and the stochastic noise affecting only the phase of the oscillation in a generic Wiener process. For N identical mutually coupled oscillators, Eq. 1 becomes the Kuramoto equation (16), here represented in a ω₀-rotating frame with ϕ = φ − ω₀t:

The noise terms ξ_j(t) are independent stochastic Gaussian functions with zero mean and diffusion constant D, δ-correlated in time: <ξ_i(t)ξ_j(t′)> = Dδ(t − t′)δ_ij. In our experiments, the number N of identical oscillators is large, N > 10⁶.

Let P(ϕ, t) be the probability of observing a given bacterium with phase ϕ at time t. The time progress of P(ϕ, t) is given by the solution of the corresponding Fokker–Planck equation (18):

where X, Y are the real and imaginary part of the mean field

Note that the amplitude ρ of the mean field Z = ρe^iμ is the order parameter, a direct measure of the synchronization: for oscillators uniformly distributed ρ = 0, whereas ρ = 1 when all oscillators have exactly the same phase. The steady-state solution [see supporting information (SI)] of Eq. 3 is the von Mises (19) distribution:

the circular analogue of the normal distribution on a line. Here μ ∈ [−π, π) is the mean phase, k is a parameter bi-univocally related to the order parameter ρ = I₁(k)/I₀(k), and I_n(k) is the modified Bessel function of the first kind of order n. The self-consistency condition ensuing from Eq. 3 ρ_s = I₁(k_s)/I₀(k_s) = (D/ε)·(k_s/2) gives (SI) that the only steady-state solution is the uniform distribution of phases for D > ε, when the noise prevails, whereas partial synchronization is achieved for ε > D.

Mixture of Two Imbalanced Populations of Identical Noisy Oscillators.

In our experiment we mix two populations of oscillators, a first one denoted as “majority” has a number of oscillators N_M much larger than N_M, the number of oscillators in the second, “minority” population (N_M/N_M = 20). Being entrained in the same way (see Materials and Methods), both populations have initially identical phase distributions (ρ_M⁰ = ρ_m⁰), albeit centered around different averages, μ_m⁰ and μ_m⁰, respectively. If the coupling strength ε is strong enough compared with D, one would expect that the mean phase of the minority population would drift toward that of the majority population.

To derive an analytical solution for the time evolution of the phase distributions in both populations we make two main approximations (see SI): (i) we assume that the attractive force acting on all oscillators comes mainly from the majority population; (ii) we approximate the probability densities P_M(ϕ, t) for the majority and P_m(ϕ, t) for the minority population by von Mises distributions at any time point. In fact, initially and at steady state, P_M(ϕ, t) and P_m(ϕ, t) are von Mises distributions (see SI), and we subsequently interpolate between these two limits. With these approximations, the time-dependent parameters μ_M(t), ρ_M(t), and μ_m(t), ρ_m(t), which characterize the time progression of the two populations, are given by (SI)

and μ_M(t) = μ_m⁰. In Eqs. 4, εt appears as the natural reduced time. Consequently, excluding the initial conditions, the ratio D/ε remains the only parameter affecting the evolution of the minority mean phase μ_m(εt) and both order parameters ρ_M(εt) and ρ_m(εt). Fig. 1 compares the numerical simulation of Eq. 2, for different values of ε and D/ε, with the solution of Eqs. 4. The good agreement validates our previous approximations, in the parameter range of our experimental circumstances.

Fig. 1.

Comparison between the solution of Eqs. 4 (solid line) and numerical simulations of 10,500 interacting phase oscillators. The mean phases μ_M(εt) and μ_m(εt) (a), order parameter of the majority population ρ_M(εt) (b), and order parameter of the minority population ρ_m(εt) (c) are represented for three values of D/ε, 0.48 (red line), 0.96 (green line), and 1.44 (blue line). Three simulations are superimposed for each value of D/ε, with different values of the coupling constant: ε = 0.2 (dashed line), 0.1 (dash-dot line), and 0.05 (dotted line). (a Inset) Similar variation of μ_m(εt), obtained from Eqs. 4 for D/ε varying from 0.01 to 10.

It is remarkable that the influence of D/ε on μ_m(εt) is weak: Fig. 1a Inset shows similar variation of μ_m(εt) for D/ε values, from 0.01 to 10. For εt ≪ 1, μ_m(t) is independent of the diffusion coefficient value D, whereas ρ_M(t) and ρ_m(t) depend strongly on D:

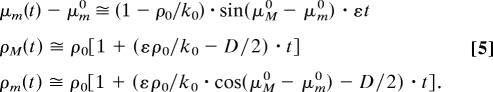We can therefore evaluate the coupling constant ε, independently of D. The appropriate physical measure is the slope of the time progression of the minority mean phase, μ_m(t). Because the precision in the estimation of the slope increases with monitoring time, our experiments are designed to follow μ_m(t) for a couple weeks continuously.

Experimental Results

We follow the temporal progression of the mean phase of the minority population by using the strain AMC462. This strain is bioluminescent, carrying a bacterial luciferase reporter that consists of two neutral site chromosomal insertions, PkaiBC::luxAB and PpsbAI::luxCDE. Although the clock is ticking in the same way as in a wild-type (WT) strain, the reporter inserted here makes it possible to observe the oscillations. The large difference in population abundance excludes the use of two color bioluminescence reporters (20), one for each population of the mixture, owing to the spectral leakage of the majority reporter signal into that of the minority. To avoid any loss of the minority signal by a 20-fold more abundant majority, we therefore use for the majority population the WT strain with no reporter, i.e., nonbioluminescent. Note that the white-light illumination of 900 lux provides each cell with at least 10⁷ more photons than the bioluminescent reporter (see SI). This excludes any feedback influence of the bioluminescent light on the bacterial clock.

Both strains were similarly entrained, ρ_m⁰ = ρ_m⁰ = ρ₀, at independent initial mean phases (see Materials and Methods) μ_m⁰ and μ_m⁰. We chose to work with four initial phases, denoted A, B, C, and D, separated by ≅π/2 rad (Fig. 2a Inset). Mixtures were made in 96-well plates, for different pairs, (μ_m⁰, μ_m⁰): from (a, A), (a, B) … to (d, C) and (d, D). Lowercase denotes mean phases of the minority and uppercase those of the majority population.

Fig. 2.

The mean phase of the minority population is unaffected by the presence of a different phase majority. (a) Recorded bioluminescence of individual wells. Red and black lines indicate wells containing only luminescent cells previously entrained at opposite phases (A and C, respectively). Orange, blue, brown, and green lines represent wells containing mixtures of a luminescent minority with a 20 times larger population of WT cells as follows: (a, A), (a, B), (a, C), and (a, D). Lowercase denotes minority and uppercase indicates majority mean phase. The mixtures have a bioluminescence level initially 20 times and finally 30 times lower than wells containing only the luminescent strain. Each experimental condition is represented by 8–12 independent wells. (Inset) The four phases of entrainment are separated by ≅π/2 rad, with A leading B, in opposition to C and lagging D. (b and c) The circadian oscillation s(t) for the luminescent strain alone (b) and for the mixtures (c), represented with the same colors as in a. s(t) = i(t)/i(t) − 1, with i(t) the well bioluminescence and i(t) its baseline obtained by a fast Fourier transform (FFT) smoothing of i(t). The oscillations of A and C still have opposite phases at the end of the experiment. For the mixtures, the oscillation of the minorities appears unbiased by the presence of different phase majorities. (d) Instantaneous mean phase of the minorities μ_m(t) extracted from s(t), represented with the same colors as in a.

In Situ Monitoring of the Relative Minority/Majority Concentration by Using the Bioluminescence Baseline.

Fig. 2a presents the bioluminescence recorded from individual wells containing mixtures of the same minority with four different majorities: (a, A), (a, B), (a, C), and (a, D), followed for ≈40 days. As a control, we also observe the luminescent strain alone, here shown for two initial mean phases A and C. For each well, the bioluminescence i(t) oscillates around a baseline i(t) that, apart from a weekly brief rise when fresh medium is added, gradually decreases all along the experiment. i(t) is the temporal mean calculated by smoothing the bioluminescence curve. The baseline value depends on the number of cells per well. At low cell numbers the well is transparent and the bioluminescence, collected from the whole well, is proportional to the absolute number of emitters. For higher concentrations of cells per well, as described in Materials and Methods, detection of the luminescence is confined only to the top layers of cells, and i(t) is proportional to the relative concentration of emitters/total number of cells in a well (see SI). We use this property to monitor the relative minority/majority population concentration. Fig. 2a shows that, initially, the wells containing the luminescent strain alone indeed emit ≅20 times more strongly than the mixtures. In time, the WT strain outgrows the reporter strain, which enhances even further the ratio between minority and majority abundance: N_M/N_M ≅ 1/30.

Experimental Monitoring of the Minority Mean Phase.

Fig. 2 b and c illustrates the circadian oscillation, s(t), for the same wells and individual time points as in Fig. 2a. The sensitivity of the bioluminescence reporter to the metabolic conditions is circumvented by defining the oscillatory signal as s(t) = i(t)/i(t) − 1. This representation reveals a remarkable well-to-well reproducibility of the oscillations. The wells containing the luminescent strain alone maintain their phase opposition until the end of the experiment (Fig. 2b). The oscillation of the minority population appears to be unperturbed by the majority presence: throughout the experiment, their oscillations overlap regardless of the majority mean phase (Fig. 2c).

It can be shown that s(t) is in fact proportional to the real part of mean field Z_m of the detected oscillators in the well. For this, we express the bioluminescence of the cell j as d_j(t) = g·[1 + bcos(ω₀t + ϕ_j)], where ω₀ and ϕ_j are the free running frequency and the phase of the oscillator j, respectively. g is the reporter gain, and b is the relative amplitude of oscillation per cell. The latter depends on the promoter monitored, here PkaiBC. Initially, b ≅ 1, then decreases during the experiment, depending on the metabolic state of the cell (see SI). The well bioluminescence is the sum of the contribution of all of the top cells and is therefore proportional to their ensemble average oscillation, i(t) ∝ <d(t)> (see SI), which finally gives: s(t) = bρcos(ω₀t + μ). The time variation of the amplitude bρ describes the apparent damping of s(t) oscillations in Fig. 2 b and c. Because b is time dependent, variable from one experiment to another, and accounts for nearly all of the amplitude damping, it is not possible to get a reliable experimental determination of ρ(t) for a quantitative comparison with the theoretical expectations (Eq. 5). By contrast, the phase of s(t) is precisely the mean phase μ, and for this reason we will employ this quantity to monitor the minority mean phase.

The Hilbert Transform is used to construct the complex analytical signal associated with the oscillation s(t) and to extract the instantaneous phase (see SI). Fig. 2d follows the temporal progression of the minority phase μ_m(t) for individual wells containing mixtures of the same minority with four different majorities: (a, A), (a, B), (a, C), and (a, D), shown in Fig. 2a. In our representation, the reference is 〈μ_{(a, A)}(t)〉, the average of wells containing a mixture with the same initial phase (see Materials and Methods) μ_m⁰ = μ_m⁰ = A. Theoretically, in the other mixtures, where μ_m⁰ ≠ μ_m⁰, we would expect the minority to drift gradually toward the phase of the majority (Fig. 1a), if the coupling is strong enough. Fig. 2d, however, shows no apparent phase deviation. The instantaneous phases spread out around zero, in a similar way to reference mixture (a, A) wells. We may conclude either that there is no intercellular interaction between oscillators or, more likely, that the experimental noise causing this dispersion masks a possible weak coupling.

Estimation of the Intercellular Coupling.

To extract from the experimental noise a possible minority phase variation, we average the individual well contributions from all of the measurements. The average is taken over equivalent experiments, i.e., wells with the same initial phase difference μ_m⁰ − μ_m⁰ between majority and minority. As described previously, the reference for each well is its corresponding average of same-phase mixtures μ_m⁰ = μ_m⁰. Fig. 3 compares the variation of the average minority phase <μ_m(t)> for three initial differences of phase: −π/2, π, π/2. Here again the minority phase variation is buried in the remaining noise and exhibits a similar variation for all three conditions. We therefore stop our quest to uncover an intercellular coupling. The precision of our experiment, however, enables us to set an upper limit for this elusive coupling constant ε.

Fig. 3.

The average minority phase <μ_m(t)> for three initial phase differences μ_m⁰ − μ_m⁰: = −π/2, π, π/2 and the reference 0, represented, respectively, by blue, brown, green, and orange lines (error bars are the standard error of the mean). For each phase, the average is taken over ≅80 individual wells. Black lines show 95% lower and upper confidence limits of the linked linear fit of the ±π/2 curves.

To this end we use Eq. 5, because the condition εt ≪ 1 is obviously valid. The expected variation of the minority phase is linear, with the slope directly related to ε: (1 − ρ₀/k₀)·ε·sin(μ_m⁰ − μ_m⁰). Here the initial order parameter (see Materials and Methods) is ρ₀ ≅ 0.67 and k₀ = 1.8. The extreme scenario is for μ_m⁰ − μ_m⁰ = ±π/2, where we would have expected the strongest variation of the minority mean phase. Fig. 3 shows the 95% confidence bands of the simultaneous linear fit (see SI) of both ±π/2 curves. The resulting 95% confidence interval confines the coupling constant ε to a value of |ε| < 1.5·10⁻³ day⁻¹. It follows that, even in the absence of noise, it would take at least 500 days, or ≈1 year, for the minority to join the majority. As will be shown in the next section, variations in the natural environmental are so large over such an extended period that this value of ε amounts in practical terms to zero.

External Force Acting on a Population of N Identical, Noisy Oscillators.

In this last section we analyzed a simpler coupling experiment. An external force, here the external lighting, is coupled to a population of identical noisy oscillators, the cyanobacteria. This experiment was designed to evaluate our ability to detect coupling and also as a quantitative test of the coupling model considered above (Eq. 1).

A particular lighting signal in front of each well (see Materials and Methods), E_j(t) = E₀·[1 + c_j·cos(ωt + θ_0,j)] is applied to a plated population of freshly entrained luminescent cells. The average applied light intensity E(t) = E₀ and frequency ω are the same for all of the wells, whereas, from well to well, the relative amplitude of the oscillatory component c_j and the initial phase θ_0,j are varied (Fig. 4a). A 1-day (24 h) entrainment period is imposed and four different entrainment phases, separated by π/2. The entrainment frequency ω is chosen to be different from ω₀ (free running frequency of the oscillator) for two reasons. First, the entrainment to a 24-h period is one of the three defining circadian clock properties and is thus a guarantee that coupling exists and can be studied. Second, a strictly resonant coupling (ω = ω₀) is trickier to impose, because the free running frequency of the oscillators ω₀(t) changes slightly in time. We denote the detuning, ν = ω − ω₀, such that ν > 0, because the cyanobacterial circadian oscillators period is >24 h.

Fig. 4.

Cyanobacterian oscillators respond to an external force as phase oscillators. (a) Entrainment lighting E(t) is applied for ≅14 days and then kept constant for the next 3 days to confirm the phase change. The light oscillates around an average of 500 lux, with a relative amplitude c = 0.4 and a 24-h period. Two of the four entrainment phases, separated by π/2, are shown. The gray vertical line highlights the transition to constant lighting. (b) The phase of the related entrained oscillators represented in a ω-rotating frame. The orange, green, blue, and brown symbols and error bars correspond to the experimental average phase <μ(t)> − μ₀ and standard error of the mean; the matching colored lines are the fits from the Adler equation with ε the only free parameter. Dashed black lines are the numerical simulations of Eq. 6, with the same ε. (Inset) The coupling constant ε increases with the relative amplitude of entrainment c.

The time-response of the oscillator mean phase μ_j(t) to the entrainment signal E_j(t) is then monitored. Fig. 4b shows the average phase variation <μ(t)> relative to the initial phase μ₀, represented in a ω-rotating frame. In this representation, the instantaneous phase of a free running oscillator (of constant ω₀) decreases linearly with a slope −ν, whereas it is constant for an oscillator locked at the entrainment frequency. In our case (Fig. 4b), the average phases start from the same point (origin) and, under the influence of entrainment, evolve toward the π/2 separated phases. These phase differences persist when the entrainment is stopped, for t > 14 days.

We can go one step further and quantify the coupling constant ε involved here. We adopt the same assumption as in Eq. 1, except that now, instead of two oscillators, there is an entrainment force of instantaneous phase θ_e(t) = ωt + θ₀, coupled to an oscillator of instantaneous phase φ_j(t). In the ω-rotating frame the equation becomes dφ_j/dt = −ν − ε sin[φ_j − Δθ], where Δθ = θ₀ − φ₀ is the entrainment and oscillator difference of the initial phases. This equation, known as the Adler equation, has an analytic solution that depends on ε, ν, and Δθ (SI): for ε > ν, the oscillator finally adopts the entrainment frequency, whereas for ε < ν, the phase rotates nonuniformly in a quasiperiodic motion (15). In Fig. 4b, the continuous lines show the simultaneous fit of the experimental curves with this solution, with ε = 0.15 day⁻¹ as the only free parameter. Δθ differs by steps of π/2 from one curve to another and ν, the same for all, is determined from the continuously illuminated wells (data not shown). As can be seen, three of the four curves are well described by this simplified model. For the fourth (brown) curve, the discrepancy with the experimental data is obvious: the average phase jumps up toward π/2, while the theoretical solution slowly decreases toward −3π/2. This is not surprising because our oversimplified model neglects the initial phase distribution (σ₀ = 0.9 rad) and the phase diffusion noise ξ_j(t) (9). We therefore simulate (see Materials and Methods), for each oscillator j of the initial distribution, the equation

where ε has the value previously obtained. The resulting mean phases, represented in Fig. 4b by the dashed curves, now describe satisfactorily all of the experimental results.

Our experimental setup therefore allows us to detect and interpret coupling. The phase oscillator model is appropriate and provides an explicit description of the dynamic change of the mean phase. The relative amplitude of the oscillatory component c manifests itself as the strength of the entrainment force. For different values of c ∈ (0, 1], the corresponding coupling coefficient ε steadily increases with c and vanishes for c ≤ 0.2 (Fig. 4 Inset).

The above experiment also probes the sensitivity of the cyanobacterial circadian clock to an external perturbation. The circadian clock appears to be quite rigid, because relative amplitudes of >50% are necessary to produce locked 24-h light entrainment.

Discussion

In situ light entrainment experiments confirm that the cyanobacterian clock responds like a classical noisy phase oscillator to small entrainment forces. In a population of identical mutually coupled noisy oscillators, the steady-state distribution of phases relies on the comparative values of the phase diffusion constant D and the coupling constant ε. If ε > D, the coupling is stronger, and the phases can be driven toward a distribution of limited width. In contrast, if the noise is stronger (D > ε), the phases ultimately are uniformly distributed between [−π, π). As a result, the outcome of apparent precision of oscillators also will depend on the ranking of D with respect to ε. Earlier single cell experiments (9) revealed robust circadian oscillators in cyanobacteria with a low phase diffusion D = 5 × 10⁻⁴ ± 3 × 10⁻⁴ h⁻¹ = 0.012 ± 0.007 day⁻¹. The estimated upper limit of ε excluded a strong coupling, ε ≤ 0.008ω₀ = 0.05 day⁻¹ (see the supplementary information in ref. 9) but was too high to allow a direct comparison with D. Here, we have reduced the upper limit of the coupling constant by a factor of 30 to |ε| ≤ 0.0015 day⁻¹. We show that the circadian clock in cyanobacteria therefore is dominated by a very low diffusion, because the coupling constant is even smaller.

The high stability of individual oscillators in cyanobacteria is therefore not related to intercellular coupling but originates from the internal wiring of the genetic and metabolic network. Their clock mechanism is not only the simplest but also the most robust. The cyanobacterial circadian oscillator appears as a simple model system for studying dynamic noise-resistant networks. What makes this oscillator noise resistant? The posttranslational core of the clock, based on the repeated interaction of the three clock proteins Kai A, B, and C is potentially less noisy than a transcription/translation clock mechanism (6). Is that enough to explain the cyanobacterian clock stability or are supplementary transcription/translation feedback loops needed to obtain this stability? Cyanobacteria offer two complementary approaches for answering this question: first, in vivo single cell experiments, by decoupling the core clock from the existent feedback loops, and, second, reverse engineering in vitro by microscale reconstituted clocks with the similar number of proteins as in vivo.

Materials and Methods

Strains, Growth Conditions, and Entrainment.

The strains used in this study are AMC 462 (21) and WT Synechoccocus sp. strain PCC 7942. Strain AMC462 carries a luciferase reporter, consisting in two neutral site chromosomal insertions PkaiBC::luxAB and PsbAI::luxCDE. Both strains were grown in modified BG-11 medium (22) at 30°C in a CO₂-controlled atmosphere and 900-lux white-lamp illumination. The phases of the cultures were set the same by light-entrainment, 12-h light/12-h dark cycles during 1 week. The two strains were then frozen in cryotubes with 150 μl·ml⁻¹ glycerol at −80°C. Freezing cyanobacteria stops the circadian clock ticking, whereas thawing them restarts it. Therefore, to obtain samples with exactly the same oscillation characteristics but different mean phases, cryotubes were thawed at different time intervals, diluted, and kept in constant conditions of light, temperature, and CO₂. The phase difference is directly related to the time interval Δt between each thawing: Δϕ = 2πΔt/T, where T is the circadian clock period. In this way we obtained cell cultures with the desired mean phase and the same distribution of individual cell phases around this mean. The standard deviation of this distribution was concordantly evaluated to σ₀ = 0.9 rad from individual cell measurements (results not shown) and from the initial amplitude of the oscillatory signal s(t = 0). This corresponds (SI) to an order parameter ρ₀ ≅ 0.67 and to a concentration parameter k₀ = 1.8.

In Situ Light Entrainment.

In the coupling with an external force experiment, we built two arrays of 96 individual white-light emitting diodes (LED), their size matching the plates. The LED arrays were designed to avoid cross-illumination of wells, in such a way that one LED illuminated exactly one well. A custom-made program varied the LED light emission, independently for six clusters per plate, each cluster containing 4 × 4 LEDs. In these experiments, a sinusoidal light signal was applied, with the same 24-h period and 500 lux average light intensity for all of the clusters but with different initial phases and amplitudes of oscillation.

Assay of Bioluminescence.

A Packard Topcount 96-well plate luminescence reader was used to follow the circadian oscillations of the luminescent strain. Each well of the 96-well plate was filled with the same amount of cells, 250 μl at an optical density measured at 750 nm, OD_750nm ≈ 0.1, that is ≈3 × 10⁷cells per well. The plates then were covered with adhesive sealing film, perforated above each well to ensure the presence of oxygen and CO₂ inside the wells. Two plates were placed in a room regulated for temperature (30°C) and CO₂ under constant white light (900 lux), to avoid any unwanted external entrainment. Every 30 min, the luminescence of each well was automatically read by two photomultipliers under darkness for 5 sec per well, i.e., 4 min per plate. Before each reading, the plates were kept in darkness for 2 min. To compensate for evaporation and nutrient depletion, fresh media was added every week to the wells.

During the experiment, the number of cells in the wells continued to grow: color photographs of the plates were taken every week showing the wells becoming greener because of the increasing chlorophyll concentration. This growth rapidly confined detection of the luminescence only to the top layers of cells, because the green-colored cyanobacteria reabsorbed the bioluminescence photons emitted by the bottom layers (see SI). In addition, the nutrient resources shared among increasingly numerous members will reduce the gain of the biochemical luminescent reaction per cell. Therefore, except for the first few days and for a weekly brief rise when fresh medium was added, the bioluminescence gradually decreased all throughout the experiment. We detected the same number of top cells, and they were emitting less. For each experimental condition, we started with 8–16 independent wells, some of which were excluded from our analysis on account of contamination, too fast evaporation, or clogged aeration of the cover film. The exclusion criterion used was the variation of the bioluminescence baseline by >40% with respect to an unperturbed well.

Numerical Simulations and Circular Statistical Analysis.

We numerically integrated the evolution of phases for 10,500 interacting phase oscillators governed by Eq. 2, by using a forward Euler scheme with time step Δt = 2.6 × 10⁻³. The initial phase of the oscillators, independently distributed, has one majority group of N_maj = 10,000, normally distributed around μ_m⁰ = π/2 and one minority group of N_min = 500 normally distributed around μ_m⁰ = 0. Initially, both groups have the same standard deviation, σ₀ = 0.9 rad. The noise ξ, a Wiener process with a diffusion constant D, is simulated by a phase jump $\xi =\pm \sqrt{D\Delta t}$ that is equally probable forward or backward at each time step. The same technique is used in the simpler case of coupling with an external force. We simulated Eq. 6 for 2,000 oscillators, initially independently distributed around 0, with the standard deviation σ₀ = 0.9 rad.

Interpretation of the results was done by using the circular analysis statistics (23). The mean order parameter <ρ> and the mean phase <μ> were determined as follows:

In this paper, the time average of a random variable x(t) is denoted by x̄ and the ensemble average by <x(t)>.