Self-organization of actin filament orientation in the dendritic-nucleation/array-treadmilling model

Abstract

The dendritic-nucleation/array-treadmilling model provides a conceptual framework for the generation of the actin network driving motile cells. We have incorporated it into a 2D, stochastic computer model to study lamellipodia via the self-organization of filament orientation patterns. Essential dendritic-nucleation submodels were incorporated, including discretized actin monomer diffusion, Monte-Carlo filament kinetics, and flexible filament and plasma membrane mechanics. Model parameters were estimated from the literature and simulation, providing values for the extent of the leading edge-branching/capping-protective zone (5.4 nm) and the autocatalytic branch rate (0.43/sec). For a given set of parameters, the system evolved to a steady-state filament count and velocity, at which total branching and capping rates were equal only for specific orientations; net capping eliminated others. The standard parameter set evoked a sharp preference for the ±35 degree filaments seen in lamellipodial electron micrographs, requiring ≈12 generations of successive branching to adapt to a 15 degree change in protrusion direction. This pattern was robust with respect to membrane surface and bending energies and to actin concentrations but required protection from capping at the leading edge and branching angles >60 degrees. A +70/0/−70 degree pattern was formed with flexible filaments ≈100 nm or longer and with velocities <≈20% of free polymerization rates.

The polymerization of soluble actin monomers between filament “barbed ends” and the plasma membrane (PM) generates the force of protrusion in cell motility (1, 2). Other proteins required for lamellipodial motility (3) are arp2/3, which nucleates (branches) free barbed ends at ≈70 degrees from existing ones (4); a PM-bound activator of arp2/3 (5); ADF/cofilin, which promotes the depolymerization of pointed ends (6) and perhaps debranching reactions (7); and capping protein, a terminator of barbed end growth (8). The generation and persistence of lamellipodia from these elements is described in the “dendritic-nucleation/array-treadmilling” conceptual model (2, 4, 9). This model can be subdivided into three main processes: the kinetics of filament (de)polymerization, branching, and capping; filament–PM interactions, which limit polymerization rates; and the diffusion of actin monomers and other soluble components. Such a system is “complex” in the sense that many copies of each component type interact to exhibit “emergent” system properties not expected from the individual rules of interaction (10). In contrast to “complicated” systems of many dissimilar components with precisely defined interactions, complex systems can self-organize and adapt to environmental change.

An important emergent property is the self-organization of lamellipodial actin filaments into orientations at ±35 degrees with respect to the direction of protrusion (11, 12). Maly and Borisy (11) predicted ±35 or +70/0/−70 degree patterns with a 2D mathematical model based on these dendritic-nucleation assumptions. A model by Atilgan et al. (13) allowed 3D branching, but required preferential arp2/3 orientation in the PM for pattern formation. The numerical model described here extends the Maly and Borisy (11) model, removing most of its simplifications and limitations. Reactions are treated stochastically, the elastic properties of the membrane and filaments are included, and the time-dependence of the distribution's evolution is obtained. We preserve the assumption that filaments remain oriented in the 2D lamellipodial plane. Our simulation exhibits orientational self-organization and permits the determination of a range of parameter values consistent with pattern stability. We reveal the transient development of the orientation pattern and the approach to steady-state protrusion velocity and filament number.

Several computer models of (rigid) bacterial propulsion by rigid filaments have been proposed (14–16), with those of Carlsson demonstrating a flat force–velocity relationship under autocatalytic branching (15, 16). Mogilner and Oster (17, 18) developed the basic theory of the actin-based elastic Brownian ratchet, which applies small-angle elastic beam theory to thermal filament fluctuations. The present model combines stochastic propulsion and elastic filament models, adding a flexible PM load and thermodynamically realistic filament–membrane interactions.

Assumptions and Methods

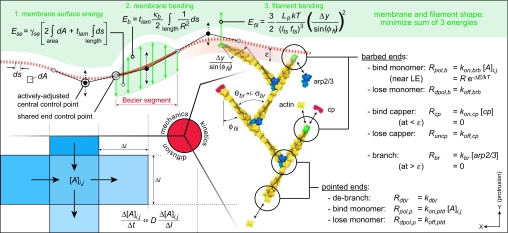
An ≈1 μm-wide (X) portion of a flexible lamellipodial leading edge (LE) was simulated, with cyclic boundary conditions for all components on the ≈1 μm Y axis edges and a fixed actin monomer concentration [A]_TE on the trailing edge. Every filament over the entire lamellipodial thickness was modeled, with 2D positions, orientations, and end states of each filament recorded individually. Over each small time step Δt, the calculation algorithm performed spatially discretized (Fick's law) diffusion and Monte-Carlo (stochastic) kinetics calculations for all components, with iterative calculations of PM and filament mechanics as required (Fig. 1 and Tables 1 and 2). Consistent with experimental indications that branching and anticapping mechanisms operate very near the LE, free barbed ends within a Y-distance ε branched new filaments at rate R_br and were blocked from the usual capping rate R_cp. New filaments deviated from the parent filament barbed end orientation by a normal distribution about the mean branch angle ±(θ_br±σ_br). Polymerization occurred at a rate proportional to the local actin monomer concentration, reduced at the LE by a Boltzmann factor based on the total system energy required for that specific protrusive step. Filaments were assumed to be either rigid or flexible and cantilevered from the nearest branch or pointed end. Values for the filament and PM mechanical properties and most of the reaction rate constants were available. The main unknowns were the effective rates of branching and capping, critical to the development of the filament distribution. With R_cp available, ε and R_br were determined from simulation (see Fig. 3), completing the standard set of parameters listed in Table 2. Model details and a simulation video depicting individual protrusive steps can be found in supporting information (SI) Methods and Movie 1.

Fig. 1.

Lamellipodia were simulated using three submodels. (Lower Left) A fixed rectangular grid demarcated regions of uniform actin concentration, subject to Fick's diffusion relation between them. (Right) Within each time step, kinetic reactions were carried out stochastically for every filament. (Upper) Minimization of PM and filament potential energies yielded quasi-SS geometries between kinetic states.

Table 1.

Symbols

R	Radius of curvature of the LE in the plane of simulation
VPM; Vfree	Velocity of the LE center of mass; free polymerization velocity
ΔE	Thermal energy required for intercalating a monomer between LE and barbed end = Δ(ΣEb + ΣEse + ΣEfil) over successive potential states
EbEse Efil	PM bending, PM surface, and filament bending potential energies
ds; dA	Differential length along LE; differential area of plasma membrane
lts	Filament terminal segment length, from barbed end to first branch
φfil	Filament orientation angle, with respect to the direction of protrusion
αd	Mean absolute filament deviation angle, measured from population mean
[A]; [A]i,j	ATP-G-actin concentration, in general; local conc. at position (i,j)
fε	Average fraction of all free barbed ends within the ε-demarcated LE zone
t1/2 N1/2	Half-time; number of branching generations to develop orientation pattern

Table 2.

Model parameters and standard values

Symbol	Value	Description	Refs.
δ	2.7 nm	Extension length of polymerizing actin monomer	—
D	6.0 μm2/sec	Cytoplasmic actin monomer diffusion coefficient	19
[A]TE	12 μM	Fixed, trailing edge actin monomer concentration	20
γse	50 pJ/nm2	Plasma membrane surface energy coefficient	18, 21
κb	80 pN nm	Bending energy coefficient, ≈20 kT	21
Lp	10 μm	Persistence length of actin filaments	22
tlam	200 nm	Lamellipodial thickness	20
kon,brb	12 /μM/sec	On-rate of actin to barbed end ≡ Rpol,b/[A]	23
koff,brb	1.4 /sec	Off-rate of actin from barbed end ≡ Rdpol,b	23
kon,ptd	0/μM/sec	On-rate of actin to ptd. end, profilin-adj. ≡ Rpol,p/[A]	24
koff,ptd	8.0/sec	Off-rate of actin from ptd. end, cofilin-adj. ≡ Rdpol,p	6
ε	2.0 δ	LE cap-protection/branch zone (Y) length	15
Rbr	0.43/sec	(Total) rate of barbed end branching ≡ kbr [arp2/3]	18, 20
Rdbr	0.05/sec	Rate of debranching for any branch point	25
Rcp	6.0/sec	Rate of barbed end capping ≡ kon,cp [cp]	26
Runcp	0/sec	Uncapping rate for any capped barbed end ≡ koff,cp	26, 27
Nfb	200 fil/μm	Free barbed ends per LE width (indirectly spec.)	20
θbr	70 deg.	Average branch angle	4
σbr	7 deg.	Branch angle SD	4
Dt	0.0004 sec	Simulation time step	—
fts	0 (≡ rigid)	Fraction of terminal segment length in fil bending	Text

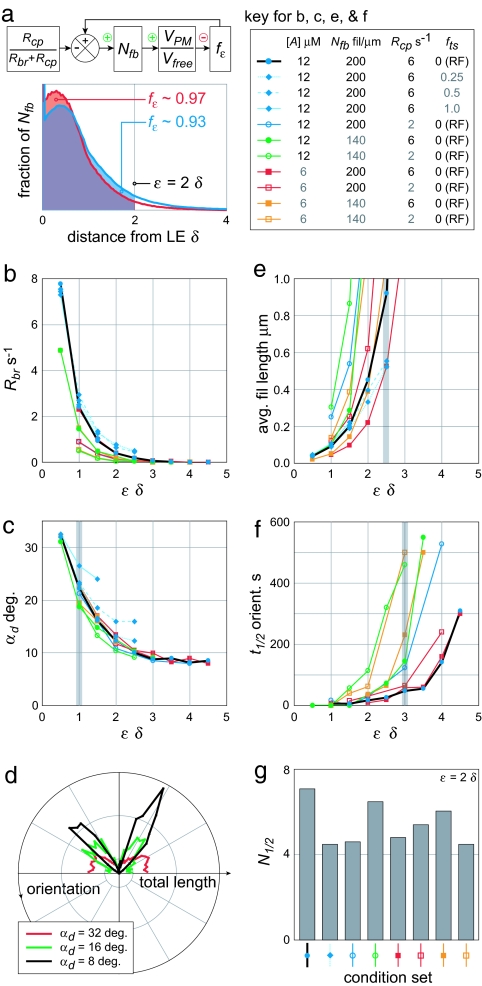
Fig. 3.

Orientation pattern and filament length were examined for several parameter sets to determine standard branching parameter values. (a) The distribution of Y-distances from free barbed ends to the LE is shown for standard conditions (R_br = 0.43/sec, f_ε = 0.93, and V_PM/V_free = 0.36, blue) and a reduced N_fb of 140 fil per μm (R_br = 0.21/sec, f_ε = 0.97, and V_PM/V_free = 0.28, red). Distances in units of δ. (b) For all conditions, the R_br required to sustain the specified N_fb increased sharply at low ε. (c) The extent of filament deviation from the average orientation (α_d) increased from near σ_br to >30 degrees at ε = 0.5 δ under all conditions. (d) Orientation patterns for three α_d values plotted, with backward-facing filaments rotated by 180 degrees to make them comparable to EM data, suggested a lower limit of ε ≈1.0 δ. (e) High ε resulted in unreasonably long filament lengths, restricting ε to < 2.5 δ. (f) The half-time to develop an SS pattern (t_1/2) from an initial 15-degree asymmetry also increased with ε, supporting ε < 3 δ. (g) The characteristic number of branching generations required to approach SS (N_1/2) was similar for all parameter sets at a given ε (2.0 δ shown).

Results and Discussion

Self-Organization of Filament Orientation Arose Under Any Initial Conditions (ICs).

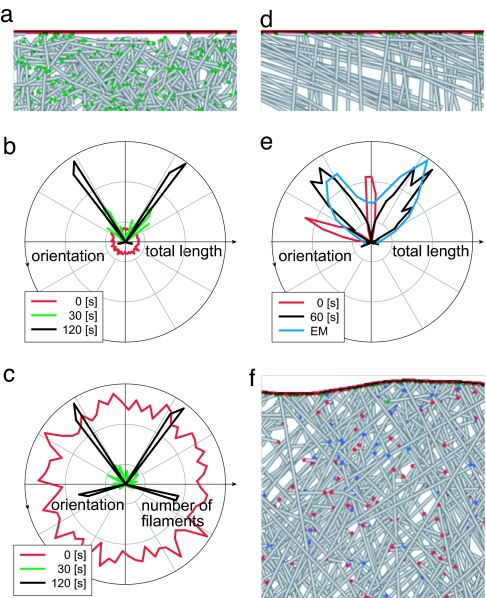
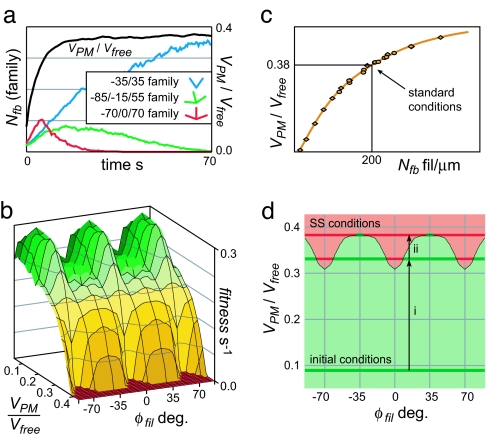
We first asked under what ICs the model system would organize filament orientation. A set of filaments at random position, orientation, and length has no order, with only the position of the branch-inducing and capping-protective LE to generate directionality. A simulation was run under these ICs (Fig. 2a), with the branch angle SD (σ_br) equal to zero and otherwise standard parameter conditions (Table 2). Results show the disappearance over 120 sec of total filament length (mass) in most orientations, with one pair of very sharp orientations at ±35 degrees dominating (Fig. 2 b and SI Movie 2). Because the branch angle did not vary, filament populations always occurred in strictly complementary families (related by exactly 70 degrees) and were not able to drift into other orientation families over successive generations of branching. This result shows that from ICs without order, very narrow populations of filaments oriented at 35 degrees show net growth, whereas others show net depolymerization.

Fig. 2.

Filaments in the model spontaneously self-organized from any ICs into preferential orientations ±35 degrees from the leading edge (LE) perpendicular. (a) ICs of simulations in b and c, showing random filament barbed-end position, orientation (0–360 degrees), and length (0–150 nm) over 0.5 × 0.35 μm of a 1 × 1 μm simulation. Fifty percent of filaments shown; standard parameter set of Table 2, except σ_br = 0 degrees; free barbed ends labeled green. (b) Polar histogram plots of total filament length versus orientation displayed a sharp preference for ±35 degree orientations, with loss of others. (c) Plotted by number of filaments, a similar pattern was observed, but with backward-facing filaments made obvious. (d) ICs of standard parameter simulations (σ_br = 7 degrees) in e and f, showing orientations near −70/0 degrees. (e) Polar plots of total length over time show adaptive behavior and compare favorably with EM measurements at SS. (f) Image of a 0.5 × 0.5 μm section at SS. Capped barbed ends labeled red, blue dots denote branches. At SS, the 1 × 1 μm simulation contained 700 filaments totaling 250 μm in length, with 200 free barbed ends.

When the number of filaments, instead of the total filament length, in each direction is plotted, we see a similar pattern with the addition of backward-facing filaments at ±105 degrees (Fig. 2c). Other orientations showed a net decrease in the number of filaments, showing that the total capping rate outpaced the total generation rate for those orientations until their numbers reached zero. Domination by length at ±35 degrees thus did not represent a system in which ±35 degree filaments became particularly long, but instead one in which other filament families were not viable. Filaments that faced backward at ±105 degrees were generated at nearly the same rate as forward-facing filaments, but rapid capping away from the LE kept their total lengths (and nonproductive monomer depletion) very low (Fig. 2b), and subsequent debranching and depolymerization reduced their count moderately (Fig. 2c).

It remained to be shown that the model could adapt from initial orientation patterns devoid of 35 degree filaments into the steady-state (SS) ±35 degree patterns. This is necessary because a feature of motile cells is their ability to reorganize filament orientations in response to changes in the direction of protrusion, without which we would not observe the ±35 degree pattern in cells that turn. Initial conditions of filaments oriented near −70/0 degrees simulated a sudden, 35 degree clockwise turn in protrusive direction from a previous SS pattern (Fig. 2d). The standard σ_br of 7 degrees was used allowing the population to drift into new orientations, but no 35 degree filaments existed initially. Orientations became symmetrical within 1 min, with a broader distribution of orientations centered on ±35 degrees (Fig. 2e). The SS distribution compared favorably to those measured via digital image-processing techniques (Radon transform) from lamellipodial electron micrographs (EMs) (11) (Fig. 2e, with an image at SS shown in Fig. 2f). We conclude that ICs of all protrusive simulations with standard parameter values evolve and adapt into ±35 degree patterns consistent with EMs.

Simulation Indicated Plausible Branching Parameters.

The standard parameter set used in Fig. 2 and the rest of this study came from both the literature and simulation. Although experimental data provided relatively direct estimates for N_fb, R_cp, and [A] values, R_br and ε were more difficult to estimate. Modeling allowed us to determine R_br, ε, and the filament bending length parameter f_ts, consistent both with estimates for N_fb, R_cp, and [A] and with experimentally accessible values such as orientation pattern and filament length.

A particular N_fb is set only indirectly, through filament turnover parameters R_br, R_cp, and ε. For a given V_PM/V_free, the profile of N_fb with distance from the LE is similar (Fig. 3a, the exact shape of which will be considered in a subsequent publication). At SS, a fraction of these free barbed ends, f_ε, are within the ε-demarcated region, and the total rates of filament branching and capping are balanced: (N_fb f_ε) R_br = (N_fb [1-f_ε]) R_cp. The SS f_ε therefore equals R_cp/(R_br+R_cp), the setpoint for a negative-feedback loop controlling N_fb and V_PM/V_free: A low V_PM relative to V_free allows filaments to keep up with the LE more often, raising f_ε above the setpoint. The resulting net branching increases V_PM/V_free. Conversely, a high V_PM/V_free results in net capping and a decrease in N_fb and V_PM/V_free.

Plots were made of the R_br values required to sustain a steady N_fb at a given ε, with two values each of N_fb, R_cp, f_ts, and [A] specified and the diffusion coefficient (D) set very high to maintain [A] uniformly (Fig. 3b). The value of [A] was not a factor in the required R_br; it affected both V_PM and V_free (= k_on,brb [A] δ) equally, and curves are superimposed. (Comparison is therefore by V_PM/V_free throughout this study.) In contrast, maintaining higher N_fb values required a higher R_br because the associated increase in V_PM/V_free diminished f_ε. A decrease in R_cp was associated with an approximately proportional decrease in required R_br, as expected. Filament flexibility was allowed in three parameter sets, and moderately raised the required R_br. The most sensitive parameter was ε itself. Decreasing ε dramatically decreased f_ε, requiring a compensatory increase in R_br.

To narrow the range of acceptable values of ε and R_br, the quality of the SS orientation distribution was assessed. Quality was quantified as the mean absolute deviation (α_d) from the mean orientation angle. The α_d values for all parameter sets were very similar at the same ε (and R_br) values, with some increase in α_d with filament flexibility (Fig. 3c). Polar histograms of orientation distributions over a range of α_d showed focused distributions at high ε and noisy and distorted distributions, incompatible with EM data, at very low ε (Fig. 2d). These results are compatible with ε values as low as 1 monomer length (δ = 2.7 nm), but not less.

To limit the upper values of ε, we analyzed average filament lengths and orientation pattern development times. Again, because large ε values were associated with low R_br, filaments turned over slowly and thus grew very long before being capped. Using EMs, conservative visual estimates of the average length of filaments within 1 μm of the LE ranged from 50 to 500 nm (data not shown). In simulations, the number of filaments was a decaying function of length, with all parameter sets consistent with a maximum 500 nm average length when ε was held to <2.5 δ (Fig. 3e). Supporting this limit were measurements of the half-time of orientation pattern development (t_1/2) from a 15 degree simulated turn (i.e., ICs of a distribution centered on +20 and −50 degrees), with full recovery defined as a SS α_d value. At ε = 3.0 δ, all parameter sets yielded a t_1/2 of 60 sec or more (Fig. 3f), corresponding to ≈3 min recovery times for a minor 15 degree turn. In comparison, fibroblasts have lamellipodial protrusion persistence times on the order of 1–2 min before retraction (28). Length and recovery time considerations were thus limited by two criteria to ε < 2.5 δ.

Of related importance to t_1/2 is the number of branching generations required for network self-organization. The product of t_1/2 and R_br yields the number of generations required for a 50% recovery in α_d after a rapid, 15 degree turn (Fig. 2g). Regardless of parameter conditions, this N_1/2 value was consistently ≈5 generations for ε = 2.0 δ. Three half-times (87.5% recovery) required 15 generations. For ε = 3.0 δ, three half-times still required ≈9 generations. These generations must be largely successive (i.e., parents branching children, then children branching grandchildren) for adaptation to occur.

Based on these studies, we chose a standard set of parameter values consisting of ε = 2.0 δ, R_cp = 6.0 /sec, and [A] = 12 μM, with which reasonable protrusion rates of 8 μm/min were achieved. Furthermore, an N_fb of 200 fil per μm was compatible with measurements of filament barbed end count (20) and length, and required an R_br of 0.43/sec. Filaments were held rigid (f_ts = 0) for simplicity except where noted.

The SS Orientation Pattern Is Sensitive to Several Model Parameters.

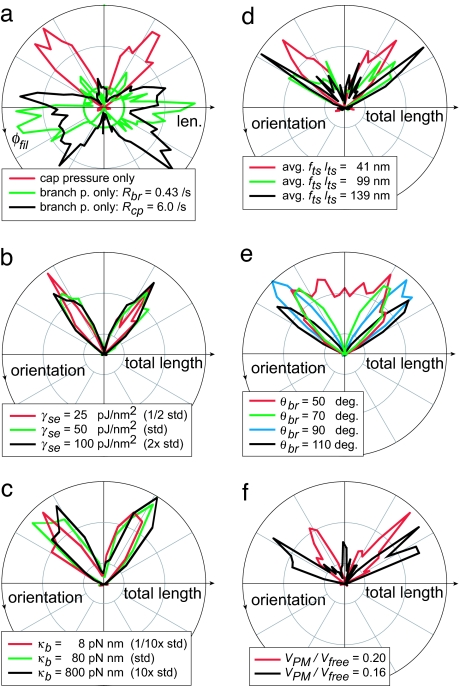
In the standard model, the same ε value limited capping protection and branching initiation. When branching was allowed at any free barbed end, regardless of position, but capping protection was maintained within ε, orientation distributions remained unchanged (Fig. 4a). These conditions were effectively similar to standard conditions because the high intrinsic capping rate quickly removed free barbed ends arising beyond ε. (Although we did not simulate branching from the sides of filaments away from their barbed ends, we predict a similar result.) In contrast, when branching was only allowed within ε and capping was allowed anywhere, the orientation pattern changed dramatically. Cases in which N_fb and R_br were maintained at standard values required a greatly diminished R_cp of 0.22 per sec, whereas those with standard N_fb and R_cp required a greatly elevated R_br of 12 per sec. Both cases resulted in distributions with most filament mass facing backward, incompatible with EM results. Protection from capping near the LE is thus essential for the formation of the ±35 degree distribution.

Fig. 4.

Sensitivity of patterns to nonbranching parameters further suggested limits to in vivo values. Polar plots include all filaments in an LE 1 × 1 μm area. (a) Deviating from standard conditions, maintaining branching pressure but allowing capping anywhere resulted in a nonphysiological, high backward-filament mass. (b) Altering surface energy (γ_se) values alone did not affect orientation pattern. (c) Varying PM bending energy (κ_B) altered the variability in LE shape but did not alter the pattern. (d) Simulations with varying filament flexibility all had average terminal segment lengths (l_ts) of ≈200 nm. When effective bending lengths exceeded ≈41 nm, orientation patterns similar to +70/0/−70 degree distributions resulted. (e) Setting the mean branching angle (θ_br) near or below 60 degrees resulted in a broad distribution. (f) Velocities of at least ≈20% of V_free were required for ±35 degree orientation patterns.

Membrane model parameters were not found to significantly affect orientation distributions over a wide range of values. Given a constant R_br, runs varying the resistance to protrusion (γ_se) retained the same V_PM and ±35 degree distribution due to the compensating effect of N_fb (Figs. 3a and 4b). This flat force–V_PM relationship is a characteristic of unrestrained autocatalytic branching, observed by Carlsson (16). Membrane flexibility, specified by the bending energy coefficient, κ_b, had a significant effect on the LE shape over length scales of <200 nm. Although the pattern is formed with respect to the LE perpendicular, this had no effect on the orientation distribution, with the same pattern attained over two orders of magnitude of κ_b variation (Fig. 4c). We attribute this stability to the LE's horizontal average orientation and rapid fluctuations relative to filament lifetime.

Conversely, filament bending stiffness had a large influence on the orientation pattern. This stiffness is dependent on the third power of effective filament bending length [(f_ts l_ts)³, with the fraction f_ts simulating cross-linking]. Standard parameter simulations with effective filament lengths averaging 0 (f_ts = 0, equivalent to rigid) or 41 nm (f_ts = 0.25) yielded ±35 degree distributions, but 99 or 139 nm lengths (f_ts = 0.50 or 0.75, respectively) resulted in distributions similar to +70/0/−70 degree triplets (Fig. 4d). These length limits are consistent with Mogilner and Oster's (17) force generation calculations. Triplets were a result of barbed-end “splaying” to higher angles under load.

The branch angle (θ_br) itself was not important to the final ±θ_br/2 distribution over values of 70–110 degrees, but smaller θ_br values resulted in a single uniform mass (Fig. 4e). Allowing splaying by filament flexibility did not revive the two-peak distribution (data not shown). Note that filaments branching from θ_br/2 no longer face backward at θ_br = 60 degrees, but rather 30 + 60 = 90 degrees. This allows them an increased opportunity to further branch and disperse the population orientation. Among θ_br values that form two-peak distributions, the t_1/2 from ICs (uniformly distributed over the range of ±90 degrees) is also sharply minimized at θ_br = 70 to 80 degrees (data not shown). A 70 degree branch angle is therefore optimized for rapid generation of a stable two-peak orientation pattern.

Changes in V_free had no effect on the orientation pattern (data not shown), but the ratio V_PM/V_free was important. Holding V_free constant, the SS V_PM was diminished by decreasing R_br (this raises the SS f_ε requirement; see Fig. 3a). An R_br of 0.06/sec yielded V_PM/V_free = 0.20 and a ±35 degree distribution (Fig. 4f). Decreasing R_br to 0.03/sec lowered the SS V_PM/V_free to 0.16 and produced an SS triplet distribution, but also lowered N_fb to 80 fil per μm. Raising γ_se to restore N_fb had no effect on the distribution or V_PM/V_free (plotted). Note that low R_br can lead to long filament lengths and slow self-organization (Fig. 3), and triplet patterns in vivo would be more suggestive of a small ε value (which instead lowers V_PM to reach the same required f_ε). Note also that, on average, a 70 degree filament advances at V_free cos (70) = 0.34 V_free, but that stochastically growing filaments bounded ahead by the PM do not maintain a high f_ε at this velocity and in fact require V_PM/V_free < 0.20 to dominate under standard values.

The Evolution of the Final Orientation Pattern and the Development of the SS V_PM Were Interdependent.

From ICs of a small number of filaments at random orientation, Fig. 5a tracks the total number of filaments in each of three complementary-orientation “families” over time. At the low N_fb and V_PM values early in the simulation, the +70/0/−70 degree triplet multiplied at the highest rate. With increasing V_PM, however, the number of filaments decreased in turn for each family until only the ±35 degree pair remained at SS V_PM.

Fig. 5.

The orientations of maximum fitness vary with V_PM/V_free, but the SS pattern is that with zero fitness at the equilibrium V_PM. (a) The sum of +70/0/−70 degree filaments grew fastest in number at low N_fb and V_PM, but only the ±35 degree population remained at SS V_PM (standard conditions with σ_br = 0 degree and a rigid PM for clarity). (b) The 3D fitness landscape for standard conditions. (c) V_PM/V_free rises with N_fb. (d) A 2D representation of b shows positive (green) or negative (red) fitness at a given velocity and orientation. At low V_PM/V_free, all orientations undergo net reproduction, raising N_fb and V_PM/V_free. The “terminal” V_PM is achieved by, and limited to, the ±35 degree family.

Following Maly and Borisy's evolutionary “fitness” concept, fitness = (rate of change of N_fb)/(N_fb) for each orientation. The value is positive if a population is growing in number, zero if constant, and negative if decreasing toward extinction. Fig. 5b shows the fitness landscape for standard branching parameters as a function of φ_fil and V_PM/V_free, with the two symmetric patterns, +70/0/−70 and ±35 degrees, having maximum fitness at low and high velocities, respectively. When either pattern is rotated slightly, the capping rate of the filament with the largest φ_fil increases faster than the branching rate of its parent, causing a net decrease in fitness. Because ≈2/3 of new filaments branching from the triplet contribute to the pattern (1/2 each of branches from ±70 degree filaments, and 2/2 branches from 0 degree filaments ≈4 of 6 new filaments), whereas only 1/2 of branches from ±35 degree filaments contribute to their pattern, the triplet has a superior reproductive rate and fitness at low velocities. At higher protrusion rates, this effect is overcome by the low f_ε of slow 70 degree filaments.

To identify the SS condition from Fig. 5b, we note that, under any model context, an increase in SS N_fb always increases SS V_PM/V_free due to the higher net rate of protrusive kinetic events (Fig. 5c). A typical path through the fitness landscape can therefore be shown as a Darwinian evolution of patterns through the flattened landscape representation in Fig. 5d. At low N_fb, all forward-facing orientations interact with the same low-velocity PM and exhibit net branching [f_ε R_br > (1-f_ε) R_cp for every φ_fil]. This leads to an increase in N_fb and V_PM and to an environment in which filaments at orientations near 0 and ±70 degrees decrease in count (Fig. 5d, i). Because any V_PM with orientations of positive fitness will ultimately result in an increased total N_fb, this cycle will continue (Fig. 5d, ii) until reaching the equilibrium V_PM and its only viable orientations, near ±35 degrees. There, f_ε R_br = [1-f_ε] R_cp for 35 degree filaments (i.e., fitness = 0), but all other orientations are driven to extinction by net capping. Given different branching parameter values consistent with a low V_PM, the triplet reproduces itself at a higher rate than the two-peak distribution, consequently mandating a slightly higher equilibrium V_PM and the extinction of the ±35 degree pattern. In either case, populations of orientations reproduce and drive environmental changes (V_PM/V_free), that lead to changes in fitness and, ultimately, to a single symmetric pattern and velocity.

Conclusions

We have developed a comprehensive 2D model of lamellipodial protrusion based on the dendritic-nucleation/array-treadmilling mechanism, incorporating diffusion, stochastic kinetics, and elastic filament and PM models. A standard set of model parameter values were determined both directly from the literature and indirectly by using the criteria that model results of filament length, orientation patterns, and development times must be consistent with observed properties. Following these criteria, free barbed ends were protected from capping and allowed to branch at R_br = 0.43/sec within a distance ε of 5.4 nm from the leading edge. This conferred the only directionality to the system.

The model accounts for the essential dynamic properties of the network, including a negative feedback loop, controlling the fraction of free barbed ends within ε, that maintained a constant SS protrusion rate V_PM regardless of load. Under standard parameter values, the system converged from any ICs to a SS V_PM/V_free of 0.38 and a free barbed end count N_fb of 200 per μm. The filament pattern also self-organized, with only a ±35 degree pattern remaining at this terminal V_PM. The system in fact displayed the hallmark adaptation to this pattern from distributions initially devoid of ±35 degree filaments. Any deviation from the symmetrical orientation increased the capping rate at the larger angle more than it increased the branching rate at the smaller angle. Changes in the direction of protrusion were thus corrected for by preferential reproduction of newly symmetrical patterns generated via branching angle “errors.”

Alternate parameter values that resulted in a SS V_PM/V_free < 0.20 (e.g., very low R_br) resulted in a −70/0/70 degree pattern. Altering V_free alone had no effect. Protection from capping within ε was absolutely required for realistic pattern formation, although branching localization was not. The pattern was robust with respect to PM surface and bending energies, but sensitive to filament bending lengths longer than ≈50 nm. These robustness and sensitivity traits describe a self-organizing filament network that resists environmental pressures in maintaining a characteristic orientation pattern and protrusion velocity.

Abbreviations

IC

initial condition

SS

steady state

PM

plasma membrane

LE

leading edge

EM

electron micrograph

RF

rigid and flexible (beam-bending) filament model

fil

filament.