Mechanism of the myosin catalyzed hydrolysis of ATP as rationalized by molecular modeling

Abstract

The intrinsic chemical reaction of adenosine triphosphate (ATP) hydrolysis catalyzed by myosin is modeled by using a combined quantum mechanics and molecular mechanics (QM/MM) methodology that achieves a near ab initio representation of the entire model. Starting with coordinates derived from the heavy atoms of the crystal structure (Protein Data Bank ID code 1VOM) in which myosin is bound to the ATP analog ADP·VO₄⁻, a minimum-energy path is found for the transformation ATP + H₂O → ADP + P_i that is characterized by two distinct events: (i) a low activation-energy cleavage of the P_γO_βγ bond and separation of the γ-phosphate from ADP and (ii) the formation of the inorganic phosphate as a consequence of proton transfers mediated by two water molecules and assisted by the Glu-459–Arg-238 salt bridge of the protein. The minimum-energy model of the enzyme–substrate complex features a stable hydrogen-bonding network in which the lytic water is positioned favorably for a nucleophilic attack of the ATP γ-phosphate and for the transfer of a proton to stably bound second water. In addition, the P_γO_βγ bond has become significantly longer than in the unbound state of the ATP and thus is predisposed to cleavage. The modeled transformation is viewed as the part of the overall hydrolysis reaction occurring in the closed enzyme pocket after ATP is bound tightly to myosin and before conformational changes preceding release of inorganic phosphate.

The mechanism of hydrolysis of adenosine triphosphate (ATP) by myosin, leading to adenosine diphosphate (ADP) and inorganic phosphate (P_i), which constitutes one of the most important enzymatic reactions responsible for energy transduction into the directed movements of adjoining actin filaments, continues to remain a subject of active debates (1–16), a significant part of which relates to what constitutes the acceptor of the proton that must be released by the “lytic” water in its nucleophilic attack on the ATP γ-phosphate.

In terms of the generally accepted kinetic scheme (1–3), the relevant ATP–myosin transformations may be described by the equation

in which M* and M** indicate conformers of myosin. As reported (1–3), reaction (Eq. 1) occurs with a near unit equilibrium constant K < 10 and the estimated rate constants k₊ ≥ 160 s⁻¹ and k₋ ≥ 18 s⁻¹. The rate constant k₊ = 160 s⁻¹ can be converted to the free-energy activation barrier ΔG^# ≈ 14.6 kcal/mol at room temperature, T = 300 K, by applying a simple transition-state theory formula (17)

However, noting that the experimental rate constants of reaction (Eq. 1) incorporate contributions from conformational changes in the protein from M* to M** leads us to expect that the activation energy of the intrinsic chemical reaction

which excludes conformational rearrangements, should be considerably <14.6 kcal/mol.

However, previous attempts (13, 15, 16) to simulate the mechanism of reaction 3 by using quantum-based simulations all have resulted in an activation energy barrier >26 kcal/mol. We reason that this discrepancy in modeled and experimental results may be attributed to the key assumption of refs. 13, 15, and 16 that the reaction mechanism is of the associative type. In this type of mechanism, a nucleophilic attack of the water molecule on the γ-phosphate of ATP consists in the formation of a penta-coordinated oxophosphorane intermediate, followed by breaking the P_γO_βγ bond and generation of ADP and inorganic phosphate. This scenario is significantly different from our findings, detailed as follows.

As shown in our previous quantum mechanics and molecular mechanics (QM/MM) simulations of the GTP hydrolysis by GTPases (18–20), the reaction energy profile consistent with an associative-type mechanism indeed leads to a high activation barrier of ≈30 kcal/mol. However, other routes have been found for the GTP hydrolysis with considerably lower activation energies (10–16 kcal/mol), which do not assume formation of a penta-coordinated oxophosphorane intermediate (18–20). For another related system, the phosphoryl transfer reaction in a protein kinase, quantum-based modeling by Valiev et al. (21) led to activation energies within the range of 7–11 kcal/mol and the conclusion that the mechanism was predominantly dissociative.

The modeling presented here follows a preliminary effort, which specifically was designed to test the “two-water hypothesis” advanced by Onishi et al. (10, 11) in which the proton acceptor is simply another water aided by the Glu residue of the salt bridge. In that approach, the computational model used was purely of the quantum type, consisting of 150 atoms derived from the 1VOM crystal structure (22). The potential energy surface was explored, and a transition state thus was found that occurred after a proton transfer from the lytic water to the second water, but because of an inadequate representation of the protein context, the conclusions required further support. Hence, in this article we use a QM/MM approach that has proved fruitful in the modeling of GTP hydrolysis (18–20). Incorporating the essential elements of the two-water hypothesis, our QM/MM calculations provide a reaction profile of the ATP hydrolysis by myosin that is characterized by modest energy changes along the reaction pathway, including the activation and reaction energies.

Simulations

The x-ray structure of the Mg²⁺–ADP–vanadate (VO₄⁻) complex of Dictyostelium discoideum myosin II motor domain solved at a resolution of 1.9 Å (Protein Data Bank ID code 1VOM) by Smith and Rayment (22) has been an important step in structural studies of ATP hydrolysis. Throughout this article, we use the numbering of residues consistent with that of the 1VOM structure. In this crystal structure, the missing heavy and hydrogen residue atoms were restored; the VO₄ moiety in the vanadate analog was replaced by a PO₃ phosphate group and a presumptive lytic water molecule, with the water's oxygen taking on the position of the replaced vanadate O₄ oxygen. In addition, the 705 water oxygen molecules were upgraded to water molecules. This complex was energy-minimized relative to the AMBER force field (23) and a distant-dependent dielectric. Complete solvation was then obtained by adding a 5-Å layer of water, followed by an energy minimization.

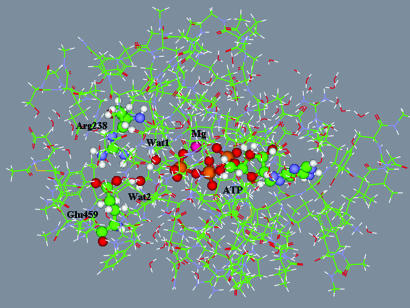
Shown in Fig. 1 is the model enzyme–substrate complex to be used for QM/MM calculations. It was obtained by eliminating all but the following residues that completely surrounded the reactive species: Leu-114, Ile-115, Tyr-116, Thr-117, Val-124, Ala-125, Val-126, Asn-127, Pro-128, Phe-129, Lys-130, Arg-131, Ile-132, Pro-133, Ile-134, Tyr-135, Thr-136, Leu-175, Leu-176, Ile-177, Thr-178, Gly-179, Glu-180, Ser-181, Gly-182, Ala-183, Gly-184, Lys-185, Thr-186, Glu-187, Asn-188, Thr-189, Lys-190, Lys-191, Val-192, Ala-218, Asn-219, Pro-220, Ile-221, Leu-222, Glu-223, Ala-224, Phe-225, Gly-226, Asn-227, Ala-228, Lys-229, Thr-230, Thr-231, Arg-232, Asn-233, Asn-234, Asn-235, Ser-236, Ser-237, Arg-238, Phe-239, Gly-240, Lys-241, Phe-242, Leu-263, Glu-264, Lys-265, Ser-266, Arg-267, Val-268, Thr-274, Glu-275, Arg-276, Asn-277, Tyr-278, His-279, Ile-280, Asp-314, Ile-315, Lys-316, Gly-317, Val-318, Ser-319, Gly-451, Val-452, Leu-453, Asp-454, Ile-455, Ser-456, Gly-457, Phe-458, Glu-459, Ile-460, Phe-461, Lys-462, Phe-466, Glu-467, Gln-468, Leu-469, Cys-470, Ile-471, Asn-472, Tyr-473, Thr-474, Asn-475, Glu-476, Phe-652, Val-653, Arg-654, Cys-655, Ile-656, Ile-657, Pro-658, Asn-659, Asn-660, Lys-661, Gln-662, Leu-663, and Pro-664. Residues Lys and Arg were assumed positively charged (protonated), whereas Asp and Glu were considered negatively charged (unprotonated). Also retained were 1,254 explicit water molecules, the magnesium cation Mg²⁺, and the unprotonated ATP molecule.

Fig. 1.

The model system for QM/MM calculations. Carbon atoms are shown in green, oxygen atoms are in red, nitrogen atoms are in blue, magnesium atoms are in magenta, and phosphorus atoms are in dark yellow. Balls and sticks distinguish the ATP moiety, magnesium cation, two reactive water molecules, and the Arg-238–Glu-459 salt bridge. Lines show the peptide chains and water molecules.

The initial position of the lytic water molecule Wat1 was derived as follows. The axial ligand (O₄) of the vanadate in the 1VOM crystal structure (22) was assumed to be the oxygen atom of Wat1, and oxygen of the crystal water W697 was assigned to Wat2 in the enzyme–substrate complex. Optimization of geometry parameters was carried out by performing QM/MM energy minimization.

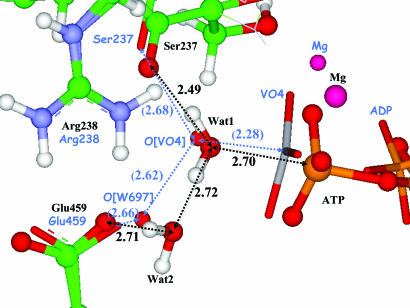
Fig. 2 shows superposition of the computed structure of the enzyme–substrate complex and the 1VOM crystal structure (22) in the vicinity of the γ-phosphate. An alignment of two structures was performed over the NCN triad of Arg-238. The computed model structure exhibits perfect hydrogen-bond network; the lytic water molecule, Wat1, is oriented perfectly for the subsequent nucleophilic attack by the hydrogen bonds with Ser-237 and Wat2. Computed distances between heavy atoms (shown in black in Fig. 2) are in fair agreement with the corresponding distances in the crystal structure (shown in blue in parentheses in Fig. 2) taking into account differences between the ADP–vanadate (VO₄⁻) complex and ATP.

Fig. 2.

Superposition of the computed minimum-energy geometry configuration of the enzyme–substrate complex (ball-and-stick representation, labeling the species and distances in black) and the 1VOM crystal structure (sticks, labeling the species and distances in blue). The distances between heavy atoms are shown in angstroms. The values in parentheses refer to the 1VOM crystal structure (22).

Results

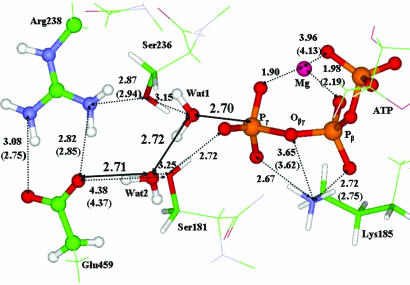
Fig. 3 illustrates an arrangement of the nearest amino acid residues and water molecules around ATP in the enzyme–substrate complex. The distances shown (in angstroms) between heavy atoms without parentheses refer to the results of QM/MM optimization. The distances in parentheses refer to the 1VOM crystal structure of the Mg²⁺–ADP–vanadate complex (22). Notable is the good agreement between the comparable theoretical and experimental distances. Also, the positions of the Ser-181, Lys-185, and Ser-236 residues (shown in sticks) relative to the QM subsystem (shown in balls and sticks) are in good agreement with the experimental data, even though their coordinates are optimized as those of effective fragments (MM part).

Fig. 3.

A fraction of the computed geometry configuration of the enzyme–substrate complex. In calculations, the phosphate groups of ATP, magnesium cation, side chain of Glu-459 and Arg-238, and water molecules Wat1 and Wat2 were included to the QM subsystem. The distances between heavy atoms are shown in angstroms. The values in parentheses refer to the 1VOM crystal structure (22).

The geometry configuration shown in Fig. 3 for the ATP–myosin complex closely resembles that of the GTP/Ras–GAP system (19); the value for the P_γO_βγ distance in ATP–myosin is exactly the same (1.78 Å) as in our previous QM/MM calculations for GTP/Ras–GAP complex, whereas the corresponding distance for methyl triphosphate in water clusters has been estimated as 1.69 Å (24). Therefore, as in the case of GTP hydrolysis in Ras and Ras–GAP (18–20), binding of ATP by myosin leads to a weakening of the P_γO_βγ bond compared with that in aqueous solution. This feature further is supported by the fact that, again as in the GTP/Ras–GAP system, the occupation number of the antibonding orbital σ*(P_γO_βγ) of ATP is approximately twice as large (0.24 a.u.) as compared with the occupation numbers (≈0.14 a.u.) of all other σ*(PO orbitals).

Although it is difficult to compare the QM/MM-optimized positions of the two water molecules, Wat1 and Wat2, displayed in Figs. 2 and 3, with positions of water molecules discussed by Onishi et al. (11), consideration of arrangements of waters relative to Glu-459 and γ-phosphate of ATP does provide support to the hydrogen-bond network proposed in the two-water hypothesis. This issue is discussed in detail in Discussion and Conclusion. The role of Ser-181, Ser-236, and Ser-237 as well as of the salt-bridge species Arg-238–Glu-459 apparently is to assist a proper orientation of these two water molecules.

An analysis of the geometry configuration shown in Fig. 3 suggests the reaction step that occurs when, upon Wat1's approaching the γ-phosphate of ATP (the initial distance is 2.70 Å), its hydroxyl binds to P_γ, and its proton is transferred to Wat2 along the hydrogen bond of 2.72-Å initial length. As in our previous QM/MM, calculations for GTP hydrolysis in Ras-GAP and Ras (19, 20), the reaction coordinate for this step was selected as the distance from P_γ to the oxygen atom of the nucleophilic water molecule Wat1. By gradually decreasing this distance from its value in enzyme–substrate (2.70 Å) and optimizing each time all other geometry parameters of the QM/MM model system, we succeeded in locating the transition state (shown in Fig. 4) that separates the enzyme–substrate complex (Fig. 3) and the reaction products (Fig. 5). According to QM/MM calculations, the energy of transition state relative to the enzyme–substrate level is 5 kcal/mol, whereas the energy of the reaction products lies 3.5 kcal/mol below the enzyme–substrate level.

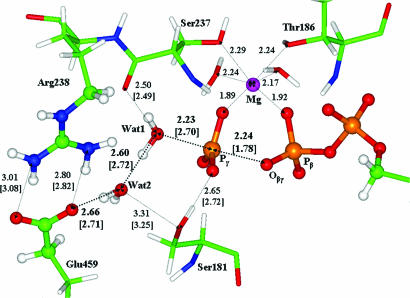
Fig. 4.

Geometry configuration of the transition state showing atoms of the quantum part in the ball-and-stick representation. Distances between heavy atoms (in angstroms) without brackets correspond to the transition state structure; distances in square brackets correspond to the geometry of the previous stationary point, the enzyme–substrate complex (Fig. 3).

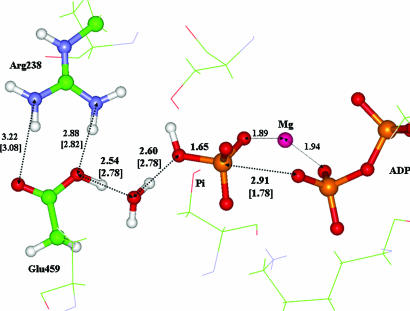
Fig. 5.

Geometry configuration of the reaction products showing distances (in angstroms). The values without brackets correspond to the enzyme–product structure; distances in square brackets refer to the geometry of the enzyme–substrate complex (Fig. 3).

The geometry configuration of transition state, illustrated in Fig. 4, is characterized by an almost planar PO₃ moiety that is well separated from ADP. The P_γO_βγ distance now is 2.24 Å compared with the initial value of 1.78 Å in enzyme–substrate. The water molecules Wat1 and Wat2 remain almost unchanged in that there is only a slight elongation (0.98 Å compared with 0.96 Å in enzyme–substrate) of the OH bond of Wat1 pointing toward Wat2.

Also illustrated in Fig. 4 is the coordination shell of the magnesium cation. Because the MgO distances experience variations within 0.02 Å along the entire reaction coordinate, the structure of this shell remains almost unchanged upon modeling the reaction (Eq. 3).

The geometry of the stationary point on the QM/MM potential energy surface corresponding to the reaction products ADP + HPO₄²⁻ is shown in Fig. 5. The direct QM/MM calculations confirm the hypothesis of ref. 11 that the chain of proton transfers required to form the inorganic phosphate HPO₄²⁻ includes both water molecules. However, we do not confirm the suggestion of ref. 11 that the stable intermediate H₃O⁺ is formed at the place of former Wat2. Instead, the minimum-energy configuration (Fig. 5) has Glu-459 as the stable proton recipient. We speculate that the protonated Glu-459 residue is a transient moiety in the entire ATP–myosin hydrolysis. Temporary protonation of Glu-459 could benefit opening the Arg-238–Glu-459 gate to facilitate the exit of inorganic phosphate (presumably in the form of H₂PO₄⁻) out of the cleft and also the restoration of the unprotonated status of the Glu residue. Modeling the large conformational changes that would be involved is not feasible with only QM/MM minimization procedures.

Discussion and Conclusion

The QM/MM simulations described in this article result in the conclusion that the energy profile for the ATP hydrolysis in myosin connecting the reagents (ATP + H₂O) and products (ADP + HPO₄²⁻) (Fig. 5) is consistent with a single elementary reaction. When the unprotonated substrate ATP is trapped in a protein environment, the P_γO_βγ bond becomes weaker, as evidenced by its elongation in the enzyme–substrate complex and by increased occupation numbers of the corresponding localized antibonding orbital. Consequently, low activation energy is required to cleave this bond and to separate the γ-phosphate group from ADP. Completion of the reaction to obtain the product HPO₄²⁻ results from a chain of proton transfers via a hydrogen-bond network that includes two water molecules and terminates in the Glu-459 residue of the salt bridge. The single transition state found for all these transformations has an energy of ≈5 kcal/mol counted from the enzyme–substrate energy level.

As mentioned above, previous attempts (13, 15, 16) to simulate the mechanism of reaction (Eq. 3) by using quantum mechanics alone or combined QM/MM methods have resulted in unrealistically high activation energy barriers. Okimoto et al. (13) reported activation barriers of 59 kcal/mol by using the HF/6–31G** method or 42 kcal/mol by using the B3LYP/6–31G** method for a small active-site molecular model in the gas phase. The proton acceptor was assumed to be the O₃ oxygen of the γ-phosphate. Li and Cui (15) used the QM/MM methodology for describing reaction (Eq. 3) in the protein environment. The authors considered two reaction routes, and both used the O₂ oxygen of the γ-phosphate as the proton acceptor. In one, the proton transfer was direct, and in the other, the proton was shuttled through Ser-236. By using the B3LYP/6–31+G**//HF/3–21+G approximation in the QM part, the rate-limiting barrier for the latter route was found to be 26 kcal/mol and only slightly larger for the former. These values may be underestimates because B3LYP approximations usually result in the underestimation of reaction barriers. The most recent QM/MM modeling for the reaction (Eq. 3) by Schwarzl et al. (16) led to very high activation barriers of 38–41 kcal/mol in the B3LYP/6–31+G**//HF/6–31G** approximation in the QM part.

The present QM/MM calculations mostly claim for adequate qualitative estimates of energy changes during the reaction (Eq. 3) but not for accurate values of the activation energy barrier (5 kcal/mol) and the reaction energy (−3.5 kcal/mol). First, the expected errors of this QM/MM approach for relative energies on potential energy surfaces may amount up to 2 kcal/mol compared with the full quantum treatment of the model system (25). Second, the high accuracy of conventional force field parameters in the molecular mechanical part of the QM/MM computational scheme is not guaranteed in the vicinity of a transition state. Third, the entropic contributions may alter energy changes along the reaction path, in particular, by increasing the computed activation barrier. The modeled transformation is viewed as the part (Eq. 3) of the overall hydrolysis reaction occurring after ATP is tightly bound to myosin and before conformational changes preceding release of inorganic phosphate. Hence, assuming the simple transition-state theory formula (Eq. 2) is correct, an experimentally based estimate for the free-energy activation barrier ΔG^# ≈ 14.6 kcal/mol for the entire hydrolysis process should be considered as an upper limit for the chemical reaction (Eq. 3) actually modeled in this work.

As emphasized in the foregoing, the part of hydrolysis with which we specifically are concerned does not encompass the myosin conformational changes that result in the fully bound state of ATP. As proposed by Onishi et al. (11), these conformation changes are described in terms of two switches (switch I and switch II) that respond to the initial binding of the ATP–Mg complex in such a way as to promote formation of the Arg–Glu salt bridge and hydrogen-bonding network that favorably position the two water molecules used in our modeling. The result of these prehydrolysis changes is closure of the nucleotide-binding cleft that constrains the substrate in a state ready for the hydrolytic event. It is this state that we have modeled and identified as the ground state of the myosin–substrate complex from which to search for the hydrolysis transition state.

Agreement of our model with experimental observations also is evidenced by (i) oxygen exchange experiments (5) that suggest a single-step elementary mechanism of the chemical reaction; (ii) the observed (4) inversion of the P_γO₃ configuration apparently seen in the computed transition state (Fig. 4); and (iii) the critical role of the salt-bridge pair Arg-238–Glu-459 underlined in many studies, including site-directed mutagenesis investigations (7, 8, 10).

We therefore consider this work to be a theoretical modeling of the ATP–myosin hydrolysis reaction (Eq. 3), resulting in reasonable energetics of the chemical transformations at this stage of the hydrolysis. It is the result of the high-resolution description of the interactions of the reactive site (QM part) with the protein environment (MM part) that is obtained with the ab initio-type QM/MM method (25–28), described in Methods, and also of not assuming an associative reaction mechanism as a guide in the modeling.

Methods

For calculations of the reaction energy profile, we use the ab initio-type QM/MM method based on the theory of effective fragment potentials (EFPs) (26). This is an approach that allows one to perform calculations close to an ab initio treatment of the entire molecular system. Molecular groups assigned to the MM part are represented by effective fragments that contribute their electrostatic potentials expanded up to octupoles to the quantum Hamiltonian. These one-electron electrostatic potentials as well as contributions from interactions of effective fragments with the QM region are obtained in preliminary quantum chemical calculations by using ab initio electron densities. The exchange–repulsion potentials to be combined with the electrostatic and polarizability terms also are created in preliminary ab initio calculations. Thus, all empirical parameters are entirely within the MM subsystem. In the original EFP-based approach (26), interactions between solvent molecules are computed as EFP–EFP interactions. In our flexible effective fragment version (25, 27, 28), we replace the EFP–EFP terms with the force field parameters, here from the AMBER library (23). The computer program used in the simulations is based on the GAMESS(US) (29) [more specifically, on its Intel-specific version, PC GAMESS (30)] quantum-chemistry package and on the TINKER (31) molecular-modeling system.

In this application, all phosphate groups of fully unprotonated ATP, the two nearest water molecules (Wat1 and Wat2 in Fig. 1), magnesium ion, and the side chains of Glu-459 and Arg-238 were assigned to the QM part. Alternative partitioning schemes to the QM and MM parts also were tested at preliminary stages. In particular, we considered including the side chains of Ser-236 and Ser-237 in the QM part instead of the Arg-238–Glu-459 salt bridge. However, we obtained a similar arrangement of the reagents for the enzyme–substrate complex as shown in Fig. 3, thus suggesting that the reaction should proceed with participation of the two water molecules but not via the side chain of Ser-236. It should be noted that the side chains of Ser-236, Ser-237, Ser-181, and Lys-185, along with other amino acid residues in the vicinity of the reaction center, are represented in our model by effective fragments in the MM subsystem and actually contribute to the QM/MM energies and forces. In total, 47 atoms constituted the quantum subsystem, and 1,800 atoms subdivided to 550 effective fragments were included in the MM subsystem.

The simulations included scans of the composite multidimensional QM/MM potential energy surface in the regions where chemical bonds or hydrogen bonds could be cleaved or formed. As a result, the basins around presumable stationary points were specified for more careful calculations of the local minima or saddle points. The stationary points were located by unconstrained minimizations (for local minima) or constrained minimizations (for saddle points) of the QM/MM energy. The location of a transition state was determined based on the criterion that the gradient of the constrained internal coordinate along an assumed reaction path must change its sign at the presumed location. The internal coordinates of all atoms in the QM subsystem and positions of effective fragments in the MM subsystem were optimized. Positions of remote effective fragments far away from the reaction center were kept fixed as in the crystal structure.

Geometry optimizations were carried out by using the Hartree–Fock approach in the QM part. The polarized LANL2DZdp ECP basis set [and the corresponding pseudopotential for phosphorus (32)] was used for all atoms except magnesium. In a series of preliminary calculations for the PO₃⁻ + H₂O reaction compared with the benchmark treatment of ref. 33, we verified that applications of the LANL2DZdp ECP parameters allowed us to achieve an accuracy corresponding to the use of more expensive all-electron 6–311++G** conventional basis set parameters. For magnesium, the standard 6–31G basis was used. It should be noted that multiple minimum-energy points could be located in geometry optimizations. We attempted to overcome this difficulty by performing in each case numerous selections of the starting sets of coordinates for minimization until the lowest energy was reached under the condition that the hydrogen-bond network in the immediate vicinity of ATP retains its structure.

Abbreviations

QM/MM

quantum mechanics and molecular mechanics

EFP

effective fragment potential.