Modeling the Combination of Amphotericin B, Micafungin, and Nikkomycin Z against Aspergillus fumigatus In Vitro Using a Novel Response Surface Paradigm

Abstract

Response surface methods for the study of multiple-agent interaction allow one to model all of the information present in full concentration-effect data sets and to visualize and quantify local regions of synergy, additivity, and antagonism. In randomized wells of 96-well plates, Aspergillus fumigatus was exposed to various combinations of amphotericin B, micafungin, and nikkomycin Z. The experimental design was comprised of 91 different fixed-ratio mixtures, all performed in quintuplicate. After 24 h of drug exposure, drug effect on fungal viability was assessed using the tetrazolium salt 2,3-bis {2-methoxy-4-nitro-5-[(sulfenylamino) carbonyl]-2H-tetrazolium-hydroxide} (XTT) assay. First, we modeled each fixed-ratio combination alone using the four-parameter Hill concentration-effect model. Then, we modeled each parameter, including the 50% inhibitory concentration (IC₅₀) effect, versus the proportion of each agent using constrained polynomials. Finally, we modeled the three-agent response surface overall. The overall four-dimensional response surface was complex, but it can be explained in detail both analytically and graphically. The grand model that fit the best included complex polynomial equations for the slope parameter m and the combination index (equivalent to the IC₅₀ for a fixed-ratio concentration, but with concentrations normalized by the respective IC₅₀s of the drugs alone). There was a large region of synergy, mostly at the nikkomycin Z/micafungin edge of the ternary plots for equal normalized proportions of each drug and extending into the center of the plots. Applying this response surface method to a huge data set for a three-antifungal-agent combination is novel. This new paradigm has the potential to significantly advance the field of combination antifungal pharmacology.

Invasive aspergillosis is a major cause of morbidity and mortality in highly immunocompromised persons (15). Risk factors for invasive aspergillosis include prolonged neutropenia, hematopoietic stem cell transplantation, solid organ transplantation, advanced AIDS, and chronic granulomatous disease (22). The expansion of the number of antifungal drugs with different modes of action that are used in the clinic and that are at preclinical stages of development has generated significant interest in combination antifungal therapy for invasive aspergillosis (4, 11, 13, 14, 25). The recent sequencing of the Aspergillus fumigatus genome will provide additional tools for the identification of novel targets for drug development (19). These important advances create a greater need to model effectively the combination of antifungal agents in vitro and in vivo.

In the past, various approaches to the assessment of synergy, additivity, and antagonism have been developed. They include older graphical isobologram methods and newer statistical response surface methods. The older methods are mostly limited to two-agent interactions; however, several statistical response surface methods can be used for three-agent and higher order combinations. Response surface methods, in particular, allow one to model and interpret all of the information present in the full concentration-effect data set; to visualize local regions of synergy, additivity, and antagonism; and even to quantify the degree of synergy or antagonism.

In the current study, we modeled the in vitro effect of amphotericin B, micafungin, and nikkomycin Z on A. fumigatus. These agents have distinct modes of action. Amphotericin B principally acts by binding to ergosterol, the major component of fungal cell membranes, leading to the disruption of the membrane and leakage of cellular metabolites and eventually cell death (21). The echinocandin, micafungin, inhibits glucan synthase, leading to the depletion of β(1-3) glucan, a fungal cell wall constituent (10). Nikkomycin Z is an investigational drug that inhibits synthesis of chitin, also a fungal cell wall constituent (17). We demonstrated a complex set of interactions among these agents. Compared to simpler models, our final model fit the data the best and gave useful information about the interaction of the three drugs.

(Preliminary results were presented at the International Society of Anti-Infective Pharmacology [ISAP] meeting, Washington, DC, December 2005, and at the 2006 American Society for Clinical Pharmacology and Therapeutics Annual Meeting, Baltimore, MD [1a].)

MATERIALS AND METHODS

Tetrazolium salt 2,3-bis {2-methoxy-4-nitro-5-[(sulfenylamino) carbonyl]-2H-tetrazolium-hydroxide} (XTT) assay. (i) Preparation of conidia.

A clinical isolate of A. fumigatus previously used in experimental aspergillosis (18, 22) was used in all studies. Using standard CLSI methods (18a), the 24- and 48-h MICs of the isolate for amphotericin B were 0.5 μg/ml, the MICs for micafungin were ≤0.03 μg/ml, and the MICs for nikkomycin Z were 64 and 128 μg/ml at 24 and 48 h, respectively. MICs correspond to the lowest drug concentration that will inhibit fungal growth based on visual inspection.

Conidia were plated on Sabouraud BHI slants with chloramphenicol and gentamicin (Becton Dickinson, MD), incubated for 7 to 10 days at room temperature, and harvested by washing the slant with 10 ml of 0.05% Tween 20 in normal saline (NS). The conidial suspension was then passed through a 100-μm filter, counted on a hemacytometer, and diluted to 2.0 × 10⁶ CFU/ml. Conidia were then diluted 1:50 in MOPS (morpholinepropanesulfonic acid)-buffered RPMI (pH 7.0). In each experiment, the number of CFU per milliliter was verified by plating serial dilutions in duplicate on Sabouraud Dextrose Emmons plates and counting colonies 2 days later.

(ii) Preparation of drugs.

Commercial amphotericin B deoxycholate (McKesson, West Seneca, NY) was reconstituted in dimethyl sulfoxide (DMSO) (100%) and diluted 1:50 in MOPS-buffered RPMI (pH 7.0) to generate a concentration of 4.44 μg/ml. Micafungin (Fujisawa, Deerfield, IL) was reconstituted in NS (5 mg/ml) and then diluted 1:50 to generate a concentration of 2.22 μg/ml in 2% DMSO MOPS-buffered RPMI (pH 7.0). Nikkomycin Z (provided by Thomas Walsh, NIH, Bethesda, MD) was reconstituted in MOPS-buffered RPMI (pH 7.0) to generate a concentration of 2.22 mg/ml.

(iii) Drug combinations.

Solutions of each drug alone were prepared as well as the various fixed-ratio binary and ternary mixtures. Drug dilutions in 2% DMSO MOPS-buffered RPMI were first made sequentially by 3.33-fold in tubes in 96-tube racks. The tubes were then randomized into new racks; and the drug solutions (100 μl/well) were applied to the wells in flat-bottom 96-well plates. Our group found that systematic growth patterns can be found in routine nonrandomized growth experiments; the additional randomization step is useful for eliminating systematic biases (6).

Five experiments, which we will refer to as experiments A to E, were performed separately. Each design point in each experiment was replicated in quintuplicate; thus, each stack included five 96-well plates, each with the same set of drug concentrations. We analyzed a total of 91 different fixed ratios (7 in experiment A, and 21 in each of experiments B through E), with 11 serial drug dilutions per fixed ratio and control wells that contained conidia, medium, and vehicle without added drug. There was a total of 5,610 data points: 91 fixed ratios (each with 11 dilutions) plus 13 control columns, 1 in experiment A and 3 in each of experiments B through E, in quintuplicate, with the exclusion of 110 wells that could not be satisfactorily read.

For these experimental designs, the assumed potency ratio on a microgram-per-milliliter basis used for micafungin-to-nikkomycin Z-to-amphotericin B was 1:1000:2. For example, a 1:4:2 ratio will correspond to a 1:4,000:4 fixed ratio of concentrations (on a microgram-per-milliliter basis).

(iv) Measurement of fungal viability.

Following the addition of drug-containing medium to each well, the conidial suspension (100 μl) was added (t = 0 h). Control wells contained conidia, medium, and vehicle used to solubilize drug, without active drug. Blank wells consisted of medium only without conidia. Plates were incubated at 37°C, and the XTT assay was performed at 24 h essentially as previously described by Meletiadis et al. (16), but with a minor adaptation. A stock solution of XTT (Sigma Chemical, St. Louis, MO) was dissolved in NS (1 mg/ml). A 10-mM solution of the electron-coupling agent menadione (Sigma Chemical) was prepared in acetone and then diluted 1:10 in NS. A working solution consisting of 4.0 ml XTT and 0.5 ml menadione was prepared immediately before use. Fifty microliters of the combination solution was added to each well, and plates were incubated for 2 h at 37°C. One hundred microliters of the supernatant was transferred to a new plate, and the optical density at 450 nm (OD₄₅₀) was determined by using a Labsystems Multiskan Plus plate reader. Final concentrations of XTT and menadione in each well were 200 μg/ml and 25 μM, respectively (16).

An additional experiment was performed to ensure that the drugs did not, by themselves, affect the colorimetric readout of the assay. Amphotericin B (2.4 μg/ml), micafungin (0.48 μg/ml), and nikkomycin Z (120 μg/ml) and the combination of all three drugs was added to medium in 96-well plates and serially diluted 3.33-fold 11 times. None of the wells contained A. fumigatus conidia. Blanks contained medium alone. Plates were incubated at 37°C for 24 h followed by the addition of XTT-menadione and the determination of the OD₄₅₀. None of the drug concentrations alone or in combination affected the OD₄₅₀ (data not shown). Another reassurance that the drugs had no direct effect on the colorimetric readout was that when exposed to fungus, none of the drugs produced a concentration-effect curve with a right tail that drifted upward with increasing drug concentration.

(v) Statistical methods and results.

For fitting models to data, we used SAS 9.1; for the graphs we used SigmaPlot version 9.0; and for some intermediary calculations, we used Microsoft Excel.

In SAS, we used the PROC NLIN procedure. In that procedure, we use the Gauss-Newton algorithm. The NOHALVE and CONVERGE PARM = 1e⁻⁸ options were used to facilitate convergence.

The procedure was run a first time using rough, graphic-based estimations of the parameters with appropriate constraints, and then those initial estimates were fine tuned and the procedure was rerun to minimize the objective function and have the procedure converge. We also tried to minimize the standard deviations of the parameter estimates.

Modeling.

(i) Weighting. For weighting, we used the inverse of the predicted variances at each design point. As a representative example, Fig. 1 shows the double-logarithmic relationship between sample variance (y axis) and sample mean (x axis) for each quintuplicate design point for pooled experiments D and E; the best-fit regression line gives an estimate of the log variance versus log mean slope that we will call Φ3 (here the estimated Φ3 is 1.59).

FIG. 1.

Variance versus mean plot to estimate weighting factor.

Such a slope estimate was calculated for experiment A (Φ3 = 2.12), experiment B (Φ3 = 1.80), experiment C (Φ3 = 2.15), and pooled experiments D and E (Φ3 = 1.59). Experiments D and E were performed very close in time, and the slope estimates were very close, so we decided to pool them for the weighting.

The weighting factor (w) for each design point used was proportional to the reciprocal of the estimated variance, w = (modeled effect)^−Φ3.

Finally, the sum of weights was calculated with the final fits and a correcting factor, F, was applied to each individual weight so that the sum of weights equals number of data points, N. F varied and had to be recalculated for each different model used.

This gave us the following weighting scheme:

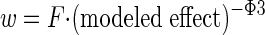(1)

(ii) Hill equation.

The basis of our modeling work in this report is the four-parameter Hill concentration-effect model presented in equation 2 below.

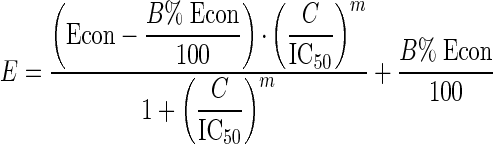(2)

In this equation, E is the measured effect (response), such as the cell mass (XTT absorbance) remaining in a culture vessel after drug exposure; C is concentration of drug; Econ is the measured effect at zero drug concentration; IC₅₀ is the median effective dose (or concentration) of drug; B% is the background of measured effect at infinite concentrations (expressed as a percentage of Econ); and m is a slope parameter. When m has a negative sign, the curve falls with an increasing drug concentration; when m is positive, the curve rises with an increasing drug concentration. When the absolute value of m is high (>5), the sigmoidal curve drops or rises rapidly; when it is low (<1), the sigmoidal curve drops or rises gradually.

We used three distinct approaches to model the data, with each sequential approach being more complex and comprehensive than the previous one. The three methods were mathematically consistent with each other, but more statistical rigor accompanied the more complex approaches.

(iii) First approach: simple Hill model.

First, we modeled each fixed-ratio combination alone by fitting the four-parameter Hill concentration-effect model described in equation 2 above to each set of single agent and each set of fixed-ratio combination concentration-effect data (91 individual curves). We allowed one Econ for each of the five experiments, and one IC₅₀, m and B% per fixed-ratio concentration-effect curve; therefore, we tabulated 278 parameter estimates.

(iv) Second approach: modified CI₅₀ approach.

For the second approach (1), the transformed x axis is C₁/IC_50,1 + C₂/IC_50,2 for a two-agent combination, or C₁/IC_50,1 + C₂/IC_50,2 + C₃/IC_50,3 for a three-agent combination. A modified Hill model is then fit to the transformed data. The estimated IC₅₀ for a fixed ratio is then called the combination index at the 50% level (CI₅₀), which itself is a measure of Loewe synergy (CI₅₀ < 1), Loewe antagonism (CI₅₀ > 1), or Loewe additivity (CI₅₀ = 1). Equation 3 was fit to data for a three-agent fixed-ratio combination:

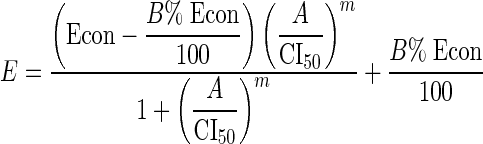(3)

with A being the total normalized amount of drugs as follows:

(4)

and C₁, C₂, and C₃ being the concentrations of drugs 1, 2, and 3, respectively, and IC_50,1, IC_50,2, and IC_50,3 being the median effective concentrations of drugs 1, 2 and 3, respectively. We allowed one Econ for each of the five experiments and one IC₅₀ or CI₅₀, m, and B% per fixed-ratio concentration-effect curve; therefore, we tabulated 278 parameter estimates, the same as with the simple Hill model approach.

(v) Third approach: overall response surface approach.

Our third data analysis approach was to fit an overall response surface to all of the data simultaneously. There was no really consistent pattern observed for B% estimated from the second approach with drug fractions, so we decided to fix B% at its estimated value for each fixed ratio for later analyses. In step 3A, the m's and CI₅₀s estimated from the second approach were then modeled as a function of drug fractions by using the following constrained polynomials.

For m

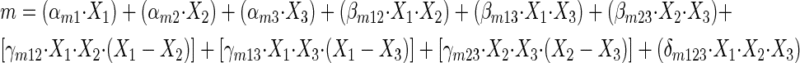(5)

and for CI₅₀

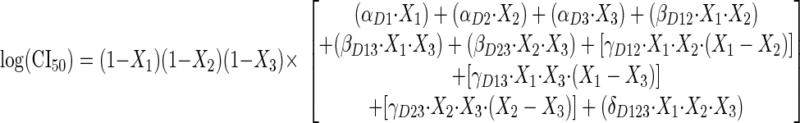(6)

with X₁ being fractions of micafungin, X₂ fractions of nikkomycin Z, and X₃ fractions of amphotericin B:

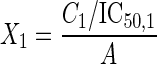(7)

(8)

(9)

All of the α, β, γ, and δ terms are polynomial coefficients (estimatible parameters). The use of these polynomials and the general modeling paradigm is from White et al. (31). The polynomials were simplified as much as possible, by stepwise eliminating terms during sequential nonlinear regression runs until all remaining terms had 95 percent confidence intervals not encompassing zero. The final estimates for the 15 polynomial coefficients from step 3A were then used as initial estimates for the grand model in step 3B.

Finally, in step 3B, we pooled all of the 5,610 data points from all five experiments and fit a grand model (equations 10 to 12) with 35 estimable parameters to all of the data simultaneously.

(10)

The grand model included 35 parameters: five Econs, one for each experiment and 15 IC₅₀s (one for each drug alone for each of five experiments, nine polynomial coefficients for m, and six polynomial coefficients for CI₅₀).

RESULTS

The final polynomials, reduced in structure to insure that all parameters had confidence intervals not including 0, are presented in equations 11 and 12:

(11)

(12)

with X equal to the vector of specific ratios of the three drugs X₁, X₂, and X₃ (equations 7, 8, and 9 above) and with θ equal to the vector of parameters (polynomial coefficients for m and CI₅₀), None of the 35 parameter estimates in the final grand model had 95 percent confidence intervals encompassing zero, confirming that they were all useful for the characterization of the four-dimensional response surface.

Figure 2 shows examples of fits with 95% confidence interval envelopes for the final fit of the grand model. The abscissa is A, the normalized sum of the drug amounts (except for the drugs alone where it is the drug concentration), and the ordinate is the absorbance from the XTT assay. The observed data, predicted values, and upper and lower population 95% confidence interval envelopes are shown.

FIG. 2.

Examples of raw data and fits with the grand model and sum of normalized concentrations versus effect showing the data points (circles), estimates (solid lines), and population 95% confidence interval envelopes (dashed lines). The red dashed line shows the CI₅₀ (the 95% confidence interval was too narrow for display). Triangles indicate the controls. Ampho, amphotericin B; mica, micafungin; nikk, nikkomycin Z.

Figure 3 shows observed data (absorbances obtained from the experiment) versus the absorbances predicted from the grand model.

FIG. 3.

Effect predicted (for the grand model) versus observed effect by experiment. The thick line is the identity line (where the predicted effect = the observed effect).

Figure 4 shows the m estimates from the modified CI₅₀ method versus the m estimates from the grand model to give an idea of the quality of the fit and the absence of bias.

FIG. 4.

m predicted with the grand model versus m predicted with modified CI₅₀ method by experiment. The thick line is the identity line (where the grand model = the CI₅₀ method).

Figure 5 shows the CI₅₀s estimated from the modified CI₅₀ method versus the CI₅₀s estimated from the grand model to give an idea of the quality of the fit and the absence of bias.

FIG. 5.

CI₅₀ predicted with the grand model versus CI₅₀ predicted with modified CI₅₀ method by experiment. The thick line is the identity line (where the grand model = the CI₅₀ method).

In Fig. 6, the upper panels include traditional isobolograms at the 50% effect level. The lower panels include plots of the CI₅₀s (log scale) versus drug fraction (X₁, X₂, and X₃ from equations 7 to 9). This figure shows that we have irregular isobols, with zones of antagonism and zones of synergy for the same two drug mixtures at different ratios when we apply the simple Hill approach or the modified CI₅₀ approach. Note that the isobols from the grand model in the upper panels and the corresponding curves in the lower panels are also asymmetrical. The ability to model asymmetrical isobols is a special unique property of our response surface modeling paradigm.

FIG. 6.

Upper panels include traditional isobolograms at the 50% effect level. Symbols are derived from IC₅₀ estimates from the first simple Hill model approach. Thick straight black lines connect the symbols. The middle curve is simulated from the final fit of the grand model. The two curves around the middle curve comprise the 95% confidence envelopes around this final fit. Lower panels include plots of the CI₅₀s (log scale) versus drug fraction (X₁, X₂, and X₃ from equations 7 to 9). Symbols are derived from CI₅₀ estimates from the second modified CI₅₀ approach. Thick straight black lines connect the symbols. For both upper and lower panels, a different symbol has been used for each of the five experiments. The middle curve is simulated from the final fit of the grand model. The two curves around the middle curve comprise the 95% confidence envelopes around this final fit. The thin straight black lines on the lower and upper panels are the additivity lines. Ampho, amphotericin B; mica, micafungin; nikk, nikkomycin Z. □, experiment B; ⋆, experiment E; ▿, experiment D; ▵, experiment C; ○, experiment A.

The estimates of the parameters from the grand model are given in Tables 1 and 2. Micafungin was the most difficult drug to model, with IC₅₀s quite different among the experiments. The IC₅₀s for amphotericin B and nikkomycin Z were more reproducible. The narrow confidence intervals for the polynomial coefficients support the validity of this final model.

TABLE 1.

Estimates of Econs and IC₅₀s of drugs alone for each experiment from the grand model (the final best-fitting model)

Experiment	Parametera	Estimate	95% Confidence interval
A	Econ	0.842	0.824-0.859
	IC50ampho	0.272	0.261-0.283
	IC50mica	0.00501	0.00425-0.00576
	IC50nikk	39.9	34.0-45.9
B	Econ	0.859	0.848-0.870
	IC50ampho	0.341	0.316-0.365
	IC50mica	0.0795	0.0688-0.0901
	IC50nikk	32.5	28.5-36.6
C	Econ	0.871	0.861-0.881
	IC50ampho	0.328	0.311-0.346
	IC50mica	0.238	0.211-0.264
	IC50nikk	30.0	26.5-33.5
D	Econ	1.08	1.07-1.09
	IC50ampho	0.351	0.325-0.377
	IC50mica	0.0335	0.0294-0.0376
	IC50nikk	22.4	19.3-25.5
E	Econ	1.42	1.41-1.44
	IC50ampho	0.294	0.271-0.317
	IC50mica	0.0491	0.0437-0.0546
	IC50nikk	14.8	13.2-16.3

^aEstimates for Econ values are shown as OD units, and those for IC values are shown as micrograms per milliliter. IC₅₀ampho, IC₅₀ for amphotericin B; IC₅₀mica, IC₅₀ for micafungin; IC₅₀nikk, IC₅₀ for nikkomycin Z.

TABLE 2.

Estimate for polynomial parameters for the grand model

Parameter	Estimate	95% Confidence interval
αD1	−8.23	−9.35-−7.11
βD13	12.5	9.99-15.1
βD23	6.57	5.23-7.92
γD12	57.3	51.0-63.7
γD13	10.2	5.97-14.4
δD123	−30.0	−41.3-−18.6
αm1	−0.931	−0.999-−0.864
αm2	−1.23	−1.35-−1.12
αm3	−7.37	−8.37-−6.37
βm12	−5.47	−6.39-−4.55
βm13	9.20	7.63-10.8
βm23	5.15	2.50-7.79
γm12	1.75	0.689-2.81
γm23	11.3	8.44-14.2
δm123	20.51	12.87-28.14

Figure 7 shows the CI₅₀s predicted with the grand model for the whole surface in a ternary plot. We also show the contours for different CI₅₀ levels.

FIG. 7.

Predicted CI₅₀ for the different normalized ratios of each drug using the grand model with the observed design points (white dots). The symbols represent the design points for all of our 91 fixed ratios (different symbols have been used for each of five experiments). Each axis represents a normalized fraction of the drug in the mixture. The background colors represent the predicted values for the CI₅₀s using the grand model, the color scheme being shown on the left side: red indicates synergy, yellow indicates additivity, and blue indicates antagonism. The solid lines are the contours for fixed predicted CI₅₀s. The arrows show in which direction to read the axis of the ternary plot. □, experiment B; ⋆, experiment E; ▿, experiment D; ▵, experiment C; ○, experiment A.

Finally, Fig. 8 shows the CI₁₀, CI₂₅, CI₅₀, CI₇₅, and CI₉₀ predicted with the grand model in the same type of ternary plot as that for Fig. 7.

FIG. 8.

Predicted CIs for different levels for the different normalized ratios of each drug using the grand model. Synergy is in red, additivity in yellow, antagonism in blue. The solid lines are the contours for fixed predicted CIs.

DISCUSSION

Our novel modeling approach was able to fit the data properly and gave us insights into the synergy and antagonism patterns for the different proportions of each of three antifungal drugs. The full model that fit the best included a polynomial equation for m and a complex polynomial equation for CI₅₀. Our comprehensive modeling paradigm had the significant advantage over the simple Hill model approach and the modified CI₅₀ approach of providing an overall fit to all the data points simultaneously. The overall fit resulted in a smooth surface and smooth irregular isobols, while not allowing any single fixed-ratio concentration profile to unduly influence the final result.

For combinations of micafungin, nikkomycin Z, and amphotericin B at the 50% effect level, we observed the most synergy with the combination of micafungin and nikkomycin Z at a normalized ratio of 3:7 (3:7,000 ratio of concentrations), with no amphotericin B in the mixture. It may be useful to study this particular binary combination at this particular fixed ratio in future in vivo studies (after taking into account the pharmacokinetic profiles of each agent in the specific study species). This synergy zone was indicated by CI₅₀ levels of approximately 0.2, indicating a fivefold increase in the activity of the mixture over the additivity prediction. The maximum antagonism was indicated by a CI₅₀ of approximately 2 or a decrease of the activity by half relative to the additivity prediction.

At the other CI levels, the most intense synergy was observed with the normalized ratios of 0/96/4 (micafungin/nikkomycin Z/amphotericin B) for CI₁₀, ratios of 0/92/8 for CI₂₅, ratios of 27/73/0 for CI₇₅, and ratios of 23/77/0 for CI₉₀, with CI values of 0.064, 0.26, 0.12 and 0.073, respectively. The most intense antagonisms were observed with the ratios of 0/77/23 (CI value of 2.8) for CI₁₀, 0/64/36 (CI value of 1.9) for CI₂₅, 0/71/29 (CI value of 5.1) for CI₇₅, and 0/54/46 (CI value of 26) for CI₉₀, respectively.

A critical question regarding our whole modeling paradigm is what should be the maximum complexity of the two polynomials that provide the flexibility to the m and CI₅₀ expressions? Equations 5 and 6, with 10 polynomial coefficients in each equation, could easily be expanded to include more terms, including higher order terms. A glance at Fig. 4, 5, and 6 might give the impression that more complex polynomials might increase the overall goodness of fit of the grand model to the data. However, our group made a decision, based upon working with several complex three-agent data sets, that the maximum practical complexity for the two critical polynomials should be that of equations 5 and 6. The decision was based on (i) lack of reproduceability of very complex patterns for the m and CI₅₀ parameters, (ii) problems in interpreting the meaning of each individual coefficient in a very large set of polynomial coefficients, (iii) biases that different experimental designs would impose upon the numbers and orders of estimated sets of polynomial coefficients, and (iv) the lack of practical interest by biologists in an extremely complex but mostly empirical model. Our compromise approach is to limit the maximum complexity of the two critical polynomials to equations 5 and 6. Note that the polynomial expressions used finally in the grand model included only nine polynomial coefficients for the m expression, and six coefficients for the CI₅₀ expression. Of the 20 total possible polynomial coefficients for the m and CI₅₀ expressions, only 15 were retained, after eliminating coefficients whose 95% confidence intervals included zero in step 3A.

Combination antifungal studies in vitro have been largely restricted to testing only two agents at a time by using a checkerboard method using the fractional inhibitory concentration (FIC). FIC = MIC_A,combo/MIC_A + MIC_B,combo/MIC_B in which MIC_A,combo and MIC_B,combo are the MICs for agents A and B in a combination, and MIC_A and MIC_B are the MICs for agents A and B when applied individually. Synergy is defined as an FIC index of <1, an additive effect as an FIC index of 1.0, a subadditive or neutral effect as an FIC index of 1.0 to 2.0, and antagonism as an FIC index of >2 (20). Using this approach, the interaction between caspofungin and either voriconazole or amphotericin B was either synergistic, additive, or subadditive among clinical isolates of Aspergillus species, but no antagonism was observed (3, 20). This FIC method is ideally suited to evaluating a large number of fungal isolates (e.g., for epidemiologic studies). While the MIC provides a single value corresponding to the lowest concentration of drug that totally inhibits fungal growth, it provides limited information about how different concentrations of a given antifungal agent affect fungal growth to various degrees. The concentration-effect relationship of antifungals extends over a broad range of concentrations instead of growth versus no growth (28). The FIC index, which is derived from MIC data, provides limited understanding of potentially complex interactions among two or more antifungal agents. For example, two drugs may have synergy within a specific concentration range and additivity or even antagonism at another concentration range. A surface response approach, in which all drug effects alone and in combination and not just the MIC effect are modeled, overcomes some of these limitations (28). However, the fundamental mathematical origin of the FIC index approach and the sophisticated response surface approach described in the report are in fact the same (12).

The combination of an echinocandin and nikkomycin Z may be attractive since they target different fungal cell wall constituents. Chiou et al. (2) showed that micafungin and nikkomycin Z had marked in vitro synergistic activity against A. fumigatus as determined by the checkerboard inhibitory assay and MTT [3-(4,5-dimethylthiazol-2-yl)-2,5-diphenyltetrazolium bromide] viability assays. Time-sequenced light and electron microscopic studies demonstrated marked transformation of hyphae to blastospore-like structures in the presence of micafungin plus nikkomycin Z, while fungi treated with a single drug showed partial recovery at 24 h. Other studies have also reported in vitro synergy between nikkomycin Z and echinocandins against A. fumigatus (7, 26), but not between nikkomycin Z and either azoles or amphotericin B (7). Consistent with these studies, we noted a large region of synergy, starting at the nikkomycin Z/micafungin combinations for equal normalized proportions of each drugs and spreading toward the center of the ternary plot, and a region of antagonism between nikkomycin Z and amphotericin B at a high nikkomycin Z/amphotericin B ratios.

Hope et al. (9) used a response surface model (8) to examine the interaction of amphotericin B and flucytosine for treatment of systemic candidiasis in mice. The combination was additive, meaning that the experimental effect did not deviate in a statistically significant manner from the null reference model (or additive surface) of the combined effect. We recently reported that the combination of amphotericin B and micafungin was more effective than either agent alone in prolonging survival in experimental aspergillosis in the p47^phox−/− mouse model of chronic granulomatous disease (5). This study did not allow any conclusion about in vivo synergy, as a single-dose regimen was used for each drug. The same A. fumigatus isolate that was used in this in vivo study was used for in vitro modeling in the current report.

There are several limitations to our study. First, because of the intensive labor involved in this modeling approach, only a single A. fumigatus isolate was used. The interactions we observed may be substantially different for Aspergillus isolates with different susceptibility profiles to the antifungal agents we modeled. For example, modeling combination regimens against Aspergillus terreus, a strain with intrinsic resistance to amphotericin B (23, 24, 29), may produce entirely different interactions. We examined the effect of drug exposure at only one time point for a 24-h continuous drug exposure, and therefore, we cannot address potential time-dependent drug interactions. An inherent limitation of in vitro studies is that they cannot model the complex pharmacokinetics and host inflammatory response that occur in vivo. The presence or absence of ischemic necrosis will affect the local inflammatory response, tissue oxygen content, tissue pH, and drug delivery to the infected site, all of which may influence the clinical efficacy of antifungal regimens (27, 30). Therefore, results of in vitro modeling should not be directly extrapolated to the clinical setting. However, detailed in vitro modeling will provide the basis for the prioritization of promising drug combinations for evaluation in animal models as well as for the optimization of dosing. This approach may be particularly useful if one of the drugs has significant potency but also substantial toxicity (e.g., amphotericin B). A combination regimen involving synergistic agents may enable us to reduce the dose of the toxic drug and have an antifungal effect equal or superior to that of any of the agents used alone.

APPENDIX

The ratios and drug concentrations normalized by the IC₅₀ estimates for each agent and all experiments are shown in Table A1.

TABLE A1.

Ratios of drug concentrations normalized by the IC₅₀ estimates for each agent and all experiments^a

Experiment or stack	Micafungin	Nikkomycin Z	Amphotericin B
Expt A	1	0	0
	0	1	0
	0	0	1
	1	0	1
	1	2	3
	4	1	2
	1	4	2
	0*	0*	0*
Expts B and C
Stack 1	1	0	0
	1	1	0
	8	1	0
	1	4	0
	4	1	1
	2	2	1
	2	1	1
	0*	0*	0*
Stack 2	0	0	1
	1	0	1
	8	0	1
	1	0	8
	1	1	4
	2	1	2
	1	1	2
	0*	0*	0*
Stack 3	0	1	0
	0	1	1
	0	8	1
	0	1	8
	1	1	1
	1	2	2
	1	2	1
	0*	0*	0*
Expts D and E
Stack 1	0	1	0
	0	0	1
	0	1	8
	0	1	2
	0	4	1
	1	4	8
	1	0	4
	0*	0*	0*
Stack 2	1	4	4
	1	1	3
	1	0	1
	4	1	4
	1	1	1
	6	1	3
	2	2	1
	1	4	4
Stack 3	3	1	1
	8	0	1
	8	1	1
	8	2	1
	1	0	0
	8	1	0
	1	1	0
	3	1	1

^a*, controls.