Cancer incidences in Europe related to mortalities, and ethnohistoric, genetic, and geographic distances

Abstract

We have previously shown that geographic differences in cancer mortalities in Europe are related to (in order of importance): geographic distances (reflecting environmental differences), ethnohistoric distances (encompassing cultural and genetic attributes), and genetic distances of the populations in the areas studied. In this study, we analyzed the relations of the same three factors to European incidences of 45 male and 47 female cancers. Differences in cancer incidences are correlated moderately, first with geographic distances, and then with genetic distances, but not at all with ethnohistoric distances. Comparing these findings to the earlier ones for cancer mortalities, we note the reversal in the importance of ethnohistory and genetics, and the generally lower correlations of incidence differences with the three putatively causal distance matrices. A path diagram combining both studies demonstrates the lack of cultural carcinogenic effects, but suggests cultural influences on procedures such as the registration of deaths in different political entities. Additionally, the relatively large correlation between ethnohistoric distances and mortality differences is caused by common factors behind the correlation of ethnohistoric and geographic distances. Geographic proximity results in similar ethnohistories. The direct effects of genetic distances are negligible and only their common effects with geographic distances play a role, accounting for the weak to negligible influence of genetics on incidence and mortality differences. Apparently, the genetic systems available to us do not substantially affect cancer incidence or mortality. We present indirect evidence that international differences in the quality of cancer rate data are greater in mortalities than in incidences.

In an earlier study (1), we showed that differences in cancer mortalities of local populations in Europe are correlated more with their ethnohistoric distances than their genetic distances. We chose to study cancer mortalities before incidences because they were available in cancer atlases yielding balanced data matrices. The present study on cancer incidences required compilation of data from several volumes (2–5) in which the number of population samples and cancers recorded varied, resulting in unbalanced data matrices. Here we analyze cancer incidence rates as we had earlier analyzed mortalities and compare our incidence findings to those for mortality.

Differences in cancer rates between populations are affected in part by their geographic distances and ethnic differences (6, 7). Epidemiologists ascribe differences in cancer rates to genetic and environmental factors. Although some of the loci used in this study have been associated with cancer (7, 8), the majority of the genetic factors we used provides only an estimate of overall genetic distances between populations. Environmental factors known to affect cancer rates include cultural factors such as dietary habits, sexual practices, occupational practices, etc. Some other environmental components representing the physical environment are present in the geographic distances we used. Still others, such as pollution, are not well described by our covariates. The ethnohistoric differences estimated in our study comprise both genetic and cultural components. We attempt to disentangle the effects of these factors by means of partial matrix correlations as detailed below.

Materials and Methods

We used three European databases: cancer incidences (2–5), ethnohistory (9), and genetics (10). For these three, as well as for the sample locations, we computed interlocality distances as described below, assembled them as matrices, and tested the significance of their association by means of Mantel matrix permutation tests (11–14). Analyses of spatial autocorrelation (15, 16) of cancer incidence rates from this study, cancer mortality rates (17), ethnohistory (9), and genetics (10) showed that these four variables are strongly spatially autocorrelated. Consequently, conventional significance tests of their association would yield overly liberal results (18). We therefore controlled for geography by using a multiple matrix extension of the Mantel test (11, 18, 19), which yielded partial correlations of distance matrices.

The cancer incidence rates (age adjusted to the world standard; ref. 7) come from four volumes (2–5) issued by the International Agency for Research on Cancer. The volumes report European incidence rates for four periods between 1968 and 1988. The number of cancer sites varies across reporting stations. The maximal number is 45 for males and 47 for females, and the maximal number of European localities per cancer site is 75 (Czechoslovakia, 2; Denmark, 1; England, 8; Finland, 1; France, 6; Germany, 3; Hungary, 3; Iceland, 1; Ireland, 1; Italy, 9; Netherlands, 2; Norway, 1; Poland, 7; Portugal, 2; Romania, 1; Scotland, 5; Spain, 7; Sweden, 1; Switzerland, 5; former USSR, 8; and Yugoslavia, 1). Our final incidence rates are averages over time based on 1–4 of these rates. For any one sex and cancer site, the incidence distances between all pairs of available localities were computed as absolute differences in average incidence rates.

Ethnohistoric distances were computed from an ethnohistoric database for Europe, compiled in our laboratory and consisting of 3,460 records of ethnic locations and movements from 2200 B.C. to 1970 A.D. Details of its construction are given (9). It can be found on the at http://life.bio.sunysb.edu/ee/msr/ethno.html. The computer program ethno (by N. L. Oden; at the same Web address) estimates the admixture of populations from specific language families, after an updating algorithm (9). The program yields vectors of estimated proportions of contribution from 17 language families and two unknown groups to the population mix at each of 2,216 land-based 1° × 1° quadrats in Europe. We do not imagine that language affiliation has any direct effect on cancer rates. We use this variable as a marker for genetic and cultural variables that may have such effects. We computed arc distances (20) from these vectors between all pairs of quadrats. The distances are estimates of the dissimilarity between the ethnic mixes of each quadrat pair. We demonstrated in a series of sensitivity experiments (9) that ethnohistoric-genetic correlations were robust against reasonable perturbations in time of movement, location, ethnic (language-family) designation, and completeness of the database. To assemble ethnohistoric distance matrices, we chose the set of quadrats that matched the locations of the cancer incidence and genetic data.

Details of our genetic database for Europe are furnished (10). It comprises 26 genetic systems with 93 allele or haplotype frequencies and is based on 3,481 samples. We computed genetic distances separately for each genetic system. Except for myelofibrosis, for which we had only (an unreliable) three genetic systems, the smallest number of genetic systems for any one cancer was 15 for males and 14 for females. For each cancer incidence locality, a computer program found the closest genetic sampling point to form a matching pair of gene-frequency and cancer incidence values. If the closest genetic point was more than 100 km from the cancer incidence locality, the point was omitted from the study. We computed Prevosti distances (21) between gene-frequency samples and assembled them into genetic distance matrices of the same size as the matching incidence matrices. The minimal matrix size (number of locality samples) for which we kept results was 20. The correlations for the separate genetic systems were then averaged to yield the coefficients given in the text and in Tables 1 and 2.

Table 1.

A summary of zero-, first-, and second-order partial correlations of cancer incidence distances (INCID) with ethnohistoric (ETH) and genetic (GEN) distances in Europe

	Males, 45 cancers			Females, 47 cancers
	ETH	GEN	n (ETH > GEN)	ETH	GEN	n (ETH > GEN)
Zero order	0.0370*	0.0492*	20	0.0197†	0.0377*	17
First order	−0.0094	0.0470*	16	−0.0264	0.0372*	16
Second order	−0.0057	0.0312*	10	−0.0046	0.0282*	12

Values in columns one, two, four, and five are averages of partial matrix correlation coefficients (11, 19) as follows: zero order in the ETH columns stands for r(INCID,ETH), first order is r(INCID,ETH.GEO), and second order is r(INCID,ETH.GEN,GEO), where GEO stands for geographic distances. For the GEN columns, interchange GEN with ETH. The significance indicators next to the averages are based on Fisher's method of combining probabilities (22). *, P ≪ 0.001; †, P = 0.030. In columns three and six, headed n (ETH > GEN), we furnish counts of the number of cancers for which correlation of cancer incidence distances with ethnohistoric distances exceeds that with genetic distances. 

Table 2.

Partial correlations of cancer incidence (INCID) distances with ethnohistoric (ETH), genetic (GEN), and geographic (GEO) distances in Europe

ICD no.	Cancer	r(INCID,ETH.GEN,GEO)		r(INCID,GEN.ETH,GEO)
		Males	Females	Males	Females
140	Lip	−0.0146	−0.0129	0.0604†	0.0882‡
141	Tongue	−0.0193	0.0041	0.0616†	0.0141
142	Salivary gland	0.0061	−0.0075	−0.0003	0.0289
143–145	Mouth	−0.0263	−0.0057	0.0857‡	0.0339*
146	Oropharynx	−0.0225	0.0120	0.0656†	−0.0315
147	Nasopharynx	−0.0126	−0.0247	0.0476†	0.0720*
148	Hypopharynx	−0.0137	−0.0238	0.0529*	0.0701†
149	Unspecified pharynx	−0.0084	−0.0002	0.0365*	0.0479
150	Esophagus	−0.0428	−0.0165	0.1342‡	0.0494‡
151	Stomach	−0.0186	−0.0156	0.0922‡	0.0687‡
152	Small intestine	0.0047	0.0086	−0.0057	−0.0389
153	Colon	−0.0153	−0.0281	0.0708‡	0.1127‡
154	Rectum	−0.0103	−0.0048	0.0344	0.0222
155	Liver	−0.0196	−0.0380	0.0567†	0.1061‡
156	Gall bladder	−0.0051	−0.0076	−0.0040	0.0069
157	Pancreas	−0.0119	−0.0114	0.0217	0.0222
158	Peritoneum	−0.0118	−0.0053	0.0303*	0.0202
160	Nose/sinuses	−0.0095	0.0000	0.0416*	0.0013
161	Larynx	−0.0309	−0.0022	0.0996‡	0.0160
162	Bronchus/trachea/lung	−0.0106	−0.0155	0.0239	0.0290†
163	Pleura	0.0078	0.0025	0.0045	−0.0010
164	Other thoracic	−0.0048	−0.0132	0.0098	0.0582†
170	Bone	−0.0010	−0.0103	0.0279	0.0508†
171	Connective tissue	0.0026	−0.0005	0.0085	0.0285†
172	Melanoma	0.0173	0.0030	−0.0285	−0.0099
173	Other skin	0.0185	0.0183	−0.0328	−0.0393
174	Breast	−0.0044	−0.0114	0.0624†	0.0704‡
180	Cervix uteri		−0.0020		−0.0116
181	Chorionepithelioma		−0.0195		0.1259‡
182	Corpus uteri		−0.0102		0.0364
183	Ovary		−0.0226		0.0320*
184	Other female genital		−0.0018		0.0068
185	Prostate	0.0047		0.0055
186	Testis	−0.0011		0.0079
187	Penis	−0.0073		0.0295
188	Bladder	−0.0133	−0.0051	0.0782‡	0.0304*
189	Other urinary	−0.0031	−0.0038	0.0219	0.0066
190	Eye	0.0134	0.0058	−0.0362	−0.0054
191–192	Brain/nervous system	0.0085	0.0147	−0.0168	−0.0297
193	Thyroid	0.0027	0.0123	0.0115	−0.0072
194	Other endocrine	0.0171	0.0108	−0.0382	−0.0424
200+202	Non-Hodgkin's lymphoma	0.0069	−0.0073	0.0077	0.0597†
201	Hodgkin's disease	−0.0211	−0.0018	0.0733‡	0.0213
203	Multiple myeloma	−0.0157	0.0098	0.0683‡	−0.0137
204	Lymphatic leukemia	−0.0003	0.0061	0.0047	0.0157
205	Myeloid leukemia	−0.0072	−0.0045	0.0468*	0.0219*
206	Monocytic leukemia	0.0021	−0.0051	0.0165	−0.0009
207	Other leukemia	0.0040	−0.0019	−0.0004	0.0203
208	Unspecified leukemia	0.0076	0.0112	0.0048	−0.0124
209	Myelofibrosis	0.0030	0.0031	0.0635	0.1747*
	Mean r	−0.0057	−0.0046	0.0312	0.0269
	Combined P	1.00000	1.00000	0.00000‡	0.00000‡

ICD 209 averages based on three genetic systems only. All other averages based on minimally 15 systems (males) or 14 systems (females). *, 0.01 < P ≤ 0.05; †, 0.001 < P ≤ 0.01; ‡, P ≤ 0.001. 

Geographic distances were calculated as great-circle distances (in km) between all pairs of cancer incidence localities.

We designated the four types of distance matrices as cancer incidence (INCID), ethnohistory (ETH), genetics (GEN), and geography (GEO). We computed all zero-order matrix correlations, as well as partial matrix correlations (22), between the distance matrices. The following are of interest for this study: r(INCID,ETH), r(INCID,GEN), r(INCID,GEO); r(INCID,ETH.GEO), r(INCID,GEN.GEO); and r(INCID,ETH.GEN,GEO), r(INCID,GEN.ETH,GEO). These computations were performed for each cancer site and for each genetic system, separately by sex. The zero-order correlations were obtained as by-products of Mantel tests (12, 13), with the matrix elements scaled to yield a correlation coefficient as the Mantel product. The partial correlations resulted from the Mantel product of the appropriate residual distance matrices, once the variables being held constant were removed by regression (11, 14, 18, 19). The (upper tail) significance of each matrix correlation coefficient was assayed by 999 row-column permutations (14). When needed, the resulting probabilities over all cancers or genetic systems were combined by Fisher's method (22).

Results

We report average partial correlations over all cancers in Table 1. Significantly positive averages may mask contributions from appreciably negative correlations of individual cancers. The overall significance tests reported tell us whether the null hypothesis (that no cancer incidence distances are correlated with ethnohistoric or genetic distances) can be upheld or not.

The average correlations in Table 1 appear low judged by conventional criteria. This is characteristic of correlations between distance matrices (23), which are usually far lower than those of the variables on which they are based. Moreover, the average coefficients reported here include nonsignificant as well as higher, significant r-values. Corresponding average correlations are within the same order of magnitude for males and females. Although males have somewhat higher average correlations, detailed analysis of the data failed to substantiate such a trend. To correct for spatial autocorrelation, we partial out geographic distances and obtain averages shown in Table 1 in the first-order line. For all average correlations with genetics, as well as the male zero-order correlation with ethnohistory, the overall significance is P ≪ 0.001 by Fisher's method. None of the first- and second-order partial correlations with ethnohistory are significant by this method, and none of the second-order partial correlations on which the averages for r(INCID,ETH.GEN,GEO) are based are individually significant. Table 1 also shows, for zero-, first-, and second-order partial correlations, the number of individual cancers (out of 45 male and 47 female cancer sites) for which correlation of incidence with ethnohistory exceeds that with genetics. Although the averages of INCID,GEN correlations are always higher than those of the matching INCID,ETH correlations in all three orders of the partial correlations, only in the second-order case is this inequality significant at P < 0.001 (by the Wilcoxon signed-ranks test discussed in the next section).

Details of the second-order partial correlations are featured in Table 2. The two r(INCID,ETH.GEN,GEO) vectors show a slight tendency toward negative correlation, but no individual coefficient is significant, nor is the combined probability for each sex. The values of r(INCID,GEN.ETH,GEO) are significant in 19 out of 45 cancers in the males (each significant P ≤ 0.03201); in 19 out of 47 in females (each significant P ≤ 0.04142). The combined P values are less than 0.000005 (by Fisher's method). When we omit gender-specific cancers (leaving 41 common cancers in the two sexes), the correlation vectors of males and females correspond well. Of the 19 significant second-order partial correlations in each sex, 13 are for the same cancers (0.005 < P < 0.01 by a 2 × 2 G-test).

Comparison with Mortality Results.

There are marked differences between the results of this study of cancer incidence distances and our analysis (1) of cancer mortality distances (MORT) with respect to their correlation with ethnohistoric and genetic distances. In the mortality distances, correlations are highest with geographic distances, second highest with ethnohistoric distances, and lowest (but still significant) with genetic distances. The ordering for the incidence distances is geography, genetics, and ethnohistory, with the first lower than for mortalities, the second approximately the same as for mortalities, and the last near zero and lacking significance. To investigate these differences more closely, we compared Tables 1 and 2 in this paper with the two tables in ref. 1 by testing all six possible pairwise contrasts between the following four combinations: MORT,ETH; MORT,GEN; INCID,GEN; and INCID,ETH. These comparisons were carried out separately for zero-, first-, and second-order partial correlations. A series of Wilcoxon signed-ranks tests (22) evaluated the statistical significance of these comparisons, based on a paired-comparisons design for the contrasted pairs of vectors of partial correlations for individual cancers. Number and description of the cancers in the mortality and incidence data sets did not match, so we omitted some unpaired cancers and lumped some others. Depending on the specified contrast, the pairs of cancers remaining to be tested numbered from 16 to 39. With the original data being variously subdivided (the mortalities into the European Economic Community and Central Europe, and each of these into male and female cancer rates; the incidences into male and female rates), each contrast could be tested in replication. All contrasts are represented by four separate tests, except for INCID,GEN – INCID,ETH, which is based on only two tests. We carried out these tests three times, once for each order of the partial correlations. (Table 2 in ref. 1 contains an error. Its mean r for second-order partial correlation of mortality and genetics for Central Europe is given as −0.0100, but should be −0.0133, the same as in Table 1 of that paper. Note that ref. 1 used the abbreviation CAN instead of MORT.)

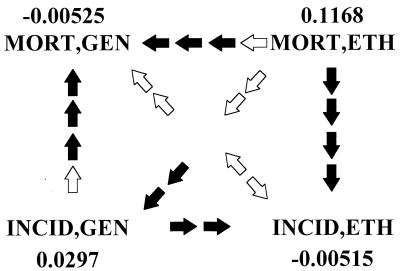
Fig. 1 summarizes the results of these tests in diagrammatic form for the second-order partial correlations. The combinations MORT,GEN; MORT,ETH; INCID,GEN; and INCID,ETH are arranged as the four corners of a square. The average partial correlations over all cancers, both sexes, and regions of Europe (where appropriate) are given next to these abbreviations. Arrows point from the higher mean correlation to the lower one. The number of solid arrows equals the number of replicates that significantly support the inequality with an experimentwise error rate of 0.0217. Hollow arrows show the direction of a nonsignificant inequality. Combination MORT,ETH has the highest average partial correlation, followed by INCID,GEN, followed in turn by INCID,ETH, which is higher than MORT,GEN by only 0.0001. Not surprisingly, the comparison MORT,GEN – INCID,ETH is nonsignificant by any single test. This contrast is positive for three tests, negative for one. Despite this near-equality of the averages for MORT,GEN and INCID,ETH, their means hide important differences between the two. The vectors comprising MORT,GEN have a moderate number of positive, significant coefficients, counterbalanced by a larger number of small, negative coefficients. The vectors yielding INCID,ETH have mostly low negative coefficients, none being significant. These statements about averages mask considerable variation among cancers and some variation among sexes and regions. We investigated the patterns of inequalities of the correlations in all cancers and found that, collectively, we can reject the null hypothesis of random assortment of the means at P < 0.00005. There are six cancers (bladder, ovary, urinary, colorectal, lung, and lymphoma) that conform or come close to the pattern of Fig. 1. Thyroid and uterine cancers have the most deviant patterns. However, refs. 6 and 7 revealed no etiological criterion that distinguishes the two groups of cancers.

Figure 1.

Comparison of second-order partial correlations for mortality and incidence. The variables are distances or differences coded: MORT, mortality; INCID, incidence; ETH, ethnohistory; and GEN, genetics. Values shown are averages over all cancers, both sexes, and regions of Europe, where applicable. Arrows point from higher to lower values. The number of solid arrows indicates the number of Wilcoxon signed-ranks tests adjudged significant at an experimentwise error rate ≤ 2.17%. Hollow arrows show the direction of a nonsignificant inequality. Of the four tests performed for the nonsignificant MORT,GEN-INCID,ETH contrast, three indicate INCID,ETH > MORT,GEN, and one indicates INCID,ETH < MORT,GEN.

The results for the zero- and first-order partial correlations (not shown) exhibit trends similar to those of the second-order partials in Fig. 1, except that most zero-order and all first-order inequalities are not significant.

A Path Analysis.

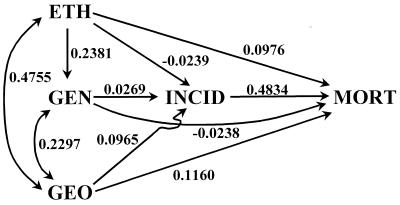
To learn more of the interaction of the variables we investigated, we constructed a path diagram (22, 24) shown in Fig. 2. The putative causes are labeled ETH, GEN, and GEO, as elsewhere in this paper. Both ETH-GEO and GEN-GEO are connected by double-headed arrows to indicate remote correlations that we cannot decompose further. The correlation r(ETH,GEN) is shown as a single-headed arrow ETH → GEN, because ethnohistoric similarity will lead to genetic similarity, whereas the converse will not hold generally. (We shall employ the symbolism A → B to indicate a path coefficient from A to B.) Ethnohistoric distances imply not only genetic distances (affected through the path ETH → GEN), but also cultural differences that directly affect the differences in cancer rates. These are shown as separate single-headed arrows ETH → MORT and ETH → INCID. Although some of the ethnic admixtures in our model are quite ancient, certain cultural traits affecting cancer incidences may persist in the modern admixed populations, serving as cultural carcinogenic factors. In contrast, MORT should be affected by recent cultural factors related to the treatment and care of cancer patients, the correctness of the diagnosis in the death certificate, and varying death registration practices in different countries and even different parts of countries. We postulate separate direct effects of GEN and GEO on INCID and MORT, indicated by single-headed arrows originating from GEN and GEO. There is also a single-headed arrow INCID → MORT to indicate the direct effect of incidence on mortality. This arrow can run only in the direction shown, because cancer must first arise before it can lead to death. We also know that incidences in these data are substantially correlated with mortalities (mean r = 0.4923 averaged over 15 cancers and both sexes).

Figure 2.

Path diagram for zero-order partial correlation coefficients (ordinary pairwise correlations) between distances or differences of the indicated variables. Double-headed arrows indicate correlations; single-headed arrows are paths from the base to the tip of the arrows. The numerical values alongside the arrows indicate magnitudes of the correlations or path coefficients.

The magnitudes of the path coefficients can be evaluated by expressing the observed correlations between all pairs of the five studied variables in terms of the path coefficients as a set of simultaneous equations which is solved by conventional means. The observed correlation coefficients are averages over all available cancers, both sexes, and, where applicable, both regions of Europe. Their values and sources are given in Table 3. Because the correlation coefficients are averages, the path coefficients computed from them can only be indicators of general trends, and are not specifically applicable to any one cancer. Note also, that the model underlying this path diagram is strictly linear, whereas the true relations among the five variables are most likely nonlinear. Thus the results of the path analysis are only a first approximation to the true relations among these variables. The numerical values obtained for the path coefficients are shown in Fig. 2 alongside the single-headed arrows, as are the values of correlations r(ETH,GEO) and r(GEN,GEO) next to the double-headed arrows.

Table 3.

Source list of zero-order partial correlations for path coefficient study of cancer incidences and mortalities

r( )	Value	Averaged over	Source of data
ETH,GEN	0.2381	gs	Ref. 9, Table 2
ETH,GEO	0.4755	ca, sx	bp
ETH,INCID	0.0284	ca, sx	bp
ETH,MORT	0.1608	ca, sx, re	Ref. 1, Table 1
GEN,GEO	0.2297	gs	Ref. 28, Table 1
GEN,INCID	0.0434	ca, gs	bp
GEN,MORT	0.0471	ca, sx, re	Ref. 1, Table 1
GEO,INCID	0.0944	ca, sx	bp
GEO,MORT	0.1999	ca, sx, re	nc
INCID,MORT	0.4923	15 ca, sx	bp

ca, cancers; gs, genetic systems; sx, sexes; re, regions; bp, by-product of present study; nc, newly computed. 

For convenience, we group the path and correlation coefficients by their magnitudes, recalling that the variables considered are distances or differences whose potential correlations are considerably less than those of their constituent variables. Strong effects (≈0.5) include INCID → MORT and r(ETH,GEO); intermediate effects (≈0.2) comprise ETH → GEN and r(GEN,GEO); weak effects (≈0.1) are shown by ETH → MORT, GEO → INCID, and GEO → MORT; and negligible effects (± 0.03) include ETH → INCID, GEN → INCID, and GEN → MORT. From Fig. 2, it appears that ethnohistoric distances directly affect genetic distances at an intermediate level and mortality differences weakly, the direct effect on incidence differences being negligible. Thus, we have no evidence for cultural carcinogenic effects, but some evidence for cultural influences on mortalities, possibly representing different mortality registration procedures of different political entities. The relatively large correlation r(ETH,MORT) is caused not only by these cultural differences but also by the common factors underlying r(ETH,GEO) which can be summarized as: geographic proximity is reflected by similar ethnohistories. These common factors act directly on mortality, and indirectly via incidences, and their summed effects are not negligible. In any case, whether mediated by genetics or culture, it is clear that the ethnohistoric affinities contribute to differences in cancer mortalities.

The direct effects of genetic distances on mortality and incidence are negligible and only their common effects with geographic distances play a role. Probably, the genetic systems we used do not substantially affect cancer rates. In contrast, geographic distances influence both incidences and mortalities appreciably, both directly (possibly reflecting environmental similarities and emphasizing the important role of the environment in cancer causation) and indirectly through their common factors with ethnohistoric and genetic distances. We have already discussed potential factors underlying ethnohistoric distances. Common factors for genetic distances must represent the spatial autocorrelation of the gene pool engendered either through isolation by distance or by the cohesiveness of ethnic units, which will result in genetically similar population samples.

From a consideration of Fig. 2, it also becomes obvious why correlation r(MORT,ETH) is greater than r(INCID,GEN). There are more indirect paths affecting the former, and they involve higher values of correlation and path coefficients than for the latter. Note that the actual values of these two correlations were empirically obtained, and that the path diagram structure was designed from a priori considerations, not from observed data.

Discussion

As in our earlier study of cancer mortalities (1), it seemed likely that cancer incidence differences are affected by ethnohistoric or genetic distances between populations, rather than the reverse. Previous work has shown that our ethnohistoric distances predict modern genetic distances (9).

Tables 1 and 2 reveal that most individual correlations and all of the average incidence correlations show higher values with genetics than with ethnohistory. Nevertheless, testing the significance of this effect by conventional methods is problematic, because we cannot assume independence of the cancers. We examined the correlation between cancer incidences empirically to get a feel for how serious a problem this might be. Of the 990 zero-order coefficients for pairs of cancers in males, 29 or 2.9% are > 0.6 and of the 1,081 zero-order coefficients for females, 27 or 2.5% are > 0.6. We doubt that dependence between incidences of different cancers is strong enough to adversely affect the Wilcoxon tests.

Cancers may exhibit a continuum from those largely driven by few genes, each with an important effect, to those affected by many genes, each with a small effect. Our genetic data, comprising contributions from 26 genetic systems, are more likely to reveal information about the latter than the former. It is therefore not justifiable to look for cancers known to have high incidences when some carcinogenic allele is present and to expect that, as a consequence, such cancers should have high correlations with our genetic data.

The average correlations and combined probabilities at the bottom of Table 2 permit general statements about the relations of ethnohistoric and genetic distances to the set of individual cancer incidences. However, we note that for a substantial number of cancers (e.g., salivary gland, small intestine, rectum, and eye), the incidence differences are not affected by either factor. If environmental or genetic factors affect these, they presumably are not in our ethnohistoric or genetic databases.

We now address the principal question emerging from a comparison of the cancer mortality study (1) and this study of cancer incidences. Why are ethnohistoric distances more strongly correlated with the cancer mortalities than are genetic distances, and why are they essentially uncorrelated with the cancer incidences, leaving the weakly correlated genetic distances as the remaining determiner of the incidences?

Earlier studies relied on mortalities because these were more widely reported than incidences, but expert opinion differs on the quality of the two rates. Advocates of mortalities claim that these are available for more countries and over longer time periods (7, 25, 26). J. C. Bailar, III (personal communication) states: “There are so many differences [in reported incidence rates] in … medical awareness, screening programs, and standards … that one cannot take the [incidence] data at face value.”

Advocates of incidence data claim that quality control is high: Expert cancer registry staffs check for internal coherence of data. “The overall validity of cancer incidence data supplied by cancer registries is certainly better than that of cancer mortality data… ” (25). Incidences are closer to causal exposures (etiology) than are mortalities and hence are better for explanatory models (25). Mortalities are unsuitable for cancer sites with good survival and will become less useful as the prognosis of various cancers improves (25, 26). F. Ederer (personal communication) believes that “… cancer mortalities are generally less accurate than incidence data because death certificates often are completed promptly, before an autopsy is done, and by physicians who may be unfamiliar with the case; also that incidence data are generally more accurate because the majority of cancer diagnoses from high quality registries are histologically confirmed.” Other deficiencies of mortalities are noted (7).

Can quality differences account for our finding that mortality is more correlated than incidence with ethnicity and geography? Many of the errors discussed above will vary more between nations than within them, and are thus inseparable in our analyses from true ethnic and geographic effects. One hypothesis consistent with our findings is that these errors are more prominent in mortality data than in incidence data, causing the higher correlations.

A recent study (27) analyzed the same incidence data set by different methods (but used fewer localities and cancers) and found that cultural factors exerted a predominant role on cancer incidences in Europe. However, the results of the two studies cannot be directly compared because the cultural factors (27) are recent demographic and socioeconomic variables, whereas ours are mostly ancient mixtures of ethnic groups characterized by their language families. Furthermore, the genetic component (27) comprises only a single genetic system (ABO), contrasted with 26 systems in our analysis.

Abbreviations

ETH

ethnohistory

GEN

genetics

GEO

geography

INCID

incidence

MORT

mortality