Abstract
Decisions based on the timing of sensory events are fundamental to sensory processing. However, the mechanisms by which the brain measures time over ranges of milliseconds to seconds remain unknown. The dominant model of temporal processing proposes that an oscillator emits events that are integrated to provide a linear metric of time. We examine an alternate model in which cortical networks are inherently able to tell time as a result of time-dependent changes in network state. Using computer simulations we show that within this framework, there is no linear metric of time, and that a given interval is encoded in the context of preceding events. Human psychophysical studies were used to examine the predictions of the model. Our results provide theoretical and experimental evidence that for short intervals there is no linear metric of time, and that time may be encoded in the high-dimensional state of local neural networks.
INTRODUCTION
All forms of sensory processing are ultimately based on decoding the spatial and/or temporal structure of incoming patterns of action potentials. The elucidation of the neural mechanisms underlying the processing of spatial patterns has advanced considerably in the past forty years. For example, the coding and representation of simple spatial patterns, such as the orientation of a bar of light, are well characterized in primary visual cortex (Hubel and Wiesel, 1962; Ferster & Miller, 2000). Indeed, much has been discovered about the mechanisms underlying the emergence of orientation selective cells, and their role in perception (e.g., Miller et al, 1989; Ferster & Miller, 2000; Gilbert et al, 2000; Schoups et al, 2001; Yang et al, 2004).
In comparison to spatial stimuli, there is a significant gap in our understanding of how the brain discriminates simple temporal stimuli, such as estimating the duration of time for which a light, or tone, is presented. Recent studies have begun to examine the neural (Kilgard & Merzenich, 2002; Hahnloser et al, 2002; Leon and Shadlen, 2003) and anatomical (Rao et al, 2001; Lewis & Miall, 2003; Coull et al, 2004) correlates of temporal processing. However, the neural mechanisms that allow neural circuits to tell time and encode temporal information are not known. Indeed, it has not yet been determined if timing across different time scales and modalities relies on centralized or locally independent timing circuits and mechanisms (Ivry & Spencer, 2004).
Timing is critical in both the discrimination of sensory stimuli (Shannon et al, 1995; Buonomano & Karmarkar, 2002; Ivry & Spencer, 2004; Buhusi and Meck; 2005) and the generation of coordinated motor responses (Mauk and Ruiz, 1992; Ivry, 1996; Meegan et al, 2000; Medina et al, 2005). The nervous system processes temporal information over a wide range, from microseconds to circadian rhythms (Carr, 1993; Mauk & Buonomano, 2004; Buhusi & Meck, 2005). We will focus on the scale of milliseconds and seconds, in which the dominant model of temporal processing is the internal clock model. A prototypical clock model includes a pacemaker (oscillator) that emits pulses that are counted by an accumulator (Creelman, 1962; Treisman, 1963; Church, 1984; Gibbon et al, 1997). Within this framework, the pulse count provides a linear metric of time, and temporal judgments rely on comparing the current pulse count to that of a reference time. This model has proven effective in providing a framework for much of the psychophysical data relating to temporal processing (Church, 1984; Meck, 1996; Rammsayer and Ulrich, 2001). However, electrophysiological and anatomical support for the putative accumulator remains elusive, and mounting evidence indicates that clock models are not entirely consistent with the experimental data (for reviews see Mauk & Buonomano, 2004; Buhusi and Meck, 2005).
A number of alternate models of timing have been suggested (see Discussion; for reviews see Gibbon et al, 1997; Buonomano & Karmarkar; 2002; Buhusi and Meck, 2005). One such class of models, state-dependent networks (SDNs), propose that neural circuits are inherently capable of temporal processing as a result of the natural complexity of cortical networks coupled with the presence of time-dependent neuronal properties (Buonomano & Merzenich, 1995; Buonomano, 2000; Maass et al, 2002). This framework, based on well characterized cellular and network properties, has been shown to be able to discriminate simple temporal intervals on the millisecond scale, as well as complex spatial-temporal patterns (Buonomano and Merzenich, 1995; Buonomano, 2000; Maass et al, 2002). Here we examine the mechanisms and nature of the timing in this model, and show that it encodes temporally patterned stimuli as single temporal objects, as opposed to the sum of the individual component intervals. This generates the counterintuitive prediction that we do not have access to the objective (absolute) time of a given interval if it was immediately preceded by another event. This prediction is tested and confirmed using independent psychophysical tasks. Together, our results provide a mechanistic account of the distinction between millisecond and second timing, and suggest that within the millisecond range, timing does not rely on clock-like mechanisms or a linear metric of time.
RESULTS
State-dependent Networks
A SDN composed of 400 excitatory (Ex) and 100 inhibitory (Inh) recurrently connected integrate-and-fire units was simulated using NEURON. The synapses in the network exhibit short-term forms of synaptic plasticity, and both fast and slow IPSPs (see Experimental Procedures). Short-term synaptic plasticity (Zucker, 1989) plays a critical role in SDNs by altering the state of the network in a time-dependent fashion after each input, which in turn produces time-dependent neuronal responses. In essence, in the same manner that long-term plasticity may provide a memory of a learning experience (Martin et al, 2000), SDNs use short-term synaptic plasticity to provide a memory trace of the recent stimulus history of a network (Buonomano, 2000).
The functional properties of an SDN can be understood if we consider the sequential presentation of two brief and identical events (e.g., two auditory tones) 100 ms apart (Figure 1A). When the first event arrives in the network, it will trigger a complex series of synaptic processes resulting in the activation of a subset of neurons. When the same event is repeated 100 ms later, the state of the network will have changed from S0 to S100. Due to the time-dependent changes in network state (imposed by short-term synaptic plasticity) the population response to the second stimulus inherently encodes the fact that an event occurred 100 ms before. In this fashion the network implements a temporal–to-spatial transformation – i.e., the presence, absence or number of spikes from a given subset of neurons will depend on the temporal structure of the stimulus. The model is stochastic in the sense that determining which neurons will be interval sensitive is a complex function of the network's random connectivity, assigned synaptic strengths and short-term plasticity (Buonomano, 2000). Once time is encoded in a spatial code it can be read-out by a set of output neurons (see below; Buonomano & Merzenich, 1995; Buonomano, 2000; Maass et al, 2002; Knüsel et al, 2004).
Figure 1. State-dependent network simulation.
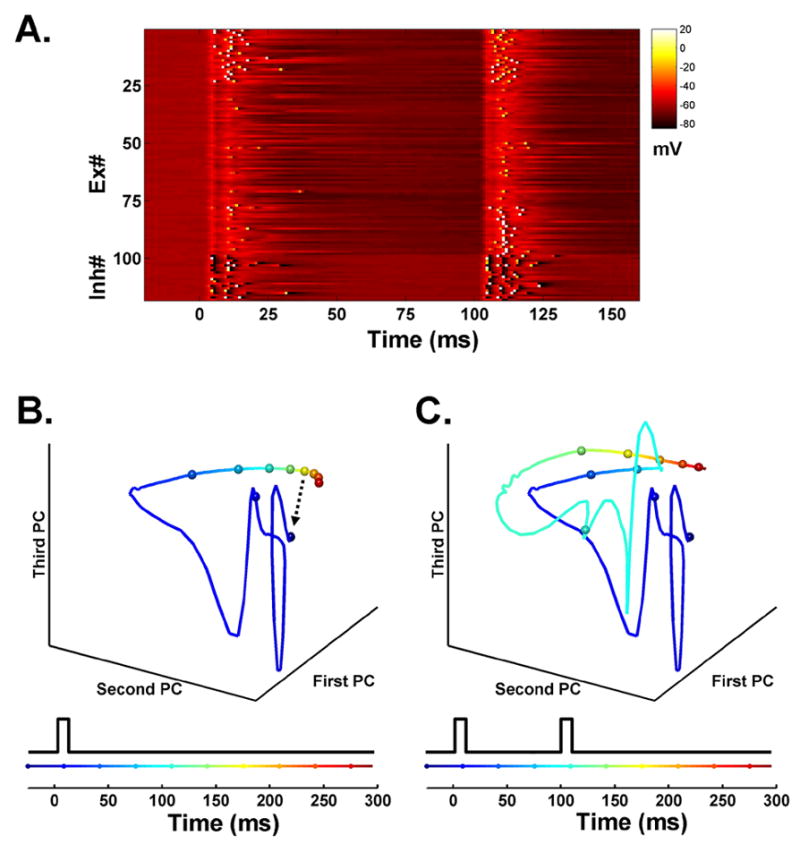
(A) Voltage plot of a subset of neurons in the network. Each line represents the voltage of a single neuron in response to two identical events separated by 100 ms. The first 100 lines represent 100 Ex units (out of 400), and the remaining lines represent 25 Inh units (out of 100). Each input produces a depolarization across all neurons in the network, followed by inhibition. While most units exhibit subthreshold activity, some spike (white pixels) to both inputs, or exclusively to the first or second. The Ex units are sorted according to their probability of firing to the first (top) or second (bottom) pulse. This selectivity to the first or second event arises because the difference in network state at t=0 and t=100 ms.
(B) Trajectory of the three principal components of the network in response to a single pulse. There is an abrupt and rapidly evolving response beginning at t=0, followed by a slower trajectory. The fast response is due to the depolarization of a large number of units, while the slower change reflects the short-term synaptic dynamics and slow IPSPs. The speed of the trajectory in state space can be visualized by the rate of change of the color code and by the distance between the 25 ms marker spheres. Because synaptic properties cannot be rapidly 'reset', the network cannot return to its initial state (arrow) before the arrival of a second event.
(C) Trajectory in response to a 100 ms interval. Note that the same stimulus produces a different fast response to the second event. To allow a direct comparison, the principal components from B were used to transform the state data in C.
In this model, there is no explicit or linear measure of time like the tics of an oscillator or a continuously ramping firing rate (see Discussion; Durstewitz, 2003). Instead, time is implicitly encoded in the state of the network - defined not only by which neurons are spiking, but by the properties that influence cell firing, such as the membrane potential of each neuron and synaptic strengths at each point in time. Thus, even in the absence of ongoing activity, the recent stimulus history remains encoded in the network. The simulation in Figure 1 consists of 500 neurons and a total of 12,200 synapses, allowing us to define the network's state in 12,700 dimensional space. Since the state of the network ultimately determines the response to the next input we can think of its evolving trajectory through this space as encoding time. Principal component analysis was performed to provide a visual representation of this trajectory (see Experimental Procedures). In response to a single stimulus, the first three principal components establish a rapidly evolving neural trajectory through state-space, followed by a much slower path settling back towards the initial state (Fig 1B). When a second event is presented at t=100 ms it produces a perturbation in state-space different from the t=0 event (Fig. 1C). Similarly, additional presentations of the same stimulus at varying delays would continue to produce cumulative changes in network state.
The time it takes for the network to return to its initial state - its reset time - is a function of the longest time constants of the time-dependent properties. For short-term synaptic plasticity this is on the order of a few hundred milliseconds (Zucker, 1989; Markram et al, 1998; Reyes and Sakmann, 1998). The dynamics of short-term plasticity must run its course; thus the network cannot return to its initial state on command. As addressed below this property has important implications for temporal processing.
Temporal Objects
An important feature of state-dependent networks is that they naturally extend beyond simple interval discrimination to the processing of complex temporal sequences. This is due to the cumulative nature of changes in network state (Buonomano & Merzenich, 1995; Maass et al, 2002). However, potential weaknesses in SDNs arise because of both the absence of an explicit metric of time, and their sensitivity to changes in initial state.
To examine these issues we investigated the ability of the network to discriminate between 100 and 200 ms intervals (we will use the notation [100] x [200] ms), as well as two simple patterns that contain these intervals, namely a 100 or 200 ms interval preceded by a 150 ms interval ([150; 100] and [150; 200]). We calculated the information each neuron in the network contains for the discrimination of both sets of stimuli. Mutual information was determined based on the number of spikes in each neuron (see Experimental Procedures). The neurons containing information for the [100] x [200] and the [150; 100] x [150; 200] discriminations fall in largely nonoverlapping populations (Fig. 2A). This occurs even though the discrimination could in principle be based on the same [100] x [200] interval. Since the individual intervals are encoded in the context of the whole stimulus, the network cannot recognize that the [100] and [150; 100] patterns share a common feature. Nevertheless, it can discriminate between all four stimuli (Fig. 2B). Each stimulus is coded as a distinct ‘temporal object’ regardless of its component features.
Figure 2. Encoding of Temporal Patterns.
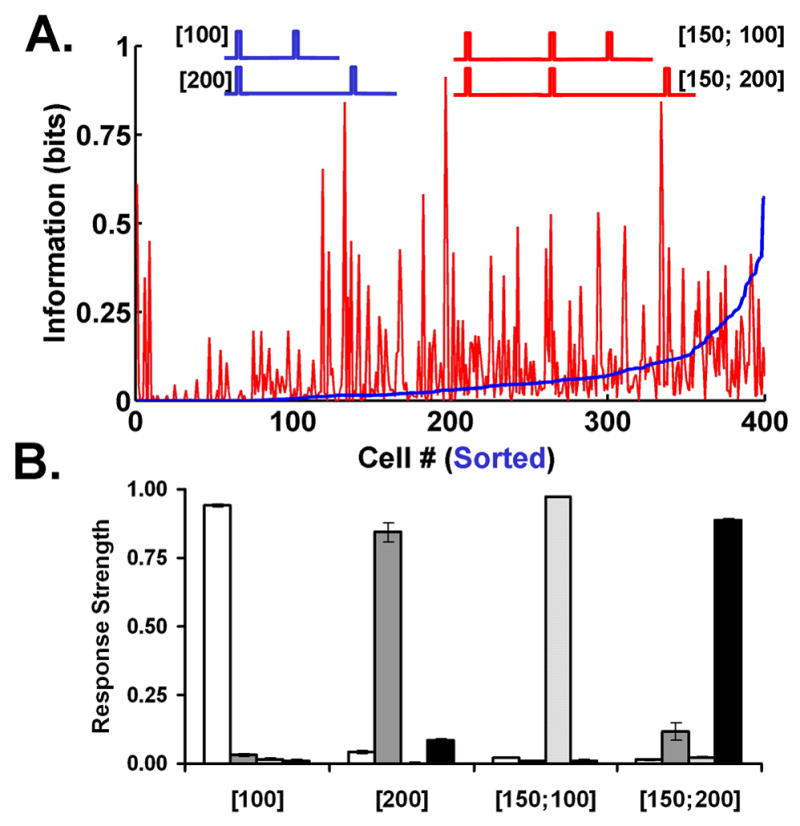
(A) Information per neuron. The blue trace displays the mutual information that each Ex unit provides for the discrimination of a 100 versus 200 ms interval (sorted). The red line shows the information for the same intervals preceded by a 150 ms interval, that is discrimination of the pattern [150;100] versus [150;200]. While individual neurons contain significant information for both stimuli, a different population of neurons encodes each one.
(B) Discrimination of all four stimuli. All Ex units were connected to four output neurons trained to recognize the network activity produced by the last pulse of all four stimuli. Average responses were calculated from six independent (different random number generator seeds) simulations. Note that a mutual information measure based on total spike count to each stimulus, as in panel A, would introduce a confound because the number of spikes is also a function of the number of events (see Experimental Procedures).
Reset Task
The prediction that emerges from the model is that if a distractor precedes a 100 ms target interval at random intervals, discrimination of the target should be impaired in comparison to a 100 ms interval with no distractor (or one preceded by a fixed distractor). This prediction was examined using psychophysical studies. We designed a task (Fig 3A) in which each trial consisted of a randomly interleaved presentation of a single two-tone (2T) or three-tone (3T) stimulus, and participants were asked to judge the interval between the last two tones. In the 3T case the first tone acts as a distractor. By independently and adaptively varying the intervals, discrimination thresholds were calculated for the 2T and 3T tracks (see Experimental Procedures). The randomly interleaved - and thus unpredictable - presentation of the 3T stimuli also ensured that the subjects did not adopt strategies to ignore the distractor. The standard interval was presented at the beginning of a trial and maintained implicitly as a result of feedback to each response (Grondin & Rammsayer, 2003; Karmarkar & Buonomano, 2003). Subjects were asked to judge whether the target interval was shorter or longer than the standard. Two classes of distractors, fixed (FIX) and variable (VAR), were examined. In the FIX condition, the distractor was always presented at a fixed interval before the target interval. In the variable condition (VAR), the distractor was presented at a range of times (±50% of the standard).
Figure 3. Reset Task: a variable distractor impairs discrimination of a short but not a long interval.
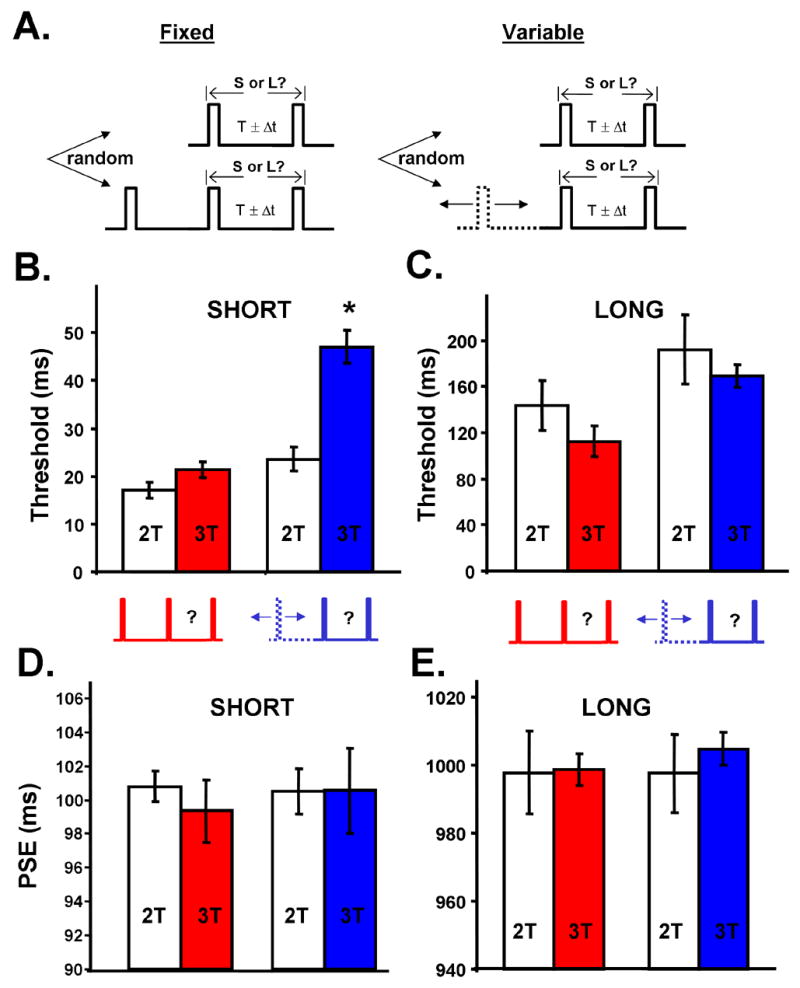
(A) Reset Task. Top rows represent the standard 2T interval discrimination task in a single stimulus protocol. Subjects are asked to press different mouse buttons if they judged the interval to be short (S) or long (L). The feedback across trials results in the creation of an internal representation of the target interval. Bottom rows represent the 3T task in which a distractor is presented at a fixed or variable (dashed) interval across trials.
(B) Thresholds for the 100 ms (SHORT) reset task. Left, thresholds for the 100 ms 2T interval discrimination (open bars) and for the 100 ms interval preceded by a distractor presented at the same interval across trials (3T-FIX, red). Right, threshold for the standard 100 ms task (open) and three-tone task in which the distractor was presented at variable intervals across trials (3T-VAR; blue). Error bars represent the SEM. The asterisk represents a significant difference from the other three groups.
(C) Reset task (represented as in A), using a 1000 ms (LONG) target interval. Neither of the main effects or the interaction was significant.
(D–E) PSE values for the same experiments shown in panels B and C, respectively. The PSE was not significantly different from the target intervals of 100 (D) and 1000 ms (E) in any condition.
This task was termed the "reset task" based on the unique constraints it places on the temporal encoding mechanisms. If a subject were using a simple stopwatch strategy, they would have to start their stopwatch at the first tone, even though it is irrelevant in the 3T trials. The true role of the second tone can only be determined retroactively by the presence or absence of a third tone. With a stopwatch, one approach could be to quickly record the time at t2 and then reset the watch. Alternately, the time at t2 and t3 could be noted and then t2 subtracted from t3 to obtain the interval between the second and third tones. We will refer to the first strategy as a clock reset mechanism and the second as temporal arithmetic. Both can be implemented with internal clock models, either because the accumulator could be reset, or because the presence of a linear temporal metric would allow for temporal arithmetic. Both clock-based models predict that performance on the 2T and 3T tracks should be similar in both the FIX and VAR conditions because the predictability of the distractor should not affect the encoding of t1–t2 and t2–t3.
In contrast, in the state-dependent network model, a reset strategy cannot be implemented because short-term plasticity cannot be reset on cue. Temporal arithmetic cannot be performed due to the absence of a linear metric of time. State-dependent networks predict that performance on the FIX condition will be similar for the 2T and 3T stimuli because the feedback at the end of each trial can be used to establish consistent states on which to build internal temporal representations for both stimuli. However, they also predict an impaired performance in the 3T-VAR trials compared to the 2T or FIX conditions, since the state of the network will not be reproducible across trials.
Subjects were first tested with a target interval of 100 ms (SHORT). Consistent with previous studies, thresholds for the 2T conditions were in the range of 20% of the target (Wright et al, 1997; Karmarkar & Buonomano, 2003). A two-way analysis of variance revealed a significant interaction between conditions (FIX x VAR) and tone number (2T x 3T; F=57.75; n=15; P<0.0001) demonstrating a dramatic impairment in the 3T-VAR condition only (Fig 3B). Indeed, the threshold in the 3T-VAR condition for a 100 ms interval was similar to that in separate (2T only) experiments on a 200 ms interval (46±3.4 ms versus 45±7; data not shown). Thus under the SHORT condition, the psychophysics supported the predictions of the state-dependent network. In contrast, when the reset task involved a target of 1000 ms (LONG) there was no effect of the variable distractor, as evident in the lack of interaction in the ANOVA (Fig 3C; F=0.087; n=12; P>0.5). Importantly, the point of subjective equality was approximately equal to the target intervals in both the SHORT and LONG experiments, independent of the presence or absence of the distractor in both the FIX and VAR conditions (Fig. 3D-E). Therefore a memory component of the task cannot account for the differences observed between the two target lengths.
The specific effect of the variable distractor on the SHORT group is consistent with the prediction of the state-dependent network model. It is unlikely that this result is due to effects such as the increased uncertainty caused by the variable distractor, as the same degree of uncertainty was present in the LONG trials without an accompanying timing impairment. Additionally, the randomly interspersed presentation of the 2T and 3T stimuli ensures the same level of uncertainty for both stimuli (in both conditions), but the 2T-VAR performance was not affected. However, to further examine the general psychophysical effects of a variable distractor, we conducted two additional controls. The first was a task in which the distractor interval was 100 (FIX) or 50–150 ms (VAR) and a 1000 ms target (Short-LONG). In addition, subjects performed a frequency discrimination task in which the target frequency was preceded by a tone either at a fixed or variable interval (see Experimental Procedures). Neither the Short-LONG [F=0.18; n=10; P>0.5] or frequency [F=0.23; n=14; p>0.5] experiments revealed a decrement in performance produced by the variability of the distractor (Fig. 4A-B).
Fig 4. Control interval and frequency discrimination tasks.
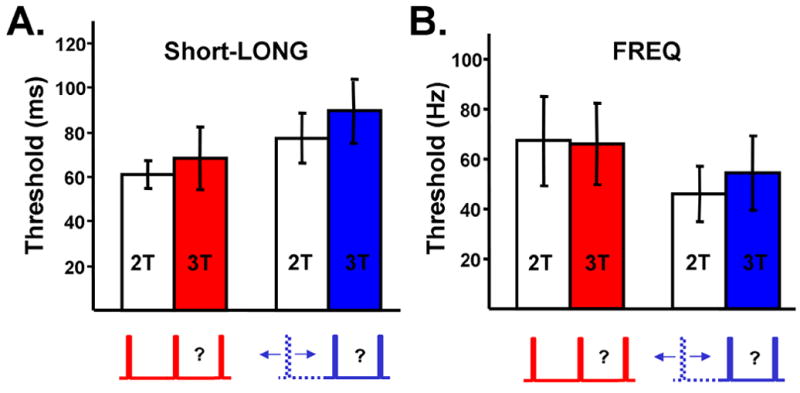
(A) Short-Long reset task. The variable distractor in these trials was between 50–150 ms, and the target interval was 1 s. When a short unpredictable distractor preceded a long target interval there was no effect of whether the distractor was Fixed or Variable.
(B) Frequency task. A tone was presented in the absence of a distractor (open bars), or in the presence of a distractor tone presented at a fixed (red) or variable (blue) interval before the target tone. Conventions and color coding as in Figure 3.
Effect of the Inter-Stimulus Interval on Performance
It is important to rule out the possibility that the impairments observed in the Reset task were not produced by some complex interaction between uncertainty and the intervals being judged, or that the distractor in the FIX condition was serving as a reference interval (see Discussion). Thus, we examined the prediction of the SDN model using a second independent psychophysical test. The SDN model predicts impaired performance under conditions when the network state at the time of the target stimulus varies across trials. This condition can also be produced by insufficient reset time before the next stimulus is presented. To test this directly, we examined performance on a traditional two-interval two-alternative forced-choice task (Wright et al, 1997) in which the interstimulus interval (ISI) was varied. In this paradigm, subjects heard both the 100 ms target and a longer comparison interval, then made a judgment as to whether the longer stimulus occurred first or second. We presented the two intervals with a mean ISI of either 250 or 750 ms. Since experimental data suggests that short-term plasticity operates on the time scale of a few hundred milliseconds (Markram et al, 1998; Reyes & Sakmann, 1998) the state-dependent model predicts that the network will not have completely returned to its initial state in the ISI250 condition, thus impairing temporal discrimination. Indeed, a comparison of the ISI250 to the ISI750 condition showed a significant decrease in performance for the shorter ISI [t=3.53; n=10; P<0.01] (Fig. 5A). Subjects also performed a frequency discrimination task under the short and long ISI conditions, where they reported if the tone pitch was higher for the first or second stimulus. There was no difference between the two conditions [t=0.53; n=10; P>0.5] (Fig. 5A), indicating that the effect of the shorter interstimulus interval was specific to process of measuring time.
Figure 5. Short interstimulus intervals impair interval, but not frequency, discrimination.
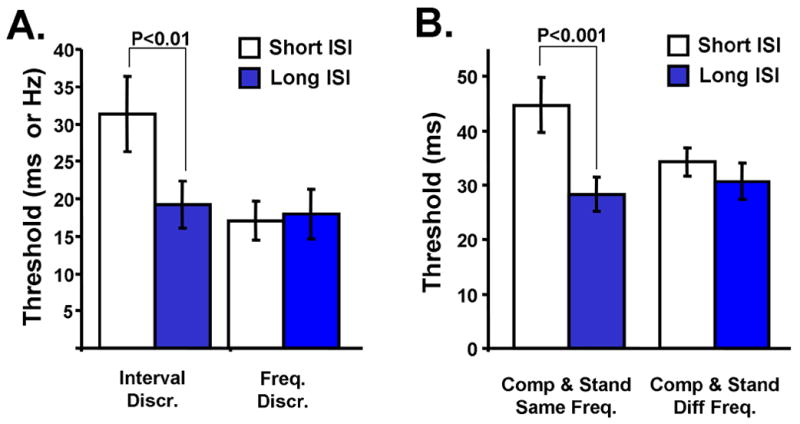
(A) Bars on the left show the thresholds for a two-interval forced-choice discrimination with a 100 ms target. When the interval between the stimuli was short (250 ms) performance was significantly worse compared to the long interstimulus interval (750 ms). In contrast, performance on a frequency discrimination task was unaltered by the interstimulus interval.
(B) Bars on the left illustrate the results for short (250 ms) and long (750 ms) ISI when both the standard and comparison intervals were presented at the same frequency. Bars on the right represent the interval discrimination thresholds when the standard and comparison stimuli were presented at different frequencies. We believe the difference in absolute interval discrimination between both studies (right bars in panels A and B) reflects interference between the different task and stimulus sets in both studies, as well as the inherent subject variability observed in timing tasks.
The state-dependent framework predicts that the two intervals are more difficult to compare, resulting in higher temporal discrimination thresholds, because their state-space trajectories have different starting points which vary from trial to trial. The total length of time from the first tone of the first stimulus to the first tone of the second is determined by the exact duration of the ISI (250 ± up to 25%). As a result, the variability in the initial state for the second stimulus is caused by the first - the first interval interferes with the second. However, if the target and comparison stimuli were presented at the same ISI but to different local networks the impairment produced by the short ISI should be decreased or absent. To examine this prediction, we took advantage of the known tonotopic organization of the auditory system. We performed interval discrimination tasks under two experimental conditions: (1) as above, a 100 ms standard and a comparison (100+ΔT ms) played at 1 kHz at ISI250 and ISI750; (2) a similar condition except that one of the stimulus intervals was played at 4kHz and the other at 1kHz. Replicating the above results, Fig. 5B shows that there was a significant increase in threshold in for the ISI250 compared to the ISI750 [t=6.85; n=9; P<0.001] in the same frequency condition. However, using different frequencies for the standard and comparison intervals eliminated any impairment in performance on the short ISI [t=0.85; n=9; P>0.3].
Interval Discrimination Despite Differences in Initial State
While the insufficient reset time in the above experiments (Fig. 5A) impaired discrimination thresholds, it did not entirely prevent subjects from performing the task. We were thus interested in returning to the theoretical model to determine how performance varied as a function of ISI, and whether some degree of timing was still possible with only a partial reset of the network. First, the trajectory of the network in state space was calculated in response to two 100 ms intervals separated by a 250 or 750 ms ISI. As shown in (Fig 6A), a 750 ms ISI allows for the network to return to a point very close to its ‘naïve’ initial state. As a result, the trajectory produced by the second stimulus closely traces that produced by the first one. In contrast, for the 250 ms ISI, the network does not return to the neighborhood of the initial state, and its trajectory for the second interval is significantly different. Measures of these distances are presented in Fig. 6B.
Figure 6. Dependence of the State-dependent Network on Initial State.
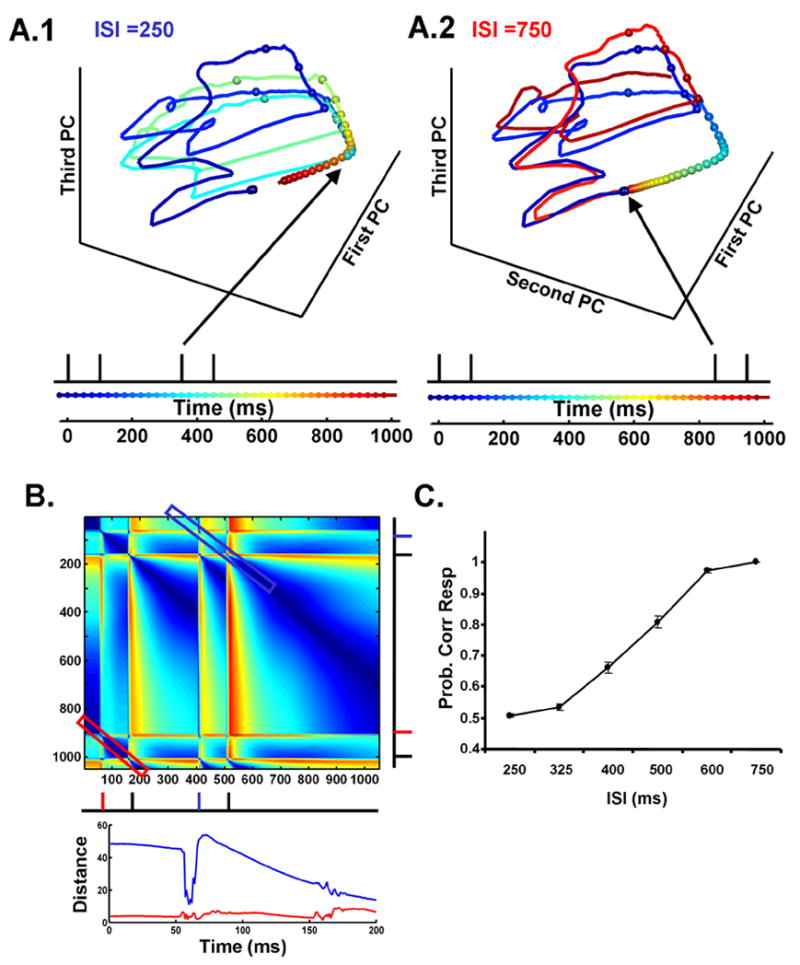
(A) Trajectory of the same network shown in Fig. 1 and 2, in response to two 100 ms intervals separated by a 250 (A1) or 750 ms ISI (A2). Note, that the trajectories under the 750 ms ISI are much closer to overlapping than in the 250 ms condition. Arrows indicated the times of the onset of the second interval.
(B) Distance matrix. The diagonal represents the distance in Euclidean space between the trajectories shown in A1 and A2 starting at 0. The distance is zero until the onset of the second tone (the noise ‘seed’ was the same for both simulations). The secondary diagonals permit the visualization of the distances between two trajectories shifted in time. This allows the comparison of the trajectory starting at the onset of the second interval (for the 250 ms ISI) and of the first interval (blue rectangle and blue line in lower panel), or the second interval of the 750 ms ISI and the first interval (red rectangle and red line in lower panel). These distances, shown in the lower panel, allows for quantification of the effect of the network not returning to its initial (resting) state before presenting the next stimulus. Note that while the initial distance is lower in the 750 ms ISI, it is not zero.
(C) Percent correct performance of networks trained to discriminate two intervals separated by varying ISIs. Average data from four stimulations. Output units were trained to discriminate intervals ranging from 50 – 150 ms. Performance was then tested by examining generalization to these same intervals when presented at varying ISIs after the presentation of a 100 ms interval. Results for the 100 x 150 ms discrimination are shown. Performance is highly dependent on the initial state of the network.
To quantify the effect of initial state on interval discrimination, Output units were trained to discriminate 100 ms from other intervals in the range of 50–150 ms. We then determined the ability of the model to perform this discrimination when the comparison intervals followed the 100 ms target by ISIs that varied from 250 – 750 ms. Performance worsened with decreasing ISIs (Fig. 6C). Importantly, performance changed in a graded manner, indicating that the reset effect is not expected to be all or none. Thus the behavior of the theoretical model is consistent with the results seen in the human psychophysical data.
DISCUSSION
The standard model of temporal processing postulates a single centralized internal clock, which relies on a pacemaker and a counter (Creelman, 1962; Treisman, 1963; Church, 1984; Grondin, 2001). The clock concept is generally taken to imply that the passage of time is counted in units that can be combined or compared linearly. In contrast, SDN models propose that for spans on the scale of tens to hundreds of milliseconds time may be represented as specific states of a neural network. Within this framework, a 50 ms interval followed by a 100 ms interval is not encoded as the combination of the two. Instead, the earlier stimulus interacts with the processing of the 100 ms interval resulting in the encoding of a distinct temporal object. Thus, temporal information is encoded in the context of the entire pattern, not as conjunctions of the component intervals.
State-Dependent Networks and the Reset Task
State-dependent network models propose that timing is a ubiquitous component of neural computations, and that local cortical circuits are inherently capable of processing both temporal and spatial information. Buonomano and Merzenich, 1995; Buonomano, 2000; Maass et al, 2002). In these models timing relies on mechanisms analogous to using the evolving state of a physical system – like the ripples on the surface of a lake – to tell time. However, as shown here (Fig. 1 and 2), reliance on the state of a complex system to tell time creates potentially serious limitations in the resulting dependence on the initial state and the lack of a linear metric of time.
Interestingly, our psychophysical results reveal the same limitations - interval discrimination is impaired by the presence of a distractor that appears at unpredictable times. However, interval discrimination was not altered if the distractor occurred at a fixed time prior to the target. Thus internal representations of the target interval can develop across trials for the 2T and 3T-FIX stimuli but not for the target interval of the 3T-VAR stimuli. This is because the state of the system at the onset of the second tone is variable. The impairment in the 3T-VAR condition is not due to the unpredictability of the distractor's presence itself, since the 2T and 3T stimuli are randomly intermixed, the unpredictability is the same under all conditions. Rather, the impairment in the 3T-VAR condition is limited to the predictability (consistency) of the interval of the distractor.
An alternate interpretation of the 3T-VAR impairment is that in the 3T-FIX condition, the distractor interval served as a reference cue for the target interval. The two-interval discrimination task, in which both a standard and comparison interval are presented on each trial was used to rule out this possibility (Grondin & Rousseau, 1991; Rammsayer, 1999; Wright et al, 1997). Performance was impaired if the time between the stimuli was 250 but not 750 ms (Fig. 5A). It could be argued that the impairment for short ISIs reflects a difficulty in segmenting or attending to rapidly presented stimuli. We find this interpretation unlikely since performance on the short and long ISI conditions did not differ when the two intervals were presented at different frequencies.
The influence of preceding stimuli on temporal judgments is surprising because much of the timing performed by the nervous system on the scale of hundreds of milliseconds is based on a continuous barrage of incoming stimuli, such as speech or Morse code recognition. The subjects in the current study were naïve, thus, a critical issue relates to the effect of learning. We speculate that training would allow subjects to improve their discrimination of intervals independent of temporal context. Indeed, state-dependent network models do not predict that spatial-temporal patterns preceded by other events are impossible to process. Rather, they propose that there must be previous exposure to a large number of instances of the stimuli so that a correspondence between the target information in a number of different contexts can be learned.
Clock Models
The standard clock models predict a linear metric of time, which implies that the clock can time the sequential intervals independent of the presence of a variable distractor across trials. However, most of these models do not explicitly address the issue of the clock reset properties. Thus it seems reasonable to consider whether a clock with some state-dependent properties could account for the impaired timing of short ISIs or intervals with a distractor. For example, one could assume that resetting or reading the time of the clock is state-dependent, and thus the reset process could inject noise into the system or be delayed dependent on the initial state.
There are two aspects of our results which could argue against a state-dependent clock mechanism. First, though a state-dependent reset of a centralized clock could explain impaired timing in the short ISI condition (Fig. 5A), it would not predict the lack of impairment in the short ISI condition with different frequencies (Fig. 5B). The second issue concerns the specificity of the reset problem. In our Reset experiments (Fig 3), a clock would be started by the first tone and stopped and reset (restarted) by the second. The third tone would again stop the clock. As mentioned above, a state-dependent reset would take time or inject noise into the process, and impair the 3T-VAR sequence compared to the 2T one. However, such a clock would also be expected to impair timing of three tone stimuli in the FIX condition. In both cases, the second tone would stop and reset the clock, because there is a 50% chance that the second tone was the end vs. the beginning of the target interval. This prediction is counter to our psychophysical results. One might then propose the use of multiple clocks, in which the first tone activates a primary clock, the second tone activates a secondary clock (and stops the first), and the third tone stops the second clock. This explanation would correctly suggest that timing is not impaired in the FIX condition, but would also hold for the VAR, again violating the dissociation found in our data.
Nevertheless, we cannot eliminate the possibility that there exists a set of assumptions which can enable clock models to account for the observed millisecond timing results. However, we argue that the SDN model provides the most parsimonious explanation of the current psychophysical data on the processing of short intervals.
Other Models of Temporal Processing
A number of other mechanistic models have been put forth to account for measuring and encoding time. These include climbing firing rate models (Durstewitz, 2003; Reutimann et al, 2004), multiple oscillator models (Miall, 1989; Matell and Meck, 2004), as well as those based on ongoing network dynamics (Medina and Mauk, 2000; Buonomano, 2005). The latter focus primarily on generating appropriately timed motor responses and will not be discussed here.
The climbing or ramping firing rate models suggest that, like many other stimulus features, time is encoded in the firing rate of neurons. Experimentally it is established that some cortical neurons undergo a more or less linear ramping in their firing rate over time (Niki & Watanabe, 1979; Brody et al, 2003; Leon & Shadlen, 2003). In their simplest form climbing models propose that firing rate represents a linear metric of absolute time. However, recent data suggests that at least in some cases these neurons are coding expectation rather than absolute time (Janssen & Shadlen, 2005). Climbing rate models have been discussed primarily in relation to timing of intervals or durations, how they would account for timing of temporal patterns has not been addressed. Thus their predictions for our tasks are not immediately clear. For the Reset task it could be argued that ramping would begin at the first stimulus. Time could be read out in the firing rate at the onset of the second and third tone – assuming activity is not reset by the second tone. However, climbing models would not predict the dramatic impairment observed in the 3T-VAR condition or the effect of short ISIs. We would speculate that ramping firing rates are likely to play an important role in the timing of expected motor responses, but less likely to be involved in the timing of rapid sensory stimuli particularly for complex tasks such as speech or Morse code.
The multiple oscillator model suggests that time is encoded in a population of oscillators with different base frequencies (Miall, 1989; Matell and Meck, 2004; Buhusi & Meck, 2006). Time can be read-out by a set of coincidence detectors. This model has the advantage of not requiring a counter/accumulator, and being capable of timing multiple consecutive intervals once the oscillators have been triggered. However, how this model will behave in the tasks examined here is again dependent on its assumptions. If each event does not reset the oscillators, this model would be expected to produce a decrease in performance in the 3T-VAR condition, consistent with our results. However, it would not necessarily predict the decrease in performance observed with the short ISIs observed in Fig. 5, since its reset mechanisms could be all or none. Furthermore, this model posits that timing is centralized. Thus it would not predict that any effect of a short ISI would be dependent on whether the frequency of the comparison stimuli were the same. We would concur that a multiple oscillator model could contribute to timing in the range of seconds (Matell and Meck, 2004; Buhusi & Meck, 2006), but would argue that it is unlikely to account for the timing on the scale of a few hundred milliseconds.
Millisecond versus second timing
Timing in both the range of milliseconds and seconds has often been considered to rely on the same underlying mechanisms (Church, 1984; Macar et al, 2002). The results described here demonstrate qualitative differences in the processing of short and long intervals. Unlike the millisecond range, timing of intervals lasting one second or longer appears consistent with mechanisms that generate a linear metric of time. For a 1 sec target subjects could accurately judge the first or second of two consecutive intervals in the reset task, even though they did not know a priori which was the target. Performance was also independent of both fixed and variable distractors preceding the target interval. This implies that subjects could independently keep track of the objective time of two sequential second-long intervals, and implies the presence of a linear metric of time. Two simple strategies by which a standard clock model could perform this task are by resetting a clock at the second tone, or by temporal arithmetic. For the long intervals we did not observe any decrease in timing accuracy in the 3T versus 2T stimuli. We would suggest that this observation is more consistent with the temporal arithmetic scenario. Specifically, that timing on the order of seconds relies on a linear metric of time, and that the second of two consecutive intervals can be calculated by subtracting the first interval from the final count.
The theoretical framework and psychophysical results described here, together with previous psychophysical (Rammsayer & Lima, 1991), pharmacological (Rammsayer, 1999), and imaging studies (Lewis & Miall, 2003), support the existence of distinct loci for subsecond and second processing. The precise boundary between these forms of temporal processing cannot yet be established. However, it seems likely that they are highly overlapping, and that timing in intermediary ranges (e.g., 400–800 ms) may be accurately performed by both the mechanisms underlying time perception and time estimation. Based on the time constants of short-term synaptic plasticity and other time-dependent neural properties we suggest that the SDN model is limited to intervals below 500 ms. Additionally, even within a specific time scale there may be multiple mechanisms contributing to timing, and thus the above models are not mutually exclusive.
Relation to previous psychophysical data
A comprehensive model of temporal processing should provide a detailed description of the neural mechanisms underlying timing, generate novel testable predictions, and account for existing experimental data. Two of the most robust features of temporal processing determined experimentally relate to the scalar property and the role of attention in subjective time estimation. The scalar property refers to the observation that the ratio of the absolute criterion interval and the standard deviation of temporal estimates tends to be constant for long intervals (Gibbon, 1977; Gibbon et al, 1997; Buhusi & Meck, 2005). However, this is not the case for interval discrimination in the range of a few hundred milliseconds (Wright et al, 1997; Mauk & Buonomano, 2004). Thus, we examined how performance scales with short intervals in the SDN model. Results showed that, consistent with the human psychophysical data, temporal resolution is proportionally worse for short intervals (Fig. S1).
Attention has been widely reported to alter estimates of time in the range of seconds (Hicks et al, 1976; Macar et al, 1994; Brown, 1997; Coull et al, 2004). Internal clock models account for attention-dependent effects in the second range, by assuming a gating mechanisms that controls the number of events generated by the pacemaker that are counted by the accumulator (Meck, 1984; Zakay & Tsal, 1989). In contrast, on the shorter time scale, divided attention or cognitive load does not appear to specifically alter temporal judgments (Rammsayer, 1991; Lewis & Miall, 2003). Therefore the SDN model would be expected to be fairly insensitive to shifts in attention. However, recent studies have revealed that temporal distortions of short intervals can be produced by saccades or stimulus features (Morrone et al, 2005; Johnston et al, 2006). These studies suggest that on short scales timing is local, and are generally consistent with the SDN model that predicts that temporal processing could occur in a number of different cortical areas on a as needed basis.
Conclusion
We propose here that cortical networks can tell time as a result of time-dependent changes in synaptic and cellular properties, which influence the population response to sensory events in a history-dependent manner. This framework is applicable to the processing of simple intervals as well as more complex spatial-temporal patterns, and does not invoke any novel hypothetical mechanisms at the neural and synaptic level. Additionally, it is proposed that timing is not centralized, and can potentially occur locally at both early and late stages of cortical processing. The psychophysical experiments examined here emerged as a direct prediction of this model, and the results are supportive of this general framework. However, establishing the neural basis for timing will ultimately require the accumulation of converging evidence from a number of different fields, of particular relevance will be the use of more complex temporal stimuli in conjunction with in vivo electrophysiology, to determine if the population response to ongoing sensory events also contain information about the preceding stimuli.
EXPERIMENTAL PROCEDURES
Neural Network Simulations
The simulated network was composed of 400 excitatory (Ex) and 100 inhibitory (Inh) recurrently connected Hodgkin-Huxley units (Buonomano, 2000). Excitatory neurons were randomly interconnected with a probability of 0.2. The mean synaptic weights were adjusted so that neurons responded with 0–3 spikes to a short stimulus, as is typical for primary sensory cortex in awake animals (Brody et al, 2002; Wang et al, 2005). Short-term dynamics of excitatory synapses were simulated according to Markram et al (1998). Short-term synaptic plasticity of Ex→Ex synapses was facilitatory, based on experiments suggesting that paired-pulse facilitation is present in adult cortex (Reyes & Sakmann, 1998; Zhang, 2004). The mean U (‘utilization’), τrec (recovery from depression), and τfac (facilitation) parameters were 0.25, 10 ms and 100 ms. All three values were randomly assigned using a normal distribution with a SD of 20% of the mean. Short-term plasticity IPSPs in the form of paired-pulse depression was implemented as previously described (Buonomano, 2000).
Mutual Information and Network Readout
Mutual information was calculated using the total number of spikes in response to a stimulus, thus providing an assumption-independent estimate of the amount of information available (Buonomano, 2005). For the discrimination between stimuli with different numbers of pulses (Fig. 2A) training of the output units was based on previously described supervised learning rules (Buonomano, 2000; Maass et al, 2002) using only the pattern produced by the last pulse. Training was performed on a set of 25 stimulus presentations and tested on 10 novel test presentations. In the stimulations shown in Figure 6, the outputs were trained to discriminate pairs of intervals (100 ms versus intervals ranging from 50 – 150 ms). In each case the shortest interval was defined as the short stimulus and the longest as the long stimulus.
Principal Component Analysis
The data set was comprised of the voltage of all Ex and Inh neurons, and the synaptic weights (which were time-varying) of excitatory and inhibitory synapses. To reduce the dimensionality of the data set, only 20% of all synaptic weights were used. The data was normalized and the principal components were calculated using the PRINCOMP function in Matlab. Although the dimensionality is very high, the dimensions are highly correlated during the silent period between events (if one cell is hyperpolarized, most cells are hyperpolarized). As a result, the first three principal components can account for a significant amount of the total variability (approximately 75% in Fig. 1B). As expected, these components do not account well for the actual response to each event, which is dominated by highly nonlinear dynamics.
Psychophysics
Subjects consisted of graduate and undergraduate students with normal hearing, and between the ages of 18 and 30 from the UCLA community.
Reset Task
These experiments were based on a single-stimulus two-alternative forced-choice protocol as described previously (Karmarkar & Buonomano, 2003). A within-subject design was used, thus each subject performed the two distractor conditions (FIX and VAR), each condition having two tracks (2T and 3T). Sessions of the FIX and VAR conditions were given on alternating days over a day period (counterbalanced). Each block within a session consisted of 120 trials: 60 2T and 60 3T. Each tone (1 kHz) was 15 ms in duration, including a 5 ms linear ascending and descending ramp. In the FIX condition, a distractor tone was presented at a fixed interval equal to that of the standard interval (SI) prior to the target. In the VAR condition the distractor occurred before the target at an interval uniformly distributed between SI±0.5*SI. Thresholds for the 2T and 3T tracks were obtained by presenting the target interval as SI±Δt, where Δt varied adaptively according to a 3-down 1-up procedure (Levitt, 1971; Karmarkar & Buonomano, 2003). Threshold was defined as two times the mean of the reversal values, which corresponds to a 79% correct performance level.
In each trial subjects made a forced choice decision as to whether the stimulus seemed shorter or longer than the target interval by pressing one of two buttons on a computer mouse. They were provided with immediate visual feedback. All stimuli were generated in Matlab and presented through headphones.
The 2T and 3T stimuli were randomly interleaved to ensure that subjects did not develop a strategy that involved ignoring the distractor tone. Additionally, the simultaneous measure of performance on a conventional two tone task and one with the presence of a distractor provided a control for nonspecific effects such as difficulty of the overall task, attention and memory. Target intervals were either 100 or 1000 ms.
A similar protocol to the one used above was also used for the frequency discrimination task. Rather then adaptively varying the interval of the tones, their frequency was varied according to F±ΔF (where F, the target frequency was 1 kHz). Tone duration was 25 ms.
Two-Interval Forced Choice Procedure
In this task subjects were presented with two intervals on each trial: a standard and the comparison (standard + ΔT) (Allan, 1979; Karmarkar and Buonomano, 2003). Subjects are asked to press one of two buttons depending on whether they judged the first stimulus or the second interval to be longer. The standard interval was 100 ms, and the interstimulus intervals for the short and long ISI conditions were 250 and 750, ms respectively.
The frequency task in the ISI experiments used the same type of stimuli, but shifted the frequency of both tones of the comparison stimulus. Note that in contrast to the single stimulus protocol, subjects could reference the target frequency on each trial as opposed to developing an internal representation of it across trials. We believe this difference, together with the absence of a distractor is responsible for the improvement in the frequency thresholds as compared to the Reset task. All subjects performed all four tasks in a counterbalanced manner.
Statistics
In the Reset task, the key analysis was the performance on the 3T-VAR task in comparison to both the 2T-VAR and 3T-FIX tasks. A difference between only one of these comparisons would suggest a ‘cross-track’ effect of the variable distractor independent of whether it was in the 2T or 3T condition, or impairment of 3T discriminations independent of whether the distractor was presented at a fixed or variable interval. Thus, we performed a two-way analysis of variance to determine if there was an interaction between the 2T/3T and FIX/VAR factors.
Supplementary Material
The SDN model was presented with three target intervals (50, 100 and 200 ms), as well as with as set of comparison intervals that were factors of 10, 20, or 50% of the target intervals. The output units were trained to discriminate between the target and each of the factors using a sample of 20 presentations of each, and than tested on a separate data set of 15 probe presentations. The percent correct for each discrimination is plotted for a total of six different simulations (in which the network 'seed' is changed). For each factor discrimination was worse for the shorter intervals. This data is consistent with human psychophysical data showing that relative to the criterion interval, discrimination is progressively worse for 50, 100 and 200 ms target intervals.
Acknowledgments
This research was supported by the NIH (MH60163). We would like to thank Jennifer Bramen, Allison Doupe, and Ladan Shams for helpful comments on this manuscript, and the many volunteers who participated in these studies.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Allan LG. The perception of time. Perception & Psychophysics. 1979;26:340–354. [Google Scholar]
- Brown SW. Attentional resources in timing: interference effects in concurrent temporal and nontemporal working memory tasks. Percept Psychophys. 1997;59:1118–1140. doi: 10.3758/bf03205526. [DOI] [PubMed] [Google Scholar]
- Brody CD, Hernandez A, Zainos A, Lemus L, Romo R. Analysing neuronal correlates of the comparison of two sequentially presented sensory stimuli. Phil Trans R Soc Lond B (2002) 2002;357:1843–1850. doi: 10.1098/rstb.2002.1167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brody CD, Hernandez A, Zainos A, Romo R. Timing and neural encoding of somatosensory parametric working memory in macaque prefrontal cortex. Cereb Cortex. 2003;13:1196–1207. doi: 10.1093/cercor/bhg100. [DOI] [PubMed] [Google Scholar]
- Brown SW. Attentional resources in timing: interference effects in concurrent temporal and nontemporal working memory tasks. Percept Psychophys. 1997;59:1118–1140. doi: 10.3758/bf03205526. [DOI] [PubMed] [Google Scholar]
- Buhusi CV, Meck WH. What makes us tick? Functional and neural mechanisms of interval timing. Nat Neursci Rev. 2005;6:755–765. doi: 10.1038/nrn1764. [DOI] [PubMed] [Google Scholar]
- Buonomano DV, Karmarkar UR. How do we tell time? Neuroscientist. 2002;8:42–51. doi: 10.1177/107385840200800109. [DOI] [PubMed] [Google Scholar]
- Buonomano DV, Merzenich MM. Temporal information transformed into a spatial code by a neural network with realistic properties. Science. 1995;267:1028–1030. doi: 10.1126/science.7863330. [DOI] [PubMed] [Google Scholar]
- Buonomano DV. Decoding temporal information: a model based on short-term synaptic plasticity. J Neurosci. 2000;20:1129–1141. doi: 10.1523/JNEUROSCI.20-03-01129.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carr CE. Processing of temporal information in the brain. Ann Rev Neurosci. 1993;16:223–243. doi: 10.1146/annurev.ne.16.030193.001255. [DOI] [PubMed] [Google Scholar]
- Church RM. Properties of the internal clock. In: Allan L, editor. Timing and perception. Vol. 423. New York: Annals of the New York Academy of Sciences; 1984. pp. 556–582. [DOI] [PubMed] [Google Scholar]
- Coull JT, Vidal F, Nazarian B, Macar F. Functional Anatomy of the Attentional Modulation of Time Estimation. Science. 2004;303:1506–1508. doi: 10.1126/science.1091573. [DOI] [PubMed] [Google Scholar]
- Creelman CD. Human discrimination of auditory duration. J Acoust Soc Am. 1962;34:582–593. [Google Scholar]
- Durstewitz D. Self-organizing neural integrator predicts interval times through climbing activity. J Neurosci. 2003;23:5342–5353. doi: 10.1523/JNEUROSCI.23-12-05342.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferster D, Miller KD. Neural mechanisms of orientation selectivity in the visual cortex. Annu Rev Neurosci. 2000;23:441–71. doi: 10.1146/annurev.neuro.23.1.441. [DOI] [PubMed] [Google Scholar]
- Gibbon J. Scalar expectancy theory and Weber's law in animal timing. Psychological Review. 1977:279–325. [Google Scholar]
- Gibbon J, Malapani C, Dale CL, Gallistel CR. Toward a neurobiology of temporal cognition: advances and challenges. Curr Opinion Neurobiol. 1997;7:170–184. doi: 10.1016/s0959-4388(97)80005-0. [DOI] [PubMed] [Google Scholar]
- Gilbert CD, Sigman M, Christ RE. The neural basis of perceptual learning. Neuron. 2000;31:681–697. doi: 10.1016/s0896-6273(01)00424-x. [DOI] [PubMed] [Google Scholar]
- Grondin S. From physical time to the first and second moments of psychological time. Psychol Bull. 2001;127:22–44. doi: 10.1037/0033-2909.127.1.22. [DOI] [PubMed] [Google Scholar]
- Grondin S, Rammsayer T. Variable foreperiods and temporal discrimination. Quarterly Journal of Experimental Psychology, Section A: Human Experimental Psychology. 2003;56A:731–765. doi: 10.1080/02724980244000611. [DOI] [PubMed] [Google Scholar]
- Grondin S, Rousseau R. Judging the duration of multimodal short empty time intervals. Perception & Psychophysics. 1991;49:245–256. doi: 10.3758/bf03214309. [DOI] [PubMed] [Google Scholar]
- Hahnloser RHR, Kozhevnikov AA, Fee MS. An ultra-sparse code underlies the generation of neural sequences in a songbird. Nature. 2002;419:65–70. doi: 10.1038/nature00974. [DOI] [PubMed] [Google Scholar]
- Hicks RE, Miller GW, Kinsbourne M. Prospective and retrospective judgments of time as a function of amount of information processed. Am J Psychol. 1976;89:719–730. [PubMed] [Google Scholar]
- Hubel DH, Wiesel TN. Receptive fields, binocular interaction and functional architecture in the cat's visual cortex. J Physiol. 1962;160:106–54. doi: 10.1113/jphysiol.1962.sp006837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivry R. The representation of temporal information in perception and motor control. Curr Opin Neurobiol. 1962;6:851–857. doi: 10.1016/s0959-4388(96)80037-7. [DOI] [PubMed] [Google Scholar]
- Ivry RB, Spencer RMC. The neural representation of time. Curr Opinion in Neurobiol. 2004;14:225–232. doi: 10.1016/j.conb.2004.03.013. [DOI] [PubMed] [Google Scholar]
- Janssen P, Shadlen MN. A representation of the hazard rate of elapsed time in the macaque area LIP. Nat Neurosci. 2005;8:234–241. doi: 10.1038/nn1386. [DOI] [PubMed] [Google Scholar]
- Johnston A, Arnold DH, Nishida S. Spatially localized distortions of event time. Curr Biol. 2006;16:472–479. doi: 10.1016/j.cub.2006.01.032. [DOI] [PubMed] [Google Scholar]
- Karmarkar U, Buonomano DV. Temporal specificity of perceptual learning in an auditory discrimination task. Learning & Memory. 2003;10:141–147. doi: 10.1101/lm.55503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kilgard MP, Merzenich MM. Order-sensitive plasticity in adult primary auditory cortex. PNAS USA. 2002;99:3205–3209. doi: 10.1073/pnas.261705198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knüsel P, Wyss R, König P, Verschure PFMJ. Decoding a temporal population code. Neural Comp. 2004;16:2079–21000. doi: 10.1162/0899766041732459. [DOI] [PubMed] [Google Scholar]
- Lehiste I, Olive JP, Streeter LA. Role of duration in disambiguating syntactically ambiguous sentences. J Acoust Soc Am. 1976;60:1199–1202. [Google Scholar]
- Leon MI, Shadlen MN. Representation of time by neurons in the posterior parietal cortex of the macaque. Neuron. 2003;38:317–327. doi: 10.1016/s0896-6273(03)00185-5. [DOI] [PubMed] [Google Scholar]
- Levitt H. Transformed up-down methods in psychoacoustics. J Acoust Soc Am. 1971;49:467–477. [PubMed] [Google Scholar]
- Lewis PA, Miall RC. Distinct systems for automatic and cognitively controlled time measurements: evidence from neuroimaging. Curr Opin Neurobio. 2003;13:250–255. doi: 10.1016/s0959-4388(03)00036-9. [DOI] [PubMed] [Google Scholar]
- Liberman AM, Delattre PC, Gerstman LJ, Cooper FS. Tempo of frequency change as a cue for distinguishing classes of speech sounds. J Exp Psychol. 1956;52:127–137. doi: 10.1037/h0041240. [DOI] [PubMed] [Google Scholar]
- Maass W, Natschläger T, Markram H. Real-time computing without stable states: a new framework for neural computation based on perturbations. Neural Comput. 2002;14:2531–2560. doi: 10.1162/089976602760407955. [DOI] [PubMed] [Google Scholar]
- Macar F, Grondin S, Casini L. Controlled attention sharing influences time estimation. Mem Cognit. 1994;22:673–686. doi: 10.3758/bf03209252. [DOI] [PubMed] [Google Scholar]
- Macar F, Lejeune H, Bonnet M, Ferrara A, Pouthas V, Vidal F, Maquet P. Activation of the supplementary motor area and of attentional networks during temporal processing. Exp Brain Res. 2002;142:475–485. doi: 10.1007/s00221-001-0953-0. [DOI] [PubMed] [Google Scholar]
- Markram H, Wang Y, Tsodyks M. Differential signaling via the same axon of neocortical pyramidal neurons. Proc Natl Acad Sci USA. 1998;95:5323–5328. doi: 10.1073/pnas.95.9.5323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin SJ, Grimwood PD, Morris RGM. Synaptic plasticity and memory: an evaluation of the hypothesis. Annu Rev Neurosci. 2000;23:649–711. doi: 10.1146/annurev.neuro.23.1.649. [DOI] [PubMed] [Google Scholar]
- Mauk MD, Ruiz BP. Learning-dependent timing of Pavlovian eyelid responses: differential conditioning using multiple interstimulus intervals. Behav Neurosci. 1992;106(4):666–81. doi: 10.1037//0735-7044.106.4.666. [DOI] [PubMed] [Google Scholar]
- Mauk MD, Buonomano DV. The Neural Basis of Temporal Processing. Annual Rev Neurosci. 2004;27:304–340. doi: 10.1146/annurev.neuro.27.070203.144247. [DOI] [PubMed] [Google Scholar]
- Matell MS, Meck WH. Cortico-striatal circuits and interval timing: coincidence detection of oscillatory processes. Cogn Brain Res. 2004;21:139–170. doi: 10.1016/j.cogbrainres.2004.06.012. [DOI] [PubMed] [Google Scholar]
- Meck WH. Attentional bias between modalities: Effect on the internal clock, memory, and decision stages used in animal time discrimination. In: Gibbon J, Allan L, editors. Annals of the New YorkAcademy of Sciences: Vol 423. Timing and time perception. New York: New York Academy of Sciences; 1984. pp. 528–541. [DOI] [PubMed] [Google Scholar]
- Meck WH. Neuropharmacology of timing and time perception. Cog Brain Res. 1996;3:227–242. doi: 10.1016/0926-6410(96)00009-2. [DOI] [PubMed] [Google Scholar]
- Meegan DV, Aslin RN, Jacobs RA. Motor timing learned without motor training. Nature Neurosci. 2000;3:860–862. doi: 10.1038/78757. [DOI] [PubMed] [Google Scholar]
- Medina JF, Mauk MD. Computer simulation of cerebellar information processing. Nature Neurosci. 2000;3:1205–1211. doi: 10.1038/81486. [DOI] [PubMed] [Google Scholar]
- Medina JF, Carey MR, Lisberger SG. The representation of time for motor learning. Neuron. 2005;45:157–67. doi: 10.1016/j.neuron.2004.12.017. [DOI] [PubMed] [Google Scholar]
- Merzenich MM, Jenkins WM, Johnston P, Schreiner C, Miller SL, Tallal P. Temporal processing deficits of language-learning impaired children ameliorated by training. Science. 1996;271:77–81. doi: 10.1126/science.271.5245.77. [DOI] [PubMed] [Google Scholar]
- Miall C. The storage of time intervals using oscillating neurons. Neural Comput. 1989;1:359–371. [Google Scholar]
- Michon JA. The complete time experiencer. In: Michon JA, Jackson JL, editors. Time, mind and behavior. Berlin: Springer-Verlag; 1985. pp. 21–52. [Google Scholar]
- Miller KD, Keller JB, Stryker MP. Ocular dominance column development: analysis and simulation. Science. 1989;245:605–615. doi: 10.1126/science.2762813. [DOI] [PubMed] [Google Scholar]
- Morrone MC, Ross J, Burr D. Saccadic eye movements cause compression of time as well as space. Nat Neurosci. 2005;8:950–954. doi: 10.1038/nn1488. [DOI] [PubMed] [Google Scholar]
- Niki H, Watanabe M. Prefrontal and cingulate unit activity during timing behavior in the monkey. Br Res. 1979;171:213–224. doi: 10.1016/0006-8993(79)90328-7. [DOI] [PubMed] [Google Scholar]
- Rammsayer TH, Lima SD. Duration discrimination of filled and empty auditory intervals: cognitive and perceptual factors. Percept Psychophys. 1991;50:565–574. doi: 10.3758/bf03207541. [DOI] [PubMed] [Google Scholar]
- Rammsayer TH, Ulrich R. Counting models of temporal discrimination. Psychonomic Bulletin & Review. 2001;8:270–277. doi: 10.3758/bf03196161. [DOI] [PubMed] [Google Scholar]
- Rammsayer TH. Neuropharmacological evidence for different timing mechanisms in humans. Quart J Exp Psychol. 1999;52B:273–286. doi: 10.1080/713932708. [DOI] [PubMed] [Google Scholar]
- Rao SM, Mayer AR, Harrington DL. The evolution of brain activation during temporal processing. Nature Neurosci. 2001;4:317–323. doi: 10.1038/85191. [DOI] [PubMed] [Google Scholar]
- Reutimann J, Yakovlev V, Fusi S, Senn W. Climbing neuronal activity as an event based cortical representation of time. J Neurosci. 2004;24:3295–3303. doi: 10.1523/JNEUROSCI.4098-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reyes A, Sakmann B. Developmental Switch in the Short-Term Modification of Unitary. J Neurosci. 1998;19:3827–3825. doi: 10.1523/JNEUROSCI.19-10-03827.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schoups A, Vogels R, Qian N, Orban G. Practicing orientation identification improves orientation coding in V1 neurons. Nature. 2001;412:549–53. doi: 10.1038/35087601. [DOI] [PubMed] [Google Scholar]
- Shannon RV, Zeng FG, Kamath V, Wygonski J, Ekelid M. Speech recognition with primarily temporal cues. Science. 1995;270:303–304. doi: 10.1126/science.270.5234.303. [DOI] [PubMed] [Google Scholar]
- Tallal P. In the perception of speech time is of the essence. In: Buzsaki G, Llinas R, Singer W, Berthoz A, Christen Y, editors. Temporal Coding in the Brain. Springer-Verlag; Berlin: 1994. pp. 291–299. [Google Scholar]
- Treisman M. Temporal discrimination and the indifference interval: implications for a model of the ‘internal clock’. Psychol Monographs. 1963;77:1–31. doi: 10.1037/h0093864. [DOI] [PubMed] [Google Scholar]
- Wang x, Lu T, Snider RK, Liang Li. Sustained firing in auditory cortex evoked by preferred stimuli. Nature. 2005;435:341–345. doi: 10.1038/nature03565. [DOI] [PubMed] [Google Scholar]
- Wright BA, Buonomano DV, Mahncke HW, Merzenich MM. Learning and generalization of auditory temporal-interval discrimination in humans. J Neurosci. 1997;17:3956–3963. doi: 10.1523/JNEUROSCI.17-10-03956.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang T, Maunsell JH. The effect of perceptual learning on neuronal responses in monkey visual area V4. J Neurosci. 2004;24:1617–26. doi: 10.1523/JNEUROSCI.4442-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zakay D, Tsal Y. Awareness of attention allocation and time estimation accuracy. Bull Psychonom Soc. 1989;27:209–210. [Google Scholar]
- Zhang Z. Maturation of Layer V Pyramidal Neurons in the Rat Prefrontal Cortex. Intrinsic Properties and Synaptic Function. 2004;91:1171–1182. doi: 10.1152/jn.00855.2003. [DOI] [PubMed] [Google Scholar]
- Zucker RS. Short-term synaptic plasticity. Ann Rev Neurosci. 1989;12:13–31. doi: 10.1146/annurev.ne.12.030189.000305. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The SDN model was presented with three target intervals (50, 100 and 200 ms), as well as with as set of comparison intervals that were factors of 10, 20, or 50% of the target intervals. The output units were trained to discriminate between the target and each of the factors using a sample of 20 presentations of each, and than tested on a separate data set of 15 probe presentations. The percent correct for each discrimination is plotted for a total of six different simulations (in which the network 'seed' is changed). For each factor discrimination was worse for the shorter intervals. This data is consistent with human psychophysical data showing that relative to the criterion interval, discrimination is progressively worse for 50, 100 and 200 ms target intervals.


