Control of protein crystal nucleation around the metastable liquid–liquid phase boundary

Abstract

The capability to enhance or suppress the nucleation of protein crystals opens opportunities in various fundamental and applied areas, including protein crystallography, production of protein crystalline pharmaceuticals, protein separation, and treatment of protein condensation diseases. Herein, we show that the rate of homogeneous nucleation of lysozyme crystals passes through a maximum in the vicinity of the liquid–liquid phase boundary hidden below the liquidus (solubility) line in the phase diagram of the protein solution. We found that glycerol and polyethylene glycol (which do not specifically bind to proteins) shift this phase boundary and significantly suppress or enhance the crystal nucleation rates, although no simple correlation exists between the action of polyethylene glycol on the phase diagram and the nucleation kinetics. The control mechanism does not require changes in the protein concentration, acidity, and ionicity of the solution. The effects of the two additives on the phase diagram strongly depend on their concentration, which provides opportunities for further tuning of nucleation rates.

The range of interactions between protein molecules in solution is comparable to their size; this range determines the typical phase diagram of protein solutions (1, 2). Similar to colloidal suspensions, in the protein concentration–temperature (C,T) plane, the transition to a higher-concentration solution, liquid–liquid (L–L) phase separation, occurs at lower temperatures than the separation between the solution and the solid phase (e.g., crystals; refs. 3 and 4). Thus, the second liquid phase is metastable. Recent simulations (5) and theory (6) predict that, as the system approaches the critical point for L–L phase separation (C^crit,T^crit), the nucleation barrier ΔG is reduced, and the rate of crystal nucleation is enhanced. Besides growing density fluctuations, the proposed enhancement mechanisms emphasize wetting of the nucleus surface by the liquid. On further cooling below T^crit, the enhancement of nucleation tapers off. Both parts of this prediction have been questioned (7, 8). One theory points out that gelation that occurs in a rather broad area around C^crit,T^crit (see for instance, ref. 4) arrests all motion in the solution, and no nucleation enhancement should be expected (7). On the other hand, another set of simulations foresee even faster nucleation in the region of L–L demixing beyond the critical point (8). In view of the practical importance of the protein crystal nucleation and the need for a better understanding of the phase behavior of protein solutions, we set out to study experimentally the nucleation kinetics around the L–L separation boundary. We probe not only the region around C^crit,T^crit but also the area around the L–L separation boundary at lower protein concentrations. In this way, we test the correlation between nucleation kinetics and L–L separation in a broader range of conditions that may be closer to those in living organisms or to those encountered in laboratory practice.

Furthermore, the L–L boundary can be shifted to higher or lower temperatures by (i) varying the acidity and ionicity of the solution (4, 9) or (ii) other modifiers of the protein intermolecular interactions, e.g., nonadsorbing polymers (10, 11). If an area of enhanced nucleation exists around the L–L boundary, such shifts provide for a nucleation control mechanism in this area. However, changing the pH and the electrolyte concentration is not possible under physiological conditions or may take laboratory or technological systems out of the crystallization conditions (12) because of changed distribution of the attractive sites on the molecular surface (13, 14). Thus, our second goal was to test whether nucleation can be controlled by shifting the L–L phase boundary and to find suitable additives of type ii.

Methods

We used a technique that yields steady-state homogeneous nucleation rates as the slope of the dependence of the number of nucleated crystals on the time allocated for nucleation (15). Heterogeneous nucleation is substantially faster and affects only the intercept of this dependence. Each rate data point results from statistics over 2,000 independent crystallization runs under identical conditions.

The same set up was used to determine the L–L phase boundary, T_L–L(C). For these tests, arrays of 20 identical solution droplets were monitored under the microscope as the temperature was lowered in 0.5°C increments, with 15 min between the steps. At a certain setting, immediately after the temperature was lowered, the solutions became cloudy. Typically, this transition happened simultaneously for all 20 droplets. Further T lowering by a few steps brought about no detectable changes in the solution. After that, T was raised in steps, and typically, the droplets became clear at temperatures within 0.5°C from the T at which they had become cloudy. The average of the T(cloud) and T(clarify) was taken as T_L–L. Where applicable, these determinations agree well with previous data (4).

Further tests were carried out by using thin layers of solution on sealed slides under a differential interference contrast-equipped microscope with a magnification of ×1,000. Immediately after the temperature was lowered by 1°C to a value below the T_L–L, motion in the solution was detectable. In a few seconds, droplets of a few tenths of a micrometer were visible that quickly grew to sizes of about 1–5 μm. The droplets partook in Brownian motion, gradually sedimented downward pulled by earth's gravity, and disappeared within a few seconds after temperature was raised back by 1°C to the setting above T_L–L (http://www.cmmr.uah.edu/protein/movies.html).

To determine the location of the spinodal at the solution compositions used in the nucleation experiments, we used static light scattering, as described in refs. 16 and 17. We extrapolated the temperature dependence of the reciprocal intensity, I⁻¹, of the light scattered at 90° to the temperature where I⁻¹ reaches zero (D. N. Petsev and O.G., unpublished work). This temperature was taken as the temperature of the spinodal for the given solution composition.

Results and Discussion

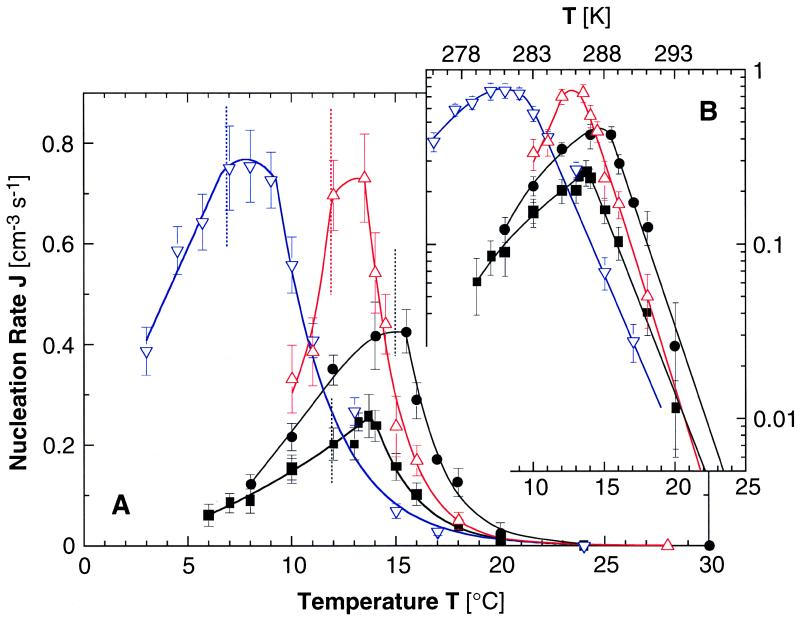
Fig. 1 presents the dependencies of the homogeneous nucleation rate J on the temperature T recorded at four solution compositions. In all cases, we see that as T is lowered, J increases, reaches a maximum near the T_L–L, and then decreases as the system enters the L–L separation region. Because J = J₀ exp(−ΔG*/k_BT) and log₁₀J = const −0.43 × ΔG*/k_BT, Fig. 1B maps the corresponding variations of the nucleation barrier ΔG* with temperature.

Figure 1.

(A) Dependencies of the rate of homogeneous nucleation of lysozyme crystals J on temperature T at pH 4.5 by 50 mM sodium acetate buffer and 4% (wt/vol) NaCl. ■, lysozyme concentration C_lys = 50 mg/ml, no additives; ●, C_lys = 80 mg/ml, no additives; ▿, C_lys = 50 mg/ml, 5% (vol/vol) glycerol; ▵, C_lys = 50 mg/ml, 0.2% (wt/vol) PEG 5000. Vertical dotted lines indicate respective temperatures of L–L separation T_L–L. Curves are just guides for the eye. (B) Semilogarithmic plots.

Factors that may underlie the J increase as T is lowered before the maximum are as follows. (i) Supersaturation for crystallization increases as the system moves away from the solubility line. (ii) The system approaches the spinodal lying below the binodal T_L–L(C) (16), similarly to the theoretical predictions for approaches to C^crit,T^crit (5, 6, 8). At the spinodal, (∂²ΔG/∂C²)_T = 0 (ΔG being the free energy of the solution; ref. 18), and the density fluctuations amplitudes are higher than at points off of it; the critical point is a location on the spinodal where the correlation length of the density fluctuations is limited only by the size of the container. (iii) In the approach to the binodal T_L–L(C), phenomena akin to wetting of the crystal nuclei surfaces by the liquid could be enhancing nucleation, as suggested in refs. 5 and 6. A prerequisite for such enhancement of crystal nucleation is faster nucleation of the liquid droplets than of crystals. At the critical point, where the surface energy of the liquid vanishes, the rate of liquid nucleation is limited only by solute transport to the liquid nuclei and the attachment kinetics. However, even away from the critical point at the binodal, nucleation of liquids may be faster than crystal nucleation; in contrast to crystal nucleation, liquid nucleation involves a single order parameter, density (6). As discussed in Methods above and in ref. 4, in the studied system, nucleation of liquid droplets is indeed significantly faster than the nucleation of crystals.

Note that factors ii and iii have not been considered separately by theory. The theoretical treatments of nucleation enhancement caused by L–L separation (5, 6, 8) concentrate on the region around the critical point, where the binodal and spinodal touch.

To evaluate the effect of supersaturation increase (i, described above), we note that, at 20°C, the concentration of a solution without additives and in equilibrium with crystals (solubility, see also Fig. 2A), C_eq = 3.4 mg/ml, whereas, for T = 14°C, C_eq = 2.3 mg/ml (19). For a solution containing 50 mg/ml lysozyme, these correspond to effective supersaturations σ = ln(C/C_eq) of 2.7 and 3.1, respectively. (The variable σ is a crude estimate of the protein chemical potential difference between solution and solid Δμ/k_BT. The possibility to account for solution nonideality that leads to the deviation between σ and Δμ/k_BT is discussed in ref. 20.) Previous experimental determinations of the nucleation rates at a constant temperature of 12.6°C and similar lysozyme and NaCl concentrations indicate that, in this supersaturation range, away from the L–L separation region, J varies according to the empirical formula exp(−44/σ²); close to T_L–L(C), this dependence is weaker (20). This dependency should not be sensitive to temperature-induced changes in the surface free energy of the nuclei not related to the L–L separation: surface free energy affects the nucleation kinetics through the nucleus size, but we found that, in this supersaturation range, away from the L–L separation boundary, this size is fixed and equal to four or five molecules (20). Thus, substituting in the above empirical formula, we find that this σ increase should lead to at most a 4-fold increase of the nucleation rate. The actual increase between these two temperatures is ≈25-fold. We attribute the residual ≈6-fold increase to the L–L separation-related factors ii or iii described above.

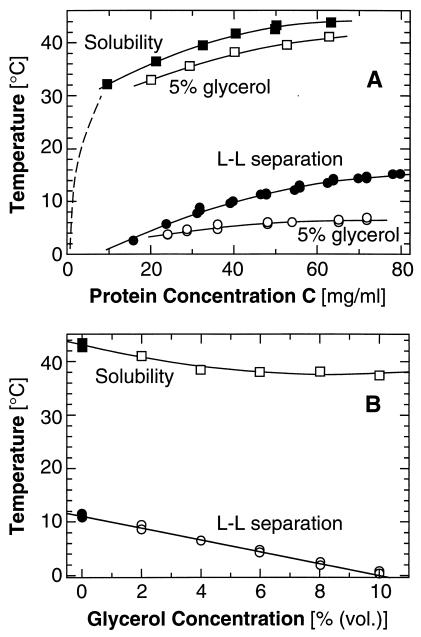
Figure 2.

Effects of glycerol on the phase diagram of a lysozyme solution containing 4% (wt/vol) NaCl at pH 4.5 by 50 mM sodium acetate buffer. (A) Changes in the solubility and L–L separation boundaries introduced by the addition of 5% (vol/vol) glycerol. Dashed line, solubility from ref. 19. (B) Dependence of the solubility and L–L separation temperatures on the concentration of glycerol in a 50 mg/ml lysozyme solution.

For further tests of this conclusion, we carried out J(T) determinations at a protein concentration of 80 mg/ml. The results in Fig. 1 show a ≈17-fold increase in J as T decreases from 20 to 15°C. The corresponding supersaturations are 3.15–3.5. In this σ range, the critical cluster contains one or two molecules; J is a very weak function of σ (20); and increase in J under these conditions is almost entirely attributable to factors related to the L–L phase separation. This higher protein concentration is closer to the critical point, and correspondingly, the effect on J is stronger.

Experiments at protein concentrations of 150 and 200 mg/ml revealed the expected (5, 6) extremely high crystal nucleation rates close to C^crit,T^crit. However, a few minutes after T was lowered to the chosen value, solution gelation (4, 21) occurred, and accordingly (7), nucleation was arrested. These observations show that gelation indeed plagues nucleation around the critical point. A recent theory suggests that nucleation around C^crit,T^crit can be thermodynamically uncoupled from gelation by fine tuning the range of protein intermolecular interactions (22). The above observations indicate that nucleation and gelation could also be separated because of different characteristic times.

On further lowering of T in the L–L demixing region, the nucleation rate decreases with lower T (see Fig. 1), despite the higher crystallization supersaturation. This trend seems to correspond to the slower nucleation at T < T^crit noted in refs. 5 and 6 and can be attributed the competition between the nucleation of crystals and of liquid droplets (6). The maximum in J(T) is reached around T_L–L and not at a T between T_L–L and the spinodal, as could be expected from the combination of enhancement on approach to the spinodal and suppression below T_L–L. This observation seems to suggest that the nucleation rate enhancement is mostly due to the wetting of the nuclei surfaces by the liquid around T_L–L as discussed in factor iii described above, rather than stronger density fluctuations. Still, one may argue that the binodal T_L–L(C) and the spinodal are within ≈1°C at the given protein concentration and that the nucleation enhancement is due to stronger fluctuations on approach to the spinodal.

To distinguish definitively between these possibilities, formulated as factors ii or iii above, we determined the location of the spinodal for the studied solutions. Our first results indicate that the spinodal is below the L–L separation line by 2–8°C, depending on the protein concentration. At 50 and 80 mg/ml, the differences are ≈6 and 4°C, respectively. Hence, the maxima in J in Fig. 1 are likely due to wetting or wetting-like effects by the liquid phase.

Note that the excess number of molecules in the region that contains the critical cluster, in the sense of refs. 23 and 24, in conditions similar to those used in this study, varies with supersaturation as 10 ± 1, 4 or 5, or 1 or 2 molecules (20). It would be difficult to assign some of them to the crystal and others to the liquid that wets it. Hence, the macroscopic concept of wetting, although readily comprehensible (25), should be applied with caution to microscopic processes (see discussion in ref. 6).

We still fail to understand the observation that the maximum value of J in Fig. 1 is consistently reached at T > T_L–L by 1–1.5°C. Analogous deviation was obtained in terms ΔG* for the C^crit,T^crit region in ref. 6 but was not addressed in the discussion.

The finding of a maximum in crystal nucleation rate near the L–L separation boundary suggests that shifting this boundary to lower temperatures can reduce J. One may attempt such shifts, by increasing the repulsion between the protein molecules (7, 10, 11). Recent work with a trypsin inhibitor suggests that glycerol increases such repulsion (26). Glycerol is rejected preferentially from the surroundings of the protein molecules (27), stabilizes their native structures (28), enhances their folding in aqueous media (29), and is even used as a food additive. The J(T) curve in the presence of glycerol in Fig. 1 shows that, indeed, T_L–L is lowered by 5°C, and, at temperatures above the T_L–L for solutions without glycerol, the nucleation rate is lowered by a factor of about three. The viscosity increase caused by 5% (vol/vol) glycerol is only ≈13% (30) and should affect the nucleation rate by the same factor (31). These facts and the similarity of the slopes of the J(T) lines with glycerol and without any additives in Fig. 1B indicate that glycerol predominantly affects the nucleation kinetics through the shifts in the phase boundaries.

The effects of glycerol on the solubility and the L–L curves differ, with the T_L–L point undergoing a stronger shift (Fig. 2). This discrepancy allows J(T) to reach values higher by a factor of three than the maximum value without glycerol before it reaches the new T_L–L point and is turned down. Fig. 2B shows that the effects of glycerol on the solubility and the L–L separation are monotonic functions of the additive and protein concentrations. Hence, we expect higher glycerol concentrations to suppress the nucleation rate further at T > T_L–L without additive.

In other applications, enhancement of crystal nucleation is sought. Polyethylene glycol (PEG) is expected to act only on the solution entropy and cause attraction between colloid particles because of the system's drive to minimize the excluded volume inaccessible to the polymer between two particles (10, 11, 32, 33). It has been suggested that such nonadsorbing, nonbridging polymers should enhance nucleation (5). Our results on J(T) in the presence of 0.2% (wt/vol) PEG 5000 are also presented in Fig. 1. This low concentration of PEG does not measurably affect the solubility or the L–L separation points (Fig. 3). Despite that, the rate of nucleation is increased 3-fold at T_L–L and less than that at higher or lower Ts. The slope of the J(T) line in Fig. 1B is steeper than for the other three cases, indicating that PEG affects the way density fluctuations respond to T. Using PEG of various molecular masses in concentrations higher than 0.5% resulted in very fast nucleation often accompanied by solution gelation or amorphous precipitation of the protein, indicating strong isotropic intermolecular attraction (13).

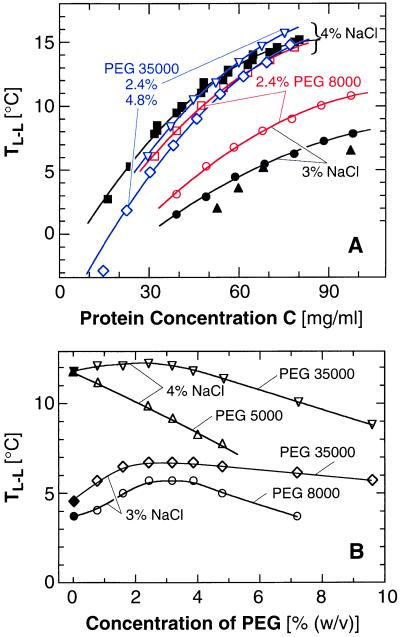
Figure 3.

Effects of PEG with molecular mass and concentration indicated in the plots on the L–L separation in a lysozyme solution containing 3 or 4% (wt/vol) NaCl at pH 4.5 by 50 mM sodium acetate buffer. Closed symbols, no additive; open symbols, PEG added as indicated in the plots. Curves are just guides for the eye. (A) Changes in the L–L separation boundary introduced by the addition of PEG. ▴, data of ref. 4 for 3% (wt/vol) NaCl. (B) Dependence of the L–L separation temperature on the concentration of PEG in a 50 mg/ml lysozyme solution.

The effect of PEG on J is considerably stronger than that of glycerol. To elucidate PEG–protein interactions further, in Fig. 3, we show T_L–L as a function of protein and PEG concentrations for two concentrations of NaCl and for PEG 5000, 8000, and 35000. These plots indicate that the action of PEG on T_L–L (Fig. 3) cannot be understood simply in terms of enhanced attraction caused by restricted volume accessible to nonadsorbing noninteracting polymers. Recent models (10, 34) allowing for interactions between the polymer molecules predict that, as the PEG concentration increases into the semidilute regime (where the polymer coils overlap), the attraction between the protein molecules should gradually taper off. This behavior may underlie the maximum in the dependence of T_L–L on the PEG concentration in Fig. 3B. However, even these models do not predict the lowering of T_L–L in the presence of PEG seen in Fig. 3, corresponding to PEG-induced repulsion between protein molecules. The emerging complex picture of the interactions in a PEG–protein system agrees with recent direct force measurements (35). They show strong, nonentropic attraction at high polymer–protein separations, corresponding to low PEG concentrations, and strong repulsion at short separations.

Strong attraction between protein molecules in the presence of low PEG concentrations has been observed in light-scattering studies (36). This attraction should affect nucleation kinetics and may be the reason behind the different slope of logJ(T) in the presence of PEG as shown in Fig. 1B, as well as the lack of correlation between the nucleation kinetics enhancements and the shifts of the L–L phase boundary. On the other hand, because the polymer does not affect the protein conformation and biological activity (37–39), the attraction between the PEG and the proteins should not be related to specific sites on the molecule. Thus, the observed nucleation enhancement with PEG is applicable to physiological conditions and in pharmaceutical technology.

Conclusions and Perspectives for Further Work.

The mechanism of nucleation control illustrated herein is not confined to the two studied additives: other substances that shift the liquid–liquid phase boundary and that should help enhance or suppress the nucleation rate of ordered solid phases are discussed in refs. 40 and 41. By using suitable additives, the interactions between the protein molecules may be modified such that a few important objectives can be achieved. The mechanism discussed above may be applied to limit the number of crystals to a desired few in crystallographic studies of protein structure (12, 42) or to suppress crystallization and aggregation in the human body, processes that underlie protein-condensation diseases (43, 44). In other cases, this mechanism may prompt strategies for enhancement of nucleation of hard-to-crystallize proteins or help to achieve fast simultaneous nucleation of multiple crystallites that then can grow to the uniform size needed for sustained release (45).

Many aspects are still not well understood. The temperature of maximum enhancement is higher than T_L–L by 1–2°C. Furthermore, near the critical point for L–L separation, we found interplay between fast nucleation of crystals, gelation, and amorphous precipitation. No unified theory exists for the thermodynamics of the four or five phases and the ensuing kinetics of the various phase transformations. Such a theory will have to account for the different ranges of interactions that may lead to gelation and the two types of phase separation (22) as well as for the anisotropy of the protein interactions (13, 14). Such a theory may address the issue raised by another set of recent results: can the L–L phase transition be viewed as an extension of crystal nucleation when the critical size tends toward zero (20)? If polymer additives are considered, concentration-dependent polymer solution behavior and specific interactions between polymer and protein molecules should be addressed (34–36).

Abbreviations

PEG

polyethylene glycol

L–L

liquid–liquid (phase separation)