Magnesium-Cationic Dummy Atom Molecules Enhance Representation of DNA Polymerase β in Molecular Dynamics Simulations: Improved Accuracy in Studies of Structural Features and Mutational Effects

Summary

Human DNA polymerase β (pol β) fills gaps in DNA as part of base excision DNA repair. Due to its small size it is a convenient model enzyme for other DNA polymerases. Its active site contains two Mg²⁺ ions, of which one binds an incoming dNTP and one catalyzes its condensation with the DNA primer strand. Simulating such binuclear metalloenzymes accurately but computationally efficiently is a challenging task. Here, we present a magnesium-cationic dummy atom approach that can easily be implemented in molecular mechanical force fields such as the ENZYMIX or the AMBER force fields. All properties investigated in this paper, that is, structure and energetics of both Michaelis complexes and transition state (TS) complexes were represented more accurately using the magnesium-cationic dummy atom model than using the traditional one-atom representation for Mg²⁺ ions. The improved agreement between calculated free energies of binding of TS models to different pol β variants and the experimentally determined activation free energies indicates that this model will be useful in studying mutational effects on catalytic efficiency and fidelity of DNA polymerases. The model should also have broad applicability to the modeling of other magnesium-containing proteins.

Introduction

All cells rely on DNA polymerases to replicate their DNA molecules¹ and repair them if they have been damaged.² These enzymes catalyze the incorporation of nucleotides into a DNA molecule.^3,4 In the case of DNA replication, the DNA molecule is synthesized from a single strand DNA template, to which a primer strand is annealed, thus forming a partial DNA double strand (duplex). In the case of DNA repair, DNA polymerases fill up single-stranded gaps resulting from excision of the damaged strand. Prior to the incorporation reaction, a deoxynucleoside triphosphate (dNTP) is bound opposite the template nucleotide and downstream of the 3′-terminal primer nucleotide. After deprotonation, O3′ attacks the dNTP α-phosphorous (αP) and yields a transition state (TS) with a pentacoordinate phosphorous. Ultimately, elimination of pyrophosphate yields the primer product extended by one nucleotide. Mammalian DNA polymerase β (pol β) fills in single-nucleotide gaps as part of base excision repair and represents a popular model enzyme due to its small size.^4–6 It employs two bivalent magnesium ions.^4,7–9 The dNTP-binding Mg²⁺ [Mg(b)] binds the triphosphate of the incoming dNTP, thus positioning it for productive incorporation. Probably, this Mg²⁺ ion also plays a key role in catalysis by stabilizing the leaving group.¹⁰ The catalytic Mg²⁺ [Mg(c)] catalyzes the reaction by both stabilizing the O3′ nucleophile and stabilizing the pentacoordinate TS. A recent high-resolution crystal structure (PDB accession code 2FMS⁹) of human pol β reveals that both Mg²⁺ ions are coordinated octahedrally: Mg(b) by nonbridging oxygens of the α-, β-, and γ-phosphates of the dNTP and by side-chain oxygens of Asp190 and Asp192, and a water molecule; Mg(c) by a nonbridging oxygen of the dNTP α-phosphate (serving as a bridging ligand between the two Mg²⁺ ions), the primer O3′, the other two side-chain oxygens of Asp190 and Asp192, a side-chain oxygen of Asp256, and a water molecule (Figure 1A). In a previous crystal structure of pol β, (PDB accession code 1BPY⁸), the metal ion in the Mg(c) binding site was coordinated tetrahedrally with unusually large metal-ligand distances for a Mg²⁺ ion. A new high-resolution structure (PDB accession code 2FMQ⁹), in which Mg(c) is replaced by a Na⁺ [Na(c)] (Figure 1B), exhibits the same coordination geometry, suggesting that in the 1BPY structure the metal ion in the catalytic site was Na⁺ rather than Mg^2+.4,9

Figure 1.

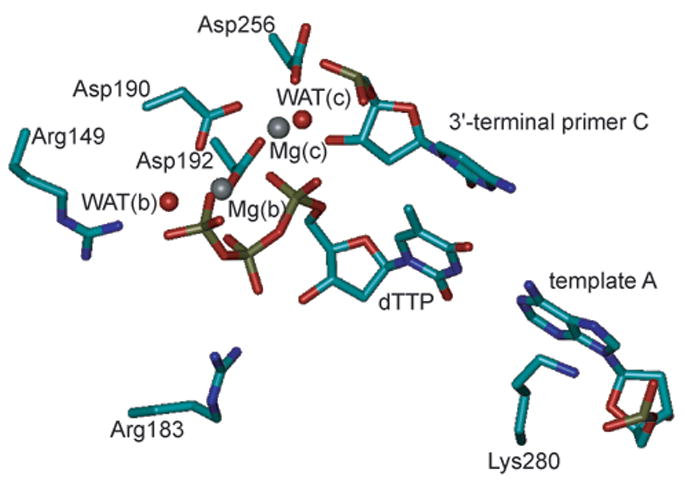
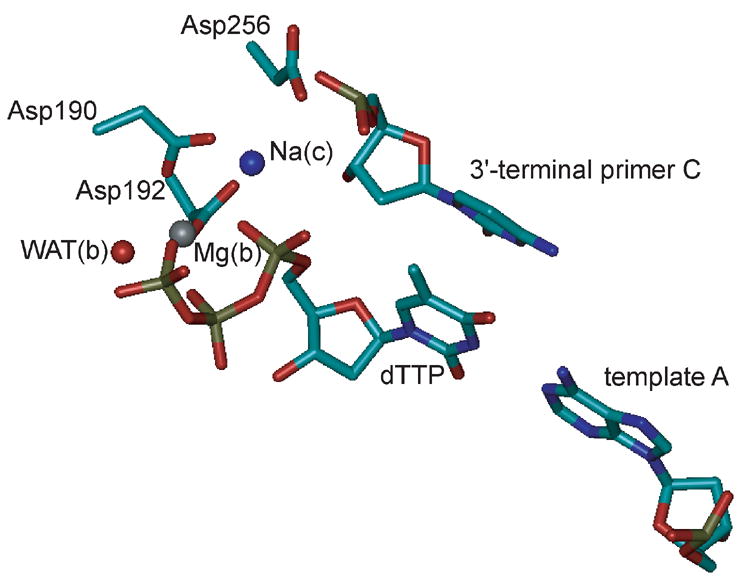
Representation of the active sites of (A) the MgMg structure and (B) the MgNa structure used for MD simulations. The imido nitrogen bridging the α- and β-phosphate groups of the dUTP analogue in the crystal structures was mutated to a phosphodiester oxygen and the uracil part was mutated to thymidine, thus generating dTTP. The side chains and Cα atoms of amino acids are shown as sticks, colored by atom (cyan, C; blue, N; red, O), and labeled at the Cα atom. Nucleotides are shown as sticks, colored by atom (copper, P), and labeled at the base. Oxygens of water molecules are shown as red spheres. Mg²⁺ions are shown as grey spheres and the Na⁺ ion as a blue sphere. (A) The two Mg²⁺ ions Mg(b) and Mg(c) and their ligands are shown. Both metal ions are coordinated octahedrally. In addition, the templating nucleotide (template A) and amino acids that were mutated in this study (Arg149, Arg183, and Lys280) are shown. (B) The Mg²⁺ ion Mg(b) and the Na⁺ ion Na(c) and their ligands are shown. While Mg(b) is coordinated octahedrally, Na(c) is coordinated in a distorted tetrahedral fashion with relatively large Na(c)-ligand distances (2.19–2.74 Å). Note that the water molecule coordinated to Mg(c) [WAT(c)] in the MgMg structure is missing in the MgNa structure and that O3′ of the primer C is not ligating Na(c) (3.54 Å) and is not positioned for nucleophilic attack on the dTTP αP (4.70 Å). The figures were generated with VMD,⁴⁶ version 1.8.3.

Computer simulations can help elucidate certain aspects of the function of DNA polymerases such as the effect of mutations on conformational changes^11,12 or energetics.^13–16 Magnesium ions are usually represented as ions with a formal point charge of +2 that interact with the protein environment and the substrate through nonbonded interactions. In binuclear sites as in pol β, however, high charges can lead to instabilities, resulting in an alteration of the proper coordination of the Mg²⁺ ions by the ligands and repulsion between the two Mg²⁺ ions. Although such artifacts can be avoided by imposing positional restraints on the Mg²⁺ ions or restraining the distances between the Mg²⁺ ions and their ligands, it is desirable to find solutions to represent the Mg²⁺ ions without using restraints. The combination of quantum mechanical and molecular mechanical (QM/MM) approaches (for a review see Ref.17) presents such a solution, however, at computational cost. In addition, instructive work has been done on the optimization of van der Waals (vdW) parameters of metal ions used in molecular mechanical (MM) force fields.^18–20 The goal of this study is to find a computationally efficient and accurate solution that can be easily implemented in different force fields such as the AMBER²¹ or the polarizable ENZYMIX²² force fields used in the MOLARIS program suite.^22,23 The focus will be placed on the Åqvist-Warshel (AW) model²⁴ that uses cationic dummy atoms and has proven very useful in accurately representing the energetics and structures of systems with transition metals such as octahedrally coordinated bivalent manganese ions²⁴ and tetrahedrally coordinated bivalent zinc ions in mononuclear^25–27 and binuclear^28–30 metalloenzymes. The underlying idea of this approach is to represent the partially covalent and partially electrostatic nature of the coordinative bond by locally splitting up the space between the transition metal atom and the ligand into a covalent bond (between the metal atom and a cationic dummy atom) and an electrostatic interaction (between the cationic dummy atom and the partially negatively charged ligand). Such models allow for stable coordination geometry by placing the cationic dummy atoms at the defined positions around the central metal atom and for a smaller repulsion between the metal ions in binuclear sites by distributing the positive charge over the cationic dummy atoms.

Here we test if such a treatment is suitable for the octahedrally coordinated bivalent earth alkali magnesium ions in the binuclear active site of pol β. Our magnesium-cationic dummy atom model (MD₆²⁺) is validated using the recent high-resolution crystal structures of human pol β⁹ with either two Mg²⁺ ions (MgMg structure, PDB accession code 2FMS) or a Mg²⁺ ion in the dNTP binding site and a Na⁺ ion in the catalytic site (MgNa structure, PDB accession code 2FMQ) as a benchmark. The MD₆²⁺ model is compared to models with standard ENZYMIX and AMBER one-atom representations for the Mg²⁺ ions as well as to the one-atom Mg²⁺ ion used in our previous studies.^14,16 Using the MD₆²⁺ model, both crystal structures are modeled more accurately. Furthermore, the MD₆²⁺ model’s potential to reproduce catalytic efficiencies from experiment⁶ is tested by calculating binding free energies of TS models of different dNTPs to different pol β variants using the all-atom LRA method.^31,32 The success of these simulations promises that the MD₆²⁺ model will be a useful element for future theoretical studies on the function and fidelity of DNA polymerases.

Results

Structures of pol β-DNA-dTTP ternary complexes

Several van der Waals values for bivalent traditional one-atom magnesium ions were tested in combination with the nonpolarizable or polarizable ENZYMIX force field or the AMBER force field. Using these different constellations in MD simulations of two crystal structures⁹ of human pol β, one exhibiting two magnesium ions (MgMg structure, Figure 1A) and one exhibiting a magnesium ion and a sodium ion (MgNa structure, Figure 1B) in the binuclear active site, the crystal structures were best reproduced with the Mg²⁺ ions used in our previous studies (vdW radius R* = 1.300 Å, well depth ε = 0.06).^15,16 The performance of these Mg²⁺ ions will be examined in more detail and compared to the MD₆²⁺ model below. All other traditional one-atom Mg²⁺ ions were not able to maintain both the MgMg and MgNa structures. Using the standard AMBER Mg²⁺ ions (R* = 0.7926 Å, ε = 0.8947)¹⁸ within the AMBER force field, the coordination of both Mg(b) and Mg(c) in the MgMg structure changed: Mg(b) lost contact to its ligands Asp192 and O2B (a nonbridging β-phosphate oxygen of the dNTP) and was instead coordinated by O3B (the oxygen bridging the β- and γ-phosphates of the dNTP); Mg(c) lost contact to its ligands O3′ of the primer and O1A (a nonbridging α-phosphate oxygen of the dNTP coordinating both metal ions in the crystal structure⁹). In the MgNa structure with Na(c) being represented as the standard AMBER Na⁺ ion (R* = 1.868 Å, ε = 0.00277),¹⁸ Mg(b) lost contact to O3G of the dNTP and a water molecule, while Na(c) was coordinated by both side-chain oxygens of Asp256 instead of only one as in the crystal structure.⁹ The MgMg structure was modeled quite accurately when using the standard ENZYMIX Mg²⁺ ions (R* = 0.735 Å, ε = 50.567) in combination with the nonpolarizable ENZYMIX force field and even more accurately when using the polarizable ENZYMIX force field. However, the MgNa structure, in which Na(c) was represented by the standard ENZYMIX Na⁺ ion (R* = 1.745 Å, ε = 0.00444), was not maintained: Na(c) lost contact to O1A but was additionally coordinated by two water molecules, giving rise to five-fold coordination as opposed to the four-fold coordination observed in the crystal structure.⁹ With the polarizable force field, the deviations from the crystal structure were smaller than with the nonpolarizable force field, but still significant.

Even though using Mg²⁺ ions with R* = 1.300 Å and ε = 0.06^15,16 yielded the best structural results among the traditional one-atom Mg²⁺ models, there were some significant discrepancies between the crystal structures and the modeled structures, i.e., increased Mg(b)-Mg(c), Mg(b)-Na(c), and O1A-Mg(b) distances. In order to overcome these deviations in modeled pol β structures without using restraints, we developed a new model for bivalent magnesium ions. In this model, the magnesium ion is represented by a central atom (M) positioned at the crystallographic position of the metal ion and six cationic dummy atoms (D) that are positioned octahedrally around and covalently connected to M (Table 1) and interact with the ligands through nonbonded interactions. Using the resulting MD₆²⁺ model in adiabatic charging free energy perturbation (FEP) calculations, the density function theory (DFT) calculated and experimentally observed solvation free energy could be reproduced (Table 2). Furthermore, the structural and energetic behavior of this model in small model complexes (Figure 2) in the gas phase and in solution was tested with the ENZYMIX and AMBER force fields and corresponded well with data from DFT calculations and X-ray crystallography (Tables 3 and 4). Overall, the MD₆²⁺ model was successfully employed with all tested force fields. Using the polarizable ENZYMIX force field gave more accurate results than using the nonpolarizable version; however, also the computationally more efficient nonpolarizable force fields gave accurate results within the confines of molecular mechanics force fields.

Table 1.

Force field parameters for MD₆²⁺ molecules

		K		r0
Bond		[kcal/(mol*Å2)]		(Å)
M-Dia		640		0.900
Di-Dj ≠ i		640		1.273
		K		θ0
Angle		[kcal/(mol*rad2)]		(deg.)
Di-M-Di		55		180
Di-M-Dj ≠ i		55		90
M-Di-Dj ≠ i		55		45
Di-Dj ≠ i-Di		55		90
Di-Dj ≠ i-Dk ≠ j ≠ i		55		60
Atom	Mass	Charge	AvdWb	BvdWc
M	6.3	−1.0	70.00	41.00
D	3.0	+0.5	0.05	0.00

^aTo distinguish positions, dummy atoms at opposite corners of the octahedral molecule are called D_i, whereas those adjacent to D_i are called D_{j ≠ i} and D_{k ≠ j ≠ k}.

^bA_vdW = [ε (2R*)¹²]^1/2

^cB_vdW = [2ε (2R*)⁶]^1/2

Table 2.

Comparison of solvation free energies of MD₆²⁺ with ab initio and experimental data.^†

	AC-FEP using the ENZYMIX force fielda
	reg.b	pol.c	DFTd	Experimente
Solvation free energy (kcal/mol)	−456.3	−456.2	−460.8	−454.2

^†The solvation free energies of MD₆²⁺ were calculated with an adiabatic charging-free energy perturbation (AC-FEP) approach using the ENZYMIX module of the MOLARIS program. The corresponding values obtained for Mg²⁺ in DFT calculations and in experiment are given for comparison.

^aFor these calculations, MD₆²⁺ was immersed in a surface-constrained⁴² 20 Å radius sphere of TIP3P⁴³ water molecules, a 22 Å radius sphere of Langevin dipoles, and a surrounding continuum solvent model.²²

^breg. designates that the regular, nonpolarizable ENZYMIX force field was used.

^cpol. designates that the polarizable ENZYMIX force field was used.

^dThis value is taken from Pavlov et al.³⁶ In that study, [Mg(H₂O)₆](H₂O)₁₂²⁺ was minimized and then the energy was calculated at the B3LYP/6-311+G** level.

^eThis value is taken from Noyes (1962).³⁵

Figure 2.

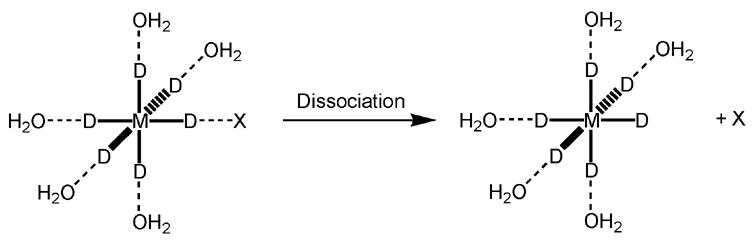
Scheme of the model complexes used for the calculations presented in Tables III and IV. The measured distances are the distances between the central atom M and the ligand X of interest in the intact complex shown on the left. Dissociation energies were calculated as the difference between the energy of the intact complex [MD₆(H₂O)₅]²⁺X (left side) and the sum of the energies of the fragments [MD₆(H₂O)₅]²⁺ and X resulting from dissociation (right side). For DFT calculations, the MD₆²⁺ molecule was replaced by a Mg²⁺ atom.

Table 3.

Comparison of calculated distances and dissociation energies in [MD₆(H₂O)₅]²⁺X complexes in the gas phase with ab initio calculations.^†

	distance (Å)				dissociation energy (kcal/mol)a
	ENZYMIX				ENZYMIX
Ligand X	reg.b	pol.c	AMBER	DFT	reg.b	pol.c	AMBER	DFT
H2O	2.06	2.10	2.09	2.15	41	42	47	34
CH3OH	2.10	2.11	2.09	2.09	37	43	48	43
PO3−	2.02	2.06	2.15	1.94	237	246	221	200
HPO42−	1.97	1.97	2.16	1.91	446	418	434	348

^†The model complexes used are shown schematically in Figure 2. These complexes were minimized using the ENZYMIX or AMBER force field. The force field parameters of MD₆²⁺ (Table I) were fit to reproduce the corresponding values of [Mg(H₂O)₅]²⁺X obtained from DFT calculations at the B3LYP/6-311++G** level.

^aThe energy required to remove the ligand X from the complex (see Figure 2).

^breg. designates that the regular, nonpolarizable ENZYMIX force field was used.

^cpol. designates that the polarizable ENZYMIX force field was used

Table 4.

Comparison of calculated distances in [MD₆(H₂O)₅]²⁺X complexes in solution with experimental data.^†

	distance (Å)
	ENZYMIX
Ligand X	reg.a	pol.b	AMBER	Experiment
H2O	2.05	2.07	2.09	2.07c
CH3OH	2.09	2.09	2.08	2.19c
PO3−	2.02	2.07	2.14	2.03–2.19d
HPO42−	2.02	2.04	2.07

^†For these calculations, the complexes were immersed in a surface-constrained⁴² 20 Å radius sphere of TIP3P⁴³ water molecules, a 22 Å radius sphere of Langevin dipoles, and a surrounding continuum solvent model.²² For comparison, the corresponding distances in X-ray crystal structures are given.

^areg. designates that the regular, nonpolarizable ENZYMIX force field was used.

^bpol. designates that the polarizable ENZYMIX force field was used.

^cThese values are taken from Harding;⁴¹ the ligands in protein X-ray crystal structures corresponding to methanol are serine and threonine.

^dThese values are taken from the pol β structures recently published by Batra et al.;⁹ the ligands in the X-ray crystal structure corresponding to PO₃⁻ and HPO₄²⁻ are different magnesium-coordinating, nonbridging triphosphate oxygens.

The MD₆²⁺ model was then tested in MD simulations of the MgMg and MgNa structures of pol β using either the AMBER force field or the ENZYMIX force field in its nonpolarizable and polarizable forms for the protein and DNA residues. Using this approach, the crystal structures were reproduced more accurately than when using the traditional one-atom representation for the Mg²⁺ ions. This is demonstrated exemplarily with the AMBER force field by critically analyzing the ability of the traditional one-atom Mg²⁺ ions with R* = 1.300 Å and ε = 0.06^15,16 and the MD₆²⁺ model to accurately reproduce the two crystal structures⁹ in unconstrained MD simulations over 1 ns at different temperatures (100 K, 200 K, and 300 K). Three critical distances were measured in 200 configurations collected over the course of each simulation: the distance between the two magnesium ions, the distance between Mg(b) and O1A, and the distance between Mg(b) and O2B. The progressions of these distances in both models over time are shown in Figure 3 for the MgMg structure and in Figure 4 for the MgNa structure. The average values ± standard deviations are reported in comparison to the corresponding distances in the X-ray crystal structures in Table 5. The distances between the other ligands and the metal ions were in agreement with experimental values (Table 4) and are not reported.

Figure 3.

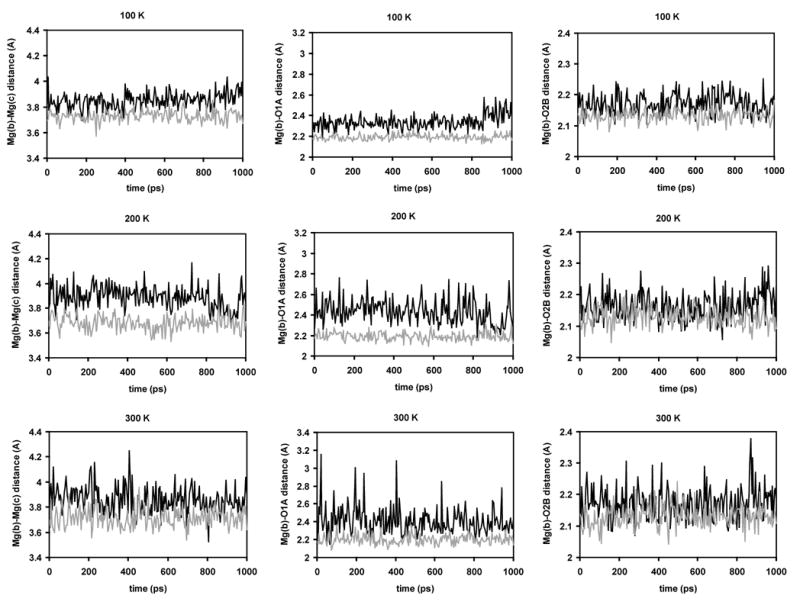
Critical distances in the active site of the MgMg structure over the course of 1 ns MD simulations at different simulation temperatures (panels A, B, and C: 100 K; panels D, E, and F: 200 K; panels G, H, and I: 300 K) using the regular Mg²⁺ model (black) and the MD₆²⁺ model (grey). Panels A, D, and G show the Mg(b)-Mg(c) distance; panels B, E, and H the Mg(b)-O1A distance; and panels C, F, and I the Mg(b)-O2A distance.

Figure 4.

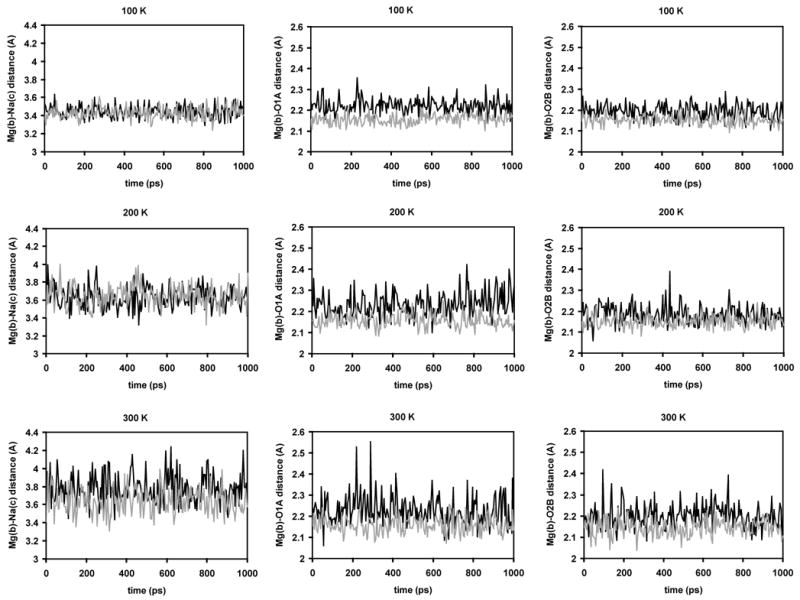
Critical distances in the active site of the MgNa structure over the course of 1 ns MD simulations at different simulation temperatures (panels A, B, and C: 100 K; panels D, E, and F: 200 K; panels G, H, and I: 300 K) using the regular Mg²⁺ model (black) and the MD₆²⁺ model (grey). Panels A, D, and G show the Mg(b)-Na(c) distance; panels B, E, and H the Mg(b)-O1A distance; and panels C, F, and I the Mg(b)-O2A distance.

Table 5A.

Critical distances in simulations of the MgMg structure

Temperature (K)	Structure/Model	Mg(b)-Mg(c) distance (Å)	Mg(b)-O1A distance (Å)	Mg(b)-O2B distance (Å)
	Crystal structure9	3.43	2.06	2.04
100	MgMg MD6MD6	3.85 ± 0.06 3.73 ± 0.04	2.34 ± 0.06 2.19 ± 0.03	2.17 ± 0.03 2.13 ± 0.02
200	MgMg MD6MD6	3.89 ± 0.09 3.68 ± 0.06	2.43 ± 0.12 2.19 ± 0.04	2.16 ± 0.04 2.13 ± 0.03
300	MgMg MD6MD6	3.86 ± 0.10 3.71 ± 0.07	2.41 ± 0.15 2.20 ± 0.05	2.17 ± 0.05 2.13 ± 0.03

In simulations of the MgMg structure, the average Mg(b)-Mg(c) distance increased compared to the crystal structure in both approaches, however much more significantly in the MgMg (two traditional one-atom Mg²⁺ ions) model (by 0.38–0.46 Å or 12–13%) than in the MD₆MD₆ (two MD₆²⁺ molecules) model (no more than 0.3 Å or 9%) (Figure 3, panels A, D, and G). For the average Mg(b)-O1A distance, the discrepancy between the two models was even more pronounced: this distance was increased by 0.28–0.37 Å or 14–18% in the MgMg model compared to less than 0.15 Å or 7% in the MD₆MD₆ model (Figure 3, panels B, E, and H). The average Mg(b)-O2B distance was in fair agreement with the crystallographic distance in both models: it was slightly increased by no more than 0.13 Å or 7% in the MgMg model and by no more than 0.1 Å or 5% in the MD₆MD₆ model (Figure 3, panels C, F, and I). In all cases, the standard deviations, an indicator for the fluctuation of the measured distances around the average value, were larger in the MgMg model than in the MD₆MD₆ model. Overall, the MD₆MD₆ model represents the MgMg crystal structure more accurately. Only the Mg(b)-Mg(c) distance increased noticeably by up to 9%. All the magnesium-triphosphate oxygen distances were between 2.13 and 2.20 Å and therefore in excellent agreement with the experimentally observed distances (Table 4). In contrast, in the MgMg model both the Mg(b)-Mg(c) distance and the Mg(b)-O1A distance deviated significantly from the crystal structure by up to 13% and 18%, respectively. These distances are likely correlated, because O1A as a bridging ligand keeps the Mg(b)-Mg(c) distance short. Their correlation can be observed in Figure 3: at 100 K, both distances increase after 850 ps (panels A and B); at 200 K, both distances decrease between 900 and 950 K (panels D and E); at 300 K, both distances peak at, e.g., 20 ps, 405 ps, and 635 ps (panels G and H).

We also analyzed the position of the primer 3′ hydroxyl relative to αP in the Michaelis complex of the MgMg structure simulated at 300 K with both approaches. The position of this residue might give insights into the subsequent nucleophilic attack of the deprotonated O3′ on αP. In the crystal structure, the O3′-αP distance is 3.40 Å and the angle O3′-αP-N3A (bridging nitrogen between αP and β P) is 160º.⁹ In the MgMg model simulated at 300 K, the O3′-αP distance was 3.32 ± 0.14 Å and the O3′-αP-O3A angle was 169 ± 5º, in good agreement with the X-ray crystal structure. In the MD₆MD₆ model simulated at 300 K, these values were 3.18 ± 0.09 and 170 ± 4º, deviating a little more from the crystal structure.

In simulations of the MgNa structure, the average Mg(b)-Na(c) distance increased compared to the crystal structure in both approaches. In contrast to the MgMg structure, the increase in both models was comparable at 100 K and 200 K. In the MgNa model, the average distance increased by 0.05–0.22 Å or 1–7%; in the MD₆Na model, it increased by 0.03–0.26 Å or 1–8%. However, at 300 K, the Mg(b)-Na(c) distance was noticeably increased in the MgNa model (by 0.38 Å or 11%), whereas it was increased only by 0.23 Å or 7% in the MD₆Na model. The Mg(b)-O1A distance was acceptable in both models, slightly above 2.2 Å in the MgNa model and slightly below 2.2 Å in the MD₆Na model. Similarly, the Mg(b)-O2B distance was around 2.2 Å in the MgNa model and around 2.15 Å in the MD₆Na model and therefore in good agreement with the crystal structure in both models. In all cases, the standard deviations were equal or larger in the MgNa model than in the MD₆Na model. Overall, using the MD₆²⁺ model, the MgNa crystal structure could be reproduced with higher fidelity than with a traditional one-atom Mg²⁺ ion; however, the deviations in the MgNa model are moderate compared to the MgMg model.

We tested both approaches, the regular Mg²⁺ ions and the MD₆²⁺ model, for their potential to restore the geometry of the MgMg structure by starting from the MgNa structure and replacing the Na⁺ ion in the catalytic metal binding site by the two magnesium models. In the following, these two models will be referred to as MgNa->MgMg and MgNa->MD₆MD₆, respectively. The conformation of the 3′-terminal sugar of the primer had to be changed from 2′-endo to 3′-endo⁴ in order to allow coordination of O3′ to Mg(c). Within a few ps of simlation at 300 K, octahedral coordination of Mg(c) as opposed to distorted tetrahedral coodination in the starting structure was restored in both models and maintained during prolonged 1.1 ns of simulation at this temperature. In the MgNa->MgMg model, O3′ and a water molecule had joined the three side-chain oxygens of Asp190, Asp192, and Asp256 and O1A of the dTTP as Mg(c) ligands. The Mg(b)-Mg(c) distance and the Mg(b)-O1A distance were relatively high with 3.88 and 2.40 Å, respectively, and very similar to the simulated MgMg model started from the MgMg structure (Table 5A). In the MgNa->MD₆MD₆ model, O3′ and the second side-chain oxygen of Asp190 completed octahedral coordination of Mg(c), with Asp190 now serving as a bidentate ligand for Mg(c) and one of its side-chain oxygens as a bridging ligand for both magnesium ions, thus keeping the Mg(b)-Mg(c) distance low at 3.26 Å. In the MgNa->MgMg model, the O3′-αP distance was 3.24 Å and the O3′-αP-O3A angle was 165º; in the MgNa->MD₆MD₆ model, the respective values were 3.10 Å and 164º, compared to 3.4 Å and 160º in the crystal structure. Thus, although both structures deviated slightly from the MgMg crystal structure,⁹ they both restored the main features of the pre-TS structure: octahedral coordination of both magnesium ions and proper orientation of the primer O3′ for nucleophilic attack on αP of the dNTP.

In summary, the main advantage of the MD₆²⁺ model over the Mg²⁺ model, especially in the MgMg structure, is that we can reproduce the crystal structure accurately without having to apply positional restraints on the Mg²⁺ ions or distance restraints between the Mg²⁺ ions and their ligands. This should also facilitate the determination of binding free energies of dNTP substrates and TS models to pol β. The performance of both models in such calculations will be examined in the next sections.

Structural comparison of modeled Michaelis and TS complexes

Prior to the all-atom LRA calculations, the Michaelis and TS complexes were equilibrated at 30 K and then simulated at 310 K for 100 ps. Some structural features deviated significantly between the resulting Michaelis and TS complexes apart from the artificially imposed restraints in the TS complexes (shortened O3′-αP distance and extended αP-O3A distance), most notably the distance between O3A and Mg(b). In the crystal structure, the N3A-Mg(b) distance is 3.25 Å. Since it is hard to directly compare N3A (the (α, β)-phosphate bridging imido nitrogen in the crystal structure⁹) to O3A (the bridging oxygen modeled at this position), we also want to mention that the O3A-Mg(b) distance in the 1BPY crystal structure,⁸ which is more comparable to our model, is 3.38 Å. In the simulated Michaelis complex of the WT bound to dTTP, this distance was 3.11 Å and 3.05 Å, using the Mg²⁺ model and the MD₆²⁺ model, respectively, slightly smaller than in the crystal structures. In the simulated WT-TS complex, this distance was significantly decreased to 2.55 Å and 2.62 Å, using the Mg²⁺ model and the MD₆²⁺ model, respectively.

Determination of binding free energies of dNTPs and TS models to pol β variants

Previously, we have investigated the effects of mutations on catalytic efficiencies of pol β using traditional one-atom Mg²⁺ ions, the positions of which were restrained with 10 kcal/(mol*Ų) to correct for possible force field deficiency.¹⁶ Although we obtained good agreement between our calculations and the experimental data, the observed correlation was qualitative rather than quantitative. Furthermore, since we used data from different experimental studies that were carried out under slightly different conditions, it was hard to assign the cause for outliers to either the computational or experimental procedures. Here, we only investigate pol β variants that were measured experimentally under the same conditions in the same laboratory,⁶ assuming that this provides a self-consistent data set. The investigated mutations are all in proximity to the incoming nucleotide or nascent base pair (Figure 1A) and have a significant effect on catalytic efficiency (Table 6). Arg149 is at a distance of 4.6 Å from the γ-phosphate of the incoming dNTP. The R149A mutation increases K_d about 6.5-fold compared to wild type, resulting in 6- to 7-fold decrease in k_pol/K_d for incorporation of dTTP opposite A (A:T) and dCTP opposite G (G:C). Arg183 is at a distance of 3.0 Å from the β-phosphate. For A:T, the R183A mutation increases K_d about 4-fold and decreases k_pol/K_d about 100-fold. For G:C, this mutation increases K_d about 3-fold, but decreases k_pol/K_d only 15-fold. Lys280 is at a distance of 3.4 Å from the template base. The K280A mutation increases K_d for G:C about 3-fold while not affecting k_pol, leading to about a 3-fold decrease in k_pol/K_d. The deduced differences in ΔG_bind are within 2 kcal/mol and the differences in Δg^‡_enz are within 3 kcal/mol. Since these residues are in the active site, they are likely to affect dNTP binding and catalysis rather than conformational rearrangements, which would be hard to capture in the time scale of our simulations.

Table 6A.

Dissociation constants for dNTP (K_d) determined in pre-steady state experiments for the incorporation of T opposite A (A:T) and C opposite G (G:C) for several pol β variants.⁶

	A:T		G:C
Pol β variant	Kd (μM)	ΔGbind (kcal/mol)	Kd (μM)	ΔGbind (kcal/mol)
WT	5.4	−7.5	1.9	−8.1
R149A	35	−6.3	12	−7.0
R183A	21	−6.6	5.9	−7.4
K280A	n.a.a	n.a.a	6	−7.4

We computed the free energies of binding of either dTTP opposite template A (A:T) or dCTP opposite template G (G:C) in the different pol β variants using the MgMg model and the MD₆MD₆ model in all-atom linear response approximation (LRA) calculations and plotted the experimentally determined values ΔG_{bind, exp}. versus the calculated values ΔG_{bind, calc}.. With the MgMg model, we were able to reproduce the experimental trend, however, with a poor correlation (R² = 0.44, Figure 5A). Using the MD₆MD₆ model, a better correlation was obtained (R² = 0.70, Figure 5B).

Figure 5.

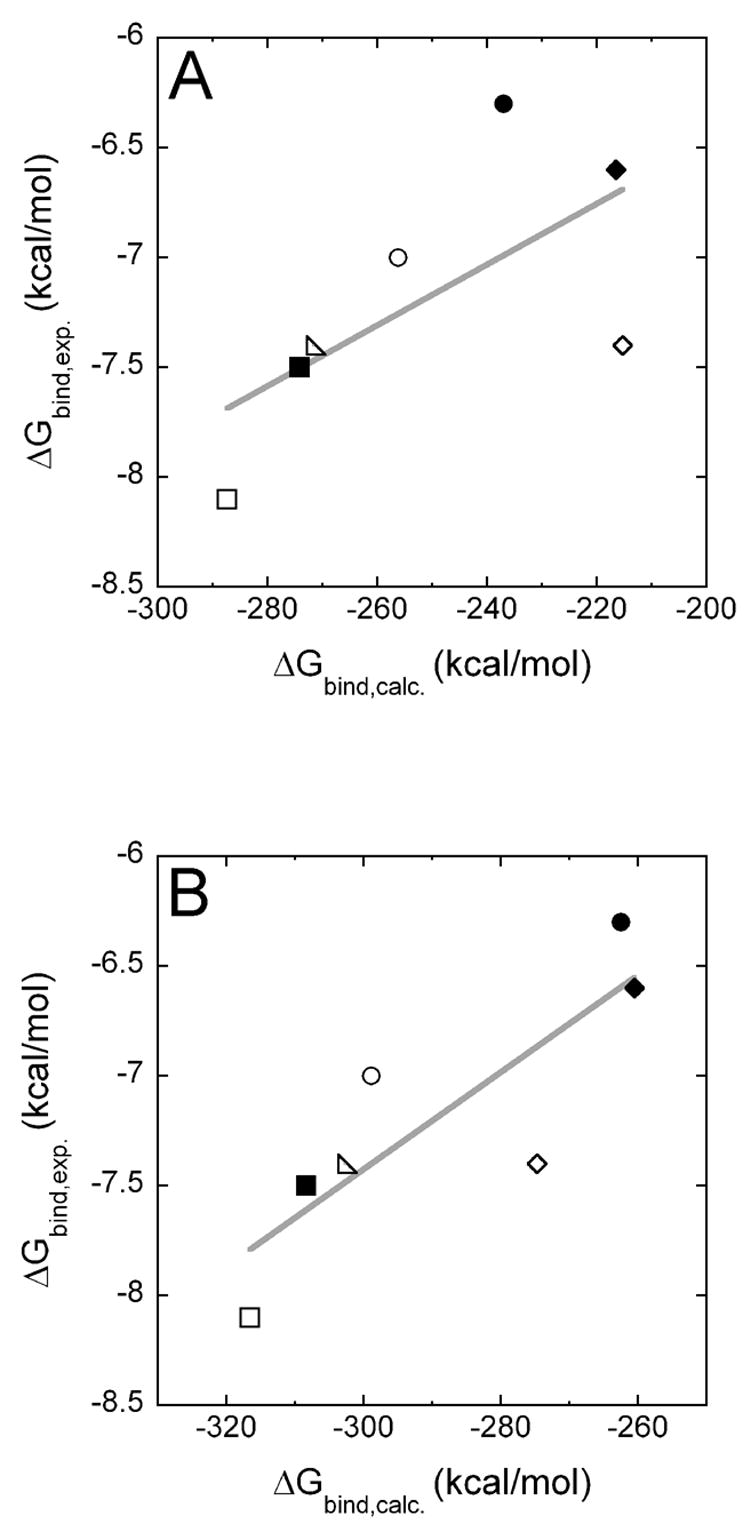
The experimentally determined pre-steady-state substrate binding energies ΔG_{bind, exp}. are plotted versus the calculated substrate binding free energies ΔG_{bind, calc}., which were obtained using the regular Mg²⁺ model (panel A) or the MD₆²⁺ model (panel B). The following pol β variants/nascent base pairs (template base:incorporated base) are shown: ■ WT/A:T; ● R149A/A:T; ◆ R183A/A:T; □WT/G:C; ○ R149A/G:C; ◇ R183A/G:C; △ K280A/G:C.

We then computed the free energies of binding of the TS models dTTP-TS and dCTP-TS opposite A and G, respectively, to the different pol β variants using both models. With the MgMg model, we obtained a reasonable correlation between the experimentally determined binding free energies of the TS Δg^‡_{enz, exp} and the calculated values Δg^‡_{enz. calc.} (R² = 0.75, Figure 6A). Using the MD₆MD₆ model, an excellent correlation was obtained (R² = 0.95, Figure 6B).

Figure 6.

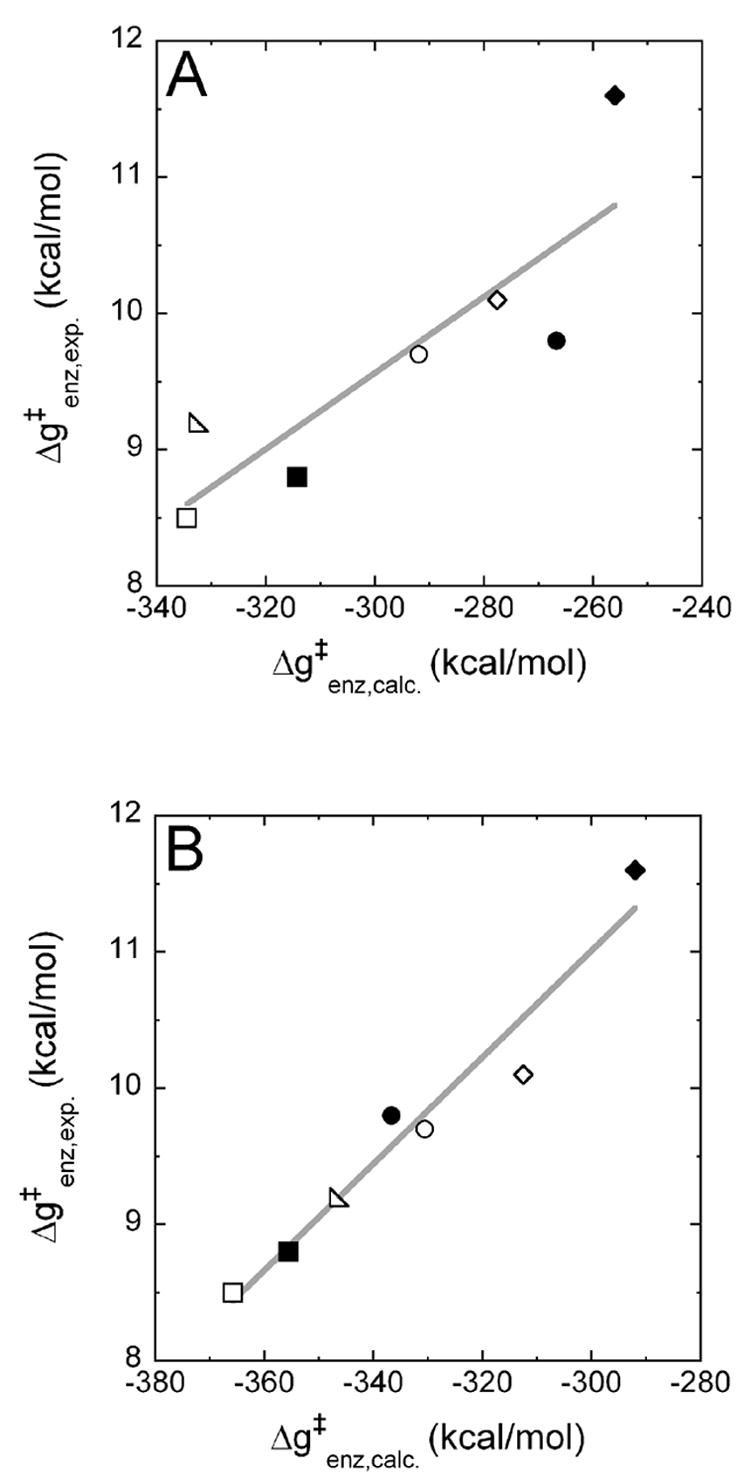
The experimentally determined equilibrium TS binding energies Δg^‡_{enz, exp}. are plotted versus the calculated TS binding free energies Δg^‡_{enz, calc}., which were obtained using the regular Mg²⁺ model (panel A) or the MD₆²⁺ model (panel B). The following pol β variants/nascent base pairs (template base:incorporated base) are shown: ■ wild type (WT)/A:T; ● R149A/A:T; ♦ R183A/A:T; □ WT/G:C; ○ R149A/G:C; ⋄R183A/G:C; △ K280A/G:C.

In all cases (Figures 5 and 6), there was no obvious separation between the values for A:T and those for G:C, indicating that the parameterization and the partial electrostatic charges used in our calculations give a good representation of both incoming dNTPs. Note that the absolute computed values for the binding free energies are of a different magnitude than the experimental values. This can be attributed mainly to the fact that we have not used a dielectric constant in our all-atom representation of the molecular systems (see detailed discussion in Ref.16). When we divide the computed values by the experimental values, for instance, for the Michaelis complexes, we obtain an effective dielectric constant of 35 for the MgMg model and 40 for the MD₆MD₆ model, values in the range of the effective dielectric constants usually used to calculate charge-charge interactions in proteins.³³

Discussion

Structural model with improved accuracy

The use of magnesium-cationic dummy atom molecules (MD₆²⁺) rather than traditional one-atom representation for Mg²⁺ ions follows up on the early AW model²⁴ and subsequent studies.^25–28 It combines the benefits of nonbonded interactions in reproducing solvation free energies and in keeping the metal site flexible with the benefits of covalent bonds, such as stable coordination geometry. Attaching cationic dummy atoms to the central metal atom at defined positions leads to more directed electrostatic interactions with ligands and delocalization of the charge to prevent repulsion in binuclear sites. As evidenced by our detailed comparison of the structures of Michaelis complexes obtained from MD simulations using both models, the MD₆²⁺ model always performed better. In particular, the Mg(b)-Mg(c) distance and the distance between Mg(b) and O1A of the incoming dNTP were much closer to the X-ray crystallographic distances in the MgMg structure.⁹ The MD₆²⁺ model was also superior in reproducing the crystallographic structure of the MgNa structure,⁹ although the Mg²⁺ model also performed satisfactorily in this case. We attribute this mainly to the fact that Na⁺ has a smaller positive charge than Mg²⁺, resulting in a smaller repulsion between the active site metals. In the MgMg structure obtained with the Mg²⁺ model, the major deviations from the crystal structure seem to originate from the repulsion of the two metal ions, which also affects the Mg(b)-O1A distance (Figure 3). Apart from that, Mg²⁺ is always coordinated octahedrally with reasonable magnesium-ligand distances. Therefore, the MD₆²⁺ model should be especially effective in modeling binuclear metalloproteins, in which two magnesium ions are at a small distance.

Originally, the idea of using cationic dummy atoms was used to account for charge transfer between ligands and transition metals by moving parts of the positive charge toward the ligands. Here, we report the successful application of this model to the earth alkali metal magnesium. Although it is not a transition metal, it is capable of forming complexes, which involve empty d-orbitals. This provides a physical rationale for using cationic dummy atoms in this case. It will be interesting to see whether the MD₆²⁺ model will also be useful in modeling the structure of other binuclear magnesium proteins.

The fact that we could translate the MgNa structure into the MgMg structure with both models suggests that the unexpected coordination of the Mg(c) ion in the previous crystal structure 1BPY⁸ was due to a substitution of the magnesium ion by a sodium ion. These two ions cannot be distinguished in X-ray crystal structures because they exhibit the same electron density.⁴ In general, MD simulations could be employed more frequently to validate the identity of metal ions in crystal structures.

Small positional restraints were used in the calculations of binding free energies of dNTPs and dNTP-TS models to the enzymes (see Computational Procedures for details). These were not necessary to maintain the positions or coordination of the magnesium ions or the protein but only to maintain the structure of the DNA. That is, the simulations indicated that the DNA structure may not correspond to the most stable configuration of the model used because of the 90º bend and the partially single-stranded DNA. This instability was observed with both the traditional one-atom representation for the magnesium ions and the MD₆²⁺ model. In the Michaelis complexes, which very closely resemble the crystallographic structure, the integrity of the DNA structure could be maintained by applying a very small restraint of 0.03 kcal/(mol*A²). In the TS complexes, where the primer O3′ is connected to Pα of the incoming dNTP, a larger restraint of 0.5 kcal/(mol*A²) was necessary to keep the upstream duplex DNA intact.

Improved energetics

Using the MD₆²⁺ model, we could reproduce experimental kinetic data in computer simulations more accurately than using regular Mg²⁺ ions. For the calculation of binding free energies of dNTP substrates, R² improved from 0.44 using the Mg²⁺ model (Figure 5A) to 0.70 using the MD₆²⁺ model (Figure 5B). Previously, we have already experienced that direct calculation of the binding of the TS gives better results and correlations than separate calculations of the binding and catalytic steps.¹⁶ Therefore, we want to focus on the calculation of binding free energies of TS models to different pol β variants to obtain Δg^‡_enz, which corresponds to the catalytic efficiency k_pol/K_d. With the Mg²⁺ model, we obtained a moderate correlation between experiment and computation (R² = 0.75, Figure 6A), but the correlation obtained with the MD₆²⁺ model is excellent (R² = 0.95, Figure 6A) and gives us confidence that we will be able to reproduce and predict the catalytic efficiencies of other mutations. In future studies, we want to extent our procedure to the incorporation of incorrect dNTPs in order to elucidate the molecular mechanisms of DNA polymerase fidelity.

Possible mechanistic implications

It is impossible to obtain a conclusive mechanistic picture without performing an actual simulation of the reaction process (eg. Ref14). However, it might be useful to speculate about some mechanistic features by considering the simulated reactant state and TS. More specifically, the Michaelis complexes simulated with both models resemble the productive pre-TS conformation more than the crystal structure, that is, the distance between the nucleophile O3′ and αP is shorter (3.18 Å in the MD₆MD₆ model and 3.32 Å in the MgMg model compared to 3.40 Å in the crystal structure) and the angle O3′-αP-O3A is closer to 180º (169º in the MD₆MD₆ model and 170º in the MgMg model compared to 160º in the crystal structure). A possible explanation for this observation is that the imido nitrogen N3A in the cocrystallized dUTP analogue has a smaller electronegativity than O3A in dNTP, thus withdrawing less electron density from αP and keeping O3′ farther away from αP. This scenario is in agreement with the fact that no chemistry is observed with the dUTP analogue, while dNTPs are incorporated very rapidly. At any rate, our simulations suggest that O3′ of the primer will be positioned in a very favorable position for nucleophilic attack on αP, and even more so in the MD₆MD₆ model than in the MgMg model.

After nucleophilic attack and formation of the pentacoordinate αP in the TS, pyrophosphate (P₂O₇⁴⁻) is eliminated and the tetracoordinate αP restored. The distance O3A-αP is extended in the TS to about 2.2 Ź⁴ and then further extended until the O3A-αP bond breaks. Since the TS resembles the product state to some extent, we can hypothesize on the elimination step and the nature of the product state. In the TS complex modeled with either Mg²⁺ or MD₆²⁺, O3A moves closer to Mg(b) compared to the Michaelis complex: the O3A-Mg(b) distance in the TS model is 2.6 Å compared to 3.1 Å in the modeled and 3.25 Å in the crystallized Michaelis complex. Thus, it seems feasible that O3A further approaches Mg(b) as the O3A-αP bond breaks during the elimination step and that the eliminated pyrophosphate coordinates Mg(b) in a tridentate fashion: with the two nonbridging oxygens of the β- and γ-phosphates that already coordinate it in the Michaelis complex plus O3A. The [Mg(P₂O₇)]²⁻ chelate complex generated in this way would be very stable and could leave the active site after the catalytic cycle, as has been proposed previously.³⁴ This possibility supports the idea that the dNTP-binding magnesium ion could serve as a “shuttle” for import of the dNTP and export of pyrophosphate. Without the magnesium ion, these molecules would be four-fold negatively charged, which would likely inhibit their transfer into and out of the protein.

Concluding Remarks

The magnesium-cationic dummy atom (MD₆²⁺) model presented here is an effective approach to model pol β using molecular mechanics. Its computational efficiency is comparable to that of regular traditional one-atom Mg²⁺ ions. However, all properties investigated in this paper, that is, structure and mutational effects on energetics of both Michaelis complexes and TS complexes were represented more accurately using the MD₆²⁺ model than using the traditional one-atom representation for Mg²⁺ ions. For small model complexes, the MD₆²⁺ model gave good results using both the nonpolarizable and polarizable ENZYMIX and the AMBER force fields. Likewise, it enabled us to accurately reproduce ternary pol β /DNA/dNTP structures with all tested force fields. We expect that the MD₆²⁺ model can be easily implemented in other commonly used force fields and that it will be useful to study other magnesium-containing proteins. The excellent agreement (R² = 0.95) between calculated binding free energies of dTTP-TS and dCTP-TS models to different enzyme variants and the corresponding experimentally determined activation free energies suggests that the magnesium-cationic dummy atom model will assist the investigation and prediction of mutational effects on catalytic efficiencies and DNA polymerase fidelity.

Computational Procedures

Refinement of the magnesium-cationic dummy atom model

The Mg²⁺ ions were represented by octahedral molecules (MD₆²⁺) with covalent bonds between the central magnesium atom (M) and the cationic dummy atoms (D) and between adjacent dummy atoms, following the early AW model²⁴ and subsequent studies.^25–28 The vdW parameters and the charges were obtained by a systematic refinement which involved the following steps: the vdW coefficients A and B and the charges of M and D were chosen by fitting the simulated solvation free energy of Mg²⁺ in water to the corresponding observed free energy (−454.2 kcal/mol³⁵) and by fitting the calculated energy of the [Mg(H₂O)₆](H₂O)₁₂²⁺ complex to the corresponding result of a DFT calculation (−460.8 kcal/mol³⁶). This high solvation free energy could be achieved by increasing the charge of the dummy atoms D to +0.5 and by imposing a charge of −1.0 on the central atom M to keep the overall charge of the MD₆²⁺ molecule at +2.0. The calculated solvation free energy of the MD₆²⁺ model was evaluated by an adiabatic charging FEP procedure^37,38 using the POLARIS module of the MOLARIS program suite.^22,23 The corresponding results using the nonpolarizable and polarizable ENZYMIX force field were −456.3 kcal/mol and −456.2 kcal/mol, respectively (Table 2). The vdW coefficients of M were also adjusted to approximate distances and dissociation energies between Mg²⁺ ions and different ligands determined in gas-phase DFT calculations (B3LYP/6-311++G**) carried out with the Gaussian03 program.³⁹ In addition to the Mg²⁺ ion and the ligand of interest, five water molecules were included to saturate the other coordination positions in these calculations (Figure 2). The results of the DFT calculations and the corresponding gas-phase MM calculations with the MD₆²⁺ molecule of these model complexes using the ENZYMIX²² and AMBER²¹ force fields implemented in the MOLARIS program²³ are reported in Table 3. The ENZYMIX force field was used either in its nonpolarizable or in its polarizable form. Charges of the ligand molecules in the MM calculations were taken from the ENZYMIX and AMBER libraries (H₂O and CH₃OH) or were calculated at the B3LYP/6-311++G** level using a PCM solvation model⁴⁰ implemented in Gaussian03.³⁹ Furthermore, the relevant distances between ligands and MD₆²⁺ were also determined after minization of these systems in solution. The results are shown in Table 4 and compared to the corresponding distances in high resolution crystal structures of magnesium-containing metalloproteins, where CH₃OH of the model complexes is compared to serine and threonine⁴¹ and PO³⁻ and HPO₄²⁻ are compared to phosphate groups that coordinate to Mg²⁺ through nonbridging oxygens.⁹ In our implementation of the AMBER force field in MOLARIS, we have previously changed the vdW radii of nonbridging phosphate oxygens (AMBER atom types O2 and O3) and carboxylate oxygens (AMBER atom type O2) from 1.66 Å to 1.9 Å (O2) and from 1.7 Å to 1.9 Å (O3), because these gave more accurate structures in long MD simulations.¹⁵ We also tested the original AMBER vdW radii, but were not able to reproduce mutational effects as accurately as with our modified vdW radii.

Structures of pol β-DNA-dNTP ternary complexes

The coordinates of the recently published X-ray crystal structures of human pol β⁹ were used for this study. The MgMg structure (PDB accession code 2FMS) features two Mg²⁺ ions in the dNTP-binding and the catalytic site [Mg(b) and Mg(c)], while the MgNa structure (PDB accession code 2FMQ) exhibits a Mg²⁺ ion in the dNTP-binding site [Mg(b)] and a Na⁺ ion in the catalytic site [Na(c)]. Both structures contain human pol β in the closed conformation bound to a single-gap DNA substrate with a dUTP analog [2′-deoxyuridine-5′(α, β)-imido triphosphate] positioned for incorporation opposite the template adenine. In the dUTP analog, the phosphodiester oxygen bridging αP and β P is replaced by an imido group, which prevents the S_N² reaction. Therefore, a deoxycytidine could be used at the 3′ terminus of the primer rather than a dideoxycytidine.^4,9 For calculations modeling the Michaelis complex of dTTP bound opposite adenine, the imido group of the dUTP analog was replaced by an oxygen and the uracil base was replaced by thymine (Figure 1). For calculations modeling the Michaelis complex of dCTP opposite guanine, the template adenine was “mutated” to guanine and the incoming dTTP was “mutated” to dCTP. The partial charges of the triphosphate parts of the dNTPs were calculated at the B3LYP/6-31G* level using a PCM solvation model⁴⁰ implemented in Gaussian03,³⁹ and the partial charges of the ribose and bases were adjusted from the AMBER²¹ libraries to yield a formal charge of −4.0 for both dTTP and dCTP. The main portion of the negative charge was located on the triphosphate. The other nucleotides of the DNA and the protein residues were represented either by the AMBER²¹ or the ENZYMIX²² amino acid and nucleic acid libraries. Sodium ions were modeled as standard ENZYMIX (R* = 1.745 Å, ε = 0.00444) or AMBER (R* = 1.868 Å, ε = 0.00277)¹⁸ Na⁺ ions. Magnesium ions were represented either by the standard ENZYMIX (R* = 0.735 Å, ε = 50.567) or AMBER (R* = 0.7926 Å, ε = 0.8947)¹⁸ Mg²⁺ ions, as the one used in our previous studies (R* = 1.300 Å, ε = 0.06),^15,16 or as the MD₆²⁺ molecules described above and in Table 1. In the latter case, the position of M was chosen as the crystallographic position of Mg²⁺ and the positions of the dummy atoms D were chosen between the positions of the Mg²⁺ ions and their ligands, 0.9 Å from the Mg²⁺ ion. The resulting structures including crystal water molecules were immersed in a 20 Å sphere of surface-constrained all-atom solvent (SCAAS)⁴² of TIP3P⁴³ water molecules and a 22 Å sphere of Langevin dipole water molecules, surrounded by a continuum water model.²² The center of these spheres was positioned at the geometric center of region I (the incoming dNTP). To test whether the MgNa structure could be transferred into the MgMg structure in MD simulations, Na⁺ was replaced by Mg²⁺ or MD₆²⁺, yielding the two models MgNa->MgMg and MgNa->MD₆MD₆. Since no coordination of Mg(c) by O3′ was achieved starting from the 2′-endo conformation of the 3′-terminal primer sugar in the MgNa structure, we changed its conformation to 3′-endo as in the MgMg structure.

Structures of pol β-DNA-dNTP TS complexes

To generate TS models for the incorporation of dCTP and dTTP (dCTP-TS and dTTP-TS), a 1.7 Å bond was added between the deprotonated O3′ of the 3′-terminal primer cytidine and αP of the dNTP; the bond between αP and the (α, β)-phosphodiester oxygen O3A was extended by using a harmonic restraint with a reference distance of 2.2 Å and a force constant of 1,000 kcal/(mol*Ų). In the product state, this bond is cleaved, yielding a pyrophosphate leaving group.⁴ The partial charges of dCTP-TS and dTTP-TS were determined in the same fashion as described above for dCTP and dTTP, except that now the dCTP and dTTP had a formal charge of −4.5 and the attacking 3′-terminal primer cytidinate had a formal charge of −0.5, resulting in TS models with a charge of −5.0.

Molecular dynamics (MD) simulations of pol β-DNA-dTTP ternary complexes

Four Michaelis complexes, the MgMg structure with two Mg²⁺ ions (MgMg), the MgMg structure with two MD₆²⁺ molecules (MD₆MD₆), the MgNa structure with one Mg²⁺ and one Na⁺ ion (MgNa), and the MgNa structure with one MD₆²⁺ molecule and one Na⁺ ion (MD₆Na), were relaxed for 11 ps at 30 K. The resulting structures were then simulated at 100 K, 200 K, and 300 K for 1 ns, during which snapshots were collected every 5 ps for subsequent analysis. All simulations were carried out with the ENZYMIX module of MOLARIS,²³ using a very small positional restraint of 0.03 kcal/(mol*Ų) for all atoms within the explicitly treated simulation sphere of 20 Å radius. The two structures MgNa->MgMg and MgNa->MD₆MD₆ were relaxed for 11 ps at 30 K, simulated for 1.1 ns at 300 K, and analyzed at the end of the simulations.

All-atom LRA simulations of Michaelis and TS complexes

Several point mutants of pol β were prepared, focusing on mutations of charged residues to alanine in proximity to the nascent base pair (Figure 1A). For the wild type (WT) and the mutants R149A, R183A, and K280A of rat pol β, pre-steady state kinetic constants (k_pol and K_d) for the incorporation of nucleotides into single-nucleotide-gapped DNA molecules have been determined in the same experimental study⁶ and are therefore assumed to be self-consistent. These pol β variants were used for the present study. Human and rat pol β share 96% sequence identity and none of the deviating amino acids are near the active site. Therefore, the studied mutations close to active site should have the same effects in rat and human pol β.⁴⁴ The incorporation of dCTP opposite template G (G:C) was studied for all variants and the incorporation of dTTP opposite template A (A:T) was studied for all variants except K280A, for which no experimental data are reported.⁶ The equilibrium substrate binding constants (K_d) and the corresponding substrate binding free energies ΔG_bind as well as the catalytic efficiencies (k_pol/K_d) and the corresponding activation free energies Δg^‡_enz for these variants are summarized in Table 5. In an effort to reproduce these experimental data, the binding free energy of dNTP to the enzyme corresponding to ΔG_bind and the binding free energy of dNTP-TS to the enzyme corresponding to Δg^‡_enz were computed in a thermodynamic cycle employing the all-atom linear response approximation (LRA), as reported previously.¹⁶ In that study, the all-atom LRA approach yielded significantly better agreement between experiment and computation than the much less expensive but less rigorous semimacroscopic protein dipole/Langevin dipole (PDLD/S) method in its LRA version (PDLD/S-LRA).⁴⁵ The latter is therefore not reported here. Mutations were introduced into the MgMg structure⁹ by truncating the amino acid side chains to alanine side chains. Prior to these calculations, all systems were equilibrated for 101 ps at 30 K and for 100 ps at 310 K (the temperature at which the experiments were carried out⁶) using a positional restraint of 0.5 kcal/(mol*Ų) for all atoms in regions I and II. Region I contained the dNTP or dNTP-TS model, that is, the incoming dNTP plus the attacking O3′ of the primer. Region II contained all other atoms in the explicitly treated simulation sphere. This relatively small restraint mainly served to maintain correct base pairing during the simulations. The all-atom LRA calculations were carried out over 5 ps on 30 automatically generated MD configurations for the uncharged and charged states using the POLARIS module of MOLARIS.²² These configurations were collected over the course of 150 ps of simulation at 310 K.

Table 5B.

Critical distances in simulations of the MgNa structure

Temperature (K)	Structure/Model	Mg(b)-Na(c) distance (Å)	Mg(b)-O1A distance (Å)	Mg(b)-O2B distance (Å)
	Crystal structure9	3.40	2.05	2.03
100	MgNa MD6Na	3.45 ± 0.06 3.43 ± 0.06	2.22 ± 0.04 2.15 ± 0.02	2.20 ± 0.03 2.15 ± 0.02
200	MgNa MD6Na	3.62 ± 0.13 3.66 ± 0.12	2.22 ± 0.05 2.16 ± 0.03	2.19 ± 0.05 2.15 ± 0.03
300	MgNa MD6Na	3.78 ± 0.16 3.63 ± 0.14	2.24 ± 0.07 2.16 ± 0.04	2.20 ± 0.06 2.14 ± 0.04

Table 6B.

Catalytic efficiencies (k_pol/K_d) determined in pre-steady state experiments for the incorporation of T opposite A (A:T) and C opposite G (G:C) for several pol β variants.⁶

	A:T		G:C
Pol β variant	kpol/Kd (s−1M−1)	Δg‡enz (kcal/mol)	kpol/Kd (s−1M−1)	Δg‡enz (kcal/mol)
WT	4,100,000	8.8	6,600,000	8.5
R149A	685,000	9.8	920,000	9.7
R183A	43,000	11.6	440,000	10.1
K280A	n.a.a	n.a.a	2,000,000	9.2

^an.a., not available.

Abbreviations used

Pol β

DNA polymerase β

MD

molecular dynamics

LRA

linear response approximation

PDLD/S

semimacroscopic protein dipole/Langevin dipole

TS

transition state

dNTP

deoxynucleoside triphosphate

WT

wild type

FEP

free energy perturbation