Abstract
We demonstrate that “brute force” quantum-mechanics/molecular-mechanics computations based on ab initio (i.e., first principles) multiconfigurational perturbation theory can reproduce the absorption maxima of a set of modified bovine rhodopsins with an accuracy allowing for the analysis of the factors determining their colors. In particular, we show that the theory accounts for the changes in excitation energy even when the proteins display the same charge distribution. Three color-tuning mechanisms, leading to changes of close magnitude, are demonstrated to operate in these conditions. The first is based on the change of the conformation of the conjugated backbone of the retinal chromophore. The second operates through the control of the distance between the positive charge residing on the chromophore and the carboxylate counterion. Finally, the third mechanism operates through the changes in orientation of the chromophore relative to the protein. These results offer perspectives for the unbiased computational design of mutants or chemically modified proteins with wanted optical properties.
Keywords: excited states, quantum mechanics/molecular mechanics
Recently, protein mutants displaying properties such as high binding affinities and novel catalytic activities (1, 2) have been designed by using computational methods based on molecular mechanics. In a close context, substrate selectivity has been simulated by using more advanced tools based on density functional theory and molecular mechanics paving the way to the design of mutations that convert receptors into enzymes (3). However, the design of mutants with specific spectral properties, such as color and luminescence, represents a more complex problem. In these cases, the quantum chemical method used must be capable to describe both ground and electronically excited states of the protein chromophore. The ab initio (i.e., first-principles) complete-active-space self-consistent-field (CASSCF) method (4) is a multiconfigurational method offering maximum flexibility for an unbiased description of the electronic and equilibrium structure of a molecule (i.e., with no empirically derived parameters and avoiding single-reference wavefunctions). Furthermore, the CASSCF wave function can be used for subsequent multiconfigurational second-order perturbation theory (5) computations (CASPT2) of the dynamic correlation energy of each state ultimately leading to a nearly quantitative evaluation of the excitation energies of organic compounds (6, 7). The CASPT2 ability to describe exotic bonding has been recently assessed (8).
In a previous study (9), we implemented the ab initio CASPT2//CASSCF protocol (where equilibrium geometries and electronic energies are determined at the CASSCF and CASPT2 levels, respectively) in a quantum mechanics/molecular mechanics (QM/MM) scheme (10–12) allowing for the evaluation of the excitation energy of chromophores (treated quantum mechanically) embedded in a protein environment (described by a MM force field).
The absorption and fluorescence maxima of diverse proteins such as the visual pigment rhodopsin (Rh) (13) (see Fig. 1) and the green fluorescent protein (14) were reproduced within a few kcal·mol−1. The quality of the used quantum chemical method has also allowed to reproduce the difference between the absorption maximum (λmaxa) of Rh and of its retinal chromophore in methanol solution (i.e., the so called opsin-shift; ref. 15) with a <2 kcal·mol−1 error (see also Fig. 2A).
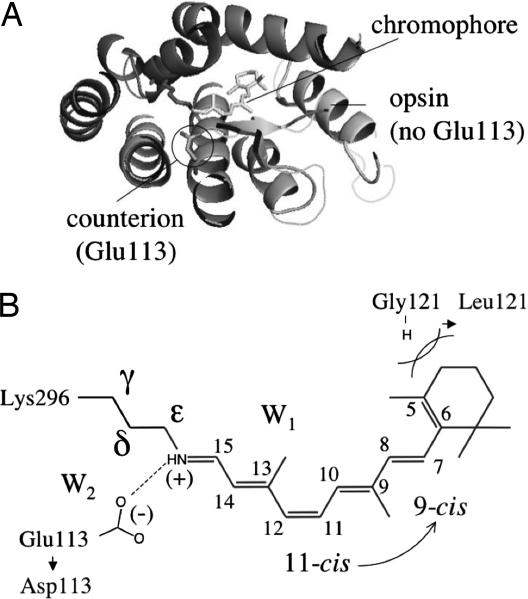
Fig. 1.
The structure of Rh. (A) View of rhodopsin (from the cytoplasmatic side). The Glu-113 carboxylate is the only ionized group in the chromophore cavity. (B) Structure of the retinal chromophore. The light gray labels indicate the mutations of residues 113 (E113D) and 121 (G121L) and the 11-cis → 9-cis change leading to isorhodopsin.
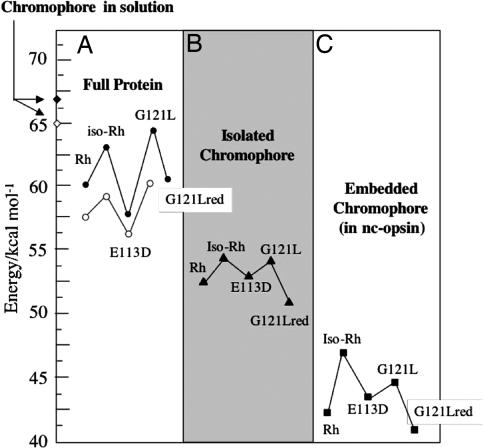
Fig. 2.
Analysis of the excitation energies of Rh, iso-Rh, E113D, G121L, and G121Lred. Filled symbols indicate computed values; open symbols indicate experimental values. The excitation energies of the chromophore in methanol solution are from ref. 13. The excitation energies for the isolated and embedded chromophores are determined by using the equilibrium structure of the corresponding proteins.
Here, we use CASPT2//CASSCF/6–31G*/AMBER QM/MM computations (see Methods and supporting information, which is published on the PNAS web site, for details) to unveil the molecular factors responsible for the changes in the absorption maximum (i.e., in color) of three rhodopsins. Although, due to their high cost, CASPT2//CASSCF/AMBER computations cannot presently be used for screening large sets of mutants, the rhodopsins were chosen in such a way to represent different limiting cases. As illustrated in Fig. 1, the first is isorhodopsin (iso-Rh) (16) a protein with the same amino acid sequence of Rh but incorporating a 9-cis rather than 11-cis retinal chromophore. The second is a mutant (E113D) (17) incorporating a change in the Glu-113 carboxylate counterion of Rh (i.e., the only ionized residue present in the protein cavity). In contrast, the third is a mutant (G121L) (18) incorporating a change in the nonpolar amino acid Gly-121 that is replaced by a bulkier one (leucine). The fact that the modified Rh (i) feature an observed λmaxa value <20 nm far from that of wild-type Rh and (ii) display λmaxa changes induced by chemically different structural variations makes them challenging candidates for computational modeling and analysis. In particular, the fact that bulkier residues or changes in chromophore conformation induce a λmaxa change of the same magnitude as seen when modifying the charged counterion, calls for an understanding of the color tuning mechanism that goes beyond the effect of the change of polar residues.
Results and Discussion
Color tuning in rhodopsins has been investigated in the past in the context of color vision (19). Three different molecular factors have been proposed to play a role: (i) the increased or decreased conjugation of the retinal polyene chain (20, 21); (ii) the placement of charged, polarized or polarizable groups close to the chromophore chain (22–25); and (iii) the weakening of the interaction between the positive charge of the chromophore and its negative counterion (26, 27). Factor ii is usually considered dominating and past work on rhodopsins has mainly focused on the effect of the insertion of polar residues in the protein cavity (28). Less attention has been paid to the changes due to factors leading to chromophore deformation/reorientation. Despite their different λmaxa, the pigments investigated here feature, when excluding the counterion, the same composition in polar residues. Thus, they provide a unique basis to determine which factors operate when factor ii is not modified.
In Table 1 we report the λmaxa evaluated at the S0 equilibrium structure of the selected rhodopsins. It is apparent that the computed quantities reproduce the observed values with a systematically blue-shifted error of <35 nm (<4.5 kcal·mol−1). It is also apparent that the relative changes in excitation energies (see Fig. 2A) are reproduced with a <2 kcal·mol−1 error. Similarly the change in f is consistent with that of the extinction coefficients. The error coming from the use of the 6–31G* basis with a correlated wavefunction has been estimated by recomputing the λmaxa of Rh with the ANO-S basis. This yields a smaller 10-nm red-shifted error (see supporting information), indicating that a better basis could predict better absolute excitation energies. However, because we focus on λmaxa changes and due to excessive computational costs, ANO-S testing has not been performed for the other rhodopsins.
Table 1.
Calculated and observed λmaxa values (nm) and vertical excitation energies (kcal·mol−1)
The quality of our models prompts for an analysis of the geometrical and electronic factors determining the λmaxa changes. Accordingly, the excitation energy of each model is compared with that of the corresponding isolated chromophore taken with the geometry found in the protein (see Fig. 2B) and to that of the protein deprived of the Glu-113 or Asp-113 carboxylate charges (see Fig. 2C), from now on called “nc-opsin” (i.e., in nc-opsin the Amber partial charges have been set to zero for the entire Glu-113 or Asp-113 residues).
Effect of the Opsin Residues.
The origin of the protein absorption centered at ≈60 kcal·mol−1, can be understood when the excitation energies of the isolated chromophores (see Fig. 2B) are taken as reference values. In fact, these fall in a red-shifted region centered at ≈53 kcal·mol−1. It is thus apparent that the opsins induce a blue-shift of the chromophore λmaxa. Notice that, for the case of Rh, the difference in excitation energy of the relaxed gas-phase chromophore (the N-methylated form of the 6-s-cis,11-cis retinal protonated Schiff base) (29) and of the isolated Rh chromophore (this work) is 0.2 kcal·mol−1. This demonstrates that the λmaxa change induced by the protein environment is due to effects other than the limited changes in chromophore structure (the main differences are a ≈10° increase in the C6 C7 single bond torsion and a planarization of the -C12
C7 single bond torsion and a planarization of the -C12 C11
C11 C10
C10 C9
C9 C8
C8 C7- moiety in the gas-phase structure). The blue-shift effect of opsin is further disentangled by looking at the values of the excitation energy of the same chromophores inserted in nc-opsin. In this condition, the chromophore feels the electrostatic potential generated by the cloud of partial charges of the protein residues but does not feel the counterion. As shown in Fig. 2C, such potential has an opposite effect as the excitation energy region is now centered at 45 kcal·mol−1. Thus, it is apparent that, in contrast with the full opsin, nc-opsin induces a red-shift of the chromophore λmaxa. As a consequence, we conclude that the counterion induces a blue-shift.
C7- moiety in the gas-phase structure). The blue-shift effect of opsin is further disentangled by looking at the values of the excitation energy of the same chromophores inserted in nc-opsin. In this condition, the chromophore feels the electrostatic potential generated by the cloud of partial charges of the protein residues but does not feel the counterion. As shown in Fig. 2C, such potential has an opposite effect as the excitation energy region is now centered at 45 kcal·mol−1. Thus, it is apparent that, in contrast with the full opsin, nc-opsin induces a red-shift of the chromophore λmaxa. As a consequence, we conclude that the counterion induces a blue-shift.
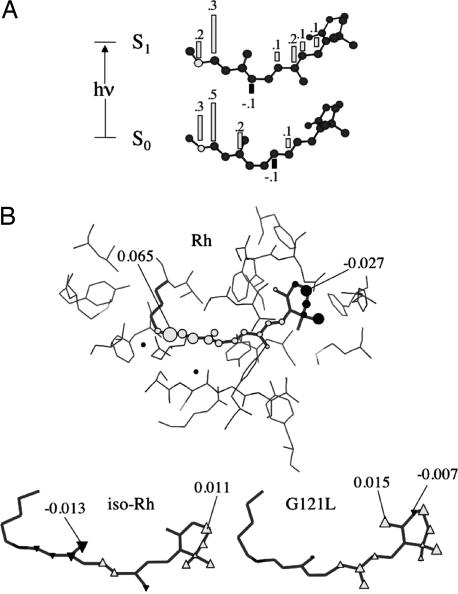
The results discussed above are explained on the basis of the charge transfer nature of the spectroscopic state of the retinal chromophore (see Fig. 3A) (30–33). As previously reported (13), in Rh, the 34% of the chromophore charge, originally located on the -NH CH- moiety, is shifted toward the β-ionone upon S0 → S1 vertical excitation. An electrostatic potential stabilizing, in the excited state, the positive charge near the β-ionone region or destabilizing it in the Schiff base region, for the ground state, will result in a decreased S0 → S1 excitation energy (34).
CH- moiety, is shifted toward the β-ionone upon S0 → S1 vertical excitation. An electrostatic potential stabilizing, in the excited state, the positive charge near the β-ionone region or destabilizing it in the Schiff base region, for the ground state, will result in a decreased S0 → S1 excitation energy (34).
Fig. 3.
Electrostatic effects on the retinal chromophore. (A) Change in the charge distribution along the backbone of the Rh chromophore. (B) Electrostatic potential (numbers give the max and min values in atomic units) generated by the AMBER partial charges of nc-opsin (see text) on the atoms of the retinal chromophore of Rh. (Lower) Change, with respect to Rh, in electrostatic potential (numbers give the max and min values in atomic units) on the atoms of the chromophores of iso-Rh and G121L. Open triangles indicate an increase, whereas filled triangles indicate a decrease.
According to Fig. 2C, the electrostatic potential generated by the nc-opsins always decreases, with respect to the isolated chromophores, the S1–S0 energy gap. Indeed, as shown in Fig. 3B, for Rh, nc-opsin destabilizes the S0 state (notice the positive potential in the -NH(+) CH- region) consistently with computed red-shift. Accordingly, in opsin, the negative counterion, that forms a salt bridge with the -NH(+)
CH- region) consistently with computed red-shift. Accordingly, in opsin, the negative counterion, that forms a salt bridge with the -NH(+) CH- moiety, counterbalances and surmounts the nc-opsin potential thus accounting for the resulting blue-shift with respect to the isolated chromophores.
CH- moiety, counterbalances and surmounts the nc-opsin potential thus accounting for the resulting blue-shift with respect to the isolated chromophores.
Effect of the Chromophore Structure.
Comparison of Fig. 2 A and B demonstrates that, relative to Rh, the increase in excitation energy seen in iso-Rh and in G121L is also present in the isolated chromophores. This finding establishes that, in these systems, the observed changes in λmaxa is, at least partially, a consequence of a change in the structure of the chromophore (i.e., factor i above). This conclusion does not apply to the E113D mutant whose chromophore (see Fig. 2B) displays, with respect to the Rh chromophore, a <0.3 kcal·mol−1 change in excitation energy.
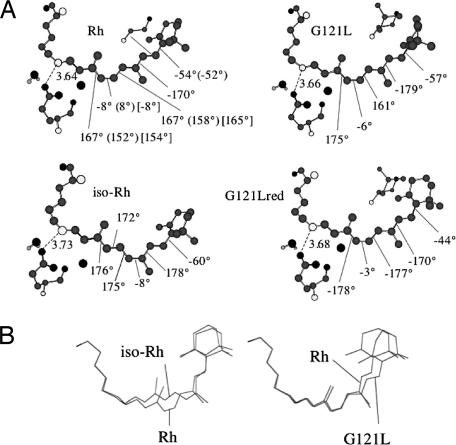
In a recent report (29) we have shown that, in the gas-phase, the excitation energy of the retinal chromophore is sensitive to the deformation of the conjugated π-framework. Here, the equilibrium structures of iso-Rh and G121L (see Fig. 4A) indicate that the excitation energy change is achieved through a complex deformation spanning the entire  C13
C13 C12
C12 C11
C11 C10
C10 C9
C9 C8
C8 C7
C7 C6
C6 fragment (of course, for iso-Rh such effect is due to the change in conformation of the chromophore that has to re-locate itself in the opsin cavity). Indeed, although iso-Rh and G121L feature a 6° and 4° increase in the C5
fragment (of course, for iso-Rh such effect is due to the change in conformation of the chromophore that has to re-locate itself in the opsin cavity). Indeed, although iso-Rh and G121L feature a 6° and 4° increase in the C5 C6
C6 C7
C7 C8 dihedral angle, respectively (i.e., too small to account for the excitation energy changes, because we found a ≈1 kcal·mol−1 excitation energy decrease for each 10° twisting of the β-ionone; see supporting information), there is also an 8° and 9° increase of the C10
C8 dihedral angle, respectively (i.e., too small to account for the excitation energy changes, because we found a ≈1 kcal·mol−1 excitation energy decrease for each 10° twisting of the β-ionone; see supporting information), there is also an 8° and 9° increase of the C10 C9
C9 C8
C8 C7 dihedral and a 9° and 8° increase in the C14
C7 dihedral and a 9° and 8° increase in the C14 C13
C13 C12
C12 C11 dihedral. The conclusion that the conformational control of a fragment (not of a single torsion) is one of the mechanisms of color tuning is also consistent with the analysis of the G121Lred conformer (see Fig. 2) of the G121L mutant. Such conformer, located 1 kcal·mol−1 higher than G121L, features, with respect to Rh, a β-ionone ring with a 10° decreased C5
C11 dihedral. The conclusion that the conformational control of a fragment (not of a single torsion) is one of the mechanisms of color tuning is also consistent with the analysis of the G121Lred conformer (see Fig. 2) of the G121L mutant. Such conformer, located 1 kcal·mol−1 higher than G121L, features, with respect to Rh, a β-ionone ring with a 10° decreased C5 C6
C6 C7
C7 C8 dihedral angle (suggesting an augmented conjugation). However, it also features an 11° and 10° increased C14
C8 dihedral angle (suggesting an augmented conjugation). However, it also features an 11° and 10° increased C14 C13
C13 C12
C12 C11 and C12
C11 and C12 C11
C11 C10
C10 C9 dihedral, respectively. Such deformation yields an excitation energy 4 kcal·mol−1 lower than that of G121L in both the protein and isolated chromophore.
C9 dihedral, respectively. Such deformation yields an excitation energy 4 kcal·mol−1 lower than that of G121L in both the protein and isolated chromophore.
Fig. 4.
Structural changes of the retinal chromophore. (A) Structure of the ground state energy minima of Rh, iso-Rh, G121L, and G121Lred. The chromophore structure of the E113D is very close to the one of Rh and it is not reported. The values in parentheses correspond to crystallographic data from ref. 51. The values in brackets correspond to NMR data from ref. 58. (B) Superposition of the frameworks of Rh and iso-Rh chromophores (Left) and of the Rh and G121L chromophores (Right).
Effect of the Counterion.
As discussed above, the interaction of the chromophore with its counterion is also a means of color-tuning (i.e., factor iii). Although this has been experimentally established (17), multireference perturbation theory provides an atomic level description of this effect in a real mutant. As shown in Fig. 2 B and C, both the isolated and nc-opsin embedded E113D chromophore features an excitation energy close to the one of Rh (actually slightly blue-shifted). This finding indicates that the red-shifted λmaxa of E113D in Fig. 2A is due to a change in the chromophore–counterion interaction that is only present in the full protein. Indeed, although the computed chromophore geometries of E113D and Rh are found to be substantially identical, the Asp-113 shorter side chain leads to a ≈0.9 Å increase in the counterion–Schiff base distance (we found a ≈1 kcal·mol−1 excitation energy decrease for each 0.1-Å increase in counterion–chromophore O N distance; see supporting information). This change, which decreases the stability of S0 with respect to S1, is almost absent in G121L and iso-Rh, where the carboxylate–Schiff base distance change, with respect to Rh, is <0.1 Å (see Fig. 4A).
N distance; see supporting information). This change, which decreases the stability of S0 with respect to S1, is almost absent in G121L and iso-Rh, where the carboxylate–Schiff base distance change, with respect to Rh, is <0.1 Å (see Fig. 4A).
Effect of the Chromophore Orientation.
A color-tuning factor, not directly related to factors i–iii, is revealed through further inspection of Fig. 2. In fact, despite the unchanged charge distribution in the five nc-opsins (i.e., the replacement of glycine with the neutral leucine residue in G121L does not alter the opsin generated electrostatic potential, see supporting information), the excitation energy decrease seen for the iso-Rh chromophore upon embedding in nc-opsin is ≈1.5 kcal·mol−1 smaller than for the other rhodopsins (compare Fig. 2 B and C). Such behavior must be related to a distinctive interaction of the iso-Rh chromophore with the electrostatic potential generated by the protein (the steric interactions have the same effect on S1 and S0 energies). In this context, one should note that, in the protein cavity, the orientation of the chromophore in iso-Rh and G121L strongly deviate from that seen in Rh. Indeed, as shown in Fig. 4B, in iso-Rh there is a displacement in the region that goes from the -NH CH- to the -C9
CH- to the -C9 C8- bond preceding the β-ionone region. In contrast, in G121L, the chromophore deviates in the β-ionone region. Such changes have the obvious consequence that the displaced backbones feel a different electrostatic potential. As shown in Fig. 3B, in iso-Rh, the chromophore experiences a decrease of repulsive potential in the region of the Schiff base and a more limited decrease of negative potential in the β-ionone region. Therefore, S0 will be less destabilized (consistently with a reduced red-shift in nc-opsin). This idea is confirmed by the analysis of the electrostatic potential on the G121L chromophore. Consistently with its different orientation, this chromophore does not show changes in the protonated Schiff base region and, thus, the magnitude of the S0 destabilization matches that of Rh. The G121L chromophore also displays a decrease in negative potential in the β-ionone region (with respect to Rh). However this seems to have only a limited effect that may be related to the fact (13) that, in Rh, the charge translocation, occurring upon S0 → S1 excitation, does not go beyond the -C10
C8- bond preceding the β-ionone region. In contrast, in G121L, the chromophore deviates in the β-ionone region. Such changes have the obvious consequence that the displaced backbones feel a different electrostatic potential. As shown in Fig. 3B, in iso-Rh, the chromophore experiences a decrease of repulsive potential in the region of the Schiff base and a more limited decrease of negative potential in the β-ionone region. Therefore, S0 will be less destabilized (consistently with a reduced red-shift in nc-opsin). This idea is confirmed by the analysis of the electrostatic potential on the G121L chromophore. Consistently with its different orientation, this chromophore does not show changes in the protonated Schiff base region and, thus, the magnitude of the S0 destabilization matches that of Rh. The G121L chromophore also displays a decrease in negative potential in the β-ionone region (with respect to Rh). However this seems to have only a limited effect that may be related to the fact (13) that, in Rh, the charge translocation, occurring upon S0 → S1 excitation, does not go beyond the -C10 C9- fragment (see Fig. 3A). Finally, from comparison of Fig. 2 A and C, it is apparent that the difference in excitation energy of the iso-Rh and G121L chromophores is reduced and even inverted when passing from a nc-opsin to an opsin environment. Part of this effect is accounted for by the larger counterion–Schiff base distance computed for iso-Rh (see Fig. 4A) that result in a lesser S0 stabilization leading to a lower excitation energy.
C9- fragment (see Fig. 3A). Finally, from comparison of Fig. 2 A and C, it is apparent that the difference in excitation energy of the iso-Rh and G121L chromophores is reduced and even inverted when passing from a nc-opsin to an opsin environment. Part of this effect is accounted for by the larger counterion–Schiff base distance computed for iso-Rh (see Fig. 4A) that result in a lesser S0 stabilization leading to a lower excitation energy.
The idea of generating, with the help of a computer, mutants or chemically modified rhodopsins of a wanted color is a dream that remains to be fulfilled. However, we have shown that an unbiased QM/MM method based on ab initio multireference perturbation theory coupled with the standard AMBER force-field, provides a state-of-the-art computational tool that can successfully reproduce λmaxa changes. Most importantly, we have demonstrated that such changes are reproduced even when the proteins do not differ in charged or polar residues.
The analysis of the excitation energy of rhodopsin demonstrates that opsin is designed in such a way to counterbalance (offset) the effect of its own counterion. Indeed, the fact that the protein excitation energy is intermediate between that of the chromophore in solution and in the gas-phase (see Fig. 2 A and B) indicates that the field generated by opsin reduces the effect of the counterion more effectively than methanol (a solvent will always compensate for the effect of the counterion; ref. 35).
The color tuning factors documented above will also operate in more common mutants characterized by a different composition or distribution of charged or polar residues. These comprise mutants mimicking the absorption properties of blue, green, and red cone pigments (28), those involved in retina diseases (36), and even the residues changes responsible for the variations in the color vision of primates (37, 38). In all these systems, the electrostatic effects will be unavoidably interlinked to a change in the chromophore geometry and cavity reorientation. For this reason, we believe that computational tools of the type applied above offer, when coupled with modern 3D structure prediction methods, new perspectives not only for the design of mutants or chemically modified rhodopsins but also for vision research.
Methods
Wanko et al. (39) have recently reviewed the application of QM/MM to the evaluation of the excitation energy of rhodopsins. Accordingly, here we only mention the few results that may help the reader to put our methodology in the correct perspective. Warshel et al. (40) reported the first QM/MM computation for an atomic-level model of bacteriorhodopsin (bR) using a QCFF/PI Hamiltonian with the polarizable protein force field of the program ENZYMIX (40). An improved version of this method was used to model the bR excitation energy profile (11). After this initial effort, other QM treatments of the chromophore have been used. For instance, Sakurai and coworkers (41, 42) used a semiempirical INDO/S, coupled to their protein polarizable force field, to model the excitation energies of Rh, bR, and other rhodopsins. More recently, time-dependent density functional theory has been tested by Vreven and Morokuma, who applied TD-B3LYP coupled to the (fixed charge) AMBER force field to bR (43). Only a few QM/MM investigations used ab initio QM. Gao et al. (44) used the CIS method couple to a modified CHARMM force field to evaluate the excitation energy of bR. Yamada et al. (45) used an RHF/6–31G/AMBER scheme to investigate the ground state (S0) stability of PSB11 protonated state in Rh. Hayashi et al. (46–48) reported a CASSCF//HF/DZV/AMBER computation of the λmax of bR and other rhodopsins. Although these authors correctly predict λmax changes, the λmax absolute values were strongly blue-shifted. More recently, a SAC-CI//SCF/AMBER investigation of Rh, bR and two sensory rhodopsins (49) and a SORCI//SCC-DFTB/CHARMM of bR and one sensory rhodopsin (50) have been reported. Although the excitation energies of these systems are reproduced in both cases, the retinal structure is determined by using a single-reference theory. In principle, this may impose a variational limit to the correct description of the chromophore bond lengths and torsional angles. Indeed, as documented elsewhere (39), the retinal bond alternation is sensitive to the nature of the wave function used in the geometry optimization. In this context, the CASPT2//CASSCF level offers a genuine multireference QM treatment.
The ground state (S0) Rh model used in our CASPT2//CASSCF/6–31G*/AMBER computations is derived from monomer A deposited in the Protein Data Bank (ID code 1HZX; ref. 51). In the context of the present work, the crystallographic structure is assumed to provide an acceptable model of the average environment of the chromophore, and no protein solvent (membrane lipids and external waters) is added. In fact, within our fixed charge model, the excitation energy should be mainly determined from the protein region close to the chromophore, and therefore the protein solvent has not been considered. This assumption is supported by the reevaluation of the λmax of Rh using a reduced model consisting of the 27 residues surrounding the chromophore (i.e., the Palczewski's cavity and the two crystallographic waters; see supporting information for details). In fact, it is shown that the recomputed excitation energies differs <1 kcal·mol−1 from the original value of Table 1. With the exception of Lys-296, the residue charges are described by the standard AMBER force field (52) and thus the residue polarizability or/and dispersion effects are not explicitly treated. [As originally pointed out by Warshel (10, 40), a correct model should include the protein solvent and account for the solvent and protein polarizability.] On the other hand, the effect of the residue polarizability and dispersion on the absolute excitation energy has been shown to be limited [for bR, Warshel et al. (11) estimated an effect of <1,500 cm−1; see also the work by Ren et al. (53), Matsuura et al. (42) and Rajamani et al. (44)] and shall fall into the reported blue-shifted <4.5 kcal·mol−1 error (however, notice that cancellation effects cannot be excluded). Given the substantially constant protein matrix of the set studied here, the error on excitation energy changes will be much smaller). With the exception of the Glu-113 counterion [forming a salt-bridge with NH(+)], the Rh cavity is set neutral consistently with the experiment (54). Although the protein is kept frozen during the optimizations, the Lys-296 side chain, the position/orientation of two TIP3P water molecules (W1 and W2 in Fig. 1), and the chromophore are relaxed to generate the protein equilibrium structure. The optimizations have been stopped when the maximum force is <0.0015 hartree/bohr and the rms displacement is <0.004 bohr. Due to the excessive computational cost, no second derivative computations could be performed to rigorously determine the nature of the stationary point. Improved crystallographic structures (1L9H and 1U19 in the Protein Data Bank; ref. 55) have recently become available that feature a better resolved position of the W2 water. Although this position differs by that defined by our model, W2 is still hydrogen bounded to the Glu-113 O1 center. Furthermore, the correct W2 hydrogen bond network is still under debate (56). Because, as documented above, our Rh models can reproduce the observed spectral properties of the corresponding systems, we maintain the chosen W2 position (13). To probe the effect of this choice on the Rh λmaxa, we have moved W2 to a position/orientation consistent with the 1L9H and 1U19 structures and reoptimized our Rh model (see supporting information for details). The results show that, despite a nonnegligible change in the geometry of the Schiff base region, the recomputed excitation energy differs <1 kcal·mol−1 from the original value of Table 1. Because there is no published crystallographic structure for iso-Rh, E113D, and G121L, their models have been derived from the Rh model. The ground state model of iso-Rh is constructed by replacing the 11-cis retinal chromophore of Rh with its 9-cis stereoisomer and repeating the optimization procedure described above (here we assume that, with the only exception of the Lys-296 that is fully relaxed, the average position of the other cavity residues will remain unchanged; the idea is that the conformationally flexible Lys-296–chromophore moiety will adapt to the opsin cavity without perturbing the original residue packing). The model of E113D has been derived by replacing the Glu-113 side chain with the side chain of the aspartic acid. Such guess structure is then relaxed by using the same procedure but including the variables describing the side chain of the aspartic acid residue in the optimization. The construction of the G121L model has required a less straightforward procedure. First, we have replaced the Gly-121 residue with leucine and included the leucine side chain in the optimization. Starting from the obtained energy minimum, we have looked for the different conformers of the β-ionone ring as a function of torsional deformation about the C6 C7 bond (see Fig. 1). Two low-lying conformers (G121L and G121Lred) were located that differ by ≈1 kcal·mol−1 in energy. For all models, at the S0 equilibrium geometries, a three-root state average CASPT2 computation is carried out using the MOLCAS-6 program (57) to evaluate the vertical excitation energy of the allowed (S0 → S1) transition (assumed to correspond to the λmaxa energy) and the associated oscillator strength. The values for the S0 → S2 transition have also been determined for consistency (see supporting information).
C7 bond (see Fig. 1). Two low-lying conformers (G121L and G121Lred) were located that differ by ≈1 kcal·mol−1 in energy. For all models, at the S0 equilibrium geometries, a three-root state average CASPT2 computation is carried out using the MOLCAS-6 program (57) to evaluate the vertical excitation energy of the allowed (S0 → S1) transition (assumed to correspond to the λmaxa energy) and the associated oscillator strength. The values for the S0 → S2 transition have also been determined for consistency (see supporting information).
Supplementary Material
Acknowledgments
In memory of Prof. Fernando Bernardi. We thank the Fondazione Monte dei Paschi for funding and the Consorzio Interuniversitario for granted calculation time. We are grateful to Prof. Stefan Haacke for many useful comments. This work was supported by the Università di Siena (Progetto di Ateneo 03). N.F. is grateful for Marie Curie fellowships HPMF-CT-2001-01769. P.B.C. is grateful for a Postdoctoral Fellowship from the Ministerio de Educación y Ciencia de España.
Abbreviations
- CASSCF
complete-active-space self-consistent-field
- QM/MM
quantum mechanics/molecular mechanics
- Rh
rhodopsin
- bR
bacteriorhodopsin
Footnotes
The authors declare no conflict of interest.
This article is a PNAS direct submission.
References
- 1.Bolon DN, Mayo SL. Proc Natl Acad Sci USA. 2001;98:14274–14279. doi: 10.1073/pnas.251555398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Dwyer MA, Looger LL, Hellinga HW. Science. 2004;304:1967–1971. doi: 10.1126/science.1098432. [DOI] [PubMed] [Google Scholar]
- 3.Gherman BF, Goldberg SD, Cornish VW, Friesner RA. J Am Chem Soc. 2004;126:7652–7664. doi: 10.1021/ja036879a. [DOI] [PubMed] [Google Scholar]
- 4.Roos BO. In: Advances in Chemical Physics: Ab Initio Methods in Quantum Chemistry. Lawley KP, editor. Vol 2. Chichester, UK: Wiley; 1987. pp. 399–445. [Google Scholar]
- 5.Andersson K, Malmqvist P-A, Roos BO, Sadlej AJ, Wolinski KJ. Phys Chem. 1990;94:5483–5488. [Google Scholar]
- 6.Roos BO, Fülscher MP, Malmqvist P-A, Merchan M, Serrano-Andrés L. In: Quantum Mechanical Electronic Structure Calculations with Chemical Accuracy. Langhoff SR, editor. Dordrecht, The Netherlands: Kluwer Academic; 1995. pp. 357–438. [Google Scholar]
- 7.Garavelli M, Celani P, Bernardi F, Robb MA, Olivucci M. J Am Chem Soc. 1997;119:11487–11494. [Google Scholar]
- 8.Gagliardi L, Roos BO. Nature. 2005;433:848–851. doi: 10.1038/nature03249. [DOI] [PubMed] [Google Scholar]
- 9.Ferré N, Olivucci M. Theor Chem. 2003;632:71–82. [Google Scholar]
- 10.Warshel A. Nature. 1976;260:679–683. doi: 10.1038/260679a0. [DOI] [PubMed] [Google Scholar]
- 11.Warshel A, Chu ZT. J Phys Chem B. 2001;105:9857–9871. [Google Scholar]
- 12.Gao J. Acc Chem Res. 1996;29:298–305. [Google Scholar]
- 13.Andruniów T, Ferré N, Olivucci M. Proc Natl Acad Sci USA. 2004;101:17908–17913. doi: 10.1073/pnas.0407997101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sinicropi A, Andruniów T, Ferré N, Basosi R, Olivucci M. J Am Chem Soc. 2005;127:11534–11535. doi: 10.1021/ja045269n. [DOI] [PubMed] [Google Scholar]
- 15.Honig B, Dinur U, Nakanishi K, Balogh-Nair V, Gavinowicz MA, Arnaboldi M, Motto MG. J Am Chem Soc. 1979;101:7084–7086. [Google Scholar]
- 16.Hurley JB, Ebrey TG, Honig B, Ottolenghi M. Nature. 1977;270:540–542. doi: 10.1038/270540a0. [DOI] [PubMed] [Google Scholar]
- 17.Sakmar TP, Franke RR, Khorana HG. Proc Natl Acad Sci USA. 1989;86:8309–8313. doi: 10.1073/pnas.86.21.8309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Han W, Lin SW, Smith SO, Sakmar TP. J Biol Chem. 1996;271:32330–32336. doi: 10.1074/jbc.271.50.32330. [DOI] [PubMed] [Google Scholar]
- 19.Mathies RA, Lugtenburg J. In: Handbook of Biological Physics. Stavenga DG, de Grip WJ, Pugh EN, editors. Vol 3. Amsterdam: Elsevier; 2000. [Google Scholar]
- 20.Blatz PE, Liebman P. Exp Eye Res. 1973;17:573–580. doi: 10.1016/0014-4835(73)90086-9. [DOI] [PubMed] [Google Scholar]
- 21.Kakitani H, Kakitani T, Rodman H, Honig B. Photochem Photobiol. 1985;41:471–479. doi: 10.1111/j.1751-1097.1985.tb03514.x. [DOI] [PubMed] [Google Scholar]
- 22.Kropf A, Hubbard R. Ann NY Acad Sci. 1958;74:266–280. doi: 10.1111/j.1749-6632.1958.tb39550.x. [DOI] [PubMed] [Google Scholar]
- 23.Neitz M, Neitz J, Jacobs GH. Science. 1991;252:971–974. doi: 10.1126/science.1903559. [DOI] [PubMed] [Google Scholar]
- 24.Beppu Y, Kakitani T. Photochem Photobiol. 1994;59:660–669. [PubMed] [Google Scholar]
- 25.Honig B, Greenberg AD, Dinur U, Ebrey TG. Biochemistry. 1976;15:4593–4599. doi: 10.1021/bi00666a008. [DOI] [PubMed] [Google Scholar]
- 26.Morton R. Biochemistry. 1955;59:128–134. [Google Scholar]
- 27.Baasov T, Friedman N, Sheves M. Biochemistry. 1987;26:3210–3217. doi: 10.1021/bi00385a041. [DOI] [PubMed] [Google Scholar]
- 28.Kochendoerfer GG, Lin SW, Sakmar TP, Mathies RA. Trends Biochem Sci. 1999;24:300–305. doi: 10.1016/s0968-0004(99)01432-2. [DOI] [PubMed] [Google Scholar]
- 29.Cembran A, Gonzáles-Luque R, Altoè P, Merchán M, Bernardi F, Olivucci M, Garavelli M. J Phys Chem A. 2005;109:6597–6605. doi: 10.1021/jp052068c. [DOI] [PubMed] [Google Scholar]
- 30.Mathies RA, Stryer L. Proc Natl Acad Sci USA. 1976;73:2169–2173. doi: 10.1073/pnas.73.7.2169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bonacic-Koutecky V, Köhler K, Michl J. Chem Phys Lett. 1984;104:440–443. [Google Scholar]
- 32.Bonacic-Koutecky V, Schöffel KJ, Michl J. Theor Chim Acta. 1987;72:459–474. [Google Scholar]
- 33.Birge RR, Murray LP, Pierce BM, Akita H, Balogh-Nair V, Findsen LA, Nakanishi K. Proc Natl Acad Sci USA. 1985;82:4117–4121. doi: 10.1073/pnas.82.12.4117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Arnaboldi M, Motto MG, Tsujimoto K, Balogh-Nair V, Nakanishi K. J Am Chem Soc. 1979;101:7082–7084. [Google Scholar]
- 35.Warshel A. J Phys Chem. 1979;83:1640–1652. [Google Scholar]
- 36.Padrón-García JA, Crespo-Otero R, Hernández-Rodriguez EW, Garriga P, Montero LA, García-Piñeiro JC. Proteins. 2004;57:392–399. doi: 10.1002/prot.20204. [DOI] [PubMed] [Google Scholar]
- 37.Jacobs GH, Deegan JF, Jr, Tan Y, Li W-H. Vision Res. 2002;42:11–18. doi: 10.1016/s0042-6989(01)00264-4. [DOI] [PubMed] [Google Scholar]
- 38.Jacobs GH, Deegan J. F., II Vision Res. 2003;43:227–236. doi: 10.1016/s0042-6989(02)00565-5. [DOI] [PubMed] [Google Scholar]
- 39.Wanko M, Hoffmann M, Strodel P, Koslowski A, Thiel W, Neese F, Frauenheim T, Elstner M. J Phys Chem B. 2005;109:3606–3615. doi: 10.1021/jp0463060. [DOI] [PubMed] [Google Scholar]
- 40.Warshel A, Chu ZT, Hwang J-K. Chem Phys. 1991;158:303–314. [Google Scholar]
- 41.Houjou H, Inoue Y, Sakurai M. J Phys Chem B. 2001;105:867–879. [Google Scholar]
- 42.Matsuura A, Sato H, Houjou H, Saito S, Hayashi T, Sakurai M. J Comp Chem. 2006;27:1623–1630. doi: 10.1002/jcc.20432. [DOI] [PubMed] [Google Scholar]
- 43.Vreven T, Morokuma K. Theor Chem Acc. 2003;109:125–132. [Google Scholar]
- 44.Rajamani R, Gao J. J Comp Chem. 2002;23:96–105. doi: 10.1002/jcc.1159. [DOI] [PubMed] [Google Scholar]
- 45.Yamada A, Kakitani T, Yamamoto S, Yamato T. Chem Phys Lett. 2002;366:670–675. [Google Scholar]
- 46.Hayashi S, Ohmine I. J Phys Chem B. 2000;104:10678–10691. [Google Scholar]
- 47.Hayashi S, Tajkhorshid E, Pebay-Peyroula E, Royant A, Landau EM, Navarro J, Schulten K. J Phys Chem B. 2001;105:10124–10131. [Google Scholar]
- 48.Hayashi S, Tajkhorshid E, Schulten K. Biophys J. 2002;83:1281–1297. doi: 10.1016/S0006-3495(02)73900-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Fujimoto K, Jun-ya H, Hayashi S, Shigeki K, Nakatsuji H. Chem Phis Lett. 2005;414:239–242. [Google Scholar]
- 50.Hoffmann M, Wanko M, Strodel P, König PH, Frauenheim T, Schulten K, Thiel W, Tajkhorshid E, Elstner M. J Am Chem Soc. 2006;128:10808–10818. doi: 10.1021/ja062082i. [DOI] [PubMed] [Google Scholar]
- 51.Teller DC, Okada T, Behnke CA, Palczewski K, Stenkamp RE. Biochemistry. 2001;40:7761–7772. doi: 10.1021/bi0155091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Singh UC, Kollman PA. J Comp Chem. 1986;7:718–730. [Google Scholar]
- 53.Ren L, Martin CH, Wise KJ, Gillespie NB, Luecke H, Lanyi J, Spudich JL, Birge RR. Biochemistry. 2001;40:13906–13914. doi: 10.1021/bi0116487. [DOI] [PubMed] [Google Scholar]
- 54.Fahmy K, Jager F, Beck M, Zvyaga TA, Sakmar TP, Siebert F. Proc Nat Acad Sci USA. 1993;90:10206–10210. doi: 10.1073/pnas.90.21.10206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Okada T, Sughihara M, Bondar A-N, Elstner M, Entel P, Buss V. J Mol Biol. 2004;342:571–583. doi: 10.1016/j.jmb.2004.07.044. [DOI] [PubMed] [Google Scholar]
- 56.Furutani Y, Shichida Y, Kandori H. Biochemistry. 2003;42:9619–9625. doi: 10.1021/bi034592k. [DOI] [PubMed] [Google Scholar]
- 57.Andersson K, Blomberg MRA, Fülscher MP, Karlstöm G, Lundh R, Malmqvist P-A, Neogrády P, Olsen J, Roos BO, Sadlej AJ, et al. Lund, Sweden: University of Lund; 2002. MOLCAS 6.1. [Google Scholar]
- 58.Verdegem PJE, Bovee-Geurts PHM, De-Grip WJ, Lugtenburg J, De-Groot HJM. Biochemistry. 1999;38:11316–11324. doi: 10.1021/bi983014e. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.