Blood flow velocity effects and role of activation delay time on growth and form of platelet thrombi

Abstract

Mural thrombi are composed dominantly of platelets and develop under a blood flow. Portions can break off and are carried in the blood flow as emboli. Thrombus growth rates are affected by the velocity of the blood flow, but they do not simply increase with it, they exhibit a maximum, with subsequent decrease. Whereas this variation indicates an interaction of biochemical and physical processes, studies have concentrated widely on understanding only the biochemical processes. Here we show results of simulation of thrombus formation in 3D flows by accounting for the movements of individual platelets. Each platelet follows prescribed rules for interactions while the local flow around the thrombus continuously adjusts to the growing structure of the thrombus, also when embolization occurs. With an activation delay time assigned to each platelet we demonstrate the dependence of thrombus growth rate on blood velocity as found experimentally by Begent and Born [Begent N, Born GV (1970) Nature 227:926–930]. With activated platelets having mutual tensile action sustainable up to a prescribed distance we achieve thrombus growth faster than with shorter maximum distances that make a thrombus less porous; when the prescribed maximum distance is large enough the thrombus shape is not like a “hill” but like a “carpet.” We find that thrombus growth rate is enhanced by modest pulsatility but less so when pulsations are amplified in part because of more embolization.

Acute thrombogenesis in a flowing bloodstream can occur on damaged tissues in normal circulation (1). It has also been observed in blood flow over vascular prostheses (2) and in artificial internal organs, such as prosthetic heart valves (3). The thrombi are composed predominantly of platelets, and they can develop even in the presence of systemic anticoagulants such as heparin (4).

Blood flow velocity effects were investigated systematically in vivo by Begent and Born (1), who obtained quantitative data on thrombus growth rates for a range of blood flow rates. Their study remains the clearest time-resolved in vivo study of the effect of blood flow rates on thrombus formation. Richardson (5) subsequently proposed that Begent and Born's observations were consistent with a shear-flow aggregation process (6, 7) in which an activation delay time of the platelets is allowed for, a delay time between each platelet's close encounter with the thrombus and its development of ability to adhere to the thrombus, and which was estimated then to be the order of 0.1–0.2 s. A predicted consequence of this finding was that the height-to-length ratio for thrombi would be lower in blood flows, where a significant fraction of the activated platelets escaped the primary thrombus before their activation delay time had elapsed; this was demonstrated later by Born and Richardson (8). More recent experiments by Petrishchev and Mikhailova (9) in vivo and van Gestel et al. (10) in vitro produced qualitatively similar results as the ones of Begent and Born but they lack the quantitative details required for validating simulation results.

At the time of Begent and Born's studies there were handicaps to carrying the implications further. The biological handicap was the lack of specific knowledge of cell membrane channels and receptors, and therefore of cell mechanics by which an activation delay time could be mediated (and varied). The computational handicap was that computing capability then available was inadequate to consider the movements of, say, 50,000 individual platelets in a blood flow where thrombus growth is initiated at one location on a wall. This latter handicap now has diminished, and this article describes what is found in running simulations of the Begent and Born flow situations and what can be predicted about thrombus formation in pulsatile flows. The latter is a circumstance important to clinical conditions such as thrombo-embolic stroke and myocardial infarction involving thrombus formation on fissured atherosclerotic plaques in carotid and coronary arteries.

Numerical Simulations

Simulations representing 3D blood flow were performed for a 50-μm-diameter straight tube, with 500-μm length at several different steady blood flow rates. Platelets are considered uniformly distributed in the inflow, with the latter having a parabolic velocity profile at entry. The mean velocity distribution alters downstream, over time, as a thrombus forms on the wall and acts as an obstacle to the flow; there is an interaction between the flow and the structure formed by the thrombus. The time-dependent computations continuously update the geometry of the thrombus with regard both to size and shape. This procedure was followed for blood flow rates both below and above the rate, which is expected to provide the maximum relative rate of growth. This approach provided simulation results, which can be compared with the experimental data of Begent and Born (1).

Simulations were extended to investigate the effect of pulsatility of blood flow. The inflow was prescribed to have a steady component and a simple harmonic component, the amplitude of the fluctuating component being ε times the steady component, with values of ε ranging from 0.1 to 0.7. The frequency ω of the fluctuating component was 1 Hz. The product of the activation delay time τ and the frequency ω is a dimensionless parameter. Both might be modified pharmacologically and largely independently, so behavior of thrombus growth at other values of the product are prospectively interesting to determine whether there are zones of behavior worth targeting and reasons for possible differences in thrombus growth between small animal (higher ω) and large animal (lower ω) observations, while τ differs less between the relevant species.

Biological Model

With the mode of supply of ADP used by Begent and Born (1), one can expect that there is a period in which the concentration of ADP builds up parallel to the axis of the blood vessel, and therefore the axial location at which the ADP concentration caused by the iontophoresis is large enough to initiate activation of platelets advances upstream for a while. The footprint of ADP concentration around the outside of the vessels Begent and Born used was likely to have an elliptic form progressively “wrapping around” the side of the vessel close to the iontophoresis needle tip and changing in its axial- and circumferential-direction spans for some time. In the experiments, the size of this footprint likely increased progressively with time.

In the simulation approach, it has been important to explore a selection of rules applied for every platelet regarding the interplatelet and platelet–wall interactions. Thrombi, except those plugging a vessel wall puncture, have a degree of loose-packing compared with, say, sedimentary behavior of solid grains packing with solid-surface contact. Fibrinogen and fibrin strands have a part of this process and were recognized early as essential cofactors in aggregation; platelet “stickiness” develops when the platelet membrane acquires the ability to bind fibrinogen (11).

Falati et al. (12) used confocal and wide field microscopy to image thrombus formation with platelets, fibrin, and tissue factor in real time. Vessel wall injury was induced by a pulsed nitrogen dye laser (nonpuncture injury). Platelets were visible in attachment by 4 s after injury. Polanowska-Grabowska and Gear (13) had shown that platelets can adhere very rapidly to collagen exposed on a surface. Falati et al. (12) found colocalization of the platelets and the fibrin in the thrombus. Tissue factor was localized on the upstream edge of the thrombus and along the vessel–wall interface. Falati et al. (12) did not provide an electron micrograph of any thrombi. Falati et al. (14) later provided additional information on tissue factor accumulation in developing thrombi. Plasma fibronectin is also known to have a role in thrombus growth and stability (15).

Activation of platelets initiated by ADP can occur at a finite distance of separation from a growing thrombus for platelets approaching it, because of diffusion of ADP from the thrombus (or from an extravascular iontophoretic source). These aspects of platelet interaction invoke use of two length scales. Another issue for incorporation in an interaction model is that of a repulsive force function in the event of close approach. Energy landscapes have been described for single molecular bonds (16), which can be studied under ingeniously designed and carefully controlled laboratory conditions that assure single bonds only are involved. Thrombi develop in vivo with multiple bonds, and so a more generalized form of energy landscape is applied for the calculations reported here. The links used in the model here incorporate the effects of many individual bonds.

One extra choice available is that for the adhesive footprint of the thrombus on the wall to which it attaches: given a seeded location (where a few platelets are adherent, a computational-model replacement of the use of iontophoretic application of ADP to initiate thrombosis), should any activated platelet be allowed to attach anywhere it comes sufficiently close to the wall surface downstream? Or should a geometrically defined patch on the wall limit the extent where that may happen? Our simulations reported here cover these two cases. A range of choice of footprint rules for the computation may be needed to represent adequately typical different causes of thrombus formation, such as highly localized vascular injury, or fissures at atherosclerotic plaque caps, or flow over manufactured surfaces as in needles or over artificial-organ components. Even within one footprint type, there can be an effect of the relative locations of the small number of seed platelets present at the beginning, which also has been explored somewhat.

Results

The simulation predicts thrombi growth with shapes and patterns similar to those observed experimentally. Fig. 1 shows one frame from the results of Begent and Born (1) and a pair of frames from a simulation of such a thrombus growth (see also Movie 1, which is published as supporting information on the PNAS web site). There is an early, brief (up to ≈3 s) phase of rapid growth, which would not have been detected in Begent and Born's experiments because of the difficulty of seeing distinctly a mural grouping of so few platelets, followed by a slower yet exponential rate of growth.

Fig. 1.

Evolution of thrombus growth. (a) Thrombus growing on a blood vessel wall in vivo is shown. [Reproduced with permission from ref. 1 (Copyright 1970, Nature Publishing Group).] (b) Similarly scaled computer model showing the early growth stage of thrombus is shown. Blue indicates unactivated platelets, green indicates triggered platelets, and conversion after a characteristic time delay to activated is indicated by red. (c) Later stage in thrombus growth at steady flow is shown. (d) Shown is a late stage in a similar computation, where adhesion of activated platelets is allowed at all locations downstream.

Thrombi initiated under the same flow conditions may have a varied small-growth time, but have major growth at an exponential rate that has no set relation to variation in the small-growth time, and embolization of part of a thrombus can readily resolved in the computation even for thrombi as small as 10 platelets.

The number of platelets accumulated in a thrombus for replicate computing runs at one flow velocity is shown in Fig. 2a. The lines correlating each run in the exponential-growth phase have closely similar slopes, and the time taken to that phase from the initiation of flow varies somewhat. This result is similar to that reported by Begent and Born (1), except that they had no way for observing the variation of the short initial phase because the number of platelets adhering to the wall then was too small, being below the resolving power of their microscope, nor did they run a number of replicate runs at each flow rate to determine statistics of the variability of the growth-rate factor as a function of blood flow rate. The slope of the exponential growth for the model was calculated as a mean and standard variation from the replicate runs.

Fig. 2.

Growth of platelet thrombi in a blood vessel. (a) Accumulation of platelets in a thrombus is shown. Conditions are the same as Fig. 1 b and c with flow rate of 100 μm/s. Solid lines are used to correlate exponential growth phase; slopes are plotted in Fig. 3a. (b) Flow structure interaction is illustrated by flow(stream) lines close to developing thrombus, with the flow going from the left front to right rear, offering a perspective view. For clarity most unactivated platelets have been omitted.

The model used provides for flow-structure interaction, as illustrated in Fig. 2b. Fig. 2b displays, in 3D at one instant in time, some flow lines computed at locations lying closely over a thrombus in an early stage of its growth. The streamlines, of which a small number are displayed, have clearly adapted to the local obstruction to flow presented by the thrombus and make their way around it. This process continues as more and more platelets aggregate into the thrombus.

Thrombi initiated at other flow rates also have their major phase of growth exponential in time, and the growth-rate coefficient has a maximum as a function of flow rate. We note that the growth-rate coefficient, which can be deduced from using a natural-logarithm scale for the vertical axis in the right-hand graph in figure 7 of ref. 1, does not fall within the range of those listed in figure 5 of the same paper but is somewhat below the lowest value in that figure 5, pointing to a scaling-factor error in the vertical axis of the latter as confirmed by Begent and Born; however, we lack the original data to be able to perform a more accurate comparison.

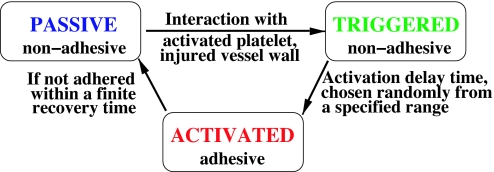
Fig. 5.

In our model, platelets can be in three different biological states: passive, triggered, and activated. In the passive state, platelets are not adhesive, which is a normal state of the platelets in blood. If a passive platelet interacts with an injured wall or an activated platelet it becomes triggered and after an activation delay time it becomes activated and adhesive. The activation delay time is chosen uniformly at random from a specified range. If after a finite recovery time an activated platelet does not adhere to anything it returns back to a passive state.

Investigation of thrombus growth was repeated for a number of different flow rates in the vessel. Qualitatively similar results were obtained. Values of the slope of the exponential growth are shown as a function of the vessel flow rate in Fig. 3a. Broadly similar to the results from Begent and Born, it was found the exponential growth rate initially rose with flow rate, but there was a peak and for higher blood flow rates the growth rate fell. This is an effect of the activation delay time; at higher flow rates, more of the activated platelets escape capture into the primary thrombus. Some runs were computed at a flow rate >500 μm/s with zero activation time to check this peak and to verify that lower growth rates were not simply caused by accumulation of the effects of repeated embolization of portions of the growing thrombus. If the wall downstream is readily adhesive to activated platelets, one typically sees a secondary thrombus develop there. Indeed, after some growth, secondary thrombi can grow with a higher capture effectiveness there than at the leading thrombus.

Fig. 3.

Effect of blood flow velocity. (a) Exponential thrombus growth rate coefficients as a function of flow rate in small vessel 50 μm in diameter is shown. The mean values are shown as circles, individual values from replicate computer simulations are indicated by asterisks, and the trend of the mean growth rate coefficients as a function of flow rate matching qualitatively the trend from Begent and Born (1) is shown. (b) For four flow rates, the effect of sinusoidal flow pulsations (mean of replicate computer simulations) is shown for various relative amplitudes ε of pulsation compared with steady-flow means (○) and standard deviations (vertical bars). △ indicates ε = 0.1; ▷ indicates ε = 0.3; ▽ indicates ε = 0.5, and ◁ indicates ε = 0.7.

Porosity of thrombus is significant to good capture efficiency of approaching platelets.

The sensitivity of the results to the assumed values for various parameters was investigated. When the minimum distance of the longer-range attraction was halved (making a more compact thrombus), the thrombus growth rate was stunted, with more platelets being deflected in the flow over the thrombus than being caught by it. (This possibility was anticipated in figure 1 in ref. 8 and is borne out by the current simulations.) It appears that the opportunity for enough plasma to filter through the thrombus is significant in maintaining a high platelet capture efficiency.

However, when the minimum distance of the longer-ranged attractive force is increased far enough, e.g., for a 50% increase of that distance at a flow rate of 300 μm/s, the steady flow may (according to some computational results) push the thrombus into more of a “carpet” form lying close to the wall at early growth times, because the equivalent mutual tether length is too long to require the linked platelets to form a pile, and the carpet may not require many platelets that have become added to it to adhere to the wall to hold the thrombus until embolization.

The number and mutual positioning of “seed” platelets have an effect on the small-time growth period.

Although it might seem optimum in some sense to use just one adherent platelet as the initial seed, this choice extends considerably the computing time required to reach a thrombus of N platelets, N ≫ 1, because with basically exponential growth it takes as the same order of time interval to go from one to two platelets as it does to go from 100 to 200 in a thrombus, so starting with more than one fixed seed platelet to initiate a thrombus saves considerable computing time. However, there is then an effect from the spacing and configuration of the seed set of platelets. If one seed platelet was close enough to streamlines that had passed over a proximal seed platelet the early capture rate seemed higher.

The limitation of thrombus surface-attachment opportunity in the downstream direction, when applied as a boundary condition in our computations, with a fixed location of the downstream boundary, leads to thrombi that can overhang the distal end of the attachment zone, but the part of the thrombus that overhangs distally has compliant behavior and can be flattened in contact with the wall or can peel up. When in the up position, the growth rate of the thrombus slows considerably. However, after some time in the up position it can make a relatively rapid transition to the down position again, and the thrombus resumes a growth rate typical of a thrombus without a raised tailpiece. While one of us (P.D.R.) has observed the up position of a rear portion of a thrombus in flow-chamber experiments, we do not have measurements of the corresponding thrombus growth rate changes as they were not being made at that time.

For a given blood flow rate, there is a range of net thrombus growth rates that likely contribute to the variability of observed “bleeding times,” those times running until leakage at a standard cut (skin) or through a puncture (tube) effectively stops. For flow rates >400 μm/min, running a dozen or so computations with replicate initial conditions gave an even larger variation in time taken to reach the larger thrombi sizes, likely to be needed to achieve thrombotic occlusion of a distal vessel puncture, over the range of two-to-one or more found at lower flow rates. Fig. 4 illustrates these times for thrombi of 70 platelets.

Fig. 4.

Ranges of bleeding time (as assessed by time to form a thrombus of 70 platelets) as a function of the blood flow velocity in the tube were determined. At all velocities the range is at least a factor of 2.

The effect of pulsatility was investigated by imposing a sinusoidal variation of velocity to the inflow,

with ε being the amplitude of pulsatility relative to the mean flow. The period of oscillation was 1 s. A shorter period was not considered, to keep the pulsatility period distinct from the activation delay time. Thrombus formation was computed for a range of values of mean flow, and with ε = 0.1, 0.3, 0.5, and 0.7. Again, exponential growth was observed, and for this flow geometry the mean values of the exponentional coefficients (five replications for each set of conditions) lies within the 95% error range of the results for purely steady flow except for ε = 0.1, for which the growth rates were higher. Upon examining the time-resolved thrombus size in detail, it was seen that with large enough ε it appears possible that a small embolus can be peeled away from the thrombus cyclically in a way not found with steady flow or ε = 0.1, and thus the cumulations with time at the higher ε have a noticeable sawtooth appearance, with the temporarily higher thrombus growth rate partly offset in the mean because of the loss of the emboli.

Thus, to first order in a straight flow geometry and with conditions precluding recirculation, the effect of sinusoidal pulsations at a typical human heart rate is to cause thrombi to develop at a rate closely related to that for steady flow at the corresponding mean flow conditions, and highest relative to that at ε = 0.1.

Discussion

It must be noted that the thrombus-formation modeling described here was for an initially uniform flow passage with parallel streamlines. Here we demonstrate that the concept of platelet activation delay time can be integrated into a computer model of mural thrombus formation, which accounts for motions of all platelets individually involved and incorporates a small number of physical parameters and functions to represent physico-chemical factors such as cell adhesion molecule behavior, fibrinogen, and so forth for the scale represented in the model. It may be discovered in vivo that the activation delay time is affected by the vascular location in which thrombi grow, and by the ability of the endothelium to produce NO and other agents. There may be some effect of vascular location on the energy landscape relevant to adhesion and aggregation that typically occurs there; the observation of Poole et al. (17) that in a large vessel, such as the aorta, platelets tend to form monolayers on damaged areas of the wall without aggregating into mural thrombi may reflect that the typical interplatelet linkage distance is greater there so that a flat form of thrombus occurs, as our simulations predicted. Obviously, there are difficulties in obtaining measurements of interplatelet distances in thrombi, especially in vivo, but some effort on this issue to distinguish possible variations depending on vascular location and blood velocity would be worthwhile for improving details of the model for application in such circumstances. The later phenomenon of clot retraction implies the prior existence of nonzero distances between the platelets that comprise it, and that possess contractile components in the cytoskeleton, and no attempt is made here to model that.

Although effects of blood flow rate on platelet adhesion and aggregation, and on thrombus growth, have been known for decades, in many experimental studies the flow conditions are not recorded or controlled for, nor are electron micrographs of thrombi routinely reported. Such incompleteness of experimental information makes it difficult to improve representational details applied in computer modeling (see Simulation Methodology). It has been noted that in the use of light-dye methods for thrombus initiation the vessel-wall injury varies with the intensity of the light applied, but reports of light intensity used, and of the extent of primary vascular injury, are often missing. There are, of course, some representational details used in the model that may be robust, in the sense that modifications of values of some parameters may make modifications of outcome that are too small to distinguish by presently available methodology in experiments [the standard deviations in the thrombus growth rates as a function of blood velocity measured by Petrishchev and Mikhailova (9) are comparable with variations that arise in our computational model, but also imply that such experiments may be limited for comparing with small refinements of the model]. For example, in modeling the interplatelet attractive forces it seems sufficient for the present to use one fixed force-distance relation for a fixed finite time, although in practice it must vary over time [likely connected in part to the variations of platelet cytosolic free calcium with time (10)] and be associated with a mix of engaged cell-surface receptors and composition of linking molecules. In modeling platelet-platelet repulsive forces, modifications to the platelet membrane stiffness (as by α-tocopherol) may require a corresponding adjustment, but potentially also to the attractive force because α-tocoperol also down-regulates GPIIb promoter activity (18). If a negative feedback regulation associated with platelet-borne MMP-9 (19) is confirmed to play a role, it could be necessary to include its effect in the activation aspects of the model used here. If there are subpopulations with different reactivies, as implied by Van Gestel et al. (10), they, too, can be incorporated by adaptation of the model. In a study to assess thromboembolism associated with pulsatile flow, Sukavaneshvar et al. (20) observed in an ex vivo model that flow pulsatility induced increases in both thrombosis and embolism.

The model may lead to improvements in assessing the impact of various platelet-active drugs, observed and measured in specific flow conditions, in altering thrombus formation in a variety of other flow conditions. Hopefully, our model will spur new experiments to determine some of the parameters of thrombi previously overlooked and lead to models more sophisticated in representation of biochemical and physical processes that matter most.

Simulation Methodology

For our simulation, we assumed platelets in concentration of 300,000 per mm³, 3 μm equivalent diameter, a vessel diameter of 50 μm, parabolic velocity profile at the inlet and mean blood flow velocities of 100–800 μm/s, overlapping the major range of Begent and Born's experimental conditions (1). Applying the force coupling method (21), the equation of motion is

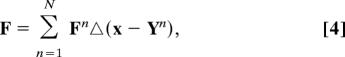where the coupled force associated with the nth platelet is distributed around its center-point Yⁿ as

with a being the platelet radius, with the force vector

and the postsuperscript is annotation designating the nth platelet, not a power. The first term allows for the difference between the density of platelets in comparison to an equivalent volume of the suspending fluid, and the second term representing the force exerted between the nth platelet and other platelets or the vessel wall surface. The individual platelet velocity is obtained from a local, volume-averaged fluid velocity as

The interaction force term includes, for any platelet, a repulsive portion when the platelet is approaching and has come within a specific distance of another platelet or wall surface. If both the nth platelet and another (or the location on the wall) it encounters are in the active state the link is created between them. No more than one link can be created between each pair of activated platelets (or the activated platelet and the wall). For activated platelets with links in addition to the repulsive force, there is also an attractive force, shown at the larger distances of separation; this is zero at smaller, finite distances to permit loose packing of mutually adhering platelets. The looseness of packing is significant for a thrombus because it provides a space through which the suspending fluid can seep. It also recognizes the linking role of fibrinogen without attempting to model it in detail. We note that Guy and Fogelson (22) have made computational estimations regarding the role of fibrinogen, based on the collision of two spherical particles with fibrinogen available in the suspending fluid, one particle being already activated, and consider bond completion and bond rupture; because of the many platelets considered in our model, a simpler form of relation that does not assess aspects of fibrinogen concentration is used here.

In our model, each platelet carries with it an activation-distance corona. Before a platelet is triggered it is tested at each step in time to determine whether an activated platelet has its center within twice the activation-distance corona of its own center; if so, the platelet is coded as having its activation triggered, and within a time span (freshly) randomly chosen between two time interval limits it becomes activated (see Fig. 5). (These are larger than the time step used in the flow computations.) The finite extent (1.5 platelet radius) of the activating corona beyond the perimeter of the platelet allows in this model for diffusion of activators such as ADP without attempting a more exact determination of the convective field involved. If an activated platelet has not adhered within a finite recovery time it returns to its initial passive state. Throughout these conditional aspects the model is intended to make practical allowances for physico-physiological aspects in ways that avoid requirement of concurrent solutions for e.g., time-dependent ADP transport to be generated as these would be computationally prohibitive at the present time. Much detailed biochemistry is condensed, and only the associated major changes in physical forces are modeled here. The model is chosen to allow computations to march forward in time, without iteration. Each time a computation is performed with constant values of parameters and the same flow rate, there is some variation from the results of otherwise similar runs when the random-number generator for determining individual platelet activation delay times is freshly seeded. Thus, replication runs are made to explore the corresponding variability of thrombus growth.

The governing flow equations are solved by using the spectral/hp element solver NEKTAR (23) marching forward in time steps, the position vectors for all of the platelets being updated (and all associated near-neighbor conditions being checked) for each time step. The force coupling method seems more reliable when the average particle density is modest, and so the suspension of red cells is treated as a continuum. The impact of this assumption is believed to be small because the Smoluchovski number, ratio of shear gradient encounter rate to random-walk collision rate, for platelets in the flow considered here is quite high, and an augmentation of platelet diffusivity would not have a significant effect. We focus on the onset of the aggregation and consider small aggregates of size ≈100 μm. For aggregates of this size the increase of platelet near-wall concentration caused by the presence of the red blood cells should have minor effects on the results obtained here (24). The few other cells typical of whole blood such as the leukocytes are omitted from the model as being too low in number density to have a significant dynamic effect. Even so, using this model has consumed significant amounts of supercomputer time (hundreds of thousands of hours) over a period of 2 years, including sensitivity studies.

At the beginning of the computation, the fluid in the vessel is empty of platelets but the entering flow has them approximately uniformly distributed in it. However, by the time there are platelets sufficiently close to the seed platelets on the vessel wall to be activated, there is full priming of the flow at smaller radii with platelet-laden blood. To initiate thrombus growth at a known location, typically three activated platelets were placed close together on the vessel wall at the initiation of flow. (In pulsatile flows of large amplitude, these were observed to oscillate somewhat back and forth in the flow direction, a natural consequence of the model and sometimes seen in actual flows.) Approaching platelets, which come close enough to these, become triggered; while a few triggered platelets escape downstream, many become activated while still close enough to adhere, and through continuous repetition of this process the platelets aggregate as a mural thrombus.

Interaction potentials applied with soft matter are typically quadratic. Hence, our interaction force term (F_interaction = F₁ + F₂ + F₃ + F₄) is piecewise linear, the part for closer approach having the repulsion force rising linearly with decreasing distance. Specifically, the force acting on the platelet approaching the wall or another platelet is

for r/a ≤ R, where a is the platelet radius and r is a distance from the center of the platelet to the wall or the surface of the other platelet. The force is directed along the normal to the wall or the vector connecting the centers of the platelets. From the distance at which that has become zero, a region of zero force is applied, F₂(r) = 0 for R ≤ r/a ≤ L (representing where connecting proteins, especially fibrin, may be slack), beyond which an attractive force rises linearly with increasing distance,

for L ≤ r/a ≤ M, representing a combination of connecting protein/filopodia and cell membrane elasticity. The force between activated platelets rises up to a point where typically the connections are not long enough to reach, or have broken from, the neighbor platelet, with the force dropping to zero at an out-of-range position,

for M ≤ r/a ≤ B. The attraction force is directed along the vector between the center of the platelet and the attachment point on the wall or the center of another platelet. The values of parameter R, L, and B are set to 1, 1.5, and 3.5, respectively, while

the constant α is set to 4 × 10⁻⁹ N. These parameters were chosen based on physical considerations and systematic simulations to evaluate the sensitivities of the model. For example, we have performed 36 simulations for three different values of α corresponding to ×1/10, ×1/3, and ×3 the above value (at flow rate 400 μm/s), and all results were within the range established by the value of α = 4 × 10⁻⁹ N at the same flow rate. Finally, the activation delay time is assumed randomly uniformly distributed over the range 0.1 to 0.2 s, selected for each platelet once, but differently in otherwise replicate runs. The platelet recovery time is set to 5 s (5).