Abstract
Plutonium possesses the most complicated phase diagram in the periodic table, driven by the complexities of overlapping 5f electron orbitals. Despite the importance of the 5f electrons in defining the structure and physical properties, there is no experimental evidence that these electrons localize to form magnetic moments in pure Pu. Instead, a large temperature-independent Pauli susceptibility indicates that they form narrow conduction bands. Radiation damage from the α-particle decay of Pu creates numerous defects in the crystal structure, which produce a significant temperature-dependent magnetic susceptibility, χ(T), in both α-Pu and δ-Pu (stabilized by 4.3 atomic percent Ga). This effect can be removed by thermal annealing above room temperature. By contrast, below 35 K the radiation damage is frozen in place, permitting the evolution in χ(T) with increasing damage to be studied systematically. This result leads to a two-component model consisting of a Curie–Weiss term and a short-ranged interaction term consistent with disorder-induced local moment models. Thus, it is shown that self-damage creates localized magnetic moments in previously nonmagnetic plutonium.
Keywords: disorder, magnetism, radiation damage
Among the interesting properties of plutonium is a complex phase diagram, which at ambient pressure exhibits six distinct solid-state phases below the melting temperature. These phases are narrowly spaced in energy, with the five lowest-energy phases separated by <2 mRyd, placing them on a molecular-energy scale as compared with the more typical 10–20 mRyd scale typical of metals such as neighboring Np and Am (1). Although there is no theoretical consensus as to the origin of the low-density fcc δ-phase of Pu (1–7), there is an understanding that the organization of the spin and orbital moments play a key role in stabilizing this phase. The lack of significant magnetic moments is a central issue among theorists and inspired a recent experimental review (8) painstakingly describing the evidence against the existence of magnetic moments in plutonium. Recent μSR+ studies for α- and δ-phase Pu further support this absence of magnetic moments, placing the upper bound on frozen moments at 0.001 Bohr magneton (μB) (9). However, all solid Pu phases possess large magnetic susceptibilities, suggesting they border on becoming magnetic. Consistent with this observation and general predictions of narrow 5f bands in plutonium are large electronic contributions to the specific heat in both α-Pu and alloy-stabilized δ-Pu, qualifying each as a highly correlated electron system (10).
Often, local magnetic moments can be induced in nearly magnetic systems by imposing a suitable perturbation. One such method is to increase disorder by introducing a low concentration of impurities via chemical substitution. For example, when very dilute quantities of Fe, Co, or Ni are doped into nonmagnetic Pd, they induce remarkably large magnetic moments by polarizing the surrounding lattice (11, 12). Similarly, one-half atomic percent (at. %) Pu doped into La depresses the superconducting Tc = 5.9 K by nearly 2 K, effectively acting like a magnetic impurity, whereas actinides such as U and Am reduce Tc by only 0.2 K (13). Surprisingly, the converse experiment: doping nonmagnetic impurities such as Zn or Li into the antiferromagnetic Cu–O planes of the high-temperature superconducting cuprates (HTSCs) also induces significant local moments (as large as 1 μB per impurity) on the neighboring Cu atoms (14, 15). Similarly, magnetic moments arise from point defects (vacancies in the copper-oxide planes) produced by electron irradiation of HTSCs, where the irradiation permits a systematic study of samples as a function of defect concentration (damage) (16). Plutonium-239, with a half-life of 24,110 years, radioactively decays by emission of a 5.04 MeV α-particle and corresponding 85.8 keV U recoil, which produce numerous defects in the underlying lattice. These defects primarily consist of vacancies (unoccupied lattice sites) and interstitials (displaced atoms that come to rest in a location between the normal lattice sites). The resulting self-damage increases the magnetic susceptibility in a manner indicative of local moments, which would not be all that surprising were the underlying plutonium magnetic. That these moments develop in a nonmagnetic system is quite remarkable and implies that this perturbation provides an observational window into the heretofore hidden nature of the 5f electrons, effectively driving them toward a more localized state.
One advantage of exploiting the radiation damage from nuclear decay is that by measuring the magnetic properties as a function of time it permits continuous observation of how the influence of damage evolves. However, the defects produced by the radioactive decay of 239Pu are more complex than the isolated vacancy and interstitial pairs (Frenkel pairs) created by an electron or proton beam. Molecular dynamics models indicate that the decay α-particle travels ≈10 μm in δ-Pu, losing most of its energy by scattering from electrons, but near the end of its range (the last 0.8 μm), it begins to scatter ballistically with atoms producing ≈265 vacancy and interstitial pairs. By contrast, the U recoil travels only ≈0.012 μm initiating a dense displacement cascade of ≈2,300 vacancies and interstitials, ≈70% of which are estimated to recombine (17) during the following tens of picoseconds as the lattice rapidly cools. Previous work (18–21) examined changes in resistivity and volume attributable to self-damage in plutonium. Recently, the temperature-dependence of the resistivity of vacancies and vacancy clusters Pu(Ga) was shown to exhibit a −ln(T) behavior, suggesting a defect-induced Kondo-like behavior (22), analogous to that seen in hole-doped superconductors subjected to electron irradiation (16). Here we report the discovery and characterization of time- and temperature-dependent magnetic susceptibility caused by accumulating damage in α-Pu and δ-Pu(4.3 at. % Ga) (hereafter denoted δ-Pu), which is fully reversible by thermal annealing.
Results
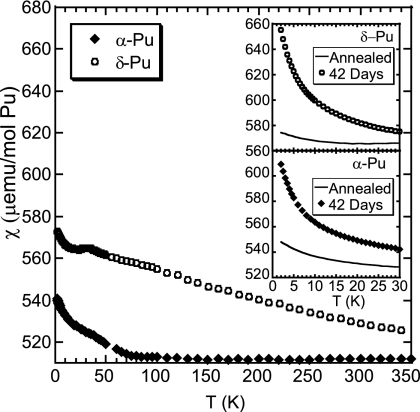
The magnetic susceptibility, defined as χ(T) = M/H, of freshly annealed (350 K for 1 h) α-Pu and δ-Pu specimens measured between 2 K < T < 350 K is shown in Fig. 1. By noting the scale of Fig. 1, it is evident that the dominant contribution to χ(T) in both specimens is the temperature-independent Pauli susceptibility, which is particularly clear in the case of α-Pu, where χ(T > 100) = 511 ± 1 μEMU/mol, consistent with other reported values (23). Lower temperatures reveal a Curie impurity tail contributing <5% to the overall signal, dominated by the 231-ppm Fe impurities present in the samples as a result of the manufacturing process. The temperature-dependence of the data below 40 K fit a Curie–Weiss law: χ(T) = C/(T − θ) where C, the Curie constant, is proportional to the square of the effective moment and θ, the paramagnetic Weiss temperature, provides a measure of the exchange energy. Such a fit results in an effective magnetic moment of 4.16 μB per Fe, somewhat less than the 5.92 μB per Fe (4.90 μB per Fe) expected were all of the Fe impurities effectively trivalent (divalent) with S = 5/2 (3/2) but not unreasonable as some fraction of the Fe has likely been subsumed into intermetallic Pu6Fe (24).
Fig. 1.
χ(T) for annealed α-Pu and stabilized δ-Pu(4.3 at. % Ga). The Curie tail in α-Pu is consistent with ≈200 ppm Fe impurities, whereas the gentle slope in δ-Pu may arise from small quantities of PuGax (2 ≤ x ≤ 3) second phases. (Inset) The low temperature χ(T) for annealed specimens and after aging the specimens for 42 days at or below 30 K.
The χ(T) for δ-Pu is more complex, although still dominated by a Pauli term, with the magnetic susceptibility increasing <10% when cooled from 350 K and from 2 K. There are several features in the χ(T) plot: a low-temperature Curie tail attributable to the same impurities observed in the α-Pu sample and a small peak at ≈33 K, likely attributable to second phases of PuGa3 and PuGa2 at the level of a few hundred ppm (25, 26). If these second phases rise to a concentration of order 0.1%, which could result from incomplete homogenization of the Ga, they would fully account for the gentle slope observed for T > 40 K. This slope also is consistent with previous observations of Ga-stabilized δ-Pu (27), which did not extend to sufficiently low temperatures to rule out second phases. Isothermal magnetization measurements to 5.5 T at 5 K on both specimens after annealing at 350 K for 1 h are strongly linear and thus support the interpretation of the Pauli term as the dominant contribution.
The magnetic susceptibility increases as a function of time, initially at the rate of several hundred ppm/h at 5 K for both specimens. When the specimen is maintained at low temperatures, the magnetic susceptibility continues to increase so that after a month the lowest temperature values have increased >10% above the magnetic susceptibility of the originally annealed specimen, as illustrated in Fig. 1 Inset. Here, χ(T < 30 K) is plotted for specimens aged 42 days at T ≤ 30 K along with the data of freshly annealed samples, demonstrating the strong temperature-dependence that develops as the sample accumulates damage at low temperatures.
Any study of radiation damage must carefully assess the relationship between the radioactively generated damage cascades and thermally activated annealing that tends to alter and eventually remove damage. There are two important temperatures to identify: (i) the temperature where significant annealing commences and (ii) the temperature at which the damage is completely annealed away apart from the radio-decay products, predominately U and He. Finally, some assessment of which point defects are most responsible for changes in the magnetic properties should be considered.
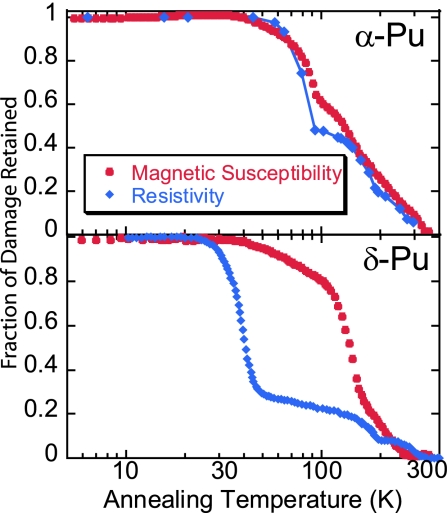
In the present work, damage is accumulated for several weeks at 5 K, after which the specimen is soaked for a fixed time (isochronal) at successively higher annealing temperatures (TAn), with each anneal followed by a measurement at 5 K. From this data, the resulting fraction of the excess magnetic susceptibility retained after each anneal, i.e., ƒχ = [χ(T = 5 K)∣TAn − χ(T = 5 K)∣T350 K], can be extracted. The ƒχ data then are normalized and plotted (red circles) as a function of TAn in Fig. 2 for both specimens. For comparison, Fig. 2 includes data from previously reported experiments (18, 22) that used resistance to study the annealing of accumulated damage (blue diamonds) on specimens with similar but not identical annealing protocols or compositions. It is noteworthy that the δ-Pu resistive annealing curve was obtained on a specimen with a different Ga concentration (3.3 at. % Ga) and after a significantly shorter damage-accumulation period (3 days) than the other data reported here. All four measurements consistently show a flat region below 30 K, indicating little or no annealing takes place up to this temperature; the defects are frozen in place. Above this temperature, the onset of annealing is indicated by the decrease in signal magnitude with signs of specific stages related to the activation energies for interstitials, vacancies, and their aggregates. Finally, the data provide an estimate of the temperature for complete annealing where vacancy clusters dissolve and the specimens are “reset” to an undamaged condition. This reset occurs at ≈315 K for α-Pu and ≈300 K for δ-Pu. Of course, decay products (U and He) accumulate and cannot be removed by this procedure, but their contribution to the overall magnetic susceptibility is below the threshold of detection in these experiments. By remaining at T < 30 K, the samples dope themselves with damage cascades proportional to time and can be effectively returned to a zero time state by annealing above room temperature.
Fig. 2.
Isochronal annealing curves for α-Pu and Ga-stabilized δ-Pu illustrating that damage is frozen in place below ≈30 K. The red circles are the magnetic susceptibility measurements from this work, and the blue diamonds are resistivity data taken from refs. 18 and 22.
On the whole, the magnetic susceptibility annealing shows evidence for distinct annealing stages similar to the resistive annealing, but a comparison of the two techniques provides additional insight. The situation for the α-Pu is qualitatively similar in annealing behavior over the entire temperature range of the annealing study for both techniques. However, for the δ-Pu, it appears that the large drop observed in the resistive annealing above 30 K is missing from the magnetic susceptibility annealing curve. This annealing stage is believed to be where interstitials begin to move and annihilate with nearby vacancies or become trapped near other local defects such as impurities. Instead, the most dramatic reduction in the magnetic susceptibility annealing curve is “deferred” until well above 100 K, which, based on the resistive annealing curve, approaches stages usually associated with vacancy interactions. These results suggest that interstitials do not contribute as significantly to the excess magnetic susceptibility in the δ-phase as do the vacancies, an idea that is reasonable considering the fcc delta phase(15.92 g/cm3) is significantly less dense than the monoclinic alpha phase (19.84 g/cm3). The idea that “spinless” vacancies may induce magnetic moments on the surrounding lattice also is consistent with the conclusions drawn from radiation damage and doping studies of HTSC compounds (16).
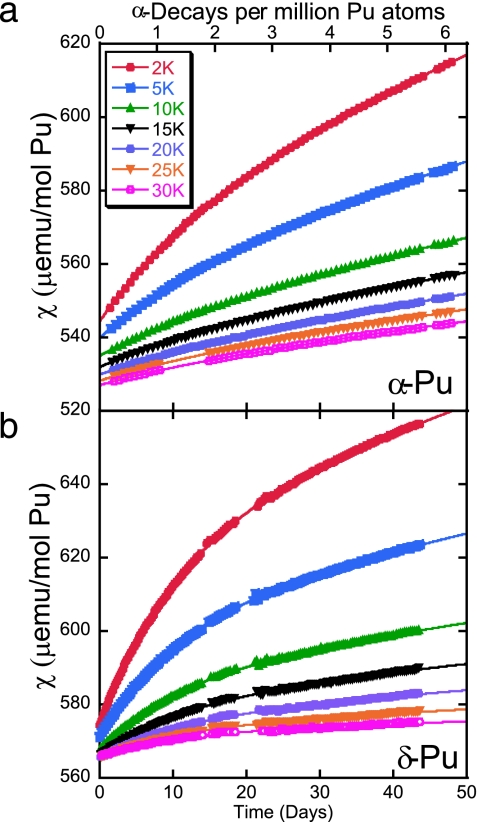
For each sample, the magnetic susceptibility was measured as the temperature was repeatedly cycled from 2 to 30 K for a period exceeding 40 days. Fig. 3 illustrates the time (damage)-dependence of the magnetic susceptibility for several representative isotherms. The points are actual data, and the lines are best fits to the following equation:
where χi(T) is the initial magnetic susceptibility of the annealed specimen. The later two terms describe the excess magnetic susceptibility arising from the self-damage and therefore explicitly depend on time and are zero when t = 0. The different time-dependences reflect two distinct contributions where the coefficients, χv(T) and χ′D(T), are free parameters for each isotherm with no assumed T-dependence. The prime on the coefficient in the third term, χ′D(T), emphasizes that the contribution to the magnetic susceptibility from this term is per unit time, i.e., μEMU/mol per day. Attempts to fit other probable models, such as a stretched exponential, led to coefficients that fluctuate strongly with temperature and thus fail to provide a self-consistent description of the data.
Fig. 3.
Representative isothermal magnetic susceptibilities for α-Pu and δ-Pu (4.3 at. % Ga) plotted as a function of time (number of α-decays). The lines are fits to Eq. 1 described in the text.
Discussion
Phenomenologically, the damage cascade generated by each α-decay may be considered to increase the magnetic susceptibility within an effective volume, δV of arbitrary shape and not necessarily simply connected. This effective volume must be at least as large as the damaged region, although there is no a priori reason it cannot be significantly larger, provided δV ≪ V, the sample volume. Thus, the overall fraction of the sample magnetically influenced by the first decay is given by δV/V. Assuming the susceptibility within δV is not further altered by subsequent and overlapping δVs, the expected volume fraction damaged by the second α-decay is just (δV/V)(1 − δV/V), where the second term is the fraction of the sample uninfluenced by the previous event. Similarly, for the nth event, the expected volume fraction influenced is
The total volume fraction of the sample magnetically influenced by damage after n events is simply the sum over all of the individual volumes, which after integration is (1 − exp[−n(δV/V)]). Recasting this as a function of time, t = n/λ, where λ is the α-decay rate of the specimen, and defining a characteristic time, τ, as: 1/τ = (δV/V)λ, then Eq. 2 becomes: (1 − e−t/τ). This is simply the time-dependence of the χv(T) term described in Eq. 1.
The 32 α-Pu isotherms are all described by a single characteristic time: τα = 15.8 ± 0.5 days, whereas τδ = 11.2 ± 0.3 days describes all 37 δ-Pu isotherms, subsets of which are plotted in Fig. 3. Converting these characteristic times to effective volumes per cascade yields 9,900 nm3 (≈500,000 atoms) for α-Pu and 13,600 nm3 (≈550,000 atoms) in the case of δ-Pu. Both quantities agree within 10% in terms of atoms influenced, despite the 40% longer characteristic time for the α-Pu sample. To put these numbers in context, consider that a recoiling U atom travels 12 nm in δ-Pu, which if treated as the diameter of a sphere encapsulating the recoil cascade, equates to 35,000 atoms, an order of magnitude smaller than suggested by Eq. 1. Of course, the origin of the larger effective volume may just reflect extended features such as strain fields or longer-ranged magnetic interactions not evident from molecular dynamics calculations.
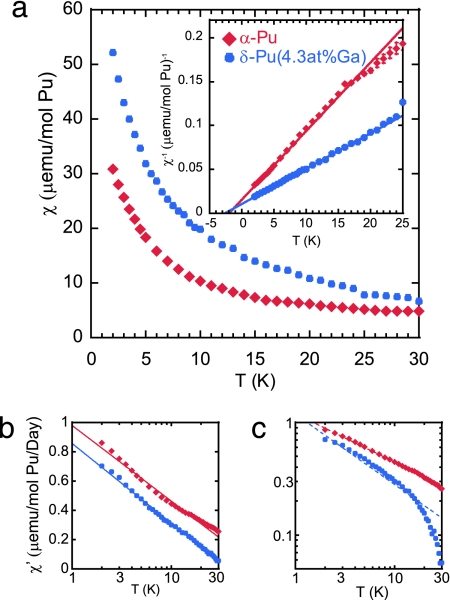
The fits of the data to Eq. 1 result in a systematic and monotonic temperature dependencies of the coefficients, χv(T) and χ′D(T), as illustrated in Fig. 4. The contribution from χv(T) is shown in Fig. 4a, whereas the Inset shows the inverse magnetic susceptibility as a function of temperature, demonstrating that it fits well to a Curie–Weiss law: χ(T) = C/(T − θ). The fit requires no temperature-independent term (i.e., χo in a modified Curie–Weiss fit), either positive or negative in value, indicating that there is no appreciable change in Pauli susceptibility because of the damage. Therefore, the conduction bands are not appreciably altered within the bubble regions. The Curie constant, C, obtained from the fit is 128 μEMU/mol·K for α-Pu (248 μEMU/mol·K for δ-Pu), equivalent to an average effective moment of 24.6 μB per α-particle decay in α-Pu (33.4 μB per α-particle decay in δ-Pu) or, by using the number of atom estimates obtained above, an average moment of 0.033 μB per α-Pu (0.045 μB per δ-Pu).
Fig. 4.
Temperature-dependence of self-damage contributions. (a) The contribution from χv. (Inset) A Curie–Weiss fit. (b and c) χ′D as semilog plot (b) emphasizing −ln(T)-dependence (solid lines) and as a log–log plot (c) showing power law fits (dashed lines).
This average moment is most probably concentrated in discrete clusters with larger magnetic moments scattered throughout the effective volume instead of a uniform moment evenly spread throughout the volume. In analogy with the defect-induced moments of the HTSCs, the cluster of Pu atoms surrounding a vacancy would possess a moment attributable to increased localization of the 5f electrons. The Curie–Weiss behavior observed in both the electron-irradiated and nonmagnetic Zn-doped HTSCs is caused by Kondo-like behavior of the Cu ions surrounding the impurity. Kondo systems have Curie–Weiss behavior at high temperatures and then below a characteristic energy scale set by TK (the Kondo temperature), the conduction electrons antiferromagnetically couple with the local moments to form a nonmagnetic ground state. Typically, the Kondo temperature is approximately one-quarter of the paramagnetic Weiss temperature, which is θP = −2.0 K for α-Pu (−2.8 K for δ-Pu) with the negative sign indicating antiferromagnetic correlations. So if damage is inducing Kondo behavior, TK is <1 K, and Curie–Weiss behavior is expected in the experimentally measured temperature range, whereas the comparable magnitude of θP for both allotropes implies little sensitivity to the details of the local crystal structure. This picture is consistent with the isochronal annealing data of δ-Pu, which show that the damage-induced magnetic susceptibility changes most rapidly when the vacancies become mobile. Of course, a Pu vacancy in the fcc δ-phase has 12 nearest neighbors, and the monoclinic α-phase has a comparable number,† whereas there are only 4 relevant nearest neighbors in the planar HTSCs, so each vacancy should influence more atoms in Pu. Furthermore, the self-damage cascades in Pu are more complicated than the isolated vacancies or Zn atoms of the HTSC materials.
These more complicated damage cascades may explain the χ′D(T)t term. Although linear in time, it likely represents the leading term of an exponential with a much longer characteristic time and thus a correspondingly smaller effective volume, thereby remaining in the dilute limit. Taken as short-ranged interactions, they will contribute appreciably only when multiple defects are in close proximity, such as are expected within the cascade resulting from the U recoil. Similarly, such dense concentrations of defects may be a second-order effect that begins to grow in regions of overlapping damage where the defect density surpasses a critical threshold. Fig. 4b shows the temperature-dependence of this term plotted on a semilog scale to emphasizes the fit of χ′D(T) ∝ −ln(T) and that α-Pu and δ-Pu have remarkably similar slopes of −0.224 μEMU/mol of Pu per day and −0.236 μEMU/mol of Pu per day respectively. This −ln(T) behavior is described by the Kondo disorder model, initially proposed by Bernal et al. (28) to explain UCu5−xPdx and later expanded theoretically by Miranda et al. (29, 30). Unlike the standard Kondo model, which assumes a dilute concentration of localized spins, here disorder creates a broad distribution of low-TK values that lead to a logarithmic temperature-dependence in the magnetic susceptibility and non-Fermi liquid behavior. The implication is that TK depends on the local density of defects, and the inherently random nature of the self-damage will naturally lead to a distribution of defect densities. Because TK depends on damage-induced disorder, the local symmetry of undamaged regions is not relevant, which is reflected in the consistent slopes for both allotropes.
A second model, also developed to describe UCu5−xPdx, has been presented by Castro Neto and coworkers (31, 32), where disorder drives a competition between the Kondo effect and the Ruderman–Kittel–Kasuya–Yosida (RKKY) interaction. In the RKKY interaction, the conduction electrons couple local moments together, either ferromagnetically or antiferromagnetically, depending on the distance between the moments. This model postulates a Griffiths phase (33), wherein clusters of local moments are magnetically coupled within a nonmagnetic background. Here, when defect-induced local moments are sufficiently close, they begin to couple together magnetically, leading to χ(T) ≈ T−1+λ and a prediction of non-Fermi liquid behavior. Over limited temperature ranges, a weak power law proportional to T−1+λ with λ ≈ 1 can be difficult to distinguish from logarithmic behavior. The lines of Fig. 4c show the result of least-squares fits to the data with λ = 0.57 (0.38) for α-Pu (δ-Pu). The fit is improved as compared with the −ln(T) fit for α-Pu but markedly worse in δ-Pu, so there is a clear distinction between the two allotropes in this interpretation.
It is worthwhile to make note of the relative magnitudes of the two time-dependent contributions: the χ′D(T) term is larger for α-Pu than for δ-Pu in contrast to the χv(T) term, where the δ-Pu contribution is larger. A relative contribution also shows that χ′D(T)t ≈ χv(T) after 25 days for α-Pu, but it takes nearly 70 days for δ-Pu. Because the Castro Neto model is built on a competition between the RKKY and Kondo energies, one possible explanation is that the RKKY interaction strength is so much weaker in δ-Pu as to not have significant influence. This is not an unreasonable assertion. Normally the RKKY interaction is long-ranged, but disorder weakens the interaction strength, making it decay exponentially with distance and thus become effectively short-ranged (31, 34). If the average distance between magnetically interacting defects for both α-Pu and δ-Pu is the same in units of atomic separations, then as δ-Pu is ≈20% less dense, this will correspond to a larger absolute distance and weaker coupling strength. Additionally, 1 of every 25 atoms in δ-Pu is a nonmagnetic Ga, further decreasing the RKKY interaction strength and simultaneously increasing the disorder inherent to the δ-Pu phase. Supplementary studies looking at the influence, if any, of Ga concentration will help clarify this issue.
These radiation damage-induced changes in the magnetic susceptibility suggest increased f-electron localization and, consequentially, reduced metallic bonding. It would not be surprising to see similar changes in other thermodynamic properties such as heat capacity and the lattice stiffness. Indeed, just such an effect has been reported by Migliori et al. (35), where a measurable lattice softening as a function of time (over ≈50 h) is observed between 50 and 150 K in δ-Pu(2.36 at. % Ga).
Conclusions
Perhaps the most remarkable conclusion drawn from these magnetic measurements is that the radiation damage induces clear evidence of localized magnetic moments in a system where none are observed in the pure state. Both α-Pu and δ-Pu have large Pauli susceptibilities indicative of narrow bands at the Fermi surface. A temperature-dependent magnetic susceptibility arises from self-damage at low temperatures without measurably distorting these conduction bands. Isochronal annealing experiments confirm that these increases are attributable to accumulating radiation damage and may be removed by thermal annealing. Analysis of the time-dependence of the damage-induced magnetic susceptibility leads to two distinct terms, with differing temperature dependencies. The dominant term at early times may be ascribed to a volume considerably larger than expected from models of the damage cascade alone, which fits well to a Curie–Weiss law and provides clear evidence of local moments. A second contribution proportional to the number of α-decays grows more slowly, showing indications of non-Fermi liquid behavior. This contribution can be fit to a −ln(T) temperature-dependence for both allotropes, suggesting a disordered Kondo model, whereas the α-Pu phase also is a candidate for the quantum Griffiths phase model. Both models arise from disorder-driven interactions coupling local moments with the conduction electrons, suggesting a complex interplay between the defects and electronic properties that provide insight into the fundamental nature of plutonium.
Experimental Details
Two specimens were prepared from an aliquot of Pu, which had been electro-refined 2 years before the experiments: α-Pu (99.98% pure) and δ-Pu (4.3 at. % Ga). Each was machined into 1 × 2 × 2 mm bars and then mechanically and chemically cleaned of oxide, yielding specimens of 56.8 mg and 45.4 mg, respectively. The isotopic composition for both specimens were similar, having been determined by inductively coupled plasma mass spectroscopy: 239Pu (93.7%), 240Pu (5.86%), and 238Pu (0.17%), whereas the magnetic impurities (in atomic ppm) were; Fe (231), Ni (24), Cr (12), and Mn (10). Specimens were coated with ≈5 μm polyimid to contain radioactive spall, sealed under helium in a 20-cm-long cartridge-brass tube and measured in a superconducting quantum interference device (SQUID) magnetometer (MPMS-5; Quantum Design, San Diego, CA). All measurements were made in a constant applied magnetic field of 3 T, for which the background contribution attributable to the tube was <1%, and, as most results reported here are differential measurements (i.e., changes in signal as a function of time), it self-cancels. The high thermal conductivity of the tube acts as a heat sink for the sample and ensures thermal stability. The maximum self-heating effect was measured as ≈0.05 K at 2 K. Repeated measurements at each temperature showed no trend indicative of a thermal lag between the system thermometer and the sample.
Acknowledgments
This work was performed under the auspices of the U.S. Department of Energy by the University of California Lawrence Livermore National Laboratory under Contract W-7405-Eng-48.
Abbreviations
- μB
Bohr magneton
- at. %
atomic percent
- HTSC
high-temperature superconducting cuprate
- RKKY
Ruderman–Kittel–Kasuya–Yosida.
Footnotes
The authors declare no conflict of interest.
The definition of nearest neighbor is less clear in a low-symmetry monoclinic structure that includes eight inequivalent lattice sites. Using the less-dense delta fcc interatomic distance as the limit for nearest neighbors results in 12 ± 1, depending on the lattice site considered.
References
- 1.Soderlind P, Sadigh B. Phys Rev Lett. 2004;92:185702. doi: 10.1103/PhysRevLett.92.185702. [DOI] [PubMed] [Google Scholar]
- 2.Soderlind P, Landa A, Sadigh B. Phys Rev B. 2002;66:205109. [Google Scholar]
- 3.Savrasov SY, Kotliar G. Phys Rev Lett. 2000;84:3670–3673. doi: 10.1103/PhysRevLett.84.3670. [DOI] [PubMed] [Google Scholar]
- 4.Savrasov SY, Kotliar G, Abrahams E. Nature. 2001;410:793–795. doi: 10.1038/35071035. [DOI] [PubMed] [Google Scholar]
- 5.Bouchet J, Siberchicot B, Jollet F, Pasturel A. J Phys Condens Matter. 2000;12:1723–1733. [Google Scholar]
- 6.Shorikov AO, Lukoyanov AV, Korotin MA, Anisimov VI. Phys Rev B. 2005;72 024458. [Google Scholar]
- 7.Shick AB, Drchal V, Havela L. Europhys Lett. 2005;69:588–594. [Google Scholar]
- 8.Lashley JC, Lawson A, McQueeney RJ, Lander GH. Phys Rev B. 2005;72 054416. [Google Scholar]
- 9.Heffner RH, Morris GD, Fluss MJ, Chung B, McCall S, MacLaughlin DE, Shu L, Ohishi K, Bauer ED, Sarrao JL, et al. Phys Rev B. 2006;73 094453. [Google Scholar]
- 10.Lashley JC, Singleton J, Migliori A, Betts JB, Fisher RA, Smith JL, McQueeney RJ. Phys Rev Lett. 2003;91:205901. doi: 10.1103/PhysRevLett.91.205901. [DOI] [PubMed] [Google Scholar]
- 11.Clogston AM, Matthias BT, Peter M, Williams HJ, Corenzwit E, Sherwood RC. Phys Rev. 1962;125:541–552. [Google Scholar]
- 12.Bozorth RM, Wolff PA, Davis DD, Compton VB, Wernick JH. Phys Rev. 1961;122:1157–1160. [Google Scholar]
- 13.Hill HH, Lindsay JDG, White RW, Asprey LB, Struebing VO, Matthias BT. Physica. 1971;55:615–621. [Google Scholar]
- 14.Mendels P, Bobroff J, Collin G, Alloul H, Gabay M, Marucco JF, Blanchard N, Grenier B. Europhys Lett. 1999;46:678–684. [Google Scholar]
- 15.Bobroff J, MacFarlane WA, Alloul H, Mendels P, Blanchard N, Collin G, Marucco JF. Phys Rev Lett. 1999;83:4381–4384. doi: 10.1103/PhysRevLett.86.4116. [DOI] [PubMed] [Google Scholar]
- 16.Rullier-Albenque F, Alloul H, Tourbot R. Phys Rev Lett. 2003;91 doi: 10.1103/PhysRevLett.91.047001. 047001. [DOI] [PubMed] [Google Scholar]
- 17.Diaz de la Rubia T, Caturla MJ, Alonso E, Fluss MJ, Perlado JM. J Comput Aided Mol Des. 1998;5:243–264. [Google Scholar]
- 18.Wigley DA. Proc R Soc London A. 1965;284:344–353. [Google Scholar]
- 19.Lee JA, Mendelssohn K, Wigley DA. Phys Lett A. 1962;1:325–327. [Google Scholar]
- 20.Mortimer MJ, Marples JAC, Lee JA. Int Met Rev. 1975;20:109–120. [Google Scholar]
- 21.Elliott RO, Olsen CE, Vineyard GH. Acta Metal. 1963;11:1129–1138. [Google Scholar]
- 22.Fluss MJ, Wirth BD, Wall M, Felter TE, Caturla MJ, Kubota A, de la Rubia TD. J Alloy Compd. 2004;368:62–74. [Google Scholar]
- 23.Fournier J-M, Troc R. In: Handbook on the Physics and Chemistry of the Actinides. Freeman AJ, Lander GH, editors. Vol 2. New York: North-Holland; 1985. [Google Scholar]
- 24.Moore KT, Wall MA, Schwartz AJ. J Nucl Mater. 2002;306:213–217. [Google Scholar]
- 25.Boulet P, Colineau E, Wastin F, Javorsky P, Griveau JC, Rebizant J, Stewart GR, Bauer ED. Phys Rev B. 2005;72:64438. doi: 10.1103/PhysRevLett.93.147005. [DOI] [PubMed] [Google Scholar]
- 26.Boulet P, Colineau E, Javorsky P, Wastin F, Rebizant J. J Alloy Compd. 2005;394:93–95. [Google Scholar]
- 27.Meot-Reymond S, Fournier JM. J Alloy Compd. 1996;232:119–125. [Google Scholar]
- 28.Bernal OO, MacLaughlin DE, Lukefahr HG, Andraka B. Phys Rev Lett. 1995;75:2023–2027. doi: 10.1103/PhysRevLett.75.2023. [DOI] [PubMed] [Google Scholar]
- 29.Miranda E, Dobrosavljevic V, Kotliar G. Phys Rev Lett. 1997;78:290–293. [Google Scholar]
- 30.Miranda E, Dobrosavljevic V, Kotliar G. J Phys Condens Matter. 1996;8:9871–9900. [Google Scholar]
- 31.Castro Neto AH, Castilla G, Jones BA. Phys Rev Lett. 1998;81:3531–3534. [Google Scholar]
- 32.Castro Neto AH, Jones BA. Phys Rev B. 2000;62:14975–15011. [Google Scholar]
- 33.Griffiths RB. Phys Rev Lett. 1969;23:17–19. [Google Scholar]
- 34.Jagannathan A, Abrahams E, Stephen MJ. Phys Rev B. 1988;37:436–441. doi: 10.1103/physrevb.37.436. [DOI] [PubMed] [Google Scholar]
- 35.Migliori A, Ledbetter H, Lawson AC, Ramirez AP, Miller DA, Betts JB, Ramos M, Lashley JC. Phys Rev B. 2006;73 052101. [Google Scholar]