Feasibility of cooling the Earth with a cloud of small spacecraft near the inner Lagrange point (L1)

Abstract

If it were to become apparent that dangerous changes in global climate were inevitable, despite greenhouse gas controls, active methods to cool the Earth on an emergency basis might be desirable. The concept considered here is to block 1.8% of the solar flux with a space sunshade orbited near the inner Lagrange point (L1), in-line between the Earth and sun. Following the work of J. Early [Early, JT (1989) J Br Interplanet Soc 42:567–569], transparent material would be used to deflect the sunlight, rather than to absorb it, to minimize the shift in balance out from L1 caused by radiation pressure. Three advances aimed at practical implementation are presented. First is an optical design for a very thin refractive screen with low reflectivity, leading to a total sunshade mass of ≈20 million tons. Second is a concept aimed at reducing transportation cost to $50/kg by using electromagnetic acceleration to escape Earth's gravity, followed by ion propulsion. Third is an implementation of the sunshade as a cloud of many spacecraft, autonomously stabilized by modulating solar radiation pressure. These meter-sized “flyers” would be assembled completely before launch, avoiding any need for construction or unfolding in space. They would weigh a gram each, be launched in stacks of 800,000, and remain for a projected lifetime of 50 years within a 100,000-km-long cloud. The concept builds on existing technologies. It seems feasible that it could be developed and deployed in ≈25 years at a cost of a few trillion dollars, <0.5% of world gross domestic product (GDP) over that time.

Projections by the Intergovernmental Panel on Climate Change are for global temperature to rise between 1.5 and 4.5°C by 2100 (1), but recent studies suggest a larger range of uncertainty. Increases as high as 11°C might be possible given CO₂ stabilizing at twice preindustrial content (2). Holding to even this level of CO₂ will require major use of alternative energy sources and improvements in efficiency (3). Unfortunately, global warming reasonably could be expected to take the form of abrupt and unpredictable changes, rather than a gradual increase (4). If it were to become apparent over the next decade or two that disastrous climate change driven by warming was in fact likely or even in progress, then a method to reduce the sun's heat input would become an emergency priority. A 1.8% reduction is projected to fully reverse the warming effect of a doubling of CO₂ (5), although not the chemical effects.

One way known to reduce heat input, observed after volcanic eruptions, is to increase aerosol scattering in the stratosphere (6). Deployment of 3 to 5 million tons/year of sulfur would be needed to mitigate a doubling of CO₂. This amount is not incompatible with a major reduction in the current atmospheric sulfur pollution of 55 million tons/year that goes mostly into the troposphere. The approach we examine here to reduce solar warming is to scatter away sunlight in space before it enters the Earth's atmosphere. The preferred location is near the Earth–sun inner Lagrange point (L1) in an orbit with the same 1-year period as the Earth, in-line with the sun at a distance ≥1.5 million km (Gm) (Fig. 1). From this distance, the penumbra shadow covers and thus cools the entire planet.

Fig. 1.

Shadowing geometry. (Left) Schematic. The L1 point and the common Earth–moon barycenter remain in-line as they both orbit the sun with a 1-year period (not to scale). (Right) Time-averaged view from Earth. The Earth wobbles with a 1-month period relative to the penumbral shadows cast from a sunshade at 1.5 and 2.4 Gm (dashed circles).

A major technical hurdle to be overcome is the instability of the orbit, which is at a saddle point. A cloud of scattering particles introduced there would dissipate in a few months. But a cloud of spacecraft holding their orbits by active station-keeping could have a lifetime of many decades. Stabilizing forces could be obtained by modulating solar radiation pressure, with no need for expendable propellants. The same controls could be used, if desired, to stop the cooling at any time by displacing the orbit slightly. In addition to longevity, space shading has the advantages that the composition of the atmosphere and ocean would not be altered further, beyond their loading with greenhouse gases, and because only a single parameter is modified, the flux of solar radiation, the results should be predictable.

Because of its enormous area and the mass required, shading from space has in the past been regarded as requiring manufacture in space from lunar or asteroid material and, thus, as rather futuristic. Here we explore quantitatively an approach aimed at a relatively near-term solution in which the sunshade would be manufactured completely and launched from Earth, and it would take the form of many small autonomous spacecraft (“flyers”).

Shading Efficiency and Radiation Pressure

Early (7) recognized that the orbit of a lightweight sunshade would be disturbed by radiation pressure. With the balance point moved farther away from L1 toward the sun, the area would need to be increased for a given flux reduction. This effect can be characterized by the blocking efficiency ε, defined as the fraction of the light blocked by a spacecraft that otherwise would have illuminated the Earth. It depends on the Earth's motion within the Earth–moon system as well as the orbital distance. Although the barycenter of the combined system and the L1 point sweep around the sun with uniform angular speed, the Earth's wobble in reaction to the moon can carry it partly out of the penumbral shadow (Fig. 1 Right). The average efficiency taken over a month, allowing for solar limb darkening, is plotted as a function of distance in Fig. 2a. ε = 68% for L1 at distance 1.5 Gm, and it drops to 25% at 3 Gm. To reduce the solar flux by a fraction f, the total area A of sunlight that must be blocked by the spacecraft at given distance is given by A = fπR_E²/ε, where R_E is the Earth's radius. The sunshade area for our goal of f = 0.018 varies from 3.4 million km² at 1.5 Gm distance to 9.4 million km² at 3 Gm (Fig. 2a). The total mass of the sunshade is given by M = Aρ_s, where ρ_s is its average areal density. It is shown as a function of equilibrium orbital radius in Fig. 2b for densities from 2.5 to 40 g/m².

Fig. 2.

Sunshade properties for 1.8% flux reduction. (a) Shadowing efficiency and total area. (b) Total mass for different reflectivities R and areal densities ρ_s in g/m².

The equilibrium orbital radius depends on the strength of radiation pressure. It is convenient to define the effective reflectivity R as the ratio of the pressure experienced by the sunshade to the maximum possible for 100% specular reflection at normal incidence. For orbits with the same 1-year period as the Earth, the balance between gravity and radiation pressure is then given by:

Here, r is the orbital radius from the sun, ω_E and r_E are the angular frequency and radius of the Earth's orbit, M_S and L_S are the mass and luminosity of the sun, and M_E is the Earth's mass. The equilibrium orbital radius depends on the ratio R/ρ_s, and Eq. 1 allows the determination of ρ_s (and hence total sunshade mass) as a function of R and orbital distance r_E–r. Fig. 2b shows results for f = 0.018, with reflectivities R from 3.2% to 100%. The figure can be used to determine any two of the quantities M, r–r_E, R, and ρ_s, given the other two.

In general, the total mass is reduced for sunshades with low areal density, but very low densities can be orbited near the L1 point only if they have very low reflectivity to minimize radiation pressure. For sunshades with density ≤40 g/m², for any given reflectivity, the total mass is minimized at a distance of ≈2.5 Gm. Thus, for a high reflectivity (R ∼ 1), the density required at this distance is 40 g/m² and the mass is ≈270 million tons, marked “McInnes (1)” in Fig. 2b. Such a sunshade might be manufactured in space from an iron asteroid, which would have to be formed into ≈10-μm-thick foil (8). An opaque sunshade could be built with lower mass if its reflectivity were reduced by applying coatings that absorb light energy on the sunward side and reemit it as heat mostly on the Earthward side (8). Reflectivity as low as R = 0.3 might be achievable, given a sun-side coating with 90% solar absorption and 10% emissivity. The corresponding minimum mass at 2.5 Gm would be 80 million tons, marked “McInnes (2)” in Fig. 2b.

Further reduction of the overall mass will be crucially important for a sunshade that could be launched relatively soon from Earth. To achieve the required lower reflectivities, a transparent screen is needed that deflects the transmitted sunlight by a couple of degrees, enough to miss the Earth but not enough to transfer significant radiation pressure. Early (6) envisaged a 10-μm-thick glass Fresnel screen with dielectric reflectivity R = 8% and areal density 25 g/m². Together with 5 g/m² of supporting structure, ρ_s ≈ 30 g/m². The equilibrium distance is then 1.58 Gm, and for f = 1.8% the required area is 3.6 million km². But, still, the mass is high at 100 million tons (marked “Early” in Fig. 2b).

A more efficient optical design is needed to deflect the light with a screen of lower areal density. For example, Fig. 2 shows that a sunshade with R = 10% and ρ_s = 5.6 g/m² could be orbited at 2.25 Gm distance, where it would need area 5 million km² and would weigh 27 million tons. A still lower mass of 11 million tons could be achieved with R = 3.2% and ρ_s = 2.5 g/m². The next section explores the physical lower limits of density and reflectivity for refractive screens.

Optical Design to Minimize Mass and Reflectivity

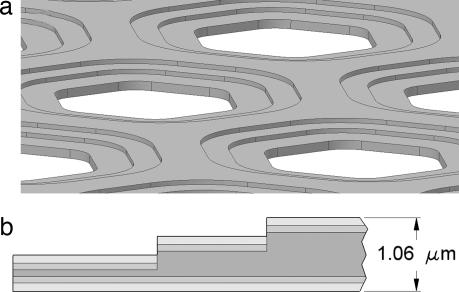
The lightest refracting screen that can significantly reduce on-axis transmission is a very thin transparent film pierced with small holes making up half the total area. The thickness is chosen such that transmitted light at the peak wavelength λ_p of sunlight is retarded by half a wave. Destructive interference then takes place for the directly transmitted beam at λ_p, with the energy deflected into diffraction peaks at angle θ = λ_p/2s, where s is the separation of the holes. Because from near L1 both the sun and Earth subtend 0.01 radians, θ ≥ 0.02. s thus must be ≤15 μm to diffract away light at λ_p = 0.6 μm. The axial component of radiation pressure for the transmitted light is reduced by a factor ≈θ² and is thus negligible.

Such a simple screen is not ideal, because the on-axis transmission rises to 30% when averaged over the full solar spectrum. A screen with reduced transmission over a broad spectral band may be constructed at the expense of increased areal density by introducing steps in the film thickness. In general, if there are m_l thickness levels of the same area (including one of zero thickness), with steps in optical depth of λ/m_l, the on-axis transmission is given by

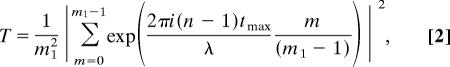where t_max is the maximum thickness and n is the refractive index. Fig. 3a and b shows a design for a four-level screen (m_l = 4) that yields on-axis transmission 〈T〉 = 10%, averaged over the solar spectrum.

Fig. 3.

Refractive screen. (a) Detail with holes are on 15-μm centers. (b) Detail of the antireflection coating, drawn to scale. The silicon nitride core with n = 2 shown in darker gray has thickness of 97,367 and 637 nm. The inner coating has index 1.587 and thickness 94 nm (medium gray), and the outer index is 1.26 and thickness 119 nm (light gray).

The thickness of screens of this type is proportional to (n − 1)⁻¹ and is thus minimized by use of a high-index material. On the other hand, reflectivity of an uncoated surface increases strongly with index, as (n − 1)²/(n + 1)². Thus a high-index, low-density material will be advantageous only if used with a thin, broad-band antireflection coating. This can be realized in a two-layer coating with the indices and thicknesses chosen so that the three reflections from the different interfaces have the same amplitude but interfere destructively at two wavelengths, one where the successive phase differences are at 120° and the other the half-wavelength where the phases are at ≈240°. An example of such a design, applied to the screen of Fig. 3a, is shown in Fig. 3b. The design is for a film of silicon nitride, chosen because it will not deteriorate in many decades of solar exposure and also is commonly manufactured in freestanding films <1-μm-thick. It has high index (2.0) and low density (3,100 kg/m³ in film form) and is also very stiff. The step-thicknesses of the silicon nitride shown in Fig. 3b were adjusted to allow for the path length increase of the coatings. The result is R = 2.62% and an average areal density ρ_s = 1.4 g/m². This film is adopted as the baseline design for the remainder of this article.

An ideal sunshade with the above reflectivity and density would orbit at 2.2 Gm and, for 1.8% flux reduction, would require area 6 million km² and would weigh ≈7 million tons (marked “screen material alone” in Fig. 2b). A practical sunshade will be heavier when structural and control elements are included. These additions are estimated to triple the average density of the complete flyer, to ρ_s = 4.2 g/m², based on the discussion below. The reflectivity also will be higher. Our baseline design adds 0.9% for opaque structural elements and 1 ± 1% for reflecting control elements, for a total R = 4.5 ± 1%. With these parameters, the orbit would be 1.85 Gm from Earth. At this distance, the blocking efficiency ε is 54%, the total sunshade area, increased by 10% from Fig. 2a to allow for the on-axis screen transmission, is 4.7 × 10⁶ km², and the mass is 20 million tons total (marked “Baseline Design” in Fig. 2b).

From the Earth to L1

Is it at all realistic to transport a total payload mass of 20 million tons from Earth? If, for the sake of argument, we allow $1 trillion for the task, a transportation cost of $50/kg of payload would be needed. The present cost for multistage rocket transportation to high orbit is ≈$20,000/kg. For very high volume, it is reasonable to suppose that the cost might brought to a level approaching fuel cost, not unlike car and airline transportation. Thus, the cost to low-Earth orbit for a two-stage system using kerosene/liquid oxygen fuel might approach $100/kg (9), with additional costs to get to L1. Here, we explore the potential for still lower costs by using electromagnetic launch followed by ion propulsion.

In electromagnetic launch, the payload is driven by a current-carrying armature in a magnetic field. From the analysis below, it seems that there is no fundamental reason why launch from Earth by linear acceleration to escape velocity of 11.2 km/sec should not be possible, even allowing for atmospheric slowing and heating. Once the launch vehicle is clear of Earth's gravity, additional propulsion will be necessary to reach L1. If auxiliary rockets were used, the potential for large savings from the initial electromagnetic launch could not be fully realized. But ion propulsion is an ideally suited, low-cost alternative that adds only a small additional mass to the vehicle and is now space-proven by the SMART1 spacecraft to the moon.^†

The potential for very low transportation cost can be seen by consideration of launch energy cost. Kinetic energy at escape velocity is 63 MJ/kg = 17 kW·hr/kg (1 kW·hr = 3.6 ×10⁶ J). Taking into account the mass of the armature and the ion-propulsion fuel, and the loss in conversion from electrical to kinetic energy, the energy for launch (as shown below) will be ≈10 times this final payload energy. At the current cost to industry of 5.3¢/kW·hr, the launch energy cost would be $9 per kg of payload. The additional major cost for energy storage is likely to be comparable, thus the $50/kg target for transportation is not unrealistic.

Atmospheric Drag and Heating.

On exiting the evacuated launch tube, the launch vehicle will be subject for about a second to strong drag and heating as it transits the atmosphere. Equating the loss of momentum of the vehicle to that gained by the displaced air, Δv/v = pδ/ρ_Vg, where p is the atmospheric pressure, δ the drag coefficient, ρ_V the areal mass density of the vehicle, and v its velocity. Based on experience with space reentry vehicles designed for minimum drag, δ = 0.1 should be realizable. To minimize the energy loss, the launch would be vertical from a high site. A realistic goal would be an atmospheric entry point at 5.5 km elevation (18,000 feet) where p = 50 kPa, half that at sea level. Setting as a goal Δv/v = 1/8, an initial velocity of 12.8 km/sec would be needed for escape velocity of 11.2 km/sec above the atmosphere, and the vehicle will need an areal density ρ_V = 4 tons/m².

The drag results in loss of 25% of the initial kinetic energy. Most will go into moving and heating the displaced air, but some will heat the vehicle itself. To prevent damage, an ablative shield must be used, as for space vehicles designed for atmospheric reentry. Based on past experience, it would seem that such a shield could be designed to weigh only a small fraction of the total vehicle mass. Measurements of a test vehicle with a low-drag (δ = 0.06) carbon nosecone entering the Earth's atmosphere at 6 km/sec showed an ablative loss of ≈0.1 kg, for a mass-loss to energy-loss ratio of 0.14 kg/GJ (10). A similar ratio of 0.25 kg/GJ was measured for the Galileo probe, which entered Jupiter's atmosphere at 47 km/sec and was brought to rest by a carbon ablation shield designed for high drag (11). In our case, a 4 ton/m² vehicle losing 77 GJ/m² would suffer an ablation loss of 20 kg/m², if the loss rate were 0.25 kg/GJ. Even if the rate were twice as much, and the ablator including safety factor weighed 100 kg/m², it would still make up only 2.5% of the vehicle total of 4,000 kg/m². Based on the above considerations, it seems reasonable to suppose that atmospheric drag should not prevent Earth launch, but clearly modeling with codes such as those used for the Galileo heat shield needs to be undertaken. A full-scale test at 12.8 km/sec could be made with a rocket-propelled reentry vehicle (10).

Electromagnetic Launch to 12.8 km/sec.

Two types of electromagnetic launchers, rail and coil, have been studied over the years. In the rail type, the current in the armature is delivered by rails with sliding contact, and the driving magnetic field perpendicular to the armature current provided by a combination of the rail current and external coils. Laboratory experiments with rail systems have demonstrated acceleration of projectiles of a few grams to ≈8 km/sec and ≈1 kg to 2–3 km/sec (12). In the coil type, the armature is a cylinder with no contact, carrying a ring current maintained by magnetic induction. The magnetic field is provided by a long solenoid comprised of many short coils that are energized successively in synchronization with the armature accelerating along the axis. A 30-coil test system has been used in the laboratory to accelerate a 240-g armature to 1 km/sec with a comoving field of 30 T (13). The average accelerating pressure measured at 150 MPa reached nearly half the theoretical limit of B²/2μ₀. For comparison, the same pressure applied to a 1-m-diameter armature would yield a thrust of 10⁸ N, four times that of the Saturn V first stage.

Designs to harness such prodigious magnetic force to deliver payloads into orbit have been worked out for both launcher types but have never been attempted. The reasons are high up-front costs, the restriction to payloads able to survive very high acceleration, and the difficulty of launch into low-Earth orbits. Such orbits can be reached only by launch at low elevation angle, which incurs substantial aerodynamic drag, and with the addition of a supplemental rocket. However, these difficulties do not apply in our case, where a high volume is to be carried to very high orbit, and there is the possibility of ruggedizing the simple payloads to withstand high g force. The coil type is the better choice to survive a very large number of launches, given active control to prevent mechanical contact during launch. (Rail launchers inevitably suffer wear from the electrical connection required between the armature and rails.)

Previous designs for 6 km/sec coil-type space-launchers can serve as a starting point for a higher-velocity system. Table 1 gives the characteristics of two published designs, the first by Marder (14), based on simplified analytical expressions, and the second, fully optimized with a design code, by Lipinski et al. (15). Both envisage use fields of ≈24 T, similar track lengths of <1 km, and similar energy input of ≈65 GJ. The main difference is that Marder's design assumes as an input a conservative electrical to mechanical efficiency of 30%, whereas the Lipinski design finds a higher efficiency of 50% for the optimized configuration. Thus, the latter design can drive a substantially heavier launch vehicle (1,820 vs. 1,000 kg) for the same energy.

Table 1.

electromagnetic launcher designs

Launcher design	Marder (analytic)	Lipinski (code)	High-velocity concept
Launch velocity v, km/sec	6	6	12.8
Track length s, m	720	960	2,000
Average acceleration, g force	2,300	2,000	4,200
Launch time t, sec	0.24	0.38	0.31
Vehicle mass, kg	1,000	1,820	3,100
Vehicle diameter, m	0.76	0.72	1
Vehicle density ρV, kg/m2	2,200	4,470	4,000
Field strength B, tesla	25	22.4	35
Armature mass, kg	—	600	1,000
Efficiency	0.30	0.50	0.4
Stored energy, GJ	60	65	635

To reach higher velocity v, the pressure on the armature must be increased, as v²ρ_V/s, where ρ_V is the vehicle mass density and s is the length of the launch track. For systems of similar geometry and the same ratio of achieved to magnetic pressure B²/2μ₀, the field thus must be increased as v√(ρ_V/s). To reach the desired 12.8 km/sec with acceptable field strength, a track length s = 2,000 m is baselined. Then, scaling from the optimized Lipinski design a field of 32 T is required for the targeted vehicle density of 4,000 kg/m². Marder's analysis gives the same field if an energy efficiency of 45% is assumed.

An important issue for the higher-velocity launcher is to control Joule heating of the armature. During the launch interval t, the temperature must not get high enough to cause the armature to yield under the high-magnetic-field pressure. The characteristic length for the depth of the eddy current and field penetration is the skin depth δ ∼ √(ηt/μ₀), where η is the armature resistivity (16). Both the 6- and 13-km/sec designs envisage use of aluminum armatures and have the same t ≈ 0.35 sec. The skin depth δ ≈ 0.1 m is thus the same and is less than the armature diameter d. In this circumstance, the eddy current density will increase in proportion to the field strength and thus the temperature will rise as B², a factor of 1.8 for the high-velocity launcher. This increase should be acceptable provided that the initial field rise is moderated to avoid high surface heating. Conductivity may be improved if necessary by precooling the armature with liquid nitrogen and possibly by incorporation of carbon nanotubes, if this is not too expensive. Computer models and subscale tests clearly are needed.

Ion Propulsion.

Going from a highly eccentric orbit with 2-month period and 1.5 Gm apogee to L1 requires changes in velocity totaling ≈1 km/sec. Given also some margin to correct for errors in launch velocity, a total of Δv = 2 km/sec is wanted. The propulsion force of ≈0.2 N available from ion propulsion will be sufficient, when applied over a few months. The mass of fuel needed is relatively low, because of its high ejection velocity, ≥20 km/sec. Thus, the Dawn spacecraft to the asteroids will carry 30% of its mass in xenon fuel to obtain a total Δv of 11 k/sec.^‡ For our task, a mass of ≈5% of the launch vehicle should be sufficient. Argon, which might be stored by adsorption in carbon, would be preferred to xenon to remove fuel as a significant factor in the transportation cost.

The Sunshade as a Cloud of Autonomous Spacecraft

Previous L1 concepts have envisaged very large space structures. The alternative described here has many free-flyers located randomly within a cloud elongated along the L1 axis. The cloud cross-section would be comparable to the size of the Earth and its length much greater, ≈100,000 km. This arrangement has many advantages. It would use small flyers in very large numbers, eliminating completely the need for on-orbit assembly or an unfolding mechanism. The requirements for station-keeping are reduced by removing the need for the flyers to be regularly arrayed or to transmit any signals.

The cross-sectional area of the cloud with random placement must be several times larger than the area of sunlight to be blocked, or the individual flyers will shadow one another and lose efficiency. On the other hand, if they are spread out too far off the axis, their penumbral shadows will move off the Earth. For randomly distributed flyers with the design parameters established above, namely a residual on-axis transmission of 10% and 1.85 Gm of distance, the optimum cloud cross-section size is a 6,200 × 7,200-km ellipse. For this choice, the average off-axis shadowing efficiency is 51% (compared with 54% on-axis), and the loss from shadows overlapping is 6.5% (Fig. 4a). These two losses combined result in a 13% reduction in blocking, compared with the maximum achievable for the same number of elements in a tightly controlled, close-packed array, which would have a 7.6 times smaller cross-sectional area. The additional flyers needed to make up for the losses of the random configuration result in an increase in the total mass from 20 to 23 million tons, given the same areal density. In reality, the mass penalty may be smaller or even negative because small flyers will require lighter structural supports and simpler controls for station keeping.

Fig. 4.

Flyer configuration. (a) Projection of the full depth of the flyer cloud onto a plane transverse to the L1 axis (detail covering 5 × 15 m). The areal density shown is for the optimized case with flyers randomly distributed over 7.6 times their total area, resulting in 6.5% shadowing from overlaps. (b) A single 0.6-m-diameter flyer with the thin refracting disc faceted to improve stiffness. The three 100-μm-thick tabs have 2% of the disc area and contain the MEMS solar sails, tracker cameras, control electronics, and solar cells.

Position and Momentum Control.

The key requirements for autonomous control are to hold within the cloud envelope, to move slowly, and to keep facing the sun. The position must be actively controlled to prevent axial instability, which if left uncorrected will result in exponential increase in velocity with an e-folding time of 22 days. There is an independent need to control velocity, to minimize the chance of collisions between the randomly moving flyers, which even at low speed could set them spinning out of control. Control to ≤1 cm/sec, for example, will keep the collision probability to 10% per century per flyer.

To provide position and velocity information, special spacecraft with radio beacons in a global positioning system (GPS)-like system will be scattered through the cloud. Each flyer will incorporate a radio receiver to sense its velocity and position. In addition, it will carry two small tracker cameras mounted back-to-back to track the sun, Earth, and moon, to determine orientation.

Control of lateral and rotational motion will be accomplished by varying the radiation pressure on each flyer, with mirrors covering 2% of the flyer area and tiltable about an axis pointing to the flyer center. In the normal equilibrium configuration, half the mirrors would be turned so as to let the sunlight pass by and half would be set close to normal incidence to reflect back the sunlight. By appropriate rotations of the different mirrors, the lateral and angular acceleration in all six degrees of freedom can be set independently. From Eq. 1, the ±1% change in overall reflectivity of the flyers allows control of axial position to ±70,000 km and a maximum lateral acceleration (without changing the axial force) of ±5.10⁻⁶ m/sec². Thus, flyers can easily be held within the elliptical envelope, requiring an outward acceleration of ≈8 × 10⁻⁷ m/sec² 5,000 km off the axis. Shadowing could be stopped temporarily if desired by placing the flyers into halo orbits about the L1 axis.

Flyer Size and Design for Launch at High Acceleration.

The preferred option is to eliminate completely construction, assembly, or unfurling in space by having rigid flyers completely fabricated on Earth and launched in stacks. A mechanism built into the launch vehicle would be used to deal the flyers off the stack, a steady process that could take around a year. This approach avoids any requirement for space rendezvous or infrastructure of any sort, except for the local beacon system.

Although aerodynamic considerations constrain the vehicle mass density to be ≥4,000 kg/m², they do not favor a specific diameter. However, several factors argue for keeping the flyers small. To survive the high acceleration of launch, the smaller the flyers are, the less overhead will be needed for structural elements, and the easier it will be to make the sail-tilting mechanisms and to achieve high stacking density. A lower limit will be set ultimately by how small the control sensors and computer can be made, but a mass of no more than 0.1 g total seems reasonable. Based on these arguments, a flyer size of <1 m is adopted, to fit in a launch vehicle diameter of 1 m with cross-sectional area of 0.78 m² and total mass of 3,100 kg.

As a specific example, consider flyers with optical screens 0.6 m in diameter. The solar sails adding 2% to the flyer area would be housed in three control ears sticking out 0.1 m, as shown in Fig. 4b. At an average areal density of 4.2 g/m², each unit will weigh 1.2 g. The 1.4-μm-thick refractive film weighing itself 0.4 g would be supported by a 3.6-μm-thick, chicken-wire-like web of hexagonal cells, for a total thickness of 5 μm. The ears will be 100-μm-thick to accommodate solar cells, electronics, and optical trackers.

To pass the acceleration load directly down, the flyers would be tightly stacked for launch, with the webs lined up one above the other and in contact. The added thickness of the ears is allowed for by making their width 1/60 of the circumference and by clocking successive flyers in the stack by one tab width. In this way, the tabs will stack directly on their 20th nearest neighbors, also transmitting their acceleration load straight down. The tiltable mirrors to fit within the 100-μm ear thickness will be made by using MEMS (MicroElectro-Mechanical-Systems) technology and will be switched between open and closed positions by electrostatic force. By keeping the dimension of the mechanical elements very small in this way, the g force should not be a problem. Similarly, it should be possible to manufacture control electronics in the ears to survive 4,000 × g, as demonstrated by gun launch of a global positioning system.^§ Once rugged flyer prototypes are developed, their operation with radiation pressure control would be tested in space. They would be taken to L1 initially by conventional rocket propulsion.

The mass of 3,100 kg for the launch vehicle will break down approximately as 1 ton for the flyers, 1 ton for the armature (scaled by area from the Lipinski design), and 1 ton for the structure and remaining items. To prevent the build up of very high loads, the flyers will be stowed in a number of short stacks, each supported by a shelf to transfer the local load to the outer cylindrical wall and thence down to the armature. Each 1,000-kg payload will contain 800,000 flyers. The payload height, set by the stacking separation of 5 μm, will be 4 m plus the thickness of the shelves. The remaining elements with 1,000-kg budget will include the structure and nonstructural items whose mass was already estimated, the ablation shield (≈80 kg), and the ion-propulsion fuel (≈150 kg) and motor, along with the mechanism to destack and release the flyers and vehicle spacecraft elements for communications and orientation.

Discussion

None of the technical issues explored above invalidate the space sunshade concept. To take it further, more analysis and experiments are needed, and the benefits and costs must be further explored, particularly in relation to Earth-based approaches. In making such a comparison, it will be important to understand flyer lifetime. Currently, spacecraft in high orbits such as communications satellites last for ≈20 years, failing in part from loss of solar power of 1% a year caused by cosmic rays. Lifetimes ≥50 years should be achievable for the much simpler flyers, provided that radiation damage is mitigated by derating the solar cells, and the control electronics is made highly redundant. The mirror mechanisms should not be a limitation, because lifetimes >10¹⁰ operations are achieved by MEMS mirrors in TV displays.

At the end of their life, the flyers will have to be replaced if atmospheric carbon levels remain dangerously high. The dead ones that find their way back to Earth could present a threat to Earth-orbiting spacecraft, but hopefully no greater than the annual flux of a million, 1-g micrometeorites, or the 30 million debris objects in low-Earth orbit that weigh ≈1 g. This issue needs to be analyzed. Similarly, the 20 million spent armatures would be directed into solar orbit or to the moon, but a small fraction might take up eccentric orbits and eventually reach the Earth intact. It seems, however, that this threat could be held to a level no more than that presented by the ≈100 1-ton natural objects that hit the Earth annually (17).

The total cost of the first full sunshade implementation will include development and ground operations, as well as the flyer production and transportation. Of these, transportation is the best understood at present, although a significant cost not yet addressed will be for storing the electrical energy for release during the short launch interval. Here, because of the large scale of the project, the key parameter is the cost per launch amortized over the lifetime of the storage medium. Capacitors of the type used to store 0.3 GJ at the National Ignition Facility would be suitable, if upgraded for million shot lifetime. Flywheel storage such as used currently to deliver ≈5 GJ to the JET torus at rates up to 800 MW (18) also could be adapted to supply high power over the 0.3-sec launch interval and should have potential for even longer lifetime. Batteries optimized for very fast discharge and long life are another possibility. A reasonable goal for cost of highly mass-produced storage with million cycle lifetime is 2¢/J. This corresponds to 7¢/kW·hr, comparable to the cost of the electrical energy itself.

To transport the total sunshade mass of 20 million tons, a total of 20 million launches will be needed, given flyer payloads of 1,000 kg. If it became necessary to complete the sunshade deployment in as little as 10 years, a number of launchers working in parallel would be needed. If each one were operated a million times on a 5-min cycle, in all, 20 would be required. To propel the 3.1-ton vehicles to escape velocity with 40% efficiency, each launcher will need 640 GJ of energy storage, which at 2¢/J will cost $13 billion. Allowing also $10 billion for the 2-km-high, largely underground launch structure, and another $6 billion for other costs such as for magnet wire and high-speed switches, then the total capital cost of each launcher would be ≈$30 billion. The first such launcher could serve not only to verify and start sunshade construction but also to test other systems requiring large mass in high orbit. (It could be used, for example, to transport a prototype space solar electric system weighing ≥100,000 tons to geosynchronous orbit, at a cost less than the National Research Council target for financial viability of $400/kg (19), or to deliver a similar mass of freight to the moon.) For all 20 million launchings the capital cost would be ≈$600 billion and the electrical energy cost $150 billion.

The environmental impact of launch must be considered in addition to its cost. In the worst case, if electrical energy were generated with coal, ≈30 kg would be required for each kg transported to L1. But each kilogram of the sunshade mitigates the warming effect of 30 tons of atmospheric carbon, a thousand times more. Note that if the launch were by rockets with kerosene/liquid oxygen fuel, the carbon consumed would be comparable. It takes ≈20 kg of kerosene to place 1 kg in low-Earth orbit with an efficient two-stage rocket (9), and likely twice this to escape the Earth. On the other hand, the fuel cost for rocket launch is much higher. Kerosene costs currently $0.73/kg, compared with ≈$0.02/kg for coal delivered to power stations. This difference underlies in part the economy of magnetic launch.

The production costs for the flyers as described here are unclear, as a completely unprecedented scale of mass-production is needed. An aggressive target would be the same $50 cost per kilogram as for launch, for $1 trillion total. To date, spacecraft have been mass-produced only in quantities ≤100. The Iridium satellites, for example (20), at $5 million each cost ≈$7,000/kg, an order of magnitude less than for one-off spacecraft but still over a hundred times too high. Strategies for completely automated production of 16 trillion flyers will have to draw on, but go far beyond, experience from the highest volume mass production in other fields. Some highly complex systems produced by the millions already come close to our cost target, for example, laptop computers at ≈$100/kg. At a volume a million time larger still, new economies of scale should further reduce cost, for example, mass-production of flyer mass-production lines themselves. Although further studies are needed, it seems that $50/kg for the flyers is not unreasonable. And if flyer construction and transportation costs each can be held in the region of $1 trillion total, then a project total including development and operations of <$5 trillion seems also possible. If the 50-year lifetime is achieved, the cost per year averages to $100 billion, (0.2% of current world gross domestic product) and would decrease after that when only flyer and energy storage renewal is needed.

In conclusion, it must be stressed that the value of the space sunshade is its potential to avert dangerous abrupt climate change found to be imminent or in progress. It would make no sense to plan on building and replenishing ever larger space sunshades to counter continuing and increasing use of fossil fuel. The same massive level of technology innovation and financial investment needed for the sunshade could, if also applied to renewable energy, surely yield better and permanent solutions. A number of technologies hold great promise, given appropriate investment (3).

Abbreviations

L1

inner Lagrange point

Gm

million km.