Poisson-Boltzmann Calculations of Nonspecific Salt Effects on Protein-Protein Binding Free Energies

Abstract

The salt dependence of the binding free energy of five protein-protein hetero-dimers and two homo-dimers/tetramers was calculated from numerical solutions to the Poisson-Boltzmann equation. Overall, the agreement with experimental values is very good. In all cases except one involving the highly charged lactoglobulin homo-dimer, increasing the salt concentration is found both experimentally and theoretically to decrease the binding affinity. To clarify the source of salt effects, the salt-dependent free energy of binding is partitioned into screening terms and to self-energy terms that involve the interaction of the charge distribution of a monomer with its own ion atmosphere. In six of the seven complexes studied, screening makes the largest contribution but self-energy effects can also be significant. The calculated salt effects are found to be insensitive to force-field parameters and to the internal dielectric constant assigned to the monomers. Nonlinearities due to high charge densities, which are extremely important in the binding of proteins to negatively charged membrane surfaces and to nucleic acids, make much smaller contributions to the protein-protein complexes studied here, with the exception of highly charged lactoglobulin dimers. Our results indicate that the Poisson-Boltzmann equation captures much of the physical basis of the nonspecific salt dependence of protein-protein complexation.

INTRODUCTION

The binding free energies associated with the formation of macromolecular complexes are generally extremely sensitive to ionic strength. For example, the binding of proteins to nucleic acids and to the surface of membranes containing anionic phospholipids exhibits a strong salt dependence that has been extensively studied both experimentally and theoretically (1–5). The underlying principles are well understood and the calculated nonspecific salt dependence of binding free energies based on the nonlinear Poisson Boltzmann equation (NLPB) are generally in remarkable agreement with experimental measurements. The salt-dependence of protein-protein interactions has also been studied experimentally (6–11) and it is often found that increases in ionic strength weaken binding affinities for hetero-dimeric complexes. Experimental measurements on homo-dimers and tetramers, where all subunits have the same net charge, have detected both decreases (12) and increases in affinity (13–15) with increasing salt concentration. In this work, we test whether the Poisson-Boltzmann equation can be used to provide a quantitative description of this set of experimental observations.

Numerical solutions to the linear PB equation (LPB) have been applied with considerable success to protein-protein binding free energies but much of the focus has been on a single system involving the Barnase-Barstar complex (16). Our goal in this article is to test the applicability of the LPB through applications to a larger set of complexes than has been studied previously, and to understanding principles that govern the salt dependence of binding in these systems. No attempt will be made to model specific ion binding effects, and Hofmeister-type salting in and salting out effects (17–19).

The nonlinear PB equation has proved remarkably successful in describing the magnitude of salt effects on the binding of ligands, peptides, and proteins to nucleic acids and to membranes (1,3–5,20,21). This success is perhaps surprising given the high charge densities, and resultantly high counterion concentrations, in the systems involved. However, the availability of a complete expression for the electrostatic free energy within the framework of the nonlinear PB (22), as well as numerical algorithms that effectively solve the equation (23–28), have made it possible to test the approach, and in many cases remarkable agreement with experiment has been obtained. On this basis one might expect that the PB equation would work quite well for proteins; however, this is not necessarily the case. Nucleic acids have a large and fairly uniform negative charge density that results in a large accumulation of positively charged counterions in their vicinity. In contrast, proteins can be highly charged or close to neutral and their charge distribution is often not uniform. This in turn suggests that the electrostatic potentials of protein may exhibit a sensitivity to factors such as conformational flexibility and pK_a shifts in specific residues that are not present in more highly charged nucleic acids. In addition, the often complex and nonuniform change distribution of proteins results in complexities that are not present in nucleic acids. In this study, we investigate protein-protein complexes that exhibit a range of electrostatic interactions with the goal of identifying common principles and of testing the ability of the PB equation to deal with different types of complexes.

The properties of the five hetero-dimeric and two homo-dimeric/tetrameric complexes studied in this work are summarized in Table 1. We carry out finite difference Poisson-Boltzmann calculation, as implemented in the Delphi program (29), to analyze the nonspecific salt dependence of the binding free energy of each of these complexes, and to compare the results with experimental data. To understand the underlying source of the ionic strength dependence of binding, we partition the salt-dependent free energies calculated into standard screening terms and into self-energy terms that describe the interaction of a charge distribution with its own induced ion atmosphere. As will be discussed, the self-energy of each monomer also includes screening effects among charges that belong to the same monomer. In general screening is found to make the largest contributions but self-energy effects can also be significant, especially if charged groups that interact strongly with the ion atmosphere in the free subunits are buried upon association. We find, in parallel with previous work, that a proper understanding of nonspecific salt effects requires that the detailed charge distribution of the monomers and of the complex be taken into account.

TABLE 1.

Crystal structures studied in this work

Complex	PDB code	Interface surface area (Å2)	Complex charge	Charge of the free monomers	Experimental δΔΔG(I)/δln[I] [kcal/mol2]	Calculated with LPB δΔΔGel(I)/δln[I] [kcal/mol2]	Calculated with NLBP δΔΔGel(I)/δln[I] [kcal/mol2]
E9Dnase-Im9 (10) (B-A)	1EMV	1465	−3	B = +5; A = −8	2.17	1.29	1.31
Barnase-Barstar (8) (A-D)	1BRS	1585	−4	A = +2; D = −6	0.96	0.67	0.74
Thrombin-Hirudin (54) (H-I)	4HTC	2748	−4	H = +3; I = −7	0.82	0.90	1.29
Tem_1-Blip (55) (A-B)	1JTG	3168	−6	A = −6; B = 0	0.40	0.38	0.34
Amy2-Basi (6) (A-C)	1AVA	2275	−6	A = −4; C = −2	0.35	0.37	0.34
Hemoglobin tetramer (56) (AB-CD)	1A3N	3540	+2	AB = CD = +1	0.16	0.23	0.27
Lactoglobulin dimer (57) (A-B)	1BEB	1167	+26	A = B = +13	−1.62	−0.82 (−2.48)	−0.53 (−1.53)

The corresponding letter (chain letter) for each monomer in the complex is indicated in parentheses in column 1. The salt in all cases was NaCl. In case of lactoglobulin dimer, the results obtained with all acidic groups neutral are shown in parentheses in columns 2–7.

METHODS

Preparing structures for the finite-difference Poisson-Boltzmann calculations

We selected five hetero-dimeric and two homo-dimeric/tetrameric protein-protein complexes whose binding free energies have been measured at different salt concentrations and whose three-dimensional structures were solved to a resolution >2.0 Å (see Table 1). Protein-peptide complexes were not included in this study since we assumed that the interacting monomers undergo no conformational change upon binding, an assumption that is clearly not correct for flexible peptides. In addition, complexes with incompletely determined three-dimensional structures or where there were measurements indicating significant proton uptake induced by the binding (30) were excluded.

Hydrogen atoms were added to each structure with CHARMM 22 (31) and missing atoms and side chains for Tem_1-Blip were built using SCAP (32). The structures were energy-minimized with the conjugate gradient method using TINKER (33) with the CHARMM 22 force field, until an energy gradient of 0.01 kcal/mol per Å was reached. The GB/SA method (34–36) was used to compute the solvation energy during the minimization. Ca⁺² ions are present in the PDB structure of Amy2-Basi and Tem_1-Blip were included in the electrostatic calculations. We do not expect Ca⁺² ion occupancy to be strongly affected by ionic strength since most of the liganding groups are in direct contact with the Ca⁺² ion and thus are well within the Debye length of the ion atmosphere. Still, assuming that Ca⁺² ions are present both at all ionic strengths and in separated monomers is an assumption of the calculations. N-acetyl-D-glucosamine, for which standard charges are not available, was deleted from the crystallographic structures of Thrombin-Hirudin. This is expected to have little effect on the calculations because its binding site is located on the surface of the complex far away from the interacting interfaces. The heme groups in the hemoglobin tetramer were modeled using a simple charge distribution assigning −0.5e to the nitrogens and +2.0e on the Fe, resulting in a neutral heme.

The salt dependence of lactoglobulin dimer formation was measured at pH 3, which requires that the ionization states of the titratable groups be adjusted from what is normally assumed at pH 7. This was done with the multi-conformation continuum electrostatics (37,38) method using default parameters and calculating the pK_a values of ionizable residues using the structure of the dimer. Protonation/deprotonation events induced by the complex formation were not considered. Acidic residues with calculated pK_a values <3 were assumed to be protonated, which was accounted for by reducing the negative charge on the carboxyl oxygens so as to achieve electroneutrality. The remaining residues, Asp-33, -96, -129, -137, and Glu-134, were kept ionized. To assess the sensitivity of the results in respect to the protonation state assumed for each ionizable group, an additional set of calculations was performed in which all acidic groups were assumed to be neutral.

Calculation of the electrostatic component of the binding energy

The electrostatic component of the binding energy (ΔG_el) is calculated as the difference of the electrostatic free energies of the complex and of the free molecules,

(1)

where 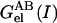is the electrostatic free energy of the complex, and and 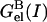are the electrostatic free energies of the monomers A and B, respectively, at a given ionic strength, I. Each energy was calculated with Delphi (29) and partitioned into three components (23),

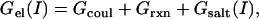(2)

where G_coul is the Coulomb energy calculated in a homogeneous medium of dielectric constant 2, G_rxn is the corrected reaction field energy (29), and G_salt(I) is the contribution of the mobile ions to the electrostatic energy. The last term in Eq. 2 was calculated as the grid energy difference at particular salt concentration minus the grid energy calculated at zero salt (39). The grid energy is the sum over products of charge and potential at each grid point in the finite difference lattice. The charge at each grid point is obtained from partial atomic charges based on an extrapolation procedure (40). Of the three terms on the right-hand side of Eq. 2, only G_salt(I) is salt-dependent. Thus, the salt dependence of the binding free energy (ΔΔG_el(I)) is the difference in the electrostatic component of the binding energy (Eq. 1) calculated at some salt concentration I and at zero salt concentration:

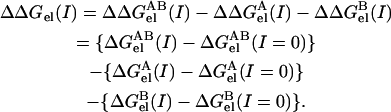(3)

Since salt affects the stability of both the complex and the individual molecules, the salt dependence of the binding energy reflects the difference between the effects of salt on the complex and on the free molecules.

The various energy terms were calculated at different ionic strengths. Since we are interested only in the electrostatic component of the binding free energy, and in particular in its salt dependence, the total binding free energy, which includes many other terms, need not be calculated. It is then most convenient to report all values for a given protein with respect to a reference state, which corresponds to the experimental binding energy at the lowest ionic strength for which it was measured.

Calculations of the salt dependence of the Coulomb interactions and the self-energy of the groups

The electrostatic component of the binding energy can be further broken into two components:

1. Screened Coulomb interactions between charges of molecules A and B, respectively; and

2. change of the self-energy of the charges due to the complex formation.

To calculate the effect of the salt concentration on the magnitude of the screened Coulomb interactions atoms, only the atoms of one of the monomers were charged, and the potential they produce was collected at the nuclei of the atoms of the second molecule in the complex. These potentials were multiplied by the corresponding atomic charges so as to yield a pairwise interaction energy between molecules A and B. The dependence of this energy on ionic strength (ΔΔG_screening(I)) describes the contribution of salt to the screening of electrostatic interactions between the two macromolecules. The salt dependence of the self-energy was calculated from the difference of the grid energies of the charged molecule (A or B, respectively) obtained in the presence of the uncharged partner and in isolation (ΔΔG_self(I: X), X – A,B). Thus, the total salt-dependent contribution to binding is given by

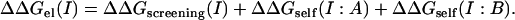(4)

Equations 3 and 4 describe the same quantity (ΔΔG_el(I)) calculated using two different numerical protocols. ΔΔG_el(I) in Eq. 3 is obtained entirely from the grid energy, which only uses lattice points. In contrast, the first term in Eq. 4 (ΔΔG_screening(I)) is calculated as a sum over all charges of one monomer multiplied by the corresponding potential generated by the other monomer at the coordinates of atomic nuclei. Thus, the salt effects calculated in Eqs. 3 and 4 will be slightly different due to numerical error. In addition, despite the fact that the self-energy contribution is calculated as a grid energy difference in both protocols (Eqs. 3 and 4), the distribution of the real charges onto the grid is not the same, since some of the grid points in the interfacial region may have contributions from the real charges of both monomers. In contrast, one of the monomers is uncharged in the protocol utilizing Eq. 4 and thus the residual grid effect may not be the same. This may result to slightly different ΔΔG_el(I) calculated with Eqs. 3 and 4.

Parameters of the electrostatic calculations

The calculations were performed assuming that all Arg, Asp, Glu, and Lys residues are ionized in both free and bound states. Histidines were considered to be neutral, a fact that is well documented in the case of Barnase-Barstar (8). We adopted the simplification of keeping all ionizable residues in their default charge state. To reduce the complexity of the problem the possibility of ionization changes, upon complex formation, suggested either by the experimental data (6,41), or theoretical simulation (42–45) as well as pK_a shifts induced by changes in the salt concentration (42,46), were not considered. The results were obtained with an internal dielectric constant of 2 and external dielectric constant of 80. However, the calculations were repeated with an internal dielectric constant of 4 and 20 so as to test the sensitivity of the results to this parameter. The force-field parameters (radii and partial charges) were taken from CHARMM 22 (31). Additional runs were performed with the Parse parameter set (35). The results were obtained using the LPB, but were repeated with the NLPB as well. In case of the NLPB, the free energy was calculated as described by Sharp and Honig (22) and includes electrostatic stress and osmotic pressure terms.

The molecular surface was generated using a water probe with radius of 1.4 Å. Initially a two-step focusing technique was applied to reduce the effect of the setup of the boundary conditions. The first run was performed at 20% filling and the resulting potential map was used to derive boundary conditions for a second run achieving the highest possible resolution for each complex with a filling of 80%. The grid size was kept constant at 297 and the ionic radius of the mobile ions was 2.0 Å. In the case of Tem_1-Blip, three focusing runs were needed to achieve stable results with respect to the grid resolution, and a three-steps focusing protocol starting from 10% filling was applied. In all cases, variance of the potential to within 0.0001 kT/e was used as a convergence criterion, except for lactoglobulin dimer where more stringent cutoff of 0.00001 kT/e was used to assure the convergence. This change was required to obtain proper convergence for the highly charged lactoglobulin dimer.

RESULTS

Comparison to experimental data

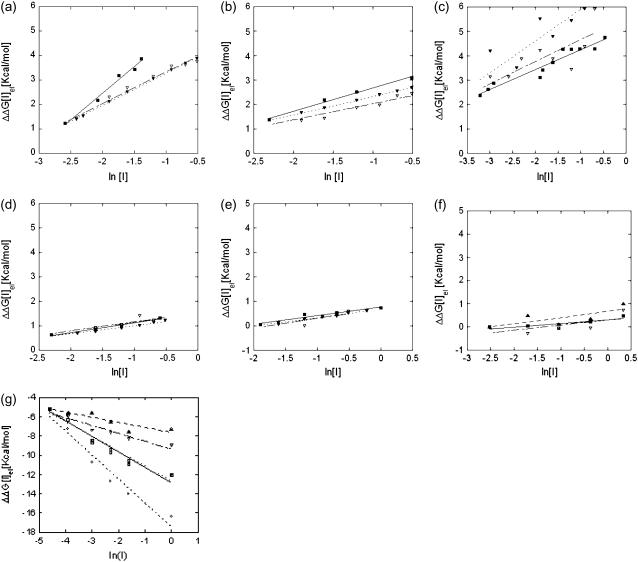
Fig. 1 shows the experimental and calculated salt dependence of the binding free energies for the seven complexes studied in the article (Table 1) plotted as a function of the logarithm of the ionic strength. The complexes are presented in descending order with respect to the slope of the experimental curve. The slopes of the fitted lines are also listed in Table 1 for both the LPB and NLPB calculations. In all hetero-dimeric complexes and in the homo-tetrameric complex, the experimentally observed binding free energies decrease with increasing ionic strength, an observation that is reproduced by both the LPB and NLPB calculations. In addition, the calculated magnitude of the slope of the salt dependence is in good agreement with experimental results, with the exception of the E9Dnase-Im9 complex. Our results using the LPB for the Barnase-Barstar complex are almost identical to those reported by Dong et al. (14) and the agreement with experiment is somewhat improved if the NLPB is used.

FIGURE 1.

Comparison of the experimental and calculated salt dependence of binding free energies. Calculations were performed using the CHARMM 22 parameter set (31), an internal dielectric constant of 2, and a focusing boundary protocol: ▪, ΔΔG (I) experimental data; ▿, ΔΔG_el (I) linear data; and ▴, ΔΔG_el (I) nonlinear data. The solid line is the linear least-square fit of the data: (a) E9Dnase-Im9 complex; (b) Barnase-Barstar complex; (c) Thrombin-Hirudin complex; (d) Tem_1-Blip complex); (e) Amy2-Basi complex, (f) Hemoglobin tetramer; and (g) Lactoglobulin dimer. The results obtained keeping all acidic groups neutral are shown with ○ for the LPB and with □ for the NLPB.

As can be seen in Fig. 1 and Table 1, the slopes of the calculated values of (δΔG(I)/δln[I]) obtained with the NLPB are generally very close to those obtained with the LPB. This is consistent with the fact that the net charge of the complexes and individual molecules are relatively small compared, for example, to nucleic acid systems where the counterion densities around the protein are large and hence the NLPB must be used. Indeed, only for the lactoglobulin dimer, which is predicted to have an ionization state with a net charge of +26e, do the effects of nonlinearities in the PB equations appear to be significant. For this ionization state, both the LPB and NLPB calculations underestimate the slope of the salt dependence of the binding free energy (see Table 1). However, as mentioned above, the experiments were done at pH 3, which required that we predict the ionization state of each of the acidic residues. Multi-conformation continuum electrostatics calculations predict that most of the carboxylic acids are neutral at pH = 3 (a list of the groups that are predicted to be ionized is provided in Methods). When the calculations were repeated keeping all acids neutral, the calculated salt dependence increased significantly (Table 1). The LPB calculations, in this case, overestimate the experimental slope by factor of 2, while the calculations with NLPB equation almost perfectly match the experimental data. It is clear that the results are very sensitive to the protonation states assigned to the ionizable groups as has also been found in a previous study of oligomeric assembly in a halophilic protein (42). Thus, the calculations are clearly successful in reproducing the negative sign slope that is observed experimentally, but the magnitude of the slope depends on the ionization state assumed for the monomer and the dimer.

Effect of parameters of the calculations

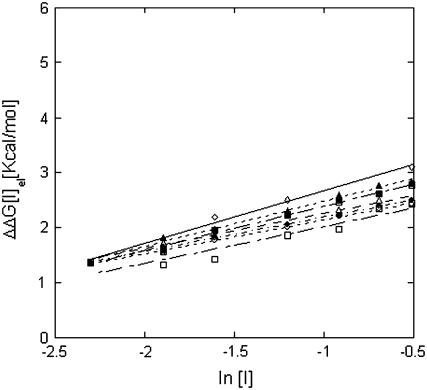
All calculations were repeated using the Parse (35) parameter set instead of CHARMM 22 (31) (Fig. 2). Fig. 2 reports results for the Barnase-Barstar although the sensitivity test was carried out on all complexes. Fig. 2 also shows the salt dependence of the binding free energy calculated with different internal dielectric constants. The best choice for this parameter is a subject of some controversy with values used for different applications, or in different laboratories, ranging from 1 to 20. We recalculated the results with internal dielectric constant of 4 and of 20 (note that in all cases salt was excluded from the interior of the macromolecules). As expected, the choice of parameter set or internal dielectric constant had only a marginal effect on the calculated salt dependence. In contrast, the absolute binding energy was found to be very sensitive to the parameters of the computational protocol and the force field that is used (data not shown).

FIGURE 2.

Salt dependence of the binding free energy (ΔΔG_el (I)) for the complex Barnase-Barstar calculated using different protocols. ◊, Experimental data; □, CHARMM 22 parameter set (31), ɛ_i = 2; ▵, CHARMM 22 parameter set; ɛ_i = 4; ○, CHARMM 22 parameter set, ɛ_i = 20; ▪, Parse parameter set (35), ɛ_i = 2; ▴, Parse parameter set, ɛ_i = 4; and •, Parse parameter set, ɛ_i = 20.

Individual free energy contribution: screening and self-energies

There are a number of possible sources for the dependence of binding free energies on salt concentration. Perhaps the simplest explanation involves the screening of Coulomb interactions between the charges on the two monomers when they form a complex. This explanation encounters difficulties in trying to explain why increasing ionic strength decreases the binding affinity of two monomers with the same net charge, although this is certainly possible if the charge distribution is not uniform.

Another source of salt effects involves changes upon binding of the interaction of the charge distribution of a free monomer with its own induced ion atmosphere. If the monomers had a uniform charge distribution, binding would always reduce the interaction of each monomer with its own ion atmosphere (47) and thus salt effects would destabilize the complex. This effect is seen in all of the hetero-dimeric complexes although the effect is generally small and in all cases but one, weaker than screening.

However, self-energy effects for nonuniform charge distributions are more complex as can be seen for hemoglobin and lactoglobulin, where self-energy contributions are found to increase the binding free energy as the salt concentration increases (the effect is almost zero for hemoglobin). This is due to the screening of favorable interactions between oppositely charged groups on the same monomer, for example in salt bridges. (In this sense the self-energy term of as nonuniform charge distribution includes screening terms between groups on the same subunit.) Indeed it has been shown (48) that increasing the salt concentration reduces the electrostatic energy of a salt bridge. If such a group is buried in a dimeric interface and is thus removed from the ion atmosphere, increasing salt will drive dimer formation through a destabilization of the monomer.

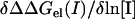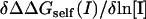To determine whether screening of self-energy effects dominates for a particular protein-protein complex we calculated the salt dependence of the screening and the self-energy separately (see Methods). The results are summarized in Table 2, which contains the values of reported in Fig. 1 and the two individual terms, and obtained from a linear fit of ΔΔG_screening(I) and ΔΔG_self(I) to ln[I], respectively (data not shown). Note that the two individual terms should sum to yield 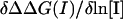as described by Eq. 4, but since these quantities are calculated numerically in different protocols they do not match exactly (see Methods). As is evident from Table 2, screening accounts for essentially the entire salt dependence for all the complexes, listed except for Temi_1-Blip, where the self-energy term dominates and the lactoglobulin dimer where the self-effect is significant.

TABLE 2.

Calculated values of the slope of the fitting lines

Complex	LPB*	NLPB†	Sum‡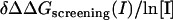
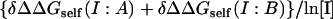E9Dnase-Im9 (10) (B-A)	1.29	1.31	1.32	1.31	0.01
Barnase-Barstar (8) (A-D)	0.67	0.74	0.58	0.50	0.08
Thrombin-Hirudin (54) (H-I)	0.90	1.29	1.36	1.26	0.10
Tem_1-Blip (55) (A-B)	0.38	0.34	0.31	0.00	0.31
Amy2-Basi (6) (A-C)	0.38	0.34	0.33	0.30	0.03
Hemoglobin tetramers (56) (AB-CD)	0.23	0.27	0.18	0.22	−0.04
Lactoglobulin dimer (57) (A-B)	−0.81 (−2.48)	−0.53 (−1.53)	−0.62 (−2.41)	−0.49 (−1.95)	−0.13 (−0.46)

In case of lactoglobulin dimer, the results obtained with all acidic groups neutral are shown in parentheses.

^*Linear Poisson-Boltzmann equation.

^†Nonlinear Poisson-Boltzmann equation.

^‡Sum = .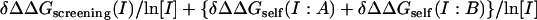

Despite the fact that Amy2-Basi (A: −4, C: −2) and the hemoglobin tetramers (AB = CD = +1) are like-charged complexes, binding affinity decreases with increasing salt and screening is the dominant salt-dependent term. In the case of the Amy2-Basi complex most of the net charge is not in the interfacial region and there is some degree of charge complementarity near the interface. Indeed, as can be seen in depictions of surface potential using Grasp2 (49) (data not shown) there are large patches of oppositely charged residues on either side of the interface that are clearly responsible for most of the observed salt dependence. The same complementarity is observed for hemoglobin dimers, where Asp-126 forms salt bridge with Arg-141 across the interface of the tetramer.

In contrast to the other complexes, for the Temi_1-Blip complex self-energy effects are larger than screening effects. The absence of screening is probably because the net charge on 1-Blip is zero and it is zero in the interfacial region as well. On the other hand, there are a significant number of charges in the interfacial region on both monomers that are removed from the solvent upon binding. These residues form a complex network of interactions involving both like-charge and opposite-charge pairs. Increasing the salt concentration makes the monomers more stable and thus results in a positive slope of th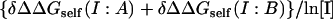e line.

In case of the lactoglobulin dimer, screening dominates, but the self-energy contribution is also significant and the slope of the 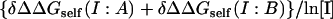line has a negative sign (Table 2). A negative slope was also calculated when all acidic residues were assumed to be neutral (Table 2). Thus, screening and self-energy terms work in the same direction to yield the one complex in our data set for which increasing the salt concentration strengthens binding. The screening effect is consistent with the expectation that increasing salt will weaken unfavorable interactions between highly charged monomers. However, the self-energy term also favors binding due to the screening of favorable interactions in the free monomers but not when they are buried in the dimer (see general discussion above). Specifically, complex formation buries the Asp-137–Arg-148 salt bridge at the center of the interface. The favorable pairwise interaction between these two groups is essentially salt-independent in the complex, but is weakened in the monomers as salt increases. We performed additional calculations neutralizing both Asp-137 and Arg-148 (by readjusting the partial charges of the nitrogen hydrogens) and the resulting slope of the 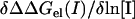line is −0.62 kcal/mol (compared with −0.81 kcal/mol in Table 1). Thus, this salt bridge accounts for ∼25% of the calculated salt dependence.

DISCUSSION

In this article, we have calculated the dependence of binding free energy on ionic strength for seven protein-protein complexes and compared the results to experimental measurements. The proteins that form these complexes differ in size and net charge and form interfaces that bury between ∼1500 Ų and ∼3200 Ų accessible surface area (Table 1). Three of the hetero-dimeric complexes are formed from monomers with net charges of opposite sign, one complex is formed from monomers with net charges of the same sign, and in one case one of the monomers is neutral due to the presence of a Ca⁺² ion. The homo-dimeric/tetrameric complexes are made of subunits that carry the same net charge. As can be seen in Table 1, the agreement between the calculated and experimental slopes is quite good with the exception of the E9Dnase-Im9 and lactoglobulin, where the calculated slope is extremely sensitive to the assumption made about protonation states. Given that we have not accounted for conformational changes, for pK_a shifts upon complexation and for uncertainty of the ionization states, the overall agreement suggests that application of the PB equation to static structures describes much of the physical basis of the nonspecific salt dependence of binding. Still, the fact that we have underestimated the salt dependence of the E9Dnase-Im9 complex by a factor of 2 is disturbing and we see no obvious reason why the calculations should be off more for that complex than for the other complexes.

The success of the PB equation in reproducing experimental measurements of the salt dependence of binding is consistent with earlier work on protein binding to DNA (1,5) and to negatively charged membrane surfaces (2,3). The success is likely because the results depend in large part on long-range electrostatic interactions that contribute to binding rather than on the detailed docking geometry. This reduces the sensitivity of the results to details of the force field and to sub-Ångström accuracy of a crystal structure, factors that complicate full binding free energy calculations.

Consistent with the long-range nature of electrostatic interactions involving salt effects, the results are not sensitive to the force field that is used or to the internal dielectric constant assigned to the protein. Thus, the electrostatic potential in solution, which is where the mobile ions are located, is not sensitive to the details of how the protein is described. In addition due to the relatively low charge density on the interacting proteins, nonlinearities do not generally play an important role as they do for nucleic acids and membrane surfaces. On the other hand, obtaining accurate results does require that care is taken in carrying out the calculations; for example, it is necessary to apply the focusing technique (39) to ensure that the results are reproducible at different grid sizes. Other investigators (16) have examined the effect of different representations of the molecular surface and of different values of the internal constant dielectric on the salt dependence of the binding energy, and have also found that the results are not sensitive to the above parameters.

In six of the seven complexes studied here, the screening of Coulomb interactions provides the dominant contribution to the calculated salt dependence of binding. This is true even for like charged monomers that bind so that interacting surfaces have complementary charge distributions. There is much precedence for this. Many DNA binding proteins have a net negative charge but the DNA binding interface is invariably positive. In another example, it has been shown that there are strong attractive interactions between the negatively charged β,γ transducin heterodimer and negatively charged membrane surfaces (3). Here again the effect is due to the highly polarized charge distribution of the protein surface that allows a positively charged patch to interact directly with the negatively charged membrane.

As described above, screening does not appear to play an important role in the salt dependence of the binding affinity of the Temi_1-Blip complex. We attribute this to the fact that 1-Blip is electrically neutral in its entirety, and in the interfacial region. On the other hand, self-energy effects appear to be important for this complex and indeed account for essentially all of the observed salt dependence of binding. The self-energy effect is also an important factor for the lactoglobulin dimer although screening appears to make a more significant contribution. As discussed above, self-energy effects are due to the favorable interaction of a charge distribution with its own ion atmosphere but also due to screening effects within each protein that are altered upon complex formation. The contribution of self-energy effects to complex formation is due almost exclusively to the charges that are buried in the interface In the Temi_1-BLIP complex, three ionizable groups in Temi (two Glu and one Lys) and three in 1_BLIP (one Asp, one Glu, and one Lys) are either fully or partially buried upon complex formation. The loss of their favorable interaction with the ion atmosphere accounts for much of the salt dependence of binding. In contrast, eight charged groups are buried upon lactoglobulin dimer formation (two Asp and two Arg for each monomer), and four of them form a salt bridge in the monomers (Asp-137–Arg-148). In this case their burial makes them less susceptible to the screening effects of salt so that now salt drives dimer formation. It should be mentioned that self-energy effects have been shown to contribute to protein stability (50) and to pK_a shifts (46). In the latter case, H-NMR data suggested that increases in the salt concentration stabilize the charged state of a histidine despite the fact that this residue is not involved in electrostatic interactions.

The results of this study suggest that numerical solutions to the PB equation are capable of accounting for much of the contribution of nonspecific salt effects to protein-protein interactions. The ionic strengths studied in this work are in the physiological range and it is possible that the agreement with experiment would not be so good at higher ion concentrations. On the other hand, the success of the NLPB in treating nucleic acid and membrane systems suggest that this is not necessarily a problem (1–3). Our results are consistent with previous studies that have also found that the PB equation successfully accounts for experimentally observed salt effects on proteins. These include studies of the salt dependence salt-bridge formation to proteins stability (42,51,52) and of the salt dependence of the coupling free energy between the N-terminus and the side chain of Asp 23 for the ribosomal protein I9 (53).

There are of course well-known shortcomings to the PB equation and, in particular, its treatment of divalent ions is expected to be less successful than its treatment of monovalents. More generally, the PB equation treats the response to the potential of both the water and the ions with a continuum assumption and thus neglects any effects at the atom scale (see, e.g., recent discussion by Elcock and co-workers (48)). Other salt effects that are not accounted for in the context of the PB equation include ion-specific effects such as those observed in the Hofmeister series (17,18), and cases where ions bind to specific sites. It should be stressed that all of the experimental measurements summarized here were carried out in NaCl and it is possible that different effects would have been observed if other ions were used. On the other hand, our results clearly indicate that nonspecific salt effects account for much of the experimentally observed effects in ion strength ranges studied in this work. It would be of interest to learn how well other theories of salt effects might account for the data used in this work. At this stage, the literature based on the PB equation appears quite separate from recent theoretical studies based on salt effects on water activity. A theory that accounts for both types of contributions would thus be of considerable interest.