A Virtual Hair Cell, II: Evaluation of Mechanoelectric Transduction Parameters

Abstract

The virtual hair cell we have proposed utilizes a set of parameters related to its mechanoelectric transduction. In this work, we observed the effect of such channel gating parameters as the gating threshold, critical tension, resting tension, and Ca²⁺ concentration. The gating threshold is the difference between the resting and channel opening tension exerted by the tip link assembly on the channel. The critical tension is the tension in the tip link assembly over which the channel cannot close despite Ca²⁺ binding. Our results show that 1), the gating threshold dominated the initial sensitivity of the hair cell; 2), the critical tension minimally affects the peak response, (I), but considerably affects the time course of response, I(t), and the force-displacement, F-X, relationship; and 3), higher intracellular [Ca²⁺] resulted in a smaller fast adaptation time constant. Based on the simulation results we suggest a role of the resting tension: to help overcome the viscous drag of the hair bundle during the oscillatory movement of the bundle. Also we observed the three-dimensional bundle effect on the hair cell response by varying the number of cilia forced. These varying forcing conditions affected the hair cell response.

INTRODUCTION

The hair cell is a sensory cell in the inner ear where the mechanical stimuli terminate and the electrical signals toward the afferent nerves initiate. Mathematical models of hair cell mechanotransduction have been developed to better understand hair cell function. These mathematical models require a number of biophysical parameters. To categorize, first, there are mechanical/structural parameters such as the geometric gain, stiffness of the gating spring, and damping coefficient. Second, the mechanoelectric transduction parameters are related to the transduction channel or adaptation. Regarding the transduction channel, previous mathematical models have two parameters—the gating swing δ and single channel gating force z (1–4). Those two parameters are related to each other by z = k_g δ γ, where k_g is the stiffness of the gating spring and γ is the geometric gain. Although previous mathematical models provided much insight into hair cell transduction, they greatly simplified the mechanical features of hair bundles.

This is the second of two articles presenting a computational model of the hair cell. In the first article, we proposed the virtual hair cell. A gating spring theory was incorporated into a three-dimensional (3-D) finite element (FE) model of the hair bundle. Our proposed model explored the behavior of each individual channel in the hair bundle. Channel kinetics was defined at the single transduction channel level. As a consequence, the virtual hair cell requires descriptive channel kinetics parameters. In addition to the gating swing, we introduced the channel gating threshold ΔF and the critical tension F_crit. ΔF is the tension in excess of the resting tension that is required to activate a channel when it is not bound with calcium and in its closed state. F_crit is the force over which the open channel cannot close despite calcium binding to the fast adaptation modulator. Also the virtual hair cell has parameters related to the fast adaptation such as the binding rate of Ca²⁺ to the fast adaptation modulator and the resting tension. We focused on the early response of hair cells when the slow adaptation effect is negligible. Therefore the virtual hair cell here does not need many of the model parameters related to the slow adaptation or calcium dynamics.

In this work, we investigated the effect of the transduction parameters used in our virtual hair cell. We present the time response to various step force stimuli and response displacement, I-X, and force displacement, F-X, relationships. Additionally we show the effect of different contact configurations for applying the force stimulus.

METHODS

Mechanical model and properties

The simulated hair cell is from a turtle (Trachemys scripta) utricular hair cell located ∼20 μm lateral from the point of polarity reversal. The geometry was measured from microscopic images and presented in detail elsewhere (5). The stereocilia heights range from 9.2 to 2.4 μm. There are 1 kinocilium, 52 stereocilia, and 42 tip links. The Young's modulus of the stereocilia is 0.75 GPa. The stiffness of tip link assembly (TLA), which defines the entire structure from actin core to actin core including the tip link, transduction channel, and gating spring, is 5 pN/nm. The stiffness of shaft links is 0.75 pN/nm. The upper lateral links have a resting stiffness of 0.001 pN/nm and stiffen as they deform. The TLAs slacken as they are compressed. These material properties are estimated by matching the static FE model with other experiments (5). The viscous damping was considered by assigning structural damping coefficients to make an overall effective damping approximately equal to the experimentally determined value of 200 nN·s/m (6). We used the FE method to solve the structural dynamic response of the hair bundle. A custom-made program was written in MATLAB (7) to perform this analysis.

Single channel gating

The transduction channel has four states: closed C, open O, calcium bound open O·Ca, and calcium bound closed C·Ca. At the resting state, we assume the channel is closed (C) and the TLA has a resting tension of F_R. The transduction channel is activated by an increased tension in the TLA (C→O). The additional tension required to open a channel is defined as the gating threshold ΔF. The open channel stays open if the tension in the TLA exceeds a critical value, F_crit, otherwise it closes as the Ca²⁺ binds to the fast adaptation modulator. A first order reaction was assumed for the Ca²⁺ binding to the fast adaptation modulator. In the reaction relationship, the association constant was assumed to be proportional to the [Ca²⁺] at the fast adaptation site C_SS, whereas the dissociation constant was constant. Default properties for this channel gating are F_R = 25 pN, ΔF = 1.5 pN, F_crit = 24 pN, and C_SS = 35 μM.

Simulations

Thirty-two step forces ranging from −50 to +700 pN were applied to the hair bundle for 2 ms. The positive value of force denotes the excitatory direction and the negative the inhibitory direction. The stimulus force had a sigmoidal rise from zero to its full magnitude in 0.05 ms. The applied force was distributed on the tips of three foremost (tallest) cilia including the kinocilium to match the forcing condition of a glass fiber parallel to the apical surface. To isolate the effect of the gating of mechanoelectrical transduction (MET) channels, one series of simulations was performed with channel gating, and one without. These will be referred to as the active and passive hair cell, respectively. When testing the effect of the transduction parameters, only the tested parameter is changed whereas the others remain at their default values. The only exception is when testing the effect of the resting tension, where the gating swing was changed according to the resting tension, which will be explained later. The response-displacement (I-X) relationships were fitted using the second order Boltzmann equation. The force-displacement (F-X) relationships were fitted according to F = F_p(X) − Ap_o(X), where F_p(X) is the passive force-displacement relation, A is a constant, and p_o(X) is the Boltzmann equation.

The details of these modeling and simulating procedures are found in our previous studies (5,8–10)

RESULTS

Effect of resting tension

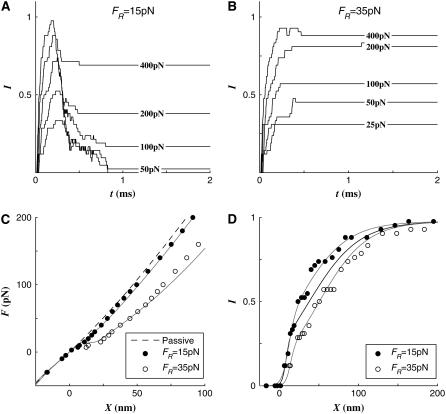
The resting tension in the TLA (F_R) is provided by the tugging force of multiple myosin molecules (11). Our tested hair bundle deformed by 32, 52, and 70 nm for resting tensions of 15, 25, and 35 pN, respectively. We assigned different gating swings for different resting tensions so that the tension drops to near zero when a channel is open. The reason for this is discussed later. The gating swings, δ, were 3, 5, and 8 nm for the resting tension of 15, 25, and 35 pN, respectively. All the other parameters remained their default values.

When F_R = 15 pN, more channels reclosed (O→C·Ca) than when F_R = 25 pN, whereas fewer channels reclosed when F_R = 35 pN (Fig. 1, A and B). Small F_R and δ values resulted in small differences between the passive and active hair bundle F-X relations (Fig. 1 C, F_R = 15 pN). Large F_R and δ resulted in a near zero minimum dynamic stiffness and greater deviation from the passive F-X relations (Fig. 1 C, F_R = 35 pN). Unlike most other simulation results, it was difficult to curve fit the F-X relations when F_R = 35 pN using a prescribed force-displacement equation. As the F_R and δ increased, the instantaneous (measured at peak X and I) activation curve shifted to the right and the operating range increased (Fig. 1 D). As the F_R and δ increased, the fast adaptation became less apparent (Fig. 1, A and B). At F_R = 35 pN, there was little difference in the I-X curve measured at the peak and t = 2.0 ms.

FIGURE 1.

Effect of resting tension (F_R). (A) The activation I(t) curve when F_R = 15 pN: The peak response is reached when t ∼ 0.25 ms. At small applied forces, a greater fraction of open channels closed again. (B) The I(t) curve when F_R = 35 pN: The fast adaptation was not obvious. Most open channels remained open. (C) The F-X curve: The difference between active and passive F-X curves at F = 100 pN was 3 and 23 nm when F_R = 15 and 35 pN, respectively. The dashed line indicates the passive F-X curve. (D) The I-X curve: As the resting tension increased the I-X curve shifted to the right. The blue line is the I-X curve when F_R = 25 pN.

These differences in the F-X and I-X relationships are not solely due to the different resting tensions, but also due to the different gating swings (δ) and the differences between F_R and F_crit. The latter value is a tension over which the channel cannot close again despite the binding of Ca²⁺. The effects of δ and F_crit are shown later.

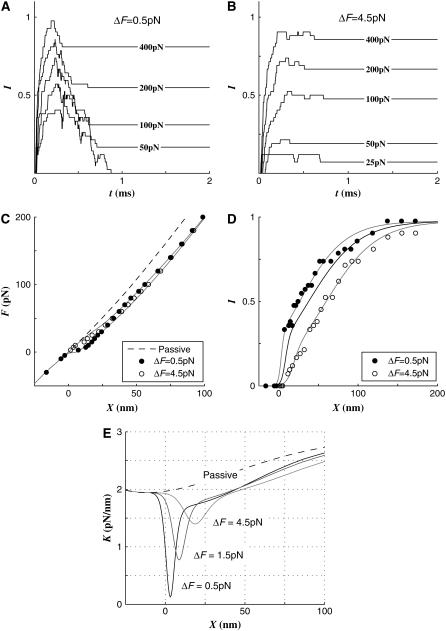
Effect of gating threshold, ΔF

We defined the channel gating threshold ΔF as the additional tension over the resting tension which is required to activate a channel. Therefore, with a default ΔF = 1.5 pN, the transduction channel is open at 26.5 pN or 1.5 pN over the resting tension of 25 pN. We also tested ΔF = 0.5 pN and 4.5 pN, which are one-third and three times the default value, respectively.

Smaller ΔF resulted in higher peak and smaller final activations (Fig. 2, A and B). The slope of the F-X relations in negative or large deflections (X < 0 or X > 100 nm) were the same despite different ΔFs. However, in the transient F-X region (0 ≤ X ≤ 25 nm), a smaller ΔF yielded a more dramatic bifurcation from the passive F-X curve (Fig. 2 C). The difference becomes clearer in the stiffness-displacement, K-X, relations as shown in Fig. 2 E. The minimum stiffness point shifted to the left (from X = 20 to 3 nm) and the compliant well got deeper and narrower as ΔF decreased. The activation curve got steeper as ΔF decreased (Fig. 2 D). Note the remarkably steep initial rise in the I-X curve when ΔF = 0.5 pN. As small as 3 pN of stimulus force resulting in X = 1.5 nm at t = 2.0 activated 14 out of 42 channels at the same moment, and all 42 channels sporadically activated within 2 ms. On the contrary, when ΔF = 4.5 pN, it took 15 pN to initiate the activation.

FIGURE 2.

Effect of gating threshold. Two different ΔFs, smaller and greater than the default value of 1.5 pN, were compared. A and B compare the channel activations along time at different ΔFs. The smaller ΔF resulted in greater peak current and smaller residual current after the fast adaptation. (C) When ΔF = 4.5 the active F-X curve bifurcates from the passive curve at a greater displacement. However, as the displacement increases the two active curves become closer. (D) As ΔF increases, the activation curve shifts to the right. At ΔF = 0.5 pN, the hair cell was very sensitive at its resting state and as small as 3 pN of stimulus activated more than 30% of channels. The solid lines are the curve fits of data points measured at ΔF = 0.5, 1.5, and 4.5 pN, respectively. The data points at ΔF = 1.5 were not shown.

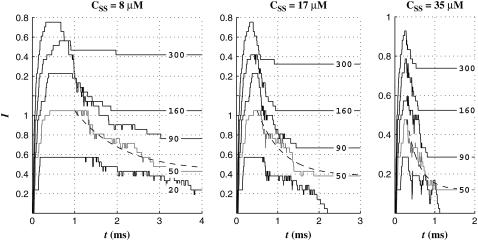
Effect of [Ca²⁺] at bundle tip, C_SS

The speed of the fast adaptation in the computer model here is governed by the binding constant (Eq. 1 in Nam et al. (5)). This binding constant is considered proportional to C, the [Ca²⁺] at the Ca²⁺ binding site. Such a postulation is supported by experiments that showed the fast adaptation speed dependent on the extracellular [Ca²⁺] (12–14). As designed, the virtual hair cell showed decreasing fast adaptation speed as the steady-state [Ca²⁺] at the fast adaptation site, C_SS, decreases (Fig. 3). At F = 50 pN, the time constant of the fast adaptation was 0.9, 0.6, and 0.3 ms when C_SS = 8, 17, and 35 μM, respectively. The I-X or F-X relationships were not affected by C_SS, which is unlike experimental observations (15,16). This discrepancy comes from the model artifact and is discussed later.

FIGURE 3.

Effect of [Ca²⁺] at bundle tip, C_SS. As the [Ca²⁺] at the bundle tip when the channel is open, C_SS, increases from 8 to 35 μM, the speed of fast adaptation increases. Unlike the adaptation speed, the magnitudes of responses were minimally affected by C_SS. At F = 50 pN, the response decay was fit with an exponential curve (dashed line). The time constants were 0.9, 0.6, and 0.3 ms from left to right.

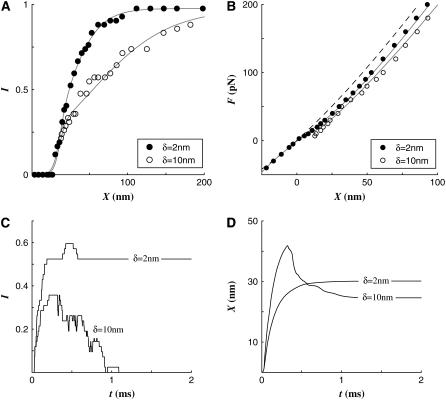
Effect of gating swing, δ

In the gating spring theory of hair cells, an elastic spring called the gating spring discretely elongates or shrinks as the channel is opened or closed. This excursion is called the gating swing (1) and was estimated from a few to a dozen nanometers (1,17). In our simulations, we have observed that the opening of a channel relaxes the tension in the neighboring gating springs (TLAs) and thus results in reduction of opening chances of adjacent channels. By the same reasoning, the closure of an open channel increases the tension of its neighboring channels. This interaction due to gating excursion dominates the hair cell kinetics as the gating swing becomes greater.

We investigated the effect of two different gating swings, 2 and 10 nm. Had we used a linearly elastic TLA, the TLA would experience a compressive stress exceeding 20 pN when δ = 10 nm. Our rationale is as follows: The tension reduction in the TLA due to gating is approximated by the product of the TLA stiffness and the gating swing or 5 pN/nm × 10 nm = 50 pN. As the tension in the TLA when the channel is open is 26.5 pN, the gating spring is subjected to 23.5 pN of compressive force as the channel is open. (In the simulation, the tension reduction is smaller than this theoretical value by a few piconewtons because of the viscous effect.) This high compressive force would be enough to buckle the tip link. Therefore to mimic reality we assigned a nonlinear material property for TLAs so that they slacken as the compressive force exceeds 5 pN.

The operating range, defined as the displacement over which the cell shows a variation in its activation level, was narrower when δ was small (Fig. 4 A). The initial sensitivity of the two cases was similar because the gating threshold was the same, but as the first wave of channel activity passes at X ∼ 25 nm, the two activation curves follow different paths. When δ = 10 nm, the opening of the channels in tall stereocilia prevented the opening of other channels until the force was increased enough to activate another cluster of channels at X = 50 ∼ 100 nm. On the contrary, the I-X relations were smoother when δ = 2 nm. In the F-X relationship, the two curves depart from the passive curve at a similar point reflecting similar initial activations of the two cases (Fig. 4 B). After bifurcating from the passive F-X curve, the hair cell with δ = 10 nm deviated further than the hair cell with δ = 2 nm (Fig. 4 B). Because TLAs were set to slacken when compressed, the F-X curve when δ = 10 nm was not much different from the F-X curve when δ = 5 nm. Because a smaller gating swing results in less tension drop due to channel opening, the tension in the TLAs easily exceeded F_crit so the fast adaptation was minimal when δ = 2 nm and vice versa (Fig. 4 C). In the computer model, the fast twitch is a direct consequence of the fast adaptation. The fast twitch was obvious when δ = 10 nm but did not appear when δ = 2 nm (Fig. 4 D).

FIGURE 4.

Effect of different gating swings. (A) The I-X curve became broader as δ increased from 2 to 10 nm. The operating ranges were 60 and 155 nm when δ = 2 and 10 nm, respectively. (B) As the gating swing increased, the F-X curve deviated more from the passive F-X curve. At F = 100 pN, the displacement was greater by 6 and 14 nm for δ = 2 and 10 nm, respectively, than for the passive displacement of 47 nm. (C) The activation profiles at F = 50 pN show that smaller δ activated more channels and had more channels remain open. (D) The bundle displacement responses at F = 50 pN show that because there was no fast adaptation there was no fast twitch when δ = 2 nm. On the contrary when δ = 10 nm, the twitch was as great as 17 nm (measured as the peak minus the displacement at t = 2.0 ms).

Effect of F_crit

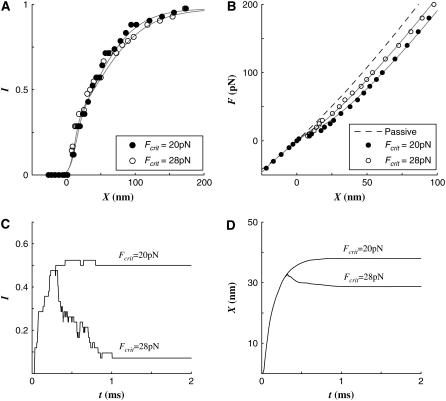
In experiments, it was observed that at small stimuli, most open channels are quickly closed again, whereas at larger stimuli the open channels tend to remain open (18). Experiments showed that at a small displacement, fast adaptation dominates the hair cell activation kinetics, but at larger displacement ranges the slow adaptation prevails (18). To obtain this characteristic, we introduced a critical tension in TLA, F_crit. In the virtual hair cell, if the tension in the TLA exceeds F_crit, the channel does not close despite the Ca²⁺ binding to the fast adaptation site. To produce a similar response to that observed in experiments, we found that F_crit should be similar to the resting tension. Accordingly we chose 24 pN as F_crit.

If F_crit is too low, the tension in TLA easily exceeds the critical value and fast adaptation rarely occurs. If F_crit is too high, most opened channels will close again even at large stimuli. These effects are shown in Fig. 5. Two different F_crit values (20 and 28 pN) were simulated. F_crit did not affect the instantaneous I-X relations (Fig. 5 A). Because the F_crit determined the amount of the fast adaptation (Fig. 5 C) and the fast twitch (Fig. 5 D), the F-X relation when F_crit = 28 deviated further from the passive curve than when F_crit = 20.

FIGURE 5.

Effect of F_crit. (A) The instantaneous I-X relationships were not affected by F_crit. (B) As F_crit decreased, the F-X curve deviated more from the passive F-X curve. At F = 100 pN, the displacement was greater by 14 and 21 nm when F_crit = 20 and 28 pN, respectively, compared to the passive displacement of 47 nm. (C) The activation profiles at F = 50 pN show that with F_crit = 20 pN there was little fast adaptation (reclosed channels). On the contrary with F_crit = 28 pN, most of the open channels were closed again. (D) The bundle displacement responses at F = 50 pN show that no twitch appeared when F_crit = 20 pN, but small twitch (5 nm) was observed when F_crit = 28 pN.

Effect of different attachment conditions

How our modeled hair cell is attached to the gel layer in the turtle utricle in vivo is unclear. The bundle kinematics is often described as a single degree of freedom (DOF) system; the displacement of the bundle is represented by a single parameter, i.e., the angular displacement or bundle tip displacement. In the single DOF model, the attachment condition does not make any difference because all the stereocilia in the bundle will deform together. Our hair bundle model has ∼6000 DOFs. The different attachment conditions produced different hair cell responses.

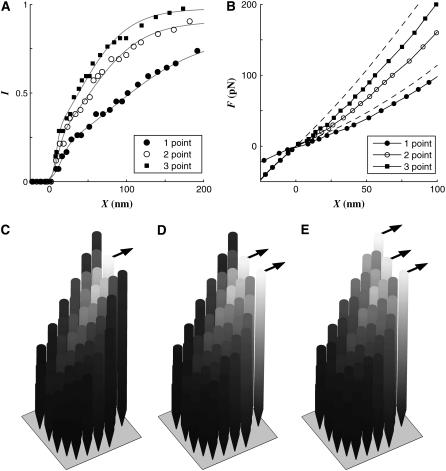
To investigate the significance of the attachment condition of the hair bundle to the gel layer and to show that the bundle tip displacement alone cannot fully represent the magnitude of stimulus, we simulated different forcing conditions. In the previous simulations shown, the force was applied at the tips of the three tallest cilia. We simulated two other cases. In one case, the force was applied at the tips of the two tallest cilia including the kinocilium and in the other case the force was applied only at the tip of kinocilium (Fig. 6). The I-X and F-X relationships were affected by the forcing conditions more than any other channel kinetics parameters previously shown. At X = 50 nm, the hair cell was activated by 31%, 48%, and 59% of its maximal activation as the number of forced cilia increased from one to three (Fig. 6 A). With a stimulus force of 50 pN, the bundle deflected by 60, 40, and 32 nm as the number of forced cilia increased from one to three (Fig. 6 B). The contour plots (Fig. 6, C and D) show the different local deformation patterns of the bundle depending on the forcing conditions.

FIGURE 6.

Effect of force constraints. The concentrated forces were applied only at the kinocilium for the one-point force condition or at the tips of the two tallest hairs including the kinocilium for the two-point force condition. Different force boundary conditions resulted in different responses. The results were compared with the default three-point force case. (A) The I-X curve became steeper as the force is distributed from one point to three points. (B) The bundle was less deformed as the force was distributed from one point to three points. Note that the bundle displacement was represented by the tip displacement of the kinocilium in the excitatory direction. Bottom: Contour plots of the bundle displacement in the excitatory direction. The force of 250 pN is applied at the tip of kinocilium (left) and distributed at the tips of two (center) and three (right) cilia. The relative displacement was coded in brightness. The displacement propagates from the forcing point(s), which indicates the local deformation of the bundle.

When more than three cilia in the tallest row were forced, it made only a slightly different response from the three-point forcing case. In our tested hair cell, three or more of the tallest cilia should be attached to the gel layer to make the hair cell most efficient and activate maximally with the smallest exciting force.

DISCUSSION

Difference between the parametric study and experiment

Through this parametric study, we investigated how variation in model parameters affects the response of our virtual hair cell and suggest a possible parameter set to produce realistic results. It should be noted that some of our results in this work would be difficult to exactly duplicate by experiment. Many parameters which can be independently varied in a computational study are not independent to each other in real hair cells. For example, when we tested the effect of the resting tension in Fig. 1, the channel opening tension F₀ was also increased to maintain a constant ΔF. The effect of different ΔFs was separately tested later. In an actual experiment F₀ may not change with a change of F_R. For another example, when we studied the effect of C_SS in Fig. 3, the resting tension remained at 25 pN despite the change of C_SS. This freedom to perform such a theoretical study enabled us to observe the effect of individual biophysical parameters related to the hair cell MET that would be otherwise difficult or impossible to separately observe through experiment.

Gating sensitivity

The gating sensitivity, z, is a frequently evaluated parameter of the two-state transduction channel model. Its physical interpretation is the tension drop in the gating spring due to channel opening (19,20). According to this theory, the gating sensitivity is related to the slope of I-X curve; a greater value results in a steeper I-X curve. Because it has a unit of force, it sometimes is called the single channel gating force (1,21).

The gating sensitivity, defined as the tension drop in the gating spring due to channel opening, is 25 pN in our study. The geometric gain correlates the gating sensitivity considered at the gating spring to that considered at the tip of the bundle (1,20). The geometric gain is defined as the elongation of the gating spring when the bundle tip is deflected by a unit length. The geometric gain, γ, approximated from the hair bundle geometry, is 0.027 in our model, which is ∼¼ of that found in the bullfrog saccular hair bundles (1) and similar to values of the mouse utricular hair bundles (22). The gating sensitivity considered at the tip of the bundle is then 25 pN × 0.027 = 0.68 pN. This gating sensitivity that we have used for our simulations is close to the upper bound of the values estimated from the analysis of experiments (1,20,23,24).

Our results, however, did not conform to the gating sensitivity theory. Unlike previous theories, the operating range of the simulated hair cell increased as the tension drop due to channel opening increased. As the tension drop in the TLA due to channel opening increased from 15 to 35 pN, the I-X relationship shifted to the right and no noticeable slope change was seen in the I-X curve (Fig. 1 D). According to our simulated results, the slope of the I-X curve is more closely related to ΔF, the difference between the resting tension and channel opening tension. As ΔF decreases, the slope of the I-X curve increased and the trough of K-X curve became deeper and narrower (Fig. 2, D and E).

Gating threshold ΔF determines the initial sensitivity

Unlike the single DOF mechanical model of the hair bundle, when a force is applied at the tip of our bundle, the force is unevenly distributed to the transduction channels. When the force is applied at the taller edge of the bundle, the tension in TLAs had a gradient, gradually decreasing from the taller to the shorter edge of the bundle. In our model, when a stimulating force of 1 pN is distributed over the three tallest cilia, the tension increase in 42 TLAs of the bundle ranged from −0.01 to 0.26 pN with a mean of 0.074 pN.

The gating threshold ΔF determines the initial sensitivity of the hair cell. With a smaller ΔF, the hair cell responded at a smaller deflection and the initial rising of the I-X curve was steeper (Fig. 2 D). With ΔF = 1.5 pN, it needed 1.5/0.26 ≈ 6 pN to activate at least one channel. With ΔF = 0.5 pN, it needed only ∼2 pN to initiate the activation. With an applied force as small as 3 pN, more than 30% of the channels were activated when ΔF = 0.5 pN, but there was no channel activity when ΔF = 1.5 pN (Fig. 2 D).

The gating threshold (ΔF) and the resting tension (F_R) determine the energy margin before a transduction channel is opened. This is a small energy barrier for a channel to overcome before changing its states from closed to open (C→O). We defined the gating threshold force, ΔF, as the additional tension above the resting tension in the TLA to open a channel. Default values of F_R and ΔF in our study are 25 pN and 1.5 pN, respectively, and the stiffness of the TLA is 5 pN/nm. TLAs in our model elongate by 5 nm due to the resting tension of 25 pN. A gating spring further elongates by 0.3 nm before the channel opens. With these values, the energy required to open a transduction channel is 7.7 pN·nm. This is ∼2k_BT, where k_B is the Boltzmann constant and T is the absolute temperature. For other ΔFs tested in this study, the energy required to open a transduction channel is 0.6 k_BT and 5.8 k_BT when ΔF is 0.5 and 4.5 pN, respectively. These values are within the expected range (19).

Role of resting tension

Resting hair cells exert force on the tip links to increase the sensitivity (11,25). Our results confirm this explanation; the increased F_R reduces ΔF and results in enhanced sensitivity (Fig. 2). We consider whether another possible role of the resting tension is related to the mechanical amplification of the hair cells.

The hair cells can oscillate spontaneously (26,27). The spontaneous oscillation is thought to help tune and amplify the input signals. Theories have suggested a four-stroke cycle to explain the spontaneous oscillations (2,28). The channel opening and closing explains the two fast strokes among the cycle of spontaneous oscillations (2,28). The bundle tip moves toward the excitatory direction when the channels open and toward the inhibitory direction when the channels close. Considering that the hair bundles are in a highly viscous fluid, the fast movements result in high viscous drag, which costs considerable energy to the hair cells.

We believe that the resting tension helps to overcome the fluid viscous drag in the excursion to the excitatory direction. By sustained resting tension, the elastic energy is stored in the hair bundle. Like the releasing of a flexed bow, when the tension is released by the channel opening, the stored elastic potential is transformed to the kinetic energy to overcome the fluid drag. If the released elastic potential prevails over the fluid drag, even a negative stiffness can be produced. In this manner, the resting tension in the hair cell TLAs may help to amplify the stimulus signals.

Based on such a consideration, when the effect of resting tension was investigated, we assigned the maximum gating swings to maximize the restored potential energy as the channel opens. For a given resting tension, the restored elastic potential increases as the gating swing increases. On the other hand, it is unlikely that the slender tip link in the TLA can sustain a significant compressive force. Therefore, the effective gating swing (δ) was limited by the constraint of δ ≤ F_R/k_TLA, where k_TLA is the TLA stiffness.

Interestingly, our results showed that increasing the elastic potential energy reduced the instantaneous stiffness (Fig. 1). When F_R = 15 pN and δ = 3 nm the restored elastic potential energy due to channel opening is ΔU ≈ 45 zJ (45 × 10⁻²¹ J) per a channel. When F_R = 35 pN and δ = 8 nm the restored elastic potential energy due to channel opening is ΔU ≈ 240 zJ per a channel. The minimum bundle stiffness was 1.5 pN/nm when ΔU ≈ 45 zJ and near zero when ΔU ≈ 240 zJ.

Single degree of freedom mechanical model of hair bundle

Most previous mathematical studies of the hair cell used a single DOF mechanical model to approximate the hair bundle deformation. Such a model can determine displacement at any point in the bundle from the bundle's angular displacement and a simple trigonometric calculation. However, Iwasa and Ehrenstein (29) note that a single DOF mechanical model is a necessary but not sufficient condition to ensure the parallel channel gating assumption. They identify a second condition, where the displacements and tensions in all tip links are identical for a given bundle displacement. Table 1 in Furness et al. (30) shows that a single DOF mechanical model does not ensure even pulling of tip links during bundle deformation. Some additional “fine-tuning” mechanism is required to meet the second condition (29). If these two conditions do hold, the magnitude of stimulus can be represented solely by the angular displacement of the bundle. If this is true, different stimulating methods do not result in different responses as long as the time courses of bundle displacement are the same. On the contrary, our model predicts that different stimuli result in different responses.

Our hair bundle model allows relative movement between the stereocilia. It is not a single DOF system. With current experimental resolution it would be difficult to observe the relative separation movement between the cilia. However, a simple experiment can test the single DOF mechanical model of hair bundle. For example, we predict that the hair cell stimulated by the glass fiber or fluid-jet exhibits different I-X profiles. In our previous studies, hair cells responded differently when they were stimulated by a concentrated force like a glass fiber stimulus and when they were stimulated by a distributed force like a fluid-jet stimulus (6,31). Even though the dynamic responses of the bundle tip displacement were the same, depending on the types of stimuli, the hair cell responded differently. In this work, we added new results. Even the same glass fiber stimulations resulted in different responses according to the attachment condition of the fiber.

Some hair cells have known attachment conditions to the gel layer. The bullfrog saccular hair bundles are linked via bulbous tip of the kinocilium and experimental stimuli are applied as such. For some hair cells like the turtle utricular cell simulated here, how hair bundles are attached to the gel or otoconial layer is unclear. In mammalian auditory outer hair cells, the tips of the tallest row of stereocilia are attached to the tectorial membrane. But, in the experimental preparations it is difficult to stimulate the outer hair cells as they are in vivo by pulling the entire first row of the hair bundle at the same time. Our results indicate that how the stimulating glass fiber contacts the hair bundle may affect the hair cell sensitivity considerably. And this may partially explain the wide variation in experimental results depending on the experimental methods.