Entropy and Barrier-Controlled Fluctuations Determine Conformational Viscoelasticity of Single Biomolecules

Abstract

Biological macromolecules have complex and nontrivial energy landscapes, endowing them with a unique conformational adaptability and diversity in function. Hence, understanding the processes of elasticity and dissipation at the nanoscale is important to molecular biology and emerging fields such as nanotechnology. Here we analyze single molecule fluctuations in an atomic force microscope, using a generic model of biopolymer viscoelasticity that includes local “internal” conformational dissipation. Comparing two biopolymers, dextran and cellulose (polysaccharides with and without local bistable transitions), demonstrates that signatures of simple conformational change are minima in both the elastic and internal friction constants around a characteristic force. A novel analysis of dynamics on a bistable energy landscape provides a simple explanation: an elasticity driven by the entropy, and friction by a barrier-controlled hopping time of populations between states, which is surprisingly distinct to the well-known relaxation time. This nonequilibrium microscopic analysis thus provides a means of quantifying new dynamical features of the energy landscape of the glucopyranose ring, revealing an unexpected underlying roughness and information on the shape of the barrier of the chair-boat transition in dextran. The results presented herein provide a basis toward probing the viscoelasticity of macromolecular conformational transitions on more complex energy landscapes, such as during protein folding.

INTRODUCTION

Single molecule force spectroscopy has become an important tool for exploring the influence of force on the structure and stability of biological macromolecules (1), as well as for testing fundamental models of polymer elasticity (2,3). The protocol underlying many force probe experiments is the linear increase of tensile force on a single biomolecule with time (4). An emergent theme from such constant loading rate experiments is the propensity for conformational change in biomolecules, from reversible or near-reversible processes such as chair-boat transition in polysaccharides (5–8), the “overstretching” transition in DNA (9,10) and RNA hairpin unfolding (11), to the irreversible unfolding of concatamers of protein domains (12–14). In addition, conformational changes are ubiquitous in many processes in molecular biology, such as the action of molecular motors in muscle and cellular transport (15,16) and allosteric signaling in regulatory proteins (17,18). However, despite their importance, the physical processes that underlie these transitions, particularly the role of conformational elasticity and internal friction, are poorly understood.

Despite the success of constant loading rate experiments, they can provide only limited information; the elastic response function for each molecule under reversible conditions, and at most global dynamical information, such as the rate of unfolding of a protein, from irreversible stretching. A case in point is the polysaccharide dextran, which exhibits a reversible plateau in its force-extension response, due to a local chair-boat transition that has been shown to be effectively two-state in nature (8,19,20). Such experiments provide the free energy difference and distance between states; however, unlike the observation of hopping between folded and unfolded states of an RNA hairpin (11), the dynamics of this transition cannot be probed, since each monomeric hopping processes is too small (<1 Å) and too fast for stretching experiments to probe. A fuller understanding of the response of single biopolymers during forced unfolding or refolding could be provided by analysis of the local linear viscoelastic response. Significantly, local dissipation would give access to finer-scale conformational dynamics; for example, the rates of transitions between different states along the unfolding or refolding pathways of a protein. A close analogy is found in the macroscopic rheology of complex fluids, whose dissipative mechanical spectra reflect dynamics of various structural, molecular, and topological transitions (21).

Recent experiments (22–29) measuring the viscoelastic properties of single biomolecules as a function of force, including polysaccharides and proteins, have gone some way to achieving this goal. The results show highly nontrivial features, particularly in the dissipative part of the spectra, where measured frictions are many orders-of-magnitude larger than solvent friction, suggesting an internal source of dissipation. Experimental signatures of internal sources of dissipation in synthetic polymers and ligand binding (for example, to myoglobin) have been previously identified, often appearing as an anomalously weak (fractional) dependence of dynamics on solvent viscosity (30,31). Here, in the case of dextran, the effective friction to elongation exhibits a minimum at a force that coincides with the plateau in the force-extension trace, indicating it arises through a process related to the local internal conformational transitions in the chain (22,28). In addition, although it is clear that a plateau in the force-extension response should give rise to a minimum in the elastic constant, the underlying statistical mechanics of this change are not well understood (5,6). Here we seek to understand the origins of these features in the viscoelasticity of dextran and by doing so give broad insight to the nature of elasticity and friction for simple conformational transitions.

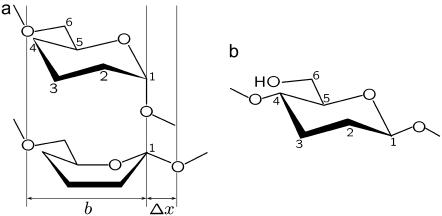
Dextran and cellulose are biological polymers composed of glucose monomers, a six-membered ring molecule, which have a number of stable conformations (32) (Fig. 1). They differ by the way the glucose ring is linked into the backbone of the polymer. In dextran, which is an α-(1→6)-linked polysaccharide, the C1–O1 bond is axial to the plane of the ring and thus force promotes conversion from the nominally stable chair state to a more elongated boatlike conformation (6,32–34), where this linkage becomes equatorial (20,35), as shown in Fig. 1 a. This gives rise to dextran's characteristic plateau in its force extension response (Supplementary Material, Fig. S1). In contrast, the glucose ring in cellulose, which is β-(1→4)-linked, is already near maximum elongation, since all its linkages are equatorial to the plane of the ring (Fig. 1 b), resulting in an almost ideal freely jointed chain (FJC) force-extension response (6,7) (Supplementary Material, Fig. S1). We see the bistable nature of the transition in dextran and its absence in cellulose provides an ideal experimental test to enable us to understand the characteristic viscoelastic response of simple forced conformational transitions. This in turn should provide a natural starting point for our understanding more complex conformational transitions such internal structural transitions during protein unfolding or refolding.

FIGURE 1.

Structure of dextran and cellulose. (a) Simplified diagram of the molecular structure of dextran, which is an α-(1→6)-linked polysaccharide of glucose, where the monomer length is defined by the distance between adjacent non-ring oxygens on the backbone, as shown schematically. The α-linkage at C₁ is axial in the lowest energy ⁴C₁ chair conformation (32) (above), which under application of a tensile force-field promotes one of a number of more elongated boat or skew-boat conformations, of which the ^1,4B is shown (below) (6,32–34). The increased length Δx gives rise to a plateau in force-extension measurements (Supplementary Material, Fig. S1) as the more elongated boatlike conformations are populated under increasing force. (b) Cellulose, on the other hand, is a β-(1→4)-linked polysaccharide of glucose, whose equatorial linkage at C₁ in the chair state means the monomer is already near maximum elongation and its force-extension behavior follows simple polymer elasticity models due to reduction of chain entropy at high stretch (Supplementary Material, Fig. S1).

The article is structured as follows: first we provide an overview of the experimental technique of thermal noise force spectroscopy (28), whereby the fluctuations of single polysaccharide molecules are measured in a force-clamp AFM system. We then analyze the force-dependent power spectra of these fluctuations using an extension of the well-known Rouse model of a polymer, which includes local conformational internal friction. This allows measurement of the elastic, internal friction and solvent friction constants of both cellulose and dextran as functions of force, which we collectively term the viscoelastic force spectra. To provide microscopic interpretations of the parameters of the extended Rouse model, we then build up a model at a more refined level of detail. A treatment of bistable population dynamics calculates the effective elastic and friction constant of conformational change on a bistable discrete landscape, representing the chair-boat transition. We then add to this a molecular model of viscoelasticity of an FJC at high stretch. Together, these tools then provide a means of quantifying the viscoelastic force spectra of dextran, importantly revealing previously unseen dynamical features of the energy landscape.

MATERIALS AND METHODS

Dextran and carboxymethylated cellulose were prepared from powder (dextran, D-5251, lot No. 69H1267, average MW = 473,000; and cellulose, 419338, lot No. 071913PA, average MW = 700,000) purchased from Sigma (Deisenhofen, Germany). These samples were dissolved in pure water at a concentration of 10% and 0.025% (w/w), respectively. An aliquot of the polysaccharide solution was dropped onto a clean glass coverslip (10 mm diameter, 0.2 mm thickness from Agar Scientific, Essex, UK) and dried overnight at room temperature. The glass coverslip was rinsed extensively with pure water to remove loosely bound polysaccharide leaving approximately a monolayer covering. All polysaccharide force spectroscopy experiments were carried out in pure water at room temperature, using V-shaped, broad, short silicon nitride cantilevers (NP, Digital Instruments, Santa Barbara, CA) with a nominal spring constant of 580 pN/nm (measured 350 pN/nm). Before each experiment, the system was left to equilibrate thermally for at least 1 h to minimize thermal drift.

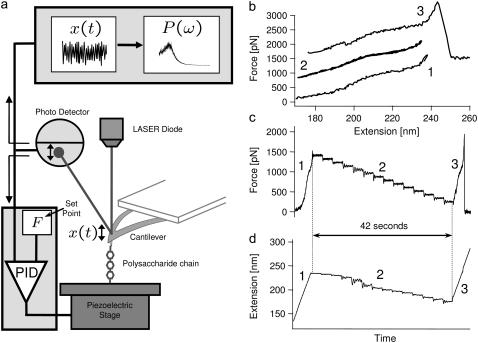
The protocol used for thermal force-clamp spectroscopy is as described in Kawakami et al. (28); we summarize the procedure here. The first part of the experiment follows conventional force-spectroscopy protocol for polysaccharides (5,8), where the cantilever is pressed into a polysaccharide monolayer with a force ∼10 nN for ∼1 s, after which it is retracted from the substrate at a constant speed, shown by the red curve in Fig. 2 b. When a predetermined force setpoint is reached, the force-clamp protocol is initiated, which involves either reducing force in discrete steps of ∼100 pN and being held for ∼3 s (blue curve in Fig. 2 b), or reducing force slowly and continuously at ∼8 pN/s. In some measurements we have used this latter continuous approach; however, both procedures produce the same results within the errors of each method. In either method the force is controlled using a proportional-integral-derivative (PID) feedback loop with a response time of ∼10 ms, whereby the cantilever substrate separation is adjusted to maintain a certain cantilever deflection. Intuitively, a response time of ∼10 ms means the feedback loop cannot respond to fluctuations faster than 10 ms; a simple linear-response model of the feedback system shows it to provide an effective high-pass response with fractional error on the bare cantilever/polymer signal that decreases as 1/(ωT), where T is the feedback response time. In our experiments, we fit to the cantilever fluctuations from a normal frequency of 4 kHz to 40 kHz (i.e., ω = 25 to 250 krad/s), giving a fractional error that varies from 0.004 to 0.0004. These unimpeded high frequency cantilever+polymer fluctuations represent a Gibbs ensemble with an average force F shared between cantilever and molecule. After the force-clamp phase, the cantilever is again retracted from the substrate at a constant speed, up to a critical force when the polymer detaches, as shown by the green curve in Fig. 2 b. Immediately after detachment, the power spectral density (PSD) of the free cantilever is recorded as the cantilever is brought toward the substrate in 30 nm steps. These free cantilever PSD are then fit using a simple harmonic oscillator model (SHO), 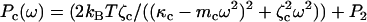, obtaining the cantilever effective stiffness κ_c, friction constant ζ_c, and mass m_c (and where P₂ represents the low frequency DC response of the cantilever higher harmonics). These parameters then serve as constraints in the curve fits to the power spectra of the cantilever and molecule system.

FIGURE 2.

Force-clamp thermal noise spectroscopy. (a) Schematic diagram of the experimental setup for thermal noise spectroscopy. Panels b, c, and d show the force-clamp protocol used: (b) typical experimental force-extension traces showing a retract, approach, and retract cycle, using dextran as the sample polymer, where the traces have been offset for clarity. The characteristic shape of the final curve (curve 3), which in the case of dextran exhibits a shoulder indicative of the chair-boat conformational transition in dextran (5), confirms that only a single molecule was attached. (c) Experimental-force time trace and (d) extension time trace, where the numbers correspond to the same sequence in panel b. The force-clamp phase (phase 2) lasts for a total of 42 s, where the dextran polymer is held for 3 s at each of 14 discrete forces (the initial and final extensions, phases 1 and 3, are shown on an expanded timescale).

The instrumentation consists of a commercially available AFM system—a Picoforce AFM with Nanoscope IIIa controller (Digital Instruments, Santa Barbara, CA) integrated with two other PCs, which provide maximum flexibility for the system. The commercially available software from Digital Instruments (Nanoscope v6.1) was used only for automatic approach of the cantilever to the substrate. All other functions such as monitoring of the deflection of the cantilever and control of the scanner position were performed using custom software with Igor Pro software (WaveMetrics, Lake Oswego, OR). Picoforce closed-loop control was turned on during all experiments. A second PC was used to control scanner motion via a standard PCI I/O board (16 bit D/A, NI-6014, National Instruments, Austin, TX) and a third PC, equipped with a PCI I/O board (for dextran, 12 bit A/D, NI-6024E; for cellulose, 16 bit D/A, NI-6014), was used to record the deflection signal with a high sampling rate of 200 kHz resulting in the highest accessible frequency in the Fourier-transformed thermal oscillation power spectrum, 100 kHz (Nyquist frequency). The force-clamp is achieved using the cantilever deflection signal sampled at ∼4 kHz and time-averaged for 12 ms before comparison with a set point. The difference between the averaged cantilever deflection and setpoint value is an error signal that is input to a software PID feedback loop, which drives the scanner z position. The power spectral density (PSD) of the cantilever fluctuations were calculated using an in-built function in Igor Pro, using 50% overlapping Hahn-type windowing with 8192 points per window. Fitting to the PSD was constrained between 4 and 40 kHz, due to mechanical noise from scanner at 1–3 kHz and a broad noise source from the quadrant photodiode at ∼50 kHz induced by a constant cantilever deflection. In addition, by being sufficiently far from the Nyquist frequency (100 kHz) we avoid significant problems with aliasing. We find that typically 1–3 s of the cantilever/molecule system's fluctuations must be recorded to produce a PSD of sufficient quality to be fit by our model.

To model the combined single molecule and cantilever system, we treat the force-clamp experiment as two linear system elements in parallel, since the change in extension of the polymer and cantilever are the same at their point of contact. It can be shown (see Appendix A) that for a system in parallel the total dynamic compliance of the system J_T(ω) is given by

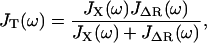(1)

where J_X(ω) is the dynamic compliance of the cantilever, for which we use a SHO model (J_X(ω) = (κ_c − m_cω² + iζ_cω)⁻¹). This is just the frequency-dependent extension of the parallel addition that arises naturally in our experiment. We then use the fluctuation dissipation theorem P(ω) = −2 k_BTJ″(ω)/ω (36) (J″ represents the imaginary part of the complex function J) and Eqs. 1 and 5 to calculate the total power spectrum of the cantilever+RIF polymer. This enables measurement of the elastic, internal friction and solvent friction constants, as functions of force, for example, as shown by the RIF model fits to the power spectra of cellulose in Fig. 3. In fitting the PSDs to the RIF+cantilever model, we constrain the chain solvent friction to be between 0 < ζ_s < 0.1 μg kHz, since a reasonable estimate of the solvent friction is given by 6πηΔR ≈ 4 × 10⁻³ μg kHz, where ΔR ≈ 200 nm is a typical end-to-end length in the experiment, representing the effective hydrodynamic radius of the chain (37). For consistency, as we have shown in previous work (28), we confirm that calculating the elastic spectrum directly from the numerical derivative of extensible FJC fits (Supplementary Material, Fig. S1) agrees very well with the elastic constant determined from the thermal spectroscopy method using the RIF+cantilever model to analyze the PSD (not shown).

FIGURE 3.

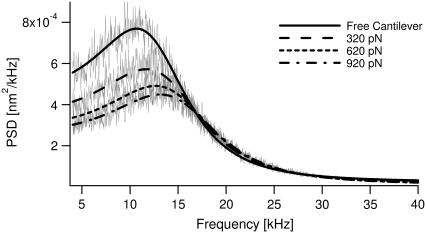
Force-dependent PSD of a single molecule of cellulose. Comparison of the PSD of fluctuations of cantilever tip, when free and with a single cellulose molecule attached, held with forces of 320 pN, 620 pN, and 920 pN (in gray lines from top to bottom, respectively). The lines in black correspond to fits using either a simple harmonic oscillator model for the cantilever (solid), or the RIF model of the biopolymer combined with the cantilever (broken lines as shown in the legend) described by Eqs. 1 and 5.

Fitting to elasticity and internal friction

In both the elastic and internal friction force spectra, there are a number of different physical processes that underlie the observed behavior, as discussed in the main text. A reasonable assumption is that the noise on each physical process is uncorrelated, so that the total power spectrum is the sum of the power spectra of each process. The DC term for each PSD will be ∼ζ/κ² and so in the low frequency regime of the experiments, the rules for summing the elastic and friction constants of the different processes are then

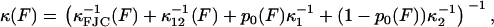(2)

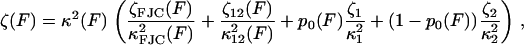(3)

where the subscripts have the following meanings: FJC refers to the elastic and friction constants of a freely jointed chain; 12 refers to the effective elastic and friction constants due to the bistability between the short and extended states, 1 and 2 (as modeled in Microscopic Explanation, Eqs. 6 and 7); 1 or 2 is the effective elastic and friction constant of the short and long states; and p₀ is the probability of occupying the short state 1. In fitting to the internal friction force spectra, we use the parameters extracted from fitting to the elastic spectra as a constraint to the fits. Experiments at higher frequency will require higher order expansions of the PSD of each process or frequency-dependent elastic and friction constants. For the bistable friction term ζ₁₂ (Eq. 7 in main text), we used trial and error with fits with different fixed values of τ₂₁(F = 0), to find values of the zero-force backward hopping time that correspond to the bound calculated on x₁, the distance to the transition state from the short state. We checked that the values of τ₁₂(F = 0) also determined from the fits, were consistent with detailed balance ( ).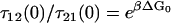

THERMAL NOISE FORCE SPECTROSCOPY

We determine the viscoelasticity of dextran and cellulose, using a recently developed technique for measuring the Brownian dynamics of single molecules under force-clamp conditions (28). Fig. 2 a summarizes the experimental apparatus and procedure, with details given in Materials and Methods. The principle of the experiment is to hold a single molecule between tip and substrate of an AFM at constant force, while observing the thermal fluctuations of the cantilever. The fluctuations contain inherent viscoelastic information, which we obtain via calculation of their frequency power spectral density (PSD). A conventional proportional-integral-derivative (PID) feedback loop with a response time of ∼10 ms, monitors the cantilever deflection signal and adjusts the piezo substrate position to maintain a constant average force (F) or force-clamp on the molecule between the tip and substrate. Here, the limited time-response of the piezo makes perfect force-feedback control of the fluctuations (38) impractical and so as discussed in Materials and Methods, the statistical mechanics of the high frequency extensional fluctuations we measure, represent a constant force Gibbs ensemble of the cantilever and single molecule combined. A key idea of this technique is that by controlling the force we probe the local viscoelasticity of single biomolecules as they explore their energy landscape under near equilibrium conditions (as shown by Fig. 2, b and c, for dextran). Measurement of the force-dependent power spectra is exemplified in Fig. 3 for cellulose, where it is clear that the PSD peak position, width, and amplitude are dependent on the response of the biopolymer.

THE ROUSE-WITH-INTERNAL-FRICTION (RIF) MODEL ANALYSIS OF PSD

To quantify these changes and extract viscoelastic information from the thermal spectroscopy power spectra, we model the biopolymer using a modified Rouse model that includes local conformational internal friction in addition to solvent friction. The Rouse model is a generic and highly successful description of the coarse-grained dynamical behavior of flexible polymers (39,40). It ignores long-range hydrodynamics (41), but we note that in the typically highly extended conformations in our experiment, they give only logarithmic corrections to local drag. The Rouse with internal friction (RIF) polymer (42,43) is represented as a series of beads with solvent friction ζ_s0, connected by spring and dashpots of elastic constant κ₀ and internal friction ζ_i0. In the continuum limit, internal friction adds an extra term in the standard Rouse equation, which describes a dissipative force proportional to the rate of change of local conformation, represented as the coarse-grained curvature of the chain,

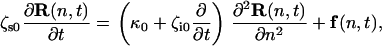(4)

where R(n,t) represents the space curve of the polymer with contour variable n, subject to a local Langevin force f(n,t), which is uncorrelated for different times. We note a similar continuum model was developed by Poirier and Marko (44), relevant to the study of internal friction in stiff biopolymers, such as chromatin or DNA. Normal mode solutions of Eq. 4 decay in a single exponential manner with a mode-dependent relaxation time, 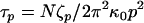, where p is the mode number, and the effective mode friction is 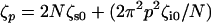. AFM experiments probe the end-to-end vector of the polymer, whose response can be found by summing over all odd modes; in frequency space this gives the following useful closed form expression for the dynamic compliance,

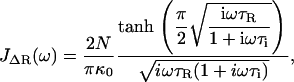(5)

where τ_R = N²ζ_s0/π²κ₀ is the contribution to the relaxation time of the first mode due to solvent friction and τ_i = ζ_i0/κ₀ is the mode-independent contribution to the relaxation time due to internal friction. This model successfully encompasses the behavior of both types of friction; in the limit of large internal friction (τ_R ≫ τ_i), Eq. 2 reduces to a single-mode spring and dashpot model, 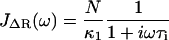and when solvent friction dominates to the Rouse model, given by the limiting form, 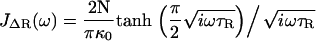, up to a critical frequency 1/τ_i, when the internal friction of high curvature modes dominates to give single mode relaxation again. The fluctuation-dissipation theorem (36), P(ω) = −2 k_BTJ″(ω)/ω is then used to calculate the total power spectrum P(ω) of a RIF polymer combined with a SHO response of the cantilever (see Materials and Methods and Appendix A), where J″(ω) is the imaginary part of a response function J(ω). This model is then used to fit the experimental PSD (for example, as shown in Fig. 3 for cellulose), which then allows extraction of the viscoelastic force spectra of the single molecule: the elastic, internal, and solvent friction constants as functions of force.

RESULTS: VISCOELASTIC FORCE SPECTRA

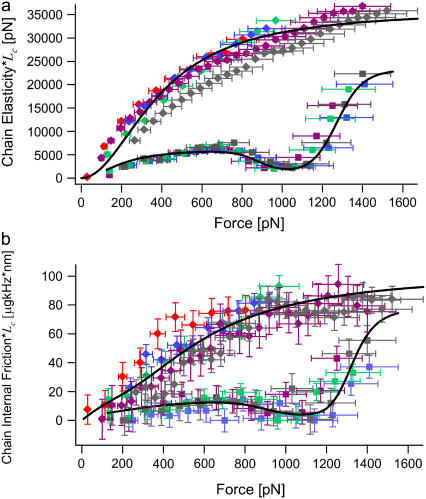
Shown in Fig. 4 a are the effective monomer elastic constants of cellulose and dextran, from the RIF model fits and normalized by contour length, obtained from FJC fits to force-extension data (Supplementary Material, Fig. S1). As previous studies have shown (5–8), at low force (in these experiments), the increase in the elastic constant of cellulose and dextran is due to the reduction of chain conformational entropy as it approaches its contour length, after which contour length elongation with a constant stretching elasticity becomes more favorable. At higher force, however, the minimum in the elastic spectra for dextran at ∼1000 pN, which is absent in the cellulose spectrum, marks a clear signal of the conformational transition in the former.

FIGURE 4.

Viscoelastic force spectrum of cellulose and dextran. (a) Elasticity force spectrum and (b) internal friction force spectrum multiplied by contour length of each molecule L_c (giving the inverses of the compliance and mobility per unit length) for cellulose (solid diamonds) and dextran (solid squares, where L_c is obtained from FJC fits to their respective force-extension traces (Supplementary Material, Fig. S1)). Data points represent measurements using thermal force-clamp spectroscopy, where different colors represent separate single molecules. The solid lines represent curves generated using the full elastic constant (a) and internal friction (b) expressions given in Eqs. 2 and 3, using the average of the parameters determined over all of single molecule experiments (see main text), apart from ζ_θ = 0.6 μg nm² kHz (half the upper bound in the main text) and bistable internal friction parameters derived in the text consistent with a fixed zero-force backward interconversion time τ₂₁(0) = 100 ns (i.e., x₁ = 0.053 nm, τ₁₂(0) = 1 s). Horizontal error bars represent an ∼10% systematic error between experiments in determining the true force scale, through errors in measuring cantilever elasticity and cantilever deflection sensitivity. Vertical error bars represent errors from the fits to the PSDs.

The key advance afforded by using the RIF model in analyzing the PSD is the new information about the two sources of dissipation, not distinguished in previous work (22,23,28,29); the solvent friction and internal friction of the single biomolecule. We find consistently from the RIF analysis that solvent friction is very small within the errors of this experiment (≤0.01 μg kHz). Hence, these chains satisfy 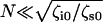(37), where N ≈ 400, which indicates that dissipation is dominated by internal friction at high stretch, and explains the success of the spring and dashpot model in previous modeling of the dissipation of dextran (22,23,28,29). The internal friction force spectrum itself exhibits nontrivial behavior as shown by the comparison of cellulose and dextran in Fig. 4 b, which, in the case of dextran, is in good agreement with previous measurements (22,23,28,29). At low force, where we expect the polymers to be dominated by the physics of an FJC, we note that both polysaccharides show an increasing internal friction with force followed by a plateau. At higher forces, the spectra of cellulose and dextran differ; qualitatively, the minimum in the internal friction force spectrum of dextran at ∼1000 pN coinciding with the minimum in the elastic constant, strongly indicates that it arises from the conformational transition of the glucose ring.

MICROSCOPIC EXPLANATION

To link the features of the experimental elastic and friction force spectra to the conformational transition in dextran, we present a simple model of population dynamics on a discrete bistable energy landscape, which we show predicts the same viscoelastic signature of simple forced transitions, as seen in Fig. 4. The parameters of the discrete bistable model are as described in Fig. 5 a, in which we assume populations obey Boltzmann statistics and dynamics follow Arrhenius transition rates for hops of fixed length Δx. Using an approach similar to the literature (45,46), the effective response of the populations at a frequency ω can be calculated by applying an oscillatory force f₀ cos ωt to the energy landscape, giving rise to nonequilibrium rate constants, λ₁₂(t), λ₂₁(t). The resulting master equation, 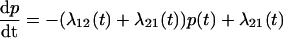, can be solved in linear response (f₀x ≪ k_BT, where x is some typical length scale of the energy landscape) to give in-phase elastic, and out-of-phase dissipative oscillatory populations, such that the ensemble extensional response of the monomer is a first-order relaxation process with effective elastic and friction constants given by

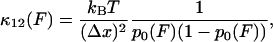(6)

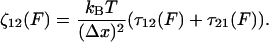(7)

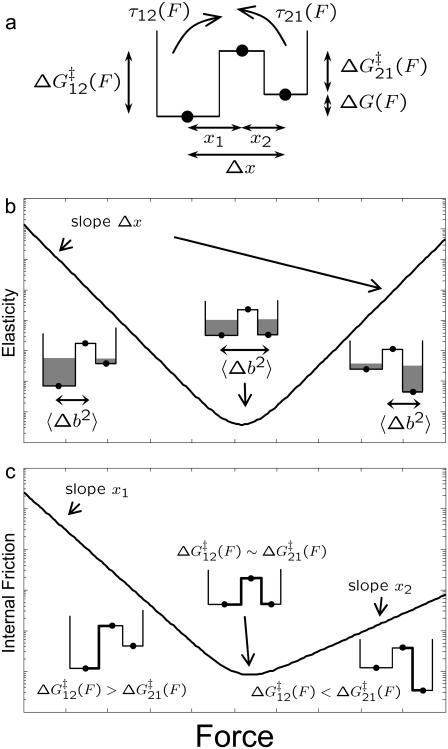
FIGURE 5.

Viscoelastic force spectrum on a discrete bistable landscape. (a) Schematic diagram of the discrete free energy landscape used to calculate the elastic and internal friction force spectra (Eqs. 6 and 7). (b) Elasticity force spectrum on a discrete bistable landscape; force controls free energy difference ΔG(F) = ΔG₀ − FΔx and hence spread 〈Δb²〉 and elastic constant κ₁₂(F) = k_BT/〈Δb²〉) (shaded regions indicate relative populations of two states). Elasticity is entropic in nature as the elastic constant decreases in direction of increasing entropy of monomers. (c) Internal friction force spectrum for a discrete bistable landscape; force controls activation barrier heights (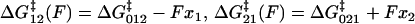), and therefore also the internal friction. Hence, at a given force, internal friction is dominated by the activation barrier that is largest, as indicated by the thick lines in diagrams.

Here, p₀(F) = (1 + e^−βΔG(F))⁻¹ is the equilibrium Boltzmann probability for the short state, and 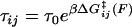are the hopping times between states, with β = 1/k_BT and 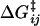the free energy barriers for interconversion. The prefactor to the exponential is given by τ₀ = 2πζ_b/κ_b, where ζ_b and κ_b are the effective friction and curvature of the barrier, and arises from reexpressing the Kramers' first passage problem on a continuous free energy landscape (47) G(x) to a discrete description, where the local density of states of the wells and the barrier are subsumed into the effective free energy differences, as shown in Fig. 5 a. In this description, τ₀, has the simple interpretation of representing the time to diffuse across a distance corresponding to the characteristic thermal width of the barrier .

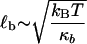Plotting these (Fig. 5, b and c, on a natural logarithmic scale to emphasize their exponential nature) we see a characteristic minimum in both the elastic and internal friction force spectra. In the former case, it is clear that the source of the change in elasticity is entropic in nature and not enthalpic as previously thought (6): force controls the shape of the energy landscape or the relative populations of monomers in short or extended states and hence, the effective configuration space that the monomer can explore. So Eq. 6 is an expression of the equipartition theorem κ = k_BT/〈Δb²〉, where 〈Δb²〉 = (Δx)²p₀(1 − p₀) is the mean-square fluctuations of the monomer for a binomial process. In Fig. 5 b at low (high) force, ΔG(F) is large and positive (negative), hence monomers are confined to the short (long) state, fluctuations 〈Δb²〉 are small and the effective stiffness is large. As force increases (or decreases from high force) the energy difference reduces, populations spread across the two states and the effective size of the box 〈Δb²〉 increases, causing the stiffness to decrease exponentially. The stiffness exhibits a minimum at a critical force 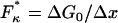, when ΔG(F) = 0 and 〈Δb²〉 is maximum, corresponding to a state of maximum entropy, when the probabilities to be in either of the states are equal. This elastic constant is purely entropic, since any enthalpic contributions to the free energy difference ΔG₀ contribute only linearly to the free energy as the ensemble extension of the monomer is increased.

A surprising consequence of Eq. 7 is that to fully describe the dynamics on a bistable landscape, a new characteristic hopping time, 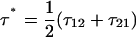, in addition to the recognized relaxation time, 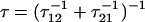, is required. Internal friction is controlled by the energy barriers of the discrete landscape through this hopping time, which is a sum of the times to interconvert from state 1 to 2 and back, from state 2 to 1. Applying a force to the monomers changes the activation barriers to interconversion, which changes the average time to interconvert and thus ultimately, the internal friction. Fig. 5 c shows schematically how the internal friction should vary with force on a discrete bistable landscape. As force lowers the barrier 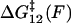of interconverting from 1 → 2, the internal friction should decrease, passing through a minimum at a critical force 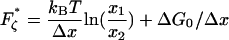, found by differentiating Eq. 7 (when x₁ = x₂ the minimum occurs at exactly 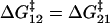). The internal friction then increases again at high force as the barrier for the reverse transition ( 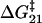) dominates and τ₂₁ becomes large. Interestingly, while the hopping time passes through a minimum, the corresponding relaxation time for populations perturbed from equilibrium must pass through a maximum, since relaxation is dominated by the smallest barrier; on average fluctuations away from equilibrium occur on the hopping timescale τ*, while relaxation back to equilibrium occurs on the timescale τ. We see Eq. 7 is a microscopic fluctuation-dissipation relation for a discrete bistable landscape, which links friction to the timescale for fluctuations due to activated barrier-hopping.

Finally, a useful rule-of-thumb relationship for the position of the transition barrier, x₁ or x₂ (Δx = x₁ + x₂), can be found by the difference in forces at which the minima occur in the elastic ( 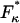) and internal friction spectra ( ):

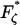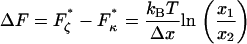(8)

VISCOELASTIC FORCE SPECTRA AS A PROBE OF ENERGY LANDSCAPES

To understand the entire force regime (∼100 → 1500 pN), in addition to the viscoelasticity of the bistable conformational transition, we need to include the physics of the chain at low and intermediate forces before the critical force at which the conformational transition occurs. At low force we use a frictional freely jointed chain (FFJC) model (see Appendix B) of rods interconnected with joints with constant friction ζ_θ. The relaxation of small rotational fluctuations of the rods at high stretch (F ≫ k_BT/b ∼4 pN for b ∼ 1 nm) gives an elastic constant 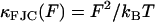and internal friction 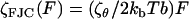. We account for the very local viscoelasticity of stretching a dextran monomer in the short or extended states, using constant stretching elasticities κ₁, κ₂, and internal frictions ζ₁, ζ₂, respectively. We assume that these processes add mechanically in series, since they provide independent and additive extensions to the overall chain length (see Materials and Methods).

Elastic spectrum

Fitting to the elastic force spectra of cellulose and dextran (normalized by contour length), we find excellent agreement as shown in Fig. 4 a, where the solid line represents the total elastic constant (Eq. 2 in Materials and Methods) generated using the average of the parameters determined over a number of single molecule experiments (cellulose, κ₁ = 36,000 ± 18,000 pN/nm, b = 1 ± 0.5 nm; and dextran, ΔG₀ = 16.5 ± 0.4 k_BT, Δx = 0.066 ± 0.005 nm, κ₁ = 10,000 ± 1000 pN/nm, κ₂ = 39,000 ± 2000 pN/nm, and b = 0.63 ± 0.02 nm). These values agree well with the literature (5,6,8,48). We can describe broad features of the whole elastic force spectra for both cellulose and dextran: at low force (below 800 pN), stiffness increases as entropy is lost due to the orientation of monomers along the line of force and finally reaches a plateau representing a constant stiffness due to the enthalpy of stretching the bonds comprising the glucose ring. However, the response of dextran differs dramatically at higher force as the more extended state becomes thermodynamically favorable. Within the framework of the bistable model presented, the subsequent decrease in stiffness can be understood since it becomes more entropically favorable for the chain to elongate.

However, closer examination of the elastic spectra suggests the broad picture just painted, exclude some interesting finer-scaled features. In the elastic spectrum of dextran, at ∼400–500 pN, the model slightly, but consistently, underpredicts the elastic constant below this force and overpredicts it above this force. This plateau may be explained by the entropic elasticity of other internal states of the α-(1→6)-linked glucose ring. One possibility is rotation about the C5–C6 bond in dextran (5); however, NMR experiments (49) measuring glucose rotamer populations and detailed molecular dynamics studies (20) both suggest significant elongation from this mechanism should only occur at forces, ∼≤100 pN. Similar undulations or plateaus can also be observed beyond 800 pN in cellulose, suggesting entropic contributions to stretching, as well as enthalpic backbone elongation; although in this case the number of datasets is more limited. To understand these features in structural terms will require a combination of more data and detailed molecular dynamics and/or ab initio simulations. More generally, detection of these previously unseen features indicates the increased sensitivity afforded by the direct measurement of elasticity from thermal fluctuations.

Internal friction spectra

In performing fits to the internal friction spectra, all elastic parameters are constrained to values obtained from fits to the elastic spectra (see Materials and Methods). Below we discuss quantitative values of each of these friction processes separately, even though actual fits were performed globally across the whole force range.

Firstly, we examine the effective internal friction associated with stretching the glucose monomers in their various conformations. For cellulose, we find ζ₁ = 110 ± 50 μg kHz and for dextran, ζ₁ = 25 ± 10 μg kHz and ζ₂ = 120 ± 50 μg kHz, for the short and extended states, respectively. Strikingly, these numbers are roughly seven orders-of-magnitude larger than the friction expected due to solvent (ζ = 6πηb ∼ 10⁻⁵ μg kHz for b ∼ 1 nm). The most plausible source for such a high local effective friction is roughness in the free energy landscape. A model of dynamics on a rough Gaussian landscape with RMS energy fluctuations ɛ (50) predicts a sensitive enhancement to the effective friction constant ζ* = ζ exp(ɛ/k_BT)², giving an effective roughness for stretching cellulose and dextran as ɛ ≈ 4 k_BT. For comparison, recent constant loading rate experiments (51) on the protein imp-β, using theoretical results by Hyeon and Thirumalai (52), suggest a Gaussian roughness of order ɛ ≈ 5.7 k_BT. In the case of these polysaccharides, this roughness may arise from transition barriers between the many conformations that the glucose ring can adopt; for example, there are in total 14 canonical chair, boat, and twist-boat conformations, separated by 12 half-chair and 12 envelope conformational transition states (32,34), which will contribute to extension and may become more or less favorable under tension. Accounting also for the three discrete rotational states of the hydroxyl groups of the six carbon atoms of glucose, there are ∼30,000 identifiable canonical conformations of the glucose ring. If we then include solvent effects that may promote or disrupt inter- and intramolecular hydrogen bonding as well as other water-mediated structures (53), it is not too difficult to see that, in principle, this may give rise to a very rugged landscape, as barriers are overcome for stretching a polysaccharide chain.

At low force, we see a similar picture for the joint friction of the FFJC model, obtaining values of the order ζ_θ ∼ 1 μg nm² kHz (cellulose, ζ_θ = 0.9 ± 0.7 μg nm² kHz; while for dextran errors from fits suggest ζ_θ < 1.2 μg nm² kHz). These numbers are roughly six orders-of-magnitude greater than the friction of a rod of length b rotating in a solvent (ζ_θ ∼πηb³/4 ∼ 10⁻⁶ μg nm² kHz (54)). We can again appeal to an underlying molecular explanation, where joint friction is due to hopping between dihedral angular states, with an average hopping time of τ_hop ∼ ζ_θ/k_BT ≈ 0.25 ms. Again, these very slow dynamics are suggestive of an underlying roughness to the rotational free energy (ɛ ≈ 3.7 k_BT, where ζ*/ζ ∼ 10⁶).

In the case of dextran, the marked decrease in internal friction at ∼1000/pN, contains information on the dynamics of interconversion between the short and extended states, for which Eq. 7 provides a simple model. However, due to the low frequency restriction of the data, fits are in general underdetermined. To further constrain our fits, we use Eq. 8. Inspecting Fig. 4, a and b (solid squares), indicates that ΔF ≈ 0 ± 100 pN, given that the spacing of points in the spectra is ∼100 pN. However, negative values of ΔF imply from Eq. 8 a transition state that is closer to the short state (x₁/x₂< 1), which is not feasible on geometric grounds, given that its curvature is roughly four-times smaller than the extended state (κ₁/κ₂ ≈1/4) and that the forward free energy barrier must obey 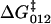> ΔG₀(= 16.5 k_BT). Hence, a reasonable assumption is that 0 < ΔF < 100 pN, implying the transition state is closer to the more extended state, in the region 0.033 < x₁ < 0.053 nm. Fitting to the friction spectra, so as to satisfy this constraint on x₁, we find 1 ns < τ₂₁(0) < 100 ns and 0.01 s < τ₁₂(0) < 1 s (see Materials and Methods, above). From Kramers' theory (47) of activated diffusive barrier crossing, the prefactor to the exponential Boltzmann factor is related to the curvature κ_b and friction ζ_b of the barrier, which when mapped onto a discrete landscape is given by τ₀ = 2πζ_b/κ_b. A priori, we do not know the value of either the friction or curvature of the barrier. If we assume that ζ_b is simply solvent friction and thus of order ∼10⁻⁵ μg kHz, then using the bound on the zero-force backward hopping time τ₂₁(0), as an upper limit for τ₀, we find that the curvature of the barrier is bounded by (0.1 < κ_b < 10) pN/nm, which is very shallow. 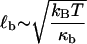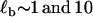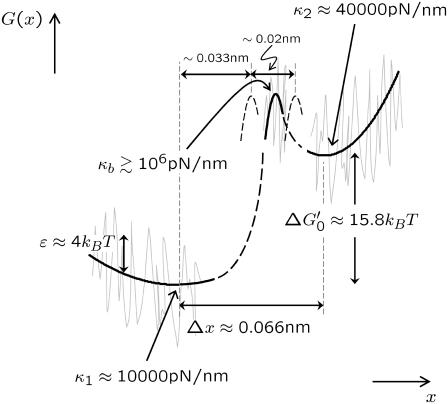The thermal width for such a barrier , would then be between nm, which is larger than separation between states Δx ∼ 0.05 nm. A more realistic estimate can be found by assuming the barrier is rough in similar fashion to the roughness in the wells representing the short and extended states, as discussed above. If we assume ζ_b ∼ 10 → 100 μg kHz, then the approximate bound on the barrier curvature is (10⁶ < κ_b < 10⁹) pN/nm, which is very sharp. This gives a far more reasonable estimate of the thermal barrier width of 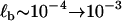nm. We see that the analysis of the effective bistable friction of barrier hopping, also strongly suggests that there is a roughness to the underlying landscape of dextran. To summarize our quantitative findings, Fig. 6 shows a graphical to-scale reconstruction of the free energy landscape based on the parameters extracted from the modeling of the viscoelastic force spectra of dextran.

FIGURE 6.

To-scale reconstruction of continuous free energy landscape of α-(1→6)-linked glucose, based on parameters extracted from theoretical modeling of the viscoelastic force spectra of dextran. Dashed features indicate areas of landscape that are uncertain; for example, position of barrier, or information unattainable with current experiments like the activation barrier heights. Barrier curvature shown is κ_b = 10⁶ pN/nm. Shaded lines indicate a roughness to the landscape with RMS deviation ɛ ≈ 4 k_BT, as a plausible interpretation for significantly enhanced friction of wells. 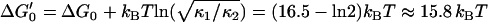is the free energy difference between the minima of a continuous landscape, which excludes the entropy of vibrations of the wells.

CONCLUSIONS

In summary, we have shown how macroscopic ideas of elasticity and friction can be extended to the study of the energy landscape of conformational transitions. Eqs. 6 and 7 are in essence microscopic equivalents of the equipartition theorem and the diffusive fluctuation-dissipation relation, where the spatial and temporal properties of the fluctuations are determined by the shape of the energy landscape, which in turn determines its effective elastic and friction constants. In the case of dextran, applying tension to its energy landscape drives the chain to a state of increased entropy, where the elastic and friction constants decrease as the populations become more spread and barriers are lowered. Of particular importance is the necessary distinction between the hopping time that defines the average timescale of the fluctuation of populations away from equilibrium and the more commonly used relaxation time for populations to return to equilibrium on a bistable landscape; as Eq. 7 shows clearly it is the hopping time τ* that controls the effective friction or dynamical resistance to conformational change on a bistable landscape. The difference between these two times is an effective parallel combination of barrier transition times, τ_ij for the hopping time and a series combination for the relaxation time, so that it is the largest barrier that dominates the friction, while it is the smallest that dominates relaxation. Using these ideas we have obtained new information on the dynamical properties of the energy landscape of the chair-to-boat transition of the α-(1→6) glucopyranose ring, such as the shape and position of the barrier and its local roughness: properties that are unattainable using conventional force spectroscopic techniques on single polysaccharide chains. These results suggest that such experiments combined with appropriate theoretical modeling, applied to more complicated examples of conformational change, such as stretching transitions in DNA and RNA, and in particular to emerging data on the elasticity and dissipation from the fluctuations of unfolding and refolding proteins, could potentially reveal previously unseen fine-scaled dynamical information about these mechanical processes. However, these ideas have wide implications beyond the immediate results presented, from applications to the field of molecular nanotechnology (55), where the microscopic theory of bistable elasticity and friction may guide and constrain engineering design, to understanding fundamental mechanical processes of molecular biology, such as the action of molecular motors (15,16), allosteric signaling (17,18), and mechanotransduction (56).

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

APPENDIX A: FREQUENCY RESPONSE OF PARALLEL SYSTEM ELEMENTS

Here we derive the total dynamic compliance or response function J_T(ω) for the cantilever and polymer in parallel, which each have response functions J_X(ω) and J_ΔR(ω), respectively. Starting in the time domain, we can write down the solution for the cantilever and polymer motion as

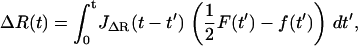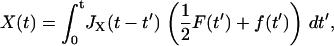where F represents an external force applied to the system and f the internal force that they share according to Newton's Third Law. By definition, the Green's response of the whole system is its response to a unit impulse of force, so we let F(t) = ηδ(t), where δ(t) is the Dirac δ-function and η the size of impulse. This gives

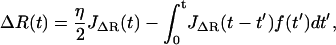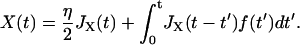Taking the Fourier Transform of these (presuming all response functions are zero for t < 0) we find

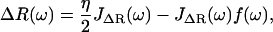(9)

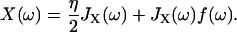(10)

Thus, using the fact that the cantilever and polymer displacements must be the same for all times (ΔR(t) = X(t)), we can solve for the internal force f(ω),

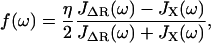which can then be plugged back into Eq. 9 or 10, to give the total dynamic compliance as the displacement response due to a unit δ-function input:

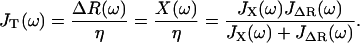APPENDIX B: FRICTIONAL FREELY JOINTED CHAIN (FFJC) AT HIGH STRETCH

To model the molecular viscoelasticity of a polymer at forces which are small (F < 500 pN), we develop a frictional FJC (FFJC) model of rods interconnected with joints with constant friction and calculate the form of ζ_FJC(F). We focus on a single monomer, assuming that each rod of the FJC is statistically independent, so the stiffness of each rod will add mechanically in series to the stiffness of the whole chain. Typical monomer/rod lengths for polysaccharides are b ∼ 1 nm, so our experiments are in the regime where F ≫ k_BT/b and the elastic spectrum can be calculated from statistical mechanics as

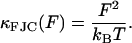(11)

To model the internal friction of a FJC we again focus on a single monomer/rod in the high force regime and consider that to rotate such a rod there is some friction ζ_θ opposing this motion, which we presume is constant and associated with the internal friction of joints between rods. In the spirit of the FJC, we assume that this friction force depends only on the rate of change of angle with respect to the applied force and is independent of the orientation of other rods in the chain. The rotational equation of motion for a segment or rod of length b held under a large tensile force F (Fb ≫ k_BT) will be

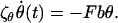(12)

Now we consider how these dynamics project onto the line of applied force. The change in projected length of the monomer compared to its actual length will be Δb = b(1 − cos θ), which in the small angle limit gives

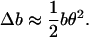(13)

Differentiating Δb, and using Eqs. 12 and 13, we find its equation of motion to be

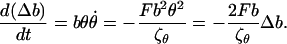(14)

This has an exponentially decaying solution 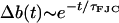, with time constant

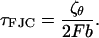(15)

Now τ_FJC = ζ_FJC/κ_FJC and thus, using Eq. 11, the effective friction along the z direction is then

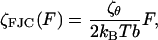which predicts a linear increase of the internal friction constant with force, presuming ζ_θ is constant.