Quantitative Membrane Electrostatics with the Atomic Force Microscope

Abstract

The atomic force microscope (AFM) is sensitive to electric double layer interactions in electrolyte solutions, but provides only a qualitative view of interfacial electrostatics. We have fully characterized silicon nitride probe tips and other experimental parameters to allow a quantitative electrostatic analysis by AFM, and we have tested the validity of a simple analytical force expression through numerical simulations. As a test sample, we have measured the effective surface charge density of supported zwitterionic dioleoylphosphatidylcholine membranes with a variable fraction of anionic dioleoylphosphatidylserine. The resulting surface charge density and surface potential values are in quantitative agreement with those predicted by the Gouy-Chapman-Stern model of membrane charge regulation, but only when the numerical analysis is employed. In addition, we demonstrate that the AFM can detect double layer forces at a separation of several screening lengths, and that the probe only perturbs the membrane surface potential by <2%. Finally, we demonstrate 50-nm resolution electrostatic mapping on heterogeneous model membranes with the AFM. This novel combination of capabilities demonstrates that the AFM is a unique and powerful probe of membrane electrostatics.

INTRODUCTION

Several lipid species found in biomembranes are charged at physiological pH. Their presence in lipid bilayer membranes results in electrostatic surface potentials different from the bulk electrolyte and thus alters the local concentrations of ions and small molecules (1). While these changes in the surface electrostatics can affect biomembrane function in a nonspecific manner, the large variety of charged lipid species and their anisotropic distribution within biomembranes suggest that the charged lipids participate in specific interactions as well. For example, the phosphoinositides, anionic lipids with valency up to 4 at neutral pH, have been linked to a surprising number of biological processes, including enzyme activation, cytoskeletal attachment, ion channel activation, and exocytosis (2). The specificity appears to rely on a combination of electrostatic, hydrophobic, and enthropic interactions (3). McLaughlin and Murray have argued that this multiplicity of function is achieved in part due to phosphoinositide regulation by electrostatic effects on the spatial organization of lipids in the membrane (4). In addition to formal lipid charges such as those on the phosphoinositides, a significant density of molecular dipoles exists at the transition between the headgroup and hydrophobic regions of the membrane (5). These dipole moments can significantly affect the membrane surface potential, especially for zwitterionic lipid membranes with no net formal charge (6,7). The dipole potential has been linked to biological functions such as protein adsorption and insertion into membranes (8,9), as well as effects of anesthetics (10).

A thorough understanding of these electrostatic contributions to biomembrane function would ideally begin with a complete characterization of the potential throughout the membrane. However, such a characterization can neither be predicted precisely nor measured unambiguously, even for simple model membranes composed of a single lipid. The difficulty arises due to the extreme complexity of the electrostatic environment, which includes a high density of formal charges, molecular dipoles, bound water molecules, and counterions in a soft interface at the site of large dielectric anisotropy. Despite this complexity, the Gouy-Chapman theory, which assumes a nondiscrete surface charge density and treats the aqueous phase as a constant dielectric medium, can be applied to lipid membranes to describe effective surface potentials at long range. The analysis can be augmented by charge regulation mechanisms to accurately model experimental measurements of the lipid membrane surface potential (11). How this effective membrane surface potential depends on the detailed molecular structure in the bilayer interface is unclear.

Many probes and techniques have been developed to measure the electrostatic potentials of lipid membranes, each having their own strengths and limitations. Following Cevc, they fell into two classes (1). The first class observes electrostatic effects on an inherent property of the membrane without the addition of extraneous molecules. These methods include titrations, ion distribution studies, and ζ-potential and conductance measurements. While these methods should be nonperturbing, it can be difficult to eliminate contributions from nonelectrostatic interactions. The other class relies on molecular probes associated with the membrane whose properties are sensitive to the electrostatic environment. While molecular probes are typically sensitive and can provide high spatial and temporal resolution, one must be mindful of the probe's impact on the membrane system and the accuracy of model used to interpret or calibrate the data.

The atomic force microscope (AFM) is a highly noninvasive probe of membrane electrostatics. The AFM images the biomolecular structures in aqueous solution with nanometer-scale resolution by scanning a sharp probe over the sample and measuring force interactions (12–14). As an imaging tool, the AFM is unique since it yields structural information on single biomolecules under near-native conditions. The AFM can also hold the tip over a specified position and measure force as a function of tip-sample separation. This force-curve analysis has been applied to molecular recognition interactions (15–17), protein unfolding (18), and nonspecific hydrophobic, hydration, van der Waals, and electrostatic interactions (19,20). By working at low electrolyte concentrations (0.5–5 mM) and tip-sample separations greater than a few nanometers, one can reach a regime where electrostatics dominates the long-range tip-sample interaction.

Soon after AFM imaging was demonstrated in fluid (21), Butt derived the electric double layer force (22) between a spherical tip and planar sample in electrolyte solution based on an expression for the pressure between two charged planes in an electrolyte (23). The force can be described by

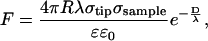(1)

where R is the tip radius, λ is the Debye screening length, σ_tip and σ_sample are the tip and sample charge densities, and D is the tip-sample separation (23). This derivation required several assumptions, including small surface potentials, tip-sample separations larger than the Debye length, and tip radii larger than the separation, R ≫ D ≫ λ.

Despite these approximations, this expression successfully described experimental measurements in terms of the force dependence on tip-sample separation, tip radius, electrolyte concentration, and pH (20,24–30). It has been widely applied to electrostatic interactions between Si₃N₄ probe tips and inorganic surfaces, as well as lipid membranes (29–34). Another approach is to numerically simulate the tip-sample force by solving the nonlinear Poisson-Boltzmann equation under certain boundary conditions (23,35–38). To get the membrane surface electrostatic information, one can interpret the experimental data with Eq.1 or with a numerical simulation. To make a quantitative measurement using an analytical approach, one must measure all the constant parameters in Eq. 1. If one uses a numerical approach, the proper boundary conditions must also be chosen.

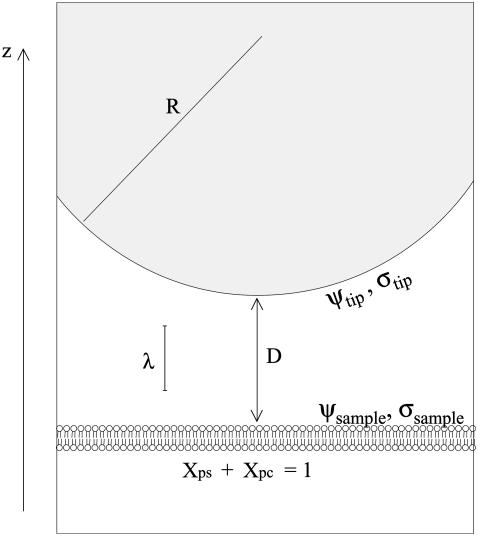
This article addresses three aspects of the AFM as a probe of membrane electrostatics. First, due to its high sensitivity, the AFM can detect screened double-layer forces at separations up to several Debye lengths, making it an extremely noninvasive probe. Second, the AFM can provide a quantitative measure of the effective membrane surface potential based on a simple electrostatic model. Third, the AFM can image electrostatic properties with resolution at the nanometer scale beyond that which is possible with optical microscopy. Fig. 1 displays a scaled schematic of the tip-sample region and defines parameters used throughout the article.

FIGURE 1.

A scaled schematic diagram of the tip-sample region. The tip is characterized by its radius (R), surface potential (ψ_tip), and charge density (σ_tip). The lipid membrane is characterized by its mole fractions of PS (X_ps) and PC (X_pc) lipids, as well as its surface potential (ψ_sample) and charge density (σ_sample). The tip-sample separation is represented by D along the z axis, and the electrolyte is characterized by the Debye length, λ.

MATERIALS AND METHODS

Preparation of supported lipid membranes

Lyophilized dioleoylphosphatidylserine and dioleoylphosphatidylcholine (PS and PC, Avanti Polar Lipids, Alabaster, AL) were dissolved in chloroform and mixed at varying PS mole fractions: X_ps = 0.05, 0.1, 0.2, 0.3, 0.4, and 0.5. The mixtures were dried under nitrogen gas, placed under low vacuum for 1 h, and then hydrated with deionized water for a final lipid concentration of 2 mg/mL. The lipid solutions stood overnight in a dark, room-temperature environment followed by vigorous agitation for 1 h. The resulting multilamellar vesicle solutions were refrigerated and stored for up to two weeks. Supported lipid bilayer membranes for AFM analysis were formed on mica substrates by vesicle fusion (39). A 100 μL drop of the multilamellar vesicle solution at a lipid concentration of 20–200 μg/mL (diluted from stock in deionized water) was placed on the substrate for 20 min at 35–40°C. Higher lipid concentrations were needed for the mixtures with a greater proportion of PS. The sample was then rinsed with deionized water and placed under an ∼0.5 mM solution of Tris buffer at pH 7 for AFM imaging and analysis in fluid tapping mode (Multimode NanoScope IV, Veeco Metrology, Santa Barbara, CA).

Force curve acquisition and analysis

All AFM experiments were carried out with silicon nitride probes (DNP, cantilever C, Veeco Probes). Both tip and sample were immersed in 0.5 mM Tris buffer (pH 7) throughout the experiment. To record force curves over lipids, the AFM tip was situated over a lipid membrane by first imaging the topography (see Fig. 2 a) and then positioning the tip over the lipid region. For reference measurements, force curves were recorded over the silicon nitride chip of a probe from the same wafer as the tip. The gold coating on this chip was first etched with aqua regia to reduce interference from the reflected AFM laser beam. Force curves were recorded with the Nanoscope software (version 5.30r1) with 10,240 data points over an 800-nm scan range at 1.4 Hz, with tip retraction triggered for a maximum cantilever deflection corresponding to ∼5 nN.

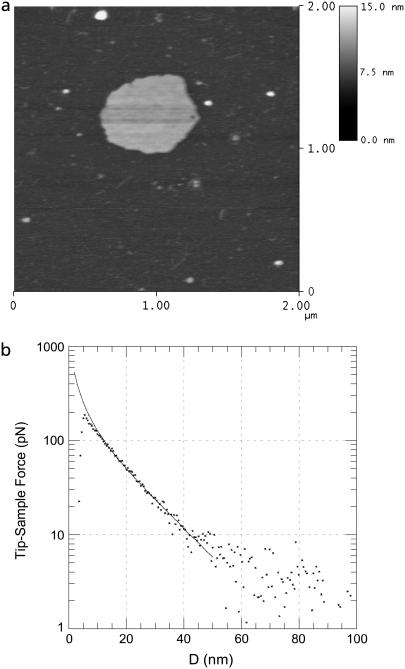
FIGURE 2.

AFM analysis of a lipid membrane. The topographic image (a) of a supported lipid membrane on mica displays the expected height. The force curve (b) demonstrates the high force sensitivity achieved after the analysis and averaging described in Materials and Methods. The points represent the measured data and the line is from a numerical simulation.

The raw force curves (cantilever deflection voltage on the y axis versus z piezo position on the x axis) were exported and read into MatLab (Natick, MA) where they were converted to force versus tip-sample separation, D, by the following methods which are similar to those described previously (24,34):

1. A y-axis offset was applied to set the deflection voltage equal to zero for large tip-sample separation.

2. An interference intensity function was fit to the large tip-sample separation region and the resulting function was subtracted from the entire force curve to compensate for optical interference between reflections from the cantilever and the sample surface.

3. A line was fit to the contact region of the force curve to determine the cantilever deflection sensitivity, s, so that the curve could be converted from tip deflection voltage to relative tip deflection position in nm.

4. The cantilever deflection was subtracted from the sample z position to convert the force curve to a plot of tip deflection versus tip-sample separation, D, rather than sample position.

5. The point of zero tip-sample separation was defined as the intersection of the lines that fit the large tip-sample separation and the contact region of the force curve.

6. The cantilever deflections were converted to forces with the measured spring constant (see below).

7. Hundreds of such force curves were averaged before carrying out the electrostatic analysis described below.

Tip charge density measurement

The tips were made of silicon nitride, which has both silanol and silylamine surface functional groups resulting in an amphoteric surface with charge density that varies with electrolyte concentration and pH (40). To calibrate measurements for the unknown tip charge density, σ_tip, one can measure force curves over the sample of interest and a reference surface with known surface charge density (41). This provides a quantitative measurement of σ_sample, which is of the proper order of magnitude, but the result is limited by the accuracy of the reference value. For example, alumina has been used as a reference surface and values for its charge density can be found in the literature, but such values may depend strongly on electrolyte conditions and surface history (42). To better characterize σ_tip we employed a reference surface identical to the tip. Silicon nitride tips were taken from a wafer (DNP, Veeco Probes), which provided silicon nitride reference surfaces with an identical preparation, stoichiometry, and history as the tip. Force curves were recorded over the identical silicon nitride reference surface and used to find σ_tip by the analysis described below. This strategy has been applied in the past using tips and reference surfaces covered with identical self-assembled monolayers (36).

Tip radius measurement

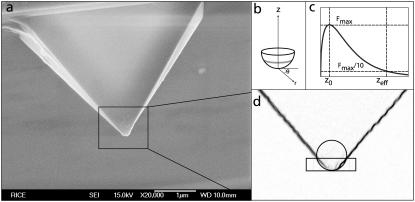
The radius of each individual AFM tip was measured from scanning electron microscope (SEM) images (Fig. 3). When the radius was determined by simply inscribing a circle in the tip image, the result was very sensitive to the tip shape and the arbitrary vertical extent of the tip that was considered. We therefore developed a procedure based on the vertical extent of the tip, which contributes to the tip-sample force. For a hemispherical tip facing a plane surface, the electric double-layer force contribution from a circular strip at height z is approximately proportional to

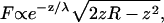(2)

based on the derivation of Eq. 1 (23). This function peaks at some height 0 < z < R, demonstrating that the largest force contribution is not from the tip apex, as expected due to its vanishing surface area. For each SEM image of a tip, an initial guess of the radius, R_initial, was entered into Eq. 2, and the height where the force contribution falls to 1:10th of its maximum value, z_initial, was determined. A rectangle of height z_initial was drawn over the SEM image, based at the tip apex, and a circle was inscribed such that it contacted the apex and the two intersecting points between the rectangle and tip edge. The radius of this circle was inserted into Eq. 2 and the processes repeated until successive estimates converged to give the final tip radius. No conducting layer was deposited on the tip before imaging; the silicon nitride is conductive enough for the mean ± SE. A carbon layer less than 1-nm thick may coat the tip during imaging, but we consider that the radius of tip does not change appreciably during the mean ± SE imaging process. The surface chemistry of tip may be changed after the mean ± SE image. To exclude this effect, all the radius measurements were carried out after the AFM experiments.

FIGURE 3.

The determination of tip radius, R, by electron microscopy. A scanning electron micrograph of the tip (a) is scaled, inverted, and edge-filtered to enhance the tip periphery (d). The force contributions from different sections of the tip (b) show a peak above the apex (c). This calculation enables a recursive procedure (d) for defining the tip radius in terms of contributions to the electrostatic force.

Spring constant measurement

The cantilevers employed have a nominal spring constant k = 0.32 N/m. For improved accuracy, the spring constant of each tip was directly measured by the added mass method (43). Briefly, the thermal resonance frequency of the cantilever was measured before and after the addition of a known mass, M, by micromanipulation, yielding frequencies ν₁ and ν₂, respectively. The known mass was a 6-μm spherical silica bead with a well-defined shape and density (Bangs Laboratories, Fishers, IN). The shift in resonant frequency yields the spring constant using the following relation:

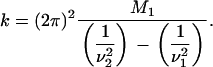(3)

Measured values for the cantilever spring constants ranged from 0.25 to 0.35 N/m.

Charge density determination: analytical

Force curves were analyzed with Eq. 1. The natural logarithm of the force was plotted versus tip-sample separation and fit to a straight line,

(4)

such that the slope yields the Debye length and the y intercept yields the factor in parentheses. For the force curve data from the reference silicon nitride samples, σ_tip = σ_sample, so the y intercept provides the tip charge density with the other parameters measured as described above. Next, the process was repeated using the force curves from the lipid samples and the measured σ_tip value to obtain the sample charge density, σ_sample. The error was determined by propagating uncertainties from the tip radius (R), spring constant (k), sensitivity (s), and fit parameters.

Charge density determination: numerical

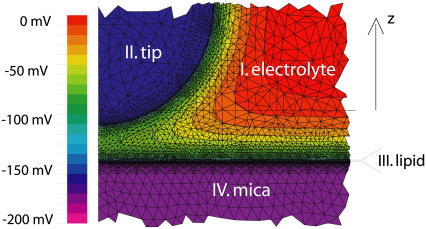
Force curves were also analyzed with numerical solutions to the full nonlinear Poisson-Boltzmann equation using a commercial software package (FlexPDE 5.0.8, PDE Solutions, Antioch, CA). To simulate the interaction between a silicon nitride AFM tip and a supported lipid membrane, the domains displayed in Fig. 4 were set up. Region I corresponded to the electrolyte, where the Poisson-Boltzmann equation was defined as

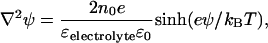(5)

with electrostatic potential ψ, 1:1 monovalent electrolyte ion density n_o, electron charge e, Boltzmann constant k_B, and dielectric constant ɛ_electrolyte = 79. Region II represented the silicon nitride tip (ɛ = 7), region III represented a 5-nm thick layer to simulate the lipid membrane (ɛ = 2), and region IV represented the mica (ɛ = 6). To simulate the reference measurement between the silicon nitride AFM tip and the flat silicon nitride substrate, regions III and IV were merged into one layer and set to ɛ = 7. The Laplace equation ∇²ψ = 0 determined the potential in regions II–IV. At the interface of the tip and the electrolyte, as well as at the interface of the lipid membrane and the electrolyte, constant field boundary conditions were applied (35) to define the charge densities on the sample and tip,

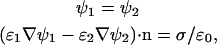(6)

where 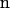represents the surface-normal direction pointing to the electrolyte solution, ψ₂ is the potential in the electrolyte, and ψ₁ is the potential of material on the other side of interface (22). FlexPDE employs a modified Newton-Raphson iteration procedure to solve the equations. An adaptive mesh was generated within the domain at the beginning of simulation. The program then iterated the mesh-refinement procedure until a tolerance of 10⁻⁵ was achieved. The electrostatic potential and the electric field were evaluated at the tip-electrolyte boundary and exported for force calculations.

FIGURE 4.

A portion of the grid used for numerical simulations of the tip-sample interaction.

Rotation of the simulation domain about the z axis generates a closed surface S for the boundary of the tip layer. The total force applied on the tip is given as the surface integral

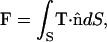(7)

where 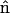is a unit vector normal to the surface and T is the total stress tensor,

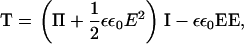(8)

which includes both an osmotic pressure term

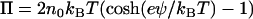(9)

and a Maxwell stress term. I is the unit dyadic. The tip-sample force measure by AFM can be described as the z component of the surface integral,

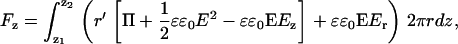(10)

and calculated numerically based on the electrostatic field values and potentials exported from the simulation (37,44). Z₁ and Z₂ are the z-axis limits of the sphere. By changing the tip-sample separation, force curves were simulated. These curves were compared to the silicon nitride reference data, and σ_tip and σ_sample were adjusted to achieve a good match. Once the tip charge density was known, the same procedure was carried out on the lipid data to determine its charge density.

Gouy-Chapman-Stern model of the charged membrane

The charge density and surface potential over the mixed PC/PS membranes were calculated in the following way. X_PS and A, the membrane area per lipid, together give the surface density of PS lipids. However, electrolyte cations can bind to form a Stern layer on the PS headgroups to reduce the membrane charge density. If one assumes that this binding follows a Langmuir isotherm, the charge density due to the remaining charged lipids is

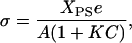(11)

where C is the molar concentration of the cation, and K is its association constant to the lipid headgroup. However, one must consider that the surface potential will alter the surface cation concentration according to the Boltzmann relation,

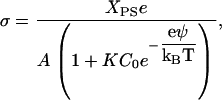(12)

where C₀ is the bulk molar concentration of the electrolyte and ψ is the surface potential. The charge density is related to the surface potential by the Grahame equation, so Eq. 12 can be rewritten as

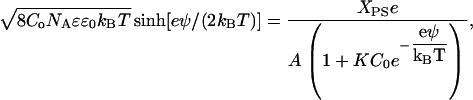(13)

where N_A is Avogadro's number. Equation 13 yields the predicted surface potential as a function of X_ps based on three well-characterized parameters: the area occupied per lipid molecule (A), the electrolyte concentration (C_o), and association constant of the electrolyte cation to the PS headgroup (K).

RESULTS AND DISCUSSION

To test the quantitative surface charge density measurement method for biomembrane analysis, we have measured force curves over supported lipid membranes of zwitterionic PC with increasing mole fractions of anionic PS (X_ps) to increase the surface charge density and potential in a predictable way. Electrostatic measurements were made in buffer with different tips on membranes with X_ps varying from 0.05 to 0.5. AFM imaging guided the tip to a position over the lipids and confirmed that it remained there throughout the force-curve measurements. Fig. 2 displays such an image and an example force curve from an X_ps = 0.2 membrane which has been averaged and processed as described above. The curve demonstrates the extreme sensitivity of the AFM for electrostatic measurements, since double layer forces are observed at a tip-sample separation >60 nm, which corresponds to over four Debye lengths.

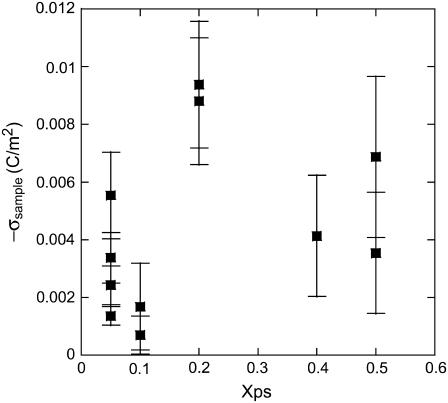
All parameters in Eq. 1 were measured as described above. Each measured σ_sample therefore requires force curves over the lipid membrane and over the reference silicon nitride surface. Fits to Eq. 4 yield σ_sample as a function of X_ps, plotted in Fig. 5. The error bars reflect contributions from the uncertainty in each parameter. The use of Eq. 1 clearly leads to a result that shows no discernable trend, and the variation cannot be accounted for by the error. This is not entirely unexpected, considering the approximations that go into the derivation of Eq. 1. In our measurements, the tip radii are significantly larger than the Debye length. In addition, the values of D that must be fit approach λ at short range and exceed R at long range. Also, the surface potentials greatly exceed the range where the linearized Poisson-Boltzmann equation is applicable. Note that the negative result of Fig. 5 does not necessarily mean that the functional dependences in Eq. 1 are inaccurate. Several experiments have confirmed that Eq. 1 accurately predicts the force dependence on D, R, λ, and pH, but usually by only varying one parameter (20,24–30,45). Also, the analytical model significantly underestimates the magnitude of the sample charge density.

FIGURE 5.

The lipid membrane charge densities determined by applying Eq. 1 to the experimental force curves. The data do not follow the expected trend with phosphatidylserine mole fraction.

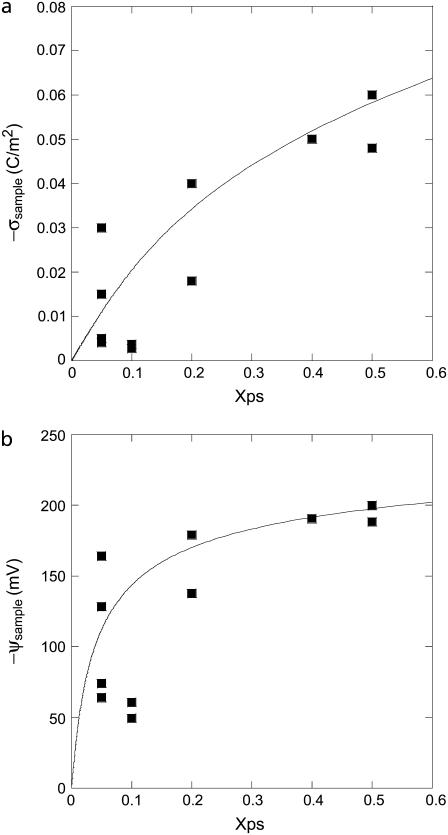
To achieve quantitative measurements of σ_sample, we turned to numerical simulations that do not require such restrictive approximations. Force curves were simulated based on numerical solutions of the full nonlinear Poisson-Boltzmann equation. The analysis was carried out by manually adjusting σ_sample in force-curve simulations and comparing to experimentally measured force curves in the long-range region (1–4 Debye lengths). The reference silicon nitride data were used to characterize σ_tip in a similar manner to that used in the analytical procedure. Unlike the analytical results, the numerical data follow the trend displayed in Fig. 6. The numerical results are in quantitative agreement with a simple Gouy-Chapman-Stern model of the membrane, which accounts for charge regulation (47). In the model, electrolyte cations can bind to the PS headgroups to form a Stern layer that neutralizes their contribution to the effective surface charge density. The cation binding is described by a Langmuir isotherm and the effect of the surface potential on the cation surface concentration is taken into account. The model therefore has only three input parameters: the bulk electrolyte concentration, the area per lipid, and the binding constant of the electrolyte cation to the PS headgroup. Note that the solid line in Fig. 6 is not a fit, but rather the results of this model for C_o = 0.47 mM, A = 0.7 nm², and K = 1 M⁻¹ (11).

FIGURE 6.

Lipid membrane charge densities and surface potentials determined by a numerical analysis of the experimental force curves. The data (squares) follow the curves predicted by the Gouy-Chapman-Stern model (line).

In the numerical simulations, charge regulation was not included in the boundary condition (47) since a simple constant field boundary condition was applied evenly to the entire sample surface. Rather, charge regulation was demonstrated by adjusting the boundary conditions to fit the data, and then showing that the resulting charge densities match the Gouy-Chapman-Stern charge regulation model. This method of analysis is not exact since the presence of the tip locally alters the surface potential, thus requiring a boundary condition that allows a spatially varying surface field. However, the omission did not cause a significant deviation since the data were analyzed only for separations where the interaction was significantly screened. Analysis of the numerical simulations revealed that the difference in membrane surface potential between points directly below the tip and off to the side where the tip had no effect was only 0.2–2%. In addition, note that the force signal is largely determined by the membrane region directly below the tip, with variations in the potential elsewhere having little effect.

Two other charge regulation mechanisms were not considered. The effect of the surface potential on protonation of the PS headgroup was not included since the pK of the headgroup is <2, very much lower than the pH of the buffer (48). Also not included was a charge regulation mechanism specific to lipid membranes that takes into account the mobility of the charged lipids (49). Unlike an inorganic surface, charged headgroups in a fluid lipid membrane can move and redistribute in response to a potential. Calculations of this effect find that it can be significant for cases such as DNA bound to a cationic membrane, but the difference between a mobile lipid model and a homogenous fixed lipid model drops significantly beyond one-fifth Debye length. However, as described above, the tip's effect on the potential at the membrane is small and only data beyond one Debye length were included in the calculation. Our approximate treatment of charge regulation and boundary conditions appears justified by the excellent agreement between the data and theoretical model with no adjustable parameters.

Fan and Federov have described numerical simulations of the interaction between an AFM tip and a deformable anionic lipid membrane considering both electrostatic and hydrodynamic interactions as well as the equilibrium shape of the membrane (38,50). These calculations can provide insight into the forces and motions of biomembranes during AFM imaging of living cells. Note that our experiments do not require a hydrodynamic analysis since we studied supported membranes, which are not highly deformable. Our quantitative results suggest that if the nonlinear Poisson-Boltzmann equation were employed in the simulations of Fan and Federov, an improved analysis of cell AFM imaging could be performed. In addition, one could include other factors such as mobile charge lipids (49) and cytoskeletal elements to achieve truly realistic simulations for better interpretation of AFM images.

Sachs recently demonstrated that significant repulsive image forces can occur between the tip and sample due to their low dielectric constant relative to that of the electrolyte (51). This interaction, which was calculated numerically, is not represented in Eq. 1 and could therefore cause erroneous charge density measurements. Note that our numerical analysis also includes contributions from image charges, since the force is calculated from a general thermodynamic relation. The inaccurate analytical results presented here, however, are not due to the exclusion of the image force. The analytical result underestimates the charge density while one would expect an overestimate due to the presence of an unaccounted force. Therefore, under these conditions of low ionic strength and large tip-sample separation, which are different from those calculated by Sachs, the double-layer force is likely much larger than the image charge force.

The above results demonstrate that the AFM is a sensitive, minimally invasive, and quantitative tool for membrane electrostatics. To demonstrate nanometer-scale lateral resolution we use fluid electric force microscopy (FEFM) (32). In this technique, the AFM probe first scans the sample topography, and then repeats that topography with the tip lifted to measure the double-layer force at constant D. An image is created based on the measured force during the lift scan. In electrolyte, Eq. 1 suggests that the lift scan contrast is proportional to the local surface charge density. We have previously demonstrated that FEFM can map the charge of single DNA molecules and cationic lipid membranes. Here we image a heterogeneous membrane composed of PC, sphingomyelin, and cholesterol on mica with electrostatic contrast. This lipid composition is well known to form a mixture of liquid-ordered regions rich in sphingomyelin and cholesterol, as well as liquid-disordered regions rich in DOPC (52). These “lipid rafts” may be analogous to domains in biomembranes. Although they have not been conclusively observed in a living cell (53), lipid rafts are easily observed by AFM (54) and fluorescence microscopy in model systems (55). Recently, selective protein associations to lipid rafts have been observed at the single-molecule level by AFM for GPI-anchored proteins, SNAREs, and bacterial toxins (56–58). The mechanism of selective associations is not well understood, and electrostatic effects could certainly be a factor. However, at first glance one would not expect a significant electrostatic contrast in a raft system since phosphatidylcholine and sphingomyelin have similar zwitterionic headgroups. FEFM allows us to check this directly.

AFM images of these model membranes reveal domains with slightly increased height, which have been presumed to correspond to the more rigid liquid-ordered phase. The FEFM image in Fig. 7 reveals a difference in the charge density between the liquid-ordered and liquid-disordered phases with ∼50-nm imaging resolution. Although no force curves were measured over the different phases, we estimate that the liquid-ordered phase is ∼20-mV more positive than the liquid-disordered phase based on the cantilever deflection. Since PC and sphingomyelin headgroups have a similar zwitterionic structure, and cholesterol is uncharged, the source of this contrast may be a change in dipole potential in the headgroup region between the two domains (5). Supporting this view, we observe a negative surface potential over single-component zwitterionic membranes such as pure PC. We are currently investigating the source of this interaction in terms of either dipoles or net formal charges on the surface due to counterion binding.

FIGURE 7.

AFM topography (a) reveals regions of liquid ordered (L_o) and liquid disordered (L_d) lipid domains based on their height. Simultaneous charge density mapping by FEFM (b) demonstrates that the L_o phase is less repulsive to the tip, and therefore more positive than the L_d phase. The scale in panel b is raw tip deflection in mV.

CONCLUSION

Here we have demonstrated three novel aspects of the AFM for measuring electrostatic properties of lipid membranes:

1. The AFM probe is highly noninvasive, detecting double-layer forces over four Debye lengths from the sample and causing only 1–3 mV changes in the membrane potential below the probe tip.

2. The AFM can yield a quantitative measure of the surface potential relying only on the nonlinear Poisson-Boltzmann equation and the assumptions of Gouy-Chapman theory to interpret the data. The approximate analytical formula, which is still in use (59), significantly underestimates the surface potential under typical AFM conditions.

3. The AFM maps electrostatic variation on heterogeneous membranes with ∼50-nm resolution.

The combination of these novel properties suggests that the AFM could be a powerful probe for unraveling electrostatic effects in lipid membranes. For instance, although the AFM only measures an effective surface potential from a Gouy-Chapman model, one could infer molecular details in the membrane through dependences on Debye length, pH, and the inclusion molecules that partition in the headgroup region. Furthermore, the mapping capabilities can be applied to heterogeneous model membranes, without the ambiguity of the partitioning of molecular probes, and possibly to direct observation of mobile lipid charge regulation. Finally, natural biomembranes excised from cells and deposited on a solid substrate could be mapped at low electrolyte concentration to look for evidence of domain formation.