Abstract
We have employed atomic-scale molecular dynamics simulations to address ion leakage through transient water pores in protein-free phospholipid membranes. Our results for phospholipid membranes in aqueous solution with NaCl and KCl salts show that the formation of transient water pores and the consequent ion leakage can be induced and be driven by a transmembrane ionic charge imbalance, an inherent feature in living cells. These processes take place if the gradient is large enough to develop a sufficiently significant potential difference across the membrane. The transport of cations and anions through the water pores is then seen; it discharges the transmembrane potential, considerably reduces the size of a water pore, and makes the water pore metastable, leading eventually to its sealing. The ion transport is found to be sensitive to the type of ions. It turns out that Na+ and Cl− ions leak through a membrane at approximately the same ratio despite the fact that Na+ ions are expected to experience a lower potential barrier for the permeation through the pore. This is because of strong interactions of sodium ions with the carbonyl region of a phospholipid membrane as well as with lipid headgroups forming pore “walls,” considerably slowing down the permeation of sodium ions. In contrast, we observed a pronounced selectivity of a phospholipid membrane to the permeation of potassium ions as compared to chloride ions: Potassium ions, being larger than sodium ions, interact only weakly with phospholipid headgroups, so that these interactions are not able to compensate for a large difference in free-energy barriers for permeation of K+ and Cl− ions. These findings are found to be robust to a choice of force-field parameters for ions (tested by Gromacs and Charmm force-fields for ions). What is more, a potassium ion is found to be able to permeate a membrane along an alternate, “water-defect-mediated” pathway without actual formation of a pore. The “water-defect-mediated” leakage involves formation of a single water defect only and is found to be at least one order of magnitude faster than the pore-mediated ion leakage.
INTRODUCTION
One of the long-standing problems in membrane biophysics is related to the ion permeation across protein-free lipid membranes (1–3). This is assumed to be driven by the ionic concentration gradient across the membrane, as it is an inherent feature in plasma membranes. Although the ion transport in living cells is mainly governed by ion channels, lipid membranes themselves are not perfect barriers. Instead, ions as well as water and other small hydrophilic molecules can leak passively in small amounts across a membrane (2,3). Such an unassisted ion transport is of prominent interest because membranes strive to maintain the ionic electrochemical gradient used for a variety of activities such as ATP synthesis, transport of nutrients, and conveyance of electrical signals. Therefore, any ion leakage is coupled to energy transduction and cellular function.
In the past, two mechanisms for ion transport through a lipid membrane have been proposed. According to the first mechanism, ion permeation is described within the solubility-diffusion theory, implying that ions partition into the membrane's hydrophobic core and diffuse across the membrane (4). The alternative mechanism is based on the fact that the formation of transient water pores in lipid membranes is an energetically favorable route for the transport of hydrophilic compounds such as ions (2,3). This pore-mediated ion leakage is believed to be the dominant pathway for cations in sufficiently thin lipid membranes (5–8). A very recent computational study by Tieleman and Marrink (9) also suggests that permeability of ions through protein-free lipid membranes is pore mediated. Although maintaining the electrochemical gradient across the cell membrane is essential, insight into the mechanism of pore-mediated ion leakage is highly desirable to better understand the processes related to transient defects in cell membranes. It is also noteworthy that formation of transient water pores in biological membranes is central for many other important cellular processes, including fusion events, maintenance of osmotic balance, and drug and antibody delivery into cells.
In this article, we employ atomic-scale molecular dynamics (MD) simulations to study the leakage of ions through transient water pores in protein-free phospholipid membranes. We show that the pore-mediated ion leakage can take place in the absence of any external fields or mechanical stress. Rather, the ion leakage is induced by a transmembrane ionic charge imbalance, which is an inherent feature in living cells. The transmembrane ionic charge imbalance, which is explicitly incorporated into our computational model, induces the formation of transient water pores in phospholipid membranes, provided that the imbalance is large enough to give rise to a sufficiently significant potential difference across the membrane. The subsequent transport of ions through the resulting pore is then observed (Fig. 1). This ion leakage, being driven by the transmembrane density gradient of cations, leads to the discharge of the transmembrane potential and eventually makes the water pores metastable. A preliminary article highlighting a brief view of this work was published elsewhere (10).
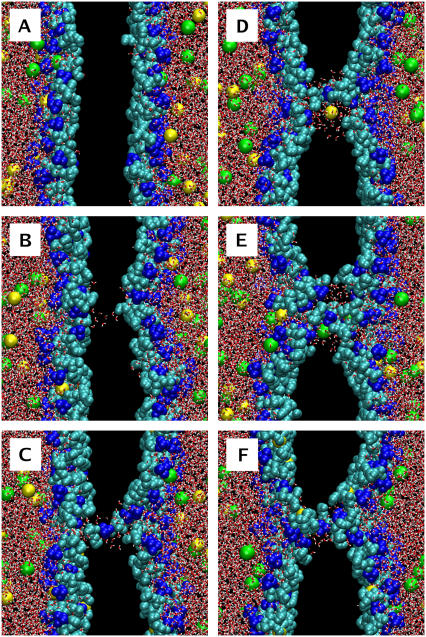
FIGURE 1.
Pore formation and subsequent pore-mediated ion transport induced by an ion charge imbalance of six Na+ ions (pore6-NaCl_8 system, see Table 2): (A) 0 ps, the initial structure; (B) 1420 ps, a single water defect appears; (C) 1490 ps, redistribution of lipid headgroups to the membrane interior; (D) 1710 ps, leakage of a sodium ion; (E) 2090 ps, leakage of a chloride ion; and (F) 10 ns, a metastable water pore. Water is shown in red-white, choline groups of lipid headgroups in blue, phosphate and glycerol groups in cyan, Na+ ions in yellow, and Cl− ions in green. Nonpolar acyl chains of lipids are not shown. Excess of Na+ ions is on the left-hand side.
The main objective of this thorough study is to shed light on the atomistic details of a pore-mediated ion leakage across a lipid membrane under the influence of a transmembrane ionic charge imbalance. The problems of pore formation and its evolution in time on ion leakage as well as the sensitivity of the ion permeation to the type of ions are addressed. We performed our MD simulation study on dimyristoylphosphatidylcholine (DMPC) bilayers in aqueous solution with monovalent salt. The cases of NaCl and KCl salt were considered separately; the transmembrane density gradient in bilayer systems was created correspondingly by sodium (or potassium) cations. Although the sequence of events and most of the features are found to be similar for DMPC membranes with NaCl and KCl salt, we report a pronounced selectivity of the membranes to the permeation of potassium ions as compared to chloride ions. This feature is not observed in the case of sodium and chloride ions, most likely because strong interactions of Na+ ions with the carbonyl region of DMPC membranes considerably slow down the permeation of the cations, cancelling the expected difference in free-energy barriers for permeation of Na+ and Cl− ions (11,12). These results were found to be insensitive to a force field employed for ions. Finally, we also report an alternative, “water-defect-mediated” pathway of permeation of a potassium ion through a DMPC membrane without formation of a pore.
METHODS
Model and simulation details
We have performed atomic-scale MD simulations on lipid bilayers comprised of zwitterionic DMPC lipids. Force-field parameters for DMPC lipids were taken from the united atom force field of Berger et al. (13). The force field was shown to correctly reproduce the experimentally measured area and volume per lipid. Recently, we have used this force field for studies of mixtures of DMPC and cationic lipids (14,15), and an essentially similar force field has been employed in studies of dipalmitoylphosphatidylcholine bilayers and their mixtures with cholesterol, alcohols, and drugs (16–19). Water was modeled using the simple point charge model (20). For sodium, potassium, and chloride ions we employed the set of parameters originally developed by Straatsma and Berendsen (21) and supplied within the GROMACS force field (22). In general, a choice of force-field parameters for ions is known to affect the structural properties of aqueous solution with NaCl salt (23). In this study one of our major results is related to the observed differences in permeation of sodium and potassium ions. To shed light on the sensitivity of this effect to the force-field parameters employed for ions, the simulations of systems with the highest ion imbalance were repeated with ion parameters used in the Charmm force field; these parameters were originally developed by Roux and Beglov (24) and are available online at http://thallium.bsd.uchicago.edu/RouxLab/downloads/charmm/parameters/ions.dat. The ion parameters employed in our study are summarized in Table 1.
TABLE 1.
Lennard-Jones parameters of ions employed in this study
| Ions | σ (nm) | ɛ (kJ/mol) |
|---|---|---|
| Na+ (Gromacs) | 0.25752 | 0.061774 |
| K+ (Gromacs) | 0.64541 | 0.56651 × 10−4 |
| Cl− (Gromacs) | 0.44480 | 0.44559 |
| Na+ (Charmm) | 0.24299 | 0.19629 |
| K+ (Charmm) | 0.31426 | 0.364001 |
| Cl− (Charmm) | 0.40447 | 0.62760 |
Following the original parameterization (13), the Lennard–Jones interactions were cut off at 1 nm without shift or switch functions. For the long-range electrostatic interactions, we used the particle-mesh Ewald method (25,26), which has been shown to do well in membrane simulations (16,27,28). The simulations were performed in the NpT ensemble with temperature being kept constant with the use of the Berendsen thermostat (29) with a coupling constant of 0.1 ps; lipid bilayers and water with salt ions were separately coupled to the thermostat. Temperature was set to 323 K, which is well above the main transition temperature of a DMPC bilayer (297 K) (30); i.e., the studied DMPC bilayers were in the fluid, liquid-disordered phase. For completeness, we also studied the temperature dependence of ion leakage and pore formation by carrying out additional MD simulations for systems with the largest ionic charge imbalance at the physiological temperature T = 310 K. Pressure with a reference value of 1 bar was controlled by the Berendsen barostat (29) with a coupling constant of 1.0 ps. All lipid bond lengths were constrained using the LINCS algorithm (31), and the SETTLE scheme (32) was used to constrain the water geometry. The time step used was 2 fs, and the simulations were performed using the GROMACS suite (22).
To model a transmembrane ionic charge imbalance explicitly, a double-bilayer setup (i.e., two lipid bilayers in a simulation box) was employed (33, 34). Initial configurations were prepared on a basis of two preequilibrated DMPC bilayers of 128 lipids each, solvated in a box with ∼10,200 water molecules, amounting to ∼42,000 atoms (this structure was taken from Gurtovenko (34)). In the double-bilayer system, the two DMPC bilayers separate the “inner” (between the bilayers) and the “outer” water reservoirs. Here, the terms “inner” and “outer” are used for the sake of convenience only, because periodic boundary conditions are applied in all three dimensions.
For simulations with NaCl salt, sodium and chloride ions were then added to the two water phases, replacing randomly chosen water molecules. The number of chloride ions was set to be the same in both water reservoirs, namely 20 Cl− ions corresponding to ∼0.22 M. The excess of Na+ ions was created in the “inner” water phase (between two bilayers) with respect to the “outer” reservoir, so that the “inner” water reservoir always has a higher concentration of cations than the “outer” one. The condition of electroneutrality in the whole double bilayer system was fulfilled.
The initial transmembrane imbalance of sodium ions was systematically varied from 1 Na+ ion per bilayer (corresponding to the overall imbalance of 2 Na+ ions between water reservoirs) to 6 Na+ ions per bilayer. The corresponding systems were referred to as “poreN-NaCl” where N stands for the initial excess of Na+ cations per bilayer (corresponding to the imbalance of 2N cations between reservoirs). The length of simulations was as follows: 50 ns for the pore1-NaCl system, 50 ns for pore2-NaCl, 20 ns for pore3-NaCl, 100 ns for pore4-NaCl, and 60 ns for pore5-NaCl. Most of the runs were 50–60 ns in length; the run for the pore4-NaCl system was extended up to 100 ns to ensure that the pore formation at such a value of ion imbalance did not occur within a 100-ns time span. For the system with the largest ionic charge imbalance of 6 Na+ ions (pore6-NaCl system), we performed 10 different simulation runs from 10 to 15 ns each by varying initial conditions to gain insight into characteristic times of pore formation. For each pore6-NaCl system we allowed at least 6–7 ns for ion permeation after a pore had been formed. Therefore, the systems characterized by long times before pore formation (pore6-NaCl_3, pore6-NaCl_6, and pore6-NaCl_10 systems) were simulated for more than 10 ns (Table 2). To check whether our results are sensitive to a force field employed for ions, the above 10 simulations for pore6-NaCl systems were repeated with Charmm parameters for ions (Table 1). One of the runs (pore6-NaCl_1, Table 2) was extended up to 150 ns to evaluate the lifetime of a pore. Additionally, we performed two 10-ns runs (pore6-NaCl_11 and pore6-NaCl_12) (Table 2) at lower (physiological) temperature of T = 310 K. Also, to test possible size effects, the total number of atoms in the two systems (pore5-NaCl and pore6-NaCl_1) was doubled, amounting to two bilayers of 256 lipids each in a box with more than 20,000 water molecules (∼84,000 atoms in total); each system was simulated for 10 ns. No significant size effects were found.
TABLE 2.
Summary of MD simulations of pore6-NaCl bilayer systems
| System* | Tsim† (ns) | Tpore‡ (ns) | ΔV§ (V) | Na+ leaked | Cl− leaked | Nwater¶ | Rpore‖ (nm) |
|---|---|---|---|---|---|---|---|
| 1 | 150 (10) | 0.5 (1.2) | 2.85(2.49) | 5 (1) | 0 (3) | 88Na (79Na) | 0.94 (0.89) |
| 2 | 10 (10) | 0.7 (0.45) | 2.77 (3.54) | 2 (2) | 2 (2) | 59Na (63Cl) | 0.77 (0.79) |
| 3 | 13 (10) | 6.3 (2.6) | 2.22 (2.28) | 1 (1) | 3 (3) | 57Na (71Cl) | 0.76 (0.84) |
| 4 | 10 (10) | 1.3 (0.25) | 2.58 (3.57) | 2 (1) | 2 (3) | 60Na (31Na) | 0.78 (0.56) |
| 5 | 10 (10) | 0.2 (0.75) | 3.10 (2.64) | 3 (1) | 3 (3) | 88Cl (53Cl) | 0.94 (0.73) |
| 6 | 13 (10) | 5.6 (0.8) | 2.61 (2.61) | 3 (2) | 2 (3) | 106Na (81Na) | 1.03 (0.90) |
| 7 | 10 (10) | 1.0 (1.75) | 2.38 (2.75) | 0 (2) | 3 (2) | 82Cl (44Na) | 0.91 (0.66) |
| 8 | 10 (10) | 1.4 (3.0) | 2.12 (1.97) | 2 (3) | 2 (1) | 54Na (20Na) | 0.74 (0.45) |
| 9 | 10 (10) | 1.7 (0.35) | 1.97 (2.96) | 1 (4) | 3 (1) | 44Na (50Cl) | 0.66 (0.71) |
| 10 | 15 (10) | 6.9 (1.2) | 2.34 (2.21) | 2 (2) | 2 (2) | 75Cl (16Na) | 0.87 (0.40) |
| 11** | 10 | 1.0 | 2.68 | 2 | 2 | 77Na | 0.88 |
| 12** | 10 | 3.1 | 2.85 | 1 | 3 | 74Cl | 0.86 |
Shown in parentheses are data for simulations with Charmm parameters for ions.
Total time of a simulation run.
Time before pore formation.
Transmembrane potential induced by an ionic charge imbalance before pore formation.
Corresponds to the leakage of the first ion, the type of the first leaked ions being indicated as a superscript.
Corresponding radius of the inner part of a water pore assuming an ideal cylindrical shape.
Simulation run at T = 310 K.
For simulations with KCl salt, we followed the same scheme for creating an excess of cations in the double-bilayer systems. The initial imbalance of potassium ions per bilayer was varied from 1 K+ (the system referred as to “pore1-KCl”) to 6 K+ (“pore6-KCl”) in the same fashion as for simulations with NaCl. The systems pore1-KCl to pore5-KCl were simulated for 20 ns each. For the system with the initial transmembrane imbalance of 6 K+ ions (pore6-KCl), 10 different simulation runs of 10 ns each were performed by varying initial conditions. To test possible sensitivity of results to a force field used for ions, these 10 runs were repeated with Charmm parameters for potassium and chloride ions.
To shed light on differences in the interaction of NaCl and KCl salts with DMPC lipid membranes, two 40-ns simulation runs were performed on single-bilayer systems (128 DMPC lipids, ∼5000 water molecules, and 20 pairs of anions and cations). These runs were also repeated with the Charmm parameters for ions to reveal possible force-field-related effects.
Analysis
The electrostatic potential and the electric field across a lipid membrane were calculated from Poisson's equation by integrating over charge densities, which were determined directly from MD simulations. The field and the potential were chosen to be zero in the middle of the “inner” water phase between the two bilayers. The membrane plane was chosen as the xy plane; thus, the z component was aligned in the membrane normal direction and z = 0 was chosen to be in the middle of the “inner” water reservoir, i.e., in the middle of the reservoir with high cation concentration. Only the initial part of the trajectories before actual pore formation was used for calculating the electric field and the potential, which were further averaged over the two bilayers in a simulation cell.
The transient water pores induced by ionic charge imbalance are subject to considerable fluctuations in size, and their shape is nonuniform across the membrane. Because a detailed study of the shape of the pores is beyond the scope of this article, we made only a rough estimate of the pore size. To do that, we closely followed the approach developed by Leontiadou et al. (35): the size of a transient water pore in a membrane was characterized by counting the number of water molecules Nwater within 0.5 nm from the membrane center. To estimate the radius of a pore in the membrane interior, Rpore, it was assumed that the central part of a pore is cylindrical in shape and contains Nwater molecules at the same density as in bulk water (35). Similar to water molecules, the number of lipids in the central part of a pore was calculated by counting the number of lipid headgroups within 0.5 nm from the middle of a bilayer.
An imbalance of ions per bilayer was calculated as follows. First, we computed the center of mass positions for both bilayers, Z1 and Z2. Then, ions with Z1 < z < Z2 were assigned to the “inner” water bath (and to the “outer” bath otherwise). Half of the difference in numbers of ions inside the two water baths then gives us the ionic charge imbalance per bilayer. Note that the initial imbalance of sodium (potassium) ions in all simulations was set to be nonzero, whereas the imbalance of Cl− ions was always nil.
RESULTS AND DISCUSSION
Pore-mediated ion leakage induced by the transmembrane density gradient of sodium ions
We start with the discussion of ion leakage through transient water pores induced by a transmembrane charge imbalance of sodium ions. The largest ionic imbalance considered in this study was 6 sodium ions imposed at the two sides of a DMPC bilayer of 128 lipids (corresponding to the overall imbalance of 12 Na+ ions between two water reservoirs). We performed 10 independent simulation runs to evaluate if pore formation events and the details of ion leakage are sensitive to initial conditions. The summary of the MD simulation runs for the systems with the imbalance of 6 Na+ ions (pore6-NaCl systems) is presented in Table 2. Below we present common features of pore formation coupled to the subsequent ion transport on a basis of one representative system, pore6-NaCl_8 (Table 2).
For this particular system, the imbalance of 6 Na+ ions per bilayer induces on average a transmembrane voltage of ∼2.12 ± 0.15 V across the membrane (Fig. 2). The applied transmembrane density gradient of sodium ions gives rise to the formation of a water pore, which starts after ∼1.4 ns of simulation (Figs. 1 and 3). The pore formation begins with the creation of a single water defect spanning the entire membrane (Fig. 1 B); this chain of water molecules then expands rapidly within ∼1 ns (Figs. 1 C and 3). At this stage one observes a considerable redistribution of lipid headgroups from the water-lipid interface to the membrane interior, surrounding and stabilizing the pore.
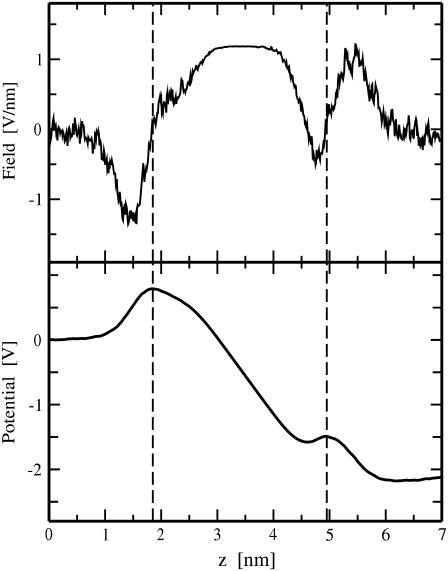
FIGURE 2.
Electric field (top) and electrostatic potential (bottom) versus distance z from the middle of the water phase between the two bilayers of the pore6-NaCl_8 system. Only the initial part of the MD trajectory (1.4 ns) before pore formation was used for the calculation; the field and the potential were averaged over the two bilayers. Dashed lines indicate average positions of phosphorus atoms of lipids for the two bilayer leaflets.
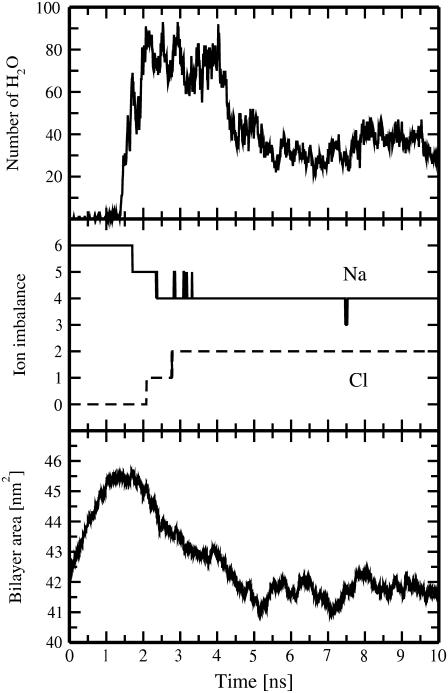
FIGURE 3.
Time evolution for the number of water molecules in a pore within 0.5 nm from the bilayer center (top), for the transmembrane imbalance of Na+ and Cl− ions (middle), and for the area of the membrane (bottom). Shown are results for the pore6-NaCl_8 system.
We note that, as a rule, the pore formation was observed in one of the two bilayers only, as the other bilayer stayed intact. This can be explained as follows. Before pore formation, a double bilayer system is symmetric, i.e., the two bilayers are equivalent. The pore can be formed spontaneously in either of the two bilayers with equal probability. After a pore has been formed in one of the bilayers, the ionic leakage through this bilayer makes the situation asymmetric: the drop in the transmembrane potential as a result of the ionic leakage considerably reduces the probability of pore formation in the other bilayer. Therefore, the formation of pores in both bilayers is possible only if there is nearly simultaneous pore formation in both bilayers. This is, however, a very rare event. The pore formation in both bilayers was observed in only 1 simulation (of ∼50 simulations presented in this study) for the system pore6-KCl_2 with Charmm parameters used for ions (Table 3). Also, no multiple pore formation (more than one pore per bilayer) was observed in simulations with NaCl salt.
TABLE 3.
Summary of MD simulations of pore6-KCl bilayer systems
| System* | Tpore†(ns) | ΔV‡ (V) | K+ leaked | Cl− leaked | Nwater§ | Rpore¶ (nm) |
|---|---|---|---|---|---|---|
| 1 | 0.9 (0.5) | 3.15 (2.49) | 5 (4) | 0 (1) | 47K (62Cl) | 0.69 (0.79) |
| 2 | 1.1 (2.3##) | 2.31 (2.82) | 3 (3) | 1 (0) | 32K (31K) | 0.57 (0.56) |
| 3 | 1.4 (0.6) | 2.60 (2.73) | 2 (4) | 2 (1) | 78Cl (114Cl) | 0.88 (1.07) |
| 4 | 0.7 (1.0) | 2.01 (2.40) | 5 (2) | 0 (2) | 17K (77K) | 0.41 (0.88) |
| 5 | 0.9 (0.7) | 3.33 (2.78) | 1 (1) | 3 (2) | 65K, Cl (68Cl) | 0.81 (0.83) |
| 6 | 1.9 (1.9) | 2.12 (2.70) | 4 (4) | 0 (1) | 17K (77K) | 0.41 (0.88) |
| 7 | 0.6 (0.65) | 2.48 (2.64) | 4 (4) | 2 (1) | 79Cl (47K)†† | 0.89 (0.69) |
| 8 | 2.8 (1.5) | 2.19 (2.52) | 3 (4) | 1 (1) | 33K (49K) | 0.58 (0.70) |
| 9 | 1.5 (3.0‡‡) | 1.74 (2.43) | 4 (4) | 1 (0) | 33K (15K) | 0.58 (0.39) |
| 10 | 2.4** (1.2) | 2.54 (2.61) | 4 (4) | 1 (1) | 67Cl (29K) | 0.82 (0.54) |
Shown in parentheses are data for simulations with Charmm parameters for ions. Each system was simulated for 10 ns.
Time before pore formation.
Transmembrane potential induced by ionic charge imbalance before pore formation.
Corresponds to the leakage of the first ion, the type of the first leaked ions being indicated as a superscript.
Corresponding radius of the inner part of a water pore, assuming an ideal cylindrical shape.
Corresponds to the leakage of the second ion. The first ion (K) crosses the membrane along an alternative water-defect-mediated pathway well before the actual pore formation (1950 ps).
The formation of water pores occurs in both bilayers almost simultaneously. The formation of a pore in the second bilayer is delayed by 100 ps with respect to that in the first one.
Corresponds to the leakage of the second ion. The first ion (K) crosses the membrane along an alternative water-defect-mediated pathway in the very beginning of the pore formation at around t = 0.7 ns (the process involves ∼11 water molecules).
The simultaneous formation of two pores occurs in the same bilayer.
The overall picture of pore formation is very similar to that reported in MD simulations of electroporation in lipid membranes under the influence of an external (constant) electric field (36–38). This is not very surprising because in both cases a lipid membrane is exposed to a rather high transmembrane electric field. For the pore6-NaCl_8 system, one has a transmembrane electric field of ∼0.30 V/nm (averaged over the simulation box). This value is of the same order of magnitude as reported in existing MD studies of electroporation in lipid membranes (36–38). However, one has to emphasize the stochastic nature of the electric field induced by a transmembrane ionic density gradient. The field considered in this work, which is determined by instantaneous positions of ions, is subject to considerable fluctuations in time and space with respect to its average value. This may be one of the reasons why we observed a lower threshold value of the average electric field required for pore formation as compared to the minimal value of 0.4 V/nm reported in MD simulations of membrane electroporation under externally applied constant electric field (37).
After a water pore has become large enough for ion permeation, we observe the transport of sodium and chloride ions through the pore along the Na+ density gradient (Figs. 1 and 3). To bring the system to equilibrium, i.e., to discharge the transmembrane potential, Na+ and Cl− ions permeate the membrane in opposite directions. Correspondingly, transmembrane imbalance of sodium (chloride) ions decreases (increases) on ion permeation. Interestingly, the first sodium ion crosses a membrane before pore expansion has been finished (Nwater ≈ 54, Table 2), whereas the second ion (Cl−) permeates through a fully expanded pore (Nwater ≈ 80, Fig. 3).
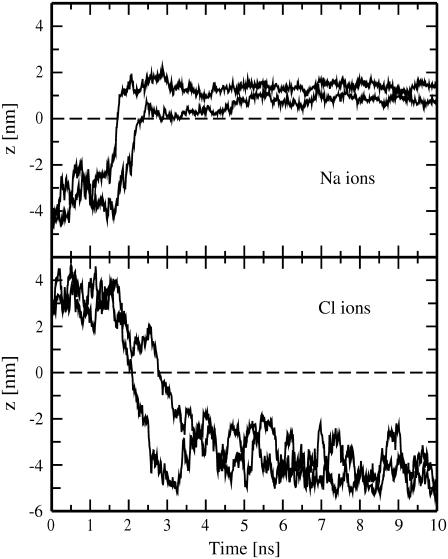
The permeation of ions through the pore and the size of the pore are both controlled by the induced transmembrane potential: The higher the potential difference between two sides of a membrane, the faster the ion leakage through the pore and the larger the pore itself. After fast permeation of the first two (sodium and chloride) ions, another pair of Na+ and Cl− leak through the membrane in ∼0.5-ns intervals (Fig. 3). As one can see from the trajectories of four leaked ions shown in Fig. 4, the ion leakage, discharging the transmembrane potential difference, slows down the rate of transmembrane ionic transport.
FIGURE 4.
MD trajectories of sodium (top) and chloride (bottom) ions leaked through transient water pores versus time. z denotes ion positions along the direction of the bilayer normal and is set to zero in the center of the bilayer (indicated by a dashed line). Shown are results for the pore6-NaCl_8 system.
One has to emphasize that, as far as sodium ions are concerned, there is an additional factor that can affect the Na+ transport through a membrane: Sodium ions strongly interact with phosphatidylcholine lipid headgroups, preferably with their carbonyl regions (15,34,39,40). These interactions seem to be not very important at high values of an ionic imbalance but can slow down the Na+ transport considerably at lower imbalances after the initial ion leakage has taken place. The difference in leakage of sodium and chloride ions is evident from Fig. 4: Cl− ions come to the pore region from bulk water, cross the membrane, and diffuse to bulk water on the other side of the bilayer. In contrast, most of Na+ ions after crossing the membrane bind to the carbonyl region of its opposite side. At rather low transmembrane voltage, sodium ions are able to bind also to the carbonyl oxygens of lipid headgroups in the interior of a pore, spending remarkable time inside the pore (see the trajectory of the second leaked Na+ in Fig. 4, top). We note that, although not seen for the pore6-NaCl_8 system, sodium ions also can start crossing a membrane while being bound to the membrane surface (i.e., not from bulk water).
The leakage of four ions through the membrane reduces the overall ionic charge imbalance to +2e, discharging the transmembrane voltage down to ∼0.7 V. This value of the voltage was estimated on the basis of the intact double bilayer system with a transmembrane imbalance of 2 Na+ referred to as pore2NaCl (see Methods). Such a considerable drop in the transmembrane voltage significantly decreases the number of water molecules inside the pore, making the pore too small in size to be still permeable for ions (Fig. 3). The drop in the number of water molecules for the pore6-NaCl_8 system was ∼60% compared to its maximum value.
It is also noteworthy that the pore formation and the subsequent ion leakage are accompanied by changes in the area of a membrane, as seen in Fig. 3 (bottom). Note that we intentionally presented in Fig. 3 the area of a membrane as a whole rather than the area per lipid because the latter quantity (which is calculated as the membrane area divided by the number of lipids in a leaflet) becomes meaningless for a membrane with a pore. The average value of the area per lipid at t = 0 for an initially intact DMPC membrane at T = 323 K was ∼0.66 nm2, which matches the available experimental data well (41–43). The initial transmembrane charge imbalance causes expansion of a membrane (amounting to ∼10% compared to its initial area) and, correspondingly, makes the membrane thinner. The steady expansion lasts up to the pore formation in the membrane. Immediately after the pore has been fully formed, the membrane starts to compress. Its initial compression is caused most likely by the redistribution of lipid headgroups toward the pore interior, whereas at later stages it is governed by the drop in the pore size and binding of sodium ions to the membrane surface.
To summarize, the above features of pore formation and ion leakage events are typical of all MD simulation runs performed for bilayer systems with the imbalance of 6 Na+ ions (Table 2). However, because of the stochastic nature of the transmembrane electric field induced by the ionic density gradient, details scatter significantly. In particular, the typical time before pore formation varies from 0.2 ns (pore6-NaCl_5 system) to 6.9 ns (pore6-NaCl_10 system), i.e., by more than one order of magnitude. The average transmembrane potential induced by the ion imbalance ranges from ∼1.97 V (pore6-NaCl_9 system) to ∼3.10 V (pore6-NaCl_5 system), corresponding to the electric field (averaged over the simulation box) from ∼0.28 V/nm to ∼0.44 V/nm. Remarkably, the highest transmembrane potential comes about in the system with the fastest pore formation (pore6-NaCl_5). We note, however, that the results for the average transmembrane voltage should be taken with caution because they are statistically not equivalent: Only parts of trajectories (of different lengths) preceding pore formation were used for calculating the potential.
In all, we witnessed 43 ion leakage events in 10 simulation runs: 21 leaked sodium ions, and 22 leaked chloride ions, i.e., a DMPC membrane does not demonstrate selectivity to the permeation of Na+ and Cl− ions through transient water pores. In recent studies by Dzubiella and colleagues (11,12) for a generic hydrophobic pore connecting two water reservoirs with different Na+ concentrations (the set-up is reminiscent to that used in our work), mostly the permeation of sodium ions was witnessed, whereas Cl− permeation was found to be a rare event. This difference in permeation of Na+ and Cl− ions was directly related to the difference in free-energy barriers of ion permeation, which correlated well with solvation energies of the ions in water (12).
In our case the situation is different because transient water pores in membranes are hydrophilic, as their “walls” are lined by lipid headgroups. As mentioned above, sodium ions are able to bind to carbonyl regions of lipid headgroups, whereas chloride ions are not (15,34,39,40). This binding of Na+ ions, leading to formation of tight complexes of lipids, was proposed as an explanation for slowing down of the lateral lipid self-diffusion under the influence of NaCl salt, which was observed in fluorescence correlation spectroscopy experiments (39) as well as in salt-induced phase separation in POPC membranes witnessed in small-angle x-ray scattering experiments (44). Thus, the lack of selectivity regarding the permeation of Na+ and Cl− ions through a membrane in our case is most likely associated with the fact that a difference in free-energy barriers of ion permeation is compensated by the strong interactions of sodium ions with hydrophilic walls of pores (lipid headgroups) as well as with the carbonyl region of the phospholipid membrane.
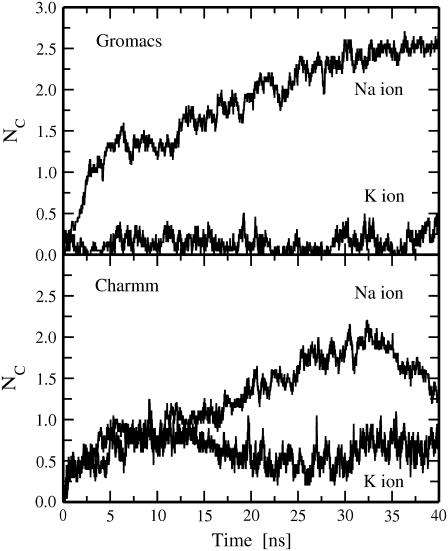
It is instructive to test how these findings are sensitive to a force field used for ions. To do that we repeated 10 simulation runs for pore6-NaCl systems with Charmm parameters for sodium and chloride ions (24) (Table 1). The results are summarized in Table 2. All general features observed in simulations with the Gromacs force field for ions also hold for Charmm parameters. Furthermore, of 42 leaked ions, 19 leaked ions in the simulations employing Charmm parameters were sodium ions, and 23 ions were chloride, i.e., we again did not observe a selectivity of a DMPC membrane for the permeation of Na+ and Cl− ions. This, in particular, suggests that strong interactions of Na+ ions with lipid headgroups also occur in the case when Charmm parameters are employed for ions. Indeed, sodium ions demonstrate substantial coordination with carbonyl oxygens of DMPC lipids as seen in single bilayer simulations with both Gromacs and Charmm force-field parameters employed for ions (Fig. 5). The coordination numbers of Na+ ions with lipid carbonyl oxygens were calculated by counting the total numbers of the carbonyl oxygens within the first hydration shell of a Na+ ion; the shell radius was extracted from corresponding radial distribution functions. Note that the coordination numbers in Fig. 5 were computed by averaging over all Na+ ions in the system. Averaging over only adsorbed sodium ions gives us the average number of lipids bound to a sodium ion: 3.13 ± 0.13 lipids bound to a Gromacs sodium ion and 2.03 ± 0.25 to a Na+ ion when the Charmm force field is employed (the averaging was performed over the last 10 ns of 40 ns trajectories). Thus, the interactions of lipids with Charmm sodium ions are found to be somewhat weaker than lipid interactions with Gromacs sodium ions. However, they still seem to be strong enough to be able to compensate for a difference in free-energy barriers for permeation of Na+ and Cl− ions through water pores.
FIGURE 5.
Time evolution of coordination numbers of cations (sodium and potassium ions) with lipid carbonyl oxygens as observed from single bilayer simulations with Gromacs (top) and Charmm (bottom) force fields employed for ions; see text for details.
The size of a transient water pore also varies considerably for different simulations; the number of water molecules Nwater in pores open for ion leakage ranges from 44 to 106 (Table 2). Assuming an ideal cylindrical shape for a pore, this corresponds to a variation in the radius of the inner part of a pore from 0.66 to 1.03 nm. In the case when Charmm parameters were employed for ions, the lower limit of the pore size was observed to be somewhat smaller (∼16 water molecules in a pore; see Table 2). One can also notice from Table 2 that, as a rule, sodium ions need somewhat smaller pores for permeation as compared to chloride, although this feature here is considerably less pronounced than in the case of potassium ions (see following section).
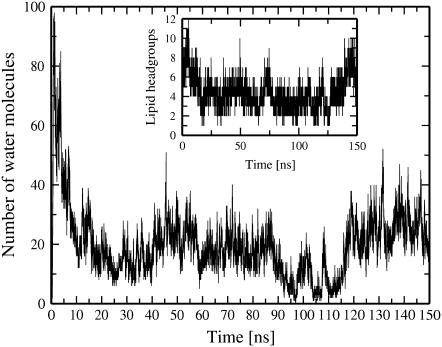
After the ion leakage and the corresponding remarkable drop in the transmembrane potential difference have taken place, the size of a pore decreases considerably (up to ∼80% compared to its maximum value within several nanoseconds after pore formation). To evaluate the lifetime of a pore, we extended one of our runs (pore6-NaCl_1 system) to 150 ns (Fig. 6). As seen, the pore stays open for the entire course of the simulation. Interestingly, the number of water molecules in the central part of the pore drops almost to zero in the time interval from 90 ns to 110 ns; however, lipids inside the pore do not follow the water content trend, preserving the pore.
FIGURE 6.
Time evolution for the number of water molecules in a pore (within 0.5 nm from the bilayer center) for the extended simulation of the pore6-NaCl_1 system. The corresponding number of lipid headgroups in the interior of the pore is shown in the inset. The leakage of ions occurs during the first 10 ns of the MD trajectory.
We recall that for the pore6-NaCl_1 system the leakage of ions finishes after the initial 10 ns, so that for the rest of the simulation there remains a residual ionic charge imbalance of 1 e+ corresponding to a transmembrane voltage of ∼0.21 V. This small residual transmembrane potential most likely does not play a crucial role in stabilizing a pore. For comparison, for the system pore6-NaCl_5, one finds the system has to fully discharge (Table 2). The resealing of the membrane was not observed, however. On the other hand, we witnessed spontaneous pore closure for other systems at similar values of the residual transmembrane potential (see below). Therefore, one can conclude that after a drop of the transmembrane voltage below some critical value because of ion leakage, a water pore becomes metastable.
To study possible effects of temperature, we performed two independent simulations at a lower (physiological) temperature of T = 310 K (see systems pore6-NaCl_11 and pore6-NaCl_12 in Table 2). These simulations suggest that the general picture and the sequence of events remain the same; the results fit well within the ranges found for T = 323 K, so that noticeable temperature effects were not revealed.
The formation of a transient water pore coupled to the subsequent ion transport was also observed at a smaller initial charge imbalance of 5 Na+ ions per bilayer (pore5-NaCl system), corresponding on average to a transmembrane voltage of 2.0 ± 0.14 V. Remarkably, the pore was formed after 5 ns and closed after ∼60 ns (see Gurtovenko and Vattulainen (10) for details). No pore formation was observed for initial imbalances smaller than five sodium ions, at least within the time span of 100 ns, as seen from the simulation of the pore4-NaCl system.
Ion leakage induced by the transmembrane density gradient of potassium ions
We turn now to a discussion of ionic transport induced by a transmembrane density gradient of potassium ions. For the bilayer systems with KCl salt, the largest ionic imbalance was also set to 6 K+ ions (pore6-KCl systems). The summary of 10 independent simulations of the pore6-KCl systems is presented in Table 3.
For most of the systems with 6 K+ imbalance, the general features and a sequence of events remain the same as those for bilayers with NaCl (pore6-NaCl systems). The initial ionic imbalance induces the potential difference across a membrane that varies from 1.74 to 3.33 V (see Table 3). This gives rise to the formation of a pore in a membrane, the typical time before pore formation ranging from 0.6 ns to 2.8 ns, i.e., somewhat less than for systems with 6 Na+ imbalance (see Table 2). The details of the pore formation do not differ much from those observed for systems with NaCl.
After a transient water pore has expanded sufficiently, we can observe the transport of potassium and chloride ions through the pore along the K+ density gradient. What is quite different here compared to membrane systems with Na+ imbalance is that one finds a pronounced selectivity of a DMPC membrane for potassium ions: Of 46 ion leakage events observed for the pore6-KCl systems, we found that 35 leaked ions (or 75%) were K+ ions, and only 11 ions were chloride (see Table 3). The selectivity for pore-mediated K+ ion permeation is in agreement with the results of a recent study of ion transport through a hydrophobic nanopore and can be explained by the fact that the free-energy barrier to permeation through the water pore of a potassium ion is much lower than that of a chloride ion (12). It is found to be considerably lower than the barrier of a smaller sodium ion because sodium ions are more preferentially solvated in water than potassium ions (12,45).
We recall that Na+ and Cl− permeation across a DMPC membrane was found to be almost the same (see the preceding section) because the above difference in free-energy barriers to permeation was compensated by the strong interactions of sodium ions with the carbonyl region of the membrane. In contrast, the interactions of K+ ions with DMPC lipids are found to be considerably weaker. As is seen from the plot of the coordination number of a potassium ion with lipid carbonyl oxygens shown in Fig. 5 (top), there is almost complete lack of stable binding of K+ ions to lipid headgroups. After averaging over only adsorbed ions, we found that a K+ ion binds, on the average, to 1.47 ± 0.69 lipids, which is much smaller than the value of 3.13 ± 0.13 found for sodium ions. Note also large fluctuations in the value of the number of bound lipids in the case of K+ ions, which are an indication of the fact that the binding of K+ ions is indeed unstable and erratic.
These findings combined with a large difference in free-energy barriers for permeation of K+ and Cl− ions through a pore (12) can explain the pronounced selectivity of phospholipid membranes to potassium ions compared to chloride ions. The fact that for permeation a potassium ion needs a pore of smaller size than a chloride ion is also clearly seen from the results for the pore sizes corresponding to the leakage of the first ion (see Table 3): In most cases K+ permeates the pore first; the K+ permeation often starts well before the pore has been fully formed and most likely has not been expanded sufficiently to be permeable for Cl− ions.
An important question is whether the observed remarkable difference in permeation of potassium and sodium ions (pronounced selectivity for K+ ions compared to Cl− ions versus lack of the selectivity in the case of Na+ ions) is sensitive to the force-field parameters employed for ions. In general, a sodium ion is smaller than a potassium ion. Because they both have the same charge, the surface charge of a Na+ ion is larger than that of a K+ ion. As a result, a sodium ion more strongly attracts water oxygens (i.e., the distance between water oxygens and ionic nuclei is smaller in the case of sodium ions) and has a more ordered first hydration shell. This can also be applied with some limitations to the interactions between a lipid carbonyl oxygen and an ion when the former replaces a water oxygen from the ionic first hydration shell on ion adsorption on the membrane surface. Given this, we can therefore expect that the interactions of Na+ ions with lipid carbonyl oxygens are stronger than those of K+ ions. This should hold for any force fields used for ions as long as a Lennard–Jones diameter of Na+ ions is smaller than that for K+ ions.
The Lennard–Jones parameters of the Gromacs force field for potassium and sodium ions seem to exaggerate the size difference of these ions. In particular, the Gromacs value of σ of a K+ ion employed in this work (see Table 1) is much larger than those used in other studies (12,24,46,47). It is, therefore, crucial to test how robust the selectivity for potassium permeation is to Lennard–Jones parameters employed for ions. For doing that, we repeated 10 simulation runs for pore6-KCl systems with Charmm parameters for potassium and chloride ions (24) (see Table 1); note that the Charmm value of σ for a K+ ion is less than half as large as that employed in the Gromacs force field. The results of the simulations are summarized in Table 3. First, all general features observed in simulations of pore6-KCl systems with Gromacs parameters for ions are found to be preserved. Interestingly, for one of the pore6-KCl systems (pore6-KCl_9), we observed a formation of two pores in the same bilayer. Second, it appears that the pronounced selectivity for permeation of potassium ions also holds for simulations that employed the Charmm force field for ions: The majority of leaked ions (34 of a total 44) are potassium ions (see Table 3).
Because a K+ ion in simulations with Charmm parameters is much smaller than that in simulations employing Gromacs-based parameters for ions, the first hydration shell of K+ is more ordered, leading to noticeably stronger coordination of a K+ ion with lipid carbonyl oxygens (see Fig. 5). At the same time, in simulations using the Charmm force field for ions, the binding of K+ ions to lipid headgroups is still weaker than the binding of Na+ ions because of the above-mentioned size differences of the ions (see Fig. 5, bottom, and Table 1). In particular, the average coordination number of K+ ions in Charmm force-field-based simulations (averaged over adsorbed ions only) is found to be 1.92 ± 0.32, whereas it is 2.03 ± 0.25 in the case of Na+ ions (note also large fluctuations of the coordination numbers). To summarize, despite the fact that the interactions between potassium ions and lipid headgroups are found to be stronger in simulations where the Charmm force field is used, these interactions appear to be still too weak to be able to compensate for a large difference in free-energy barriers for permeation of K+ and Cl− ions. Thus, the selectivity of phospholipid membranes to permeation of potassium ions is found to be robust to variations in force-field parameters employed for ions.
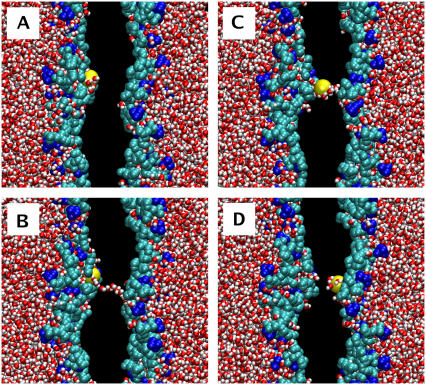
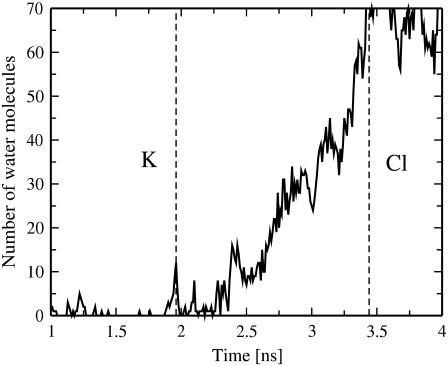
Remarkably, for one particular bilayer system with the transmembrane imbalance of 6 K+ (pore6-KCl_10), we found an alternative mechanism of fast permeation of a potassium ion through a membrane without actual pore formation (Fig. 7). Similarly, as in the early stage of pore formation described above, the process starts with the formation of a single water defect: Two water fingers penetrate the hydrophobic core from both sides of a membrane to meet each other and to form a chain of water molecules spanning the entire membrane (Fig. 7 B). The major difference with the pore formation is that now one of the water fingers (on the left-hand side) comes with a potassium ion, implying that some of water molecules in the finger belong to the first hydration shell of the ion. Further penetration of the water fingers leads to the formation of a water defect, with the potassium ion now sharing both fingers (Fig. 7 C). In ∼15 ps the water defect becomes metastable and eventually disappears. It turns out, however, that most of water molecules in the hydration shell of the ion now belong to another water finger (on the right-hand side), so that the K+ now permeates through the membrane (Fig. 7 D). We refer to this mechanism of ion permeation as “water-defect-mediated.” This permeation is found to be very fast; the whole process visualized in Fig. 7 takes ∼40 ps. The water defect involves only a small amount of water molecules. As one can see from Fig. 8, the water-defect-mediated event of K+ ion permeation is mediated only by a dozen water molecules.
FIGURE 7.
“Water-defect-mediated” permeation of a potassium ion through the membrane observed for the pore6-KCl_10 system (see Table 3): (A) 1926 ps, a potassium ion penetrates into the interfacial region of the membrane; (B) 1944 ps, appearance of two “water fingers,” one of them coming with the K+ ion; (C) 1960 ps, formation of a single water defect that spans the entire membrane and carries the potassium ion; (D) 1966 ps, the closure of the water defect, leading to the permeation of the potassium ion. Water is shown in red-white, choline groups of lipid headgroups in blue, phosphate and glycerol groups in cyan, and the leaked potassium ion in yellow; acyl chains of lipids and the rest of ions are not shown. Excess of K+ ions is on the left-hand side.
FIGURE 8.
Time evolution for the number of water molecules in the interior of the membrane (within 0.5 nm from the bilayer center) for the pore6-KCl_10 bilayer system.
The above water-defect-mediated permeation of a potassium ion is a rare event: An ion should spontaneously appear at the site where the formation of a pore (a single water file) has just started. The fact that such a mechanism was observed for a potassium ion and not for a sodium ion can again be explained by rather weak interactions of K+ ions with lipid headgroups, making it possible for K+ ions driven by a transmembrane field to penetrate rather deep into the membrane. Yet, the water-defect-mediated permeation can hardly be related to a very high potential developed in the system because the average transmembrane potential observed in the pore6-KCl_10 system is rather moderate compared to the rest of the simulation runs with K+ ions (see Table 3). Remarkably, we were able to reproduce the water-defect-mediated permeation of a potassium ion in one of the simulations (pore6-KCl_7) employing Charmm parameters for ions. The only minor difference in this case was that the water defect after ion permeation had been accomplished gave rise to the formation of a water pore instead of its disappearance observed in the Gromacs force-field-based simulation of the pore6-KCl_10 system.
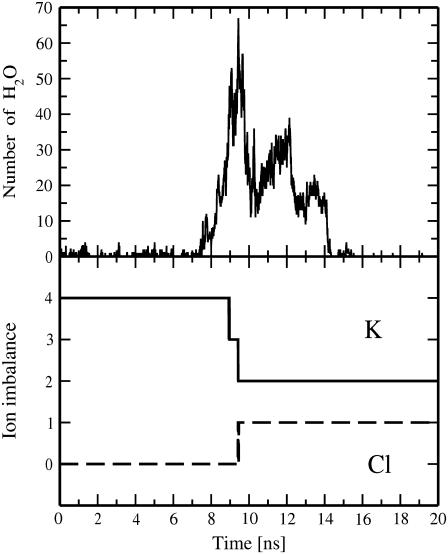
The ion leakage through transient water pores was also witnessed in bilayer systems with the initial transmembrane ionic imbalance of five and four K+ ions; the latter is smaller than the threshold imbalance observed for systems with NaCl salt (see preceding section). For the pore4-KCl system, the imbalance of four K+ ions develops the transmembrane voltage of ∼1.64 ± 0.2 V, corresponding to the electric field of ∼0.23 V/nm (averaged over the simulation box). This leads to the formation of a transient water pore after ∼7.4 ns and the subsequent transport of two K+ and one Cl− ions across the membrane (Fig. 9). The above ionic leakage discharges the transmembrane potential down to ∼0.49 V (the residual ionic charge imbalance in the system after 10 ns is 1 e+). It turns out that the pore spontaneously closes and the membrane reseals within ∼5 ns after the permeation of three ions has completed (Fig. 9). Thus, our simulations revealed that a metastable water pore in a DMPC membrane can stay open from 5 ns to at least 150 ns (see also the previous section).
FIGURE 9.
Time evolution for the number of water molecules in a pore within 0.5 nm from the bilayer center (top) and for the transmembrane imbalance of K+ and Cl− ions (bottom) for the pore4-KCl system.
SUMMARY AND CONCLUSIONS
Using realistic atomic-scale MD simulations, we explicitly modeled the process of pore-mediated ion permeation through protein-free phospholipid membranes (see Fig. 1). This permeation is driven by the transmembrane density gradient of cations, which is an inherent feature of living cells. The ionic imbalance at the two sides of a membrane induces the transmembrane potential, which plays a dual role: On one hand, it leads to the formation of a transient water pore spanning the entire membrane on a nanosecond time scale; on the other, it controls the subsequent transport of ions through the resulting pore. The leakage of ions through the pore discharges the transmembrane potential, drastically reducing the size of the pore and making it metastable. Eventually the pore spontaneously reseals. Its lifetime observed in our simulations ranged from 5 ns to at least 150 ns.
The transmembrane ionic imbalance is of biological relevance because it is believed to determine the resting membrane potential in cells; the potential is typically of the order of 100 mV. In cellular membranes this value of the potential corresponds to the average ion concentration gradient across the membrane. Thermal fluctuations present in living cells can lead to higher values of the membrane potential. However, it is unlikely that the local fluctuations in ion concentrations on the two sides of a cell membrane are able to give rise to a 10-fold increase in the transmembrane potential so that it would be comparable with potentials employed in this MD computational study (the threshold value of the potential leading to pore formation was found to be ∼1.64 V (see above). In general, atomic-scale MD simulations have obvious limitations regarding the system size and time scales accessible. In particular, to increase the probability of pore formation, we were forced to lower the energy barrier for pore formation by increasing the ionic charge imbalance across the membrane and, correspondingly, the transmembrane potential. As is clear for systems with the initial imbalance of four, five, and six K+ ions across a membrane of 128 lipids, the overall picture of pore formation and ion leakage remains the same when the initial ionic imbalance goes down. This lends support to a conclusion that the same mechanism may also be applied for smaller ionic imbalances on time scales not accessible by current atomic-scale MD simulations: It is likely that pore formation and subsequent ion leakage at smaller ionic imbalances would be much slower but would still occur. Our arguments here are fully consistent with those successfully employed in MD studies of membrane electroporation (36–38) and phosphatidylserine externalization (48,49).
Forty independent MD simulations of systems with the highest initial imbalance of six cations revealed the stochastic nature of the induced transmembrane electric field: The field is defined by instantaneous positions of ions and, therefore, exhibits substantial fluctuations with respect to its average value. As a result, the characteristic time before actual pore formation ranges from 200 ps to almost 8 ns, i.e., by more than one order of magnitude. In turn, the average values of the transmembrane potential induced by the cationic density gradient can differ by a factor of 2.
Comparative studies of the ion leakage induced by a transmembrane imbalance of sodium and potassium ions revealed that the sequence of events and most of the features are very similar for bilayer systems with both NaCl and KCl salt. However, there is a sensitivity of permeation through the pore to the type of ions that is most likely related to the difference in free-energy barriers to permeation of ions through the pore. For bilayer systems with NaCl salt, a sodium ion is expected to experience lower potential barrier for the permeation as compared to a chloride ion (12). However, strong interactions of Na+ ions with lipid headgroups considerably slow down their permeation through hydrophilic water pores, so that Na+ and Cl− ions are found to leak through the membrane at nearly the same ratio. In contrast, in the case of KCl salt, we found a pronounced selectivity of the membrane to the permeation of K+ ions as compared to Cl− ions: Three-fourths of all leaked ions were potassium ions. This is mostly because potassium ions, being larger than sodium ions, interact only weakly with the carbonyl regions of phospholipids, so that their interactions are not able to compensate for a large difference in free-energy barriers for permeation of K+ and Cl− ions through a pore. It appears that these findings are very robust to a choice of force-field parameters for ions. We did not observe any essential difference while using Gromacs and Charmm (24) force fields for ions.
Remarkably, we discovered that a potassium ion can permeate through a phospholipid membrane along an alternate, water-defect-mediated pathway without formation of a pore (see Fig. 7). The permeation event involves formation of a single water defect and is found to be very fast (the entire process takes ∼40 ps) as compared to the formation of a pore, which occurs on a nanosecond time scale and involves redistribution of lipid headgroups toward the membrane interior. In a certain sense the water-defect-mediated mechanism of ion permeation might be even more relevant for living cells than the pore-mediated pathway: The transmembrane potential caused by large local fluctuations in ion concentrations at two sides of a cell membrane most likely develops over extremely short times.
To conclude, our computational study provides an atomic-scale picture of ion permeation through protein-free lipid membranes, a problem of long-standing discussion. We demonstrate a hypothetical but physically plausible possibility of ion leakage along the pore- and the water-defect-mediated pathways because of large local fluctuations in ion concentrations on two sides of a phospholipid membrane. In living cells, the density gradients of cations across a membrane are an inherent feature. Understanding the mechanism of unassisted transmembrane transport of ions as well as other charged species can also offer valuable insight into a variety of practical problems such as drug and antibody delivery, binding of cationic antibacterial proteins to the membrane surface, and DNA transmembrane translocation.
Acknowledgments
A.A.G. thanks Alexander Gurtovenko for pointing out the “water-defect-mediated” pathway of permeation of a potassium ion through a membrane. This work has been supported by the Academy of Finland (I.V.) through Grant No. 80246 and by its Center of Excellence Program. The simulations were performed at the Finnish IT Center for Science and on the HorseShoe (DCSC) supercluster at the University of Southern Denmark.
References
- 1.McConnell, H. M., and R. D. Kornberg. 1971. Inside-outside transitions of phospholipids in vesicle membranes. Biochemistry. 10:1111–1120. [DOI] [PubMed] [Google Scholar]
- 2.Toyoshima, Y., and T. E. Thompson. 1975. Chloride flux in bilayer membranes: Chloride permeability in aqueous dispersions of single-walled, bilayer vesicles. Biochemistry. 14:1525–1531. [DOI] [PubMed] [Google Scholar]
- 3.Deamer, D. W., and J. Bramhall. 1986. Permeability of lipid bilayers to water and ionic solutes. Chem. Phys. Lipids. 40:167–188. [DOI] [PubMed] [Google Scholar]
- 4.Finkelstein, A. 1987. Water movement through lipid bilayers, pores, and plasma membranes: Theory and reality. Wiley Interscience, New York.
- 5.Lawaczeck, R. 1998. Defect structures in membranes—routes for the permeation of small molecules. Ber. Bunsen-Ges. Phys. Chem. 92:961–963. [Google Scholar]
- 6.Jansen, M., and A. Blume. 1995. A comparative study of diffusive and osmotic water permeation across bilayers composed of phospholipids with different head groups and fatty acyl chains. Biophys. J. 68:997–1008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Paula, S., A. G. Volkov, A. N. VanHoek, T. H. Haines, and D. W. Deamer. 1996. Permeation of protons, potassium ions, and small polar molecules through phospholipid bilayers as a function of membrane thickness. Biophys. J. 70:339–348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bordi, F., C. Cametti, and A. Motta. 2000. Ion permeation across model lipid membranes: A kinetic approach. J. Phys. Chem. B. 104:5318–5323. [Google Scholar]
- 9.Tieleman, D. P., and S.-J. Marrink. 2006. Lipids out of equilibrium: Energetics of desorption and pore mediated flip-flop. J. Am. Chem. Soc. 128:12462–12467. [DOI] [PubMed] [Google Scholar]
- 10.Gurtovenko, A. A., and I. Vattulainen. 2005. Pore formation coupled to ion transport through lipid membranes as induced by transmembrane ionic charge imbalance: Atomistic molecular dynamics study. J. Am. Chem. Soc. 127:17570–17571. [DOI] [PubMed] [Google Scholar]
- 11.Dzubiella, J., R. J. Allen, and J.-P. Hansen. 2004. Electric field-controlled water permeation coupled to ion transport through a nanopore. J. Chem. Phys. 120:5001–5004. [DOI] [PubMed] [Google Scholar]
- 12.Dzubiella, J., and J.-P. Hansen. 2005. Electric-field-controlled water and ion permeation of a hydrophobic nonopore. J. Chem. Phys. 122:234706. [DOI] [PubMed] [Google Scholar]
- 13.Berger, O., O. Edholm, and F. Jahnig. 1997. Molecular dynamics simulations of a fluid bilayer of dipalmitoylphosphatidylcholine at full hydration, constant pressure, and constant temperature. Biophys. J. 72:2002–2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gurtovenko, A. A., M. Patra, M. Karttunen, and I. Vattulainen. 2004. Cationic DMPC/DMTAP lipid bilayer: Molecular dynamics study. Biophys. J. 86:3461–3472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gurtovenko, A. A., M. Miettinen, M. Karttunen, and I. Vattulainen. 2005. Effect of monovalent salt on cationic lipid membranes as revealed by molecular dynamics simulations. J. Phys. Chem. B. 109:21126–21134. [DOI] [PubMed] [Google Scholar]
- 16.Patra, M., M. Karttunen, M. T. Hyvönen, E. Falck, P. Lindqvist, and I. Vattulainen. 2003. Molecular dynamics simulations of lipid bilayers: Major artifacts due to truncating electrostatic interactions. Biophys. J. 84:3636–3645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Falck, E., M. Patra, M. Karttunen, M. T. Hyvonen, and I. Vattulainen. 2004. Lessons of slicing membranes: Interplay of packing, free area, and lateral diffusion in phospholipid/cholesterol bilayers. Biophys. J. 87:1076–1091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Falck, E., J. T. Hautala, M. Karttunen, P. K. Kinnunen, M. Patra, H. Saaren-Seppala, I. Vattulainen, S. K. Wiedmer, and J. M. Holopainen. 2006. Interaction of fusidic acid with lipid membranes: Implications to the mechanism of antibiotic activity. Biophys. J. 91:1787–1799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Patra, M., E. Salonen, E. Terama, I. Vattulainen, R. Faller, B. W. Lee, J. Holopainen, and M. Karttunen. 2006. Under the influence of alcohol: The effect of ethanol and methanol on lipid bilayers. Biophys. J. 90:1121–1135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Berendsen, H. J. C., J. P. M. Postma, W. F. van Gunsteren, and J. Hermans. 1981. Interaction models for water in relation to protein hydration. In B. Pullman, editor, Intermolecular Forces. Reidel, Dordrecht. 331–342.
- 21.Straatsma, T. P., and H. J. C. Berendsen. 1988. Free energy of ionic hydration: Analysis of a thermodynamic integration technique to evaluate free energy differences by molecular dynamics simulations. J. Chem. Phys. 89:5876–5886. [Google Scholar]
- 22.Lindahl, E., B. Hess, and D. van der Spoel. 2001. GROMACS 3.0: A package for molecular simulation and trajectory analysis. J. Mol. Model. (Online). 7:306–317. [Google Scholar]
- 23.Patra, M., and M. Karttunen. 2004. Systematic comparison of force fields for microscopic simulations of NaCl in aqueous solutions: Diffusion, free energy of hydration and structural properties. J. Comp. Chem. 25:678–689. [DOI] [PubMed] [Google Scholar]
- 24.Beglov, D., and B. Roux. 1994. Finite representation of an infinite bulk system: Solvent boundary potential for computer simulations. J. Chem. Phys. 100:9050–9063. [Google Scholar]
- 25.Darden, T., D. York, and L. Pedersen. 1993. Particle mesh Ewald: An N log(N) method for Ewald sums in large systems. J. Chem. Phys. 98:10089–10092. [Google Scholar]
- 26.Essman, U., L. Perera, M. L. Berkowitz, H. L. T. Darden, and L. G. Pedersen. 1995. A smooth particle mesh Ewald method. J. Chem. Phys. 103:8577–8592. [Google Scholar]
- 27.Patra, M., M. Karttunen, M. T. Hyvönen, E. Falck, and I. Vattulainen. 2004. Lipid bilayers driven to a wrong lane in molecular dynamics simulations by subtle changes in long-range electrostatic interactions. J. Phys. Chem. B. 108:4485–4494. [Google Scholar]
- 28.Anézo, C., A. H. de Vries, H. D. Höltje, D. P. Tieleman, and S. J. Marrink. 2003. Methodological issues in lipid bilayer simulations. J. Phys. Chem. B. 107:9424–9433. [Google Scholar]
- 29.Berendsen, H. J. C., J. P. M. Postma, W. F. van Gunsteren, A. DiNola, and J. R. Haak. 1984. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 81:3684–3690. [Google Scholar]
- 30.Cevc, G., and D. Marsh. 1987. Phospholipid Bilayers: Physical Principles and Models. John Wiley & Sons, New York.
- 31.Hess, B., H. Bekker, H. J. C. Berendsen, and J. G. E. M. Fraaije. 1997. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 18:1463–1472. [Google Scholar]
- 32.Miyamoto, S., and P. A. Kollman. 1992. SETTLE: An analytical version of the SHAKE and RATTLE algorithms for rigid water models. J. Comput. Chem. 13:952–962. [Google Scholar]
- 33.Sachs, J. N., P. S. Crozier, and T. B. Woolf. 2004. Atomistic simulations of biologically realistic transmembrane potential gradients. J. Chem. Phys. 121:10847–10851. [DOI] [PubMed] [Google Scholar]
- 34.Gurtovenko, A. A. 2005. Asymmetry of lipid bilayers induced by monovalent salt: Atomistic molecular dynamics study. J. Chem. Phys. 122:244902. [DOI] [PubMed] [Google Scholar]
- 35.Leontiadou, H., A. E. Mark, and S.-J. Marrink. 2004. Molecular dynamics simulations of hydrophilic pores in lipid bilayers. Biophys. J. 86:2156–2164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Tieleman, D. P., H. Leotiadou, A. E. Mark, and S.-J. Marrink. 2003. Simulation of pore formation in lipid bilayers by mechanical stress and electric fields. J. Am. Chem. Soc. 125:6382–6383. [DOI] [PubMed] [Google Scholar]
- 37.Tieleman, D. P. 2004. The molecular basis for electroporation. BMC Biochem. 5:10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Tarek, M. 2005. Membrane electroporation: A molecular dynamics simulation. Biophys. J. 88:4045–4053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Böckmann, R. A., A. Hac, T. Heimburg, and H. Grubmüller. 2003. Effect of sodium chloride on a lipid bilayer. Biophys. J. 85:1647–1655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Pandit, S. A., D. Bostick, and M. L. Berkowitz. 2003. Molecular dynamics simulation of a dipalmitoylphosphatidylcholine bilayer with NaCl. Biophys. J. 84:3743–3750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Nagle, J. F., R. Zhang, S. Tristram-Nagle, W. Sun, H. I. Petrache, and R. M. Suter. 1996. X-ray structure determination of fully hydrated Lα phase dipalmitoylphosphatidylcholine bilayers. Biophys. J. 70:1419–1431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Petrache, H. I., S. W. Dodd, and M. F. Brown. 2000. Area per lipid and acyl length distributions in fluid phosphatidylcholines determined by 2H NMR spectroscopy. Biophys. J. 79:3172–3192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Costigan, S. C., P. J. Booth, and R. H. Templer. 2000. Estimations of lipid bilayer geometry in fluid lamellar phases. Biochim. Biophys. Acta. 1468:41–54. [DOI] [PubMed] [Google Scholar]
- 44.Rappolt, M., G. Pabst, H. Amenitsch, and P. Laggner. 2001. Salt-induced phase separation in the liquid crystalline phase of phosphatidylcholines. Coll. Surf. A. 183:171–181. [Google Scholar]
- 45.Lynden-Bell, R. M., and J. C. Rasaiah. 1995. Mobility and solvation of ions in channels. J. Chem. Phys. 105:9266–9280. [Google Scholar]
- 46.Aqvist, J. 1990. Ion-water interaction potentials derived from free energy perturbation simulations. J. Phys. Chem. 94:8021–8024. [Google Scholar]
- 47.Shrivastava, I. H., D. P. Tieleman, P. C. Biggind, and M. S. P. Sansom. 2002. K+ versus Na+ ions in a K channel selectivity filter: A simulation study. Biophys. J. 83:633–645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Vernier, P. T., M. J. Ziegler, Y. Sun, W. V. Chang, M. A. Gundersen, and D. P. Tieleman. 2006. a. Nanopore formation and phosphatidylserine externalization in a phospholipid bilayer at high transmembrane potential. J. Am. Chem. Soc. 128:6288–6289. [DOI] [PubMed] [Google Scholar]
- 49.Vernier, P. T., M. J. Ziegler, Y. Sun, M. A. Gundersen, and D. P. Tieleman. 2006. b. Nanopore-facilitated, voltage-driven phosphatidylserine translocation in lipid bilayers—in cells and in silico. Phys. Biol. 3:233–247. [DOI] [PubMed] [Google Scholar]