A Virtual Hair Cell, I: Addition of Gating Spring Theory into a 3-D Bundle Mechanical Model

Abstract

We have developed a virtual hair cell that simulates hair cell mechanoelectrical transduction in the turtle utricle. This study combines a full three-dimensional hair bundle mechanical model with a gating spring theory. Previous mathematical models represent the hair bundle with a single degree of freedom system which, we have argued, cannot fully explain hair bundle mechanics. In our computer model, the tip link tension and fast adaptation modulator kinetics determine the opening and closing of each channel independently. We observed the response of individual transduction channels with our presented model. The simulated results showed three features of hair cells in vitro. First, a transient rebound of the bundle tip appeared when fast adaptation dominated the dynamics. Second, the dynamic stiffness of the bundle was minimized when the response-displacement (I-X) curve was steepest. Third, the hair cell showed “polarity”, i.e., activation decreased from a peak to zero as the forcing direction rotated from the excitatory to the inhibitory direction.

INTRODUCTION

Hair cells in the inner ear receive mechanical stimuli to emit electric impulses. Tens to hundreds of modified microvilli and a kinocilium atop a hair cell form a hair bundle. Various extracellular link structures bind the hair bundle together (1). Among those links, the tip links at the top of stereocilia are believed to be serially connected to the transduction channels (2,3). The prevailing theory of hair cell transduction says that the tension in the tip links delivers the energy required to activate the transduction channels (4). The hair cell is an active system that maintains its sensitivity by continuously adjusting the tension in the gating spring (5).

Mathematical models have been used to analyze the experimental results of hair cell mechanotransduction. They have provided an elegant test bed to develop theories that explain the prominent characteristics of hair cells such as frequency selectivity and amplification (6–11). Recent analytic studies of hair cell mechanotransduction investigate four areas—hair bundle mechanics, the transduction channel, slow adaptation, and fast adaptation (10,11). In those studies, the adaptation models have become sophisticated in an effort to explain the experimental data. Despite the increasing knowledge of the hair bundle structure, however, the mechanical representation of the hair bundles in the analytic studies remains surprisingly simple. In most studies, the hair bundle is represented by a single degree of freedom spring-damper complex (6–11). A mechanical system has one degree of freedom if one value can be used to describe its state. For hair bundles, either tip deflection or angular displacement has been used in one degree of freedom models. The simplicity of this mathematical model has helped to develop various transduction channel theories, but at the same time the simple mechanical representation of the hair bundle has limited application.

This study introduces a computational model of hair cell mechanotransduction that faithfully describes the mechanical characteristics of hair bundles. This study extends previous efforts to create realistic hair bundles (12–15). We applied gating spring theory of hair cell transduction to a finite element (FE) model of the hair bundle. Our model differs from existing analytic hair cell models in two ways: 1), for a structural analysis of the hair cell, a full three-dimensional (3-D) structural model of the hair bundle is used instead of the single degree of freedom model, and 2), the transduction channels open and close individually instead of opening and closing collectively. Two criteria determine when to open or close the transduction channels—the tip link tension and the Ca²⁺ binding to the fast adaptation modulator. Tip link tensions are computed by dynamic FE analysis. Fast adaptation kinetics is regulated by the variation of Ca²⁺ concentration at the tip of each stereocilium. We confined the scope of this study to the early stage of hair cell activation within 2 ms after the onset of excitement. This is too short a time for any significant effect of slow adaptation to appear. Therefore, the slow adaptation is not considered in this study.

We introduce the resulting virtual hair cell and investigate the model features by various simulation results. The structure is based on the geometry measured from a hair cell in the turtle utricle. Imitating an in vitro experimental technique that uses a flexible glass fiber to simulate the hair bundle (16), we applied a series of force steps for 2 ms to the virtual hair cell and obtained the displacement and channel activation responses. The virtual hair cell could reproduce the characteristics observed in experiments such as fast twitch (17–19) and nonlinear stiffness (6,20,21).

METHODS

Finite element model of hair bundle

Our FE modeling procedures are described in previous works (13,14). For geometric information, we used a turtle (Trachemys scripta) utricular hair cell. The modeled hair cell is a type II hair cell in the striolar region, 20-μm lateral from the point of polarity reversal (22,23). The model geometry is shown in Fig. 1. Detailed geometric properties for the same hair bundle were listed elsewhere (24). Structural components of our hair bundle model are the kinocilium, stereocilia, and various extracellular links such as the tip link assembly (TLA), upper lateral links, shaft links, and kinocilial links. Note that in this hair bundle model the TLA represents more than just the tip link whose major constituent is Cdh23 (25). The TLA represents the mechanical equivalent of the entire structure extending from the core of one stereocilium to the core of the other, including the Cdh23 filaments, the actual transduction channel, and all connections to the actin fiber in the stereocilia. The stiffness of the TLA is dominated by the most compliant element in the complex. The most compliant element can be the ankyrin repeats of the transduction channel or another springy protein (26–28).

FIGURE 1.

FE model of a hair cell. Geometric information such as stereocilia arrangement and heights are obtained from confocal microscopic images (23) and the link configurations are inferred from the literature (1,61,62). (Left) The bundle has 52 cilia including 1 kinocilium and 42 tip links. The kinocilium was labeled with ‘K’ in the circle. Center: The hair bundle model includes several different structural elements—TLA, upper lateral links (UL), shaft links (SL), and kinocilial links (KL). (Right) The FE model of the hair bundle used for this study is shown in a 3-D view. Bars in the bottom right corner of each plot indicate 1 μm.

The Young's modulus of stereocilia is 0.75 GPa. The stiffness of the TLA is 5 pN/nm. The stiffness of upper lateral and shaft links are 0.001 and 0.75 pN/nm, respectively. These mechanical properties were estimated by matching our mechanical model with other experiments and are presented in full elsewhere (24). TLAs are designed to slacken as they are compressed. The upper lateral links stiffen as they elongate to prevent the bundle from excessive splay at large stimuli. Also the upper lateral links stiffen as the stereocilia surfaces come close to contact, preventing the neighboring stereocilia from sticking together (24). A computer program was written in MATLAB for this study (29).

Resting tension

The TLAs are tensed at the bundle's resting state (3,30). The resting tension is regulated by the myosin motors (reviewed in Gillespie and Cyr (31)). The resting tension in the TLAs helps to maintain the sensitivity of hair cell mechanotransduction (31). We selected a resting tension level of 25 pN. This choice of resting tension is examined and discussed later. We did not simulate the myosin motors that actually provide the resting tension. The pretension was not applied by pulling the tip links along the shaft of stereocilia. Rather, we achieved the pretension by static analysis as follows. First, the TLAs were removed from the hair bundle, and the pulling forces of 25 pN were substituted for the TLAs. After the static analysis, the distances between the TLA attachment sites were assigned as the elongated lengths of the TLAs. Finally the tensed TLAs replaced the tensile forces. This static method is simple to implement and mechanically equivalent to the resting tension maintained dynamically by the molecular motors. This method is justified only when it is simulated for a brief time before any significant effect of the slow adaptation appears.

Dynamic analysis and fluid viscous drag

To solve the equations of motion of the hair bundle, an implicit integration scheme called the Newmark method is used (32). The time step size of 2 μs was chosen as a compromise between computational resources and temporal resolution. Fluid drag on the hair bundle is considered as follows. Each individual stereocilium is modeled as a cylinder subjected to a developed steady-state flow. When a bundle moves in the fluid, the drag force on each stereocilium is computed from the relative velocity between the fluid and the portion of the cilium exposed to the flow. The viscous damping inside the bundle is also considered by adding structural damping. This damping in the bundle was adjusted to make the overall effective damping ∼200 nN·s/m, which is within the range of the reported damping coefficient (6,21,33). The effective damping is equivalent to a single damping coefficient when the bundle is considered as a single degree of freedom spring-damper system. The structural dynamic analysis procedures, including the equations of motion and the time integration scheme, were previously reported (34).

Fast adaptation regulated by Ca²⁺

As in previous studies (6,10), we assumed the Ca²⁺ reaction rate of the fast adaptation modulator regulates the channel reclosure. Like the fast adaptation mechanism suggested by Vilfan et al. (11) and Cheung and Corey (35), our fast adaptation modulator generates the force that closes the channel instead of relaxing the channel. In this computational model, the fast adaptation motor is located at the transduction channel assumed to be at the upper end of the tip link (Fig. 2).

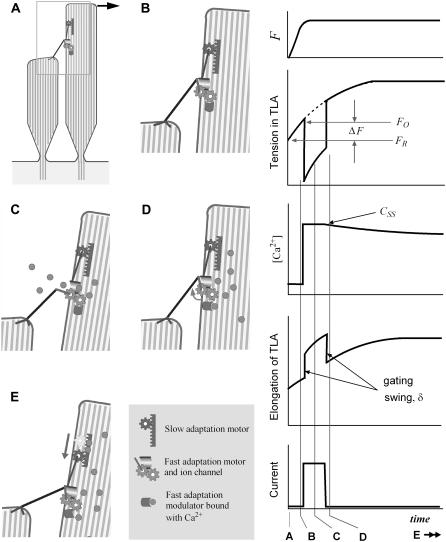
FIGURE 2.

Mechanism of mechanoelectric transduction in the presented model. Our computer model considers the transduction channels to be serially connected to the tip links. The transduction channel and adaptation motor are located at the upper end of the tip link. Although the slow adaptation is not modeled or simulated in this study, it was included in this illustration. (Left) At rest, the channel is closed (A), and the TLA has a resting tension of F_R. As the bundle deforms, the tension in the TLA increases (B). When the tension exceeds the opening tension level, F_O, the channel opens (C). Due to the gating swing (δ) the tension in TLA drops. The cations flow in due to the resting potential between extracellular and intracellular fluid. As Ca²⁺ at the site of the fast adaptation modulator increases, the channel closes and the tip link pulls back the taller stereocilium (D). By sliding down the upper end of the tip link (slow adaptation), the tension of TLA is decreased to its resting level (E). (Right) The time response of a single channel from our proposed model. From top to bottom, the applied force to the bundle, tension in the TLA, [Ca²⁺] at the fast adaptation site, elongation of the TLA, and transduction current of the single channel. The vertical lines A–D correspond to the images labeled A–D to the left. This study simulates for 2 ms after the onset of excitation, before the slow adaptation (E) becomes apparent.

The probability of Ca²⁺ binding to the fast adaptation modulator, p_B, is described by the first order differential equation

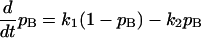(1)

(1a)

where k₁ is the binding rate constant, k₂ is the dissociation rate constant, C is the [Ca²⁺] at the fast adaptation site, and α is a constant. Parameters of α = 0.1 and k₂ = 0.25 were chosen to achieve the reported fast adaptation time constant of 0.1 ∼ 1.0 ms (36,37). Related channel kinetics parameters are summarized in Table 1.

TABLE 1.

Properties related to channel gating

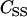	35 μM	Steady-state [Ca2+] at the binding site when channel stays open
FR	25.0 pN	Resting tension
ΔF	1.5 pN	Channel gating threshold
δ	5 nm	Gating swing
Fcrit	24 pN	Critical tension above which open channels remain open regardless of [Ca2+]
α	0.1 μM−1 ms−1	Ca2+-binding rate to the fast adaptation modulator
k2	0.25 ms−1	Ca2+-dissociation rate from the fast adaptation modulator

The [Ca²⁺] at the fast adaptation site, C, is bimodal. When the channel is open, the ionic diffusion is driven by the electric potential and thus is faster than pure diffusion. The electron-dense insertional plaques at the ends of tip links in the bilipid layer are believed to house the adaptation motors (31). Considering the size of an insertional plaque is ∼50 nm in diameter (38), the [Ca²⁺] at the slow adaptation site was estimated to reach its steady state within a few tens of microseconds (39). It is believed that the fast adaptation happens at an even closer site from the ion pore than the slow adaptation. The time to reach C_SS, the steady-state [Ca²⁺] at the site of fast adaptation (see Fig. 2), is expected to be less than a few microseconds (39). This is much faster than the fast adaptation timescale, which has a time constant of 0.1 ∼ 1 ms. Therefore, in our computer model, C jumps to its steady-state value, C_SS, right after the channel opens. When the channel is closed, Ca²⁺ diffusion is driven by the [Ca²⁺] gradient and the diffusion time constant is expected to be much larger than our simulated time periods of 2 ms (40). Because of this fast Ca²⁺ inflow and slow Ca²⁺ dissipation, the Ca²⁺ diffusion relations do not affect the simulation's response presented here, which is within 2 ms of excitation. If we simulate for longer time periods (>10 ms), the Ca²⁺ diffusion rate should affect the responses.

Transduction channel model

In our model, the transduction channel is located at the upper end of the tip link (Fig. 2). The modeled transduction channel has four states: closed C, open O, calcium bound open O·Ca, and calcium bound closed C·Ca (Fig. 3). This four-state description is comparable to Choe et al.'s six-state channel (8) and Fettiplace et al.'s four-state channel diagram (41).

FIGURE 3.

Transduction channel has four states. From the resting closed state the channel opens (C→O) when the tension in the TLA exceeds the channel opening tension (F > F₀). The opened channel is closed by fast adaptation (O→O·Ca →C·Ca). However, if the tension exceeds a critical value (F > F_crit) the open channel stays open despite calcium binding (O→O·Ca). The Ca²⁺-bound closed channel becomes an unbound closed channel as the Ca²⁺ diffuses (C·Ca→C). In this study, the slow adaptation is not simulated.

The transduction channel is activated by an increased tension in the TLA (C→O). When the channel is open, the transduction current is carried by inflowing cations. As the Ca²⁺ concentration increases to reach its steady state (in this study 35 μM) and the Ca²⁺ ions bind to the fast adaptation site, a morphological change occurs in the transduction channel that causes the channel to close (O→O·Ca →C·Ca). This fast reclosure is called the fast adaptation. A sharp transient reversal in the bundle displacement, called the fast twitch, has been attributed to the channels near the tip of bundle closing (18).

Experimentally, the effect of the fast adaptation decreases as the magnitude of excitation increases (36). We define a critical tension in the TLA, F_crit, to account for this. We suppose that when the tension in the TLA exceeds F_crit, the channel does not close despite the [Ca²⁺] at the binding site (O→O·Ca). If the stimulus is sustained, the channel closes eventually by decreased tension due to the slow adaptation (O·Ca→C·Ca).

Single channel gating

Channel opening and closing is mechanically described by the gating swing, δ. In our simulation, the length of TLA is increased by the gating swing instantly after the channel opening and decreased after closure. The gating swing in this study is 5 nm. The effect of varying the gating swing distance is examined in the companion work (24). If the applied stimulus is sustained for more than a few milliseconds, the increased tension in the tip links is relaxed by the upper end of the tip links' sliding down. This slow adaptation takes a longer time than the fast adaptation.

Other model studies are based on statistical mechanics represented by the Boltzmann relationship (7,8,10,11). In combination with the parallel arrangement assumption (4), all the channels in the hair cell are assigned the same open probability, which is a function of the bundle tip displacement. Unlike other hair cell transduction models, our model features individual gating of the transduction channels.

In our study, individual channels open and close based on the tip link tension and the Ca²⁺ kinetics. The ion channel at the end of TLA opens as the tension in the TLA reaches the channel opening tension, F₀. There are Ca²⁺-binding sites (the fast adaptation modulator) near or at the ion channel. The [Ca²⁺] at the binding site increases quickly as the channel opens (39). As the Ca²⁺ binds to the fast adaptation modulator, the channel closes. The open channel remains open if the tension in the TLA is greater than F_crit. In this study F_crit = 24 pN, which will be examined and discussed later. Fig. 2 illustrates the single channel-gating scenario.

Simulations and data analysis

Thirty-two step forces ranging from −50 to +700 pN were applied to the taller edge of the hair bundle for 2 ms. To simulate the test conditions analogous to many in vitro experiments that used flexible glass fibers to stimulate hair cells, the force had a sigmoidal rise from zero to its full magnitude in 0.05 ms. The applied force was distributed on the tips of the three tallest cilia, including the kinocilium, to match glass fiber forcing. To isolate the effect of the gating of mechanoelectrical transduction (MET) channels, two series of simulations were performed, one with and one without channel gating, referred to hereafter as the active and passive hair cell, respectively.

We defined the hair cell activation level, I, as the fraction of open channels. This is analogous to the channel open probability, p_o, in other studies. The choice of I refers to transduction current, as our results will be compared to experimental studies presenting current. In previous studies, the channel open probability as a function of displacement, p_o(X), was approximated by the second order Boltzmann relation (36,42–45)

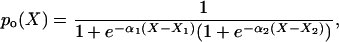(2)

where X is the bundle displacement measured at the tip of the bundle and α₁, α₂, X₁, and X₂ are constants. We used Eq. 2 to curve fit our simulated I-X data as it has been shown effective as a fit of data and will allow comparison of parameters.

For each applied force the peak displacement at the tip of the bundle was measured. To fit the F-X relationship, the following equation from Howard and Hudspeth was used (6). As with Eq. 2 this equation has been shown to accurately describe the data. In this equation, the applied force, F, equals the elastic reaction force of the bundle.

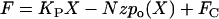(3)

where, K_P is the stiffness of bundle without the gating spring, N is the number of transduction channels, z is the gating force, and F_C is a constant. This equation was modified to fit our simulated F-X data points:

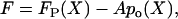(3a)

where F_P(X) is the passive force-displacement relationship, and A is a constant that best fits the curve. The function p_o(X) was taken from our fit of Eq. 2. F_p(X) was obtained from our series of passive bundle simulations and replaces the first term in Eq. 3. The same hair cell was simulated with the same conditions, but the channels were fixed at closed state (C) to obtain the passive response of hair cell.

There is an inconsistency between Eqs. 2 and 3a that we used to curve fit our simulated data. Equation 2 is based on a three-state channel model, and Eq. 3a is from the two-state model. This inconsistency is discussed later. We fit our data with these equations to demonstrate that our model fits experimental studies which have been interpreted with these equations.

RESULTS

Channel gating and fast adaptation

In our simulations, the channels in the taller end of the bundle were opened first (Fig. 4). As individual channels opened and closed, the bundle deformed to balance the internal forces with the externally applied force. The reclosure of channels caused the tension in the neighboring tip links to increase and thus elicited a cascade of channel activations (Fig. 4). Usually the number of open channels peaked within 0.2 ms after the force was fully applied. Occasionally other peaks followed the first peak and were caused by the cascaded opening of channels in shorter stereocilia (Fig. 5 B). The channel reclosures lasted for 0.5 ∼ 1.0 ms, and the fast adaptation finished within 2 ms. The Ca²⁺ association coefficient k₁ in Eq. 1 determines the speed of the fast adaptation. For small stimulus forces, a small number of channels opened and most closed again. For large forces, more channels opened and most remained open (Fig. 5 B). Our results show that the recoil of the bundle can happen due to the channel reclosure (Fig. 5, A and B). Using the parameters in Table 1, the maximum rebounding displacement was 10 nm when the force magnitude was 15 pN. This corresponded to when a number of channels near the tip of the bundle closed. The recoil could reach over 20 nm when tested with a higher F_R and a smaller F_crit than the values in Table 1.

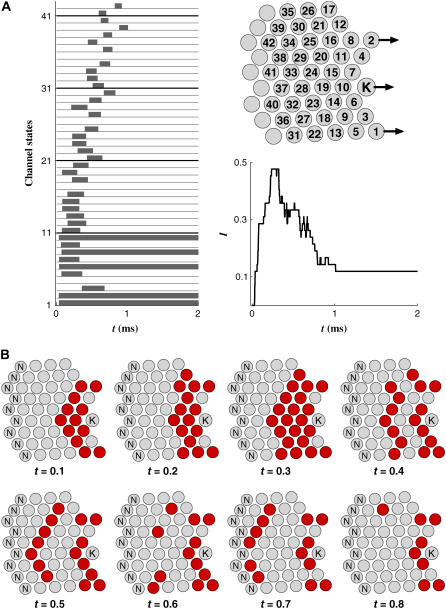
FIGURE 4.

Simulation of hair cell mechanotransduction: single channel activations. A hair cell with 42 transduction channels was subjected to a step force of 50 pN. The bundle tip was displaced by 30 nm. (Right top) Top view of the bundle shows the channel identification numbers in the circles indicating stereocilia. Analogous to the glass fiber stimulation, the force is applied at the taller edge of the bundle. (The three arrows indicate the location of applied force acting on the tips of the cilia.) (Left top) Each of 42 channels opened and closed individually according to the prescribed gating criteria. The channels in the tall stereocilia opened first, and the activation propagated toward the short stereocilia. Channels 1 and 2 opened at the very beginning of stimulation and stayed open. Channel 3 opened and closed around 0.5 ms. Only four channels were not activated during the simulation, and they were mostly peripheral channels (Channels 4, 17, 26, and 35). (Right center) The hair cell activation level, analogous to the whole cell current, I, is shown. Even though most channels were activated once during the simulation period of 2 ms, the maximum number of channels open at the same time was 20 (I = 20/42 = 0.48). Five channels remained open after the fast adaptation, and those unclosed channels were near the taller edge where the force was applied. (Bottom) Sequential plots of channel activations are shown with a 0.1-ms interval. Darker circles indicate the stereocilia with the open transduction channels. The stereocilia marked with ‘N’ are those without a transduction channel. The channel activations propagate from the taller edge toward the shorter edge.

FIGURE 5.

Responses of the virtual hair cell. A total of 32 step forces were applied ranging from −50 to 600 pN. Each case was simulated for 2 ms. Of those 32 simulations, three time responses were selected in A and B—force magnitudes of 20, 60, and 140 pN. (A) Tip displacement along time: Solid lines are the response of active hair cells, and dashed lines are from passive hair cells with no channel activity. (B) Channel activations along time: The hair cell activation level, I, was defined as the number of open channels at the time divided by the total number of channels. For small forces, fewer channels opened and all of them were closed again. As the force stimulus increased, more channels opened and more channels remained unclosed. (C) F-X curve: For the active response with channel gating, the force-displacement curve undulates between 0 ∼ 25 nm (•). The active curve was obtained at peak response. When the channels were held in their closed state (passive response, dashed line), the F-X curve behaved smoothly. The curve fit of active response was from gating spring theory using Eq. 3a. At F = 50 nm, the active F-X curve shifts to the right by 8 nm from the passive curve, which is about the magnitude of the largest twitch. (D) Activation curves were obtained from a series of simulations. The tip deflection X was obtained when the bundle was deformed most (•) and at 2 ms after the fast adaptation finishes (○). The second order Boltzmann relations were used to fit the data points (solid lines). The best fit for peak response (•) is obtained with α₁ = 362 nm⁻¹, α₂ = 31 nm⁻¹, X₁ = 9 nm, and X₂ = 36 nm. The best fit for post-fast-adaptation (○) is obtained with α₁ = 76 nm⁻¹, α₂ = 20 nm⁻¹, X₁ = 38 nm, and X₂ = 79 nm. (E) The dashed line indicates the passive stiffness of the bundle. Solid lines are the active K-X curve obtained from the active F-X curve. The stiffness was 2.0 and 2.6 pN/nm at X = − 25 and 100 nm, respectively, and the minimum active (dynamic) stiffness was 8.0 pN/nm at X = 8 nm.

The dynamic response of the bundle displacement (X) and channel activation (I) is shown in Fig. 5, A and B. When there was no channel activity, the bundle reached 95% of its steady state in 0.6 ms (dashed lines in Fig. 5 A). When there was channel gating, the bundle reached 95% of steady state ∼0.1 ms earlier than when passive, which is equivalent to a time constant of 0.15 ∼ 0.2 ms (solid lines in Fig. 5 A). The active hair cell bundle deformed further than the passive bundle due to channel gating. When all channels were closed due to fast adaptation, there is no difference in steady-state displacement between the passive and active responses (Fig. 5 A, when F = 20 pN). The difference between the passive and active response became greater as the applied force increased (see Fig. 5 A: 8 and 12 nm at F = 60 and 140 pN, respectively). The fast twitch was observed when the applied force was <70 pN. The overshoot was 8 nm when F = 20 pN and 1 nm when F = 60 pN (Fig. 5 A).

Activation curve

The simulated hair cell behaved similarly to the experimental I-X curve as it was steeper when the channels began to open and gradually developed to a plateau (Fig. 5 D).

The second order Boltzmann relationship was used to fit our results. The I-X relations were obtained at peak displacement and 2 ms after the onset of stimulation. Around 0.3 ∼ 0.6 ms, the bundle arrived at its peak displacement and usually the number of open channels peaked at a similar moment. The hair cell finished its fast adaptation within 2 ms after the onset of stimulus. Due to the channel reclosure, the I-X curve at peak response is above the curve at 2 ms (Fig. 5 D). As small a force as 10 pN could sporadically activate 29 out of 42 of the transduction channels throughout the simulation period, but as large a force as 400 pN did not activate all the channels at once.

Force-displacement relation

F-X (force-displacement) relations are shown in Fig. 5 C. The passive force-displacement relation was nonlinear. The tangent stiffness smoothly increased from 1.95 to 2.78 pN/nm as the force increased from 0 to 500 pN. The active F-X relations are obtained at peak and 2 ms. The curve undulates in the displacement range between 0 and 25 nm, which means that the bundle has a stiffness varying considerably in this displacement range. In Fig. 5 C, the solid lines are the curve fits of the simulated F-X data points using Eq. 3a. As seen both in Eq. 3a and in our simulated results, the F-X relationship depends on the I-X relationship. To better fit the abrupt change of the F-X relationship in small deflection range, we weighted the small deflection range when we fitted the I-X data. The I-X data were fitted with Eq. 2 using the weighted least square method, and the data points within ±15 nm of the activation commencement were given three times greater weight than other data points.

Hair bundle stiffness

By differentiating the force F obtained using Eq. 3a, with respect to the displacement X, the stiffness versus displacement (K-X) curves were obtained as shown in Fig. 5 E. The bundle was most compliant in the displacement range from 0 to 20 nm where the activation curve in Fig. 5 D was steepest. The smallest dynamic stiffness was 0.8 pN/nm at X = 9 nm and the stiffness increased to 2.6 pN/nm at X = 100 nm.

Several experiments have shown the directional bias of hair bundle stiffness (6,7,46–48). Our simulated hair bundle was stiffer in the excitatory than in the inhibitory direction. This directional dependence of the bundle stiffness is due to the nonlinear passive stiffness. Material properties of the stereocilia, shaft links, and kinocilial links were considered constant in our study. Although the upper lateral links and TLAs in this study have a nonlinear stiffness, the nonlinear bundle stiffness was not caused by the link nonlinearity within a moderate displacement range of −50 ∼ 150 nm. Rather, the geometry of the bundle is responsible for the nonlinear passive stiffness. As the bundle deforms in the excitatory direction, the bundle diameter along the forcing direction grows, whereas the diameter orthogonal to the forcing direction shrinks. Subsequently, the links between the stereocilia are realigned toward the forcing direction. This change in the bundle configuration explains the geometric nonlinearity of bundle stiffness shown in this study. If the bundle has a tented shape so that the tips of the stereocilia almost contact each other, we expect less geometric nonlinearity.

Polarity of the hair cell

Hair cells are most sensitive in the excitatory direction and least sensitive in the inhibitory direction, a characteristic known as the polarity of the hair cells (49,50). To observe the polarity of our tested hair cell, a force of 120 pN was applied at the taller edge of the hair bundle at different angles from the excitatory-inhibitory (E-I) axis (Fig. 6). When the forcing angle was within ±30°, the hair cell has a near constant I (fraction of open channels) of 0.7. When the forcing angle was ±90°, the I drops to 0.2. There was little or no activity as the forcing angle approached 180°—the inhibitory direction.

FIGURE 6.

Polarity of the hair cell. A series of 120-pN forces were applied to the hair cell at 15° increments. The forcing angles φ were measured from the excitatory direction, i.e., 180° indicates the inhibitory direction (left). For the current versus forcing angle plot (right) the distance from the center to each point indicates the hair cell activation level, I. The angular location of each dot indicates the forcing angle. The I remained the same (∼0.7), whereas the forcing angle was within ±30°. But, as soon as the forcing angle exceeds ±60°, response reduced abruptly. Beyond ±90°, we observed negligible channel activations.

DISCUSSION

Bundle mechanics may be responsible for the asymmetry of I-X relations

This study incorporated a full 3-D mechanical model of the hair bundle and the predominant gating spring theory of the hair cells. Our simulated I-X and F-X relations fit Eqs. 2 and 3, which are frequently used to analyze experimental results of various hair cells. However, it is paradoxical that the transduction channel in this study has four states, and Eqs. 2 and 3 represent three- and two-state channel models, respectively. Although we did not derive any biophysical properties out of such equations, we reckon why the equations matched our simulated results as follows.

First, the F-X relations matched well with the two-state model in Eq. 3 because our hair bundle also has two mechanical states. The four states of the channel can be divided into two mechanical states: open or closed. The open states (O, O·Ca) have the unstrained TLA length longer than the closed states (C, C·Ca) by the length of δ. Therefore, the hair bundle in the open states deforms further and results in reduced stiffness than the bundle in either of the closed states. Second, we consider that the asymmetrical I-X relations are due to not only the number of channel states, but also the hair bundle shapes and passive structural mechanics. In gating spring theory, each transduction channel can be considered as having an independent open probability. Our simulation results showed interactions between the neighboring transduction channels. The gating event of a channel influences gating of nearby channels, and such interactions form the I-X relations. For example, in our simulations, the channels near the forced points were opened first, but as the channel opening propagates toward the periphery of the bundle it took more force to activate the channels.

Our notion that 3-D bundle mechanics is responsible for the asymmetry of the I-X relationship may reconcile seemingly conflicting observations. Whereas many reported I-X relations fit better with the second order Boltzmann curve, the I-X relations measured from a single transduction channel fit well with the first order Boltzmann curve (51). Although others have also warned that one should be very careful in attempting to understand underlying processes from a Boltzmann fit to the input-output relations (52), to our knowledge, this is the first work in which a mechanism has been proposed for the MET in a hair bundle that yields a higher order Boltzmann function with a first order Boltzmann channel.

Introducing the channel opening tension, F₀

We introduced a new parameter that is related to the MET channel kinetics: the channel opening tension, F₀. To our knowledge, no previous study has speculated on such a parameter. Previous mathematical studies described the transduction channels in a hair cell collectively and statistically. Unlike those studies, our virtual hair cell describes specific geometric location and number of the transduction channels in a hair bundle. Because of this descriptive approach, we had to introduce the channel opening tension, F₀, over which tension the transduction channel opens.

Although we newly introduced F₀ as a hair cell MET parameter, it is deduced from the existing gating spring theory. The gating spring theory of the hair cell is based on thermodynamics, which discusses the energies of discrete channel states. When we confine our discussion to the elastic potential energy of the TLA in our model, the argument is as follows: in an energetic sense, F₀ integrated over the elastic TLA deformation is the potential energy a resting closed channel reaches before it opens. Previous studies focused on the energy difference between channel states to develop the gating spring theory of the hair cell (6,53). Between any two stable states, there is an energy barrier to limit the transition between the states. In our model, the gating threshold ΔF determines the height of the energy barrier, ΔE, again by integrating the TLA force over the deflection

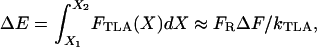(4)

where X is the TLA elongation, X₁ and X₂ are the elongation at a channel at the resting closed state and at the state where it is about to open, and F_TLA is the tension in the TLA. We chose ΔF = 1.5 pN, which makes ΔE ≈ 2 k_BT. We investigate this choice in the accompanying work by simulating different ΔF values. By definition, ΔF = F₀ − F_R. The estimated value of the F_R ranges from a few to tens of piconewtons (31). We chose F_R = 25 pN in this study. Considering the stalling force of 2 pN per myosin head (31,54), at least 13 myosin heads are required to generate our chosen resting tension. Hence, we arrive at F₀ = F_R + ΔF = 26.5 pN.

We suppose that the F₀ is intrinsic to the molecular identity of the transduction channel, which has not yet been identified. The value we used in this study, F₀ = 26.5 pN, is estimated as stated above. However, if a proper set of experiments is accompanied by an analytic study such as ours, we expect that a better estimation of F₀ can be made.

3-D hair bundle versus single degree of freedom bundle model

Most mathematical studies of hair cells assume that all transduction channels in the hair bundle are arranged in parallel and have an equal probability of activation (4,6–8,10,30,55). Based on this assumption, the applied force at the tip of the bundle is evenly distributed to all channels. This assumption is incorporated into the term N z p_o(X) in Eq. 3. The applied force, F, is equally distributed onto N channels, or N gating forces, z, contribute equally to oppose the external force, F.

Our study does not rely on the parallel arrangement assumption because we modeled the hair bundle's full 3-D geometry. Previous model studies show that the tip link tensions are not evenly distributed in the bundle (15,56,57). When force is applied at the tip of a bundle, the tip links near the excitation point have the highest tension (15,34). Our simulations show that channels near the taller edge open faster and have a higher chance to remain open because of the uneven tip link tension distribution (Fig. 4). Further, the parallel arrangement assumption has a mechanical consequence, e.g., if Eq. 3 is used to estimate the stiffness of the gating spring, it can underestimate the stiffness by several times (24). Our results recommend that one should be careful to interpret the biophysical values obtained using the simple single degree of freedom bundle mechanical model.

Because this model uses a multiple degree of freedom mechanical system, it can be used to study how the different shapes of hair bundles are related to their function. Three hair bundles, including the one used in this study, are shown in Fig. 7. The diversity of bundle shapes is striking. Bundle A is from the medial extrastriola of the turtle utricle. Bundle C is from the striola of the mouse utricle. Only a sophisticated mechanical model such as ours can reveal why there is such a variation in the bundle morphology. According to our previous efforts (34,58), a hair bundle that has a longer array along the E-I axis, like bundle A, encodes a wider range of stimulus amplitudes. A hair bundle with a shorter array along the E-I axis, like bundle C, may respond faster and encode a narrow range of stimulus amplitudes.

FIGURE 7.

Various bundle shapes. Top-down views of hair bundles and vertical columns of hair bundles along the bilateral symmetry line are shown. The geometric values were measured from the confocal microscopic images (E. H. Peterson, Ohio University, personal communication, 2005). The kinocilium is indicated with “K”. The lines of bilateral symmetry, which are also the E-I axes, are drawn on the top-down views. The scale bars indicate 1 μm. The hair bundles are from the macular surface of the medial extrastriola (A) and striola (B) in the turtle utricle and the striola in the mouse utricle (C).

A cascade of channel opening events as shown in Fig. 4 will be more apparent in bundle A than in bundle C (Fig. 7). According to our hair bundle model, transduction channels in the same column along the E-I axis are more interactive than the channels located across columns, because tip links are connected along the stereocilia columns. We expect that the extent of this channel interaction is more apparent in bundle A than in bundle C. If channel interaction is responsible for the asymmetry of the hair cell input-output relations as we argued in the beginning of the Discussion, the I-X curve of bundle A may be more asymmetric than bundle C. On the other hand, the parallel arrangement assumption implies that the transduction channels in a bundle are independent. Therefore, among the three hair bundles, bundle C may be better approximated by the single degree of freedom mechanical model, whereas bundle A may be poorly approximated.

Simulation artifacts and limitations

Although the presented virtual hair cell shows characteristics of in vitro hair cells, there are several aspects that have not been incorporated. First and most obvious is that the channel kinetics of the hair cells are known to be probabilistic. To simulate this probabilistic feature, we could have randomly distributed channel kinetic properties with the mean values presented in Table 1. We argue that incorporating these random properties may not alter the results. However, this does introduce an artifact as follows.

The zero resting current of our simulation is an artifact of our deterministic channel gating conditions. The channel opening force, F₀, is probably intrinsic to the channel molecular identity. However, unlike our model, the resting tension, F_R, in real TLAs may continuously vary with time because the tugging force provided by multiple myosin molecules should be stochastic. Therefore, ΔF, the difference between F₀ and F_R, may be distributed between zero and several piconewtons for hair cells in vivo. Further, the stochastic impact of water molecules on the bundle may easily activate channels on the verge of opening. Despite our simulation results, we do not argue that the hair cells in vivo require a few piconewtons to initiate any mechanoelectric transduction.

There is an additional artifact of our computer model. Although we simulated as if the channel kinetic parameters in Table 1 are independent, the resting tension F_R is considered dependent on the intracellular [Ca²⁺]. When we tested the effect of C_SS, we did not change F_R, and little difference in the I-X or F-X relationship resulted despite different C_SS values. Because Ca²⁺ tends to cause slippage in the actin-myosin junction, C_SS and F_R should be inversely related: an increased internal [Ca²⁺] reduces the resting tension. Decreased resting tension results in a shift of the I-X curve to the right and decreases the slope of the I-X curve. If the dependence between C_SS and ΔF is considered, decreased C_SS should result in increased sensitivity of the hair cell as seen experimentally (59,60).