Sources of Anomalous Diffusion on Cell Membranes: A Monte Carlo Study

Abstract

A stochastic random walk model of protein molecule diffusion on a cell membrane was used to investigate the fundamental causes of anomalous diffusion in two-dimensional biological media. Three different interactions were considered: collisions with fixed obstacles, picket fence posts, and capture by, or exclusion from, lipid rafts. If motion is impeded by randomly placed, fixed obstacles, we find that diffusion can be highly anomalous, in agreement with previous studies. In contrast, collision with picket fence posts has a negligible effect on the anomalous exponent at realistic picket fence parameters. The effects of lipid rafts are more complex. If proteins partition into lipid rafts there is a small to moderate effect on the anomalous exponent, whereas if proteins are excluded from rafts there is a large effect on the anomalous exponent. In combination, these mechanisms can explain the level of anomaly in experimentally observed membrane diffusion, suggesting that anomalous diffusion is caused by multiple mechanisms whose effects are approximately additive. Finally, we show that the long-range diffusion rate, D_macro, estimated from fluorescence recovery after photobleaching studies, can be much smaller than D_micro, the small-scale diffusion rate, and is highly sensitive to obstacle densities and other impeding structures.

INTRODUCTION

Diffusive processes are crucial to biological interactions. However, the environments in which these processes take place have high densities and viscosities due to molecular crowding. Biological media exhibit a large degree of complexity and heterogeneity and often exhibit substantial compartmentalization (1). Furthermore, diffusive motion and interaction in biological systems often takes place on two-dimensional membranes. Because the nature of diffusion depends strongly on the dimensions of the medium, this has important consequences. In particular, diffusion in biological media is observed to be orders of magnitude slower than predicted by theory (2). As a result of the nonclassical nature of these random motions, biological reactions are generally complex, nondeterministic as well as being frequently characterized by low numbers of reacting molecules (3).

Classically, according to the standard diffusion equation, the mean squared deviation of a protein from its starting site on a two-dimensional membrane grows linearly with time, i.e., MSD ∝ t. However, in low-order or complex biological media, this parameter is often found to vary with a positive fractional power of time that is smaller than 1, i.e., MSD ∝ t^α, where α is called the anomalous exponent (which is exactly equal to 1 for normal diffusion). This phenomenon is called anomalous diffusion or subdiffusion. Mathematically, this is significant because it indicates a breakdown of the standard form of the Central Limit Theorem and requires modified analytical models and simulation techniques based on detailed Monte Carlo simulations. An alternative approach is to realize that the presence of diffusion obstacles changes the waiting time distribution of reactions from exponential to nonexponential (4). In the continuous setting this leads to fractional differential equations of noninteger order that describe the concentrations of molecular species in crowded environments (5). Anomalous diffusion on the plasma membrane is biologically important because it may contribute to the nonrandom distribution or lateral segregation of lipid anchored and integral membrane proteins. Protein clustering in turn drives the formation of specific signaling complexes, for example, diverse experimental approaches that perturb the plasma membrane interactions of lipid anchored Ras proteins prevent Ras clustering and abrogate Ras signal output (6–9).

Anomalous diffusion has been observed experimentally in cytosol and on cell membranes. Different methods have been used to study such processes, including single particle tracking (SPT) (10–14), fluorescence recovery after photobleaching (FRAP) (14–16), and fluorescence correlation spectroscopy (17). The quantification of the degree and nature of the anomalous diffusion, however, has proven difficult due to experimental limitations (18). Nevertheless, some estimates of the anomalous exponent and other parameters have been reported; for example, one study has estimated α ≈ 0.49 ± 0.16 for diffusion of the proteins on HeLa cell plasma membrane (10).

What is the fundamental cause of anomalous diffusion? A number of hypotheses have been suggested, including interactions with picket post structures anchored to membrane skeleton mesh (2), motion impedance by fixed proteins (1), the effects of corrals and impermeant patches (19,20), and interactions with membrane microdomains such as lipid rafts (21,22). In a biological membrane each of these types of interaction is likely to contribute to subdiffusion, but their relative importance is unclear. To explore this problem further, we developed a stochastic random walk Monte Carlo model of protein diffusion on a membrane that incorporates the majority of these different types of membrane component. We interrogate the model to estimate the extent to which each membrane component in isolation, or in combination can account for subdiffusive behavior on cell membranes.

METHODS

Modeling and Monte Carlo simulations

In this investigation, Monte Carlo methods are used to simulate the spatial mobility of modeled proteins and the kinetics of chemical reaction systems on membranes. A two-dimensional lattice is used to represent the membrane. Each element of this lattice is a voxel that can be either occupied or unoccupied by a modeled protein at each time step; in the former case, a record is made of which protein occupies the voxel. For all simulations we used a lattice of dimensions 250 × 375 voxels, unless otherwise stated. Assuming a voxel to have a side of length 2 nm, this corresponds to a membrane area of dimensions 500 × 750 nm. At any time, only one modeled protein may occupy a given voxel, to ensure volume exclusion between modeled proteins. For brevity we will subsequently refer to “modeled proteins” simply as “proteins”. The two main considerations in choosing the voxel size are the size of a membrane anchored protein (so that volume exclusion can be accurate) and the dimensions of the membrane, which must be large enough to get accurate statistics but small enough to make the simulations tractable.

The lattice is seeded with proteins of different species (for each species i, let the number of proteins present in the system initially be N_i(0)). Each protein has two properties: position, specified in terms of its x and y coordinates on the lattice and species. In addition, each species has an associated characteristic “diffusion coefficient” representing the size of the random diffusive step taken by the protein during any time step. At each such step, a protein M₁ is chosen at random from the general population. Let the coordinates of this protein be (x,y). One of the voxels with coordinates (x + D_i,y), (x − D_i,y), (x,y + D_i), or (x, y − D_i) is also chosen at random, where D_i is the step size of species i. This new voxel represents the location to which the protein is moved during the current time step by Brownian motion alone. Note that in the case D = 1, this corresponds to choosing one of the voxels adjacent to the one in which the protein resides as described by Berry (1). If the new voxel is occupied, by a protein or a fixed obstacle, then the protein is placed back in its original voxel (x,y) and a collision is recorded. This is an implementation of volume exclusion so that only one protein can occupy a voxel at any time.

Larger values of D correspond to higher diffusion rates, that is, a better-mixed system. If D = 0 then the species in question is immobile. If D is nonintegral then the interpretation of D is probabilistic and the size of the diffusive step is nondeterministic—for example, if D_i = 0.5 then a protein of species i has, at each step, a probability of 0.5 of moving to one of its neighboring voxels (if unoccupied) and an equal probability of not moving at all. This is used to implement statistically subvoxel step sizes (the unitary step size must always be the size of one voxel, 2 nm). Periodic boundary conditions are imposed on the molecular positions in the lattice.

If the neighboring voxel chosen is unoccupied, then the protein is moved to its new location and the lattice is updated to reflect this event. If the voxel is occupied by protein M₂, then if M₁ and M₂ are involved in a bimolecular reaction, this reaction is allowed to take place, with a probability specified in the input and which is different for each reaction (see below). The voxels are again updated to reflect the change. In the case of a unimolecular reaction, M₁ is allowed to move to its new location if the latter is unoccupied and the reaction can then take place (again, with a given probability). If M₂ is not involved in a reaction with M₁ then M₁ does not move during this time step (1,23,24).

By using nonunitary and nonintegral step sizes, the behavior of systems with various degrees of stirring can be investigated. For example, the trajectory of a system with large D (i.e., well stirred) computed using this Monte Carlo approach can be compared with the predictions made by the stochastic simulation algorithm (SSA) of Gillespie (25), that assumes perfect stirring. In addition, by using values of D between 0 and 1, we can simulate the stochastic mobility of species in nonhomogenous and disordered media, or highly ordered media in which continuity assumptions are invalid at any scale. For example, in the cellular lipid bilayer, the lipid “mosaic” in which proteins are embedded is discrete, highly ordered and nonfluid (26); lipids and proteins can “swap places” probabilistically during any given time interval, or a protein may move a discrete distance within the layer according to a probability distribution. These processes cannot be approximated appropriately by a scheme in which a small diffusive step is taken by each protein at each step, particularly as the granularity of the lattice decreases (and begins to approximate continuous space). In such cases, which are highly biologically relevant, the stochastic movement of discrete proteins in a semifluidic environment is better approximated by a nonlinear, discrete, Markov process, which in our approach can be implemented by assigning to D a value equal to the probability of a discrete step of unit length being taken at each time step by a protein.

Theory of anomalous diffusion

If diffusion is anomalous, the mean-squared deviation (the mean of the square of the Euclidean distance from a particle's starting site) grows as a fractional power α of time (4):

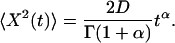(1)

Here D is the diffusion coefficient and Γ(x) is the gamma function defined as

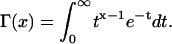(2)

The case α=1 corresponds to pure diffusion 〈X(t)²〉 = 2Dt (a linear relationship).

By measuring the anomalous diffusion exponent that can be calculated as the slope of the log-log plot of the mean squared deviation against time, we obtain a measure of the anomalous behavior of a particle. From the intercept of this curve, the (small-scale) diffusion coefficient of proteins can be estimated by

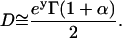(3)

In this study, the MSD has been computed by averaging the deviations of 2500 particles over the course of a single simulation, unless otherwise stated.

FRAP simulations

An important method for measuring protein dynamics is fluorescence recovery after photobleaching. This can be used to characterize the mobility of a fluorescently labeled macromolecule. Briefly, the method “bleaches” fluorescent molecules by exposure to high intensity laser radiation. The exposure does not ordinarily denature the macromolecule of interest but destroys the fluorescence of the tag. Firstly, a small area of the cell membrane is bleached. As new unbleached molecules move into this area from the outside, the fluorescence recovers over time to its prebleaching state. The recovery curve can be used to infer information about the mobility of the macromolecule under investigation (27) since the fluorescence signal will recover more slowly if the diffusion of proteins is slow or impeded.

Using our model, simulating FRAP experiments is straightforward. All proteins are given a “tag” property that has value 1 if they are fluorescent and 0 otherwise. At the beginning of the simulation, all proteins have tag values of 1. After some time—once the system has reached equilibrium with respect to spatial distributions of proteins—all proteins in a circular central area of the membrane have their tags set to 0 (while all proteins outside this area have unchanged tags). Subsequently, the total sum of the tags over the “bleached” area is recorded periodically and this procedure is repeated until this sum, representing the total fluorescence due to the bleached area, returns to its initial value. The bleached area is very small compared with the total area of the membrane to ensure full signal recovery is possible. From this data, a characteristic “half-time,” t_1/2 the time required for the fluorescence signal to return to half of its initial value can be measured. This is an indication of the speed of the recovery and can be related to the mobility of the proteins on the membrane since a faster recovery would be expected if the unbleached proteins entering the bleached area are more mobile, and conversely the bleached proteins are not prevented from exiting this area.

The relationship between the diffusion coefficient and the recovery half-time is

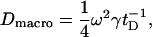(4)

where D_macro is the large-scale diffusion rate, ω is the bleach radius, γ is a correction factor (0.88 for a circular bleached area), and t_D is the characteristic time of recovery (28). The “macro” subscript refers to the fact that because of the relatively long timescales involved in FRAP experiments (and our simulations), the diffusion coefficient estimated using this method reflects the large-scale mobility of proteins. In the case of pure diffusion, one would expect the diffusion coefficient to be independent of the time and space scales (it is a constant in the diffusion equation). Recent studies, however, have suggested that diffusion is strongly impeded over large length scales so that the short-range diffusion coefficient D_micro is not in fact equal to the large-scale coefficient D_macro (27,29). We estimated D_macro using FRAP simulations in an effort to investigate whether the presence of objects on the membrane (rafts, fences, or fixed proteins) could be expected to account for the nonconstancy of the diffusion coefficient.

Simulating chemical reactions

Finally, to probe the effects of different sources of subdiffusion, the Michaelis-Menten enzyme reaction scheme was used. In this system, four molecular species react according to the equation:

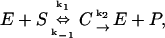(5)

where E stands for the enzyme, which is necessary for the reaction but regenerated, S is the substrate, C is a complex, and P is the product. In classical kinetic analysis, if the system is well mixed and a large number of proteins involved, this results in a system of differential equations:

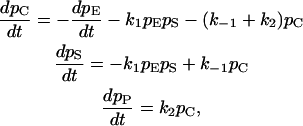(6)

in which ρ_i is the concentration of species i (a function of time t). An analytical solution valid over all time is not possible; in practice, a steady-state assumption is used in many analyses (1). The reaction rates k₁, k₋₁, and k₂ are modeled using reaction probabilities f, r, and g, respectively, because we simulate spatial behavior and hence do not assume the system to be well mixed. At each Monte Carlo step, a protein is chosen at random and its position determined. The evolution rules are as follows:

1. If the protein is of type S, a destination site is chosen at random, at a distance D_S from the chosen protein and in a direction chosen randomly between the four cardinal directions. If this destination site is unoccupied, the protein moves to it directly, whereas if the destination site is occupied by a protein of type E, a random number is chosen between 0 and 1 to determine if the first reaction will take place. If this number is lower than the reaction probability f, the original S protein and the destination site E protein are destroyed and a C protein is placed on the new site. In all other cases, the S protein remains at its initial position. Note that this is also valid if the chosen destination site is an obstacle.

2. If the chosen protein is of type E, the process is analogous to the above, that is, the result depends on the occupancy status of the randomly chosen destination site. Movement takes place if the destination site is free, a reaction takes place with a probability f if the destination is occupied by a protein of type S. In other cases, the E protein is not moved.

3. If the chosen protein is of type C, a random number R_C is chosen between 0 and 1 from a uniform distribution. If R_C < r, and provided that at least one of its nearest neighbors is unoccupied, the C protein dissociates into two proteins (of types E and S, respectively). Berry (1), following an idea of Kopelman (22), suggests that a “more physically realistic way would be to choose a site at random for the new S protein, move it to this site if unoccupied, and abort the decomposition process if occupied” and we have implemented this scheme in our algorithm. The E protein is placed at the original C site. The C protein dissociates into E and P proteins in the same way, if r ≤ R_C ≤ r + g. Finally, if R_C > r + g, the C protein is allowed to move to a randomly chosen nearest-neighbor site, if the latter is unoccupied (otherwise, it is immobile during this step).

4. If the chosen protein is of type P, it moves to a randomly chosen neighbor site (in the general sense discussed above) if this site is not occupied.

5. After each step, the simulation time is incremented by 1/N where N is the total number of proteins present in the system (disregarding obstacles). Thus, one time unit represents, on average, the time needed for each protein to move once (1).

RESULTS

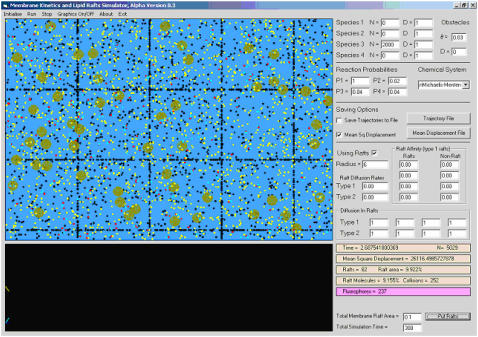
We have implemented our algorithm, which we call membrane anomalous diffusion (MAD) simulator in an in-house software package for Windows. In addition to running Monte Carlo simulations as described above, it also displays distributions of the chemical species and obstacles graphically and allows interactive input. It is possible to save the trajectory of a chemical system for later analysis, as well as raft-related variables (such as molecular concentration in rafts) and other parameters of interest (such as collision rates or the mean squared deviation). This program is intended to be a general-purpose Monte Carlo spatial simulation tool for biologically relevant model reactions on two-dimensional media. A screenshot is shown in Fig. 1.

FIGURE 1.

Screenshot of the MAD simulation package. The software operates under Windows and is available from the authors upon request. In the screenshot, black points represent fixed obstacles whereas all other points represent diffusing species. The rectangular array represents a regular obstacle arrangement simulating a cytoskeletal fence structure (see text). Lipid rafts are shown as light-colored circles. The panels on the right are used to interactively specify the input parameters to the simulation. Note that the values of D in the top right panel refer to protein step size (1 voxel per unit time).

Sources of anomalous diffusion

In this study, three possible sources of nonclassical diffusive behavior are investigated. The first of these is the presence of a significant number of fixed obstacles on the membrane, representing, for example, immobile proteins. Obstacles are represented as a separate chemical species that is inert with respect to all other species and has step size identically 0. We denote the density of random obstacles on the membrane as θ. In lattices with immobile obstacle densities below the percolation threshold—θ_T ≈ 0.4073 for this case (30)—accessible sites form a percolation cluster and diffusion on percolation clusters is known to be anomalous (1,31).

The second source of anomalous diffusion investigated here is the interaction of mobile proteins and lipids with picket posts anchored to membrane skeleton mesh (2). The fence lines between the picket posts are assumed to be at right angles to each other and distributed evenly across both dimensions, with spacing between lines (“pitch”) of d_f. Each fence line is made up of immobile picket posts (obstacles) and each voxel of the fence line is either occupied or unoccupied by a picket post. In this way, square domains are delimited by fence lines on the membrane. The only qualitative difference between fixed obstacles and fence posts is that the former are uniformly distributed on the membrane whereas the latter are randomly distributed only along fence lines.

Proteins attempting to cross from one domain to another may be rejected (and thus retained in their current domain) by collisions with the fixed fence posts; Fujiwara et al. (2) call this “hop diffusion”. The density of posts is denoted φ and the case φ = 0 corresponds to no fence whereas φ = 1 corresponds to a completely impenetrable fence. Together, the picket post spacing and picket post density characterize a fence system. Intuitively, it would be expected that, due to local confinement of proteins to membrane compartments, their mobility would be different over short timescales (local free diffusion) and long times (diffusion impeded by fence lines). Thus, we would expect to observe some degree of anomalous diffusive behavior due to the presence of fences. In this model we have not included hydrodynamic friction-like effects between picket posts that further corral proteins. Given that the effect of actin-based corralling is not fully realized in our model, we shall refer to the effects of the fence that we have modeled as reflecting collisions with picket posts.

Thirdly, we investigated whether the interaction of proteins with lipid microdomains (lipid rafts) can result in anomalous diffusion. It is believed that proteins diffuse more slowly inside rafts than outside (32) and this has been postulated as a possible source of anomalous diffusion (22). We have used a previously developed model of raft-protein interaction (24) in which a raft is modeled as a two-dimensional, circular patch of radius r_ρ and area 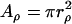. The step size of a protein in a raft is smaller than that outside raft regions and the ratio of these is the key parameter describing the interaction of a protein with a raft in this study:

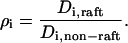(7)

Thus the motion of proteins in rafts is characterized by a step size that is different from that in the surrounding membrane. In this work, all rafts used within one simulation are of equal radii and the effect of raft dimension is investigated by running simulations with different raft radii. Another important global parameter is the total area of the membrane that is represented by rafts, p_rafts. In this study, rafts were assumed to be either fixed or to diffuse in an analogous manner to proteins, with diffusion rate relative to proteins given by the Saffman-Delbruck equation (24,33). If a raft attempts to move over a region that is occupied by another raft, it is rejected (similarly to the handling of protein-protein collisions).

Because it is believed that some proteins are excluded from rafts while others are selectively accumulated (34,35), we also introduced into the model “rejection probabilities” associated with entering and exiting a raft, respectively. When a model protein moves from a nonraft voxel to a raft voxel, it may be returned to its original location (rejected) with probability p_nr. Conversely, when exiting a raft, it may be rejected with probability p_rn. If these probabilities are 0, the proteins do not differentiate between raft and nonraft regions, except for the difference in diffusion rates they experience. At the other extreme, a probability of 1 indicates that, once a protein has entered a raft or nonraft region, it will be permanently captured in that raft or nonraft region, respectively. In this study, we investigated the extent to which exclusion of proteins from rafts can lead to anomalous diffusion of the latter by running simulations with p_nr = 1.

In all simulations described here, we have used a unit step size of 1 for a protein moving in a free medium and a unit step size of ρ (see Eq. 7, above) for a protein moving inside a raft. Using an unimpeded step size of 1 corresponds to a diffusion rate of 0.5 voxels²/time unit. In general, we can convert between simulation times and diffusion rates and their physical equivalents using the relation

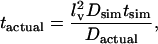(8)

where l_v is the voxel side length (2 nm here), D_sim is the diffusion rate from the simulations (0.5 voxels²/time step if diffusion is not impeded and there is no competition for voxels), t_sim is the simulation time and t_actual is the actual time. Thus assuming a diffusion rate for proteins of 0.5 μm²/s, we get that one time unit in the simulations is equivalent to roughly 4 μs, in the absence of competition for voxels.

Anomalous diffusion due to fixed obstacles

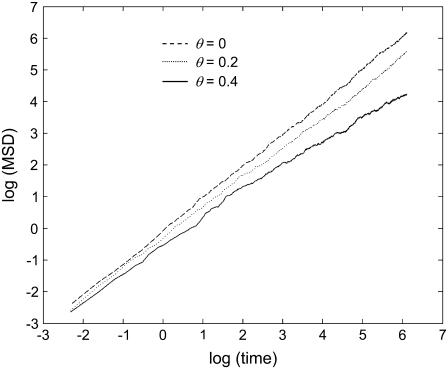
We firstly used the MAD simulator to measure the mobilities of proteins in the presence of randomly distributed fixed obstacles. Two-thousand proteins were randomly distributed on the membrane and allowed to diffuse. The squared deviations of the most central 1000 of these (excluding those close to the edges to avoid “wrap-around”) from their starting sites were recorded and averaged. Six obstacle densities are used: 0, 0.1, 0.2, 0.3, 0.4, and 0.5. The last of these is higher than the percolation threshold, so that that the relation in Eq. 1 cannot be expected to be an accurate description. All simulations were run for 600 time steps. Representative results are shown in Fig. 2.

FIGURE 2.

Mean squared deviation behavior for various obstacle densities. The mean squared deviation (MSD) of diffusing particles on the membrane (from their starting sites) plotted against time (log-log plot) for increasing obstacle densities. As diffusion is more and more impeded by the presence of fixed obstacles, the MSD grows more and more slowly with time. The gradient of the line is the anomalous exponent (α in the text) whereas the y-intercept gives the diffusion rate (Eq. 3). Under the classical diffusion framework, a line with gradient 1 and y-intercept of 0 is expected.

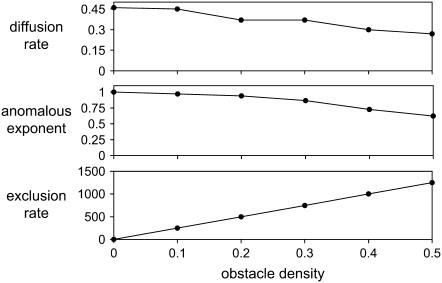
It is clear from Fig. 2 that if θ is not close to 0, the log(MSD) − log(t) curves deviate somewhat from a linear relationship with unit gradient. Furthermore, for values of θ near the percolation threshold, the curves also deviate slightly from linearity, suggesting that Eq. 1 is not accurate for obstacle densities close to the percolation threshold. In Fig. 3, the anomalous exponent has been plotted against the obstacle density. We note that at θ = 0.4, we obtained α ≈ 0.7, in close agreement with the results of Berry (1). Interestingly, Fig. 3 also shows that the diffusion coefficient, computed from the intercept of the log-log plot of MSD against time, does not vary greatly with increasing obstacle density. The method used for computing this value, based on Eq. 3, is not expected to be accurate for values of θ larger than the percolation threshold, since the small-scale diffusion of a tracer particle (protein) is not spatially symmetric due to the fixed spatial structure surrounding it (obstacles). At such high obstacle densities, proteins tend to take paths along spatial corridors that are relatively free of obstacles; thus the assumptions underlying the diffusion equation fail in these cases. For smaller values of θ, it is somewhat surprising that the diffusion coefficient remains essentially insensitive to θ.

FIGURE 3.

Effect of various obstacle densities on the anomalous exponent and diffusion rate. Small-scale diffusion rate D_micro (top) calculated using Eq. 3, anomalous exponent (middle) calculated using Eq. 1, and exclusion events per unit time (bottom) are all plotted against obstacle density, θ. These results are in agreement with the results of Berry (1) and indicate that as θ approaches the percolation threshold, the anomalous exponent falls to ∼0.7. This value is comparable to exponents estimated experimentally in live cell membranes; however, our FRAP results (see Fig. 6) suggest a biological limit of around θ = 0.3–0.35. D_micro does not fall considerably with increasing θ (compare with D_macro in Fig. 6), as expected since over short times diffusion behaves classically, not anomalously, so that there is little contribution from the presence of obstacles. As expected, the anomalous exponent and exclusion events are inversely related above a certain threshold (θ ≈ 0.2).

Anomalous diffusion due to collisions with picket fence posts

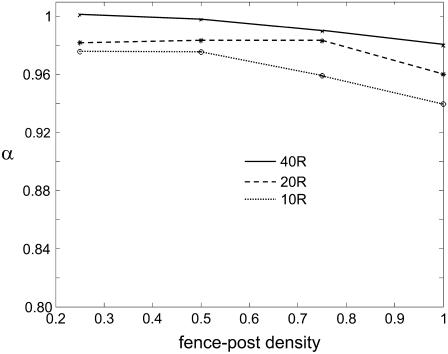
To study the effect of collisions with picket fence posts, as described previously (2,11), three fence line spacings were used, equal to 10, 20, and 40 molecular diameters (voxels, each 2 nm across as described above), respectively. For each of these, four fence-post densities were used: 0.25, 0.5, 0.75, and 1, the last of which results in completely impenetrable fence lines. As before, 2000 proteins were placed on the membrane and allowed to diffuse for 600 time steps. The anomalous exponent α was computed in each case using a log-log plot. The results show that for all of the biologically realistic fence parameters, a fence system of picket posts alone resulted in minimal anomalous diffusion since α remained between 0.94 and 1 (Fig. 4). In the extreme case of a tightly packed and completely impenetrable fence, resulting in the division of the membrane into compartments with a width of only 10 molecular diameters, α ≈ 0.94. We also checked this result by confirming that the number of exclusion events per unit time was low in each case (data not shown). We conclude that, in the absence of other interactions, either between the fence and proteins or the fence and other structures, a fence system of picket posts is not responsible for a large degree of anomalous diffusive behavior, at least in the framework of the model presented here.

FIGURE 4.

Contribution of a regular picket-fence structure to anomalous diffusion. The effect of a picket-fence structure with a picket post density 25%, 50%, 75%, and 100%, respectively, on anomalous diffusion. The three curves correspond to distances between fence lines of 40, 20, and 10 molecular diameters, respectively, from top to bottom. The anomalous exponent remains very close to unity under each condition, indicating that diffusion is close to classical predictions in the presence of a model picket post fence of this type. The numbers of exclusion events per unit time confirm this, being very similar for all the parameter sets examined (data not shown). Therefore, under this model, such a structure cannot explain any significant levels of anomalous diffusion or large differences between small-scale and large-scale diffusion.

Anomalous diffusion due to interactions with lipid rafts

We next investigated the effects of lipid rafts on the diffusion of proteins on a membrane. The dimensions and characteristics of rafts are the subject of debate (36–38), we therefore probed the effects of rafts by performing extensive combinatorial experiments. Four different raft diameters were used: 6 nm, 14 nm, 26 nm, and 50 nm (assuming each voxel represents an area of 2 × 2 nm). For each raft diameter, four values of the diffusion reduction ratio ρ were used: 0.25, 0.5, 0.75, and 1 (note that ρ = 1 corresponds to the effective absence of rafts). Finally, for each combination of these parameters, three raft membrane areas were used: corresponding to 10%, 25%, and 50% of the total membrane area. Rafts were assumed to be either fixed (immobile) or to diffuse at a reduced rate relative to proteins, calculated from the Saffman-Delbruck equation (33). Simulations were run for 600 time steps. The results in Table 1 show that the presence of rafts has a small to moderate effect on the anomalous diffusion exponent. The smallest value observed for α is 0.85, corresponding to the case where lipid rafts cover 50% of the membrane area, ρ = 0.25, and the raft diameter is 6 nm. Although this value for α indicates a significant departure from classical behavior, we note that the average value for α over all the parameters is 0.96, which represents a small difference from α = 1. The smallest value for the diffusion coefficient (D_micro), found for the same range of raft parameters was D_micro = 0.21, corresponding to a 42% reduction of D_micro on a control membrane with no rafts (24).

TABLE 1.

Anomalous exponent against raft parameters for raft partitioning proteins

Raft area 25%, fixed rafts					Raft area 50%, fixed rafts
	ρ = 0.25	ρ = 0.5	ρ = 0.75	ρ = 1		ρ = 0.25	ρ = 0.5	ρ = 0.75	ρ = 1
6 nm	0.865	0.951	0.979	0.975	6 nm	0.85	0.942	0.975	0.996
14 nm	0.944	0.98	1.005	0.974	14 nm	0.87	0.947	0.968	0.996
26 nm	0.971	1	0.989	0.974	26 nm	0.941	0.964	0.985	0.996
50 nm	0.98	0.998	0.992	0.974	50 nm	0.959	0.958	0.979	0.996
Raft area 25%, mobile rafts					Raft area 50%, mobile rafts
	ρ = 0.25	ρ = 0.5	ρ = 0.75	ρ = 1		ρ = 0.25	ρ = 0.5	ρ = 0.75	ρ = 1
6 nm	0.959	0.974	0.993	1	6 nm	0.862	0.92	0.958	0.991
14 nm	0.943	0.965	0.994	0.996	14 nm	0.921	0.944	0.974	1.000
26 nm	0.976	0.974	0.973	0.977	26 nm	0.912	0.966	0.973	0.993
50 nm	0.983	0.973	0.961	1.002	50 nm	0.952	0.964	0.977	0.965

An interesting and often ignored issue is whether excluding proteins from rafts has any significant effect on their diffusive behavior. To explore this problem, proteins were initially distributed uniformly over the membrane, but proteins attempting to enter rafts were rejected and placed at their original voxel. The effect is that after exiting rafts, proteins become restricted to nonraft regions. The system was allowed to reach a steady state in which the concentration of proteins in rafts is negligible; we then computed the diffusion rate and anomalous diffusion exponent as above for simulations of 600 time steps. Two raft radii were used (14 and 50 nm) and rafts were assumed either to be immobile (fixed) or to diffuse freely. The results in Table 2 show that if rafts are small (14 nm), fixed, and occupy a large proportion of the membrane, the anomalous diffusion exponent can be very close to the theoretical limit of ∼0.7. This is not unexpected since this situation is similar to placing a large number of obstacles on the membrane. However, even if rafts are not fixed and have a diffusion rate of 0.54, approximately half that of a protein, α can still deviate significantly from unity. If rafts are large (50 nm), α is very close to unity, regardless of whether rafts are fixed or mobile. This can be explained by noting that diffusion is affected by interactions of proteins with the edges of rafts, where proteins are rejected, and that raft area grows quadratically whereas perimeter length only grows linearly. These results suggest that exclusion from lipid rafts may go a long way toward explaining anomalous diffusion of some proteins on cell membranes, but only those proteins that do not partition into rafts. This effect is clearly sensitive to raft dimensions but since recent studies indicate raft dimensions to be in the range 6–25 nm (7,39), we conclude that this may be a significant phenomenon. Note that the diffusion rate varies systematically with raft area if rafts are mobile, but nonlinearly if rafts are fixed; this effect is due to the interplay of two factors: the ease of finding “raft-free channels” to diffuse through and the increasing inapplicability of the anomalous diffusion equation to describe protein motion along these channels. In the case of mobile rafts, the second factor is suppressed because channels are constantly being opened and closed by the motion of the rafts. The results also show that the anomalous exponent is approximately inversely related to the number of rejection events per time unit, as would be expected.

TABLE 2.

Anomalous exponent, diffusion rate, and exclusions per unit time for raft-excluded proteins in a membrane

		Diffusion rate		Anomalous exponent		Exclusion rate
Total raft area	Raft diameter (nm)	Mobile	Fixed	Mobile	Fixed	Mobile	Fixed
10%	14	0.722	0.623	0.866	0.853	85.8	72.4
25%	14	0.786	0.842	0.813	0.652	214.0	200.6
50%	14	0.825	0.544	0.745	0.634	377.9	506.0
10%	50	0.556	0.472	0.993	1.017	66.7	64.46
25%	50	0.489	0.5	1.045	0.976	64.0	59.36
50%	50	0.602	0.486	1.024	0.99	64.2	55.7

The first column shows the proportion of the membrane that is raft associated. If rafts are mobile, the diffusion rate is obtained from the Saffman-Delbruck equation (24,33). The expected diffusion rate (units of voxels²/time unit) if no objects are present on the membrane is 0.5. The last column shows the number of exclusion events per unit time in each case, which is approximately inversely proportional to the anomalous exponent, as would be expected. Note that the diffusion rate can exceed 0.5 in some cases. This is caused by proteins moving along “raft-free channels”, in which case their motion is no longer accurately described by the diffusion equation. The anomalous exponent in some cases slightly exceeds 1 for the same reason. The effect of this phenomenon on the reliability of α-values obtained in these cases is insignificant, since the difference from the expected value of D is very small and the log(MSD) − log(time) plots are all linear.

An alternative way to model the exclusion of proteins from rafts would be to allow a rejected protein to find a neighboring voxel that is not part of a raft and move there. This was not done here for three reasons. Firstly, the method used here is more physically realistic (there is no reason to assume the protein would slip along the boundary of a raft it cannot enter) and is in keeping with other modeling approaches (1). Secondly, allowing proteins to move in this way would add a further nondiffusive component to the motion of proteins, thus possibly underestimating the anomalous parameter. Third, in our simulations one time unit equals the statistical time needed for each protein to move (or attempt to move) once, on average. Allowing a protein two movements in one step would no longer conserve the step size.

Estimation of D_macro from FRAP simulations

Finally, we investigated whether the presence of objects on the membrane can result in a difference between the large-scale diffusion rate, D_macro and the small-scale diffusion rate (D_micro). To this end, we simulated FRAP experiments by “bleaching” molecules in a circular area of radius 250 nm (in a membrane of size 2 × 3 μm, to ensure full signal recovery is possible). It is necessary to have dimensions of this size as previous studies have shown that the sensitivity of FRAP to measure mobility is highly dependent on the sizes of the bleach area (40). The total number of proteins present on the membrane was 10,000 (excluding fences and obstacles). The system was allowed to reach steady state over 500 time steps before the bleaching step. Since FRAP simulations are computationally intensive, we chose only a few parameter sets for simulation. The half-recovery time (t_1/2) in each case was measured and the value of D_macro estimated from Eq. 4. We then compared the effects of different membrane objects on the diffusion rates D_micro and D_macro. The results in Table 3 show that D_macro is generally lower than D_micro and can be much lower or even, for practical purposes, 0.

TABLE 3.

Large-scale and small-scale diffusion rates for various impeded diffusion scenarios D_macro (estimated using FRAP) and D_micro (estimated using a log-log plot of MSD versus time)

Case	Dmicro	Dmacro	Dmacro/Dmicro	Anomalous exponent
No impeding structures	0.495	0.491	0.991	1.000
Fence only	0.472	0.38	0.741	0.989**
25% rafts	0.471	0.190	0.403	0.965
50% rafts	0.410	0.155	0.378	0.943
Obstacles only, θ = 0.2	0.310	0.277	0.893	0.98
25% rafts, proteins raft-excluded	0.786*	0.219	0.279	0.813
Fence + 25% rafts	0.447	0.238	0.532	0.959
Fence + 50% rafts	0.414	0.203	0.490	0.941

The picket post fences have a pitch of 80 nm and a density of 20%. Rafts are 14 nm wide and diffuse at a (relative) rate of 0.54 voxels²/time unit. (* indicates the estimate is not accurate because D_micro cannot be reliably estimated from Eq.3. ** indicates that this value is slightly lower than that shown in Fig. 5 because it was estimated over a much longer simulation time, over which anomalous diffusion became more pronounced.) The interactions of the three impeding types of objects are complex and nonlinear. Note, for example, that although exclusion from rafts results in a more rapid distancing of a particle from its initial site on the short timescale, it results in a much lower large-scale diffusion rate. It is also clear that although the D_macro/D_micro ratio is related to the anomalous exponent, the dependence is highly nonlinear; for example, in the 25% raft, raft-excluded case, a 20% difference in α (from 1) results in a fourfold drop in the ratio.

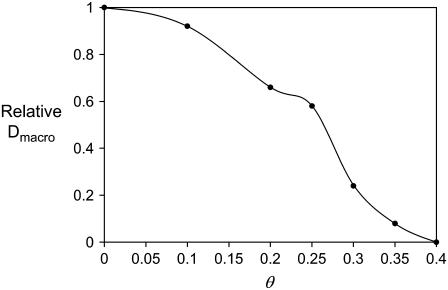
Because D_macro seems to be very sensitive to the obstacle density, we estimated D_macro for a range of such densities. The results in Fig. 5 show that between θ = 0.2 and θ = 0.35 obstacle coverage, long-range diffusion falls dramatically from a value only moderately lower than D_micro (see Table 3) to almost 0. These results are interesting because they suggest: a), that long-range diffusion depends strongly and nonlinearly on the obstacle concentration; and b), that the equivalent in vivo obstacle concentration must be lower than ∼30% since FRAP recovery is observed in live cell membranes (16).

FIGURE 5.

Effect of fixed obstacles on large-scale diffusion rates. D_macro, the long-scale diffusion rate as a function of obstacle density θ. This was calculated using Eq. 4 from simulated FRAP curves and normalized to the value of D_macro calculated in the no-obstacles case. Interestingly, D_macro falls very sharply for θ > 0.2. Note that the value of 0 obtained for θ = 0.4 is not accurate—rather, it indicates that the signal did not recover to half of its initial value in our simulations (even for very large times) and we could not extrapolate from the recovery curve what the half-recovery time would be.

The effect of obstacles on chemical kinetics

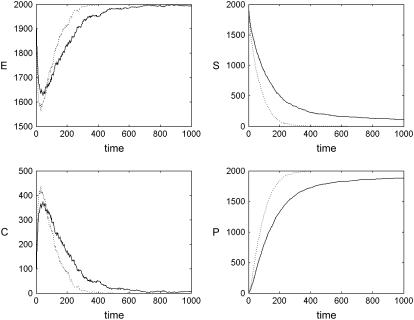
What effects do a large fixed obstacle density have on a set of chemical reactions occurring on the membrane? We addressed this question by simulating the behavior of the Michaelis-Menten system in the presence of fixed obstacles. The numbers of C and P were initially 0 whereas those for S and E were set to 2000 each. The three reaction probabilities were set at f = 1, r = 0.02, and g = 0.04, respectively, which is a good balance for the purposes of qualitative inspection (1). During the simulation, the total numbers of each type of protein were recorded. The results in Fig. 6 show that the kinetics of this reaction system is influenced to a large degree by the density of obstacles. Between an obstacle density of 0.0 and 0.4, the rate of generation of P (the product) falls dramatically (roughly by a factor of 4). If the numbers of reacting proteins are smaller, this effect is even more pronounced (data not shown) because proteins of types E and S, whose interaction is the main driving force behind the kinetics, are not as likely to be in close proximity to each other (so that the lowered mobility over long distances plays a more important role, as proteins of types E and S must travel, on average, a longer distance before meeting).

FIGURE 6.

Effect of fixed obstacles on chemical kinetics. Kinetics of the Michaelis-Menten reaction system (Eq. 5) θ = 0 (i.e., in the presence of no obstacles, dotted line) and θ = 0.4 (solid line) obstacle densities, respectively. The latter is close to the percolation threshold of θ ≈ 0.4073. When obstacles are present, the kinetics are considerably slower, especially at large times, because of the difficulty that molecules initially placed far apart have in meeting one another.

This behavior cannot be attributed to a reduction in local diffusion rate, since Fig. 3 shows that the coefficient of diffusion does not fall significantly with increasing θ. Rather, the reduction in reaction rates must be attributed to the anomalous nature of the diffusion that exhibits a transition between a linear regime on short timescales and a power-law regime over long timescales. The result is that, although over short times, proteins' movements are not significantly impeded, over medium or long times the proteins are comparatively less likely to stray far from their starting sites and mixing is impaired. This gives rise to segregation between reactants and a low reaction rate.

DISCUSSION

We have investigated the fundamental causes of anomalous diffusion on the plasma membrane using a stochastic random-walk model of biomolecule diffusion. Our results show that the most powerful constraining factor for small-scale molecular mobility is the presence of many randomly distributed, fixed (or almost fixed) obstacles. The presence of lipid rafts with biophysically realistic characteristics has a moderate effect on the anomalous diffusion exponent if proteins partition into rafts, but has a significant effect if proteins are excluded from rafts. In contrast, collisions with the picket posts of a rectangular fence have only a small influence on this exponent.

We show that as the concentration of obstacles on the membrane increases from 0 to the percolation threshold (0.4073), the anomalous exponent falls smoothly from unity to its limiting value of around 0.7. This is in agreement with previous studies (1). Smith et al. (10) showed that on the membranes of HeLa cells, MHC Class I molecules diffuse anomalously with an average anomalous diffusion exponent of α ≈ 0.49. Using obstacles as the only source of diffusion impedance, our model therefore partially reproduces the results of that study but only when a very large density of obstacles, θ > 0.6—far above the percolation threshold—is used. In fact our in silico FRAP results suggest an upper limit for θ of around 0.3–0.35 since no recovery is observed above this value, while in experiments, the fluorescence signal does recover.

If lipid rafts are present and cover a significant area of the membrane, our results indicate that α can be as small as 0.85 if proteins partition into rafts—a moderate departure from α = 1. If rafts are immobile and reject proteins that attempt to enter a raft the value of α can be as small as 0.65. If rafts are mobile (a more plausible model) and reject proteins then α = 0.75 in the most extreme case. Anomalous diffusion is most pronounced if rafts are small (6–14 nm). This is an interesting result because raft exclusion has not previously been considered as a source of anomalous diffusion. Since many more plasma membrane proteins are likely excluded from rafts than partition into these structures this result may have significant biological implications.

We find that collisions with proteins tethered to the cytoskeleton cannot, in our framework, account for a large degree of anomalous diffusion in the absence of other interactions even if the fence lines are completely impenetrable and close together (as low as 10 protein diameters). Although in such an extreme case the long-range mobility of proteins would be reduced to almost zero, the anomalous diffusion exponent is calculated on short timescales using a log-log fit and in this sense, we find that such an arrangement cannot, by itself, explain anomalous diffusion on live cells. However, it is important to note that Fujiwara et al. (2) claim that the effects of an actin fence on lipid diffusion are not exclusively due to the steric hindrance of the immobile fence posts as we have modeled here. They suggest that an additional and critical effect of the fence extends beyond the posts because of the packing of lipids around immobile obstacles. It is possible to explore this concept by using probability distributions to model the diffusion of proteins across barriers (29,41). This more sophisticated approach to modeling fences will be the subject of our future work.

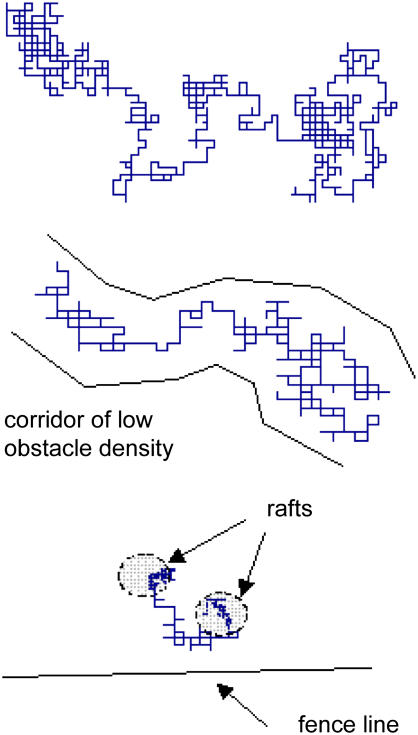
If, as seems reasonable, anomalous diffusion of proteins on a membrane reflects the combination of these three mechanisms then earlier experimental data (10) can be mostly explained. For example, if we conservatively set θ = 0.25, cover 50% of the membrane with rafts of 14 nm diameter, set ρ = 0.33, and place a picket fence system on the membrane with a spacing of 80 nm and a density of 40%, our model predicts a value of α of 0.75 and a small-scale diffusion coefficient (D_micro) that is 39% of its value in an unencumbered membrane. If the density of obstacles is increased to only 0.32, the anomalous exponent falls to 0.68, which is within the range of published values (10). In silico single particle tracking illustrates qualitatively the enormous differences between free and impeded diffusion under these various conditions. For example, Fig. 7 shows single particle tracking with no impeding structures, an obstacle density (θ) of 0.25 and the addition of rafts and picket fence posts. The trajectory is similar to those observed experimentally (13).

FIGURE 7.

Single-particle tracking simulations of impeded diffusion in three different scenarios. The position of a single particle, initially placed in the center of the simulation area, was tracked over time. Typical results are shown for three scenarios: no impeding structures (top), randomly distributed obstacles with θ = 0.3 (middle), and random obstacles with θ = 0.3 plus lipid rafts (25% of membrane area covered) and picket fences (interfence distance of 40 molecular diameters and fence-post density of 25%). Single-particle tracking simulations reveal large differences in the nature of diffusion in these three cases. In particular, two significant effects are observed: 1), the nonsymmetric nature of molecular motion in the presence of obstacles, in which molecules slip through corridors of low obstacle density, seen clearly in the middle figure; and 2), capture by lipid rafts, in which the diffusion rate of proteins is postulated to be reduced, seen in the bottom figure.

The results of our FRAP simulations are quantitatively different from an earlier simulation study on the effects of anomalous diffusion on fluorescence recovery (27). Our results indicate that the long-scale diffusion rate (D_macro) calculated using FRAP falls sharply with θ over the range 0.2–0.3 and that for θ > 0.35, no full recovery is to be expected. In contrast, the earlier study of Saxton (27) demonstrated that D_macro varies more moderately with θ and that full recovery is merely significantly slowed, not stopped altogether, even close to the percolation threshold. However, that study focused, in the case of obstacle-impeded motion, on the anomalous diffusion caused by diffusion on a percolation cluster, in which the obstacles are not distributed uniformly but can be connected, leading to the existence of lakes (obstacle-free regions) and large membrane “animals” (regions of connected obstacles). At the percolation threshold, the lattice is divided into an “ocean” on one side and a completely impenetrable obstacle block on the other. In our study, however, we have distributed obstacles uniformly on the membrane, such that the membrane is not populated with the “lakes” observed with a percolation cluster (27). In addition, we have used a rectangular lattice that has a percolation threshold of θ ≈ 0.4073 for our obstacle distribution, whereas the triangular lattice used in the earlier study (27) has a percolation threshold of θ = 0.5. In this context our results agree more closely with those of Berry (1), who used a similar rectangular lattice to ours. Taking all these studies together, we can conclude that, obstacle concentration, the distribution of obstacles, and the precise diffusion model (such as triangular versus rectangular lattice) are important parameters in characterizing the long-range diffusion of proteins. Further experimental elucidation of the likely geometries of impeding structures on cell membranes would help to focus modeling efforts in this area.

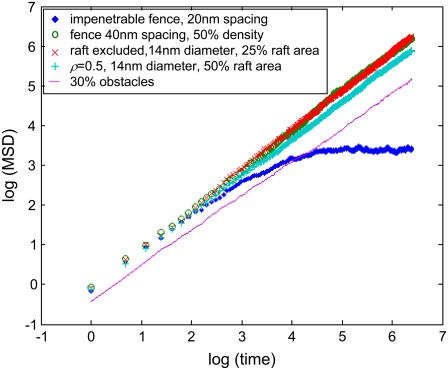
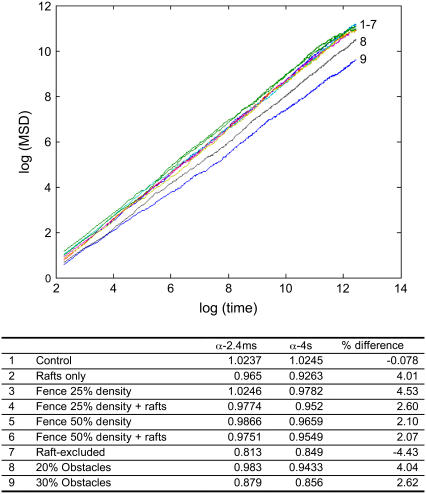
In this work, we have assumed that Eq. 1 accurately describes the phenomenon of anomalous diffusion and implicitly have assumed the linearity of the MSD versus time curves generated by our model. Of course, this assumption may not always hold, or may not hold for large times. For example, in the case of an impenetrable fence structure with a pitch of 10 molecular diameters, we obtained α = 0.94. This result cannot in fact hold for large times because in the case of an impenetrable fence, the MSD cannot exceed the pitch of the fence lines. This calls into question the fitting of a straight line to the log(MSD) − log(time) curve. In the vast majority of the parameter sets tested here, however, we checked that the MSD is indeed linear in time. A representative set of MSD curves is shown in Fig. 8. Furthermore, even when there is some departure, as in the case of the impenetrable fence (Fig. 8), fitting a line over the linear part of the curve (at shorter times) makes sense because the diffusion coefficient is inherently a short-time parameter: the difference between D_micro and D_macro we report in this work is a reflection of the fact that the diffusion equation does not apply here at long times but does apply at short times. It is conceivable that the values of α calculated by linear fitting may be time dependent for some of the parameter combinations. To explore this possibility, we ran simulations corresponding to 4 s of real time and recalculated α. The results (Fig. 9) show that the values of α calculated from 2.4 ms or 4 s of simulation are not significantly different. Thus the comparison of α-values calculated here with those of experimental studies where long observation times were used (10,14) is warranted.

FIGURE 8.

Representative log(MSD) − log(time) plots for different parameter sets. If the motion of a particle can be described accurately by an anomalous diffusion equation, then the plot of log(MSD) − log(time) is expected to be a straight line. Here we have shown five representative plots corresponding to: i), exclusion from rafts; ii), partitioning into rafts; iii), being impeded by fixed obstacles; iv), confinement by a fence of widely spaced picket posts of low-density; and v), confinement by a narrowly spaced impenetrable fence of picket posts. Only in the last case (which is not biologically plausible) is a departure from linearity apparent, and only at large times. These results support the idea that a very general class of biomolecular particle motion can be accurately captured by an anomalous diffusion approach.

FIGURE 9.

The time dependence of α. Simulations for a wide range of different scenarios, described in the lower panel, were run for 4 s of real time and plotted as in Fig. 8. Values for α were calculated over short times (2.4 ms) and long times (4 s) of simulation. The lower panel shows that the values do not differ significantly.

Finally it is important to note that there are other membrane/protein interactions that we have yet to explore. For example, physical association (rather than simple collision) with the cytoskeleton could also contribute significantly to nonclassical diffusion. Moreover, in recent work (24), we show that the mobility of rafts as well as the ability of rafts to selectively capture and exclude different proteins can change the characteristics of the random walks executed by proteins on a cell membrane.

One consequence of anomalous diffusion is that the dynamics of bimolecular reactions of the form A + B → Ø behaves as if the “rate constants” are functions of time (1). This is due to the fractal nature of the kinetics, which in turn is caused by diffusion on percolation clusters (in the case of obstacles) or equivalent structures (for rafts, fences, and other membrane components). As a result, the assumptions underlying the mass-action laws used to analyze chemical kinetics classically break down and approaches that take into account the noninteger order of the resultant reactions are needed—such as fractional differential equations. Thus, it is becoming increasingly clear that due to the heterogeneous nature of biological media and to the low numbers of proteins involved in many biomolecular reactions, ordinary differential equation methods are often not appropriate for treating many biological problems (1).

Therefore, given the complex, discrete, nondeterministic and disordered nature of biological interactions and media, spatial homogeneity cannot be assumed in many cases (as we have argued here) and techniques that take these factors into account are needed. On the other hand, direct Monte Carlo approaches suffer from the drawback of requiring large amounts of computer resources for problems of realistic dimensions, if the system is built up molecule by molecule. We argue that the best way forward is along a middle path, involving multiscale simulation methods that deal with heterogeneity and nondeterminism at the scales at which these are appropriate but can retain the powerful approach of differential equations over all other scales. For instance, for membrane chemistry simulations, it would be possible that the space can be divided into partitions, inside each of which the system can be assumed to be well-mixed, so that a rapid method such as the Stochastic Simulation Algorithm (25) can be used for small numbers of proteins in that region. The exchanges of proteins between partitions (on a large scale), can then be treated efficiently using, for instance, a stochastic difference or differential equation approach (42). The development of such methods and their application to problems involving subdiffusion in biological media will be the subject of future work.

In conclusion, we have investigated three sources of anomalous diffusion in two-dimensional rectangular biological membranes: randomly distributed fixed obstacles, lipid rafts (with proteins either partitioning into or being excluded from rafts), and a rectangular system of cytoskeletal fence posts. We find that of these, fixed obstacles and exclusion from rafts are the mechanisms most likely to cause anomalous diffusion, in the absence of other interactions. The combination of all three mechanisms, at biologically relevant levels, can account for experimentally reported anomalous diffusion levels. We argue that the presence of impediments to motion in complex biological media has important effects on biochemical interactions in these media, which should therefore be analyzed with appropriate spatial-temporal methods.