Irreducible Representation for Nucleotide Sequence Physical Properties and Self-Consistency of Nearest-Neighbor Dimer Sets

Abstract

A compact representation of usual DNA/RNA four-nucleotide sets based on molecular affinity classes is proposed. In a geometrical correspondence to this formulation, it follows that intrinsic tetrahedral symmetry correlates nucleotide properties. This representation also leads to a proper decomposition frame for any sequence-dependent physical expectation. Thermodynamic and other physical properties of nucleotide sequences are most often stated within the scope of nearest-neighbor models and decomposed in terms of dimer properties. The inverse problem of obtaining dimer set properties is, however, well known to be ill-posed due to sequence composition closure relations. Analysis of the dimer set composition and structure within the novel tetrahedral formulation provides important self-consistency relations, solving the ill posed nature of the original formulation. As an applied example, we analyze DNA oligomer duplex free energy data available on the literature. It is shown that imposition of stringent self-consistency relations does not decrease fit quality to the experimental data set. On the other hand, an improved dimer set with physically consistent free energies is obtained. Meaningful corrections to previous determinations are found when the self-consistent set is applied to calculate free energies for sequences with composition order bias.

INTRODUCTION

Widely used DNA biotechnological applications such as PCR or cDNA expression profiling rely on the knowledge of sequence specific thermodynamic parameters such as strand melting temperature. Many physical properties of DNA\RNA sequences can be calculated from a number of algorithms in the context of nearest-neighbor (NN) models. NN models give linear representations for experimental measurements on nucleotide chains usually in terms of pairwise (dimer) sequence contributions. However, the notion that NN dimer parameters cannot be assigned from experiments by solving a set of simultaneous linear equations has been given since the development of these models in the context of polynucleotide thermodynamic studies (1). This puzzling conclusion is due to the consideration of intrinsic composition closure constraints that effectively reduce the number of degrees of freedom of the model. Dimer occurrence relations are well known, allowing for decomposition of sequence properties into arbitrarily chosen reduced dimer sets. As a corollary, so-far-unknown constraints must also link the full dimer set properties in some hidden way to restore full set unity. The dimer decomposition is overstated, since the dimer set size (16 for single strands and 10 for double strands) is greater than the number of degrees of freedom of the problem (13 and 8, respectively, for circular sequences). Alternative approaches have considered decompositions into irreducible and hence smaller sets of short sequences or dimer combinations (2–5). Comparison among different laboratory sets and physical interpretation of set values becomes a difficult task due to the arbitrariness of possible renderings. The extraction of simpler and more direct dimer contributions from such sets has remained an ill-posed problem with nonunique solutions, but still embraced by a large community of biochemists (6–12). To adopt the dimer set formulation further ad hoc regularization hypotheses have been taken by different authors, such as the singular value decomposition method (9,10). Here we adopt an entirely new approach to this problem by analyzing how the nucleotide intrinsic intermolecular symmetries contribute to the structure of NN sets. In this article, we first introduce a general quantum mechanics statement giving physical properties for a sequence of heterogeneous molecules, treated as subsystems assuming any of a given complete set of molecular states. The four-nucleotide set has a corresponding four-state representation. At this point, a careful choice of the number of degrees of freedom is made that projects the representation into a three-dimensional molecular class space. Luckily, the three independent molecular classes are readily associated to main biochemical classification of nucleotides as composed of purine-pyrimidine, amino-keto, and strong-weak bases. The representation of the four-nucleotide set as a tetrahedron in three dimensions is at the heart of this work. This representation has been used to generate DNA-walks for sequence composition analysis or display. The corresponding proper space metrics has also been recently used for phylogenetic sequence comparisons (13). We proceed to contract the original quantum mechanics statement into an irreducible formulation using the four-nucleotide tetrahedron representation. This molecular symmetrical decomposition is found to provide the right number of fundamental properties (free parameters). Next we relate this decomposition to the dimer set formulation. The comparison uncovers useful and so far hidden self-consistency relations among dimers. Finally these results are applied to the analysis of DNA free energy by introducing empirical end contributions to the model. A self-consistent set has thus been fit to free energy data from 108 short duplex oligomer sequences as available on the literature. The more compact and symmetrical self-consistent set, although modeled short by two variables, is shown to provide at least as good modeling for oligomer free-energy as standard NN dimer models. The far-reaching strength of this entirely novel theoretical modeling frame for DNA/RNA sequences resides in its compactness and symmetry. One of the immediate and practical consequences of the tetrahedral model is the disclosure of the implicit dimer self-consistency relations. The constraints discovered are to avoid unphysical values and thereby increase the precision of predictions relying on dimer set values. This work concludes with an analysis of error propagation, which manifests mostly for sequences with strong composition order trend.

A QUANTUM MECHANICS FORMULATION FOR SEQUENCE PROPERTIES

Complexity in biological phenomena represents an enormous challenge and a rich field for the application and development of physical methods. To unfold simple biopolymer phenomena we start by a biochemical meaningful nucleotide representation into molecular classes and count on sound tools of quantum mechanics formulation. Quantum mechanics does not need to start with a complete spatio-temporal wave-function or Schrödinger representation. It may be well stated in the matrix or Heisenberg representation. What is needed from start is some base set for the description of the states of a system. For a system, we take a DNA/RNA sequence. The ensemble of sequence states is given by allowable sequence composition alone. We want to describe and isolate gross composition states. Inner electronic states or molecular conformation contributions, which would require a much finer level of quantum description, are so far intrinsically averaged. State transitions are of course forbidden if one neglects mutations. The sequence state will be given in terms of its molecular constitution, and a nucleotide set representation will condition the sequence representation.

The quantum mechanics expectation for any observable is given in terms of the corresponding operator E and system state |Ψ〉 as 〈Ψ|E|Ψ〉 in Dirac's notation. The state of a system composed of n particles or molecules is usually expressed as the tensorial product of their component states |b(i)〉:

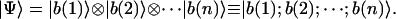(1)

For d-dimensional component states, this would lead a priori to the specification of (nd)² operator matrix elements E_μ(i)ν(j). If interaction range is limited, however, then many off-diagonal matrix elements become null and a reduced formulation can be sought. Considering only sequential NN interactions, the expectation can thus be written as

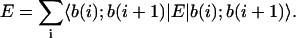(2)

Here, submatrix elements pertaining to the same component at position i (diagonal or self-matrixes E_μ(i)ν(i)), which are internal to the sequence (i ≠ 1, n), should be halved since they are counted twice in this formulation (see Fig. 1). Interactions of the free end nucleotides with surrounding molecules are ignored in this approximation and will be considered in a future work.

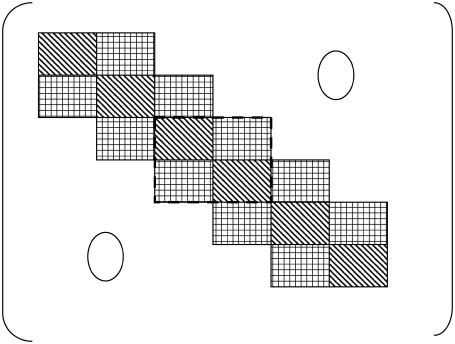
FIGURE 1.

Structure of an expectation matrix for a sequence of n = 6 identical components (molecules in arbitrary states). The components have d degrees of freedom represented through d orthogonal base states, which results in 3n-2 = 16 submatrices of size d². Only nearest-neighbor interactions are considered. This matrix, corresponding to the quantum mechanics formulation of Eq. 1 is Hermitian and periodic, allowing for a more synthetic representation. One periodic module of four submatrices implicit in Eq. 2 has been distinguished by a dashed line. Note that internal submatrices in the diagonal are counted twice according to the formulation of Eq. 2.

Further reduction of this development can be obtained considering implicit symmetries of the Hermitian E-matrix and its invariants under orthonormal base representations.

Nucleotide class-states representation

The most straightforward representation for a four-nucleotide set is a four-dimensional vector. Such “independent-nucleotides” representation has been implicitly adopted by many authors and leads to 4×4 matrixes or 16 parameter sets when considering nucleotide pairwise properties (5). This representation, however, already overstates the nucleotide composition problem from the beginning. The set representation should be more concisely established in a three-dimensional space. First note that, due to a normalization constraint, a variable composed (assuming any combination) of d + 1 different possible states may be specified by a corresponding generalized d-dimensional composition diagram, even though, ultimately, only the corners of the diagram represent pure states. To give examples, properties for a ternary mixture are well represented in a two-dimensional triangular composition diagram for support, while a binary mixture is defined from a single concentration variable. A complete and symmetrical representation for the usual DNA (or RNA) four-nucleotide set can be given within a tetrahedral decomposition scheme into a three-dimensional orthonormal base set |x〉, |y〉, |z〉. The pure nucleotide states |b(i)〉 are given as (13)

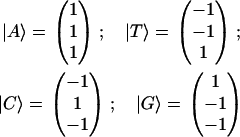(3)

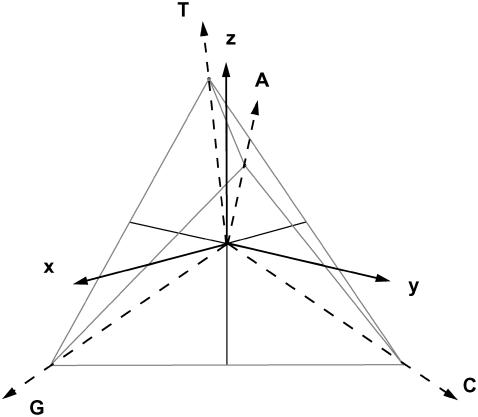
The nucleotides themselves are represented as a nonorthogonal (tetrahedral) √3-modulus vector set (Fig. 2). The four-nucleotide states are not independent, and can be expressed in terms of three independent abstract nucleotide class states. Due to this decomposition, z-component discriminates weak (two bridges, AT) versus strong (three bridges, CG) hydrogen bonding for Watson-Crick pairing; x-component discriminates purines (double-ring, AG) versus pyrimidines (single-ring, CT) nucleotide sizes and y-component discriminates amino (nitrogen-containing, AC) versus keto (oxygen-containing, GT) nucleotide radicals. The nucleotide representation is given in a tentative molecular class space. In quantum language, a |x〉 base state, for example, is a ring number or purine-pyrimidine class-state, while |A〉 = |x〉+ |y〉+ |z〉 is an adenine molecular-state decomposed in terms of proper nucleotide class subspaces. Any pure nucleotide state can thus be represented in terms of molecular class states. Each possible nucleotide pair shares one of its fundamental molecular structural characteristics as a group in a given class, which differs from the complementary pair as another group in the same class (see Eq. 3). This is perfectly well represented in the intrinsic cubic symmetry of the tetrahedron. The properties associated to each molecule are to be decomposed in terms of three differential affinity groups or classes belonging to a complete nucleotide representation. It is worth stressing that the four-nucleotide molecules display rather straightforward differential affinities, which helpfully associates each of the three proper classes to main molecular structural features. Hence, through abstract operations, each nucleotide could be modeled to mutate into another by keeping the group state of one of its three classes while converting the remaining class states. The choice of a tetrahedral set is thus natural and convenient for its intrinsic orthogonality and symmetry properties, which are related to common molecular group classifications. Nevertheless its main advantage is to fulfill the necessity for a three-dimensional bijective representation of a four-set composition.

FIGURE 2.

Orthonormal x-y-z base set and tetrahedral DNA-nucleotide set representation. Each of the three axes distinguishes a specific molecular class feature. Purines are distinguished from pyrimidines through x-coordinate. Amino are distinguished from keto through y-coordinate. Weak Watson-Crick hydrogen-bridge binding is distinguished from stronger binding through z-coordinate.

Irreducible representation

Returning to the quantum mechanics formulation, we want to exploit the remaining invariants and redundancies from the structure of the matrix operators in Eq. 2 to further reduce its number of parameters. The three-dimensional nucleotide basis should be kept in mind. The sequence-dependent states of an observable will then assume discrete values given by a most compact expansion of its expectation as

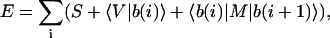(4)

in place of Eq. 2, where b(i) are still the sequence nucleotide states at coordinate i, given in terms of class states by Eq. 3, while end effects have been ignored here, i.e., the sequence is assumed to be noninteracting at both ends, or gigantic, or circular, or periodic for simplicity. The bracket notation indicates vector and dyadic contractions as usual. The expansion above is intuitive, as the first two terms represent linear contributions to a property from the sequence composition, while the third term comprises nonlinear effects due to NN interference or differential stacking interactions. Comparison with Eq. 2 allows the identification of its components. The first term is a constant or mean contribution to the observable, given as the invariant trace of the square expectation periodic matrix S = Tr(E). The trace represents a molecular-state independent contraction of the self-matrix diagonal, where, by construction, any pure nucleotide component (Eq. 3) equally squares to one (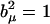). The remaining cross terms of the self-matrix similarly contract to a vector since all pure nucleotide states |b(i)〉 also have cyclically multiplicative class components (b_x = b_y b_z, etc.). This contraction gives the second term as an order-independent or global-composition contribution, with components 〈V| = 4 Re(E_y(1)z(1) E_z(1)x(1) E_x(1)y(1)). The third term is an NN or first-order sequence stacking contribution to the observable. The stacking matrix M is a second-rank tensor and has its elements given from the cross expectation matrix as M_μν = 2 Re (E_μ(1)ν(2)). The symmetrical sum of the expectation matrix Hermitian conjugates result in a fully contracted real formulation.

Decomposition of nucleotide sequence observable expectation as in Eq. 4 naturally leads to an irreducible 13-parameter description of physical properties (S, V_μ, M_μν), which we call the symmetrical set, within the NN approximation. Note that a traditional description of stacking dependent properties is often stated in terms of the NN dimer composition, i.e., as a linear combination of the 16 ordered 5′–3′ NN dimer set E_ij:

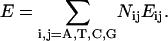(5)

The NN dimer set is, however, overspecified, i.e., only a smaller set of NN combinations can be a priori obtained from inversions of Eq. 5, since Eq. 5 is supplemented by independent composition closure relations. For implicit circular sequences these can be taken as any three of

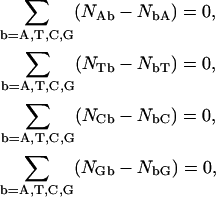(6)

reducing the number of independent dimers in the set to arbitrary 13. Similar arguments hold for linear oligomers.

In comparison, the decomposition of physical properties in the symmetrical set proposed here is in a fundamental level, since from the beginning it includes only a priori linearly independent terms and gives contributions to the observable in the hierarchic form of three expectation tensors of increasing rank, corresponding to different levels of analysis. The 16 NN expectations can otherwise be easily obtained as a linear combination of the 13 symmetrical-set tensor components. In that case it is useful to rewrite Eq. 4 in a form appropriate for NN dimer decomposition as

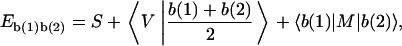(7)

where, to correctly account for additivity, as given by Eq. 5 for each dimer in a sequence, the two nucleotide linear contributions are halved.

Explicitly one has applying Eq. 3 to Eq. 7:

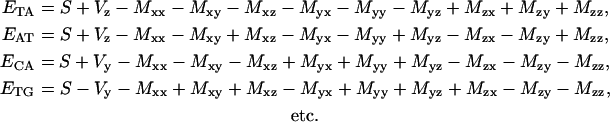(8)

Tensor elements can be either conversely determined from reported dimer values or be self-consistently derived from fits to raw polynucleotide data using Eqs. 8 and 5, or directly from Eq. 4, while from a theoretical point of view, molecular symmetry arguments or ab initio calculations could be used to guess tensor structure and values.

Double strands

For measurements concerning double strands, aside end effects, it is well known that complementary strand symmetry further reduces the problem to the statement of only 10 conjugated NN dimer pair values (see the expressions in Eq. 12 below) linked through two independent composition closure relations as

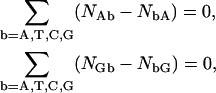(9)

so that only eight independent parameters should result, while the difficulties in defining a 10-dimer set of parameters from a given set of experimental data persist. In that case, complementary strand A/T and C/G pairing symmetry in a dimer, as expressed in Eq. 3, gives the conjugate NN base component relations

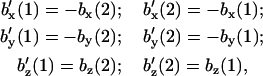(10)

where primed bases correspond to the complementary dimer and numerals correspond to the first and second nucleotide along 5′–3′ direction for each strand, i.e., both order and x,y coordinates are inverted for the conjugate pair.

The double-strand expansion can be given as a function of a single strand sequence taking into account the fore mentioned implicit symmetries (by adding contributions from both strands to Eq. 7 taking into account Eq. 10 and then redefining the tensor set, i.e., E′_b1b2 ≡ E_b1b2+ E_b′1b′2). It is clear in that case that

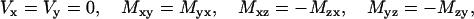(11)

correctly reducing the number of independent elementary tensor set values to 8.

From Eq. 11 and Eq. 8, decomposition for the 10 paired NNs gives a self-consistent set of expectations obeying

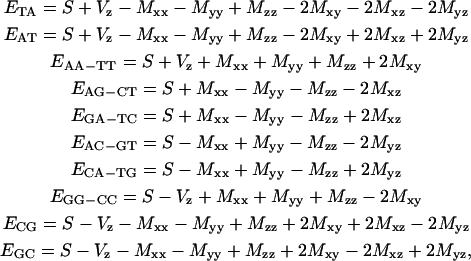(12)

while the symmetrical set of eight tensor parameters can be inferred from the inverse relations

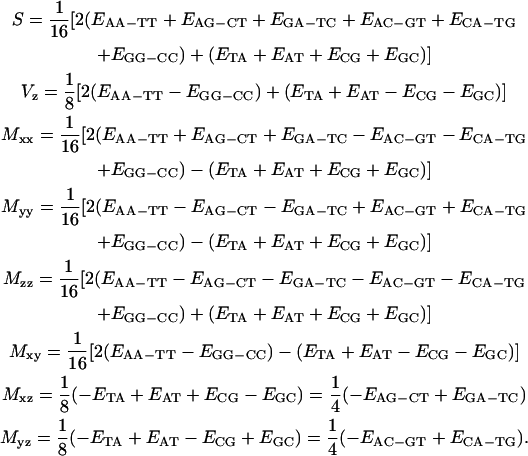(13)

This decomposition enlightens the meaning of the composition free S term as the 16-dimer ensemble mean expectation value and of V_z as the half-differential expectation between AT containing and CG containing dimers. Most important, the double determination of M_xz and M_yz values in the last two expressions in Eq. 13 should coincide for a self-consistent set of dimer values. Explicitly, self-consistency introduces links relating composition order symmetry among dimer properties as

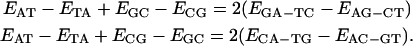(14)

Note that, analogous to the composition closure relations (Eq. 9), the dimer expectation self-consistency relations (Eq. 14) may also be combined to read

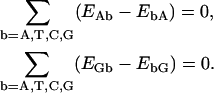(15)

COMPARISON WITH EXPERIMENTAL DATA

To compare this self-consistent formulation with double-strain DNA oligonucleotide free energy data, four extra terms corresponding to the different 5′ terminal compositions need to be considered with the dimer contributions of Eq. 7. End effects include duplex initiation and other duplex and solvent terminal interactions. However, only two parameters, that discriminate AT end pairing from CG end pairing, without 5′–3′ order discrimination, seem to be relevant and have often been included in general thermodynamic analysis of DNA (10–12). A symmetry penalty of entropic origin given as ln(2) RT = 0.43 kcal/mol, is also usually assigned for the physically distinct case of self-complementary sequences. We will adopt the same set of initiation and symmetry parameters here in order not to loose the focus on the NN set presentations.

The determination of oligonucleotide free energies has been a long-standing problem (1,14,15). SantaLucia et al. (10–12) has reviewed the data from seven laboratories and given a table of unified values for DNA dimer contributions to standard free energies at 37°C and 1M salt concentration: ΔG₃₇. This unified data set is not self-consistent a priori. Adopting an ab initio approach, we proceed to fit the same set of thermodynamic data from 108 sequences used to establish the unified NN dimer parameter set (11); using the eight parameter tensor decomposition of dimer properties (Eq. 12) plus three extra parameters: an entropic correction for symmetric self-complementary sequences; and terminal corrections for AT and CG initiations.

For example, the sequence AATG would be decomposed as

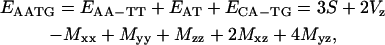(16)

plus one AT and one CG initiation contribution. A set of 108 equations linear on the eight tensor plus two initiation parameters were thus defined. The free-energy parameters for the symmetrical set were determined by minimization of nonweighted square deviations for all sequences,

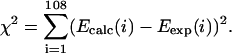(17)

The free-energy mean standard deviation from this decomposition estimate gives 0.14 kcal/mol/dimer, exactly the same deviation found from using the unified-set results, which is the order of experimental precision. The symmetrical set then becomes (in cal/mol)

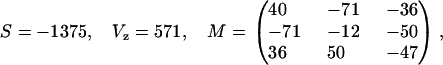(18)

plus the two initiation contributions given in Table 1.

TABLE 1.

NN standard free energies ΔG₃₇ (in kcal/mol)

Dimer set	Unified	Self-consistent
TA	−0.58	−0.57 ± 0.04
AT	−0.88	−0.91 ± 0.04
AA-TT	−1.00	−0.97 ± 0.02
AG-CT	−1.28	−1.20 ± 0.04
GA-TC	−1.30	−1.35 ± 0.03
AC-GT	−1.44	−1.28 ± 0.03
CA-TG	−1.45	−1.48 ± 0.03
GG-CC	−1.84	−1.82 ± 0.04
CG	−2.17	−2.14 ± 0.04
GC	−2.24	−2.19 ± 0.06
A-T ending	1.03	0.92 ± 0.08
C-G ending	0.98	0.85 ± 0.07
Symmetry	0.43	0.43

The unified set proposed by SantaLucia (10) is compared to the self-consistent set. Both sets have been obtained by model fits to the same 108-sequence data set (11).

The precision of the symmetrical set has been estimated from a resampling analysis including 100 random data subsets with 70 sequences as ±20 cal/mol for S and ±10 cal/mol for the remaining parameters. Accordingly, the self-consistent set for dimer free energies and deviations is given in Table 1. Comparing both dimer set results (see Table 1), deviations of the order of only 0.05 kcal/mol per NN indicate that the unified set is already close to self-consistency within experimental error. However, we notice greater discrepancies in the free energies of AG and AC dimers, which were given as almost identical to the GA and CA NNs, respectively, for the unified set. We interpret these as mean values determined from the unified set analysis, within two underestimated energy splittings between AG and GA and between AC and CA NNs. These splittings only become well resolved through self-consistency requirements of the symmetrical set (see Fig. 3).

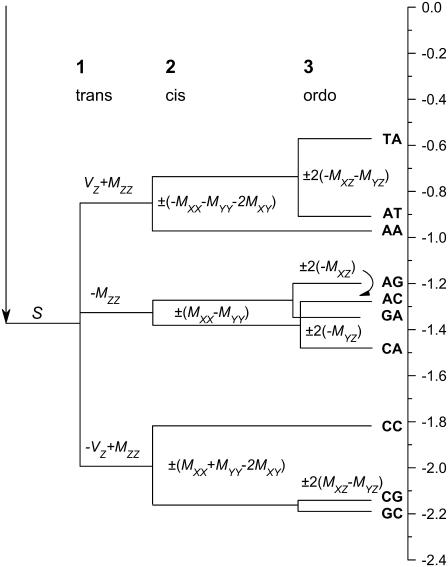
FIGURE 3.

Self-consistent free energy splitting. According to Eq. 12, dimer physical properties split after three composition levels: 1), a nonlinear Chargaff split is trans-composition or z-controlled; 2), dimer cis-composition split is x,y-controlled; and 3), nucleotide 5′3′ order split (ordo-composition) also determines NN self-consistency relations. The scale to the right is in kcal/mol.

DISCUSSION

Entropy release is mainly due to freezing of the ribo-phosphate backbone degrees of freedom and is quite insensitive to base composition. Differential entropic contributions to V_z should be correspondingly small and 2V_z estimates the linear differential enthalpy contribution of a characteristic A/T to C/G single hydrogen-bonding energy difference of H ∼ 1.1 kcal/mol. This is of good order (16) and can be taken as a reference value since no precise estimate for this quantity is universally accepted. The mean contribution S ∼ 1.4 kcal/mol to the free energy can be interpreted in terms of a relatively high mean entropy release of ∼−23 cal/(mol.K) (10) compensated by a mean enthalpy gain of −8.3 kcal/mol, which amounts to include mean hydrogen-bonding energy of order 2.5 H ∼−2.8 kcal/mol and approximately two-times stronger mean stacking interactions. This is also in accordance with estimates of mean stacking interactions (16,17). Differential stacking contributions to the standard free energy, given by M matrix elements, are one order-of-magnitude weaker while no clear dominant feature appears. Finally we wish to point out that the symmetrical representation allows for the analysis of duplex dimer physical properties in terms of composition structure at three levels (Fig. 3). In the first level, properties are split according to the number of hydrogen bonds. This “Chargaff splitting” is an AT-CG (trans-composition) split controlled by z-coordinate alone and includes a nonlinear M_zz differential stacking correction to the linear V_z three-split. In the second level, a symmetrical splitting occurs for different dimer compositions (cis-composition). This is controlled by x,y-coordinates alone. For the third level, another symmetrical split occurs for dimers in opposite 5′3′ orientations (ordo-composition). Four pairs of expectations then become distinguished by nucleotide order and since only two parameters (M_xz and M_yz) control their properties, it is this last splitting that also implies the self-consistency relations (Eqs. 14 and 15). Composition order bias, producing highly unbalanced M_xz and M_yz contributions, is seldom produced in ordinary sequences. It would be desirable to explicitly design and measure simple complementary ordered sequences such as GTAGTAG and GATGATG. Table 1 estimates a free energy difference of 5.78 − 4.40 = 1.38 kcal/mol for the symmetrical set, against only 5.30 − 4.64 = 0.66 kcal/mol for the unified set. Differential analysis of such oligomer pairs should thus provide compelling evidence against or toward the symmetrical model.

CONCLUSIONS

A geometrical representation of four-nucleotide sets as a tetrahedron (Eq. 3 and Fig. 2) allows for the association of the three most distinctive molecular group classifications with corresponding orthogonal cubic axis. Physical properties of nucleotide sequences may be calculated with an optimal set of tensor coefficients (Eq. 4) assuming projections within this tetrahedral representation. The coefficients are expressed in hierarchical differential form, so lower levels of approximation are explicitly embodied in the description. This includes an ensemble mean expectation from scalar coefficient S alone, and a global composition approximation, as expressed through V-component contributions. The symmetrical set is shown to provide a frame for the analysis of DNA duplex free energy fully compatible with experimental data (Eq. 18). Such a symmetrical set of coefficients allows for the translation among different decomposition frames. It also gives a proper irreducible representation for dimer properties (Eqs. 8 and12). It solves an old indeterminacy of dimer sets by establishing self-consistency relations among dimer coefficients (Eqs. 14 and15). A self-consistent dimer set is given in Table 1. Self-consistency relations provided by the present analysis should increase the predictive power of NN models since with lesser parameter number they should become more robust against fitting noise of experimental data. Experiments with order-biased sequences to test in depth the reliability of this model have been suggested.