Protein-Protein Association in Polymer Solutions: From Dilute to Semidilute to Concentrated

Abstract

In a typical cell, proteins function in the crowded cytoplasmic environment where 30% of the space is occupied by macromolecules of varying size and nature. This environment may be simulated in vitro using synthetic polymers. Here, we followed the association and diffusion rates of TEM1-β-lactamase (TEM) and the β-lactamase inhibitor protein (BLIP) in the presence of crowding agents of varying molecular mass, from monomers (ethylene glycol, glycerol, or sucrose) to polymeric agents such as different polyethylene glycols (PEGs, 0.2–8 kDa) and Ficoll. An inverse linear relation was found between translational diffusion of the proteins and viscosity in all solutions tested, in accordance with the Stokes-Einstein (SE) relation. Conversely, no simple relation was found between either rotational diffusion rates or association rates (k_on) and viscosity. To assess the translational diffusion-independent steps along the association pathway, we introduced a new factor, α, which corrects the relative change in k_on by the relative change in solution viscosity, thus measuring the deviations of the association rates from SE behavior. We found that these deviations were related to the three regimes of polymer solutions: dilute, semidilute, and concentrated. In the dilute regime PEGs interfere with TEM-BLIP association by introducing a repulsive force due to solvophobic preferential hydration, which results in slower association than predicted by the SE relation. Crossing over from the dilute to the semidilute regime results in positive deviations from SE behavior, i.e., relatively faster association rates. These can be attributed to the depletion interaction, which results in an effective attraction between the two proteins, winning over the repulsive force. In the concentrated regime, PEGs again dramatically slow down the association between TEM and BLIP, an effect that does not depend on the physical dimensions of PEGs, but rather on their mass concentration. This is probably a manifestation of the monomer-like repulsive depletion effect known to occur in concentrated polymer solutions. As a transition from moderate to high crowding agent concentration can occur in the cellular milieu, this behavior may modulate protein association in vivo, thereby modulating biological function.

INTRODUCTION

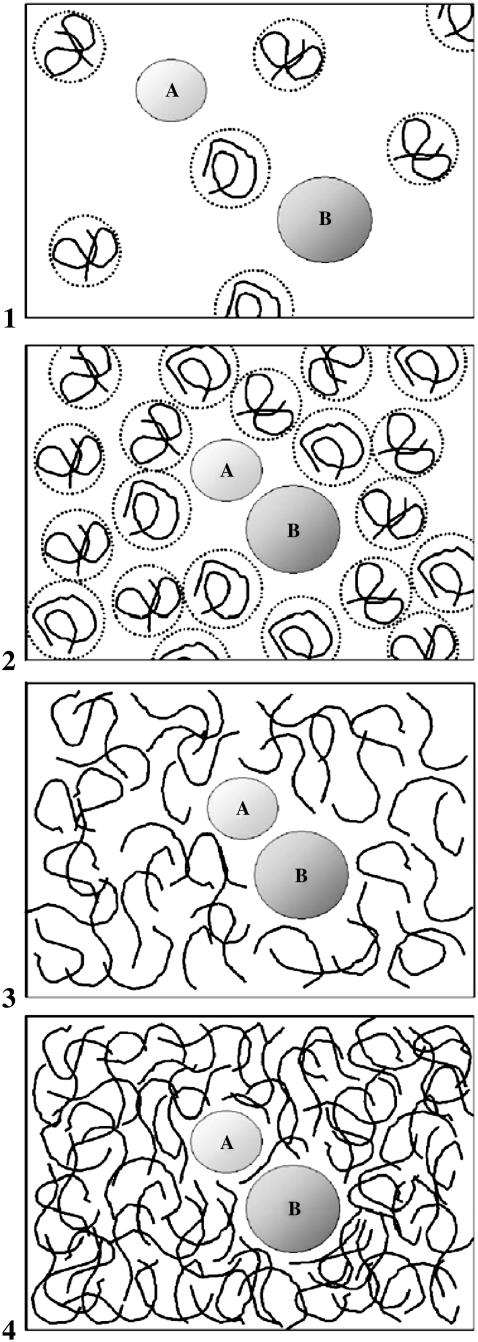
Synthetic polymers such as polyethylene glycol (PEG), Ficoll, dextran, and polyvinyl alcohol are commonly used as a means to simulate molecular crowding in the cell. The presence of high concentration of macromolecules in a solution is known to enhance enzymatic activity (1–3), stabilize protein solutions (4–7), and promote crystal growth (8,9). Polymer molecules such as PEG or dextran change their behavior in solution as a function of concentration. The character of the polymer-induced interaction changes significantly as one goes from a dilute to a semidilute solution and finally to a concentrated solution, as illustrated in Fig. 1 (10,11). In the dilute regime it is useful to regard the polymers as extended spheres (coils) with a certain radius of gyration (R_g), which depends on the number of monomers per polymer (N). However, these spheres are not rigid and are highly solvated. As density increases, the separate coil picture is no longer valid and the polymers begin to interpenetrate one another. In this so-called semidilute regime, a polymer solution consists of a network with a certain average mesh size (ξ), which is a decreasing function of polymer volume fraction (φ) according to ξ ∼ φ^−3/4.

FIGURE 1.

Schematic representation of proteins in crowded polymer solution. Proteins and polymer molecules are represented as spheres (A or B) and as flexible lines, respectively. In the dilute regime (panel 1) the polymer coils hardly interact with the proteins or themselves. The polymer concentration is too low to produce a substantial depletion attraction between the proteins, especially when working with short polymer molecules (PEG 200–600). At the crossover concentration (c*, panel 2), the polymers retain their structure but they start to overlap with each other. The repulsion and depletion interactions are roughly balanced, and the mass concentration dependence of the rate of association equals the one predicted by the SE relation. In the semidilute regime (panel 3) the polymers form a dense network. Proteins are embedded in the resulting viscous solution, but a polymer cage is still formed around the two proteins, causing a much faster relative rate of association than predicted by the SE relation. In the concentrated regime (panel 4), polymers are very dense and there is much less solvent in the system. The solvent cage around proteins is much smaller and penetration of polymer molecules to the area between the two proteins hinders complex formation, yielding low association rate values.

In ternary systems composed of polymer-water-colloid, a depletion interaction is exerted on the immersed colloidal particles by the polymer molecules (12). The strength of the depletion interaction depends on the size of the colloids and the polymer, as well as on polymer concentration (8,9,13). In dilute and semidilute polymer solutions, this interaction can be described as an effective attraction between pairs of colloids induced by the inability of the polymer molecules to enter the volume between them when their separation is smaller than the size of one polymer molecule. We have shown previously how the attractive force in a semidilute solution enhances the rate of association of a pair of proteins much above that expected from the solution viscosity (14).

In the concentrated regime the solution can be assumed to exhibit structure on a monomer scale, like a small-molecule fluid; here, polymer segments begin to pack at the colloid/protein surface. An important consequence of packing is that the effective force becomes an oscillatory function of particle separation and is repulsive for certain distances (D), notably D − b ≈ σ, where σ is the segment diameter and b is the colloid radius. Addition of a polymer to a colloid suspension is therefore expected to induce flocculation at low and moderate concentrations, whereas at high concentrations there may be a stabilizing effect due to the repulsive barrier. Such oscillatory forces have been observed experimentally on surfaces immersed in liquids, on cells in PEG solution (15), and in computer simulations (16–18). In this work we provide evidence for repulsive depletion interactions in concentrated protein-polymer solutions, where we believe this phenomenon was not observed before.

Polymers (mostly PEGs) of various sizes were used in the past to investigate protein-protein association under crowding conditions representing some aspects of the biological environment (19,20). We have found that the effect on the association rate, k_on, is surprisingly small even upon addition of PEG 8000 or Ficoll up to concentrations of 25% (21). In contrast, low MW viscogens like glycerol, EG, or sucrose slowed down association way above the predicted effect of viscosity. To understand this phenomenology, we measured the translational and rotational diffusion rates in these solutions (14). An inverse linear relation was found between the translational diffusion coefficient (D_t) and the solution viscosity for all tested viscogens up to very high viscosities, as predicted by the well-known Stokes-Einstein (SE) relation:

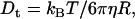(1)

with η being the solution viscosity, T its temperature, 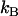the Boltzmann constant, and R the hydrodynamic radius of the diffusing species. In contrast, the rotational diffusion coefficient (D_r) was found to be affected differently by high and low MW viscogens; whereas the effect of monomeric, low MW viscogens on D_r followed the Stokes-Einstein-Debye relation

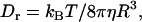(2)

high MW viscogens affected D_r to a lesser extent. The use of the diffusion-limited association (DLA) theory (22–24) to calculate k_on from the diffusion coefficients (D_t and D_r) resulted in poor agreement with experimental data. We explained the deviations of experimental k_on from DLA by a short-range solute-induced repulsion between the proteins in glycerol solution and an attractive depletion interaction generated by the polymers (14).

Crowding agents abundant in the cell include mostly proteins and nucleic acids. The cytoskeleton is known to form a dynamic network of protein filaments dividing the cell into discrete bulk areas of cytoplasm where soluble proteins interact. In addition there are many ‘natively unfolded proteins’ that can add complexity to the cytoplasmic medium (25). In this sense a synthetic linear polymer that forms network-like structures, such as PEG, mimics at least some qualitative properties of a eukaryotic cell. Although networks formed by native skeletal proteins or other unfolded proteins have different properties from networks formed by synthetic polymers like PEG, the effect they may exert on protein-protein association can be similar in nature. It was recently suggested that a generic form of polypeptide structure, resulting from the dominance of main-chain interactions, is a fibrillar aggregate (26). This implies that under certain pathological conditions (e.g., amyloid diseases) many more proteins in the cell will form networks in vivo. Under these conditions the description of protein-protein association measured in the presence of synthetic crowding agents might be of biological relevance. Our experiments on association in crowded environments thus may be seen as another means to investigate possible mechanisms of regulation and modulation of reactions and interactions within the cellular milieu.

In this article we aim to establish a relation between the rate of association, the diffusion constants, and the MW of the crowding agents over a broader range of conditions. We used a stopped-flow apparatus to measure k_on values for the association of the protein pair TEM1-β-lactamase (TEM) and β-lactamase inhibitor protein (BLIP) in the presence of up to ∼60% mass of PEGs of MW ranging from 200 to 8000. We compared these k_on values with the ones measured in the presence of several monomeric viscogens such as glycerol, ethylene glycol (EG), and sucrose. Using these data we were able to show how the nonmonotonic behavior of k_on with increasing viscogen concentrations is related to two fundamental properties of polymer solutions, namely the crossover concentration from dilute to semidilute (c*) and the radius of gyration (R_g). Our results show how the thermodynamic properties of polymer solutions affect the way proteins diffuse and associate in a crowded environment.

MATERIALS AND METHODS

Chemicals

Glycerol, ultra pure grade, was purchased from ICN (Irvine, CA). Sucrose was purchased from VWR (West Chester, PA) BDH. EG, Poly(ethylene glycol) 8000, 6000, 3350, 1000, 600, and 200, and Ficoll-70 were purchased from Sigma (St. Louis, MO). All the reagents were used without further purification.

Proteins

Wild-type TEM and the +4 BLIP analog (D163K, N89K, V165K) (27) were used throughout this study. Proteins were kept in 10 mM Hepes buffer adjusted to pH 7.2, and all measurements were conducted in the same buffer and pH. For fluorescence correlation spectroscopy (FCS) diffusion experiments, we used the BLIP A1C mutant, which was specifically labeled with the maleimide derivative of the dye Alexa 488 (Molecular Probes, Eugene, OR) and shown to be active after the labeling procedure (14). For fluorescence anisotropy experiments we used a green fluorescent protein mutant with enhanced fluorescence (eGFP), which was expressed and purified as described (14).

Viscosity measurements

Viscosity measurements were done using a Cannon-Fenske Routine Viscometer 150/I750 (Cannon, State College, PA) (21). Some of the viscosity measurements at high additive concentrations were done with a rotational viscometer (Haake Roto visco 1, Thermo Electron, Karlsruhe, Germany). Measured values of viscosity for glycerol and EG were in good agreement with published data (28).

Fluorescence anisotropy measurements

The rotational correlation time of eGFP in various viscous solutions were obtained from steady-state fluorescence anisotropy measurements carried out on a commercial spectrofluorimeter (ISS PC1, Urbana, IL) equipped with rotating calcite polarizers and a thermostated bath, which allowed maintaining the sample temperature at 25°C ± 0.2°C. For a detailed explanation of the method and a justification of using eGFP as a protein probe (instead of TEM or BLIP) refer to the Materials and Methods section in Kuttner et al. (14).

Fluorescence correlation spectroscopy

Translational diffusion was measured using a home-built fluorescence correlation spectrometer (see Kuttner et al. (14) Supporting Information). FCS measurements were conducted under temperature control at 25°C ± 0.2°C. The fluorescence correlation function was fitted to the well-known equation for a single diffusing species moving through a Gaussian-shaped sampling volume (29). From this fit we extracted the translational diffusion coefficient (D_t) for the fluorescently labeled BLIP in various solutions. As noted previously (14), no evidence for anomalous diffusion was found in any of these solutions.

Protein association measurements

The association reaction of TEM and BLIP in various solutions was measured as explained in Kozer and Schreiber (21) under second-order kinetic conditions with equal concentrations (0.5 μM) of both proteins in a 10 mM Hepes buffer solution of pH 7.2 and at 25°C ± 0.2°C. The data were fitted to a standard equation describing association under the condition of equal reactant concentrations (30).

RESULTS

Effect of crowding agents on the rate of association

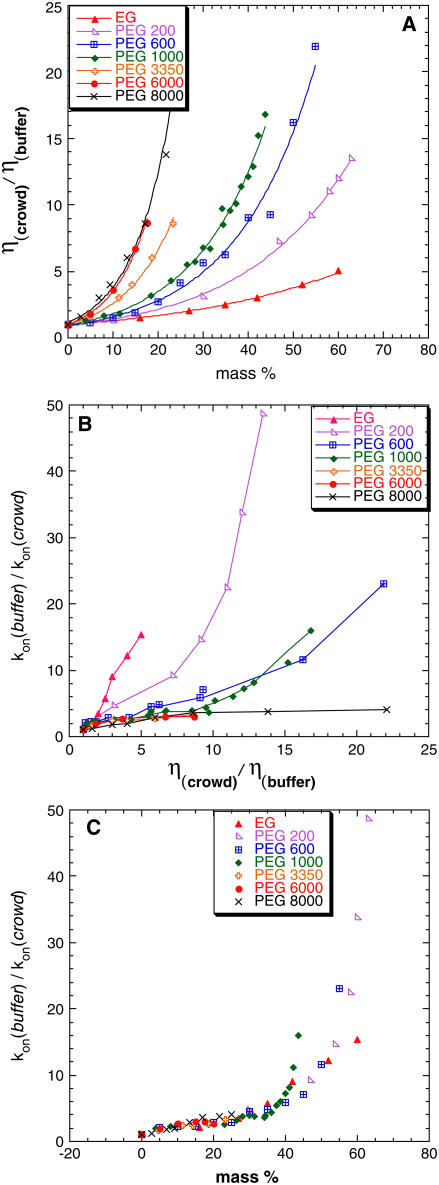
Association rate constants for TEM and BLIP were measured in the presence of EG and PEG polymers of various molecular weights (MWs) and of mass concentrations up to ∼60%. The increase in polymer mass concentration produces higher solution viscosity. The dependence of solution bulk viscosity on mass percent is presented in Fig. 2 A, which reflects the fact that lower MW molecules influence viscosities to a lesser extent than high MW molecules. Due to the complex relation between polymer mass percent and solution viscosity, plotting association data on either scale will result in a very different presentation, as can be appreciated from Fig. 2, B and C. In these figures relative inverse k_on values were plotted on a viscosity or mass percent scale. On a relative viscosity scale (Fig. 2 B) association rate constants are dependent on the MW of the viscogen. On the mass percent scale (Fig. 2 C) all data seem to approximately converge in a manner independent of the viscogen MW. This convergence is somewhat misleading, since it was shown that the association reaction of these two proteins is diffusion limited (31,32). Indeed, once the data are corrected for the viscosity of the medium (as discussed below, Fig. 4), the apparent convergence of the various curves is not observed anymore.

FIGURE 2.

Relation between solution viscosities, polymer mass percent, and rate of association. (A) Viscosities were measured by a capillary or a rotational viscometer in 25°C. Excellent agreement was found between the measured data for EG and glycerol and literature data (28). Panels B and C show the relative association times (inverse rates) for TEM-BLIP association in the presence of increasing concentrations of the indicated crowding agents as a function of the relative viscosity (B) or mass concentration (C).

FIGURE 4.

Deviations from SE behavior calculated according to Eq. 2 and plotted as a function of mass percent of the various PEGs. Data from top to bottom: PEG 8000, PEG 6000, PEG 3350, PEG 1000, PEG 600, PEG 200, and EG. Panel (B) shows data of association in the same solutions as in A but on a c/c* scale, where c* is the dilute-semidilute crossover mass concentration calculated from c* = N^−4/5 with c being the PEG mass concentration.

The relation of diffusion and association in PEG solutions

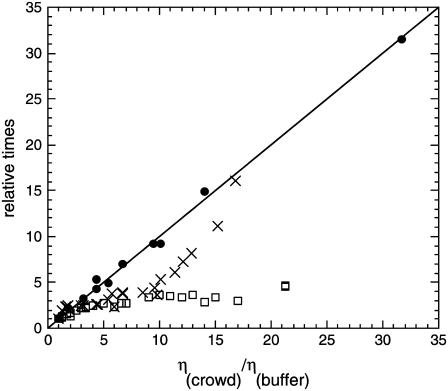
We have previously analyzed the relation of measured translational and rotational diffusion coefficients to association rates in glycerol and PEG 8000 solutions (14). Here, we extended this study to include polymers with an intermediate MW. Fig. 3 shows the relative translational and rotational diffusion coefficients as well as the relative change in the association time (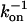) for TEM-BLIP association in PEG 1000 as a function of the relative solution viscosity. D_t clearly follows the SE relation (with a slope of 1), whereas D_r and 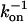do not. This result is similar to that observed for PEG 8000 (14). The reader is referred to our previous work (14) for a detailed discussion of the origin of this behavior, which stems from the difference in timescales sampled by translational and rotational diffusion measurements (hundreds of microseconds versus nanoseconds). However, for PEG 1000 we observe an additional phase; up to a relative viscosity of 10, 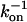seems to follow D_r, but above 10 it strongly deviates from it. Evidently, this nonmonotonic behavior cannot be attributed to either translational or rotational diffusion.

FIGURE 3.

Relative diffusion and association times (inverse rates) for TEM-BLIP in PEG 1000 as a function of relative viscosity. Translational correlation times (circles) were measured by FCS. Rotational correlation times (open squares) were calculated from steady-state fluorescence anisotropy measurements. Association (x symbols) was measured using a stopped-flow apparatus. The line represents the SE prediction and is not a fit.

The non-SE behavior of the rates of association

Fig. 3 shows that D_t is linearly related to the relative change in solution viscosity for PEG 1000. The same was found previously for glycerol and PEG 8000 and will be considered in this article to hold for all PEG solutions. For a diffusion-controlled reaction of two similar sized particles, the rate of collision (k₁) is given by the Smoluchowski relation:

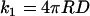(3)

with R being the sum of the effective radii of the particles and D the sum of their translational diffusion (D_t) coefficients. As the rate of collision is linear with D_t and we showed that D_t is linear with η⁻¹ for all viscogens tested, we may assume that k₁ is linear with η⁻¹ in all solutions as well. Therefore, by multiplying the measured values of k_on by the relative viscosities of the solution, we obtain a measure of the effects of viscogens on the rate of binding that is essentially independent of the rate of collision. In the SE limit the multiplied rates should be constant, and the ratio of the rate at a particular polymer mass concentration to the rate in buffer should equal unity. We define the deviation from the SE behavior as follows:

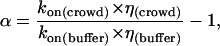(4)

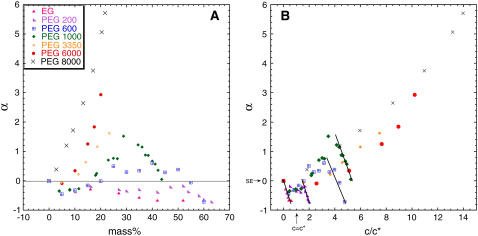
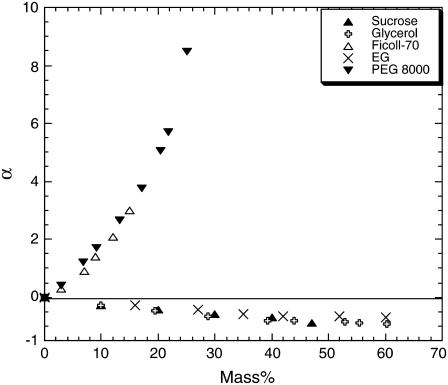
where k_on(buffer) and k_on(crowd) refer to the rate of association in buffer and in solution of a crowding agent, respectively, and η_(buffer) and η_(crowd) are the respective viscosities. The crowding agent mass concentration dependence of α can be directly attributed to events along the association pathway occurring between collision and complex formation. In Fig. 4 A, values of α are plotted as a function of the mass percent of the viscogens for the whole series of PEG solutions, and in Fig. 5 we present similar data for the small viscogens EG, sucrose, and glycerol, as well as for the polymer Ficoll-70. This data presentation allows us to take a closer look at the ‘portion’ of the association reaction that does not depend (or depends only weakly) on translational diffusion (the postcollision step of association) to appreciate the dependence of association on the type and MW of the viscogen. Positive and negative values of α signify rates of association, which are faster or slower than would be calculated at the SE limit. These nonzero values of α are due to two factors: First, the effect of rotational diffusion once the proteins have collided on the association reaction will lead to deviation from SE behavior if rotational diffusion is not linear with η⁻¹, as is indeed the case in PEG 1000 (Fig. 3) and PEG 8000 (14). Second, solution forces such as depletion or preferential hydration will also lead to nonzero values of α. Since the deviation of rotational diffusion rates from SE behavior is monotonic, it is expected to have a monotonic effect on α. However, the behavior of α is clearly nonmonotonic, and three distinct phases are observed in Fig. 4 A:

1. Negative values of α at relatively low mass percent values (0–20%) or in the presence of small crowding agents.

2. Positive and increasing values of α at moderate mass percent values (20–35%).

3. A dramatic slowdown in association rates at high mass percent values (35–60%), leading again to decreasing values of α.

FIGURE 5.

Deviations from SE behavior plotted as a function of mass percent for several additional viscogens. TEM-BLIP association was measured in the presence of Ficoll-70, glycerol, or sucrose and analyzed as explained in Fig. 4. For comparison, the data are overlaid on the data obtained for EG and PEG 8000 presented in Fig. 4.

Negative deviations from SE behavior—monomeric viscogens or dilute regimes

Under two conditions we observe negative α values: 1), in the presence of small crowding agents (i.e., EG and PEG 200), and 2), in dilute solutions of ‘medium size’ PEGs (600, 1000, and possibly also 3350). These negative values indicate that relative association rates are slower than calculated by the Smoluchowski expression (Eq. 3). The observed slow rates are not due to low 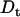values, since we account for them when multiplying k_on by the relative viscosity. Rather, they seem to be a result of a repulsive force acting between the proteins. A similar behavior was observed before in the presence of glycerol (14). This behavior was also seen in solutions of the small viscogens EG and sucrose (Fig. 5).

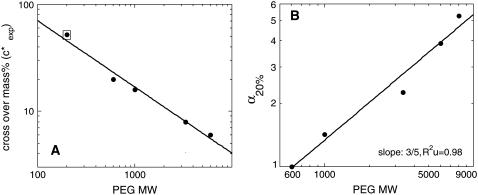
At higher mass concentrations of the medium-sized PEGs, α crosses zero and becomes positive. We designate the concentration at which a transition from negative to positive deviations from SE behavior occurs as 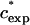. In Fig. 6 A we plot 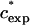as a function of MW on a log-log scale. Fitting the data we find that they can be represented in the form 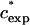∝N^ν, with ν = −0.62 (0.05). This relation is quite similar to the one describing the well-known scaling of the crossover concentration from the dilute to the semidilute regime, c*∝N^−4/5. We can therefore attribute negative α values occurring at ∼0–20% to a process that takes place in the dilute regime of the solution.

FIGURE 6.

Scaling of association rates under some key conditions with the MW (or size) of PEG molecules. (A) The crossover point from negative to positive deviation from SE behavior extracted from Fig. 4 and plotted as a function of polymer MW on a log-log scale. The PEG 200 point (in a square) is the mass concentration value that yields the smallest deviation from unity (see Fig. 4). The slope of a linear fit to the data equals 0.62 (±0.05). (B) Deviations from SE behavior at 20% polymer solutions plotted as a function of polymer MW on a log-log plot. The slope of a linear fit to the data equals 0.60 (±0.06) and is identical to the R_g dependence on polymer size: Rg ∼ N^3/5 (see text).

Positive deviations from SE behavior in semidilute PEG solutions

Positive α values are observed up to a mass concentration of ∼35% in medium and high MW PEGs. Deviations of k_on from SE behavior are more extreme in higher MW PEGs (6000 and 8000) and get smaller as MW decreases to 600 (Fig. 4 A). Fig. 6 B is a log-log plot of α values in 20% PEG solutions (α_20%) as a function of MW. Interestingly, the slope obtained from fitting the experimental points is equal on a log-scale to 0.60 (±0.06). This exponent value is similar to the one appearing in the relation between polymer length (N) and its radius of gyration in self-avoiding polymers: 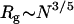. The data presented in Figs. 4 A and 6 B suggest that for TEM-BLIP association in semidilute PEG solutions 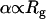. The fact that as 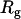of the polymer becomes larger the association rate becomes faster is explained in the discussion in terms of the depletion interaction, though the linear relation is unexpected.

Negative deviations again at high mass percentage—the concentrated regime

At mass concentrations >35% a dramatic slowdown in association rate constants is observed in solutions of PEG 200, 600, and 1000. We were not able to measure association in PEG solutions of higher MW (3350, 6000, and 8000) at mass concentrations >35% due to the high viscosities and the inefficient mixing in the stopped-flow apparatus. Interestingly, when scaling the mass concentration by c*, the crossover concentration defined above, we find that the slowdown in association rates at very high PEG concentrations follows roughly the same slope irrespective of the MW of the polymer (black lines, Fig. 4 B). Moreover, this slope is equal to that observed for the monomeric EG, suggesting that PEG polymers have the characteristics of monomers at these high concentrations.

DISCUSSION

In this study we aimed to provide a more complete description of protein-protein association behavior in polymer solutions, which may serve as a model to understand binding in the crowded environment in vivo. A remarkable outcome of the study is the importance of the thermodynamic properties of polymer solutions for the association reactions of proteins immersed in them, leading to the appearance of several different regimes in the behavior of the association rates. In the discussion, we will analyze the three observed association regimes, using current knowledge of polymer solution regimes (dilute, semidilute, and concentrated). Although this study was done on the interaction between two model proteins, TEM and BLIP, we suggest that the results are generally applicable.

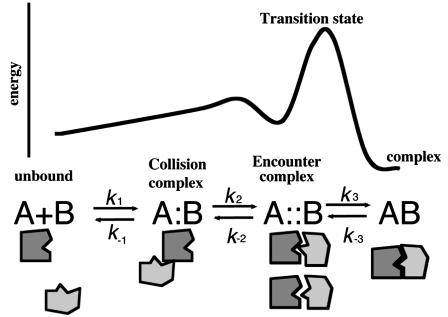
Protein complex formation can be viewed as a three-step process (Fig. 7). The initial step is a collision between two proteins in a solution. In the next step the collision must be followed by a search for the correct orientation to form an encounter complex, which after desolvation of the interface and exact structural rearrangement evolves into the final complex (31). In the absence of guiding electrostatic forces, the first step is driven solely by translational diffusion, which is directly affected by the solution viscosity and the size of the proteins (according to the Smoluchowski relation). The second step relates to rotational diffusion and to the time the two proteins spend near one another. The faster the rotation and the longer the lifetime of the collision complex, the higher its probability to evolve into an encounter complex and eventually into a final complex (31). Therefore, complementary electrostatic forces that stabilize the encounter complex increase the rate of association (27,32).

FIGURE 7.

Free energy diagram describing the pathway for protein-protein binding. Two proteins (A and B) in solution will collide with one another at a rate dictated by translational diffusion (forming a collision complex [A:B]). From here, rotational diffusion may lead the proteins to form an encounter complex [A∷B], which develops into the final complex [AB]. The theoretical collision rate is ∼10¹⁰ M⁻¹s⁻¹, whereas association, which is a combination of all processes, occurs at a rate of 10⁵ M⁻¹s⁻¹, thus on average only 1 out of 100,000 collisions is fruitful.

Similarly, if a polymer cage is formed around the two proteins, the ensuing depletion interaction will increase the probability to go from collision to encounter complex and to final complex. The main difference between the effect of electrostatic forces acting between the two proteins and the depletion effect is that electrostatic forces are directional and limited in distance and therefore act mainly on stabilizing the encounter complex, whereas depletion acts essentially uniformly along the reaction pathway past collision (or more accurately past the point where the distance between two protein molecules is smaller than the size of a polymer molecule). Therefore, depletion will similarly increase the transformation of the collision complex into the encounter complex and from encounter complex to complex. These two steps will be treated as one in the following discussion, with the first step being the collision step followed by binding (unifying k₂ and k₃ in Fig. 7). In this work we concentrate on the analysis of cosolvent effects on the steps in the association reaction leading from collision to complex formation.

The validity of our analysis in terms of the factor α (Eq. 4) relies on the assertion that k₁ is diffusion controlled (31,32) and that, therefore, α represents the variation in the above steps. The assumption that k₁ is diffusion controlled was experimentally verified by FCS measurements (Fig. 3), showing a simple linear relation between D_t and η, as predicted by the SE relation for diffusion-controlled reactions. The effect of solution viscosity will always enter at least through k₁, even if the ensuing steps are not sensitive to viscosity. An additional point of concern is whether the addition of cosolvents will not affect the electrostatic attraction between the two proteins and thereby the rate of association (31). The following three arguments lead us to think that this is not a major problem. First, the dielectric constants of 100% EG, PEG, and glycerol are ∼40, and therefore for solutions of up to 50% cosolvent the dielectric constant is >60. This is not much different from water (78.5). Second, we compared association in different PEG solutions, all of them having the same dielectric constant at similar mass percent. Third, in a previous work (21) we determined the relative k_on values for a set of electrostatically altered BLIP mutants binding TEM, ranging from protein complexes with hardly any electrostatic attraction to pairs with strong electrostatic attraction. The difference in k_on upon addition of cosolvent was shown to be independent on the electrostatic steering between the proteins, suggesting that α is independent of electrostatics (see Table 2 in Kozer and Schreiber (21)).

Repulsion in the dilute regime of PEG solutions

In the dilute regime of PEG 200, 600, 1000 (and possibly also 3350), as well as in all concentrations of EG, glycerol, and sucrose, we observe negative deviations from SE behavior (Figs. 4 A and 5), which indicate the presence of some sort of an effective repulsive force. The source of repulsion can be either weak polymer-protein attraction or a more general thermodynamic effect, namely the spatial arrangement of polymer molecules relative to the proteins. Any attraction, even weak, between EG or PEG and TEM or BLIP will translate into protein repulsion or ‘steric stabilization’ in high monomer concentration. Indeed, Minton had already discussed the issue of PEG-protein interaction in 1983 (33) and suggested that PEG interacts attractively at least with some proteins. However, the data presented in Fig. 5 suggest that in the case of the TEM-BLIP interaction there is no specific effect of EG relative to other solutes. The different monomeric crowding agents produce a similar effect on association (at least up to a mass percent of 30).

Weak binding between crowding agents and protein molecules also does not fit the inverse linear relation between D_t and viscosity, which matches the prediction of the SE relation (Fig. 3 and (14)). If crowding agents are adsorbed to the protein surface this should result in rates that are slower than SE diffusion rates, especially in the case of large polymers (34). In addition, if the repulsion between proteins is an outcome of PEG-protein interaction, it should increase with increasing concentration of PEG, slowing down the rate of association. Instead, at medium concentrations of PEG 600 and 1000 the rates of association are significantly faster than predicted by the Smoluchowski equation, as will be further discussed below.

Contrary to our observation of effective repulsion in low concentration solutions of medium-sized PEGs, measurements of the second virial coefficient (B₂) of lysozyme molecules in solutions of PEGs of MW 400 and 1000 showed effective attraction between the proteins (35). The discrepancy between the data presented by Kulkarni et al. and the data presented here might not be surprising if we realize the two experiments are fundamentally different in several respects. First, B₂ measurements are made under equilibrium conditions, whereas k_on is a kinetic parameter. It could be, for example, that the effective repulsion is in fact a nonequilibrium effect, e.g., due to lubrication forces (36). Second, the type of interaction between PEG molecules and the investigated proteins can also affect the measurements, as discussed above. It has been shown that EG and PEG molecules lead to preferential hydration of proteins (5,6). This preferential hydration is due to a solvophobic effect, i.e., to the inability of the solutes to form as many hydrogen bonds when close to the protein surface as opposed to the bulk. The stronger hydration of the proteins may affect association since it is more difficult to remove water molecules from the interface between the two proteins as they associate. It is possible that the strength of preferential hydration is different for lysozyme solutions versus TEM-BLIP solutions.

Attraction in the semidilute regime of PEG solutions

In the semidilute regime of all PEGs we observe positive deviations from SE behavior, which indicate the presence of an effective attractive force between TEM and BLIP. Attraction between colloids/proteins in nonadsorbing polymer solutions is long known from both experiments (3,35) and theoretical work (13,33,37) and is attributed to the depletion interaction. In the semidilute regime the polymer chains overlap and entangle, and protein molecules are embedded within the polymer mesh, with a depletion layer surrounding them. A depletion layer near a nonadsorbing colloid will exist if the colloid particle prefers the solvent to the dissolved polymer (7,34). One reason for such a situation to exist is that flexible polymer molecules experience an ‘entropic repulsion’ as their centers of mass approaches the colloid, a phenomenon first noted by Asakura and Oosawa in 1954 (37). The repulsion is a result of the reduced number of configurations available to the polymer near the colloid that would otherwise be accessible. The depletion layer thickness scales as R_g in the dilute regime and as the mesh size (ξ), which is a function of R_g, in the semidilute regime (10). The presence of a depletion layer around proteins can be regarded as if the effective radius of the proteins is larger or as if there exists an osmotic pressure gradient in the microenvironment around proteins, increasing the potential for protein interaction (9).

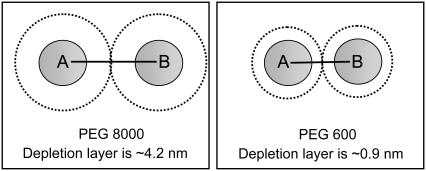
To understand how depletion layer thickness can account for faster association rates, consider the drawing in Fig. 8. When two protein particles get sufficiently close, their depletion zones overlap and the polymer molecules are excluded from the space between them. The resulting unbalanced osmotic pressure gives rise to an attractive interaction between the proteins, which depends upon the polymer size and concentration (9). In the presence of a thick depletion layer (PEG 8000), TEM and BLIP will already be caged together when the distance between their center of mass is ∼10 nm (2 × R_g). This is a large distance on a molecular scale. By the time two proteins are separated by this distance, they diffuse toward each other as in pure solvent; and because the polymer molecules essentially prevent them from translating away from each other (effectively caging them together), they will experience a longer residence time near each other, allowing for multiple collisions and rotations, making association more probable. This effect is enhanced by the tendency of the polymer cage around the two proteins to shrink to the minimum possible size, leading to a depletion force. In the presence of a thinner depletion layer (PEG 600) the two proteins must approach one another more closely before the depletion effect kicks in. Accordingly, if the depletion layer of the polymer is small compared to the size of the interacting molecules, no depletion interactions should be observed. The existence of a depletion layer may also contribute to the seemingly simple relation between k_on and the mass percent of the polymer, as observed in Fig. 2 C. Indeed, a slower translational diffusion is directly converted into a longer residence time of the collision complex, leading to faster conversion of the collision complex toward the final complex (as rotational diffusion rates are hardly affected, see Figs. 3 and 7).

FIGURE 8.

Schematic representation of the depletion layer formed by PEG 600 and PEG 8000. In the experiment we find that the slowdown of association rates in the semidilute regime is linear with R_g, which also dictates the depletion layer thickness.

We showed above that the magnitude of deviations from SE behavior is proportional to the R_g of PEG molecules in solutions of 15–22% PEG (Fig. 6 B). Can this observation be explained by the current theory of the depletion effect? In our previous publication (14) we used the following useful approximation to calculate the effect of a distance-dependent interaction potential on the association rate of two proteins (24):

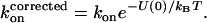(5)

In this equation, U(r) is the distance-dependent potential, evaluated at contact (r = 0). This Boltzmann-like approximation is correct for spherically symmetric interaction potentials and small interaction patches on the protein (24). The most relevant theory for the experimental conditions of our work is the PRISM theory of Schweizer and co-workers (13,38), which takes into account the polymeric nature of high concentration solutions and is also valid when 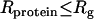. The depletion potential at contact is given in Schweizer's theory by

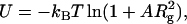(6)

where A is a coefficient that lumps together various molecular factors as well as the polymer concentration. The Boltzmann factor in Eq. 6, therefore, has a portion proportional to 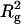, as opposed to the R_g dependence obtained from our data (Fig. 6 B). The Asakura-Oosawa theory of depletion (37) also will not give a linear dependence on R_g. Our result thus remains as a challenge for future theoretical work.

Repulsion in a concentrated regime of PEG solution

At mass concentrations of PEG above 35% we observe a dramatic decrease in k_on. This regime of polymer solutions is not characterized in our experiments as thoroughly as the dilute and semidilute due to our inability to obtain a full data set of TEM-BLIP association in very viscous PEG solutions. Yet, we wish to discuss it since the data are novel. A somewhat prosaic explanation for the slow k_on in concentrated PEG solutions is protein aggregation. As a matter of fact, PEG is known as the most potent agent to facilitate protein crystallization. Protein aggregation can result from a competition for water between PEG and proteins or the ‘salting out’ effect (8). When proteins aggregate, their effective concentration in the solution is smaller than assumed. Since TEM-BLIP association is a second-order event, lower protein concentration will result in slower association rates, as observed. However, plotting the k_obs of association under pseudo-first-order association conditions in 40% PEG 600 or 1000 shows a simple linear relation between protein concentration and k_on, with the extracted rate fitting those obtained under second-order conditions (data not shown). The linear relation suggests the absence of effects like aggregation that might change protein concentration. Second, as reported above, we found a linear dependence of D_t with viscosity up to a mass concentration of 60% in PEG 1000 solutions (Fig. 3). If indeed the protein had aggregated, we would expect to see a significant slowdown in translational diffusion with the increase in PEG concentration due to the increase in effective size. These arguments suggest that the explanation for the appearance of the third regime should be found in the physics of PEG solutions, rather than in protein aggregation.

In highly concentrated solutions, polymer chains overlap more and more, and the swelling of any chain (as in the dilute regime) is counteracted by the presence of other chains leading to a screening effect of the excluded volume interactions between monomers belonging to the same chain. When polymer chains are tightly packed, it is meaningless to describe them using parameters related to polymer length, and a better description of the solution is that of a sea of monomers with no long-distance correlation between them (10). As discussed in the introduction, the depletion interaction between two particles in concentrated solutions of polymers is not a monotonic function of their distance anymore, and it develops oscillatory behavior with an appearance of repulsive barriers at certain distances (16–18).

Physically, a repulsive barrier can arise from tight packing of monomers in the volume between two protein molecules in a manner that resists their removal during the association reaction. This can naturally lead to a strong decrease in k_on, which should in principle be MW independent. In our experiment we indeed observe a decrease in k_on in the concentrated regime, but there is some MW dependence, which can be removed if we plot the results on a c/c* scale, as done in Fig. 4 B. This figure suggests universal behavior of α in all polymer solutions (and monomeric EG) when plotted as a function of c/c*. For PEG concentrations below the concentrated regime α shows a monotonic upward relation, whereas for PEG concentrations in the concentrated regime (and for EG) a downward trend is observed with the same slope for all these cosolutes. This experimental result fits the view suggested above, that at the concentrated regime the polymers behave like monomers. Nevertheless, the repulsion seen in concentrated solutions is in fact different from the repulsion in low concentration PEG solutions, which we attributed to solvophobic preferential hydration. The depletion interaction becomes dominant over preferential hydration in the semidilute regime, and in concentrated solutions the repulsion must therefore be seen as a manifestation of depletion. We believe that this is the first time that the effect of repulsive depletion on protein interactions has been observed.

Possible biological relevance of our findings

Proteins and nucleic acid constitute at least 20–30% of the total mass (and volume) of all living organisms. Thus, the chemistry of life—as opposed to in vitro biochemical assays—always takes place within an extremely crowded medium, i.e., containing a substantial volume fraction of macromolecules. A synthetic linear polymer that forms network-like structures, such as PEG, mimics at least some qualitative properties of a eukaryotic cell, for example the cytoskeleton dynamic network of protein filaments or nucleic acids within the nucleus (25). Under certain pathological conditions (e.g., amyloid diseases) the appearance of fibrillar aggregates may further enhance crowding (26). Thus, the description of protein-protein association measured in the presence of synthetic crowding agents might be of biological relevance. Further, we may speculate that a transition from a moderate to a high crowding agent concentration can serve as a means to control protein association in vivo by altering the rate constant of the reaction. It is interesting to note that a particularly sharp transition in association rate constants was observed between the semidilute and concentrated regimes that occur at a mass percent of ∼30%, which is in the range of cellular crowding. Thus, the possibility exists that changes in crowding are related to cellular regulation and modulation of reactions and interactions within the cellular milieu. The work done here provides the biophysical basis for such phenomena.