Abstract
Two mouse strains, AKR/J and SAMP6, were assessed longitudinally for bone mineral density of the spine. They displayed very different time courses of bone accrual, with the SAMP6 strain reaching a plateau for vertebral BMD at 3 months, whereas AKR/J mice continued to increase spine BMD for at least 8 months. Among 253 F2 progeny of an AKR/J x SAMP6 cross, at 4 months of age the BMD variance was 5-6% of the mean, versus 15% for weight. Variance increased with age for every parameter measured, and was generally higher among males. The ratio of 6-month/4-month spine BMDs, termed ΔsBMD, had a normal distribution with 5.7% variance, and was largely independent of spine BMD (R=-0.23) or body weight (R=-0.12) at maturity. Heritability of the Δs BMD trait was calculated at 0.59. Genetic mapping identified two significant loci, both distinct from those observed for BMD at maturity - implying that different genes regulate skeletal growth vs. remodeling. A locus on the X chromosome, replicated in two mouse F2 populations (P<10-4 for combined discovery and confirmation), affects age-dependent BMD change for both spine and the full skeleton. Its position agrees with a very narrow region identified by association mapping for effects on lumbar bone density in postmenopausal women (Parsons et al., Hum Mol Genet 2005). A second locus, on chromosome 7, was observed in only one cross. Single-nucleotide polymorphisms (SNPs) are highly clustered near these loci, distinguishing the parental strains over only limited spans.
Keywords: chromosomal mapping, quantitative trait loci, bone mineral density, modeling and remodeling, mouse
Introduction
The best clinical predictor of osteoporosis is bone mineral density (BMD), known to have a large genetic component in mice and humans, with heritability of 60-80% [1-5], and a strong age dependence [6]. Many candidate genes, proposed on the basis of function to modulate bone metabolism and thus affect BMD, have been tested for allelic association to this trait. Although several were shown to exert genetic influence on BMD in some populations, the assessed candidate genes fail to account for the bulk of natural variation in BMD within any given population [1,6-8]. Whole-genome screens, by either linkage or association, offer the possibility of capturing the principal genes underlying genetic variation, based solely on relative influence on BMD rather than on preconceptions as to functional involvement. At present, however, full-genome association screens are not feasible at the marker densities and population sizes required.
Could the same genes as revealed by linkage studies in mice, also prove to contribute to trait variation in human populations? Although precedents exist for “trans-species polymorphism”, the evolutionary conservation of an allelic repertoire across diverse taxa [9-11], this is an area that has not previously been explored with respect to bone density. Our laboratory identified five significant quantitative trait loci (QTL) for vertebral bone density in mature mice [12], by interval mapping in F2 mouse populations generated from crosses between strains that share a common ancestor (the AKR/J strain), and consequently ∼60% of their genomes, but differ markedly in BMD.
We now report on interval mapping in mice for postmaturity change in spine BMD, a trait intended to emphasize bone remodeling over growth. Although most mouse strains continue to gain weight and to accrue bone mineral after maturity, in all mammals the adult phase of bone metabolism reflects primarily bone remadeling, the process of bone repair and maintenance. Genetic regulation of remodeling thus provides an experimental model of bone homeostasis in adults, the failure of which results in an age-dependent BMD decline which occurs at nearly constant rates in men following maturity and in women after menopause [3,5,13]. As detailed below, we discovered two loci that exert significant effects on this trait in adult mice; of these, one on the X chromosome was reproduced in two independent crosses. Remarkably, the latter region corresponds closely to a polymorphic locus significantly associated with vertebral BMD in postmenopausal women [14]. Further studies will be required, to determine whether other bone-related QTLs, defined in the mouse, can readily be translated to humans in advance of gene identification.
Materials and methods
Mouse strains
Information on the mouse strains AKR/J and SAMP6 and inter-strain crosses can be found in Methods of reference [12]. The SAMP6 strain was originally obtained from Dr. Toshio Takeda of Kyoto University in Kyoto, Japan [15,16]; the AKR/J strain was acquired from the Jackson Laboratory, Bar Harbor ME.
Mouse bone densitometry
Bone densitometry was performed by dual-energy X-ray absorptiometry (DEXA) on a QDR-2000+ instrument (Hologic, Inc., Bedford, MA, U.S.A), modified for use on mice following the procedures in Jilka et al. [17]; see also reference [12]. Mice, tagged with implanted transponders (Biomedic Data Systems), were immobilized under mild anesthesia, and spinal BMDs were scanned from just below the skull to the base of the tail. Scans were repeated at intervals of 1-2 months for longitudinal analysis.
Genetic mapping
Two interstrain crosses were initiated by reciprocal mating between strains AKR/J and SAMP6, randomly interbreeding F1 hybrid progeny to generate F2 mice for trait analysis and chromosomal mapping. In the first study, 253 mice were ordered by vertebral BMD at 4 months of age, and only the high and low quartiles (a total of 117 mice) were genotyped by analysis of DNA from tail snips; all were re-assessed for BMD at 6 months of age. For the second cross, 110 mice for which acceptable BMD scans were obtained at both 4 and 6 months of age (i.e., excluding a few mice for which either scan was obscured by a transponder overlying the spine) were genotyped and utilized for polygene interval mapping of postmaturity change in spine BMD. In each population, male and female mice were represented approximately equally. Genotyping utilized short-tandem-repeat markers (Research Genetics, Huntsville AL), shown to differentiate between these strains [12], at a mean initial spacing of ∼7 cM. Markers that produced >10% indeterminate genotypes, or >2-fold expansion of the genetic map distance to adjacent markers, were excluded from analysis.
Genotyping and linkage analysis were performed using procedures described in Benes et al. [12], with the trait “postmaturity change in spine BMD” taken as the ratio of 6-month to 4-month BMD in each mouse. Mapping by Windows QTL Cartographer [18] (NCSU, version 2.5) employed Composite Interval Mapping [19] with a window of 10 cM and a step size of 2 cM. Addition of body weight and/or mouse gender as background variables had negligible effect on the outcome. Significance levels (false-positive thresholds) were determined from 1000 permutations of phenotype with respect to genotype, using the same data-set [20].
Comparison of parental mouse strains by typing of single nucleotide polymorphisms
SNP analysis was performed using MALDI-TOF mass spectrometry of polymerase-chain-reaction products amplified using primers flanking each of 15,000 putative polymorphisms (Illumina BeadArray™, San Diego CA). Details of procedures used are available at http://zeon.well.ox.ac.uk/rmott-bin/strains.cgi and http://www.illumina.com/products/prod_snp.ilmn.
Results
Defining a new mouse trait for postmaturity change in spine BMD
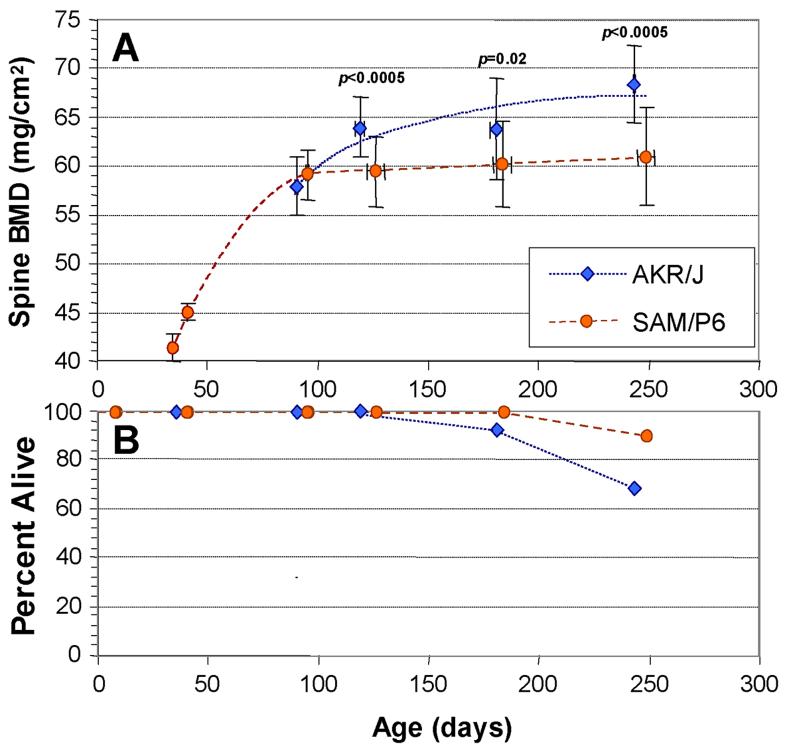
Previous studies of bone QTL in the mouse [8,21-24], including our own [12], have focused on parameters assessed at maturity (usually taken as 3-4 months of age), by which time skeletal growth is essentially compete in most strains of mice. The time course for accrual of spinal bone density is illustrated in Figure 1, panel A, for strains SAMP6 and AKR/J. The SAMP6 strain reaches a plateau or “peak” bone density by approximately 3 months of age, whereas AKR/J continues to add bone mass between 3 and 8 months. The data shown here are for both genders combined, but very similar patterns were seen for males and females separately. Even beyond the age of 8 months, AKR mice continue to increase in spinal BMD, while SAMP6 mice appear to decline (data not shown), but we cannot rule out effects of selective attrition, since both strains undergo significant mortality associated with thymic lymphoma (AKR) and “premature senescence” (SAMP6), as indicated in Figure 1B.
Figure 1.
Age-dependence of spinal BMD in the AKR/J and SAMP6 mouse strains. Bone mineral density (BMD) was determined for the spines of individual, transponder identified mice of each strain at the ages indicated (A). Mice were excluded if there was superposition of transponders with the spinal column; the remaining assay cohorts comprised 24 AKR mice and 23 SAMP6 mice. Error bars show standard deviations (SDs) for both age (x-axis) and spine BMD (y-axis). Significances are given for 2-tailed t-tests (Fisher-Behrens test for samples of unknown or unequal variance), comparing spine BMDs of strains at 4, 6 and 8 months. Survivals of the two cohorts are shown in the lower panel (B); at 8 months of age, 16 AKR and 21 SAMP6 mice remained.
Peak vertebral bone densities differ markedly between these strains; the difference in the cohort shown was 10 - 16%, somewhat below the 19% we observed previously [12]. This is in part attributable to the slightly greater mean age of the SAMP6 mice, 2 - 7 days older than the AKR mice at each DEXA scan, but may also be affected by the greater weight of SAMP6 mice (Table 1). At 3 months of age, SAMP6 males were 24% heavier than AKR males, although the difference declined to 16% by 6 months. SAMP6 females began the study 32% heavier than their AKR counterparts, declining to a 21% advantage at 6 months. This impressive difference is consistent with the deficit noted in osteogenesis [17], and the commensurate increase in adipogenesis [25], of SAMP6 mice. In contrast, spine area at each age was virtually identical in mature males of the two strains (<1% difference at 4, 6 or 8 months), and differed by <4% in females at 4 and 6 months (Table 1), even as the vertebral densities of these strains diverged (Figure 1). These data also support the contention that growth of the spine was essentially complete by 3 - 4 months, although weight-bearing parts of the skeleton did continue to increase in both size and density, with the heavier P6 cohort showing greater increases in hindlimb BMD (data not shown).
Table 1.
Other Age-Dependent Traits of Parental Mouse Strains SAMP6 and AKR/J. Significance levels are based on a stringent two-tailed Fisher-Behrens t-test (for samples of unequal or unknown variance), comparing AKR/J to SAMP6 values.
| Males | Total Weight (g) ± SD | Spine Area (cm2) ± SD | Global Bone Area (cm2) ± SD | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Age (mo) | AKR/J | SAMP6 | P< | AKR/J | SAMP6 | P< | AKR/J | SAMP6 | P< |
| 3.0 - 3.2 | 29.0±2.0 | 36.0±2.6 | 10-3 | 5.19±0.12 | 5.47±0.15 | 10-3 | 9.11±0.53 | 10.4±0.57 | 10-3 |
| 4.0 - 4.4 | 30.7±3.1 | 36.3±10 | 0.05 | 5.41±0.11 | 5.45±0.25 | NS | 9.50±0.69 | 10.5±1.1 | 10-2 |
| 6.0-6.1 | 33.7±4.1 | 39.0±6.4 | 0.02 | 5.56±0.13 | 5.54±0.32 | NS | 10.1±0.76 | 11.2±1.5 | 0.03 |
| 8.2-8.4 | 35.4±5.2 | 39.0±4.3 | 0.07 | 5.57±0.29 | 5.54±0.17 | NS | 10.4±1.19 | 11.2±1.1 | 0.10 |
| Females | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Age (mo) | AKR/J | SAMP6 | P< | AKR/J | SAMP6 | P< | AKR/J | SAMP6 | P< |
| 3.1-3.2 | 25.3±1.2 | 33.5±1.7 | 10-3 | 5.01±0.15 | 5.19±0.12 | NS | 8.02±0.47 | 10.4±0.58 | 10-3 |
| 119-129 | 29.0±2.2 | 37.2±11 | 0.05 | 5.39±0.16 | 5.41±0.11 | NS | 9.33±0.72 | 11.3±0.60 | 10-3 |
| 179-192 | 32.5±3.1 | 39.2±2.0 | 10-3 | 5.46±0.13 | 5.56±0.13 | NS | 9.57±0.66 | 11.9±0.37 | 10-3 |
| 241-251 | 29.0±7.0 | 42.3±3.6 | 10-3 | 5.14±0.77 | 5.57±0.29 | NS | 8.66±2.36 | 12.4±0.87 | 10-3 |
In selecting a parameter that reflects primarily post-maturity remodeling of the spine, the 3-month measurements were avoided to minimize the inclusion of skeletal development or “modeling”, whereas 8-month scans extend into a period of significant and differential mortality, and thus risk introducing a systematic bias for any traits associated with survival. We thus chose to examine the ratio of 6-month to 4-month densities of the spinal column, a trait herein termed “postmaturity change in spine BMD” or Δs BMD. This trait is internally controlled for individual variation in mature bone density; analyses were essentially unaltered by inclusion of body weight or mouse gender as background variables, indicating that they exert relatively little influence.
Characteristics of F2 progeny from a SAMP6 by AKR/J cross
Two reciprocal crosses were set up between mouse strains AKR/J and SAMP6, pairing males of each strain individually with females of the other strain. The F1 (hybrid) progeny of each cross “direction” were randomly interbred, and their resulting progeny (F2 mice, 253 and 110 per cross) were scanned for vertebral and global BMD at 4, 6 and 8 months of age.
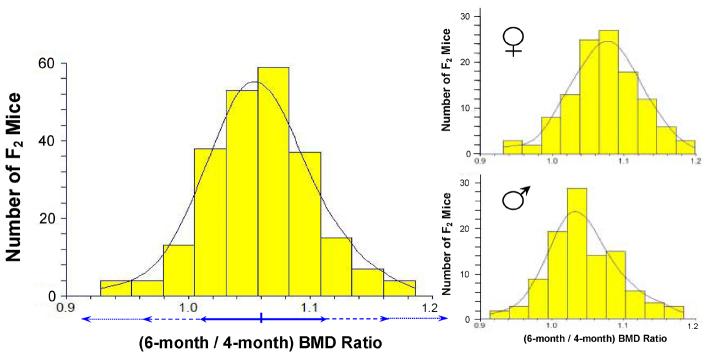
Among the F2 progeny of each cross, Δs BMD approximated a Gaussian (normal) distribution (Figure 2) with a mean ratio of 1.06 and a standard deviation of 0.06. Very few of the F2 mice declined in bone density between 4 and 6 months of age, whereas over half increased by at least one standard deviation. This outcome is consistent with expectation, for progeny segregating multiple loci that govern a quantitative trait, given that one of the parental strains slowly increased, while the other showed essentially no change, in spine BMD after 3 months of age.
Figure 2.
Distribution of individual F2 mouse ratios of spine BMDs measured at 6 and 4 months of age (each ± 7 days). F2 progeny from an AKR/J × SAMP6 cross (Cross 1, 253 mice) were scanned by DEXA. Ratios of spinal-region values for individual mice, 6-month divided by 4-month BMDs (ΔsBMD), are plotted as a histogram over the best-fit Gaussian distribution for these data. Horizontal double arrows below the histogram indicate intervals spanning ± 1, 2 or 3 standard deviations from the mean, corresponding ∼70%, 96% and 99% confidence intervals. Nearly identical results were obtained for Cross 2. Smaller panels indicate distributions separated by gender.
Much can be learned from an examination of trait distributions and inter-trait correlations within such genetically heterogeneous populations. Table 2 summarizes such trait values and correlations for the first and larger cross presented herein, comprising 253 mice. The normalized population variance, indicated by the Coefficient of Variation (CoV, mean/SD), was 2- to 3-fold higher for body weight (15.0 - 16.4%) than for BMD of the skeleton (5.1-6.4%) or of the spine (6.3 -7.7%) at all three ages tested (Table 2A). These CoV levels all increased systematically with age, and were generally higher in males than females. The CoV for Δs BMD was 5.7%, slightly below that for 4-month BMD. These levels of variation were substantially greater than would be attributable to measurement error: the CoV for technical replicates was ∼2% [12, 17], or 2.8% for the ratio of two measurements.
Table 2.
Properties of adult F2 progeny from a SAMP/6 x AKR/J interstrain cross. A total of 253 mice (131 females and 122 males) were weighed and scanned by DEXA for global and spinal BMD at 4, 6 and 8 months of age (as indicated). “Ratio 6/4” and “Sp6/4”: ratio of BMD at 6-months to BMD at 4 months. A, Body weight (wt) and BMD measures, as mean ± SD (standard deviation); B, Pearson correlation coefficients, R. Sp, spine BMD; Glo, global BMD; CoV, coefficient of variation (mean/SD).
| A | Weight-4 | GloBMD-4 | SpineBMD-4 | Weight-6 | GloBMD-6 | SpineBMD-6 | Weight-8 | GlobBMD-8 | SpineBMD-8 | Spine BMD | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (g) | (mg/cm2) | (mg/cm2) | (g) | (mg/cm2) | (mg/cm2) | (g) | (mg/cm2) | (mg/cm2) | Ratio 6/4 | |||||||||||
| All Mice (mean±SD) | 38.0 | ±5.7 | 59.2 | ±3.0 | 68.0 | ±4.3 | 43.6 | ±6.8 | 61.9 | ±3.7 | 72.2 | ±5.5 | 45.7 | ±7.5 | 62.4 | ±4.0 | 73.0 | ±5.6 | 1.06 | ±0.06 |
| CoV (%) | 15.0 | 5.1 | 6.3 | 15.6 | 6.0 | 7.6 | 16.4 | 6.4 | 7.7 | 5.7 | ||||||||||
| Females (mean±SD) | 37.0 | ±5.8 | 59.2 | ±2.9 | 68.5 | ±4.0 | 43.2 | ±6.8 | 62.4 | ±3.8 | 73.1 | ±5.2 | 45.1 | ±7.6 | 62.8 | ±4.3 | 74.0 | ±5.9 | 1.07 | ±0.06 |
| CoV (%) | 15.7 | 4.9 | 5.8 | 15.7 | 6.1 | 7.1 | 16.9 | 6.8 | 8.0 | 5.6 | ||||||||||
| Males (mean±SD) | 39.1 | ±5.4 | 59.2 | ±3.1 | 67.5 | ±4.5 | 44.0 | ±6.8 | 61.5 | ±3.7 | 71.3 | ±5.6 | 46.2 | ±7.4 | 61.9 | ±3.7 | 72.1 | ±5.2 | 1.05 | ±0.07 |
| CoV (%) | 13.8 | 5.2 | 6.7 | 15.5 | 6.0 | 7.9 | 16.0 | 6.0 | 7.2 | 6.5 | ||||||||||
| BR values | Sp4:Sp6 | Sp4:Sp6/4 | Wt4:Sp6/4 | Wt6:Sp6/4 | Sp4:Sp8 | Glo4:Glo6 | Glo4:Glo8 | Sp4:Glo4 | Sp6:Glo6 | Sp8:Glo8 |
|---|---|---|---|---|---|---|---|---|---|---|
| All Mice (mean±SD) | 0.646 d | -0.231 b | -0.117 | 0.226 b | 0.619 d | 0.693 d | 0.607 d | 0.917 d | 0.919 d | 0.912 d |
| Females (mean±SD) | 0.673 d | -0.223 b | 0.046 | 0.298 c | 0.670 d | 0.670 d | 0.604 d | 0.921 d | 0.946 d | 0.951 d |
| Males (mean±SD) | 0.617 d | -0.259 b | -0.251 b | 0.176 a | 0.562 d | 0.734 d | 0.626 d | 0.925 d | 0.892 d | 0.863 d |
Significance of Pearson (linear) correlations:
P≤0.05;
P≤0.01;
P≤0.001;
P≤10-8
Correlation coefficients between 4-month and 6-month spinal BMD readings ranged from 0.62 to 0.67 (Table 2B) whereas their ratio, Δs BMD, was much less strongly correlated with 4-month BMD (R = -0.22 to -0.26). Thus, mice at either extreme of the mature-BMD range were not substantially more likely than other mice to subsequently increase or decrease in BMD. Nearly identical trends were observed for global BMD as for spine, and correlations between spinal and global BMD were consistently quite high (0.86 - 0.95; Table 2A), indicating that most genetic and environmental sources of variation in this population are not site-specific but instead exert similar effects on diverse types of bone.
Heritability of postmaturity change in spine BMD
The heritability of a trait is a measure of the increased variance of the genetically segregating F2 generation, relative to the parental strains. Broad-sense heritability (H2) for a trait is defined as (VF2 - VP)/VF2, where VF2 is the variance of the F2 generation and VP is the mean variance of the parental strains. Considering only the females in each group, because of skewness in the male distributions, H2 is calculated to be 0.59, quite close to the heritability of 0.58 estimated for 4-month BMD in the same interstrain cross [12].
Such high heritability of a trait, reflecting random segregation of the underlying gene alleles that differ between the parental strains, indicates that the F2 progeny should be informative for genetic mapping studies.
Genetic mapping of mouse QTLs for postmaturity change in spine BMD
DNAs were obtained from fresh tail clippings of all F2 mice, and analyzed for a genomic panel of short-tandem-repeat markers at an average spacing of 7.5 cM, as described previously [12]. The resulting data were analyzed by Composite Interval Mapping [19], using Windows QTL Cartographer [18] v.2.5, for the trait of 6-month spine BMD divided by 4-month BMD in each mouse. It should be noted that the genomes of the parental strains differ at only ∼ 40% of the genome, distributed in segments on all except one pair of chromosomes. The quest for QTLs is thus narrowed to these “informative regions” of the genome, and the threshold for LOD (Logarithm of Odds) significance is accordingly reduced to 2.5 - 3.2 (see reference [12] for details).
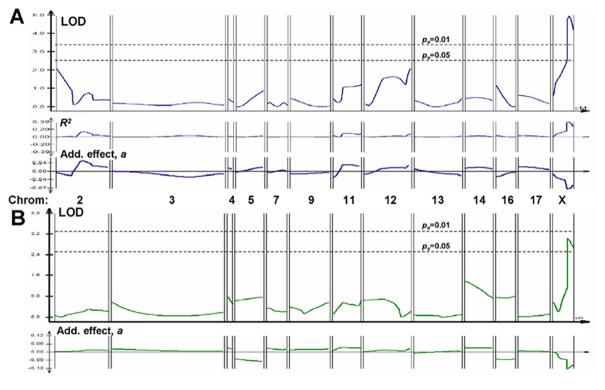
The first cross revealed only one significant QTL peak (LODmax >4.9, P<<0.01) (Figure 3A), on the X chromosome, accounting for 34% of trait variance (R2, middle panel of 3A) and reducing the Δs BMD ratio by 7% per AKR allele (additive effect a, lower panel of 3A). Very similar results were obtained for global BMD assessed for the full skeleton below the skull, but with a somewhat larger additive effect (12% per AKR allele), and genomewide significance between 0.05 and 0.01 (Figure 3B). These peaks were quite distinct from those observed for spine (or total) BMD at maturity (Figure 3C), as reported previously [12]. In each analysis, the significance threshold of pe<0.05 (or pe <0.01) is a peak LOD score that was attained or exceeded by chance, anywhere in the genome, in less than 50 (or 10) out of 1000 random permutations of genotype with respect to phenotype for this data-set [20].
Figure 3.
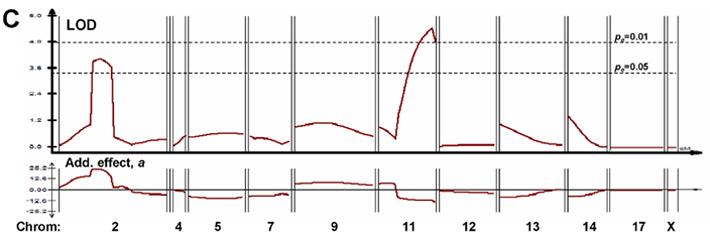
Composite interval mapping for three traits in AKR/J × SAMP6 Cross #1. (A) Mapping of postmaturity change in spine BMD (ΔsBMD) of F2 cross-progeny mice. Individual mice, identified by implanted transponders, were scanned for by DEXA at ages of 4 and 6 months. The ratio of 6-month divided by 4-month spinal BMD values was input as the trait for Composite Interval Mapping, using a window size of 10 with 3 background variables ranked by stepwise multivariate regression. Not all chromosomes are shown, due to the lack of informative markers on chromosome 15 (AKR/J = SAMP6 for all STR markers tested), and robust genotyping for only one marker each in the informative regions on chromosomes 1, 6, 8, 10, 18 and 19. None of these markers was significantly linked to ΔsBMD by simple linear regression. R2(where R is the correlation coefficient between marker allele and the trait) is plotted just below the ΔsBMD LOD scans, indicating the “fraction of variance explained” by a QTL posited at that position. (B) Mapping of postmaturity change in total skeletal BMD, excluding the skull, of F2 cross-progeny mice. This trait was analyzed exactly as described for “A” above, substituting total BMD for spinal BMD. (C) Mapping of spine BMD for F2 cross-progeny mice at 4 months of age. All panels:LOD scores, indicating likelihood of QTL location, are plotted by QTL Cartographer, v. 2.5, across the genetic map of each chromosome determined from data of this cross by Mapmaker QTL™. Horizontal dashed lines indicate empirical genome-wide significance thresholds [20] at pe=0.05 and pe=0.01, determined from 1000 permutations of phenotype against genotype. Additive effect, a, defined by multivariate regression as the average trait effect per AKR/J allele, is displayed below each QTL LOD-plot. All plots were generated by QTL Cartographer.
A second, smaller AKR/JxSAMP6 cross was constructed for the sole purpose of replicating the initial experiment. A total of 110 F2 progeny were anayzed for the Δs BMD trait (Figure 4). The most prominent QTL peak in this cross appeared on chromosome 7, with LODmax of 11.8 (pe<<0.01). This peak was not well-behaved, however, in that its magnitude was very sensitive to the analytical parameters, and it had the curious property of explaining virtually none of the population variance (R2) despite an extraordinarily large additive effect (a=+0.58) (Figure 4, lower panels). A second Δs BMD peak mapped very close to the previous position on the X chromosome, with a peak LOD of 5.8 (genomewide significance, pe<0.05), and values for variance explained (R2=0.39) and additive effect size (a=-0.06) almost identical to those observed in the first cross. It should be noted that the LOD threshold levels determined by permutation were higher in this cross (LOD 5.5 for pe < 0.05) than obtained in the first cross, perhaps as a consequence of the smaller number of animals considered. The same two peaks were obtained with males excluded, although with lower LOD values and reduced empirical significance, as expected from the reduced numbers; in addition, a new peak appeared on chromosome 3 (data not shown).
Figure 4.
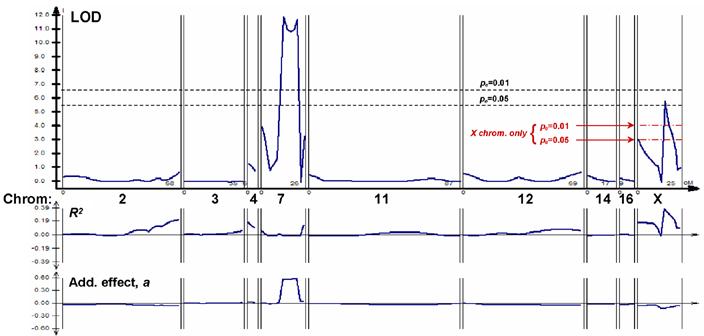
Composite interval mapping for postmaturity change in spine BMD (ΔsBMD) in AKR/J × SAMP6 Cross #2. Details are as given in the legend to Figure 3. Additional threshold lines are shown for the X-chromosome plot only; these were generated by 1000 permutations considering only the map of this chromosome, although utilizing the 3 top-ranking background variables (from other chromosomal locations) in the regression.
The empirical false-positive threshold required for detection of a comparable QTL anywhere on the X chromosome occurred at LOD 1.9 for pe < 0.05, and LOD 3.0 for pe < 0.01 (threshold lines marked only for the X chromosome in Figure 4). This reflects the reduced false-positive likelihood for replication of a QTL, when limiting the investigation to a single chromosome (or subregion of a chromosome). In that context, the QTL peak observed on the X-chromosome in the second cross was highly significant (pe <<0.01). Taken together, the results from two independent crosses imply a chance likelihood of pe <<10-4 for finding a comparable QTL anywhere in the genome and confirming it on the same chromosome.
Mapping of single-nucleotide polymorphisms (SNPs) between parental mouse strains
Through participation in a SNP typing project supported by the Complex Trait Consortium and the Wellcome Trust Centre for Human Genetics (Oxford, U.K.), we have determined the SNP genotypes for the SAMP6 strain and compared it to its parental strain, AKR/J. The complete data for 13,377 SNPs, ascertained in 477 strains and sublines, are accessible at http://zeon.well.ox.ac.uk/rmott-bin/strains.cgi, and haplotype block structures for recombinant inbred line sets are presented at http://www.well.ox.ac.uk/mouse/INBREDS/RIL/.
The SNPs and STRs differentiating between strains SAMP6 and AKR/J on the X chromosome are depicted graphically in Figure 5. It is noteworthy that no differences between AKR/J and SAMP6 genotypes were seen among 72 SNPs tested in the first 51.5 Mb of the X chromosome. Additional regions on X, totally devoid of informative SNPs, include four segments of 14 to 16 Mbp in length, located at 65-79 Mbp (43 SNPs), 105.3-121.0 Mbp (58 SNPs), 131.2-144.9 Mbp (26 SNPs), and 147-163 Mbp (43 SNPs). Similarly uninformative regions were found on chromosome 7 (data not shown), including a 19-Mbp segment from 78 - 97 Mbp, containing 110 synonymous SNPs, and several smaller regions: 13.9-21.8 Mbp (32 SNPs), 30.3-34.5 Mbp (25 SNPs), 67.3-74 Mbp (28 SNPs), 111-117 Mbp (42 SNPs), and 135-140 Mbp (26 SNPs). Because the overall fraction of informative SNPs is 24.7% (161/653) on chromosome 7, and 13.2% (53/403) on X, these long expanses of synonymous SNPs are extremely unlikely to have arisen by chance (P values from <0.025 to <10-9, based on the binomial distribution).
Figure 5.
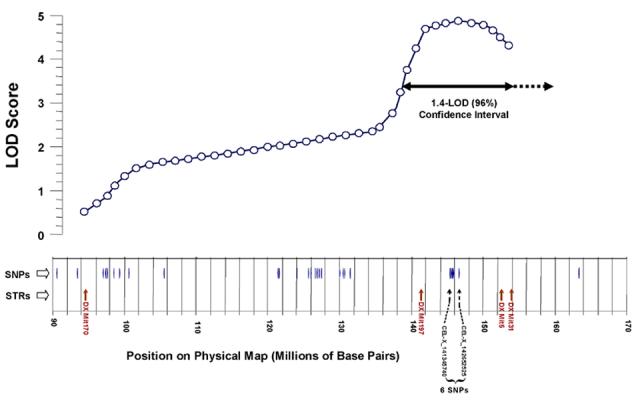
Distribution of single-nucleotide polymorphisms, distinguishing between mouse strains AKR/J and SAMP6, near the X-chromosome QTL peak. Informative SNPs are positioned with reference to the physical map of the murine X chromosome (NCBI Build 34.1), as are short-tandem-repeat (STR) polymorphisms used in interval mapping. The results of composite interval mapping in Cross 1 are depicted above these lines; selected functional-candidate genes are indicated for reference. The x-axis has been distorted slightly in aligning genetic and physical maps. A two-headed horizontal arrow below the curve marks the ∼96% confidence interval for QTL position.
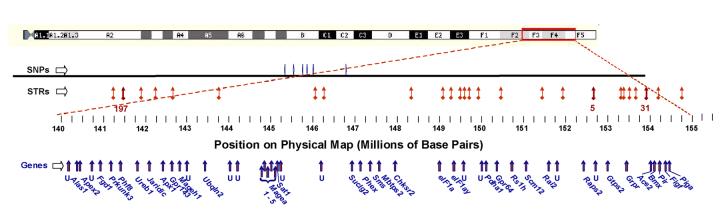
In Figure 6, the region on the X chromosome from 140 - 155 Mbp is expanded to show the 6 SNPs near the center (145.0 - 146.3 Mbp), all short tandem-repeat (STR) polymorphisms mapped to this region, and the genes identified to date. Our results for STR markers are consistent with the SNP findings: no length variation was seen among 7 consecutive STR markers positioned to the centromeric (“left”) side of DXMit170 (15 - 91 Mbp), or in 10 consecutive STR markers assayed which are distal to (to the “right” of) DXMit31 (154 - 170 Mbp in Figure 5).
Figure 6.
Genes in the polymorphic region of the X-chromosome QTL peak. The 96% confidence interval indicated in Figure 5, is shown here expanded. SNPs and STRs are indicated as in the preceding figures; three of the STRs used for mapping (DXMit197, DXMit5 and DXMit31) are indicated by arrows ( ) with numbers beneath. Approximate locations (5′ ends) of all identified gene are marked by thick arrows in the bottom row. Unknown genes are indicated as “U”; not all are shown due to space limitations.
) with numbers beneath. Approximate locations (5′ ends) of all identified gene are marked by thick arrows in the bottom row. Unknown genes are indicated as “U”; not all are shown due to space limitations.
Discussion
The benefit of QTL mapping over other approaches to finding genetic factors that contribute to bone mineral density, is that it offers an unbiased screening for all genes that differ in allelic fashion between the parental strains, provided that they exert sufficiently large effects to be detected with the numbers of cross progeny assessed [26,27]. In contrast, association studies that begin with prior identification of functional candidate genes, are thereby limited to “discovering” only determinants that were already known or suspected. At later ages, humans of either gender undergo a roughly linear decline in bone mineral density, with similar slopes in males and postmenopausal females [3,5,13]. Genetic factors contributing to differences within a species, in the ability to maintain bone homeostasis via “remodeling”, had not previously been investigated in mouse models.
In two interstrain crosses between the SAMP6 and AKR/J mouse strains, we assessed a number of parameters thought to be relevant to bone homeostasis, measuring each at two-month intervals beginning at maturity in the F2 populations. Among these, the change in bone density between 4 and 6 months of age appeared largely independent of mature BMD or weight, and showed a broad-sense heritability of almost 60%. We then sought genetic loci that contribute to this trait, post-maturity change in vertebral BMD. By multivariate mapping procedures, these can be enumerated, approximately positioned on the chromosomes, and characterized as to their individual effects on the trait in question. A highly significant locus on the X chromosome was mapped with quite similar location and properties in two crosses. The two alleles at this locus exert effects on time-dependent change in BMD that are opposite to the difference observed between the parental strains. As has been frequently noted, however, countervailing-effect QTLs will be quite common in any strains that have not undergone stringent selection for extreme trait values [12, 27].
The issue of reproducibility is critical to the field of QTL mapping. False-positive and false-negative thresholds based on a single F2 cohort, whether determined by computer simulation or by permutation, tend to overestimate reproducibility [28-32], at least in part because they fail to account for environmental and biological variation in the process of generating cohorts. We therefore considered the ability to reproduce a QTL for the Δs BMD trait, for two different bone sites (the spine and total skeleton) and in two independently generated F2 populations, to be of greater value than achieving higher numbers, and higher power, in any single experiment. The locus on the X chromosome thus fulfilled our criterion of reproducibility, with a combined probability of detecting a QTL twice on the same chromosome at the observed peak LOD values, purely by chance, of <10-4. Of course, the observed replication was considerably better than that, mapping the QTL peak to within a few cM in the two experiments, but there has been little discussion, and no consensus, on standards for calculating “coincidence” of QTL location [26].
A second, nominally significant QTL on chromosome 7 was observed in only the smaller cross. This locus exhibited some internal inconsistencies, as noted in Results, above, which led us to be skeptical of its validity. However, because the potential for missing a true QTL (i.e., of false-negative outcomes) is substantial for such relatively low-power studies [28,29], we cannot be certain that this QTL is artefactual; it remains to be confirmed in subsequent investigations.
The two strains crossed are identical for all polymorphic markers assessed, over ∼60% of their genomes [12]; thus, the mapped regions comprise only the “informative” 40%. This lowers the thresholds for significance, by reducing the size of the genome evaluated for QTLs [30], and also constrains QTL intervals insofar as we can position the boundaries between dimorphic and synonymous regions. The boundary to the “right” of the X-chromosome QTL in Figures 3 and 5 (distal to the telomeric centromere, at the left of each diagram), was defined through the analysis of single-nucleotide polymorphisms (SNPs) and short tandem repeat (STR) markers that distinguish these strains. As noted in Results, out of 17 STR markers assessed to either side of the interval mapped in Figure 5, none differ between the SAMP6 and AKR/J parental strains. Moreover, there were remarkably few SNPs distinguishing the two parental strains outside this region - none at all in the first 51.5 million base pairs and only one between marker DXMit31 and the right end of the X chromosome (Figure 5). Taken together, these results argue that a gene responsible for the Δs BMD QTL is unlikely to reside beyond the region spanned by our STR genotyping markers, since observation of a QTL both implies and requires that an underlying gene must differ between the two parental strains.
This is an example of the use of fine-mapping information to reduce an interval implicated by QTL analysis by precisely defining the boundary between two haplotype blocks. In this case, the blocks are of relatively recent conjunction, since the SAM strains arose from an unintended outcross of the AKR/J parental strain in 1971 [15,16]. Substantially greater narrowing of the differential region might be achievable, based on the clustered distribution of SNPs which differentiate between the parental strains - reflecting haplotype blocks which presumably arose from far more ancient events in the parental-strain ancestry. In view of the stochastic nature of SNP occurrence, and the relatively small sample of SNPs that were typed (well below 1% of the 2-3 million SNPs expected to differentiate, on average, between two standard laboratory mouse strains), it would not be advisable to exclude entire regions that appear SNP-deficient. As the SNP map becomes more complete, that situation will certainly change. Even at the present time, however, it would be reasonable to begin a search for positional candidate genes underlying any given QTL, in the regions of known polymorphism rather than in areas that are largely sequence-identical between parental strains. The latter regions are not necessarily bereft of all polymorphism, since short-tandem-repeat (STR) arrays are well represented there (see  symbols in Figure 6) and these generate new variants with high frequency [28,29]. Nevertheless, we found remarkably little polymorphism among such STR markers in regions of the SAMP6 genome of apparent AKR/J origin.
symbols in Figure 6) and these generate new variants with high frequency [28,29]. Nevertheless, we found remarkably little polymorphism among such STR markers in regions of the SAMP6 genome of apparent AKR/J origin.
In a related study, reported recently [14], we pursued the human X chromosome region corresponding to the interval expanded in Figure 6, by SNP association to BMD of the lumbar vertebrae. Using a population of 3224 postmenopausal women in the Aberdeen area, an association peak was observed within the X-chromosome interval implicated in the present study. Two adjacent SNPs near the right end of human region corresponding to the 96% confidence interval for the mouse Δs BMD QTL on X (Figures 5 and 6) showed significant association to BMD of lumbar vertebrae (each P<0.005), but not of the femur. These SNPs, together, comprise a haplotype which is also associated to lumbar BMD, with p<0.002. Our evidence thus supports the premise that post-maturity change in bone mass in the mouse is relevant to senescent osteopenia in humans; at the very least, it demonstrates that QTL mapping can translate directly to human population studies, thus allowing relevance to humans to be evaluated without extensive fine mapping or gene identification in the mouse. Proof of causation then requires return to an animal model in which ostegenesis can be experimentally perturbed; we are currently using transgenic mice and genetically manipulated murine bone cells for functional assessment of candidate genes in this interval.
Acknowledgments
We thank Randall S. Shelton and Timothy McClure for expert technical assistance. This work was supported by a grant from the National Institutes of Health (P01-AG13918), and by a Research Career Scientist Award to RJSR from the U.S. Dept. of Veterans Affairs.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Nguyen TV, Blangero J, Eisman JA. Genetic epidemiological approaches to the search for osteoporosis genes. J Bone Miner Res. 2000;15:392–401. doi: 10.1359/jbmr.2000.15.3.392. [DOI] [PubMed] [Google Scholar]
- [2].Hopper JL, Green RM, Nowson CA, Young D, Sherwin AJ, Kaymakci B, Larkins RG, Wark JD. Genetic, common environment, and individual specific components of variance for bone mineral density in 10-to 26-year-old females: A twin study. Am J Epidemiol. 1998;147:17–29. doi: 10.1093/oxfordjournals.aje.a009361. [DOI] [PubMed] [Google Scholar]
- [3].Hansen MA, Hassager C, Jensen SB, Christiansen C. Is heritability a risk factor for post-menopausal osteoporosis. J Bone Miner Res. 1992;7:1037–1043. doi: 10.1002/jbmr.5650070906. [DOI] [PubMed] [Google Scholar]
- [4].Gueguen R, Jouanny P, Guillemin F, Kuntz C, Pourel J, Siest G. Segregation analysis and variance components analysis of bone mineral density in healthy families. J Bone Miner Res. 1995;10:2017–2022. doi: 10.1002/jbmr.5650101223. [DOI] [PubMed] [Google Scholar]
- [5].Kanis JA, Melton LJ, 3rd, Christiansen C, Johnston CC, Khaltaev NJ. The diagnosis of osteoporosis. J Bone Miner Res. 1994;9:1137–1141. doi: 10.1002/jbmr.5650090802. [DOI] [PubMed] [Google Scholar]
- [6].Ferrari SL, Rizzoli R. Gene variants for osteoporosis and their pleiotropic effects in aging. Mol Aspects Med. 2005;26:145–167. doi: 10.1016/j.mam.2005.01.002. [DOI] [PubMed] [Google Scholar]
- [7].Bandres E, Pombo I, Gonzalez-Huarriz M, Rebollo A, Lopez G, Garcia-Foncillas J. Association between bone mineral density and polymorphisms of the VDR, ER-alpha, COL1A1 and CTR genes in Spanish postmenopausal women. J Endocrinol Invest. 2005;28:312–321. doi: 10.1007/BF03347196. [DOI] [PubMed] [Google Scholar]
- [8].Ralston SH. Genetic determinants of osteoporosis. Curr Opin Rheumatol. 2005;17:475–479. doi: 10.1097/01.bor.0000166385.62851.92. [DOI] [PubMed] [Google Scholar]
- [9].Klein J, Satta Y, O′Huigin C, Takahata N. The molecular descent of the major histocompatibility complex. Annu Rev Immunol. 1993;11:269–295. doi: 10.1146/annurev.iy.11.040193.001413. [DOI] [PubMed] [Google Scholar]
- [10].Funkhouser W, Koop BF, Charmley P, Martindale D, Slightom J, Hood L. Evolution and selection of primate T cell antigen receptor BV8 gene subfamily. Mol Phylogenet Evol. 1997;8:51–64. doi: 10.1006/mpev.1997.0406. [DOI] [PubMed] [Google Scholar]
- [11].Miller MM, Wang C, Parisini E, Coletta RD, Goto RM, Lee SY, Barral DC, Townes M, Roura-Mir C, Ford HL, Brenner MB, Dascher CC. Characterization of two avian MHC-like genes reveals an ancient origin of the CD1 family. Proc Natl Acad Sci USA. 2005;102:8674–8679. doi: 10.1073/pnas.0500105102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Benes H, Weinstein RS, Zheng W, Thaden JJ, Jilka RL, Manolagas SC, Shmookler Reis RJ. Chromosomal mapping of osteopenia-associated quantitative trait loci using closely related mouse strains. J Bone Miner Res. 2000;15:626–633. doi: 10.1359/jbmr.2000.15.4.626. [DOI] [PubMed] [Google Scholar]
- [13].Looker AC, Wahner HW, Dunn WL, Calvo MS, Harris TB, Heyse SP, Johnston CC, Jr., Lindsay RL. Proximal femur bone mineral levels of US adults. Osteoporosis Int. 1995;5:389–409. doi: 10.1007/BF01622262. [DOI] [PubMed] [Google Scholar]
- [14].Parsons CA, Mroczkowski HJ, McGuigan FE, Albagha OM, Manolagas S, Reid DM, Ralston SH, Shmookler Reis RJ. Interspecies synteny mapping identifies a quantitative trait locus for bone mineral density on human chromosome Xp22. Hum Mol Genet. 2005;14:3141–3148. doi: 10.1093/hmg/ddi346. [DOI] [PubMed] [Google Scholar]
- [15].Takeda T, Hosokawa M, Higuchi K, Senescence-accelerated mouse (SAM) A novel murine model of aging. In: Takeda T, editor. The SAM Model of Senescence. Elsevier Science; Amsterdam, Holland: 1994. pp. 15–21. [Google Scholar]
- [16].Matsushita M, Tsuboyama T, Kasai R, Okumura H, Yamamuro T, et al. Age-related changes in bone mass in the senescence-accelerated mouse (SAM). SAM-R/3 and SAM-P/6 as new murine models for senile osteoporosis. Am J Pathol. 1986;125:276–283. [PMC free article] [PubMed] [Google Scholar]
- [17].Jilka RL, Weinstein RS, Takahashi K, Parfitt AM, Manolagas SC. Linkage of decreased bone mass with impaired osteoblastogenesis in a murine model of accelerated senescence. J Clin Invest. 1996;97:1732–1740. doi: 10.1172/JCI118600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Basten CJ, Weir BS, Zeng Z-B. QTL Cartographer: A Reference Manual and Tutorial for QTL Mapping. Department of Statistics, North Carolina State University; Raleigh NC: 1998. [Google Scholar]
- [19].Zeng Z-B. Precision mapping of quantitative trait loci. Genetics. 1994;136:1457–1468. doi: 10.1093/genetics/136.4.1457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Doerge RW, Churchill GA. Permutation tests for multiple loci affecting a quantitative character. Genetics. 1996;142:285–294. doi: 10.1093/genetics/142.1.285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Masinde GL, Li X, Gu W, Wergedal J, Mohan S, Baylink DJ. Quantitative trait loci for bone density in mice: the genes determining total skeletal density and femur density show little overlap in F2 mice. Calcif Tissue Int. 2002;71:421–428. doi: 10.1007/s00223-001-1113-z. [DOI] [PubMed] [Google Scholar]
- [22].Beamer WG, Shultz KL, Donahue LR, Churchill GA, Sen S, Wergedal JR, Baylink DJ, Rosen CJ. Quantitative trait loci for femoral and lumbar vertebral bone mineral density in C57BL/6J and C3H/HeJ inbred strains of mice. J Bone Miner Res. 2001;16:1195–1206. doi: 10.1359/jbmr.2001.16.7.1195. [DOI] [PubMed] [Google Scholar]
- [23].Beamer WG, Shultz KL, Churchill GA, Frankel WN, Baylink DJ, Rosen CJ, Donahue LR. Quantitative trait loci for bone density in C57BL/6J and CAST/EiJ inbred mice. Mamm Genome. 1999;10:1043–1049. doi: 10.1007/s003359901159. [DOI] [PubMed] [Google Scholar]
- [24].Klein RF, Mitchell SR, Phillips TJ, Belknap JK, Orwoll ES. Quantitative trait loci affecting peak bone mineral density in mice. J Bone Miner Res. 1998;13:1648–1656. doi: 10.1359/jbmr.1998.13.11.1648. [DOI] [PubMed] [Google Scholar]
- [25].Kajkenova O, Lecka-Czernik B, Gubrij I, Hauser SP, Takahashi K, et al. Increased adipogenesis and myelopoiesis in the bone marrow of SAMP6, a murine model of defective osteoblastogenesis and low turnover osteopenia. J Bone Miner Res. 1997;12:1772–1779. doi: 10.1359/jbmr.1997.12.11.1772. [DOI] [PubMed] [Google Scholar]
- [26].Shmookler Reis RJ, Kang P, Ayyadevara S. Quantitative trait loci define genes and pathways underlying genetic variation in longevity. Exper Gerontol. doi: 10.1016/j.exger.2006.06.047. in press. [DOI] [PubMed] [Google Scholar]
- [27].Lynch M, Walsh B. Genetics and Analysis of Quantitative Traits. Sinauer Associates; Sunderland MA.: 1998. [Google Scholar]
- [28].Cornforth TW, Long AD. Inferences regarding the numbers and locations of QTLs under multiple-QTL models using interval mapping and composite interval mapping. Genet Res. 2003;82:139–149. doi: 10.1017/s0016672303006396. [DOI] [PubMed] [Google Scholar]
- [29].Curtsinger JW. Sex specificity, life-span QTLs, and statistical power. J Gerontol A Biol Sci Med Sci. 2002;57:B409–B414. doi: 10.1093/gerona/57.12.b409. [DOI] [PubMed] [Google Scholar]
- [30].Lander ES, Botstein D. Mapping mendelian factors underlying quantitative traits using RFLP linkage maps. Genetics. 1989;121:185–199. doi: 10.1093/genetics/121.1.185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Kruglyak L, Lander ES. A nonparametric approach for mapping quantitative trait loci. Genetics. 1995;139:1421–1428. doi: 10.1093/genetics/139.3.1421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Roberts SB, MacLean CJ, Neale MC, Eaves LJ, Kendler KS. Replication of linkage studies of complex traits: an examination of variation in location estimates. Amer J Hum Genet. 1999;65:876–884. doi: 10.1086/302528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Jeffreys AJ, Allen MJ, Armour JA, Collick A, Dubrova Y, et al. Mutation processes at human minisatellites. Electrophoresis. 1995;16:1577–1585. doi: 10.1002/elps.11501601261. [DOI] [PubMed] [Google Scholar]
- [34].Barber R, Plumb M, Smith AG, Cesar CE, Boulton E, Jeffreys AJ, Dubrova YE. No correlation between germline mutation at repeat DNA and meiotic crossover in male mice exposed to X-rays or cisplatin. Mutat Res. 2000;457:79–91. doi: 10.1016/s0027-5107(00)00130-5. [DOI] [PubMed] [Google Scholar]