Abstract
We studied the dependence of ocular torsion on eye position during horizontal optokinetic nystagmus (OKN) elicited by random-dot translational motion (tOKN) and prolonged rotation in the light (rOKN). For slow and quick phases, we fit the eye-velocity axis to vertical eye position to determine the tilt angle slope (TAS). The TAS for tOKN was 0.48 for both slow and quick phases, close to what is found during translational motion of the head. The TAS for rOKN was less for both slow (0.11) and quick phases (0.26), close to what is found during rotational motion of the head. Our findings are consistent with the notion that translational and rotational optic flow are processed differently by the brain and that they produce different 3-D eye movement commands that are comparable to the different commands generated in response to vestibular signals when the head is actually translating or rotating.
Keywords: Listing’s Law, torsion, nystagmus, macaque
INTRODUCTION
Optokinetic nystagmus (OKN) is a visual tracking eye movement that is driven by full-field optic flow. Although OKN is often studied in the laboratory by exposing a stationary subject to motion of the visual surround, in natural experience it is more often a visual consequence of one’s own motion through the environment. In this setting, OKN acts to supplement angular and linear vestibular reflexes to maintain clear vision during head movement (Miles, 1995).
Cohen, Matsuo and Raphan (1977) demonstrated that OKN consists of two components: a direct or early component (termed OKNe by Miles) that has a short latency and lower gain, and an indirect or delayed component (OKNd) that builds up slowly, possibly due to “charging” of the velocity-storage system, but with a higher gain at steady-state. Miles (1995) and colleagues have proposed that OKNd and OKNe represent different visual stabilization responses, such that OKNd acts in concert with the rotational vestibulo-ocular reflex (rVOR) to minimize retinal image motion during prolonged head rotations, and OKNe supplements the translational VOR (tVOR) to compensate for head translations. The short-latency ocular following response (OFR) is similar to OKNe but refers to the eye movement elicited by sudden motion of an already visible stimulus (Miles, Kawano, & Optican, 1986).
If OKNe/OFR and OKNd share neural circuitry with the tVOR and rVOR, it might be expected that differences between the two vestibular reflexes would be reflected in their corresponding visual reflexes. Several lines of evidence connect OKNe/OFR to the tVOR. First, the slow-phase gain of OKNe depends on viewing distance (Busettini, Miles, & Schwarz, 1991), as does the tVOR (Schwarz, Busettini, & Miles, 1989). Second, the OFR is greatest for image motion in the plane of fixation, i.e. when binocular disparity is zero (Masson, Busettini, Yang, & Miles, 2001; Yang & Miles, 2003). Third, the OFR and tVOR have similar three-dimensional (3-D) kinematics (Adeyemo & Angelaki, 2005).
Previous studies have shown that different subtypes of eye movements have different rotational kinematics; in particular, they behave differently with respect to Listing’s Law (LL). LL describes the relationship of ocular torsion to orbital position: if eye positions are expressed as rotation vectors in a head-fixed coordinate system, these vectors all lie in a plane. Strictly defined, LL refers to static fixations, i.e., when the eye is not moving. An important question, however, has been whether eye movements respect this same constraint on torsional eye position: to what extent do 3-D eye positions remain in Listing’s plane as the eye moves? In both humans and monkeys, it is well established that saccades (Ferman, Collewijn, & van den Berg, 1987; Tweed & Vilis, 1990; Straumann, Zee, Solomon, Lasker, & Roberts, 1995; Palla, Straumann, & Obzina, 1999), smooth pursuit (Ferman et al., 1987; Haslwanter, Straumann, Hepp, Hess, & Henn, 1991; Tweed, Fetter, Andreadaki, Koenig, & Dichgans, 1992; Palla et al., 1999; Tian, Zee, & Walker, 2006), and the tVOR (Angelaki, Zhou, & Wei, 2003; Walker, Shelhamer, & Zee, 2004) nearly obey LL. This is consistent with the fact that pursuit and the tVOR typically stabilize only the foveal image. In contrast, for the rVOR (Misslisch, Tweed, Fetter, Sievering, & Koenig, 1994; Palla et al., 1999; Thurtell, Black, Halmagyi, Curthoys, & Aw, 1999; Thurtell, Kunin, & Raphan, 2000; Misslisch & Hess, 2000; Misslisch & Tweed, 2000; Misslisch & Tweed, 2001; Tian et al., 2006), torsion depends less upon eye position (it is closer to head-fixed), with the goal of maintaining images stable on the entire retina (Misslisch et al., 1994). In humans, it has been shown that, like the rVOR, rOKN does not follow LL (Fetter, Tweed, Misslisch, & Koenig, 1994; Zee, Walker, & Ramat, 2002). These studies examined responses to low-frequency or constant-velocity rotational optic flow, i.e., OKNd.
Based on the hypothesis that the OFR is related to the tVOR, Adeyemo and Angelaki (2005) asked whether the OFR has similar 3-D kinematics to the tVOR and smooth pursuit. Using brief steps of full-field linear motion, they found a large amount of eye-position-dependent torsion. What this study did not address, however, was whether the difference in kinematics between the OFR and OKNd was due to the transient nature of the visual stimulus or to an inherent difference between the processing of translational and rotational optic flow, independent of timing.
Finally, additional evidence supports the idea that translational OKN (tOKN) and rotational OKN (rOKN) are processed differently, apart from a difference in timing (early vs. late). Mossman, et al. 1992 showed that tOKN and rOKN influence the response to subsequent rotation differently. Specifically, rOKN appeared to invoke the vestibular velocity-storage mechanism, but tOKN did not. They also reported that cerebellar lesions in patients affect rOKN and tOKN differently (Mossman, Bronstein, & Hood, 1991). Finally, a sustained translational stimulus invokes the perception of linearvection, whereas a sustained rotational stimulus invokes circularvection (Berthoz, Pavard, & Young, 1975).
Here, we asked whether there is a difference in the kinematics of the responses to rotational and translational visual motion during prolonged (steady-state) stimulation. Because of the difference in the normal function of these two reflexes (analogous to the difference between the rVOR and tVOR), i.e., full-field retinal versus foveal stabilization, respectively, we expected this to be the case. We also asked whether or not there is a relationship between the kinematics of corresponding slow and quick phases for rOKN and tOKN. Preliminary results have been presented in abstract form (Tian & Walker, 2005).
METHODS
Animal preparation and training
Experiments were conducted on two female and one male rhesus (Macaca mulatta) monkeys (4 to 5 kg). All surgical procedures were performed under aseptic conditions using pentobarbital anesthesia and post-operative analgesia, according to a protocol that was approved by the Institutional Animal Care and Use Committee (IACUC) of the Johns Hopkins University, including measures to minimize pain and discomfort. All aspects of animal care were approved by the IACUC and were supervised by the staff veterinarians of the Johns Hopkins University School of Medicine.
The animals were first trained to come out of their cages and sit comfortably in a primate chair. For head immobilization during experiments, a plastic head plate was attached to the skull with dental acrylic. Using noninvasive infrared oculography, animals were then trained to fixate and follow a visual target for a water reward. Once basic training was completed, eye coils were implanted. Two coils were implanted in each eye to record three-axis (horizontal, vertical, and torsion) eye position (Robinson, 1963; Judge, Richmond, & Chu, 1980; Hess, 1990). Each coil is pre-made from several turns of Teflon-coated stainless steel wire. The frontal coil is placed around the limbus and sutured to the sclera. A second smaller coil is placed roughly orthogonal to the first, usually on the superolateral aspect of the globe; this coil is more sensitive to torsional eye rotations. The lead wire from each coil was passed subcutaneously from the lateral orbital margin to the edge of the head implant where it was attached to a connector that was imbedded in the dental acrylic. For magnetic shielding (to minimize offsets in the coil signals), the lead wires were twisted tightly for their entire length and connectors were enclosed with Mumetal® (MuShield, Londonderry, NH). After recovery, training was completed and experiments were begun.
Eye Movement Recording
During each experiment, the monkey was seated in a primate chair with its head fixed in the upright position to the frame of the chair. . The limbs and body were free to move inside the chair. The chair was placed at the center of a vestibular turntable that was mounted on a rotational motor with an earth-vertical axis. The eyes were centered within a cubic frame (66 cm on a side) that generated three orthogonal magnetic fields of different frequencies (55.5, 83.3 and 42.6 kHz). Signals from each coil were demodulated by frequency detectors, filtered in hardware with a bandwidth of 0–90 Hz, sampled at 1000 Hz, and stored on computer for later analysis.
Coil signals were calibrated using the standard three-axis techniques that are used routinely in our laboratory for both human and animal experiments (Straumann et al., 1995) The signal offsets were first zeroed with a test coil in the center of a metallic tube and then the relative gains of signals from each of the three fields were determined separately. Offsets from coil connectors were minimized by shielding the connectors with Mumetal®.
Optokinetic stimulation
To elicit horizontal OKN, two types of stimuli were used. First (tOKN), a large-field (74° × 74°) random-dot pattern (500 white dots; individual dot size 0.4°) was rear-projected onto a tangent screen at a distance of 43.5 cm . The visual stimulus moved rightward and leftward at constant speed (22.8 or 45.6 cm/s, the equivalent of 30 or 60°/s at this distance with the eyes looking straight ahead), lasting 90-120 seconds. Second (rOKN), animals underwent yaw rotation on a vestibular turntable at 30 or 60°/s in the dark. When the vestibular nystagmus had subsided, the room lights were turned on while the chair continued to rotate. The first 30 seconds of rOKN were omitted from the analysis, to ensure that the slow-phase velocity had reached a steady-state. The stimulus axis was earth-vertical for both tOKN and rOKN. Finally, to determine the orientation of Listing’s plane (LP), we recorded eye positions during fixation of targets spaced every 5° on a 40° × 40° grid.
Data analysis
Data analysis was performed using custom software developed in MATLAB™ (The Mathworks, Natick, MA) and in Python (www.python.org), using the numpy and scipy packages (www.scipy.org). Using straight-ahead as the reference position, raw coil signals were first converted to rotation vectors, which describe the instantaneous eye orientation as a single rotation from the reference position. These rotation vectors (r) and their derivative (dr/dt) were then used to calculate angular velocity vectors (ω) in head-fixed coordinates according to the following equation: ω = 2(dr/dt+r×dr/dt)/(1+|r/2), where ‘×’ denotes the cross product (Hepp 1990). Positive directions are leftward, downward, and clockwise (from the animal’s perspective) for the horizontal, vertical, and torsional components, respectively (right-hand rule). Rotation vectors were expressed in Listing’s coordinates, based on primary positions calculated from the static fixation paradigm.
An interactive program was used to select slow phases for analysis, excluding quick phases, saccades, blinks, and other artifacts. To determine the axis of angular eye velocity, we calculated the median tilt angle (arctangent of the ratio of median torsional to horizontal eye velocity) for each slow phase. The tilt angle indicates the amount of axis tilt in the animal’s sagittal plane from the purely earth-vertical axis (horizontal motion) of the stimulus. A linear regression of these tilt angles was performed with respect to the measured vertical position of each slow phase to determine the tilt angle slope (TAS). Statistical comparisons were performed using one-way ANOVA (α = 0.025, applying the Bonferroni correction for two comparisons – slow-phase and quick-phase TAS – to an overall α of 0.05).
Quick phases were selected automatically using a velocity criterion of 100°/s. This ensured a robust distinction of quick phases from slow phases, which had a velocity of no more than 60°/s. It also limited the analysis to the middle portion of the quick phase, where velocities are higher, and thus the effect of noise is less. The marked quick phases were then examined interactively. Saccades other than OKN quick phases (e.g., saccades in the direction of the slow phase) and any artifacts (e.g., blinks) were manually removed.
Unlike horizontal slow phases, which were always in the direction of stimulus motion, horizontal quick phases were often associated with a coincident vertical saccade (the animal was free to look around the visual scene, see Figure 1). In fact, this is what permitted us to determine the axis of both slow and quick phases at different vertical eye positions. When assessing the axis of the quick phases, however, we deliberately limited our analysis to those quick phases with a vertical component that was considerably smaller than the horizontal component: quick phases were only included in the analysis when the peak vertical velocity was less than 15% of the peak horizontal velocity. The objective was to limit the amount of torsional eye velocity due to the vertical saccade. Because the 15% criterion was an arbitrary one, however, and could have somehow influenced the results, we determined the effect of relaxing the criterion to 25% or 50%. The differences in the TAS were small (mean slopes for each condition differed by no more than 0.02), and the main finding (the difference between tOKN and rOKN) remained the same.
Figure 1.

Angular eye orientation in head-fixed coordinates as a function of time for epochs of leftward rOKN and tOKN in the same animal. Time and position scales are as shown. Note that the torsion traces have been magnified relative to the horizontal and vertical traces to facilitate comparison of torsion in the two conditions. Here, and elsewhere, the right-hand rule is followed: positive directions are leftward, downward, and clockwise, from the perspective of the animal. For the first three traces, eye positions are shown relative to the standard coordinates of the coil frame. The fourth trace of each panel shows torsion in Listing’s coordinates. Note that there is a smaller range of torsion (in Listing’s coordinates) for tOKN, suggesting that the eye remains closer to Listing’s plane than it does during rOKN.
Determination of the axis of quick phases is more complex than for slow phases. Although it is generally stated that saccades (when the head is fixed) follow LL, studies have generally shown at least a small deviation of eye orientation from LP as the eye moves (the so-called “torsional blips”, e.g., Straumann et al., 1995). Correspondingly, the instantaneous eye velocity axis is typically not constant throughout saccades or quick phases. For the present study, the goal was to compare the overall eye velocity axis of quick phases of tOKN and rOKN. Thus, we chose to calculate an “average” axis by performing a least-squares linear regression of the torsional component to the horizontal component of angular eye velocity. The axis of eye velocity for each individual quick phase was then defined as the arctangent of the slope of this regression. Once these individual quick-phase axes were calculated, an analysis similar to that for slow phases was performed: a least-squares linear regression of axis tilt to mean vertical eye position for all quick phases yielded the TAS.
RESULTS
Figure 1 shows representative 3-D eye positions in head-fixed coordinates (horizontal, vertical, and torsional components; as well as torsion in Listing’s coordinates) during leftward rOKN (rightward rotation in the light) and tOKN (leftward dot motion) in one monkey. In both cases, there is a horizontal nystagmus with leftward slow phases. Torsional components, however, are quite different. Specifically, torsion in Listing’s coordinates is much less for tOKN, suggesting that the eye remains closer to Listing’s plane during tOKN than it does during rOKN.
In all monkeys, the eye-velocity axis of OKN slow phases varied with the vertical position of the eye in the orbit, more so for tOKN than for rOKN (Figures 2 and 3). Figure 2 shows mean tilt angles for three vertical eye positions in one monkey. Note that the axes are more similar for rOKN and more widely separated for tOKN. Figure 3 illustrates the calculation of the tilt angle slopes for the two conditions in one monkey. The tilt angles (axis) are plotted as a function of vertical eye position for each slow phase. The slope of the linear regression defines the TAS. Note that this slope is greater for tOKN (Figure 3B) than for rOKN (Figure 3A).
Figure 2.
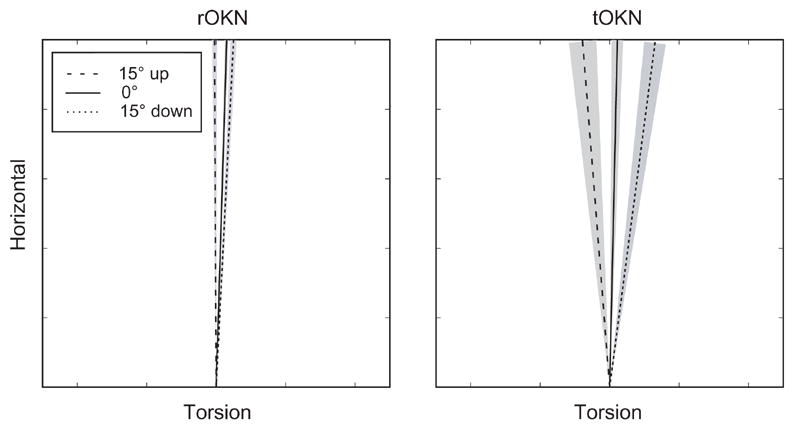
Eye velocity axis as a function of orbital position for rOKN and tOKN (M2). Each line represents the mean axis (torsional vs. horizontal eye velocity) for all slow phases within a vertical position window of 5°, centered on the indicated position. The shaded areas show the 95% confidence intervals. Axes are shown in the coordinates of the coil frame (not in Listing’s coordinates), in order to allow direct comparison with the axis of the visual stimulus.
Figure 3.
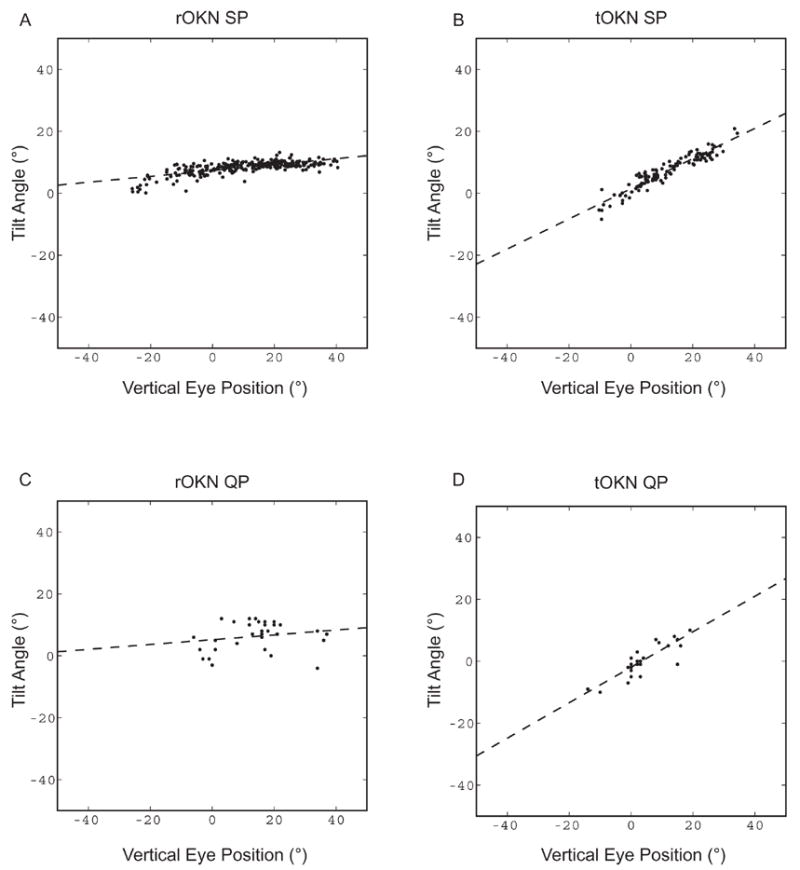
Examples of tilt-angle slope (TAS) calculations for (A) rOKN, and (B) tOKN, for rightward slow-phases in M1. For each slow phase, the tilt angle (arctangent of the ratio of median torsional to median horizontal eye velocity) is plotted as a function of median vertical eye position. The dashed line shows the result of a least-squares linear regression, the slope of which is the tilt-angle slope. (C) and (D): Calculation of TAS for quick phases. There is a smaller number of quick phases than slow phases, because quick phases that had peak vertical velocities exceeding 15% of the peak horizontal velocity were excluded from the analysis. For TAS calculations, data were expressed in Listing’s coordinates.
The kinematics of OKN quick phases reflected the difference in the kinematics of their corresponding slow phases: overall, the axis of rOKN quick phases was closer to head-fixed than that of tOKN quick phases (Figure 3C, D), although there was more variability in the axes of individual quick phases than in the axes of the slow phases (cf. Figure 3A and C).
Figure 4 summarizes the results from all three animals, plotting the mean TAS (combining data from both directions and both eyes). For slow phases, the overall mean (all animals combined) TAS was 0.11 for rOKN and 0.48 for tOKN (p < 0.012). For quick phases, the overall mean TAS was 0.26 for rOKN and 0.48 for tOKN. While this difference in the axes of quick phases missed being statistically significant (p = 0.057), the TAS was lower for rOKN quick phases than for tOKN quick phases in each animal. Similar results were obtained for 30°/s stimulus (data not shown).
Figure 4.
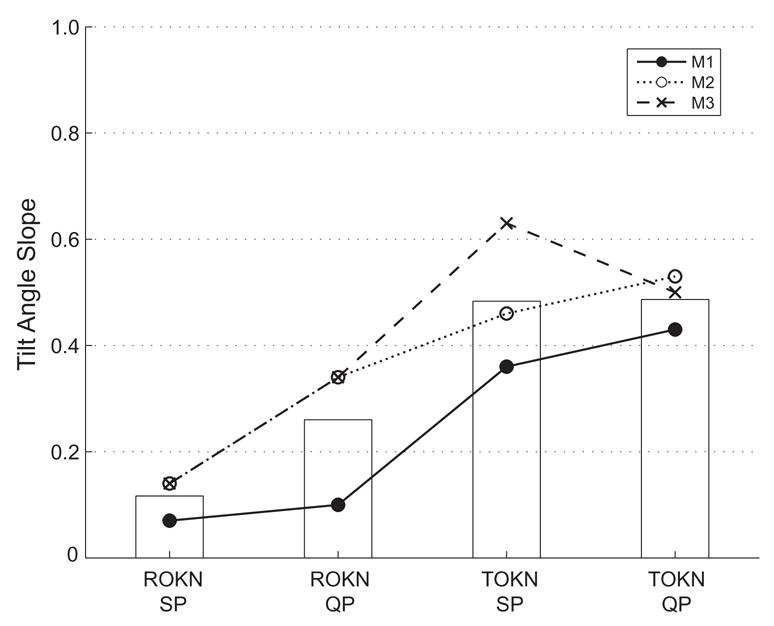
Mean tilt-angle slopes (TAS) for each condition in all animals. As indicated in the legend, each symbol and line represents the TAS (mean of both eyes and both directions) for an individual monkey. The superimposed bars indicate the mean of the values from the three animals. TAS for slow-phases were different (p < 0.012, one-way ANOVA), but the corresponding difference for quick phases did not reach significance (p=0.057).
DISCUSSION
In this study, we have shown that horizontal rOKN and tOKN have different 3-D kinematics, similar to those of the rVOR and tVOR, respectively. The rVOR and rOKN have a response that is closer to head-fixed, and the tVOR and tOKN have more eye-position-dependent torsion, i.e., they have a response closer to the predictions of LL. These findings lend further support to the notion that these visual reflexes are distinct and that they are closely tied to their corresponding vestibular reflexes, not only at the perceptual level, but also with respect to their premotor circuitry. Since the response to translation depends upon the distance of the target of interest, and is related to stabilization of images on the fovea, and the response to rotation is related to stabilization of images on the entire retina, it is not surprising that the visual equivalents of translation and rotation are processed in the same way as their corresponding vestibular reflexes.
The idea that rotational and translational optic flow are processed differently by the brain is not new (see Introduction). Prior work, however, has distinguished these reflexes largely by their relative timing, early or late, i.e., OKNe and OKNd (Miles, 1995; Adeyemo & Angelaki, 2005). Our results here are important, because they show that it is not only the timing of the response relative to the onset of the stimulus but also the nature of the visual stimulus that determines whether optic flow is interpreted as translation or rotation. A constant-velocity stimulus projected on a flat screen, even when it is prolonged and fills most of the visual field, does not elicit a response that simulates rotation. This is true even in the absence of the depth cues and motion parallax that typically accompany linear head motion.
What characteristics of the visual stimulus determine if rOKN or tOKN will be elicited?
When exposed to motion of the visual environment (optic flow), the brain must be able to interpret the nature (rotational or translational) and direction of that motion. This makes sense when one considers that the primary purpose of these reflexes is to use visual inputs to extract information about self-motion, supplementing the corresponding vestibular signals.
The vestibular system distinguishes translation and rotation by comparing signals arising from the semicircular canals and otoliths: the canals sense angular acceleration and the otoliths sense linear acceleration. Even in ambiguous cases, such as combinations of roll rotations and interaural translation, the true motion is correctly detected (Shaikh, Ghasia, Dickman, & Angelaki, 2005). In the case of optokinetic stimulation, however, the input is purely visual, whether the motion indicates rotation or translation. How then does the brain determine the type of motion from the visual stimulus alone?
In the natural world, the visual environment is not two-dimensional; it has depth. The effect of linear and rotational motion on images at various distances from the subject is different and is one possible way that rotations and translations could be distinguished. In particular, translational motion is associated with motion parallax (Miles, 1999): images of closer objects move more on the retina than those of distant objects. In the extreme case, the retinal image of an object at infinity remains stationary as the head translates. In contrast, when the head rotates, the relative motion of all images is the same, regardless of the distance, if one ignores that the axis of rotation may not be directly through the eyes. In the present study, the rotational stimulus contained depth (the animal was rotating in the light), but the translational stimulus did not. Thus, motion parallax could not have been used to detect translation, but the absence of motion parallax might have contributed to the detection of rotation. This could be tested in another study by recording the response to a rotating stimulus that does not have depth (e.g., a rotating drum).
How is tOKN related to OKNe and the ocular following response?
Based on a series of findings (reviewed in Miles, 1999), Miles proposed that the OFR is equivalent to OKNe and serves to supplement the tVOR, whereas the longer-latency OKNd supplements the rVOR during prolonged rotations. Our data do not allow us to compare rotational OKNe to the linear OFR, since the initial vertical eye position was not controlled and, therefore, could not be varied reliably over a wide range. Our results do, however, clearly support the notion that there are both rotational and translational forms of OKNd and that these have different kinematics, similar to those of the corresponding vestibular reflexes. Further studies will be required to determine if there are kinematic differences in the initial responses to these two types of stimuli or if rotational OKNe resembles OFR, with a larger tilt angle slope than that of OKNd.
What determines the kinematics of OKN quick-phases?
It is generally thought that vestibular and optokinetic quick phases share basic brainstem circuitry with the saccadic system, except that for quick phases, the burst neurons are activated by vestibular signals (reviewed in Curthoys, 2002). In the cat, this input to saccadic burst neurons comes from burst-driver neurons in the nucleus prepositus hypoglossi (Ohki, Shimazu, & Suzuki, 1988). One might then ask whether the 3-D kinematics of quick phases resemble those of saccades, which have been shown to follow LL (Ferman et al., 1987; Tweed & Vilis, 1990), at least in their average axes, ignoring the torsional “blips” that move the eye transiently out of Listing’s plane (Ferman et al., 1987; Straumann et al., 1995). Here we have demonstrated that this is not necessarily the case. Our data show that quick-phase kinematics parallel those of their corresponding slow phases: rOKN quick phases have less eye-position-dependent torsion than do tOKN quick phases. Since tOKN slow phases do obey LL, subsequent quick phases need not be concerned with taking the eyes back to Listing’s plane. On the other hand, since the slow phases of the rOKN do not obey LL (torsional orientation is taken out of Listing’s plane), subsequent quick phases also serve to take the eye back toward Listing’s plane. The mechanism might be similar to that responsible for the correction of imposed torsional offsets by subsequent saccades (Lee, Zee, & Straumann, 2000) and by rVOR quick phases (Crawford & Vilis, 1991) and for anticipatory torsional quick phases in advance of an active roll head movement (Tweed, Haslwanter, & Fetter, 1998; Crawford, Ceylan, Klier, & Guitton, 1999). In monkeys, van Opstal, et al. (1996) showed that the nucleus reticularis tegmenti pontis acts to correct torsional movements away from LP during spontaneous saccades. A similar mechanism might be operating for rOKN quick phases and could account for the greater variability in quick-phase axis (Figure 3C). The differences in functional requirements for quick phases of tOKN and rOKN impose an additional level of complexity that may be reflected in their different TAS. How this difference in kinematics is achieved is not certain, but a three-dimensional neural command — one that takes into account the kinematics of the intervening slow phases — would seem to be required.
Note that our findings are not inconsistent with the idea that orbital mechanics are optimized for Listing’s Law, an hypothesis that has been supported by experimental stimulation of the abducens nerve (Klier, Meng, & Angelaki, 2006). It does mean, however, the 3-D neural signal driving rOKN quick phases must be different from that of corresponding saccades, in order for the rOKN quick phases to violate LL. Our results are also consistent with the findings of Klier, Wang, and Crawford (2003) who showed that violations of LL during head-free gaze shifts originate downstream from the superior colliculus. In the case of rOKN quick phases, these 3-D signals likely arise in the vestibular system.
In conclusion, we have shown that the kinematics of both slow and quick phases of optokinetic nystagmus reflect the nature of the visual stimulus (rotational or translational). That the slow phases of rOKN are closer to a head-fixed axis is similar to the rVOR and likely facilitates a more stable visual image on the entire retina. The difference in quick phase kinematics may help to keep eye orientations closer to LP, when (as for rOKN and the rVOR) LL is not obeyed (Crawford & Vilis, 1991).
Acknowledgments
This study was supported by the National Institutes of Health (R01-EY01849); the Albert Pennick fund; and by the Arnold-Chiari Foundation. Dr. Walker is a Pollin Scholar. C. Bridges, A. Lasker, and D. Roberts provided technical support. The authors are grateful to F.A. Miles for a critical review and discussion of this manuscript.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Adeyemo B, Angelaki DE. Similar kinematic properties for ocular following and smooth pursuit eye movements. J Neurophysiol. 2005;93:1710–1717. doi: 10.1152/jn.01020.2004. [DOI] [PubMed] [Google Scholar]
- Angelaki DE, Zhou HH, Wei M. Foveal versus full-field visual stabilization strategies for translational and rotational head movements. J Neurosci. 2003;23:1104–1108. doi: 10.1523/JNEUROSCI.23-04-01104.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berthoz A, Pavard B, Young LR. Perception of linear horizontal self-motion induced by peripheral vision (linearvection) basic characteristics and visual-vestibular interactions. Exp Brain Res. 1975;23:471–489. doi: 10.1007/BF00234916. [DOI] [PubMed] [Google Scholar]
- Busettini C, Miles FA, Schwarz U. Ocular responses to translation and their dependence on viewing distance. II. Motion of the scene. J Neurophysiol. 1991;66:865–878. doi: 10.1152/jn.1991.66.3.865. [DOI] [PubMed] [Google Scholar]
- Cohen B, Matsuo V, Raphan T. Quantitative analysis of the velocity characteristics of optokinetic nystagmus and optokinetic after-nystagmus. J Physiol. 1977;270:321–344. doi: 10.1113/jphysiol.1977.sp011955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crawford JD, Ceylan MZ, Klier EM, Guitton D. Three-dimensional eye-head coordination during gaze saccades in the primate. J Neurophysiol. 1999;81:1760–1782. doi: 10.1152/jn.1999.81.4.1760. [DOI] [PubMed] [Google Scholar]
- Crawford JD, Vilis T. Axes of eye rotation and Listing’s law during rotations of the head. J Neurophysiol. 1991;65:407–423. doi: 10.1152/jn.1991.65.3.407. [DOI] [PubMed] [Google Scholar]
- Curthoys IS. Generation of the quick phase of horizontal vestibular nystagmus. Exp Brain Res. 2002;143:397–405. doi: 10.1007/s00221-002-1022-z. [DOI] [PubMed] [Google Scholar]
- Ferman L, Collewijn H, van den Berg AV. A direct test of Listing’s law--II. Human ocular torsion measured under dynamic conditions. Vision Res. 1987;27:939–951. doi: 10.1016/0042-6989(87)90010-1. [DOI] [PubMed] [Google Scholar]
- Fetter M, Tweed D, Misslisch H, Koenig E. Three-dimensional human eye-movements are organized differently for the different oculomotor subsystems. Neuro-Ophthalmology. 1994;14:147–152. [Google Scholar]
- Haslwanter T, Straumann D, Hepp K, Hess BJ, Henn V. Smooth pursuit eye movements obey Listing’s law in the monkey. Exp Brain Res. 1991;87:470–472. doi: 10.1007/BF00231865. [DOI] [PubMed] [Google Scholar]
- Hess BJ. Dual-search coil for measuring 3-dimensional eye movements in experimental animals. Vision Res. 1990;30:597–602. doi: 10.1016/0042-6989(90)90070-2. [DOI] [PubMed] [Google Scholar]
- Judge SJ, Richmond BJ, Chu FC. Implantation of magnetic search coils for measurement of eye position: an improved method. Vision Res. 1980;20:535–538. doi: 10.1016/0042-6989(80)90128-5. [DOI] [PubMed] [Google Scholar]
- Klier EM, Meng H, Angelaki DE. Three-dimensional kinematics at the level of the oculomotor plant. J Neurosci. 2006;26:2732–2737. doi: 10.1523/JNEUROSCI.3610-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klier EM, Wang H, Crawford JD. Three-dimensional eye-head coordination is implemented downstream from the superior colliculus. J Neurophysiol. 2003;89:2839–2853. doi: 10.1152/jn.00763.2002. [DOI] [PubMed] [Google Scholar]
- Lee C, Zee DS, Straumann D. Saccades from torsional offset positions back to listing’s plane. J Neurophysiol. 2000;83:3241–3253. doi: 10.1152/jn.2000.83.6.3241. [DOI] [PubMed] [Google Scholar]
- Masson GS, Busettini C, Yang DS, Miles FA. Short-latency ocular following in humans: sensitivity to binocular disparity. Vision Res. 2001;41:3371–3387. doi: 10.1016/s0042-6989(01)00029-3. [DOI] [PubMed] [Google Scholar]
- Miles FA. The sensing of optic flow by the primate optokinetic system. In: Findlay JM, Kentridge RW, Walker R, editors. Eye Movement Research: Mechanisms, Processes, and Applications. Elsevier; Amsterdam: 1995. [Google Scholar]
- Miles FA. Short-latency visual stabilization mechanisms that help to compensate for translational disturbances of gaze. Ann NY Acad Sci. 1999;871:260–271. doi: 10.1111/j.1749-6632.1999.tb09190.x. [DOI] [PubMed] [Google Scholar]
- Miles FA, Kawano K, Optican LM. Short-latency ocular following responses of monkey. I. Dependence on temporospatial properties of visual input. J Neurophysiol. 1986;56:1321–1354. doi: 10.1152/jn.1986.56.5.1321. [DOI] [PubMed] [Google Scholar]
- Misslisch H, Hess BJ. Three-dimensional vestibuloocular reflex of the monkey: optimal retinal image stabilization versus listing’s law. J Neurophysiol. 2000;83:3264–3276. doi: 10.1152/jn.2000.83.6.3264. [DOI] [PubMed] [Google Scholar]
- Misslisch H, Tweed D. Torsional dynamics and cross-coupling in the human vestibulo-ocular reflex during active head rotation. J Vestib Res. 2000;10:119–125. [PubMed] [Google Scholar]
- Misslisch H, Tweed D. Neural and mechanical factors in eye control. J Neurophysiol. 2001;86:1877–1883. doi: 10.1152/jn.2001.86.4.1877. [DOI] [PubMed] [Google Scholar]
- Misslisch H, Tweed D, Fetter M, Sievering D, Koenig E. Rotational kinematics of the human vestibuloocular reflex. III. Listing’s law. J Neurophysiol. 1994;72:2490–2502. doi: 10.1152/jn.1994.72.5.2490. [DOI] [PubMed] [Google Scholar]
- Mossman SS, Bronstein AM, Hood JD. Linear and angular optokinetic nystagmus in labyrinthine and central nervous system lesions. Acta Otolaryngol Suppl. 1991;481:352–356. doi: 10.3109/00016489109131420. [DOI] [PubMed] [Google Scholar]
- Mossman SS, Bronstein AM, Hood JD, Sacares P. The interaction of angular and linear optokinetic stimuli with an angular vestibular stimulus. Ann NY Acad Sci. 1992;656:868–870. doi: 10.1111/j.1749-6632.1992.tb25278.x. [DOI] [PubMed] [Google Scholar]
- Ohki Y, Shimazu H, Suzuki I. Excitatory input to burst neurons from the labyrinth and its mediating pathway in the cat: location and functional characteristics of burster-driving neurons. Exp Brain Res. 1988;72:457–472. doi: 10.1007/BF00250591. [DOI] [PubMed] [Google Scholar]
- Palla A, Straumann D, Obzina H. Eye-position dependence of three-dimensional ocular rotation-axis orientation during head impulses in humans. Exp Brain Res. 1999;129:127–133. doi: 10.1007/s002210050943. [DOI] [PubMed] [Google Scholar]
- Robinson DA. A method of measuring eye movement using a scleral search coil in a magnetic field. IEEE Trans Biomed Eng. 1963;10:137–45. 137–145. doi: 10.1109/tbmel.1963.4322822. [DOI] [PubMed] [Google Scholar]
- Schwarz U, Busettini C, Miles FA. Ocular responses to linear motion are inversely proportional to viewing distance. Science. 1989;245:1394–1396. doi: 10.1126/science.2506641. [DOI] [PubMed] [Google Scholar]
- Shaikh AG, Ghasia FF, Dickman JD, Angelaki DE. Properties of cerebellar fastigial neurons during translation, rotation, and eye movements. J Neurophysiol. 2005;93:853–863. doi: 10.1152/jn.00879.2004. [DOI] [PubMed] [Google Scholar]
- Straumann D, Zee DS, Solomon D, Lasker AG, Roberts DC. Transient torsion during and after saccades. Vision Res. 1995;35:3321–3334. doi: 10.1016/0042-6989(95)00091-r. [DOI] [PubMed] [Google Scholar]
- Thurtell MJ, Black RA, Halmagyi GM, Curthoys IS, Aw ST. Vertical eye position-dependence of the human vestibuloocular reflex during passive and active yaw head rotations. J Neurophysiol. 1999;81:2415–2428. doi: 10.1152/jn.1999.81.5.2415. [DOI] [PubMed] [Google Scholar]
- Thurtell MJ, Kunin M, Raphan T. Role of muscle pulleys in producing eye position-dependence in the angular vestibuloocular reflex: a model-based study. J Neurophysiol. 2000;84:639–650. doi: 10.1152/jn.2000.84.2.639. [DOI] [PubMed] [Google Scholar]
- Tian J, Walker MF. Program No.745.6.2005 Abstract Viewer/Itinerary Planner. 2005. Eye-position dependence of optokinetic nystagmus in the monkey. (Abstract) [Google Scholar]
- Tian J, Zee DS, Walker MF. Eye-position dependence of torsional velocity during step-ramp pursuit and transient yaw rotation in humans. Exp Brain Res. 2006;171:225–230. doi: 10.1007/s00221-005-0261-1. [DOI] [PubMed] [Google Scholar]
- Tweed D, Fetter M, Andreadaki S, Koenig E, Dichgans J. Three-dimensional properties of human pursuit eye movements. Vision Res. 1992;32:1225–1238. doi: 10.1016/0042-6989(92)90217-7. [DOI] [PubMed] [Google Scholar]
- Tweed D, Haslwanter T, Fetter M. Optimizing gaze control in three dimensions. Science. 1998;281:1363–1366. doi: 10.1126/science.281.5381.1363. [DOI] [PubMed] [Google Scholar]
- Tweed D, Vilis T. Geometric relations of eye position and velocity vectors during saccades. Vision Res. 1990;30:111–127. doi: 10.1016/0042-6989(90)90131-4. [DOI] [PubMed] [Google Scholar]
- Van Opstal J, Hepp K, Suzuki Y, Henn V. Role of monkey nucleus reticularis tegmenti pontis in the stabilization of Listing’s plane. J Neurosci. 1996;16:7284–7296. doi: 10.1523/JNEUROSCI.16-22-07284.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker MF, Shelhamer M, Zee DS. Eye-position dependence of torsional velocity during interaural translation, horizontal pursuit, and yaw-axis rotation in humans. Vision Res. 2004;44:613–620. doi: 10.1016/j.visres.2003.10.009. [DOI] [PubMed] [Google Scholar]
- Yang DS, Miles FA. Short-latency ocular following in humans is dependent on absolute (rather than relative) binocular disparity. Vision Res. 2003;43:1387–1396. doi: 10.1016/s0042-6989(03)00146-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zee DS, Walker MF, Ramat S. The cerebellar contribution to eye movements based upon lesions: binocular three-axis control and the translational vestibulo-ocular reflex. Ann NY Acad Sci. 2002;956:178–189. doi: 10.1111/j.1749-6632.2002.tb02818.x. [DOI] [PubMed] [Google Scholar]


