Protein-induced, previously unidentified twin form of calcite

Abstract

Using single-crystal x-ray diffraction, we found a formerly unknown twin form in calcite crystals grown from solution to which a mollusc shell-derived 17-kDa protein, Caspartin, was added. This intracrystalline protein was extracted from the calcitic prisms of the Pinna nobilis shells. The observed twin form is characterized by the twinning plane of the (108)-type, which is in addition to the known four twin laws of calcite identified during 150 years of investigations. The established twin forms in calcite have twinning planes of the (001)-, (012)-, (104)-, and (018)-types. Our discovery provides additional evidence on the crucial role of biological macromolecules in biomineralization.

The phenomenon of twinning in crystals (1) has been extensively studied because of its importance in crystal growth, phase transformations, and mechanical, electrical and optical properties in real crystals. In fact, twinning is one of the key mechanisms of plastic deformation in metals and ceramics (2). Quite often it serves as a structural basis for different types of ferroelectric domains (see, e.g., refs. 3–5) or structural variants in shape-memory alloys (6). Twinning in calcite was identified 150 years ago and has been thoroughly investigated and classified by mineralogists (7) and geologists (8). In the present, twinning in calcite is used as a stress and temperature indicator of geological processes (8) and of meteorite impact (9). It is commonly accepted that there are only four different kinds of twins in calcite (“The Four Twin Laws of Calcite,” according to ref. 7), which describe all possible twins produced by deformation (see, e.g., ref. 10 and references therein) and during crystal growth (7). The interest in calcite growth has been renewed in the last few decades in relation to biomineralization (11, 12), because biogenic calcite is extensively produced by living organisms. Because of deep involvement of organic macromolecules in the growth of biogenic crystals, biogenic calcite differs in some aspects from its geological counterpart. Even the unit cell of biogenic calcite is anisotropically stretched (13), an effect caused by macromolecules trapped within individual crystallites. In this article, we show that protein extracted from mollusk shells can also induce a previously unidentified form of twinning (in addition to the established four twin laws) in calcite crystals artificially grown from the protein-containing crystallization solution. This discovery sheds additional light on the great potential of biological macromolecules to affect the structure and microstructure of growing minerals, and, therefore, some of their physical properties.

Results and Discussion

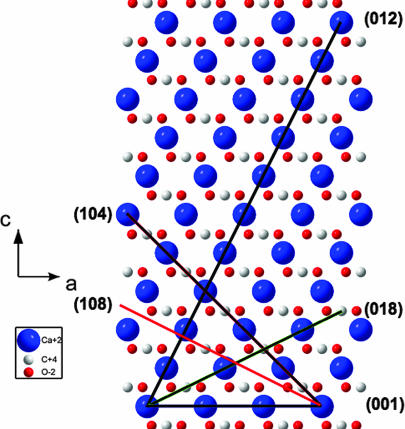
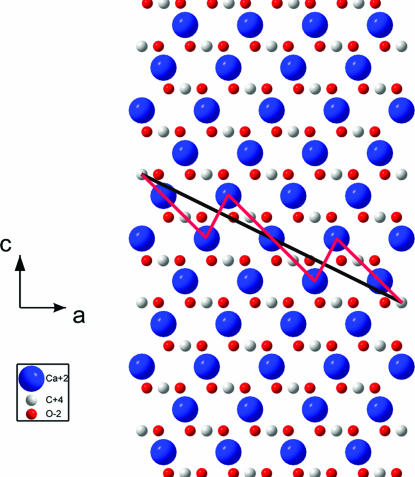
Normally, crystalline twins are defined by crystallographic planes, which relate two parts of a twinned crystal by a mirror reflection through a net plane or twofold rotation around the normal to the plane. In centrosymmetric crystals, to which calcite belongs, these two operations are equivalent. As a rule, the twin plane is a compactly packed one that prevents breaking of short (and therefore strong) bonds during the atomic rearrangements that accompany the twin formation. This observation is well illustrated by the known four twin laws in rhombohedral calcite, for which the Miller indices (hkl) of the twin planes (in hexagonal setting) are as follows: (001), (012) [or (−102)], (104), and (018) [or (−108)]. Recalling the structure of calcite in the hexagonal setting [(0,0,0) and (0,0,1/2) for Ca and (0,0,1/4) and (0,0,3/4) for the centers of planar carbonate groups (CO₃) plus internal translations +(2/3,1/3,1/3) and +(1/3,2/3,2/3)] and looking on the c–a plane of the calcite lattice (see Fig. 1), one can comprehend why only these four twin planes were identified in calcite during 150 years of investigations.

Fig. 1.

Axonometric projection of the calcite lattice in hexagonal axes on the c–a-plane (a view along the hexagon edge inclined by 120° to the translation vector a). The atoms are colored as follows: Ca, blue; C, white; O, red.

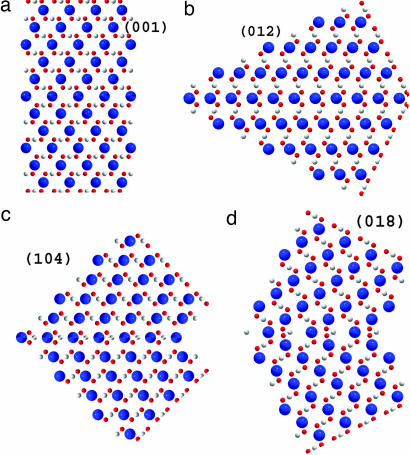
In fact, the (001)-planes are composed of pure calcium or carbonate sublayers, in which neighboring Ca atoms or carbonate groups are shifted along the translation vector a by a lattice parameter a = 4.991 Å, whereas the separation between adjacent sublayers along the translation vector c is d = c/12 = 1.422 Å. The angle between the c axes in twinned crystal parts in this case is evidently, α = 180° (see Fig. 2a).

Fig. 2.

Atomic ordering in different types of calcite twins: (001) (a); (012) (b); (104) (c); and (018) (d). The atoms are colored as follows: Ca, blue; C, white; O, red.

The (012)- or (-102)-planes (see Fig. 1) are built of pure calcium and carbon sublayers separated by d = (c/4)sin[arctan(2a/c)] = 2.154 Å. The neighboring atoms within individual sublayers are shifted by $\sqrt{a^2+{(c/2)}^2}/3=3.295Å$. An angle between the c axes in twinned crystal parts equals β = 180° − 2arccos[1/ $\beta =180°-2\arccos \left[1/\sqrt{1+(1/3){(c/a)}^2}\right]=53.74°$ (see Fig. 2b).

Twin planes (104) and (018) [or (−108); see again Fig. 1] are composed of only one type of sublayers, which contain alternating calcium and carbon atoms. For the (104)-plane, the in-plane distance between adjacent Ca and C atoms equals $\sqrt{c^2+{(4a)}^2}/12=2.189Å$ and separation between sublayers is d = [csin(arctan(4a/c)]/4 = 3.243 Å. The angle between the c axes in twinned crystal parts equals $\gamma =180°-2\arccos \left[1/\sqrt{1+(1/12){(c/a)}^2}\right]=90.76°$ (see Fig. 2c). For the (018)- plane, the in-plane distance between Ca and C atoms equals $\sqrt{{(c/2)}^2+{(4a)}^2}/6=3.618Å$, and the separation between layers is d = (c/6)cos[arctan(c/8a)] − (a/3)sin[arctan(c/8a)] = 1.961 Å. The angle between the c axes in twinned crystal parts is $\delta =2\arccos (1/\sqrt{1+(1/48){(c/a)}^2})=127.47°$ (see Fig. 2d).

At the same time, it is evident from Fig. 1 why twin planes with Miller indices of (102), (014), and (108) do not exist: they have much lower atomic occupancies. For example, the distance between neighboring Ca and C atoms along the (108)-trace is $\sqrt{{(c/4)}^2+{(2a)}^2}=10.855Å$, i.e., being much larger than that one for the (018)-plane. Dissimilarity between the (018)- and (108)-planes is clearly seen when comparing them in the rhombohedral (actual calcite symmetry) axes (HKL), by using the transformation law:

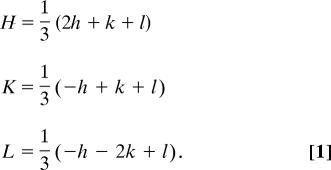By means of Eq. 1, the (018)-plane is transformed into the (332)-plane, whereas the (108)-plane is transformed into the (10.7.7)-plane. Larger Miller indices imply that the atomic planes rarely intersect the atomic positions. Bearing all these considerations in mind, we were greatly surprised when, in our growth experiments described below, we unequivocally found a formerly unknown type of twinning in calcite, i.e., via the (−118)-plane in the hexagonal setting or (7.10.7)-plane in the rhombohedral setting. This twin plane is structurally equivalent to the formerly “forbidden” planes: the (108) or (0–18)-planes.

When calcite is grown by the method described below (see Materials and Methods) with no protein in the crystallization solution, the grown crystals have regular rhombic shape with well-defined (104) cleavage faces [see supporting information (SI) Fig. 7]. Single-crystal diffraction patterns taken from such crystals always revealed rhombohedral symmetry with lattice parameters (in hexagonal axes) equal a = 4.991 (1) and c = 17.066 (1) Å, which fit well the previously reported values (13, 14). In contrast, when calcite crystals are grown in the presence of Caspartin (a 17-kDa intracrystalline protein extracted from the bivalve shell Pinna nobilis) there is an expansion of lattice parameters, by nearly 0.1% in the c-direction and 0.05% in the a-direction, depending on the protein concentration in solution (13). Lattice expansion up to 0.2% along the c-direction and 0.08% in the a-direction was also detected in biogenic calcite crystals obtained from the P. nobilis and Atrina rigida mollusk shells (13). Lattice swelling when observed, clearly indicates that the organic macromolecules enter the calcite crystallites and affect long-range crystal growth. In addition, we found that some of the crystals grown in the presence of Caspartin had morphologies differing from the regular rhombic shape (see SI Fig. 8). The crystals grown with the assistance of protein were also examined by x-ray powder diffraction and revealed characteristic calcite diffraction pattern with no diffraction peaks from aragonite or vaterite (metastable polymorphs of calcium carbonate).

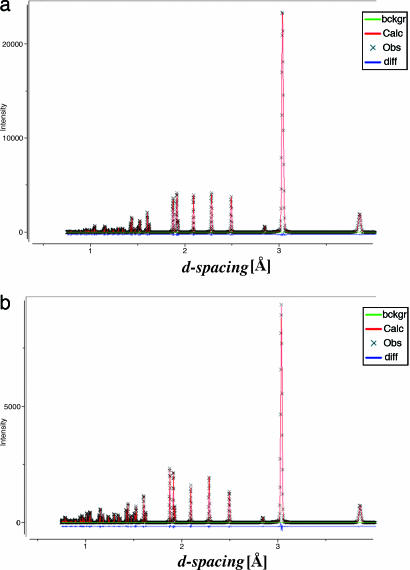
One such crystal was attached by grease to a glass rod and mounted onto a single-crystal diffractometer. By using graphite monochromatized Mo Kα radiation, 2,029 reflections were collected up to 2θ = 67.4°. The collected data yielded a monoclinic body-centered cell with the cell parameters: a₁ = 12.864 Å, b₁ = 4.989 Å, c₁ = 19.116 Å, β₁ = 90.27°, and V₁ = 1,226.8 ų. At this step, a good model (R factor 22%) was achieved for 20 molecules of CaCO₃. However, the powder diffraction pattern calculated with the extracted structural parameters was found to be very similar to that one obtained for the hexagonal calcite structure (see Fig. 3). We note, that the hexagonal unit cell of calcite with translations A₁, A₂, and C (where the vector C is perpendicular to both vectors A₁ and A₂) could indeed be reduced to the monoclinic body-centered unit cell with translations a, b, and c (where the vector b is perpendicular to both vectors a and c) by using the following relationships:

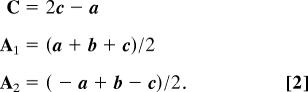Fig. 3.

Calculated powder diffraction patterns for monoclinic unit cell obtained in the single-crystal diffraction measurements (a) and standard hexagonal unit cell of calcite (b).

With the aid of Eq. 2, the hexagonal unit cell of calcite is reduced to the monoclinic one (space group I2/a) with the following unit cell parameters: a = 8.098 Å, b = 4.991 Å, c = 6.377 Å, β = 107.8°, V = 245.5 ų. Comparison of the unit cell volumes, V₁ and V, gave an integer ratio of 5:1, i.e., the reduction of 20 molecules of CaCO₃ to only 4. The latter provides the correct number of 6 molecules for the standard hexagonal unit cell if one takes into account that the volume of the body-centered monoclinic unit cell is 2/3 of the volume of the hexagonal unit cell. This analysis together with the fact that both b₁ and b values of monoclinic structures are practically equal to the length of the A₁ and A₂ translations in the hexagonal setting, forced us to consider possible variants of twinning in the a–c plane, i.e., perpendicular to the b vector. In fact, introducing a merohedral twinning into the monoclinic lattice allowed us drastic improvement of the model refinement (R = 6.7%) for the twin ratio of 0.87/0.13 [see SI Crystallographic Information File (CIF)].

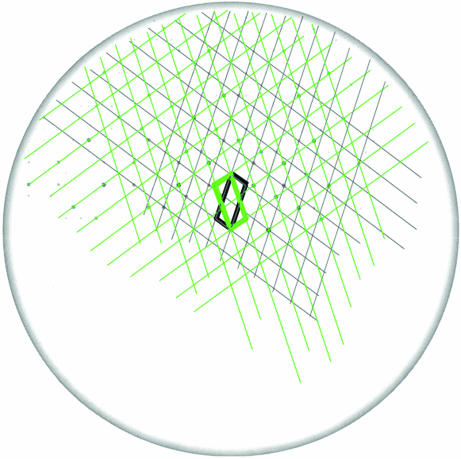
To find the twin plane, the (a*–c*)-slice in the reciprocal space was constructed for the twinned body-centered monoclinic lattice by using the maXus program package. In this slice (see Fig. 4), two lattices turned by 37° are clearly seen. The trace of the twin plane is along the direction, t* = a* + 2c*. If so, an angle between the individual lattices in Fig. 4 should be φ = 2·arccos[t*·c*/(|t*|·|c*|)] = 37.01°, which fits the observation. By using the condition, n*·t* = 0, the normal to the twin plane, n*, is obtained as n* = −2a* + c*. To receive the Miller indices of the twin plane in the hexagonal axes we used the transformation law

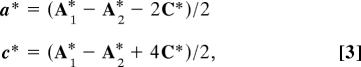which could be derived from Eq. 2 taking again into account that the volume of the body-centered monoclinic unit cell is 2/3 of the volume of the hexagonal unit cell. By applying Eq. 3 to vector n*, one obtains the twin plane in the hexagonal setting as (−118). As we mentioned before, this twin is structurally identical to the (108)-type, the latter being unknown within the established four twin laws for calcite.

Fig. 4.

Reciprocal lattice slice normal to the b*-vector-containing diffraction spots and two reciprocal lattices, corresponding to the twinned crystal parts. The unit cells of these lattices are outlined by bold black and green lines.

A further illustration of this finding is provided by constructing the (a*–c*)-slices for the known twins in calcite (not shown here). According to calculations, the known twins are characterized by completely different misorientation angles on the (a*–c*)-slices as compared with φ = 37.01° for the (−118)-twin. In fact, these angles are φ = 63.0° for the (018)-twin plane, φ = 143.3° for the (104)-twin plane, φ = 26.1° for the (001)-twin plane, and φ = 1.4° for the (012)-twin plane.

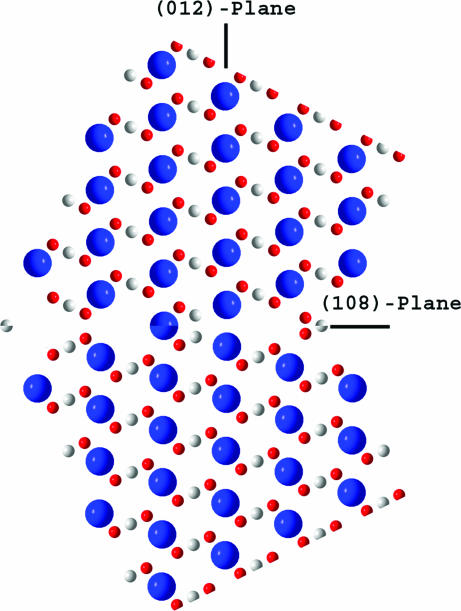
The discovered twin of the (108)-type (see Fig. 5) differs remarkably from the known one, (018), in real space as well. When comparing Figs. 5 and 2d, we find an interesting feature, specifically, almost exact continuation of the trace of the (012)-plane across the twinned crystal in the case of the (108)-twinning law (see Fig. 5). In fact, an angular change of only 1.2° occurs when crossing the twin plane. In other words, the normal to the twin plane, H = (108), practically coincides with the lattice vector L = [201], which represents the atomic rows mentioned (see Fig. 1). The deviation is merely 0.6°, so that the twin lattice common to both crystal individuals is formed (1, 15). The twin index, i, which is the ratio of the volumes of the unit cells of the twin lattice and the crystal lattice (15), equals i = (1/2)H·L = 5. This value exactly fits the ratio, V₁/V = 5, found when using the structure refinement procedures described above.

Fig. 5.

Atomic ordering in the (108)-twin. The atoms are colored as follows: Ca, blue; C, white; O, red.

Note that, according to our recent structural study (16), the (012)-plane may play an important role in the growth of biogenic calcite. In particular, we observed that crystallite sizes in calcitic shell P. nobilis, from which the specific protein Caspartin was extracted, are highly anisotropic, reaching the maximum (≈800 nm) along the normal to the (012)-plane. Under mild heat treatment at 200°C, which leads to protein degradation, the crystallite sizes are drastically reduced down to 200 nm. These findings allowed us to conclude that organic macromolecules facilitate the crystal growth in certain directions. Moreover, these molecules are apparently attached to appropriate atomic planes (and the (012)-plane has a favorable atomic structure described above) being in registry with some atomic groups of calcite (16). At this stage, we indicate deep involvement of the specific atomic plane in crystal growth and twinning, both in the presence of organic macromolecules, which may be important for further studies of biomineralization.

We believe that the proteins added to the crystallization solution play an important role in the twin formation. To strengthen this conclusion, one should consider more carefully the structure of the boundary between the twinned crystal parts (see Fig. 6). As was mentioned in the beginning of this article, the twin formation at the (−118)-plane or (108)-plane is much less realistic than at the (018)-plane because the corresponding atomic occupancies are low. The atomic occupancy would be much higher if the interface between twinned crystal parts is built of the (104)-terraces (2.189 × 4 = 8.756 Å long) connected by the (012)-oriented kinks (3.295 Å long) (see Fig. 6). The median of this zigzag line is still the trace of the (108)-plane, but individual segments are densely packed. Now under twinning, the twinned parts are connected leaving some open space, which could adopt fragments of organic macromolecules entering from the crystallization solution. In such a way, free interface energy would be greatly reduced. To clarify the atomic arrangement in the vicinity of the twin plane, which can differ from this simple geometrical picture because of lattice relaxation, the modern high-resolution transmission electron microscopy techniques may be very helpful.

Fig. 6.

Axonometric projection of the calcite lattice in hexagonal axes on the c–a-plane (a view along the hexagon edge inclined by 120° to the translation vector a). The black solid line is the trace of the (108)-plane. The red zigzag line is the suggested profile of the interface along which the twinning probably occurs. The atoms are colored as follows: Ca, blue; C, white; O, red.

The discovered twinning law in calcite provides additional evidence of the important and multifunctional role played by organic macromolecules in biomineralization. This finding demonstrates that proteins can influence the twinning process in ceramic crystals. We show that during the protein-assisted calcite growth a formerly unknown twinning form has arisen. Nowadays, it is widely accepted that in biogenic crystals specific proteins are incorporated within individual crystallites (13, 16–18). If they give rise to formerly unidentified twinning planes there, this development will influence the mechanical properties of biogenic crystals produced in nature, which in fact are different as compared with their geological counterparts (11, 12). This important issue deserves further investigation. Our findings shed additional light on the complex process of biomineralization, helping to gain deeper understanding toward the development of new methods for controlling the structure and properties of materials by using appropriate biological macromolecules.

Materials and Methods

Single crystals of calcite were grown at room temperature (22 ± 2°C) and atmospheric pressure from a solution containing Caspartin (an intracrystalline 17-kDa protein), which was extracted from the bivalve shell P. nobilis (see ref. 19). Growth experiments were accomplished in a sealed desiccator by slow diffusion of CO₂ vapor [the product of the decomposition of NH₄(CO₃)₂] into 1 ml of 10 mM CaCl₂ within the wells of a 24-well tissue culture box, tightly sealed by a transparent polyethylene film (similar to ref. 20). Purified Caspartin protein was mixed before crystallization at a concentration of 3 μg/ml with 10 mM CaCl₂. After these preparations, identical diffusion outlets were produced in all of the wells by a 21G needle. After 48 h of crystallization, the polyethylene film was removed and the grown single crystals, a few tens of micrometers in size, were first monitored by a bifocal optical microscope. Selected samples were examined by using an FEI (Eindhoven, The Netherlands) Quanta Environmental SEM. For x-ray powder diffraction measurements, a Philips X-Pert diffractometer equipped with a Cu-sealed tube and curved graphite crystal-monochromator was used. Single-crystal diffraction measurements were performed by means of a Nonius KappaCCD diffractometer equipped with a Mo-sealed tube and graphite crystal-monochromator.