Water surface is acidic

Abstract

Water autoionization reaction 2H₂O → H₃O⁻ + OH⁻ is a textbook process of basic importance, resulting in pH = 7 for pure water. However, pH of pure water surface is shown to be significantly lower, the reduction being caused by proton stabilization at the surface. The evidence presented here includes ab initio and classical molecular dynamics simulations of water slabs with solvated H₃O⁺ and OH⁻ ions, density functional studies of (H₂O)₄₈H⁺ clusters, and spectroscopic isotopic-exchange data for D₂O substitutional impurities at the surface and in the interior of ice nanocrystals. Because H₃O⁺ does, but OH⁻ does not, display preference for surface sites, the H₂O surface is predicted to be acidic with pH < 4.8. For similar reasons, the strength of some weak acids, such as carbonic acid, is expected to increase at the surface. Enhanced surface acidity can have a significant impact on aqueous surface chemistry, e.g., in the atmosphere.

In room-temperature liquid, one in 6 × 10⁸ water molecules is autoionized, yielding the standard value of pH = 7. Autoionization in crystal ice should be less favorable, because, in contrast to water, ice is a very poor solvent of ionic and polar substances (1). As recently realized (2–5), the chemistry and composition of aqueous surfaces are quite distinct from that of the bulk; therefore, autoionization behavior should be reexamined at the surface.

A number of recent computations (6–8) indicated the preference of hydronium cations for surface positions. Surface propensity of H₃O⁺ was also deduced from vibrational spectroscopy of large protonated water clusters (6), as well as vibrational sum frequency generation (8, 9) and second harmonic generation (10) spectroscopic experiments probing extended aqueous interfaces. Interestingly, zeta potential measurements and titration experiments on oil droplets dispersed in water indicated the presence of negative charges at the interface, interpreted as adsorbed OH⁻ ions (11). Similar conclusions have also been drawn from zeta potentials of air bubbles in water (12). More work is clearly needed to reconcile this apparent discord between predictions of surface-selective spectroscopies and molecular simulations on one side and electrochemical measurements on the other side.

H₃O⁺ forms three strong proton–donor bonds to H₂O, but acts as a poor proton acceptor. A surface position with only H atoms hydrogen-bonded is preferred to interior positions, because the latter are associated with disruption of the approximately tetrahedral hydrogen-bond network in water (10). The present work focuses on the effect of surface stabilization of hydronium on water autoionization and surface pH.

Calculations

Overview.

Modeling of proton-tranfer systems is a nontrivial problem, because standard (empirical) potential energy surfaces do not include a possibility of proton hopping between different water molecules or transitions between the two limiting protonated water forms (the hydronium H₃O⁺ and the Zundel ion H₂O·H⁺·OH₂). In the present study, three complementary computational approaches were used. First, constant volume and temperature (NVT) ab initio molecular dynamics simulations were carried out for liquid water with a pair of H₃O⁺ and OH⁻ ions. To assess surface effects, the simulation was carried out for both a box with 3D periodic boundaries and a slab with two open surfaces and 2D periodic boundaries. This “on-the-fly” technique enables first-principle modeling of proton transfer systems at finite temperatures; proton transfer and transitions between the different protonated-water forms are automatically included in the computational scheme. However, the high computational cost limits the dimensionality of the model system, the duration of the trajectories, and the accuracy of the electronic structure method used to evaluate the forces and the energies.

Direct simulation of autoionization is not easily feasible because of the activation barrier (see, however, a pioneering study of bulk autoionization in ref. 13). On the other hand, recombination between H₃O⁺ and OH⁻ can be readily observed in on-the-fly simulations, on a feasible time scale, enabling qualitative assessment of the autoionization energetics. On-the-fly results suggest a significant lowering of the endothermicity of the autoiozation reaction at the surface, with respect to the bulk, because of the stabilization of the protonated water at the interface.

To assess more quantitatively the extent of this stabilization, ab initio techniques were applied to calculate the energy of a protonated water cluster (H₂O)₄₈H⁺ with the proton either at the surface or in the interior. At this size, fairly accurate electronic structure calculations can be made for the system energetics. The calculations indicated substantial energy lowering upon proton transfer from the interior to the surface of the cluster. However, behavior of an aqueous solution is ultimately determined by the free-energy (rather than the energy) difference between the interior and the surface ion states. Calculations of the free-energy differences (ΔG_sb) between these states are feasible only with empirical potentials. Such calculations were performed in the third part of the study, for aqueous solutions in slab geometry of protonated-water ions in the two limiting forms (hydronium and Zundel) and of the hydroxide ion. Polarizable potentials were used, which were calibrated against cluster ab initio data. In this part, the use of potential models that do not include proton transfer is reasonable because a thermodynamic rather than a dynamic quality is calculated. The resulting ΔG_sb values were consistent with enhanced acidity of the neat water surface, because of proton preference for the surface and lack thereof for the hydroxide. The different computations are described in more detail below.

On-the-Fly Dynamics.

NVT classical trajectories were evaluated at 270 K. The nuclei moved on the Born–Oppenheimer potential energy surface, which was calculated at each time step at the Becke-Lee-Yang-Parr (BLYP) level of the density functional theory (DFT) using a double-zeta polarization basis set (DZVP). The CP2K/QUICKSTEP package was used (14); see Fig. 1 and Computational Methods for further technical details. First, a single ion (H₃O⁺ or OH⁻) was simulated in an 11-Å-thick water slab containing 71 water molecules. Throughout a 2.5-ps simulation, the cation remained at the surface. In a similar simulation, the anion underwent initially several quick proton transfer cycles between the surface and the interior, but after 0.3 ps settled in the interior of the slab for the remainder of the simulation. The latter result is consistent with recent sum frequency generation data and simulations using an empirical potential, which indicated lack of surface preference for hydroxide (8, 9).

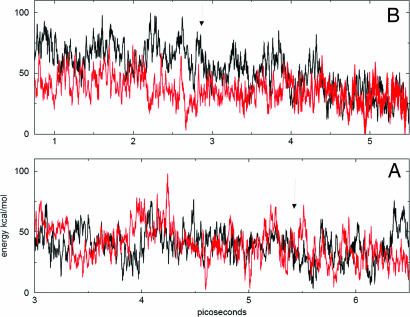
Fig. 1.

Born-Oppenheimer potential energies corresponding to NVT (at 270 K) on-the-fly trajectories of Zwitterionic systems containing an H₃O⁺, OH⁻ ion pair (black) and of corresponding neutral liquid H₂O systems without ions (red). (A) A ≈11-A-thick slab of water in a 2D periodic box. (B) A cubic box of water with 3D periodic boundaries. Arrows mark the time of the ion-pair recombination; note subsequent lowering of the energy in the black curve of B and the absence thereof in A. In A, the mean energies of the system with the ion pair, and of the neutral system, were −1,236.794 (0.017) and −1,236.791 (0.022) Hartree, respectively; the numbers in the parentheses denote standard deviation. In B, the corresponding energies were −1,099.363 (0.0180) and −1,099.413 (0.0180), respectively. In the plots, the zero of the energy was shifted, and the units were transformed to kcal/mol. The calculated mean energy differences between the Zwitterionic and neutral systems are −0.003 Hartree = −2 ± 18 kcal/mol and 0.05 Hartree = 31 ± 16 kcal/mol, for A and B, respectively.

Simulation of a slab including both ions (H₃O⁺ and OH⁻) required some effort, because, due to the limited dimensionality of the model, the ions tended to recombine before relaxing. Different initial locations were tried for the two ions. Finally, a trajectory was generated in which the two ions acquired favorable solvation shells before recombining and thus survived for 5.4 ps. During the first picosecond of this trajectory, the two ions formed an interesting solvent-separated ion pair, with the central water molecule acting as proton acceptor with respect to both ions. (In this configuration, recombination is blocked by the central water molecule; such configurations may in fact serve as intermediates in the autoionization process in water.) During this part of the trajectory, the ion pair resided in the slab interior; however, the proton underwent numerous back-and-forth transitions between the ion-pair configuration and the surface. At t ≈ 1 ps, the two ions separated; the proton moved to the surface, whereas the hydroxide adopted an interior position. The ions remained so until just before recombination (t ≈ 5.3 ps), at which time the anion emerged at the surface.

Fig. 1A shows the energy of the system along the trajectory, together with energy for a trajectory of a neutral water slab without the ions. The two energies are the same within the accuracy of the calculation. The energy difference between the autoionized and neutral system cannot be assessed quantitatively from this calculation, because of the large potential energy fluctuations of the finite dimensionality systems and the limited accuracy of the DFT/BLYP method. However, one may note the qualitative difference with respect to a bulk on-the-fly simulation, using cubic 3D periodic boundaries, for which the energy of the autoionized system clearly exceeded the energy of the neutral one (Fig. 1B). Note in Fig. 1B that the drop in potential energy is delayed by 1 ps with respect to recombination, marked by the arrow, because the surrounding water molecules need some time to relax to the new environment of the recombined ion pair. These on-the-fly results are consistent with preference of protonated water for surface sites and suggest reduced endothermicity of autionization at the liquid surface caused by surface stabilization of the cation.

Search for Low-Energy Structures of the (H₂O)₄₈H⁺ Cluster.

Because OH⁻ does not display surface preference, the crucial quantity for the present argument is the free energy lowering as the proton is moved from the H₂O bulk to the surface. The main contribution is expected to originate from the energy change caused by surface stabilization of the proton. To estimate the energy change, a search was made for low-energy structures of a protonated water cluster (H₂O)₄₈H⁺, with the proton either on the surface or in the interior. At this size, Becke three-parameter hybrid functional combined with Lee–Yang–Parr correlation functional (B3LYP) calculations can be made of the system energetics. The B3LYP method is expected to yield much more accurate energy values than the BLYP used in the slab and bulk calculations; as a matter of fact, this method benchmarked very well against more accurate ab initio calculations for autoionization in the water octamer (15).

The initial search for low-energy cluster structures used a molecular dynamics-based method as described (16). Microcanonical trajectories lasting several nanoseconds were run for the cluster at a mean temperature of ≈200 K. At this stage, the calculation used a nonpolarizable version of the empirical potential for the hydronium–water system (8). Trajectory structures were minimized every 5 ps. A bank of ≈1,200 perspective minima was thus obtained, with the hydronium either at the cluster surface or in the interior. The energies of the minima were then recalculated at the BLYP/DZVP level, following a single minimization step. Ten thus-obtained lowest-energy structures of each kind (i.e., with the proton at the surface or in the bulk) were subjected to full minimization at the BLYP/DZVP level. The final energies were then recalculated at the B3LYP level. The average energy difference between the 10 lowest energy minima with the proton in the interior and the 10 lowest energy minima with the proton at the surface was 8.7 and 10.5 kcal/mol, for B3LYP and BLYP, respectively. Three of the lowest energy minima of each kind were furthermore fully reoptimized at the B3LYP level, resulting in an 8.8 kcal/mol energy difference between a pair of lowest energy minima of each kind. This energy preference for surface structures is consistent with the values obtained by other authors (6, 7) for smaller (H₂O)_n=20,21H⁺ clusters, which, however, acquire a rather special cage-like geometry.

Calculations of ΔG_sb.

Finally, to assess the surface preferences of protonated and deprotonated water, free-energy differences ΔG_sb between the bulk and the surface for the ions are needed. For that purpose, simulations using thermodynamic integration were carried out for each ion dissolved in a slab of liquid water. The scope of these simulations necessitated the use of computationally efficient empirical potentials, which were calibrated against ab initio MP2/aug-cc-pvdz geometries and energies of small water clusters with H₃O⁺ or OH⁻. For further computational details, see Fig. 2 and Computational Methods. For H₃O⁺, the calculation predicted a free-energy preference for the surface of ≈3 kcal/mol. This value is likely a lower bound, because the empirical potential underestimates, with respect to B3LYP, the average energy difference between “in” and “out” structures of (H₂O)₄₈H⁺ clusters, yielding an average energy difference of ≈4 kcal/mol. Thus, ΔG_sb of the proton deduced from the empirical potential could be too small by up to 4 kcal/mol, because of the underestimation of this energy difference. Additional ΔG_sb calculations using an empirical potential were carried out for the proton-sharing Zundel form of protonated water H₂O·H⁺·OH₂; the ΔG_sb value obtained in the simulation was similar to that of the H₃O⁺ ion. (Zundel ions were examined, because according to our on-the-fly calculations, ≈30% of protonated water configurations resemble the Zundel rather than the H₃O⁺ ion.) In contrast to hydrated proton, no surface preference was found for OH⁻, which weakly prefers the bulk with ΔG_sb of −1 to −2 kcal/mol. A typical snapshot depicting a surface-bound H₃O⁺ and bulk OH⁻ is shown in Fig. 2.

Fig. 2.

A typical snapshot from a molecular dynamics simulation depicting a surface bound H₃O⁺ (red and white) and bulk OH⁻ (orange and white) in an aqueous slab (blue and white). The two neighboring periodic images of the solvent next to the unit cell are also depicted (shaded representation).

Using the above lower bound of the proton surface stability ΔG_sb = 3 kcal/mol, one obtains at 300 K a ≈150-fold increase in surface concentration of H₃O⁺ compared with the bulk. [This is a larger surface enhancement then observed in our previous MD simulations (8), mainly because of a refined potential and lower H₃O⁺ concentration in this study.] This value translates to pH ≈4.8 of the top-most layer of neat water (as usual, we define pH as the negative logarithm of proton concentration rather than of its activity, which is justified at these low ion concentrations). Assuming the above upper-bound ΔG_sb value for H₃O⁺ suggests surface pH possibly as low as 1.9. At the same time, the surface pOH is estimated as 7.7–8.4. We thus conclude that the surface of pure water is acidic.

Experiment

Additionally, we present experimental evidence that ice nano crystal surfaces are slightly acidic, similar to liquid H₂O surfaces. Proton activity in ice can be monitored by observation of isotopic exchange (17–20), because the only known mechanism of the reaction D₂O + H₂O → 2HDO at experimental temperatures is via proton transfer (1). In the absence of acidic impurities, the protons are provided by H₂O autoionization. [OH⁻ contribution to the exchange is much less than that of the proton, because of a significantly lower mobility (21), i.e., no isotopic exchange is observed in thick ice films grown from the vapor of very dilute ammonia-water solutions on a time scale of days at 155 K.] In the interpretation of the experimental data, advantage is taken of some of the computational results presented above. To justify that, we note that ice nanocrystals were shown to include a ≈5-Å-thick disordered surface layer and a partially disordered subsurface layer (22). Thus, it is reasonable to surmise that surface and subsurface states of the proton at the disordered nanoparticle surface are similar to those of the amorphous (H₂O)₄₈H⁺ cluster and a cold liquid. On the other hand, interior proton states are expected to be more unfavorable inside the nanocrystal than inside (H₂O)₄₈H⁺ or the liquid, because, in contrast to the liquid, crystal ice is a very poor solvent (1).

Experimental Technique.

Infrared spectroscopic observation of isotopic exchange in/on ice nanoparticles in the 110- to 150-K temperature range was carried out much as described (18). Aerosols of H₂O particles, with an average diameter in the 12- to 40-nm range, were prepared containing small percentages of intact D₂O. Gas pulses from two separate 1-liter He(g) reservoirs with the same total gas pressure, one containing 1.0% of H₂O and the other ≈0.1% of D₂O, were transmitted by coaxial tubing to the inside of a double-walled cold-condensation cell. Simultaneous release and thorough overlap of the gas pulses allowed ice nanocrystals to form with nearly uniform distribution of D₂O between and within the particles. Significant H–D exchange occurred during gas handling and within the cold-droplet phase of the nanocrystal formation process, but typically every second or third deuterium appeared as intact isolated D₂O (as exemplified by the solid-line spectrum in Fig. 3 Right).

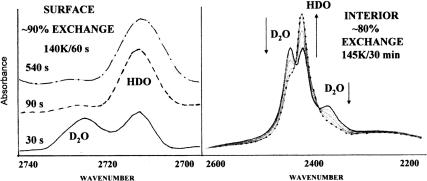
Fig. 3.

Spectroscopic signatures of proton activity using isotopic scrambling. (Left) Isotopic exchange from surface proton hopping is reflected by loss (D₂O: 2,725 cm⁻¹) and gain (HDO: 2,712 cm⁻¹) of intensity of the bands of unique surface-dangling O–D bonds. (Right) Interior proton motion causes a much slower conversion of the isolated-D₂O doublet (2,448 and 2,370 cm⁻¹) to bands of an HDO pair having two coupled OD bonds in tandem. The prominent HDO singlet (2,420 cm⁻¹) is produced by subsequent HDO rotation from passage of an orientational defect that decouples the O–D bonds (17). For the ice nanocrystal interior, the passage of orientational defects is fast compared with proton hopping (17) so the bands of the coupled HDO (2,442 and 2,400 cm⁻¹) are hidden throughout by the more intense isolated HDO band at 2,420 cm⁻¹. Less than a minute is required to complete the surface exchange at 140 K, whereas 30 min at 145 K is required to convert most of the interior D₂O to HDO.

Ultimately, the ability to monitor the exchange rates is based on distinct spectroscopic signatures of isotopically isolated D₂O and HDO (Fig. 3). Upon passage of a mobile proton defect, an isolated D₂O is converted to an HDO neighbor pair, and subsequently, through successive molecular-turn and proton-hop steps, to isolated HDO (1, 17). Fig. 3 displays typical spectroscopic results for exchange rates at the ice nanocrystal surfaces and in their interiors. Note that we rely on the opportune presence of distinct and well spaced spectroscopic features for the two environments. The assignment of the three distinct interior bands near 2,400 cm⁻¹ (Fig. 3 Right) to isolated D₂O (symmetric stretch, 2,370 cm⁻¹; asymmetric stretch, 2,447 cm⁻¹) and isolated HDO (2,420 cm⁻¹) within ice has been thoroughly documented (1, 17).

Similarly, surface free-OH and free-OD stretch bands have been studied in detail (22) and used by in numerous investigations of ice surface adsorbates. In particular, the two free-OD surface bands (Fig. 3 Left), one of D₂O (2,725 cm⁻¹) and the other of HDO (2,712 cm⁻¹), have been used to demonstrate the preference for D-bonding over H-bonding of the single-donor surface HDO molecules (23). Identification of the HDO surface spectrum in the absence of D₂O was made by using nanocrystals prepared from premixed H₂O with <5% D₂O. The temperature-dependent preference of single-donor HDO to D-bond at temperatures used in this study limits the value of the 2,712-cm⁻¹ band as a measure of isotopic exchange (23). Therefore, quantitative rates for the surface exchange have been deduced from the decrease in the 2,725-cm⁻¹ D₂O band (see Fig. 4).

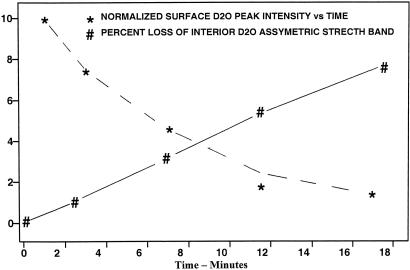
Fig. 4.

Graphical representation of interior and surface H–D exchange with time for an H₂O ice aerosol, with ≈10% D content, in He(g) at 128 K. The plots show the percent loss of the interior D₂O asymmetric-stretch band intensity (#) and the simultaneous diminution of the normalized peak intensity of the free-O–D surface band of D₂O (∗). Lines connecting data points are included as an aid to viewing.

Results.

Isotopic exchange in the ice nanocrystal interior occurs on the time scale of minutes to hours in the 150- to 130-K range, much as observed for thick ice films (17, 18). On the surface, the relative initial rate is ≈20 times faster, as deduced from data such as in Figs. 3 and 4. In the example of Fig. 3 for temperatures near 140 K, the surface exchange is nearly complete in 90 s during which time period the interior exchange is <10%. Fig. 4 shows graphically the percent loss with time of the interior D₂O asymmetric-stretch band intensity and the diminution of the normalized peak intensity of the free-O-D surface band of D₂O for a sample held at 128 K for 18 min. The latter decrease indicates a half-life of ≈7 min, whereas the decrease of the interior D₂O band by 7.8% over 18 min extrapolates to a half-life of 154 min (assuming a first-order exchange process). This result, typical of kinetic runs for numerous aerosols of “pure” ice nanocrystals, suggests a ratio of 22 for the respective rates. However, initial results, for the temperature dependence of the surface exchange rates, point to an activation energy of 5 kcal/mol, which can be contrasted with a value of ≈9 kcal/mol reported for H-D exchange within μm-thick ice films (1, 17). Thus the ratio of rates, surface-to-interior, is expected to decrease with increasing temperature.

The ≈20 ratio of surface-to-interior exchange rates indicates enhanced proton concentration at the surface and/or enhanced mobility at the surface. We shall argue here in favor of the first possibility. As noted above, ice nanocrystals were shown in the past to have disordered surfaces (22), and one expects lower mobility in the disordered medium (surface) than in the crystal one (interior). For example, it has been established that no proton transfer occurs in pure compacted amorphous ice <140 K, and that, relative to crystalline ice, a greater abundance of injected protons is required to induce H-D exchange at ≈120 K (24). Because of the surface and subsurface disorder, protonated H₂O configurations there should be similar to those in amorphous ice, liquid water, and the amorphous (H₂O)₄₈H⁺ cluster. On the other hand, proton transfer from the surface to the crystalline bulk is expected to be more endothermic than for the liquid, because, in contrast to water, crystal ice is a very poor solvent (1, 25). Further, one may note past computational results favoring a greater surface than bulk proton concentration, which showed that the O·H interaction between hydronium embedded in ice, and the proton-donating neighbor water molecule is repulsive (26).

The effect of surface impurities on the relative isotopic exchange rates is revealing. Twenty percent of a surface monolayer (ML) of H₂S enhances both the surface and interior exchange rate by only a factor of ≈2.5. Thus, at the surface the autoionization constant of water is of the same order of magnitude as K_a of H₂S, which is a weak acid. On the other hand, paralleling reports for thick ice films (21), a small amount of NH₃ adsorbate (<1% of an ML) stops the isotopic exchange altogether on the time scale of the experiment (≈30 min), evidently caused by proton trapping by the base. The exchange in the interior resumes when the ammonia coverage is increased to >10% of an ML and, with coverage >50% of an ML, the rate exceeds that of pure ice. However, now the surface exchange rate is no longer enhanced with respect to the interior. The larger amounts of ammonia generate sufficient OH⁻ so that isotopic exchange takes place despite its reduced mobility with respect to the proton (21).

Because of the poor solvation properties of crystal ice, one still expects OH⁻ to spend most of the time in noncrystalline portions of the particle. In characterization of the structures of ice nanoparticles, it has been noted that there exists a significantly distorted surface and subsurface region with a thickness of ≈1 nm (see, for example, pages 400–403 of ref. 22). The computational results suggest that OH⁻ favors the subsurface region rather than surface sites. Accordingly, the exchange induced by a large amount of NH₃ does not display any isotopic exchange enhancement of the surface, with respect to the bulk, in contrast to the pure H₂O nanoparticles. Acidity of the nanocrystal surface is a combined outcome of surface sites for the protons and subsurface sites for OH⁻.

Considering that the subsurface region differs from both the surface and the interior of the nanocrystals, it is likely that the exchange rates of that region are also unique. Kang et al. (19) have reported reactive-ion-scattering data that are consistent with a greater exchange rate in the subsurface of amorphous ice films than for the bulk. Because the nanocrystal subsurface has a distinct infrared spectrum (22), the possibility exists for extension of our methods to determine the exchange rates for this third component of the nanocrystals. However, with the present study based on relatively large nanocrystals, the subsurface D₂O/HDO bands are present as small broad components directly underlying the interior ice spectra. Studies with still smaller particles for which the subsurface bands rival the interior-ice band intensities (as for 4-nm-diameter crystals as displayed in figures 2 and 4 of ref. 22) may permit identification of the exchange rates within the subsurface.

Conclusions

Based on molecular computational and experimental evidence we have shown that the surface of neat water is acidic with pH < 4.8 because of a significant surface propensity of hydronium (but not hydroxide) ions. By argument analogous to our results for neat water, weak acid solutions can display enhanced surface acidity, i.e., surface pH reduction by at least 2.2 units, corresponding to ΔG_sb ≥ 3 kcal/mol of hydrated protons. [Note that pK_a of the acid is not necessarily reduced by the same extent, being affected additionally by ΔG_sb values of the neutral acid and the negative ion (27–29).] The case of carbonic acid is of particular interest. Under normal atmospheric conditions, bulk water exposed to the air acquires a pH of 5.7 because some of the dissolved CO₂ gas undergoes a reaction CO₂ + 2 H₂O → H₃O⁺ + HCO₃⁻ At the surface, pH will be reduced more significantly than in the bulk, because of surface propensity of hydronium ions. Enhanced acidity of water surface can have a significant impact on aqueous surface chemistry in natural atmospheric environments, cloud nucleation, thundercloud electrification, and electrochemistry (e.g., corrosion processes).

As noted in the Introduction, the present results contradict the microscopic interpretation proposed for macroscopic titration experiments and zeta potential measurements on oil emulsions and gas bubbles in water (11, 12). Those experiments indicated negatively charged surfaces. It was proposed that this effect is caused by a substantial surface propensity of OH⁻ and lack thereof for H₃O⁺. The existing controversy between molecular simulations and spectroscopic experiments on one side and macroscopic measurements on the other side, which probably cannot be fully resolved at the moment, is discussed in detail in ref. 30.

Computational Details

The ab initio molecular dynamics simulations used an on-the-fly NVT code as implemented in the CP2K/QUICKSTEP package (14). The scheme combines a Gaussian basis for the wave functions with an auxiliary plane wave basis set for the density. The DFT/BLYP functional was used in conjunction with the DZVP basis and pseudopotentials of the Goedecker-Teter-Hutter type (31). The time step was 0.5 fs. The first simulation pertained to a slab of 72 water molecules in a 13.47 × 15.56-Å 2D periodic box; the thickness of the slab was ≈11 Å. A Martyna-Tuckerman Poisson solver was used in the calculation with 2D periodic boundaries (32). In the simulations with a single ion, one of the surface water molecules was converted initially to either H₃O⁺ or OH⁻ by addition or subtraction of an H atom. Additional simulations were carried out for a zwitterionic system, after converting two water molecules to H₃O⁺ and OH⁻. The second set of simulations pertained to 64 water molecules in a cubic box of dimension 12.41 Å, with 3D periodic boundaries. For both 3D and 2D periodic boundary conditions long-range electrostatic interactions were accounted for via an Ewald summation. For the above computational parameters, the water self-diffusion constant in a 3D box is 2.50 and 0.52 10⁻⁵ cm²·s⁻¹ at 300 and 270 K, respectively, as compared with the experimental values of 2.57 and 1.13 10⁻⁵ cm²·s⁻¹ at 298 and 273 K, respectively (33, 34). The simulations were carried out finally at 270 K, because at this temperature it was easier to stabilize the hydronium-hydroxide ion pair within the finite size box.

For the free-energy calculations we used the thermodynamic integration method as implemented in a classical molecular dynamics package, Gromacs 3.3.1 (35), with a control routine (36) ensuring statistical error below a given threshold (≈1 kcal/mol). This procedure required nanosecond time scale runs, which were performed in the NVT (300 K) ensemble by using a 1-fs time step. The slab was formed by placing 432 POL3 (37) water molecules, H₃O⁺ (Eigen) or H₅O₂⁺ (Zundel), and OH⁻ into a 3D periodic unit cell of 18.7 × 18.7 × 237 Å. A 9-Å interaction cut-off with a particle mesh Ewald sum (38) for long-range electrostatic interactions was used. We tested a set of potential parameters for these ions, which we either took from literature (8) or fitted the van der Waals radius of the oxygen of the ion against ab initio MP2/aug-cc-pvdz geometries and energies of clusters containing H₃O⁺ or OH⁻ with three strongly bound water molecules. Alternatively, we aimed to match the energy difference between the surface and bulk located hydronium, as obtained in the above DFT calculations for the (H₂O)₄₈H⁺ clusters. In either case, we did not allow the ion oxygen radius H₃O⁺ to deviate >10% from those of the previously used models (8) to remain within physically reasonable potential parameters.

Abbreviations

NVT

constant volume and temperature

DFT

density functional theory

BLYP

Becke-Lee-Yang-Parr

B3LYP

Becke three-parameter hybrid functional combined with Lee–Yang–Parr correlation functional

ML

monolayer

DZVP

double-zeta polarization basis set.