Coherent neural representation of hand speed in humans revealed by MEG imaging

Abstract

The spiking activity of single neurons in the primate motor cortex is correlated with various limb movement parameters, including velocity. Recent findings obtained using local field potentials suggest that hand speed may also be encoded in the summed activity of neuronal populations. At this macroscopic level, the motor cortex has also been shown to display synchronized rhythmic activity modulated by motor behavior. Yet whether and how neural oscillations might be related to limb speed control is still poorly understood. Here, we applied magnetoencephalography (MEG) source imaging to the ongoing brain activity in subjects performing a continuous visuomotor (VM) task. We used coherence and phase synchronization to investigate the coupling between the estimated activity throughout the brain and the simultaneously recorded instantaneous hand speed. We found significant phase locking between slow (2- to 5-Hz) oscillatory activity in the contralateral primary motor cortex and time-varying hand speed. In addition, we report long-range task-related coupling between primary motor cortex and multiple brain regions in the same frequency band. The detected large-scale VM network spans several cortical and subcortical areas, including structures of the frontoparietal circuit and the cerebello–thalamo–cortical pathway. These findings suggest a role for slow coherent oscillations in mediating neural representations of hand kinematics in humans and provide further support for the putative role of long-range neural synchronization in large-scale VM integration. Our findings are discussed in the context of corticomotor communication, distributed motor encoding, and possible implications for brain–machine interfaces.

Neurophysiological recordings in nonhuman primates have revealed that neuronal discharges in primary motor cortex (M1) are correlated with various movement parameters, including hand speed (1, 2). Furthermore, recent findings show that information on hand speed may also be accessible, at a more macroscopic level, from the summed synaptic activity of neural populations by recording local field potentials (LFPs) in M1 (3). Velocity-related activity has also been found in other brain areas, including the premotor cortex (2), posterior parietal cortex (4), and cerebellum (5). Recent reports based on simultaneous multielectrode recordings (6, 7) lend further support to the hypothesis that limb kinematics are encoded in multiple cortical areas. In humans, cerebral areas involved in speed control can be detected with functional imaging (8, 9). However, the investigation of the underlying neural mechanisms requires high (millisecond-range) temporal resolution and is still poorly understood.

Evidence from a parallel body of research investigating rhythmic activity in motor cortex, its relationship to peripheral motor behavior (10, 11), and its interaction with muscle activity (12–20) suggests that neural oscillations in distinct frequency bands are related to various aspects of motor behavior and may play a functional role in corticomuscular communication. However, it is still unclear from these studies whether oscillatory brain activity is directly related to limb speed and, if so, to what extent it contributes to mediating neural representations thereof. Indeed, previous work has largely focused on the role of central oscillations in isometric motor behavior, rather than on fine-tuned skilled motor control. Here we used whole-head magnetoencephalography (MEG) and recent source-imaging solutions (21), combined with spectral analysis techniques, to investigate the putative relationship between ongoing neural oscillations and time-varying hand speed in humans performing a continuous visuomotor (VM) compensation task.

Results

We recorded neuromagnetic signals from 15 subjects while they continuously manipulated a track ball to counter the unpredictable movements of a cube randomly rotating about its center [see supporting information (SI) Movies 1 and 2]. The subjects were cued to switch between the VM task and a resting (R) condition every 8–12 sec. The track-ball displacements were acquired simultaneously with the steady-state MEG data and were used to derive the trace of the instantaneous speed of the manipulative hand movements throughout the experiment. By contrast to classical evoked response analysis, we estimated the underlying cerebral activity from single-trial data sweeps (i.e., no prior averaging) and searched for correlations between cerebral oscillations and manipulative hand speed during ongoing VM control.

Relationship Between Hand Speed and Slow Cortical Oscillations.

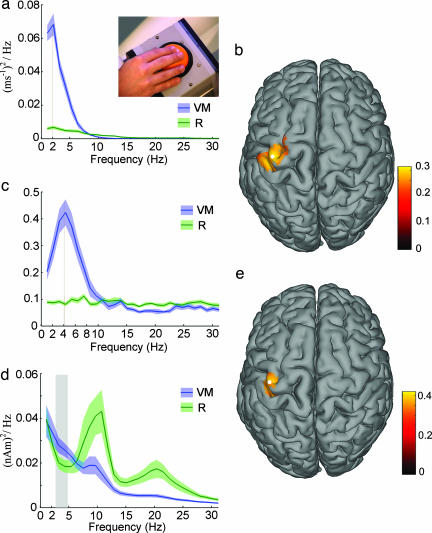
The power spectrum of the track-ball speed (TBS) during online motor control revealed that most of the hand velocity energy (92.8%) was concentrated in the low-frequency range (≤5 Hz), peaking at 2 Hz (Fig. 1a). Furthermore, applying single-trial source imaging to the raw MEG data, we obtained the trial-by-trial time course of the cortical activations at ≈12,000 brain locations for all subjects during both VM and R conditions (see Materials and Methods). The presence of correlations between the activity of the brain and the speed of the moving hand could then be investigated in the frequency domain by exhaustive evaluation of the coherence between the time-varying hand speed and ongoing cortical activity at each brain location (see Materials and Methods). To investigate task-related coupling at a population level, individual coherence maps (for VM and R) were normalized, and the task-related changes (VM vs. R) were mapped to a standard brain. The resulting map of task-related modulation of coherence between the estimated cerebral activity and TBS (Fig. 1b) demonstrates that hand speed is coherent with the activity of the contralateral primary motor and sensory areas in the 2- to 5-Hz range (P < 0.001), with maximum coherence located on the precentral gyrus [M1 hand area, Brodmann's area (BA) 4]. The profile of the coherence between the activity at this location (labeled M1) and ongoing hand speed plotted as a function of frequency (from 1–30 Hz) shows a notable peak at ≈4 Hz (Fig. 1c). In addition, the power spectrum of the activity in M1 during motor control shows a significant increase in the 3- to 5-Hz band compared with the R condition (Fig. 1d). Furthermore, to disentangle the effects of amplitude and phase on the low-frequency coupling, we also measured task-related phase synchronization (47) between all brain areas and hand speed around the frequency of maximum coherence (4 Hz) and found significant phase locking between M1 and hand movement speed (Fig. 1e; P < 0.001). Remarkably, during periods of particularly strong phase locking, the task-related synchronization between instantaneous hand speed and M1 activity can be demonstrated by simply band-pass filtering the single-trial time series of the two signals (Fig. 2).

Fig. 1.

Coherence between brain activity and hand speed. (a) TBS power spectrum during VM (blue) and R (green) conditions. (b) Cortical map of task-related Z-transformed coherence with TBS (VM vs. R) in the 2- to 5-Hz range (P < 0.001, corrected). The white dot indicates the location of maximum coherence difference (Montreal Neurological Institute coordinates: −42 −17 + 67 mm, hand area M1). (c) M1–TBS coherence spectrum during VM and R, with a peak at 4 Hz. (d) M1 power spectrum. Compared with R (green), VM (blue) has more power in 3–5 Hz (P < 0.05, corrected), followed by the well known power suppression of ≈10- and ≈20-Hz oscillations. (e) Cortical map of difference in brain–TBS phase locking ≈4 Hz (±1Hz) between VM and R (P < 0.001, corrected). The white dot indicates the location of maximum phase-locking difference. Power and coherence spectral plots (calculated with 1-Hz bin width) depict mean ± SEM.

Fig. 2.

Three-second sample of continuous VM control (one subject). (a) Track-ball trajectory with time markers from 0 to 3 sec. (b and c) Corresponding instantaneous hand speed and activity at M1, respectively. (d) Signals in b and c band-pass filtered in the 2- to 6-Hz band (i.e., ±2–4 Hz, the frequency of maximal coherence). Note that the selected sample corresponds to an epoch with high (>0.8) M1–TBS phase locking and the filtered signals are normalized.

Long-Range Neural Synchronization Between M1 and Multiple Brain Areas.

Are the speed-related slow oscillations found in M1 during VM control functionally coupled to the activity of other brain structures? To answer this question, we computed the coherence between the activity in M1 and all brain areas in the 2- to 5-Hz range, the frequency band of statistically significant M1–TBS coupling. The result (Fig. 3) shows that, during VM control, M1 activity becomes significantly coherent (P < 0.005) with the activity in multiple brain areas, including the contralateral dorsal premotor (PMd, BA6), primary somatosensory (BA3), inferior parietal (IPL, BA 40), bilateral secondary motor (SMA and pre-SMA, BA6), superior parietal lobule (SPL, BA7), left dorsolateral prefrontal cortex (DLPFC), right ventral and orbital prefrontal cortices (PFv and PFo, BA 11), ipsilateral anterior cerebellum, and subcortical areas, including the thalamus. The components of this large-scale cerebral network are largely consistent with regions known to be involved in visually guided motor behavior in humans (22). More importantly, the detection of these areas via their interaction with M1 within the same frequency range of M1–TBS coupling suggests that these areas are part of a spatially distributed functional network involved in the neural encoding of limb kinematics, providing further support for the putative role of cortical synchronization in mediating long-range communication between distant but functionally related areas in the brain.

Fig. 3.

Multiple brain areas coherent with activity at M1. Right (a), left (b), top (c), front (d), right medial (e), and left medial (f) views of the cerebral map of task-related Z-transformed coherence with M1 activity (VM vs. R) in 2- to 5-Hz range (P < 0.005, uncorrected). A white dot indicates the location of M1, the reference signal. Data represent group-level statistical analysis (n = 15). Significant values are overlaid on an inflated template brain, with gray-coded sulci and gyri identified by curvature indices.

Discussion

Synchronization Between M1 Oscillations and Hand Kinematics.

To date, most of the direct evidence for movement-related coupling between components of central and peripheral oscillations has come from studies of corticomuscular coherence (12–20). Such coherence, which is thought to reflect corticomotor communication during voluntary movement, has mostly been reported during simple isometric movements and predominantly detected at frequencies >5 Hz (but see ref. 23 for an exception). Given that the kinematics of manipulative hand movements are generated by the synergistic action of multiple muscles, and bearing in mind that the hand's mechanical properties restrict the range of achievable movement frequencies, corticomuscular synchrony may only provide indirect evidence for the presence of synchrony between global limb kinematics and oscillatory brain activity. In other words, measuring coupling between brain signals and the electromyogram may only yield limited information on whether hand speed per se has a coherent neural representation at a cortical level. The present study reveals task-related coupling directly between time-varying hand speed and oscillatory signals in M1. This finding suggests a role for slow (≤5 Hz) oscillations in motor cortex in the neural mechanisms underlying the neural control of limb speed and may also be interpreted as evidence for the existence of a neural representation of low-frequency components of limb kinematics. Such centrally encoded kinematic plans might be used by the CNS to generate the appropriate muscle forces via kinematics–dynamics transformations (24).

Localization of the Neural Activity Phase Locked to Time-Varying Hand Speed.

Earlier studies investigating velocity-related activity by using MEG or electroencephalography were restricted to rhythmic limb movements, and the analysis was performed at the sensor level, yielding limited spatial resolution (25, 26). In contrast, the results presented here overcome these limitations by using source-imaging techniques, combined with appropriate statistical inference techniques at the group level, to identify the anatomical origin of the brain activity that is correlated with hand kinematics. The improved spatial resolution (which was achieved here via MEG source imaging, allowing the shift from sensor- to source-level analysis) enabled us to pinpoint M1 (hand area, BA4) as the peak area of significant coherence detected between the sensorimotor cortex and hand speed. Second, the sustained VM paradigm used here was explicitly designed to yield smooth hand movements continuously adjusting to unpredictable pseudorandom changes in task demands. Therefore, the hand-speed profile differed considerably from the one generally obtained in tasks that impose repetitive pulsatile movements at a given frequency.

A Role for Low-Frequency Oscillations in Motor Control.

The low-frequency aspect of the coherence revealed in this study between limb kinematics and neural activity in humans is in line with recent findings in nonhuman primates. Averbeck et al. (4) investigated the accuracy with which hand velocity could be predicted from the activity of simultaneously recorded neurons while monkeys performed a tracing task. The average transfer function of the model that provided the best velocity prediction was found to be a low-pass filter. This finding reflects the fact that, similarly to our observations, hand velocity power was band-limited to frequencies <≈5 Hz, whereas the neural activity also contained power at higher frequencies. Moreover, a recent study by Rickert et al. (27) examined how different frequency components of the LFPs recorded in monkey motor cortex were modulated during center-out arm movements. Although directional tuning occurred in several frequency bands, the best prediction of arm movement direction (i.e., decoding power) was achieved by using the amplitude of the low-frequency range (≤4 Hz) of the LFP signals. Although the latter study did not specifically address the spectral aspect of speed encoding, these data suggest a prominent role for low-frequency neural activity in encoding movement parameters, consistent with our finding that 2- to 5-Hz cortical oscillations in human M1 increased in amplitude and became phase locked with hand speed during motor control.

Intrinsic Versus Task-Related Motor Oscillations.

It is important to distinguish between two closely related, although subtly different, interpretations of the low-frequency coupling found here between the M1 and hand kinematics. The first is to consider the slow 2- to 5-Hz oscillations to be an intrinsic (i.e., physiological) central motor rhythm, and the second is to view the frequency of these oscillations as reflecting the neural encoding of task-related parameters. Although linking our findings to previous reports of slow intrinsic motor rhythms (e.g., 3-Hz peripheral oscillations involved in VM control; see ref. 28) could be tempting, our experimental design and current analysis do not allow for such conclusions. However, we can reasonably assume that the low-frequency coherences (and, more specifically, the detected phase locking) reflect the central motor encoding of the limb's kinematic parameters. This interpretation is strengthened by the fact that the M1–TBS coherence peaked in the M1 and, importantly, not in the somatosensory cortex, which also makes an interpretation uniquely based on sensory feedback unlikely. Nevertheless, it might be conceivable that both intrinsic and task-related oscillations are present in our data. Further experiments will have to be designed to fully resolve this specific issue.

Cerebro–Cerebral Interactions Revealed by MEG Source Imaging.

The long-range task-related coherence detected between M1 and various brain areas in this study highlights the advantage of the whole-head source-imaging approach. The high spatiotemporal (and hence spatiospectral) resolution that has now become achievable with MEG source-imaging techniques allowed us to scan the entire brain in search of neural activity coherent with that of M1. Although the reliability of single-trial MEG source imaging is generally challenged by the low signal-to-noise ratio of raw MEG data, the present analysis indicates that this limitation might be overcome by applying source-imaging techniques to sufficiently long epochs of data, splitting the investigation into specific frequency bands, and relying on statistical inference to detect robust task-related modulations. Such an approach also requires an adapted steady-state experimental design. Although this procedure allows for the detection of long-range oscillatory coupling, one should be extremely cautious when interpreting observations of short-range coherences. The local spatial smoothing inherent to the regularized minimum norm-imaging solution makes it difficult to disentangle short-range physiological coupling and local data smearing. For instance, it is impossible to rule out that the short-range coherence reported in this study between M1 and BA3 is not at least in part due to spatial resolution limits. Moreover, although the ability of MEG to detect subcortical activations is still a matter of debate, we have strong reasons to believe that deep sources reported here do represent cerebellar and thalamic activity. First, it is likely that these areas are picked up more easily by scanning for their task-related coherence modulations with respect to a reference signal (here M1) than by performing classical source reconstructions in search of stimulus-locked activity throughout the cerebral volume. Second, our confidence comes from the permutation testing that reveals statistically significant coupling between these structures with M1 by contrasting VM with R epochs. Finally, an additional level of confidence comes from the physiological plausibility of the findings (e.g., ipsilateral but no contralateral cerebellar involvement) and evidence from an increasing number of MEG studies reporting activity in these deep structures (e.g., refs. 17, 19, 29, and 30).

Large-Scale Coherent Network Mediating VM Control.

The M1-coherent large-scale network revealed in the current study (Fig. 3) includes areas involved in functionally well established circuits, such as the frontoparietal network and the cerebello–thalamo–cortical pathway, presumably reflecting the sensorimotor processing and the motor control loop at work during the continuous VM task. This large-scale network was revealed in our study by identifying areas that display significant coherence with respect to M1 activity. Given that M1 was shown to be significantly coupled to hand speed, it is interesting to ask whether the other cerebral areas in Fig. 3, which are all coherent with M1, are also directly coupled to hand speed. Such correlations were indeed observed in our data, yet they were much weaker than the one observed between M1 and hand speed, and were thereby only visible in the unthresholded coherence maps and did not pass the statistical significance tests. This observation highlights the pivotal role played by M1; it is the cortical structure directly involved in movement execution and kinematic encoding, yet it is also part of widespread networks involved in sensorimotor transformation and motor control.

Interestingly, the frequency of the identified oscillatory networks (2–5 Hz) and the cerebral structures it comprises are similar to those reported in the oscillatory network underlying Parkinsonian resting tremor (30, 31). This further supports the hypothesis that pathological tremors might be based on physiologically preexisting cerebral networks (32, 33). Furthermore, a subset of the brain structures reported in our study was also found to be involved in the generation of the ≈8-Hz movement discontinuities that occur during slow finger movements (17). Using MEG and finger muscle recordings, the latter study revealed the central origin of the peripheral ≈8-Hz oscillations by showing that they were generated by an oscillatory network formed by the contralateral M1, the premotor cortex, the contralateral thalamus, and the ipsilateral cerebellum, which are all synchronized at ≈8 Hz.

In this study, we restricted the coherence analysis between M1 and the rest of the brain to the 2- to 5-Hz range because this was the frequency band of significant coupling between M1 and hand speed. Previous reports have suggested a functional role for cortico–cortical synchronization at higher frequencies in mediating VM integration (34–38). The data presented here extend these studies to the low-frequency range, and, more importantly, we show a direct relationship between these slow neural oscillations and hand kinematics. Therefore, if long-range neural coherence is taken to reflect functional connectivity between distant brain areas (20, 39, 40), then our results suggest that low-frequency interregional coupling could be a highly relevant index for the noninvasive investigation of normal and neurologically impaired voluntary control of limb movements.

Moreover, a better understanding of the spatially distributed nature of movement encoding may also be crucial to the development of neural prosthetic applications. Recent trends in this field include (i) improving movement decoding via simultaneous multielectrode recordings at multiple sites across the brain (6, 7), and (ii) assessing the potential application of LFPs as an alternative signal for movement prediction (3, 27, 41–43). Although further research is required to accurately relate the MEG source time series to intracranial LFP signals, we may speculate, in the light of the current findings, that the high-spatiotemporal resolution of the large-scale functional networks revealed by whole-head MEG imaging in humans may help develop neural decoding algorithms and identify behaviorally relevant target frequency bands and candidate cortical and subcortical structures for brain–machine interfaces.

Taken together, our findings extend previous reports on the role of neural oscillations in motor behavior by demonstrating that synchronization at remarkably low frequencies may be involved in the central mechanisms encoding low-level motor parameters. Incorporating these findings into a common framework that describes the role of coherent oscillations at multiple frequencies in mediating distinct aspects of sensorimotor behavior (force, speed, and covariates) at several levels (brain, muscle, and limb) may have crucial implications for the investigation of the pathophysiology of motor control.

Materials and Methods

Subjects and Behavioral Task.

We studied 15 right-handed healthy male volunteers. We recorded the ongoing magnetic activity of their brain while they continuously manipulated a track ball to counter the unpredictable movements of a cube rotating about its center (stimulus and hand movements are shown in SI Movies 1 and 2). The participants were instructed to attempt to keep the cube's angular deviation at a minimum from its initial position (blue face up) at all times. The VM task was alternated with an R condition, during which the subjects relaxed while looking at a motionless cube. The subjects were cued to switch between the two conditions every 8–12 sec, yielding continuous epochs of steady-state MEG data. The size of the projected cube and the position of the display screen yielded a stimulus that spanned a visual angle that remained below 4° throughout the experiment. All subjects gave informed consent, and the study was approved by the local medical ethics committee.

Recordings.

The cerebral activity was recorded with a whole-head MEG system (151 sensors; VSM MedTech, Coquitlam, BC, Canada) with a band pass of 0–200 Hz. Bipolar Ag-AgCl electrodes (band pass = 0.16–200 Hz) were used to record the electrooculogram monitoring both horizontal and vertical eye movements and the ECG detecting the subjects' cardiac activity. These recordings, as well as the x and y outputs from the track-ball device and markers of the behavioral conditions, were acquired in continuous mode (8-min MEG recording blocks), digitized at 1.25 kHz, and stored for offline analysis. All subjects also underwent a high-resolution 3D IR-FSPGR T1-weighted anatomic MRI scan (1.5 T; GE Medical Systems, Milwaukee, WI).

Track-Ball Kinematics.

The track-ball position signals were fed into the acquisition system and recorded simultaneously with the ongoing brain signals. The instantaneous track-ball velocity vector was then derived by low-pass filtering and two-point differentiation of the x- and y-position signals. Finally, the TBS (and thus, to first order, hand speed) was computed as the absolute tangential velocity, $\text{TBS}(t)=\sqrt{\dot{x}{(t)}^2+\dot{y}{(t)}^2}$.

Preprocessing.

The MEG data were first low-pass filtered (100-Hz cutoff), down-sampled to 312.5 Hz, and subjected to visual inspection. All data segments contaminated by eye blinks (detected via the electrooculogram signals), unwanted swallowing, coughing, or movement artifacts were rejected, and heartbeat artifacts (measured by the ECG) were corrected by using a heart-beat trace (QRS complex)-matched filter. All 8- to 12-sec continuous MEG records of each condition (VM or R) were split into nonoverlapping 1-sec epochs. Two hundred artifact-free trials were thus obtained for each condition in all subjects.

Single-Trial MEG Source Estimation.

In contrast to classical evoked response analysis of MEG data, we imaged the cerebral activity underlying the sensor measurements directly from single-trial data sweeps, i.e., without prior data averaging. We thereby preserved trial-specific temporal information, which is both crucial to the study of the spatiotemporal properties of motor encoding and fundamental to the analysis of induced brain oscillations not systematically time-locked to a given stimulus (44). The neural current density time series at each elementary brain location was estimated by applying a minimum norm-inverse solution (21) with constrained dipole orientations (normal to the cortical sheet) and standard Tikhonov regularization to all time samples of the 200 one-sec segments of sensor data (in fT) available in each condition (VM and R). This procedure yielded 200 one-sec-long time windows of ongoing cerebral activation (in units of Am) at each of ≈12,000 brain locations (corresponding to the nodes of each subject's individual cortical tessellation). The single-trial source estimations were implemented with the BrainStorm MEG and EEG Toolbox (www.neuroimage.usc.edu/brainstorm), and the segmentations and tessellations of all MRI data sets were performed with the BrainVisa (www.brainvisa.info) and BrainSuite (45) packages.

Estimating Source-Level Coherence, Phase Synchrony, and Power.

The coupling between the estimated neural time series and the TBS was investigated by coherence estimation. Coherence is a spectral measure of correlation between two signals x(t) and y(t) across frequencies; it is calculated from the cross-spectral density between the two waveforms and normalized by the power spectral density of each:

where X_i(f) and Y_i(f) are the Fourier transforms of the signals x and y for the ith data segment at frequency f, and * indicates the complex conjugate. Coherence values range from 0 (if the signals are uncorrelated) to 1 (if the signals are perfectly correlated). For the coherence estimates between brain activity and hand speed, x(t) represents the time series of the estimated current amplitude at an elementary brain location and y(t) represents the time series of the TBS. For the coherence estimations between M1 and the rest of the brain, the reference signal y(t) is no longer TBS but simply the current amplitude time series estimated at M1. The computations were carried out by using the magnitude-squared coherence function (MATLAB; MathWorks, Natick, MA) based on Welch's averaged periodogram method (applied to the n = 200 nonoverlapping 1-sec time windows). To compare coherence between conditions and perform statistical analysis across subjects, we used Fisher's Z transform of coherence (46): ${\text{Z}}_{\text{coh}}={\tanh }^{-1}(\sqrt{C})$. This procedure yields a constant variance given by $\mathrm{var}\left\{{\tanh }^{-1}(\sqrt{C})\right\}=1/2N$, where N is the number of disjoint data segments used in the coherence estimate. Both phase and amplitude coupling contribute to magnitude-squared coherence. Therefore, to single out the role of phase consistency in task-related coupling modulations, we evaluated the phase-locking value to quantify the phase synchrony between the estimated neural activity and subject hand speed. The phase-locking value between signals x and y at a given frequency f is defined as (47)

where θ(t, i) = ϕ_X(t, i) − ϕ_Y(t, i) is the phase difference between the two signals at time t in the ith segment/trial. The instantaneous signal phases ϕ_X and ϕ_Y at frequency f were determined via the Hilbert transform. Finally, the signal power of the estimated time series of the neural signals at an elementary brain location (e.g., M1) was computed by using a standard power spectral density function (MATLAB) based on fast Fourier transform applied to each data segment (n = 200 time windows), to which we previously applied a Hanning window to reduce spectral leakage.

Spatial Normalization and Statistical Nonparametric Coherence Maps.

Individual maps of cortical coherence were first computed for each condition (VM and R) by using the subject's MRI. To perform statistical testing at the population level, the cerebral coherence data needed to be interpolated to a common source space, such as the standard Montreal Neurological Institute brain. This process was achieved by spatially normalizing the individual MRI tessellation of each subject to the MNI-Talairach space [by using a standard procedure based on anatomical markers (AC-PC), the Talairach bounding box, and piecewise affine transformations] and by using a regularized linear interpolation of the functional data from the vertices of the normalized subject tessellation to the vertices of the Montreal Neurological Institute tessellation. We then averaged the coherence maps over subjects and contrasted the two conditions, VM versus R. The difference maps were thresholded at P < 0.001 by using group-level (n = 15), one-tailed paired permutation tests, which randomly exchanged the estimated values of coupling in R and VM for each subject. We used exhaustive permutations (2¹⁵ = 32,768) to estimate the empirical distribution under the null hypothesis of no difference between the two conditions. The alpha level was adjusted to the maximum statistic distribution to control for the type I family wise error rate due to multiple comparisons over the entire brain surface (48, 49). Unless otherwise stated, all coherence and power plots presented here were obtained with group-level (n = 15) statistical inference based on paired permutation tests.

Abbreviations

LFP

local field potential

MEG

magnetoencephalography

M1

primary motor cortex

R

resting

TBS

track-ball speed

VM

visuomotor.