Atomic force microscopy reveals the mechanical design of a modular protein

Abstract

Tandem modular proteins underlie the elasticity of natural adhesives, cell adhesion proteins, and muscle proteins. The fundamental unit of elastic proteins is their individually folded modules. Here, we use protein engineering to construct multimodular proteins composed of Ig modules of different mechanical strength. We examine the mechanical properties of the resulting tandem modular proteins by using single protein atomic force microscopy. We show that by combining modules of known mechanical strength, we can generate proteins with novel elastic properties. Our experiments reveal the simple mechanical design of modular proteins and open the way for the engineering of elastic proteins with defined mechanical properties, which can be used in tissue and fiber engineering.

A wide variety of proteins are placed under mechanical stress during cell adhesive interactions (1–4) and in muscle contraction (5–9). A remarkable feature of these proteins is their tandem modular construction. For example, the giant muscle protein titin is composed of several hundred Ig and fibronectin type III (FnIII) domains placed in tandem (10). These modules show low sequence homology among themselves [20–30% identity, 30–40% similarity between Ig modules in human skeletal titin (11)] and widely different thermodynamic stability (12) (2.55 to 7.36 kcal⋅mol⁻¹). The key residues of individual Ig repeat across different species, and the superrepeat patterns of avian and mammalian titins are highly conserved through evolution (11) (82.5% similarity between human and the reptile sequences), suggesting that their particular ordering is important for the elasticity of the protein. The ordering of modules is particularly striking in the protein projectin, a titin-like protein found in the muscles of invertebrates (13). Most of the projectin protein is arranged in a repeating pattern of FnIII–FnIII–Ig domains. Although the significance of these modular arrangements is unknown, it is likely that these patterns form mechanical units that determine the elasticity of the whole protein. If this view is true, it implies that, in contrast to most other proteins, the functional characteristics of elastic proteins are obtained by the summation of the mechanical strength of its modular units. To examine this hypothesis, we use protein engineering and single molecule atomic force microscopy (AFM) techniques (3, 6, 9) to construct simple tandem modular proteins and study their mechanical properties. For our studies, we have chosen to use the I27 and I28 Ig modules of human cardiac titin. These modules offer the advantage that they have been studied in detail by using NMR, steered molecular dynamics, and AFM techniques, and their thermodynamic properties are well established (9, 12, 14–17). Furthermore, because the I28 module is significantly less stable than I27 (ΔG_D−N = 3.0 kcal⋅mol⁻¹ for I28 vs. 7.6 kcal⋅mol⁻¹ for I27), we expected that these modules would show very different mechanical properties, and that these could be readily identified by AFM. Contrary to these expectations, we found that I28 domains are mechanically more stable than I27 domains, suggesting that the observed mechanical stability is not governed by thermodynamic stability but rather by the height of the kinetic barrier. We constructed a heteropolyprotein by combining I27 and I28 domains in series and found two distinct levels of unfolding forces; we first observed the unfolding of the weakest (I27) and then the unfolding of the mechanically stronger domain (I28). We also found that the mechanical stability of a tandem modular protein is not a simple sum of the mechanical stability of its modules, because I28, but not I27, domains are stabilized in the heteropolyprotein.

Materials and Methods

Protein Engineering.

We constructed polyproteins that contained eight direct tandem repeats of a single Ig domain no. 27 from the I band of human cardiac titin (I27)₈, eight tandem repeats of domain no. 28 (I28)₈, and a protein chimera containing 4 repeats of the I27-I28 dimer (I27-I28)₄, according to methods described elsewhere (17). Our method adds two amino acids, Arg-Ser, to the junction between each repeating unit. The synthetic polyproteins were cloned in an Escherichia coli recombination-defective strain, Sure-2 (Stratagene), and expressed in the M15 strain. The proteins were purified by Ni²⁺ affinity chromatography under nondenaturing conditions. Elution from the resin was with 100 mM imidazole, pH 6.0. All these proteins had two Cys in their C terminus to facilitate the attachment of the molecules to the gold-coated coverslips.

Force Spectroscopy of Single Proteins.

Our custom-made AFM apparatus, as well as its mode of operation, is identical to those that we have described recently (3, 9, 17). Calibration of the spring constant of each individual cantilever was done in solution by using the equipartition theorem, as described (18). The proteins were suspended in PBS buffer at a concentration of ≈10 μg⋅ml⁻¹ and adsorbed onto freshly evaporated gold coverslips.

Chemical Denaturation.

Single I27 and I28 domains were isolated by PCR from the polyprotein clones and subcloned into a modified pRSETA vector according to methods described elsewhere (17). Equilibrium denaturation of I27, I28, and an I27-I28 construct was performed in PBS, pH 7.4, at 25°C, as has been described elsewhere (19, 20), and each transition was fitted separately, as described. The samples were allowed to equilibrate for up to 20 h to allow equilibrium to be achieved. In kinetic experiments, unfolding was initiated by mixing 1 volume of protein with 10 or 20 volumes of concentrated GdmCl solution. In each case, the final conditions were 2 μM of protein in PBS and 5 mM DTT at 25°C. Unfolding was monitored by loss of fluorescence at 320 nm (excitation 280 nm) after manual mixing in a 1-cm pathlength cuvette. Unfolding was slow, and data were collected for more than 2,000 sec. For unfolding traces at low denaturant concentration (≈2 M), each trace was collected for >12 h. The data fit well to a single exponential [I27 or I28 alone or I27-I28 at low [GdmCl] or a double exponential equation (I27-I28 construct at high [GdmCl] plus a term to account for baseline drift because of photolysis (19, 20)]. Refolding of I27 has been described previously (17). Unfolding of I28 was performed by jumping from pH 1.5 to pH 7.4 in an Applied Photophysics (Surrey, U.K.) stopped-flow apparatus.

Results and Discussion

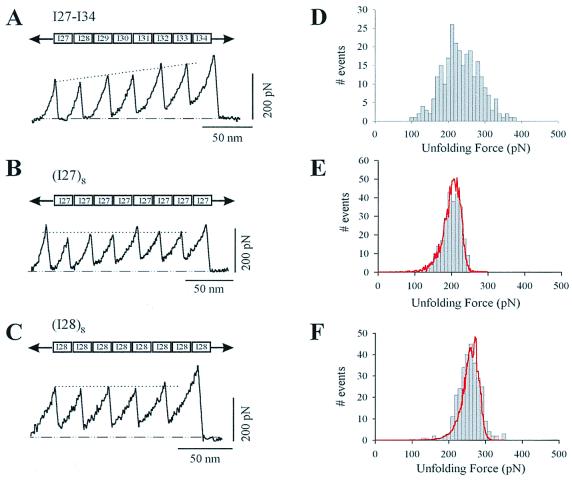
Stretching single modular proteins with an AFM generated force-extension curves showing a characteristic sawtooth pattern (Fig. 1). A series of recent AFM experiments have established that the peaks of the sawtooth patterns correspond to the sequential unfolding of the protein modules. Stretching a recombinant tandem modular protein composed of eight modules from the region of native titin encompassing the I27 to I34 modules of human cardiac titin gave a sawtooth pattern with peaks of ascending force indicating the varying mechanical stability of the modules and their hierarchical unfolding (Fig. 1A). A histogram of the unfolding forces revealed a broad distribution spanning a range of 100–400 pN (Fig. 1D). To examine the molecular origin of the hierarchical unfolding, we have studied the mechanical stability of the I27 and I28 modules. For this purpose, we constructed two direct tandem repeat proteins solely composed of either the I27 module (I27₈) or the I28 module (I28₈). Stretching the I27₈ polyprotein gave a sawtooth pattern (Fig. 1B) with a much narrower distribution of unfolding forces and a mean unfolding force of 204 ± 26 pN (Fig. 1E; n = 266). The I28 module was found to be mechanically more stable than the I27 module. The mean unfolding force for the I28₈ polyprotein was 257 ± 27 pN (Fig. 1 C and F; n = 245). This result is highly significant because it has been proposed that the mechanical stability of a module depends on its thermodynamic stability (5, 15); however, the thermodynamic stability of the I28 module is significantly lower than that of the I27 module. This discrepancy becomes clear once we consider that a mechanical unfolding event is a kinetic process, not an equilibrium measurement, and hence depends only on the unfolding activation energy.

Figure 1.

Force-extension curves for various recombinant fragments of human cardiac I band titin, measured with single-protein AFM techniques. (A) Force-extension curve for a recombinant protein composed of the I27-I34 region of I band titin. Notice the steady rise in the force peaks, indicating the hierarchical unfolding of its modules. By contrast, stretching either an I27 polyprotein (B) or an I28 polyprotein (C) produces sawtooth patterns with a relatively constant unfolding force. (D) Histogram of unfolding forces for the I27-I34 protein shows a broad peak spanning a ≈300 pN range of unfolding forces (E, F). Unfolding force frequency histograms for I27 and I28 polyproteins show a single peak at 204 ± 26 pN (n = 266) and 257 ± 27 pN (n = 245), respectively. The lines correspond to Monte Carlo simulations of the mean unfolding forces (10,000 trials) of eight domains placed in series by using a pulling rate of 0.6 nm/ms and an unfolding distance, Δx_u, of 0.25 nm for both domains. The unfolding rate constants were k_u^0, 3.3 × 10⁻⁴ s⁻¹ and 2.8 × 10⁻⁵ s⁻¹ for I27 and I28, respectively.

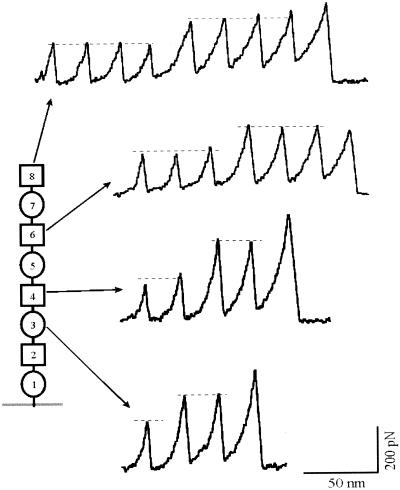
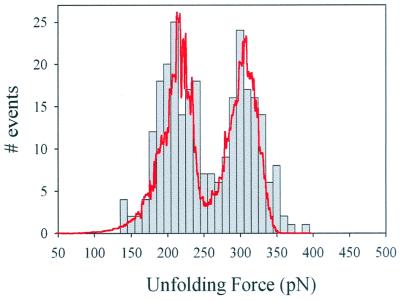
The mechanical unfolding of homopolyproteins demonstrates that it is possible to isolate and study the mechanical properties of individual modules. However, homopolyproteins never occur in native tandem modular proteins. It is possible that when different modules are placed in tandem and subject to mechanical stress, they might not function as mechanically independent units. To examine whether the serial placing of I band modules results in mechanical properties that are additive with respect to the individual modules, we constructed heteropolyproteins containing the Ig modules as heterodimers (I27-I28)₄. Fig. 2 shows force-extension curves for the heteropolyprotein. Stretching this polyprotein resulted in force-extension curves with equally spaced force peaks but with two distinct levels of unfolding forces, one located at ≈200 pN and a second level at ≈300 pN (Fig. 2, dashed lines). Because the AFM tip picks up proteins from any module at random, we do not always stretch the proteins from N and C termini. This results in a wide variety of sawtooth patterns with different combinations of I27 and I28 modules. Fig. 3 shows a frequency histogram of the unfolding forces measured from the (I27-I28)₄ heteropolyprotein. The histogram shows two separate peaks, centered at 211 pN and 306 pN. We attribute the first peak to the unfolding of I27 domains and the second peak to the unfolding of I28 domains. We first observe the unfolding of the domains that are mechanically weakest (I27) and then the unfolding of the mechanically more resistant domains (I28). Interestingly, this unfolding sequence is contrary to the construction of the protein. I27 and I28 domains are thus unfolding in a hierarchical pattern rather than in order of placement. However, given the construction of the (I27-I28)₄ protein, only some combinations are possible. Table 1 lists the number of sawtooth patterns that were observed to have a particular combination of high (≈300 pN) and low (≈200 pN) unfolding force peaks. The table shows that if we observe N high force unfolding peaks, we always observe at least N − 1 low unfolding force peaks, consistent with the construction of the protein. However, the converse is not true, and in several cases, we have found sawtooth patterns that contained up to four low force peaks without a single high force peak (Table 1). As shown in Fig. 1, unfolding forces are distributed in a probabilistic manner (Fig. 1 E and F). Because it is likely that some I28 unfolding events will occur at low forces (e.g., ≈200 pN; Fig. 1F), they will be confused as I27 unfolding events. This explains why we have observed some events composed solely of low force peaks (Table 1). The opposite cannot be true. I27 modules do not unfold at forces higher than ≈250 pN and therefore cannot be confused with an I28 unfolding event.

Figure 2.

Force-extension curves for a heteropolyprotein constructed as (I27-I28)₄. The force-extension curves always show two distinct levels of unfolding forces (dashed lines). However, the number of modules unfolding in each case varies because the AFM tip picks up the proteins at a random location resulting in the stretch unfolding of different number of modules every time a new molecule is picked up. The diagram on the left provides an explanation for the recordings and marks the number of modules that will unfold in each case (circles represent I28 modules, squares represent I27 modules). Some exclusion rules apply; for example, it is not possible to observe three or more unfolding events of one kind and less than two of the other kind (see Table 1).

Figure 3.

Histogram of the unfolding forces for the (I27-I28)₄ polyprotein. There are two clearly separated peaks, one at 211 pN and a second at 306 pN (n = 270). The line corresponds to Monte Carlo simulations of the unfolding forces (10,000 trials) of a protein chimera modeled as a double tetramer with two different domains placed in series. The unfolding rate for the first four domains was k_u⁰ = 7.0 × 10⁻⁴ s⁻¹, and the unfolding rate for the second four domains was k_u^{0 = 2.5 × 10−6 s−1. The unfolding distance for both domains was assumed to be Δx_u = 0.25 nm.}

Table 1.

Observed frequency of high and low force peaks in the (I27-I28)₄ polyprotein

	0L	1L	2L	3L	4L
0H	—	—	2	4	4
1H	—	8	6	6	2
2H	0	12	15	10	1
3H	0	0	6	11	6
4H	0	0	0	2	3

The number of sawtooth patterns showing different combinations of high and low unfolding force peaks. 

The unfolding force of I27 modules in the heteropolyproteins is similar to that of the (I27)₈ homopolyprotein. However, the I28 modules of the heteropolyprotein unfold at slightly higher forces (≈300 pN; Figs. 2 and 3) than in the I28 polyprotein (≈260 pN; Fig. 1 C and F). This suggests that the mechanical unfolding of the I28 modules is stabilized by the I27 domains in the heteropolyprotein. To examine the mechanism responsible for this stabilization, we have measured the height of the mechanical and chemical unfolding energy barrier for the I27 and I28 modules when they are isolated or tethered together.

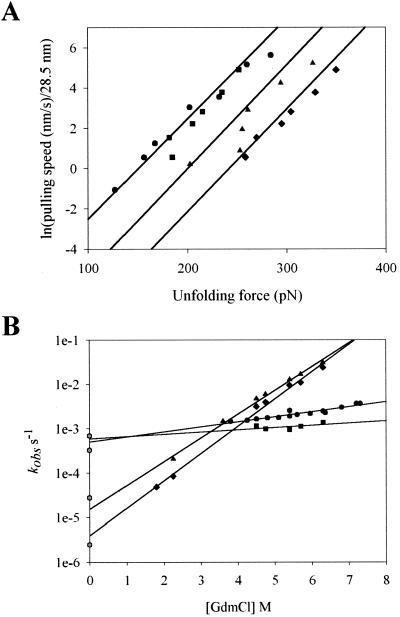
The height of the mechanical unfolding energy barrier can be calculated from the unfolding rate constant at zero force. The mechanical unfolding rate constants were estimated from the unfolding force frequency histograms (Fig. 1 E and F) and from the dependency of the unfolding force on the pulling rate (Fig. 4A). We use a Monte Carlo simulation technique to simultaneously predict the distribution of unfolding forces and their rate dependency (17, 21). The distribution of unfolding forces was predicted by Monte Carlo simulations by using unfolding rate constants, k_u⁰, of 3.3 × 10⁻⁴ s⁻¹ for I27 (Fig. 1B, red line) and 2.8 × 10⁻⁵ s⁻¹ for I28 (Fig. 1C, red line). The unfolding distance to the transition state for both domains was Δx_u = 0.25 nm. The same Monte Carlo simulations readily predict the dependence of the unfolding forces on pulling rate for both the I27 and I28 polyproteins (Fig. 4A, solid lines).

Figure 4.

Mechanical and chemical unfolding rates of I27, I28, and I27-I28 domains (A). Plot of pulling speed ÷ 28.5 vs. unfolding forces of I27 (circles) and I28 polyproteins (triangles). The data are well described by Monte Carlo simulations (solid lines) with spontaneous rates of unfolding of I27: k_u⁰ = 3.3×10⁻⁴ s⁻¹ and I28: k_u⁰ = 2.8 × 10⁻⁵ s⁻¹. The data for the (I27-I28)₄ heteropolyprotein are shown as squares for I27 and diamonds for I28 domains, respectively. These data are well described by Monte Carlo simulations with rates of I27: k_u⁰ = 7 × 10⁻⁴ s⁻¹ and I28: k_u⁰ = 2.5 × 10⁻⁶ s⁻¹ (solid lines) (B). Plot of the natural logarithm of the observed unfolding rate constant vs. denaturant concentration, for I27 (circles) and I28 (triangles) monomers. The I27-I28 dimer is shown in its separate components: I27 (squares) and I28 (diamonds) and their respective extrapolations to zero denaturant (solid lines). The corresponding unfolding rates measured by AFM and calculated for zero force are shown as hexagons.

Unfolding is a probabilistic event; hence, if the rate at which a polyprotein is pulled is slow enough, the protein can be extended at a very low force. These conditions occur when at least one module unfolds spontaneously every time the protein is extended by 28.5 nm. Hence, a plot of pulling rate/28.5 vs. unfolding force can be extrapolated to give the rate of unfolding at zero force. This plot is shown in Fig. 4 for both the I27₈ (circles) and the I28₈ (triangles) polyproteins. The Monte Carlo simulations of rate dependency for I27 and I28 polyproteins (Fig. 4, solid lines) extend over a wide range of pulling rates fitting the data points and intercepting the ordinate at points that correspond to the values of k_u⁰ used (see above). We compared these values with those obtained by chemical denaturation with guanidinium chloride (see Table 2). The rate constants for unfolding, extrapolated to 0 M denaturant k_u^H2O (Fig. 4B, solid lines), were 4.9 × 10⁻⁴ s⁻¹ for I27 and 1.6 × 10⁻⁵ s⁻¹ for I28 domains, which are close to the values obtained by AFM (Fig. 4B, hexagons). From these rate constants, we calculate that to mechanically unfold, an I27 module must overcome an activation energy barrier of ≈22.2 kcal⋅mol⁻¹ (17), and an I28 module must overcome ≈23.7 kcal⋅mol⁻¹.

Table 2.

Results of chemical denaturation experiments for isolated I27, I28 modules and I27, I28 in I27-I28 dimer

Protein	[D]50%, M	ΔGD-N, kcal⋅mol−1	ku, s−1
I27 monomer	3.04  ± 0.01	7.6  ± 0.1	4.9 (±0.5)  × 10−4
I27 in dimer	3.24  ± 0.01	8.1  ± 0.1	6.0 (±3.0)  × 10−4
I28 monomer	0.93  ± 0.01	3.0  ± 0.1	1.6 (±0.3)  × 10−5
I28 in dimer	1.10  ± 0.02	3.5  ± 0.1	4.0 (±0.9)  × 10−6

[D]_50%, the concentration of denaturant at which 50% of the protein is denatured. ΔG_D-N, calculated thermodynamic stability. k_u, estimated unfolding rate at 0 M denaturant. 

We have previously been able to determine the refolding rate at 0 force for I27 (1.3 s⁻¹) and have shown it to be an order of magnitude slower than that for the isolated I27 domain (32 s⁻¹). We were unable to observe refolding for the I28 polyprotein. It is likely that this reflects the very slow refolding rate of I28. In solution, the refolding rate of I28 is 0.025 s⁻¹, three orders of magnitude lower than that of I27. The half time for refolding of I28 in solution is ≈30 s and, if tethering affects refolding of I28 in the same way as I27, we might expect a significantly longer half time than this, a half time that is inaccessible by AFM. This means, however, that we are unable to determine the thermodynamic stability of I28 in a polyprotein by AFM. It is possible that tethering increases the stability of I28 significantly. This is unlikely, because attachment of I27 to I28 has only a small effect on the stability of I28 (ΔG_D-N increases by 0.5 kcal⋅mol⁻¹; see Table 2), which remains significantly less stable than I27 under these conditions (Table 2). The close agreement between AFM and solution studies strongly suggests that the unfolding force is not governed by thermodynamic stability (free energy difference between the folded and denatured states) but rather by the free energy difference between the folded and transition states (activation energy).

Although the I27 and I28 modules have very low sequence identity, their structure and mechanical topology are thought to be identical (16). The mechanical strength of these modules is thought to result mainly from two clusters of hydrogen bonds that break under the applied force (16). If this view is correct, the varying mechanical strength of these modules should reflect variations in the free energy associated with the backbone hydrogen bonds that form the mechanical resistance points of the modules. This simple mechanism may be sufficient to explain how both the sequence variability and the different mechanical strength of the I band provide a simple toolbox of domains that can be simply stringed together to assemble a complex elastic protein. However, as shown in Fig. 2, placing the I27 module in tandem with the I28 module increases the mechanical stability of the I28 module with respect to an I28 homopolyprotein (Figs. 1F and 2). Hence the mechanical stability of a tandem modular arrangement is not always a simple sum of the mechanical stability of its modules.

Fig. 4A shows the pulling rate dependence for the two levels of unfolding forces observed in the (I27-I28)₄ protein (squares and diamonds). As the figure shows, the rate dependency of the unfolding forces for the I27 modules (low force peaks) is not affected by their placement in the heteropolyproteins (circles vs. squares). By contrast, the rate dependency of the I28 modules in the heteropolyproteins is significantly shifted (diamonds) with respect to the I28 modules in the homopolymer protein (triangles). As before, we use Monte Carlo simulations to determine the unfolding rate constants. In this case, we simulate a heteropolyprotein composed of two types of modules, following our molecular design (Fig. 2). We can reproduce the rate dependence of the unfolding forces (Fig. 4A, solid lines) and the bimodal distribution of unfolding forces (Fig. 3, solid line) with unfolding rates of 7.0 × 10⁻⁴ s⁻¹ for the I27 domains and 2.5 × 10⁻⁶ s⁻¹ for the I28 domains. By comparing the unfolding rates of I28 in the homopolyprotein and the heteropolyprotein, we calculate that the I28 modules are stabilized by ≈1.4 kcal/mol/module (calculated as RTln(2.8 × 10⁻⁵ s⁻¹/2.5 × 10⁻⁶ s⁻¹). Interestingly, we observed a similar stabilization of the I28 module in chemical denaturation studies (see Table 2).

We determined the unfolding rates of an I27-I28 construct in solution unfolding studies. At high denaturant concentrations, the unfolding data were fit to a double exponential, as they represented the unfolding of both I27 and I28 domains. At lower denaturant concentrations (1.8–2.3 M GdmCl), a single unfolding event was observed, as I27 remains folded under these conditions. Similar to the AFM observations, the unfolding rate at 0 M denaturant was the same for I27 as for isolated I27 domains, but the unfolding of I28 was slowed significantly compared with I28 modules alone (4.0 × 10⁻⁶ s⁻¹ vs. 1.6 × 10⁻⁵ s⁻¹; see Table 2). Again, extrapolation of the chemical denaturation results for the I27-I28 dimers readily predicted the denaturation rates measured by AFM (Fig. 4B). This result demonstrates that the stabilization of the I28 module is the result, not of a mechanical effect of tethering such as torsional strain (22), but rather of the chemical structure of the neighboring pairs. Interestingly, the kinetic stabilization of I28 is seen in the presence of both folded I27 (in the case of chemical unfolding experiments at low denaturant concentrations) and unfolded I27 (in the mechanical unfolding experiments). This would indicate that the important interactions lie in the linker region. Previous studies have confirmed that there is little direct interaction of the modules in the I27I28 pair and have indicated the importance of the natural linker region, including residue Leu-89, in restricting the relative motion of the two domains (15).

Our results demonstrate that it is possible to engineer the mechanical strength of a single protein by combining Ig modules of known mechanical properties. However, our results also show that the mechanical properties are not strictly additive and may depend on either the amino acids that link the modules together or module–module interactions. These interactions may be an important component of the mechanical design of a protein. Our results also show that the mechanical strength of the Ig modules is a kinetic process that depends strictly on the height of the unfolding energy barrier and is not correlated with the thermodynamic stability of the modules, as has been proposed before (5, 12). These important molecular rules underlie the mechanical properties of elastic proteins and explain the origin of the hierarchical unfolding observed in the muscle protein titin.

The mechanical unfolding of protein modules is a dissipative process characterized by a pronounced hysteresis between the extension and relaxation curves (6). The area between these curves corresponds to the work that is dissipated as heat by the extension (1). Hence, modular proteins may function as shock absorbers, allowing the extension of bonded materials without rupture (1, 3). The engineering of a mechanically complex modular protein, as demonstrated here, shows that the amount of work dissipated by an extension can be finely engineered at the molecular level by choosing modules with different mechanical stability.

Our observations now pave the way to the full understanding of the mechanical design of elastic modular proteins. This understanding will permit the engineering of novel tissues and fibers (23, 24).

Abbreviation

AFM

atomic force microscopy