A supersymmetric model for the evolution of the genetic code

Abstract

A model is presented for the structure and evolution of the eukaryotic and vertebrate mitochondrial genetic codes, based on the representation theory of the Lie superalgebra A(5,0) ≃ sl(6/1). A key role is played by pyrimidine and purine exchange symmetries in codon quartets.

The application of group theoretical methods to spectroscopy is today part of the accepted set of techniques for the analysis of many body systems in physics. In the present paper, we consider models for the symmetries of the genetic code by using the classical Lie superalgebras. We claim that, beyond the physical language of spectroscopy in which the method is couched, the group theoretical technique is indeed able to give a succinct account of many of the currently understood aspects of the evolution of the genetic code and the observed degeneracy structure of the codon–amino acid correspondences. We present one particular model, based on the Lie superalgebra A(5,0) ≃ sl(6/1), which has many natural structural features for this purpose that conform with observation. We argue that the model is susceptible to numerical verification by using the wealth of data that are available on biologically important molecules related to DNA.

The plan of the paper is as follows. Below, the nature of analyses of the genetic code based on Lie algebra symmetries is examined via a discussion of the work of Hornos and Hornos (1) on the eukaryotic genetic code. However, it is pointed out that the central motivation for our own extension of the analysis to supersymmetries based on the classical Lie superalgebras is the quartet or family box structure of the genetic code and its pyrimidine and purine exchange invariances. {At the algebraic level, the extension is analogous to generalizations of the interacting boson model [Arima and Iachello (2) by using supersymmetry, as in Balantekin et al. (3), or Morrison and Jarvis (4)]}. A search for candidates having typical 64-dimensional representations is described, and then the A(5,0) model is presented, together with natural branching chains that are shown to reflect the structure of both the eukaryotic code (EC) and the vertebrate mitochondrial code (VMC) and variants. By way of justification, we discuss briefly how the model encompasses a description of existing biological theories of evolutionary code history. In the concluding remarks, we suggest that the Hamiltonian and other operators defined in terms of the algebra generators may provide scope for detailed numerical studies [see Bashford et al. (5)]. A preliminary version of this work has been presented in Bashford et al. (6) [see also Bashford (7)].

In 1993, Hornos and Hornos (1), proposed a novel application of group theory to the possible pathways of evolution of the eukaryotic genetic code: Symmetries evident in the code should manifest themselves in the way codons are chosen to represent different amino acids. That is, consider the 64 codons as a 64-dimensional, irreducible representation of some appropriately chosen Lie group. In the beginning of evolution, they are all supposed to code for one amino acid. Then, the presently observed amino acids are recovered by consecutive symmetry breakings. Decomposing the 64-dimensional representation with respect to a certain subgroup chain leads to the appearance of increasing numbers of subrepresentations of decreasing dimension. The number of representations present at any stage of decomposition corresponds to the number of amino acids incorporated into the genetic code; the dimension of each subrepresentation corresponds to the number of codons that code for a given amino acid. Inspection of the eukaryotic code of Table 1 shows that 21 such subrepresentations of dimension 1, 2, 3, 4, or 6 are required in the final stage of decomposition; at this final stage, the codon multiplicities are evident (and thus the degeneracy of the code). After a systematic search of semisimple Lie algebras with 64-dimensional, irreducible representations (for example, B₆ has one and D₇ has two 64-dimensional, irreducible representations), Hornos and Hornos (1) adopted the 64-dimensional, irreducible representation of C₃ [sp(6)] with numerical marks (1,1,0) and the subalgebra chain:

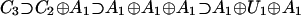1

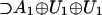By analogy with spectroscopy spin states, a “Hamiltonian” operator H was associated with the system. The eigenvalues are taken to be related to some amino acid properties, presumably a measure primarily of the size, shape, and dipole moment to reflect the ease of transport and binding to tRNA. In fact, the Grantham polarity (8) was used to numerically “fit” the subrepresentations to their corresponding amino acid and provide a tentative assignment [exhibited in figure 1 of Hornos and Hornos (1)]. Finally, Jukes’ (9) “freezing” of the genetic code also was accomplished in the model by a partial symmetry breaking, via appropriate parameter choices in the Hamiltonian model.

Table 1.

EC and VMC codes

aa	c	ac	aa	c	ac
Phe	UUU	GAA	Ser	UCU	*IGA
Phe	UUC	"	Ser	UCC	"
Leu	UUA	UAA	Ser	UCA	UGA
Leu	UUG	*CAA	Ser	UCG	*CGA
Leu	CUU	*IAG	Pro	CCU	*IGG
Leu	CUC	"	Pro	CCC	"
Leu	CUA	UAG	Pro	CCA	UGG
Leu	CUG	*CAG	Pro	CCG	*CGG
Ile	AUU	†IAU	Thr	ACU	*IGU
Ile	AUC	"	Thr	ACC	"
Ile*	AUA	UAU	Thr	ACA	UGU
Met	AUG	*CAU	Thr	ACG	*CGU
Val	GUU	*IAC	Ala	GCU	*IGC
Val	GUC	"	Ala	GCC	"
Val	GUA	UAC	Ala	GCA	UGC
Val	GUG	*CAC	Ala	GCG	*CGC
Tyr	UAU	GUA	Cys	UGU	GCA
Tyr	UAC	"	Cys	UGC	"
Ter	UAA	—	Ter*	UGA	—*
Ter	UAG	—	Trp	UGG	*CCA
His	CAU	GUG	Arg	CGU	*ICG
His	CAC	"	Arg	CGC	"
Gln	CAA	UUG	Arg	CGA	UCG
Gln	CAG	*CUG	Arg	CGG	*CCG
Asn	AAU	GUU	Ser	AGU	GCU
Asn	AAC	"	Ser	AGC	"
Lys	AAA	UUU	Arg*	AGA	UCU*
Lys	AAG	*CUU	Arg*	AGG	CCU*
Asp	GAU	GUC	Gly	GGU	*GCC
Asp	GAC	"	Gly	GGC	"
Glu	GAA	UUC	Gly	GGA	UCC
Glu	GAG	*CUC	Gly	GGG	*CCC

VMC can be obtained by changing Ile*, Ter*, Arg*, (−)*, UCU*, and CCU* to Met, Trp, Ter, UCA, (−), and (−), respectively, and all of *C, *I, and *G to U and  

^†I to G. aa, amino acid; c, codon; ac, anticodon. 

The key idea of using group theoretical symmetry breaking to model the dynamical processes of code evolution is an extremely powerful one and forms the methodological basis of our work. The main point of departure for our analysis is to give primacy to the patterns (and some of the properties) of the anticodons underlying the genetic code. Thereby, we make contact with the evolution of the anticodon carrying tRNA, with the associated tRNA synthetases and in principle with the earliest translation mechanisms. The original arguments of Jukes (9) for code evolution [see Osawa et al. (10) for a recent review] used the standard tabular representation based on codon family boxes, or quartets. In fact, addition of amino acids to a code and changes in amino acid assignment were proposed to be incorporated as the result of tRNA mutations. When splitting and duplicating, a gene for a tRNA may produce a perfect and an imperfect copy of itself. The resulting mutant’s amino acid receptor site may bond with another aminoacyl enzyme more precisely; thus, when reading mRNA, a different amino acid may be incorporated into biosynthesis, producing new (but potentially ineffective) proteins. Effectively then, the original amino acid “loses” some codons to the new one. It is argued in Jungck (11) and Di Giulio et al. (12) [see also Sueoka (13)] that codon allocation to amino acids is largely a result of error minimization to proteins affected by such processes. Given such mechanisms of codon “loss” and “capture” (9) in terms of tRNA mutations, we have “binary splitting,” that is, a quartet of codons loses codons only in pairs. (Similarly, pairs of codons may be split into singlets). In light of this, the amino acids of multiplicity 6 or 3 should be considered as 6 = 4 + 2 or 4 = 2 + 2 followed by 2 + 1 = 3 and not subrepresentations of dimension 6 or 3 as in Hornos and Hornos (1). Jukes’ arguments (9) based on family boxes in fact predicted a primordial number of 14 or 15 amino acids (depending on the evolutionary history of quartets incorporating Ter), but in the 14 subrepresentations found in the decomposition of Hornos and Hornos (1) at the A₁ ⊕ A₁ ⊕ A₁ level, dimensions of 8, 6, or 2 occur.

The details of our own analysis will be developed mainly combinatorially; a discussion of the biological context of the final model is given after it has been described algebraically. As mentioned above, inspection of the EC and VMC shows that it is natural to consider them in terms of codon quartets, or family boxes. Indeed, changing the first or second base almost invariably changes the amino acid being coded for, and it is clear that the code structure sensitively depends on the base occupying the third codon position. Jukes (9) noted that eight codon quartets code for the same amino acid regardless of whether a pyrimidine, Y (that is, either of the nucleic acid bases U or C derived therefrom), or a purine, R (that is, either A or G), occupies the third codon site whereas eight quartets are sensitive to the choice of pyrimidine or purine for this position. This phenomenon can be related to the Crick wobble rules (14) for third position pairing (the first two codon bases pair with their canonical anticodon partners). Let us focus on the VMC first (Table 1). The former eight quartets can be associated with the fact that a tRNA anticodon of the form UNN may bind to a codon with any of U, C, A, or G in the third position, and anticodons of the form GNN may bind only to codons of type N′N′Y, thus correlating with the structure of the latter eight quartets. The case of the EC (Table 1) is more complex. A commonly used tRNA for quartets in which all codons code for the same amino acid is one having an anticodon INN (with I replacing A in the first position) for codons N′N′Y, and for the NNR codons of these quartets, we have tRNAs with anticodons YN′N′. For quartets in which not all codons code for the same amino acid, a tRNA with anticodon GNN tends to cover the N′N′Y codons. The similarity of the structures of EC and VMC reflects the closeness of the VMC to the primitive code, from which the EC is believed to have descended. Finally, other variants of the EC (metabacteria codes, chloroplast codes, etc.) do not differ in amino acid assignment to codons but use different tRNAs to cover their quartets [see Osawa et al. (10) for details of anticodon assignments].

We say that codons from a given family box or quartet differing by exchange of the third codon position are invariant if they code for the same amino acid. From Table 1, we observe that the codons may be split into distinct sets of quartets, according to the type of codon exchange invariance manifested. The further notion of strong quartet invariance entails in addition that the invariant codons also should have the same associated anticodon. Thus, for the EC, the only strong invariance (of all quartets) is that of Y-Y exchange; for the VMC, eight quartets show strong invariance with respect to Y-Y and R-R transitions as well as Y-R transversions, and eight possess strong invariance under Y-Y and R-R exchanges only. These patterns are major determinants of our subsequent analysis in that we expect Jukes’ (9) quartets to appear at the final stages of the evolution both for the EC and VMC (as a result of symmetry breaking of some algebra), together with a further splitting consistent with the codon and the anticodon content of the quartets in Table 1. That is, the VMC should have either an intact quartet associated with one anticodon or a split 2 + 2 quartet associated with two anticodons; similarly, the EC should have all quartets split to 2 + 1 + 1.

To motivate the introduction of superalgebras and before embarking on the analysis leading to the favored model to be presented below, we reiterate the above discussion by demonstrating, at the quartet level, the algebraic content of the invariances mentioned above.

In a state space notation, let us explicitly introduce three letter labels spanning the 64-dimensional codon set. Bearing in mind the above discussion, the two-dimensional spaces spanned by --U, --C (with fixed first and second base letters) will play a distinguished role. On these subspaces with the ordering chosen, the most general linear transformations are of course generated by the elementary 2 × 2 matrices e_ij, with i, j = 1,2. Thus, the most general Y-Y exchange symmetry is associated with the Lie algebra gl(2). Below, we shall be concerned mainly with the simple A₁ ≃ sl(2) subalgebra generated by e₁₂ and e₂₁, representing the positive and negative simple root vectors, respectively, and ½ (e₁₁−e₂₂), the Cartan subalgebra element. In exactly the same way, we can associate an A₁ symmetry with the R-R exchange in the third codon position (the basis of the vector space being --A, --G).

The Y-Y and R-R invariances among the quartets mentioned above should be interpreted in terms of the appearance of appropriate two-dimensional subrepresentations at the algebraic level. The question arises next as to the algebraic nature of the invariance under Y-R exchange and moreover as to which algebra, combining all the symmetries, is responsible for the emergence of the basic quartet structure. Extending the line of reasoning developed above, natural candidates would be subalgebras of gl(4). Here, however, we introduce the notion of a Z₂ grading in the codon space and attempt to describe and unify the symmetries by using appropriately chosen Lie superalgebras. Besides studying this case as a logical alternative to Lie algebras, our motivations for this, as will be more apparent from the evolution scheme proposed, build strongly on the above remarks about codon patterns in the genetic codes.

We consider a codon of a quartet to be even or odd according to the grading of the base in the third codon position. In each quartet, we will always have two even and two odd codons, associating to each quartet a graded four-dimensional vector space so that the 64-dimensional codon space becomes graded 32 even and 32 odd. Thus, our analysis must lead to quartets carrying four-dimensional representations of some superalgebra, namely gl(2/2) or an appropriate subalgebra, such as sl(2/2), osp(2/2) ≃ sl(2/1) ≃A(1,0), sl(1/1), or osp(1/2) ≃ B(0, 1) [information and conventions used in the following concerning Lie superalgebras can be found in Cornwell (15), Kac (16), or Scheunert (17)]. In fact, the quartets will turn out to carry the family of four-dimensional, typical, irreducible representations of A(1,0), whose matrix representation we give explicitly for completeness [see, for example, Cornwell (15) page 249 or Gould and Zhang (18)]. Denoting the root vectors of A(1,0) as e_α1, e_−α1, h_α1, h_α2 (even) and e_α2, e_−α2, e_α1+α2, e_−α1−α2 (odd), the respective matrices of the representation are given by: e₃₄, e₄₃, (1/2)(e₃₃ − e₄₄), (1/2)(κ₊κ₋e₁₁ + μ₊μ₋ e₂₂ + κ₊κ₋e₃₃ + μ₊μ₋e₄₄), κ₊e₁₃ + μ₊e₄₂, κ₋e₃₁ + μ₋e₂₄, −κ₊e₁₄ + μ₊e₃₂, −κ₋e₄₁ + μ₋e₂₃. κ₊, κ₋, μ₊, and μ₋ are any complex parameters subject to the conditions μ₊μ₋ = κ₊κ₋ + 1 and b₂ = κ₊κ₋, where b₂ is any complex number, b₂ ≠ 0, 1, labeling the highest weight (b₁,b₂) = (0,b₂) of the four-dimensional A(1,0) irreducible typical representation.

For the invariant quartets of both the EC and VMC, ordering the basis as --U, --C (even), and --A, --G (odd), we note that A(1,0) unifies all exchanges in that the representation space remains irreducible under the A(1,0) action (in fact any grading or ordering will do). For the remaining quartets, we invoke the strong invariance substructure that takes into account the anticodon. The 2 + 1 + 1 pattern noted previously can be presented as a breaking of the A(1,0) with respect to an A₁ ⊕ U₁ subalgebra (see, for example, Gould et al. (19)], where the Y-Y invariance A₁ is generated by the even simple root of A(1,0). Then, the four-dimensional graded vector space splits into a direct sum of three irreducible vector spaces of dimensions 2, 1, and 1, with the even two-dimensional subspace carrying a doublet (spin-½) representation of A₁ (with the basis as above).

As noted previously, for the VMC (Table 1), the split quartets possess two associated anticodons. We therefore require a symmetry breaking whereby the Y-Y and R-R invariances are associated with two-dimensional subrepresentations. One possibility is to decompose the quartet with respect to a semidirect sum algebra of A₁ ⊕ U₁ ⊂ A(1,0) with the group algebra W of an appropriately chosen group. Consider the group W = Z₂ generated by the affine transformation S′_α1+2α2. The action of the latter on any element λ of the weight lattice of the four-dimensional A(1,0) representation is given by S′_α1+2α2 (λ) = S_α1+2α2 (λ) + (−2κ₊κ₋ − 1)(α₁ + 2α₂) where S_α1+2α2 is a Weyl reflection with respect to the even weight α₁ + 2α₂. Then, after lifting the action of W on the weights to an action on the weight vectors, the four-dimensional A(1,0) representation splits into two doublets, consisting of the two A₁ ⊕ U₁ singlets and the A₁ doublet as before. After appropriate identification of codons and weight vectors in the quartet, we can isolate two invariant subspaces with basis --U, --C, and --A, --G that manifest the Y-Y and R-R invariance, where A₁ + U₁ leaves invariant the first subspace and is represented on the other trivially and (the lifted action of) S′_α1+2α2 leaves invariant the second subspace and is represented on the first trivially.

There also is an A₁ ⊕ A₁ subalgebra of the enveloping algebra of A(1,0), generated by v¹ = me_α2e_α1+α2, v² = ne_−α2e_−α1−α2, v³ = (1/2)[v¹,v²] for the first A₁ and v₁ = m′e_−α2e_{α1 + α2}, v₂ = n′e_α2e_−α1−α2, and v₃ = (1/2)[v¹,v²] for the second A₁, such that m, n, m′, n′ satisfy mn = m′n′ = −[b(b + 1)]⁻¹. Such a realization of A₁ ⊕ A₁ is strictly dependent on this representation and does not constitute a genuine closed subalgebra of A(1,0). Nevertheless, with respect to this A₁ ⊕ A₁, the representation decomposes into two homogeneously graded invariant subspaces spanned by --U, --C and --A, --G, respectively (i.e., Y-Y and R-R invariance).

A third possible branching chain for the VMC involves an sl(1/1) ⊂ A(1,0) subalgebra generated by the root vectors associated with the odd simple root of A(1,0). Then, choosing as even basis --U, --A and the others as odd and the ordering as before, the representation space decomposes under sl(1/1) as a direct sum of two invariant two-dimensional subspaces, with bases --U, --C and --A, --G, respectively, thus again manifesting the Y-Y and R-R invariances, but with a reassignment of codon grading compared with that involved in the branching to A₁ ⊕ U₁ in the EC.

Finally, we turn to the analysis of representations of superalgebras leading to a preferred model possessing the detailed algebraic structure at the quartet level that we have just described. In the same spirit as in Hornos and Hornos (1), we undertook a search of the simple, basic, classical, complex Lie superalgebras A(r,s), B(r,s), C(s), and D(r,s) having typical 64-dimensional irreducible representations [see Bashford (7)]. Simplicity led us initially to examine only symmetry breakings with respect to maximal regular subalgebras; however, the choice of typical representations also is motivated by the dimensionality of the required codon space. Of the four potential candidates found with rank ≤8 [A(5,0), B(2,1), C(4), and D(2, 1;α)], the most promising one is A(5,0) ≃ sl(6/1), because the expected quartet structure, associated with an A(1,0) subalgebra as described above, arises directly. The scheme is flexible enough to accommodate both the EC and the VMC, keeping contact with well established properties of the genetic code and reproducing the currently observed structure [see Jukes (9) and in particular Osawa et al. (10)] with the final symmetry breaking also taking into account the evolution of the anticodons.

The family of 64-dimensional, irreducible typical representations of A(5,0), with Dynkin labels (0,0,0,0,0,b) where b ≠ 0,1,2,3,4,5,6 to avoid atypicality, will be considered. Of most importance at the quartet level (with the full exchange invariance) is the subalgebra chain:

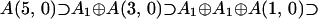2

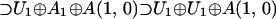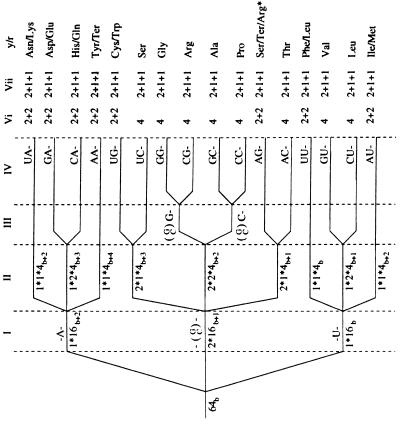
Based on this chain, the evolution proposed for the EC and the VMC is shown in Fig. 1, along with tentative codon assignments (discussed further below). The perpendicular dashed lines separate various stages of evolution (symmetry breaking) and are described as follows: stage I, the 64-dimensional representation of A(5,0) decomposes with respect to a regular subalgebra A₁ ⊕ A(3,0); stage II, the A(3,0) multiplets decompose with respect to a subalgebra A₁ ⊕ A(1,0); stage III, the A₁ doublets generated in stage I decompose with respect to an abelian U₁ subalgebra; and stage IV, the A₁ doublets generated in stage II decompose also with respect to an abelian U₁ subalgebra.

Figure 1.

Evolution of the EC and VMC. The notation is (2j₂ + 1)*(2j₁ + 1)*4_b2, and stages Vi and Vii show the differences between branchings appropriate to the EC and the VMC; refer to Table 1 for the AAN, AGN, and AUN codons.

At this stage, it is worth noting that, in both codes, the decomposition has resulted in 16 quartets or family boxes [i.e., four-dimensional representations of A(1,0)]. The crucial difference between the two codes is the mode of decomposition of the A(1,0) representations in stage V. For the VMC, the various decompositions responsible for Y-R breaking among quartets, which have been identified previously, all have the same final two doublet outcome as far as the anticodon (or tRNA) assignments are concerned, and this is shown in Fig. 1. It will be seen below from the details of the branching rules that a “freezing” is present in the evolution of the VMC, as suggested by Jukes (9). On the other hand, for the EC (see Fig. 1), the branching of the A(1,0) quartets with respect to the even subalgebra A₁ ⊕ U₁ as identified previously is a complete symmetry breaking with no “freezing” [contrary to Hornos and Hornos (1)], in the sense that each of the three final subrepresentations corresponds to one and only one anticodon.

The means by which codons tentatively can be assigned to the branching scheme are more transparent from the details at the level of the weight space, to which we now turn. We present a form of generic Hamiltonian operator for the system and its corresponding eigenvalues. We defer further justification of the model in terms of biological understanding to the discussion below, and we defer general questions about the physical interpretation of the Hamiltonian and other operators for the system to the concluding remarks. Each subrepresentation at stages I–V may be labeled in terms of its Dynkin labels (see Table 2), providing a complete weight labeling scheme. For definiteness, the various subalgebras will be given a superscript ^( ), for example A₁⁽²⁾ ⊕ A₁⁽¹⁾ ⊕ A(1,0) in the first line of Eq. 2 above. For the EC chain, the labels are (2j₂;a₄;2j₁;b₂;m₁, m₂;2j₃;c₃), where, for the family (0,0,0,0,0,b) of 64-dimensional typical representations of A(5,0) considered, the A(3,0) irreducible representations arising have Dynkin labels (0,0,0;a₄); similarly, the A(1,0) quartets are labeled (0,b₂). The A₁⁽ⁱ⁾ algebras, with angular momenta j_i, are associated the U₁ subalgebras with representation labels m_i (magnetic quantum numbers); c₃ is the U₁ label for the A₁⁽³⁾ ⊕ U₁ basis of A(1,0). For the VMC chain in the A(1,0) ⊃ sl(1/1) case, the last two labels 2j₃ and c₃ should be replaced by n₃, and for the A₁ ⊕ A₁ case, these labels should be replaced by ℓ₁,ℓ₂, being, respectively, the sl(1/1) invariant and the appropriate effective angular momenta (see Table 2 for the explicit spectra). A Hamiltonian H is derived as a linear combination of the (second order) Casimir invariants Γ of each subalgebra in the appropriate chain with arbitrary coefficients. For the EC this yields:

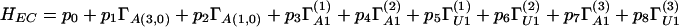3

whereas for the VMC, we must substitute in Eq. 3 p_ifor (different) parameters q_i, and the last two terms acquire additional factors (m₂ + ½)(j₂ + ½ − ½Δ), Δ ≡ b₂ − b [with Γ_sl(1/1) replacing Γ_A1³ in the case A(1,0) ⊃ sl(1/1)]. Had we chosen, for the VMC, the final decomposition of the quartets to be with respect to the semidirect sum of A₁ ⊕ U₁ with W, the state labeling would follow that of the EC, but the parameters should be chosen such that the doublets’ degeneracy with respect to W is preserved. The eigenvalues E_EC of H in terms of the numerical marks are found to be:

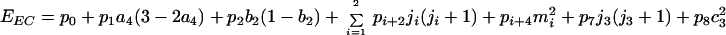4

whereas for the E_VMC, the last two terms acquire additional factors (m₂ + ½)(j₂ + ½ − ½Δ), with n₃² replacing j₃(j₃ + 1) in the case A(1,0) ⊃ sl(1/1). Note that the terms ∝(m₂ + ½)(j₂ + ½ − ½Δ) in the VMC case produce the freezing referred to by Jukes (9).

Table 2.

Non-zero highest weight labels of quartet decomposition for the the EC and VMC

2j2, a4; 2j1; b2; m1, m2;	k	ℓ
1; b + 1; 1; b + 2; ± ½, ± ½;	5, 4, 6	3, 4
1; b + 1; 0; b + 1; ± ½, 0;	3, 2, 4	2, 3
1; b + 1; 0; b + 3; ± ½, 0;	7, 6, 8	4, 5
0; b; 1; b + 1; 0, ± ½;	3, 2, 4	1, 2
0; b; 0; b; 0, 0;	1, 0, 2	0, 1
0; b; 0; b + 2; 0, 0;	5, 4, 6	2, 3
0; b + 2; 1; b + 3; 0, ± ½;	7, 6, 8	3, 4
0; b + 2; 0; b + 2; 0, 0;	5, 4, 6	2, 3
0; b + 2; 0; b + 4; 1, 0;	9, 8, 10	4, 5

The A₁ ⊕ U₁ ⊂ A(1, 0) labels (2j₃, c₃ ≡ 2b + k) take values (0, 2b₂), (1, 2b₂ + 1), (0, 2b₂ + 2). The sl(1/1) invariant n₃ ≡ b + ℓ takes values b₂, b₂ + 1. 

As could be expected, the assignments of amino acids in the representations of Fig. 1 are necessarily tentative. The quartet structure already discussed imposes the requirement to have the Z₂ gradings consistently attributed. A stronger requirement is that the 4-fold groupings of codon quartets at stage IV that are closest in the branching tree [namely, the 16 dimensional representations of A(3,0)] should correspond to a column from Table 1. The outcome of the assignment is thus the association of codons to the representations so as to form families with the same second codon position after stage II of the decomposition. Specifically, codons having C and G in the second position are chosen to be situated in the 32-dimensional representation of stage I, and those with A and U in the second position are situated on each of the 16-dimensional representations; the breaking of the A₁⁽²⁾ doublet to its abelian part U₁⁽²⁾ (the magnetic label) completes the disaggregation into families of 16. Referring to biological understandings of the origin of protein encoding, this accords with the situation of a primitive translation apparatus, wherein active enzymes could be constructed from suitably alternating hydrophilic and hydrophobic residues, with the encoding and assembly systems consistent with this. Thus, for example, Weber and Lacey (20) [see also Jungck (11)] have studied anticodon dinucleotide hydrophilicities and correlated these with amino acid properties. At the extreme ranges of hydrophilicity are the −U− and −A− families (20), with the −G− and −C− families intermediate, subject to additional modulation by the first (codon) dinucleotide base. It is this pattern that has been assimilated in stages II and III of the model, with discrimination between the −G/C− families following the initial hydrophobic/hydrophilic split. Similarly, the first base modulation is achieved by stage III/IV branching that mimics the stage I/II hierarchy. The same pattern, but based on free energy considerations, was derived in Bashford et al. (5); Jarvis et al. (6) give an alternative assignment, which, however, does not lead to a direct interpretation of the A₁ subalgebras at stages I and II in terms of base position exchange symmetries. Within the A(5,0) model, code discrimination at the level of the second and first base positions also can be seen to emerge cleanly by an alternative scheme in which A₁⁽²⁾ branches to U₁⁽²⁾ before the A(3,0) breaking; the admissibility of such patterns is a subject for further investigation (see below).

In fact, there is a rich literature on studies of correlations between physicochemical properties of amino acids and their associated codon locations in the genetic code (11–13, 21). In one of the most elegant presentations, Siemion (22) has established that, for codon orderings, according to “one-step mutation rings,” periodicities emerge. In fact, the resultant graphical 4-wheel periodic system (see figure 2 in ref. 22) can be regarded as equivalent to a concatenated weight diagram of A(5,0), first projected onto two dimensions to establish the locations of the −A−, −G/C− and −U− families of A(3,0) (for example m₂ vs. a₄ − b − 1) and then with each such 16-dimensional representation projected onto a plane perpendicular to A(1,0) (for example, m₁ vs. b₂ − a₄ − 1), whose quartet weights are then plotted in turn. “Periodicity” of indices of amino acid properties simply reflects the fact that generic Casimir operators in the chain of A(3,0) subalgebras will produce similar eigenvalues on the various components of the 16-dimensional families, whose weight labels differ systematically as a result of the shift of the fourth Dynkin label a₄ in the decomposition (Table 2).

In this paper, we have a given an analysis of the structure and evolution of the genetic code in terms of classical superalgebras and have presented a model based on the decomposition of a family of 64-dimensional, irreducible, typical A(5,0) ≃ sl(6/1) representations, which evidently matches the classification of codons in terms of exchange symmetries in codon quartets. Furthermore, it has been demonstrated that these features can be discussed naturally in terms of A(1,0) and its subalgebras, not only accounting for the codon symmetries but also giving a dynamical role to the anticodons as well, especially in the final stage of the decomposition. The model incorporates both the EC and the VMC and gives a plausible pathway for evolutionary progression from primitive codes, with few amino acids, to the present complex codes with many amino acids (thus the model would predict two primordial amino acids at stage I together with Ter). To emphasize not only the explanatory power but also the quantitative applicability of this type of model, we conclude with further remarks on the physical interpretation.

An important issue is the physical justification of the introduction of supersymmetry in the sense described previously. From a mathematical point of view, there is no difficulty with the use of superalgebras provided that a consistent Z₂ grading can be established (see, for example, refs. 23–25). In fact, the chemical structure of the nucleic acid bases reveals just such a possibility: The single (6-atom skeleton) pyrimidine ring is to be contrasted with the two-ring purine complex, which has a pyrimidine ring fused to an imidazole ring (9-atom skeleton). It also may be possible to adduce a physical grading with respect to the different electronic configurations of these molecules [it should be noted, however, that, if we implement an sl(1/1) decomposition of the A(1/0) as described above, the pyrimidine and purine doublets must be inhomogeneously graded]. For the purposes of the present work, however, we adopt the more formal approach and view the grading simply as a concomitant of the mathematical tools being used.

It was emphasized above that Fig. 1 provided only tentative codon assignments, and a generic Hamiltonian operator has been invoked to provide a semi-quantitative measure that aids fitting to arrive at a unique identification. Given a particular assignment, each subrepresentation acquires a unique label, and correspondences between the eigenvalues (Eq. 4) of E_EC (and similarly E_VMC) associated with each codon (or anticodon) and specific physicochemical properties (of amino acids or anticodons) can be made. In the discussion of the A(5,0) model, such a procedure was implied (but not carried through) for indices of anticodon dinucleotide hydrophilicity (20) (but see ref. 5 for an analysis of codon–anticodon dinucleotide free energy of formation). At the coarsest level, the parametrization of VMC freezing as discussed already can be regarded as a type of “fit.” Similarly, regressive features in the code, such as the existence of hexanumerate codons for Ser, Arg, and Leu via additional (captured) doublets at various symmetrical locations with respect to the symmetry axes of the 4-wheel periodic system of Siemion (22) [that is, the A(5,0) weight diagram], may be explained by invoking particular types of functional dependence of Hamiltonian eigenvalues on the labeling parameters. In general, it is clear that semi-empirical fits can be attempted to a variety of physical, chemical, as well as geometrical measures [for example, the conformational parameters as treated by Siemion (22, 26) and Goodman and Moore (27)]. Work along these lines is in progress.

As we saw previously, the matrix elements of the four-dimensional, typical, irreducible A(1,0) representation (0,b₂), b₂ ≠ 0, 1 depend on constrained complex parameters. This property suggests the investigation of data that involve amino acid or codon pair correlations. For example, the parameters may describe the rate (or amplitude) of particular codon substitutions (leading to mutations) by interpreting the various generators of A(1,0) as transition (or transversion) operators within a given quartet, for example, κ₊ = (--C,e_α2⋅--U). A complete analysis requires knowledge of such parameters for the 64-dimensional representation of A(5,0) and their distribution in the final A(1,0) quartets. In this context, we can also analyze the observation that a nucleotide may be influenced by its neighbors, and this is documented by the existence of directed mutational pressure of genomic G plus C content [see, for example, Sueoka (13), Mrazek and Kypr (28), and Siemion and Siemion (29)]. It has been shown in Muto and Osawa (30) that the third, and to a lesser extent the first, codon position is particularly susceptible to this phenomenon. The relevant transition operators easily are identified in terms of appropriate A(5,0) generators in the subalgebra basis of Fig. 1; beyond the A(1,0) generators themselves, appropriate shift operators and selection rules at the A₁ ⊕ A(3,0) or A₁ ⊕ A₁ ⊕ A(1,0) level may become relevant. We hope to return to these issues in future work.