A Generalized Born Implicit-Membrane Representation Compared to Experimental Insertion Free Energies

Abstract

An implicit-membrane representation based on the generalized Born theory of solvation has been developed. The method was parameterized against the water-to-cyclohexane insertion free energies of hydrophobic side-chain analogs. Subsequently, the membrane was compared with experimental data from translocon inserted polypeptides and validated by comparison with an independent dataset of six membrane-associated peptides and eight integral membrane proteins of known structure and orientation. Comparison of the insertion energy of α-helical model peptides with the experimental values from the biological hydrophobicity scale of Hessa et al. gave a correlation of 93% with a mean unsigned error of 0.64 kcal/mol, when charged residues were ignored. The membrane insertion energy was found to be dependent on residue position. This effect is particularly pronounced for charged and polar residues, which strongly prefer interfacial locations. All integral membrane proteins investigated orient and insert correctly into the implicit-membrane model. Remarkably, the membrane model correctly predicts a partially inserted configuration for the monotopic membrane protein cyclooxygenase, matching experimental and theoretical predictions. To test the applicability and usefulness of the implicit-membrane method, molecular simulations of influenza A M2 as well as the glycophorin A dimer were performed. Both systems remain structurally stable and integrated into the membrane.

INTRODUCTION

Estimates indicate that 20–30% of the human genome encodes membrane proteins (1–3). Even though the majority of current drug targets are membrane proteins such as receptors and ion channels, only 113 unique membrane protein structures are known at present (4) (August 2006, an up-to-date summary is provided by White: http://blanco.biomol.uci.edu/). The scarcity of structural data is mainly a result of substantial difficulties with overexpression and crystallization of membrane proteins (5). Due to their pharmacological role as major drug targets, there has been an increasing interest in detailed structural data as well as realistic simulation methodologies. Together with the extremely high computational cost of molecular mechanics simulations using explicit lipid-bilayer membranes (6–9), this has led to the development of a variety of implicit-membrane representations, which we briefly summarize. Knowledge-based methods include energy terms derived from a library of known protein sequences and structures (e.g., 10–12) (see also Hurwitz et al. (13) for an up-to-date review). Coarse-grained or off-lattice models have been successfully employed to study the insertion process of a variety of membrane peptides (14–16). The peptides are modeled as a linked chain of hard spheres, each representing a residue, whereas the membrane and surrounding aqueous phase are modeled by properties depending only on the membrane normal, e.g., fractional water content, polarity, and hydrophobicity. If parameterized well, this type of coarse-grained model can yield excellent results. However, these models have several limitations compared to all-atom models. 1), The potential functions used are not based on classical force fields and hence lack the extensive testing, accuracy, and versatility of the latter. 2), Peptide-peptide interactions are difficult to model correctly in the absence of side-chain atoms. 3), Complex membrane-protein functionality, like ions moving through channel pores, cannot be modeled using such simplified models.

More rigorous approaches combine standard all-atom force fields with implicit-solvent energy terms. This can be achieved by modeling both the aqueous solvent and lipid phase as a lattice of Langevin dipoles mimicking the spatial polarization of the protein environment (17). Other studies have applied distance-dependent dielectrics, as well as Gaussian screening functions to model both membrane and aqueous solvation (18). Another approach builds on atomic solvation parameter methods, which model the solvation terms as an effective surface tension multiplied by the accessible peptide surface area (19,20). More accurate is the use of the Poisson-Boltzmann equation in determining the electrostatic free energy of solvation, but its use in molecular dynamics simulations is prohibitively slow (21,22). A further overview on the large number of present and future applications of implicit-membrane models is given in recent reviews (23,24).

A much faster method, with results comparable to Poisson Boltzmann, is the generalized Born algorithm. This algorithm treats the solvent as a dielectric continuum. For spherical ions in a homogeneous isotropic dielectric, the solvation energy can be determined analytically as demonstrated by Born (25). The generalized Born solvation model extends this equation to macromolecules, which are approximated as an assortment of charged spheres (26). The immense success of this method (25,26) in globular protein and peptide folding simulations (27–31) has spurred attempts to apply the generalized Born formalism to represent the membrane environment implicitly (32–34). These models describe the membrane environment as a uniform hydrophobic slab and have been used successfully to fold and assemble small helical membrane peptides (34,35).

This study was motivated by the need for a computationally efficient implicit-membrane model, which will allow simulation of large systems and long timescales while still being accurate enough to compare reasonably well with experimental data. Statistical analyses of membrane proteins (12) as well as translocon-mediated insertion experiments of designed polypeptides (36,37) suggest that the insertion energy of a residue at a certain position along the membrane normal is a property of its local solvation environment. It therefore seems reasonable to model a membrane as a smoothly varying “solvation function” along the bilayer normal. In this study, the membrane was treated as a region that becomes increasingly apolar (i.e., increasingly inaccessible to the solvent) toward the center of the membrane. However, rather than changing the dielectric constant as a function of the membrane normal, the self-solvation energy of an atom, which accounts for the largest part of the solvation energy (38), was modified to vary smoothly between full solvation in bulk water and a limiting value for burial at the center of the membrane. At this stage of development of the method, any increased polarity at the charged bilayer interfaces was neglected. Nevertheless, most of the experimental results could be reasonably well reproduced, suggesting that the solvent exclusion properties of the membrane model account for the bulk properties of a lipid bilayer. A general problem of membrane-protein simulation lies in the correct treatment of charged residues at the interfaces. In nature, burial of a charged residue inside a membrane will almost certainly involve a change of protonation state or accompaniment by a hydration shell. Here, the charged interfaces might play an important role; however, this is beyond the means of the model described here.

The membrane model was parameterized to match the water-to-cyclohexane transfer free energies of the side-chain analogs of leucine, isoleucine, and valine (39). The model was compared to the apparent free energies of a set of translocon-inserted helices (36), the octanol and interfacial scales of Wimley and White (40,41), and cyclohexane-water transfer free energies of the remaining side-chain analogs, as well as to a recent study, that derived an implicit-membrane representation from the distributions of amino acids along the membrane normal (12). Subsequently, the membrane model was tested against a range of proteins with different membrane association and topology: 1), Transmembrane (TM) helices whose tilt and rotation angles have been determined using solid-state NMR methods in oriented lipid bilayer membranes (42); 2), a set of antimicrobial peptides known to bind to the membrane surface; 3), a set of integral membrane proteins with regular as well as irregular structures; 4), a monotopic membrane protein, which integrates only partially into the cytoplasmic leaflet of a lipid bilayer. Finally, the feasibility of the membrane model for protein dynamics simulation was confirmed by performing several simulations using both a Monte Carlo concerted backbone rotation method (27) and molecular dynamics.

METHODS

The generalized Born method

The present generalized Born membrane is based on a method developed by Spassov et al. (33), in which the membrane is modeled as a planar dielectric slab with thickness 2L, surrounded by a uniform polar solvent with a dielectric constant ɛ_w = 80. Both the protein interior and the slab are assumed to have the same interior dielectric constant of ɛ_m = 2. The generalized Born method has been described in detail in a recent review (43). The Born radii are calculated using the fast asymptotic pairwise summation of Qiu and Still (44), which has been demonstrated to yield excellent results in predicting experimental free energies of solvation as well as hydration effects on conformational equilibria (45). Spassov et al. (33) modeled the membrane by restricting the pairwise summation to solute atoms outside of the membrane. This was done by switching the volumes V_i(z_i) of atoms i inside the membrane to zero at the interfaces z = ±L. The contribution due to the membrane was modeled using an exponential switching function G(z_i, L) that changes the self-solvation term of each atom between a buried and a solvated state at the interfaces. Thus, the solvation energy for each atom is given by

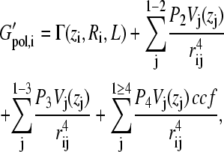(1)

where P₁–P₄ are the parameters determined by Qiu et al. (44), and ccf is a close contact function. G(z_i, L) was obtained by fitting a smooth function to the polarization energy of a singly charged ion, determined by a Poisson-Boltzmann solver, as it is moved through the dielectric slab.

A real membrane, however, is not a hydrophobic slab with a uniform dielectric constant, but rather a heterogeneous medium with a highly nonuniform distribution of charge, density, and polarizable solvent. In this study, the membrane was therefore treated as a region that becomes increasingly apolar (i.e., increasingly inaccessible to the solvent) toward the center of the membrane. The self-solvation terms G(z_i, L), as well as the atomic volumes V(z_i), were modified to vary smoothly between full solvation and a limiting value for burial at the center of the membrane. In this work, we propose a Gaussian shape

(2)

where g_bulk is the limiting value of Γ at a large distance from the membrane (i.e., z ≫ L) corresponding to the self-solvation term of the unmodified generalized Born method 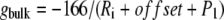, while g_center is the value of Γ at the membrane center.

The nonpolar part of the solvation free energy is modeled using an effective surface tension associated with the solvent-accessible surface area (SASA) (44). Instead of a costly calculation of the accurate surface area, a mimic based on the Born radii is used, which has been shown to be very accurate, but much faster (46). As it is moved toward the center of the membrane, the surface energy contribution of each atom is varied using a Gaussian function: For distances far from the membrane (i.e., z ≫ L), the nonpolar contribution is included with the positive surface tension of solvation in water, whereas in the center of the membrane the surface tension is negative (i.e., energy is gained by moving into this phase from the gas phase), as determined experimentally (39). Gaussians were chosen in good agreement with experimental evidence from lipid distortion (47,48), x-ray and neutron diffraction experiments on fluid liquid-crystalline bilayers (49–51), and partitioning experiments on hexane (52) in lipid bilayers.

It should be noted that the present membrane model neglects any effects due to differences in lipid composition and charge distribution of the two bilayer leaflets, as well as effects due to the transmembrane voltage. However, it is in principle possible to include these properties by replacing the Gaussians with an equivalent nonsymmetric function.

Parameterization of the Born membrane

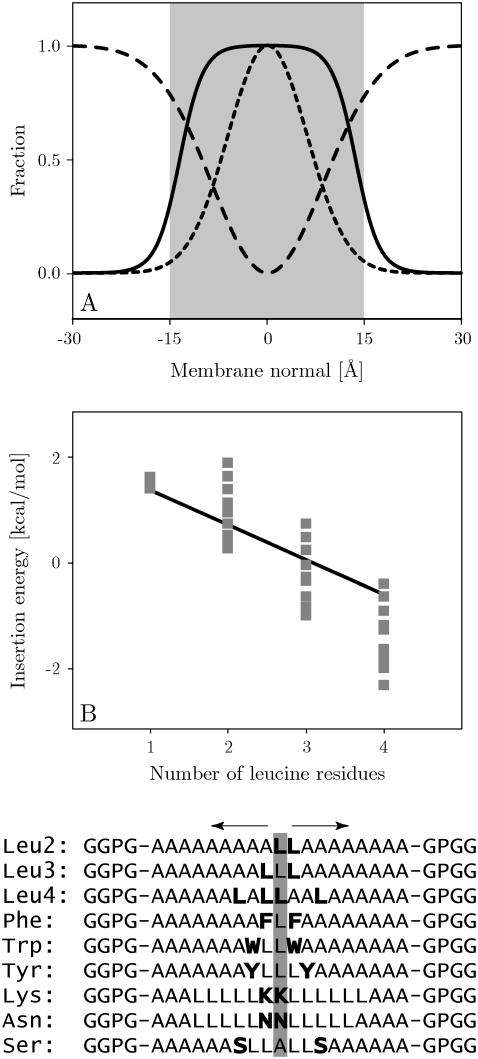
There are several adjustable parameters in the present generalized Born implicit-membrane representation. The first is the width of the membrane, given by the width of the Gaussian curve describing the self-solvation energy term in the Qiu and Still formula (44) (Eq. 1). We assumed a Gaussian with γ = −3.0 (also used for the volume term V(z)) and a membrane half-width of L = 15 Å (Fig. 1 A). The second adjustable parameter is the energy of transferring an isolated unit charge from vacuum to the center of the membrane, corresponding to the height of the Gaussian self-term g_center. This value was set to g_center = −7.67 kcal/mol, as reported in other studies (33,53). The surface tension contribution of each atom was varied as described above using a Gaussian function with γ = −1.5, interpolating between the limiting values of 12 cal/mol·Å² in the surrounding medium and −19 cal/mol·Å² in the membrane. These values were determined from a fit of the membrane insertion energy of leucine (−4.85 kcal/mol), isoleucine (−4.99 kcal/mol), and valine (−4.63 kcal/mol) side-chain analogs to the experimental water-to-cyclohexane transfer free energies (39) (see Table 2). Since these analogs are virtually neutral their experimental cyclohexane-water transfer free energies can be assumed to be only dependent on nonpolar interactions, thus providing an estimate of the effective surface tension of the membrane. The mean error for the optimal fit with respect to the experimental values was 0.24 ± 0.30 kcal/mol. Since the OPLS all-atom force field partial charges of these analogs are virtually zero the polar contribution of the implicit membrane was <0.2 kcal/mol for these analogs.

FIGURE 1.

(A) Exponential (solid) and Gaussian functions with γ = −1.5 (dashed) indicating the attractive nonpolar term, and γ = −3 (dotted) indicating the repulsive generalized Born term. (B) Calculated insertion energy of the L_nA_(19−n) set of designed peptides together with the experimental best-fit line (E_Insertion = −0.66n_Leu + 2.14). The experimental error is estimated at ±0.2–0.3 kcal/mol (36). Sequences of the symmetrical peptides used for residue-pair scans are shown below the graph. Results for the positional dependency of the insertion energy as determined by symmetrical scans of leucine pairs are shown as points in the graph. Results for the remaining scans are given in Fig. 4.

TABLE 2.

Bulk-solvent-to-membrane-center transfer free energies of the 20 natural amino acids integrated into an α-helical conformation compared with the biological scale and a statistical membrane model

Residue transfer energies (kcal/mol)
Residue	Generalized Born membrane	Biological scale	Statistical membrane	Water to cyclohexane
ALA	0.11	0.11	−0.42	−1.81
ASN	3.55	2.05	0.90	6.64
CYS	0.25	−0.13	—	−1.28
GLN	3.39	2.36	1.21	5.54
GLY	0.58	0.74	−0.30	−0.94
HIS	3.33	2.06	−0.06	4.66
ILE	−0.87	−0.60	−0.68	−4.92
LEU	−1.21	−0.55	−0.64	−4.92
MET	0.38	−0.10	−0.55	−2.35
PHE	−0.81	−0.32	−0.83	−2.98
PRO	1.93	2.23	0.65	—
SER	2.08	0.84	0.00	3.40
THR	1.71	0.52	0.00	2.57
TRP	1.12	0.30	−0.18	−2.33
TYR	0.84	0.68	−0.05	0.14
VAL	−0.59	−0.31	−0.58	−4.04
ARG	11.42	2.58	2.02	14.92
ASP	23.61	3.49	2.19	8.72
GLU	27.23	2.68	2.11	6.81
LYS	20.85	2.71	1.83	5.55

Experimental water to cyclohexane transfer free energies of side chain analogs are also shown.

Translocon-inserted polypeptides

Hessa et al. (36) challenged the endoplasmic reticulum translocon Sec61 with an extensive set of designed polypeptide segments using an in vitro assay to measure the efficiency of membrane integration (54). The peptides have the general design GGPG-X₁₉-GPGG, where the GGPG flanks serve to insulate the central 19-residue stretch from the surrounding sequence by having a low probability of secondary structure formation. In this study, all peptides were modeled as perfect α-helices with extended GGPG flanking segments. Preequilibrated side-chain conformations were used and the segment termini were acetylated (C-terminus) and methylated (N-terminus).

Calculating the minimal energy conformation

The minimal energy conformation was calculated by exploring the entire translational and rotational space of the peptide in the membrane. The principal axis of the protein was determined through diagonalization of the inertia tensor using only the heavy backbone atoms. The tilt angle was defined as the angle of the principal axis with respect to the membrane normal, whereas the rotation angle was defined as the angle of rotation around the principal axis.

The helix was translated from −50 Å to +50 Å along the membrane normal (membrane center = 0 Å) in 0.5 Å steps. At each step, the protein was rotated through all space to find the orientation of minimum energy by first tilting it with respect to the membrane normal and subsequently rotating it around its principal axis until all tilt and rotational states had been sampled with a step size of 1°. The lowest energy conformation encountered was then subjected to a rigid-body minimization to ascertain the precise location of the global energy minimum.

Experimental structures

The implicit-membrane model was tested on a range of experimental structures with different membrane topologies (see Table 1): The M2 channel segment of the δ-subunit of the nicotinic acetylcholine receptor (AchR) (1cek) (55), influenza A M2 (1mp6) (56), and the membrane conformation of FD coat protein (1mzt) (57) are single membrane-spanning α-helices. Their tilt angles are known from solid-state NMR measurements in aligned lipid bilayers (42). Since the solid-state NMR structure of the AchR M2 (1cek) lacks the charged residues at the termini, the equivalent solution NMR structures (55) (1a11) were used, which have the complete sequence. The structures of the antimicrobial peptides magainin (2mag) (58), ovispirin (1hu5) (59), and a cecropin-magainin hybrid (1f0d) (60) were determined by solution NMR in micelles. These peptides are generally believed to form amphipathic α-helices oriented parallel to the membrane in a surface-bound fashion (61–64). The transmembrane helix dimer glycophorin A (1afo) (65) has been determined by solution NMR. The relatively regular integral membrane proteins bacteriorhodopsin (1cwq) (66) and sensory rhodopsin (1h68) (67), as well as the more irregular aquaporin (1j4n, 1rc2) (68,69) and chloride channel structures (1kpk, 1kpl) (70) were all determined by x-ray crystallography. The membrane model was also challenged with the monotopic membrane protein cyclooxygenase 2 (1cx2) (71), which is known to insert only partially into one monolayer of a membrane.

TABLE 1.

Minimum energy orientations for membrane proteins of known conformation

Calculated minimum energy orientation
PDB	Protein	Organism	Tilt angle (°)	z (Å)	ΔE (kcal/mol)
1afo	Glycophorin A	Human red blood cell	14	3.7	−70.7
1cwq	Bacteriorhodopsin	Halobacterium salinarium	30	1	−29.9
1h68	Sensory rhodopsin II	Natronomonas pharaonis	3	0.7	−86.6
1j4n	Aquaporin	Bovine red blood cell	14	0.3	−83.2
1rc2	Aquaporin	Escherichia coli	8	0.7	−108.1
1kpk	Chloride channel homologue	E. coli	3	3	−90.5
1kpl	Chloride channel homologue	Salmonella typhimurium	3	3.1	−82.6
1cx2	Cyclooxygenase-2	Mouse	0	36	−95.3

The protein tilt angle, displacement of the center of mass with respect to the membrane center (z), and insertion energy (ΔE) are listed for all systems. The membrane center is located at z = 0 and negative z values correspond to shifts toward the extracellular side, whereas positive z values correspond to shifts toward the cytoplasm. For 1afo, 1j4n, 1rc2, 1kpk, 1kpl, and 1cx2, the tilt angle is given with respect to the multimer.

Molecular simulations

The simulations were run with a Monte Carlo program developed by the authors specifically for the simulation of membrane proteins in a GB/SA continuum solvent. An efficient concerted rotation sampling technique (72) is used to move the protein backbone; in addition, there are single rapid side-chain moves, with a side-chain move/backbone move ratio of 3. This method has been demonstrated to be at least as efficient as molecular dynamics sampling (73). The potential energy was evaluated with the OPLS-AA force field (74), and the Monte Carlo simulations used Metropolis sampling at a temperature of 300 K. All nonbonded interactions as well as the generalized Born energy were truncated using a cutoff of 14 Å, and the Born radii were recomputed for every configuration. The described setup has been shown to perform well in sampling DNA (75) and protein-folding simulations (27), where the native state of several polypeptides was rapidly determined starting from extended conformations. Here we report the first application of this method to the simulation of membrane proteins in implicit solvation.

Molecular dynamics simulations were performed with the GROMACS software package (76), modified to include the implicit-membrane model described above. Fixed bond lengths (77) and a time step of 2 fs for numerical integration were used. The simulation conditions and parameters were the same as for the Monte Carlo simulations and comparison of a test trajectory showed both methods to sample the same potential function.

RESULTS AND DISCUSSION

Correlation with experimental scales

The biological hydrophobicity scale was derived by calculating the insertion energies for the 19-residue helical model peptides and replacing the central residue with all 20 natural amino acids. For each peptide, the insertion energy was calculated by performing transrotational minimum-energy search in the membrane. All peptides except those with charged amino acids were found to have local minima for fully inserted configurations (z = ±2.5 Å) with small tilt angles (<10°). In their experimental derivation, Hessa et al. (36) varied the number of Leu residues in the 19-residue segment to obtain apparent free energies of insertion in the range −1.2 to 1.2 kcal/mol, since the experimental measurement is maximally sensitive at this range. Using the insertion energies of these peptides, the biological scale can subsequently be computed in a stepwise procedure (see Supplementary Material). In principle, this derivation is equivalent to replacing the central residue X of the GGPG-AAAALAAAAXAAAALAAAA-GPGG peptides with all 20 natural amino acids and subtracting the energy for X = A. Indeed, for this membrane model both methods give almost identical values and the final scale was calculated as their average (see Supplementary Material). Both the experimental and computed scales were made to coincide for alanine (see Positional dependency below).

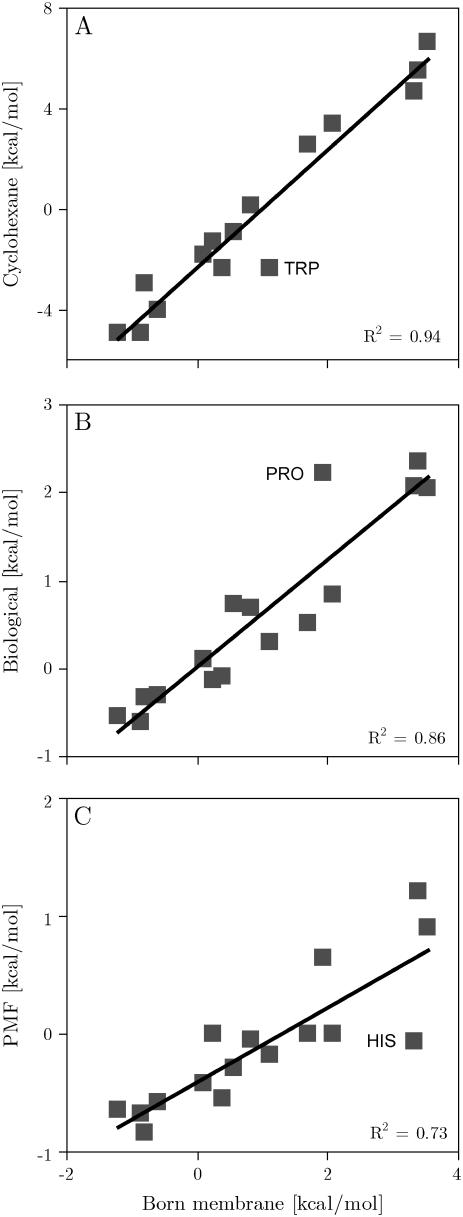
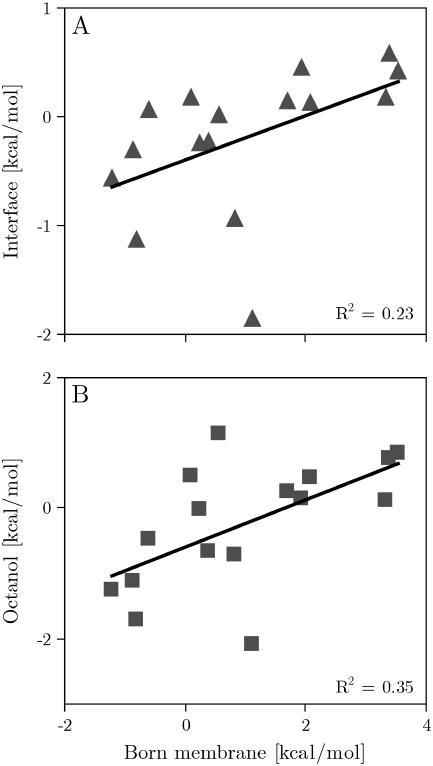
Fig. 2 compares the computationally derived scale with the experimental apparent free energies of the biological hydrophobicity scale (36). Considering the simplicity of the membrane model, both scales correlate remarkably well (C = 93%). The linear fit has a slope of 0.6 and the scales have identical origins (r_square = 0.86). Comparison with a statistical scale derived from membrane protein structures (12) gave a correlation of 87%, an offset of −0.41 kcal/mol and a slope of 0.32 (r_square = 0.73). The calculated scale also correlates remarkably well (C = 97%) with experimental transfer free energies of side-chain analogs into cyclohexane (39). On the other hand, Fig. 3 shows that there is little to no correlation with both the octanol (40) and interface scales (41). The individual energies are reported in Table 2.

FIGURE 2.

(A) Calculated insertion energy of the designed peptides versus experimental transfer free energies of side-chain analogs from water into cyclohexane. (B) Insertion energy of the designed peptides: generalized Born membrane versus the biological hydrophobicity scale (36). (C) Calculated insertion energy of the designed peptides against insertion potentials from a statistical membrane potential (12).

FIGURE 3.

(A) Calculated insertion energy of the designed peptides against the Wimley and White interfacial scale (41). (B) Calculated insertion energy of the designed peptides against the Wimley and White octanol scale (40).

Charged residues were excluded from the scale since their insertion energies are considerably overestimated by the generalized Born membrane. The energy penalties for the burial of charged residues at the center of the membrane are much higher than the corresponding values from the biological scale (23.6 kcal/mol for Asp, 11.4 kcal/mol for Arg, 27.2 kcal/mol for Glu, and 20.9 kcal/mol for Lys). Upon burial in the hydrophobic membrane core, a charged residue is likely to be either neutralized or accompanied by a shell of water molecules, which will lower its insertion energy significantly. In fact, there is no energy penalty for burial of charged amino acids with neutralized side chains (see Supplementary Material). However, simulation of ionization-state changes or the inclusion of a hydration shell, although both possible in principle, is beyond the means of the simple membrane model proposed here.

Comparison of the insertion free energies for peptides in which either one or two Ala residues have been changed to Gly, Ser, Trp, or Tyr demonstrated that the biological scale was approximately additive (36). This property was also found for insertion of the same peptides into the generalized Born membrane (see Supplementary Material).

In the experiment, lengthening of the flanking stretches from GGPG-X₁₉-GPGG to GGGGGGPG-X₁₉-GPGGGGGG through the stepwise addition of Gly residues resulted in variations to the apparent free energy of no more than ±0.2 kcal/mol, demonstrating that residues outside the H-segment have little influence on the results. The corresponding results for the generalized Born membrane found no measurable change to the insertion energy (see Supplementary Material). However, replacing the GGPG-X₁₉-GPGG flanks with NNPN-X₁₉-NPNN resulted in a 1.1-kcal/mol increase in insertion energy. The experiment found a more measured increase of 0.5 kcal/mol.

Positional dependency

To study the effect of amino acid position on the insertion energy of the designed peptides, Hessa et al. (36) performed symmetrical scans in which a pair of identical amino acids was moved from the center of the peptide toward the carboxy and amino terminus, respectively. These scans were repeated in the generalized Born membrane by building α-helical models of all peptide segments synthesized in the experiments and performing an orientational minima search in the membrane (see Methods). For each system, a Monte Carlo simulation was performed to yield the average conformational energies both in bulk solvent (z = ∞) and for the completely inserted transmembrane configuration (z = 0). The backbone was kept fixed while the side chains were sampled with flexible bonds, angles, and dihedrals. The results generally converge after 20 million steps, with a 0.5-million-step equilibration period. In general, the insertion energy is fairly insensitive to the actual side chain conformation. The maximum fluctuation of the solvation energy for flexible side chains was found to be ∼1 kcal/mol.

Fig. 1 shows the results of symmetrical scans for pairs of Leu residues together with the experimental best fit. Since we assume helical structures for both the membrane-bound state as well as for a larger separation from the membrane, the theoretical model neglects the free energy of folding the hydrophobic helix in the solvent phase. Experimentally, the structure in the solvent phase is unknown, but it is almost certainly not a helix, given the strong hydrophobicity of that structure. We found a constant ΔG = 0.6 kcal/mol per residue, which includes the free energy of folding the system in water as well as the free energy cost of immobilizing the helix in the membrane, as determined from the best fit of the experimental and computational data. Despite the uncertainty of the experimental structures, which in principle limits the accuracy of this study, both computational and experimental results can be seen to correlate remarkably well. However, although the experiment shows little to no positional dependency for Leucine the computational results found them to be slightly more favorable at the center of the membrane. This is a reflection of the fact that for hydrophobic residues the insertion energy is dominated by the nonpolar SASA term, which has the shape of a Gaussian centered on the membrane core (see The generalized Born method). Phe residue scans show a very similar behavior (Fig. 4).

FIGURE 4.

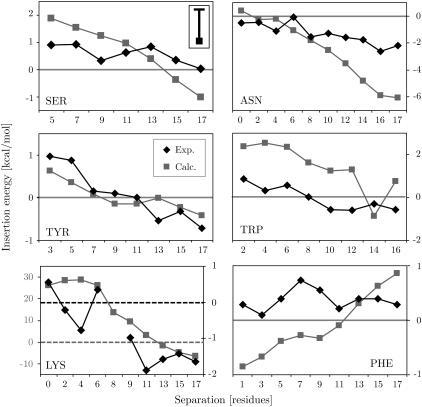
Comparison of the calculated (squares) and experimental (diamonds) positional dependency on the insertion energy for residues Asn, Lys, Phe, Ser, Trp, and Tyr. Note that the graph for Lys has two different scales for the calculated (left) and experimental (right) results due to the overestimation of burial of charged residues in the membrane by the generalized Born method (see text). The zero potential lines are indicated. The upper left panel (SER) shows the average error bar of the calculations, which fluctuate around a mean of ∼1 kcal/mol.

As expected from theory and experimental data, the polar residues Asn and Ser both show a preference for positions near the helix termini (see Fig. 4), with a larger slope encountered than the experimental data. This is due to the uncertainty of the experimental structures, which we assume to be helices for computational feasibility.

Aromatic residues are known to prefer the interface transmembrane segments (78). In this analysis, Tyr and Trp do indeed show a slight preference to locate near the interfaces. However, the penalty for inserting Trp is slightly lower in the experiments. Trp is the largest amino acid side chain and its desolvation in the membrane is likely to cause some disruption of the bilayer core, probably resulting in effects beyond those of an implicit-membrane model.

Fig. 4 shows that burial of Lys residues at the center of the membrane generally entails a large energy penalty, whereas they are favorable at the interfaces. This property matches the experimental and theoretical expectations. However, both the penalty of burial and the solvation energy at the interfaces is much larger compared to the experimental values. This is due to the general problem relating to the simulation of ionizable residues (see above).

Transmembrane and surface-bound helices

As a first test of this model, the minimum energy conformation of a set of six TM helices and antimicrobial peptides was calculated. All TM helices inserted correctly, with insertion energies in the range 1–13 kcal/mol, whereas all antimicrobial peptides were found to occupy surface-bound conformations, in agreement with experimental observations (58,62,64,79). The results closely match those from a previously reported statistical membrane potential (80) and are summarized in Table 3.

TABLE 3.

Comparison of the experimental and computational results for membrane-associated helices and membrane proteins of known conformation

Experimental and computed peptide orientations
		Experiment		Calculated
PDB	Name	Helix residues	Tilt angle (°)	Tilt angle (°)	z (Å)	ΔE (kcal/mol)
1a11	Acetylcholine M2 (1cek)	2–24	11	11 ± 5	−1.0 ± 0.9	−5.0 ± 0.9
1mp6	Influenza A M2	23–45	37	25	−1.1	−12.8
1mzt	FD coat protein	21–44	19	15	−1.5	−0.83
2mag	Magainin	4–21	∼90	85 ± 4	17.6 ± 0.9	−4.6 ± 0.8
1hu5	Ovispirin 1	4–16	∼90	89 ± 12	18.1 ± 0.6	−3.3 ± 0.4
1f0d	Magainin-cecropin hybrid	11–17	∼90	89 ± 27	21.3 ± 2.0	−2.3 ± 0.6

The residues defining the helical segment, as well as the experimental tilt angle, are listed. The helix tilt angle, displacement of the center of mass of the helix with respect to the membrane center (z), and insertion energy (ΔE) are listed for all systems. The experimental tilt angles were calculated from the aligned solid-state NMR structures deposited in the Protein Databank.

Integral membrane proteins

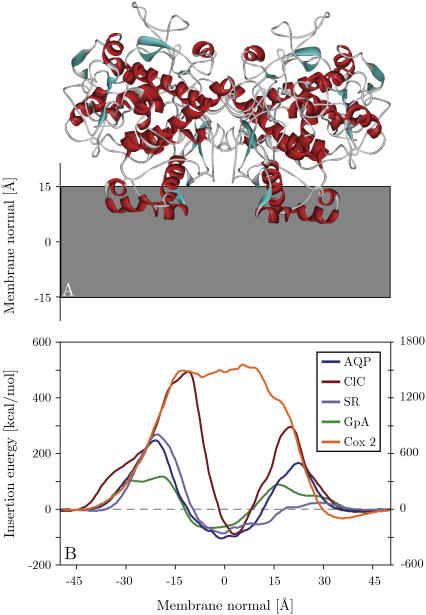
Fig. 5 shows the insertion profiles for the transmembrane section of the glycophorin A homodimer (1afo, model 12) (65), the integral membrane protein sensory rhodopsin (1h68) (67), and the more irregular structures of aquaporin from bovine red blood cell (1j4n) (68) and a chloride channel homolog from Escherichia coli (1kpk) (70). All proteins investigated have an energy minimum for inserted configurations with their center of geometry close to the core of the membrane and low tilt angles (see Table 1). Interestingly, all proteins exhibit similar energy profiles with an energy penalty for insertion from both membrane interfaces. In all cases, insertion from the extracellular side involves traversing a higher energy barrier than insertion from the cytoplasmic side. This is a reflection of the different topology of extra- and intracellular membrane protein interfaces. Generally, membrane proteins have a much larger number of charged residues at their intracellular interface (12,81), resulting in higher energy penalties for burial compared to the cytoplasmic side.

FIGURE 5.

(A) Global minimum energy conformation of cyclooxygenase 2 in the membrane. (B) Energy profiles obtained by pushing aligned proteins through the membrane. AQP, aquaporin from bovine red blood cell (1j4n); ClC, chloride channel homolog from E. coli (1kpk); SR, sensory rhodopsin (1h68); GpA, glycophorin A dimer (1afo, model 12); Cox 2, cyclooxygenase 2 (1cx2). The extracellular side is to the left. Except for Cox 2, all proteins can be seen to have a larger insertion penalty from the extracellular side, as well as a global insertion energy minimum at the membrane center. The insertion energy of Cox 2 is displayed on the y axis to the right, whereas all the other insertion energies are given on the left y axis.

Monotopic membrane protein

The monotopic membrane protein cyclooxygenase 2 (1cx2) is a homodimer that inserts partially into the cytoplasmic leaflet of the membrane and is a major target for anti-inflammatory drugs (e.g., Ibuprofen) (71). Fig. 5 shows that a fully inserted configuration carries an extremely high energy penalty, whereas the global energy minimum corresponds to a partially inserted conformation 36.0 Å from the membrane center. Interestingly, the statistical membrane potential found the same global insertion minimum orientation with the protein only slightly closer to the membrane center (33.5 Å). The tilt angle of the dimer with respect to the membrane normal was found to be 0°. Generally the orientation and partially inserted configuration closely match experimental and theoretical expectations. However, the relatively thin 30-Å membrane might overestimate the depth of insertion. Nevertheless, it is remarkable that both the statistical and generalized Born membrane models can predict the correct membrane orientation of such a complex system.

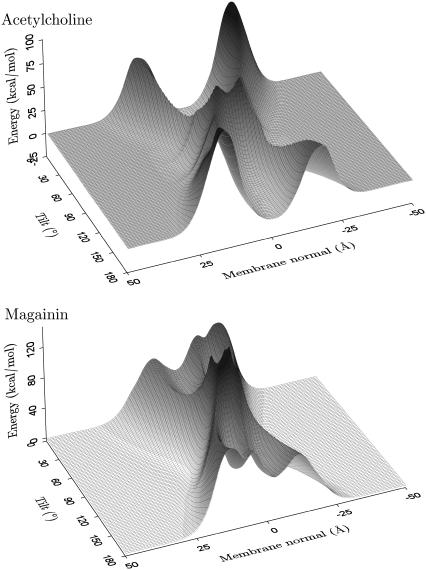
Insertion-energy landscape

To investigate the insertion-energy landscape for other, local minimum-energy orientations, the potential was plotted as a function of position along the membrane normal and tilt angle with the rotation angle optimized (i.e., the rotation angle for each position and tilt angle is such that the energy is minimal). Fig. 6 shows the resulting insertion energy landscapes for AchR M2 (1a11, model 1) and magainin (2mag, model 1). The zero point of the potential was chosen at an infinite distance from the membrane. AchR has four distinct minima, the two deepest corresponding to inserted configurations with the helices approximately parallel to the membrane normal. The other two minima are surface bound configurations with the helix axis parallel to the plane of the membrane. It should be noted that due to the symmetry of the membrane model, the cytoplasmic and intracellular minima have identical insertion energies, as do the two inserted minima. Repeating the analysis for all 10 AchR solution NMR structures gave topologically identical energy landscapes.

FIGURE 6.

Insertion energy landscape of a helix as a function of the tilt angle and center of mass position along the membrane normal for optimized rotation angle (around the long axis of the helix). The profile for the acetylcholine receptor helix M2 (1a11, model 1) is representative of all transmembrane helices investigated, displaying four distinct minima, whereas the profile for magainin (2mag, model 1) is typical of all the other antimicrobial peptides analyzed in this study with two surface-bound energy minima. The potential zero was chosen to be at an infinite distance from the membrane.

Generally, inserted TM configurations correspond to the global energy minima. The mean insertion energy (−5.0 ± 0.9 kcal/mol), tilt angle (12° ± 5°), and position close to the center of the membrane (−1.0 ± 0.9 Å) compare well to the values previously calculated for a statistical membrane potential (−4.7 ± 0.1 kcal/mol, 20° ± 5°, and 0.5 ± 0.2 Å) (80). Adsorption of the peptide onto the membrane surface is also favorable but to a lesser extent, with energy minima of −3.2 ± 0.3 kcal/mol. The minima correspond to helices bound to the interfacial membrane surface in a parallel orientation with tilt angles of 92° ± 10°. The equivalent values for the statistical membrane potential are −3.5 ± 0.4 kcal/mol and 92°±2°. At a distance of 18.5 ± 2.5 Å, the helix is farther away than the 9.3 ± 0.8 Å found previously. Nevertheless, the overall agreement between the two membrane models is remarkable. Both membranes support an insertion model where a helix will first bind to the membrane surface in a parallel orientation and subsequently change to a fully inserted transmembrane configuration. This is in accordance with general theoretical considerations (82) as well the two-stage folding model for α-helical membrane proteins (83,84). There is strong experimental evidence for independent helix formation and insertion in the first stage.

The above results are also in very good agreement with a theoretical study of the same structures (85,86), which found average energies of −4.7 ± 2.1 kcal/mol and −2.6 ± 2.4 kcal/mol for inserted and surface-bound configurations, respectively. The study used a theoretical continuum-solvent method developed by Ben-Tal (87) that has been successfully applied to estimate the insertion energies of TM peptides and proteins (88). To compare the results, the helix-coil transition free energy (ΔG_con = −2.4 kcal/mol) was subtracted, since the present data estimates the insertion energy of a folded helix.

For the antibiotic peptide magainin the free-energy landscape can be seen to differ substantially in topology. There are only two interfacial minima and the membrane region forms a large barrier spanning the entire tilt range of the helix with a 50 to 100 kcal/mol energy penalty for insertion into the membrane. The association depth (17.6 ± 0.9 Å), tilt angle (85° ± 4°), and insertion energy (−4.6 ± 0.8 kcal/mol) compare well with the statistical membrane model, which found values of 13 ± 1 Å, 87° ± 7°, and −3.5 ± 0.1 kcal/mol, respectively.

Conformational sensitivity

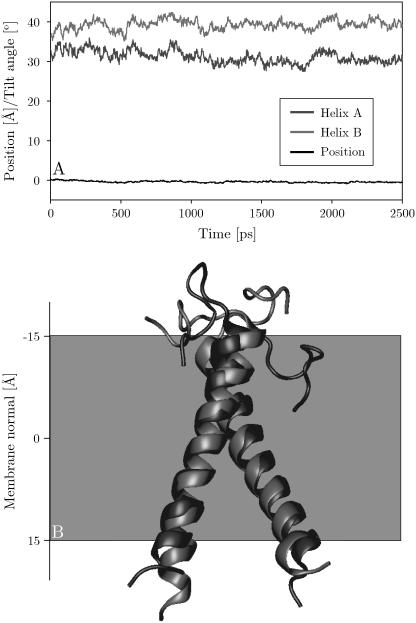
The purpose of an implicit-membrane representation is to enable significantly longer simulation times for the study of membrane proteins than are possible with an explicit lipid bilayer and solvent molecules. The present generalized Born membrane model is only a factor of ∼2 slower than a corresponding simulation in vacuum, whereas simulations using explicit lipid and solvent molecules are several orders of magnitude slower. To test the applicability of the method for modeling membrane proteins, 350 million Monte Carlo step simulations of the influenza A M2 helix (1mp6), as well as a 2.5 ns molecular dynamics simulation of the glycophorin A dimer (1afo), were performed. The simulations started from the experimental structures, with the helices inserted into the center of the membrane. The backbone root mean-square deviation (RMSD) with respect to the experimental structure over the course of the simulation was found to have an average of ∼1.8 ± 0.6 Å for influenza A and ∼1.8 ± 0.3 Å for glycophorin A. All helices remained firmly integrated near the center of the membrane in a transmembrane configuration (Fig. 7). Tilt angles of the influenza A helix with respect to the membrane normal fluctuate in the range 0–30° (average of 9° ± 5°) throughout the simulation and there is frequent bending and kinking. Fig. 7 shows the overlay of the glycophorin A dimer simulation at 0 and 2.5 ns, with an RMSD of 1.6 Å when the dimer is fitted as a whole. The system remains stable and the relative orientation of the helices is constant throughout the simulation. Both runs demonstrate that membrane systems can be reliably studied in an implicit membrane. Future work will concentrate on the role of the parameters on experimentally determined properties, such as tilt and kinking angles as well as helix-helix fluctuations.

FIGURE 7.

(A) Tilt angles of helices A and B, and center of mass position of the glycophorin A dimer simulation. (B) Initial global minimum energy configuration of the glycophorin A dimer TM domain (1afo, model 12) in black. The final structure at the end of the simulation (2.5 ns) is shown in gray. This model is representative of the 11 of 20 structures that were found to insert.

CONCLUSION

Translocon-mediated insertion experiments of designed polypeptides (36), as well as statistical analyses of membrane proteins (12), seem to indicate that the insertion properties of a transmembrane helix are determined chiefly by its solvation energy in the membrane environment. This study used the generalized Born method to derive an implicit-membrane representation based on the assumption that the bulk properties of a lipid bilayer can be captured by treating it as a region that becomes increasingly apolar (i.e., increasingly inaccessible to the solvent) toward the center of the membrane. The polar part of the limiting value of maximum desolvation at the center was taken from theoretical calculations (33,53), whereas the nonpolar part was determined by fitting the calculated insertion energies of hydrophobic side-chain analogs against those measured experimentally (39).

Subsequent comparison of the insertion energy of α-helical model peptides, containing the remaining 20 natural amino acids, with the experimental values from the biological hydrophobicity scale of Hessa et al. (36) gave a correlation of 93% with a mean unsigned error of 0.64 kcal/mol. The calculated scale also correlates remarkably well (C = 97%) with experimental transfer free energies of side-chain analogs into cyclohexane (39), though it displays little to no correlation with either the octanol (40) or the interface scale (41).

TM peptides of known orientation were found to insert and orient correctly, with an average tilt deviation of 6° from the NMR values. Antimicrobial peptides were found to orient parallel to the membrane surface, pointing their hydrophobic residues toward the membrane center while exposing their polar residues to the aqueous environment, in excellent agreement with experimental data. The free-energy landscapes showed that there is a large penalty for insertion into the membrane regardless of the tilt angle.

In general, the translational and rotational energy landscapes described represent a detailed search of the orientation space of the peptides considered. The insertion-energy surfaces are surprisingly smooth and the good overall agreement with theoretical and experimental data is encouraging. It should be noted that the insertion-energy landscapes are similar to those found for previously derived membrane potential based on 46 α-helical membrane protein structures (80).

All integral membrane proteins investigated orient and insert correctly into the implicit-membrane model, regardless of whether their structure is composed of a fairly regular arrangement of helices or not. One of the most remarkable findings of the study was that the membrane model predicts a partially inserted configuration for the monotopic membrane protein cyclooxygenase 2. The part inserted into the membrane agrees well with experimental and theoretical predictions.

Simulations of influenza A as well the glycophorin A dimer proved that both systems remain stable over the timescale of the simulations. These simulations run a factor of only ∼2 slower than the equivalent systems in vacuum, demonstrating the feasibility and applicability of the current method to large-scale membrane protein simulations.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.