Abstract
Tissue dynamics during dorsal closure, a stage of Drosophila development, provide a model system for cell sheet morphogenesis and wound healing. Dorsal closure is characterized by complex cell sheet movements, driven by multiple tissue specific forces, which are coordinated in space, synchronized in time, and resilient to UV-laser perturbations. The mechanisms responsible for these attributes are not fully understood. We measured spatial, kinematic, and dynamic antero-posterior asymmetries to biophysically characterize both resiliency to laser perturbations and failure of closure in mutant embryos and compared them to natural asymmetries in unperturbed, wild-type closure. We quantified and mathematically modeled two processes that are upregulated to provide resiliency—contractility of the amnioserosa and formation of a seam between advancing epidermal sheets, i.e., zipping. Both processes are spatially removed from the laser-targeted site, indicating they are not a local response to laser-induced wounding and suggesting mechanosensitive and/or chemosensitive mechanisms for upregulation. In mutant embryos, tissue junctions initially fail at the anterior end indicating inhomogeneous mechanical stresses attributable to head involution, another developmental process that occurs concomitant with the end stages of closure. Asymmetries in these mutants are reversed compared to wild-type, and inhomogeneous stresses may cause asymmetries in wild-type closure.
INTRODUCTION
Embryonic development comprises dynamic processes that link gene expression to morphogenesis. The processes involve a precisely orchestrated interplay between gene expression, tissue movement, and cell shape changes. The mechanisms that regulate this interplay are under intense investigation (1).
Dorsal closure is an essential stage of Drosophila embryogenesis that requires 2–3 h of spatially coordinated and temporally synchronized tissue movement and serves as a model system for research in developmental biology ((2–4), reviewed in the literature (5,6)). In addition, the cellular and molecular mechanisms involved in dorsal closure are thought to parallel those that characterize wound healing ((2,7), reviewed in the literature (8–10)). During dorsal closure, two advancing flanks of epidermal tissue demarcate an eye-shaped opening of exposed amnioserosa tissue on the dorsal side of the embryo (Fig. 1). As closure proceeds, the advancing flanks of epidermal tissue progressively cover the dorsal opening. At each canthus, i.e., corner of the eye-shaped opening, adhesion between the two advancing flanks forms a seam in a process known as zipping. The canthi anchor the purse-strings and influence their curvature, where each leading edge approximates an arc and the two arcs lie roughly in a plane.
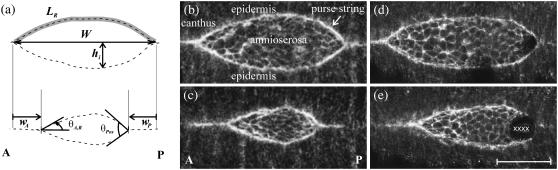
FIGURE 1.
(a) Geometric parameters that describe dorsal closure, where dashed lines are contours of the leading edges (see text). The arc length LR is indicated by the shaded line. (b,c) Confocal fluorescent images of native closure taken 1700 s apart. (d,e) Images of the single-canthus nicking protocol targeted to the posterior end, also taken 1700 s apart. In frame d, dark patches are evident near the left purse-string and the posterior canthus. Dark patches were observed occasionally and are due to the dorsal surface lying just outside the focal plane; however, scanning the focal plane verified the tissues were continuous. In frame e, the X characters indicate the location and extent of the laser perturbations. Scale bar is 50 μm. The anterior end (A) is to the left in all figures.
Genetic analysis shows that >60 genes contribute to dorsal closure (5,6,11). These include genes that encode signaling cascades, e.g., basket (bsk) encodes the Drosophila Jun-N-terminal kinase, a member of an essential signaling pathway that specifies, patterns, and regulates dorsal closure through the transcriptional activation of targeted genes (12,13). They also include genes that encode cell surface receptors and adhesion molecules, e.g., scab (scb) and myospheroid (mys), which encode the αPS3 and βPS subunits, respectively, of the integrin, transmembrane adhesion, and signaling protein (14–16). Mutations in bsk, mys, and scb affect specific cellular processes that result in an altered geometry of the dorsal opening, reduced seam formation, and failure to complete closure (17), and consequently were included in this investigation.
The mechanics of morphogenesis have also been investigated and, in some cases, the physical forces responsible for tissue movements have been identified (2,4,10,17–22). Laser perturbations have proven to be useful tools to probe such forces. Previously (2,4), we combined laser microsurgery techniques with biophysical modeling to investigate the forces involved in dorsal closure, where the laser rapidly ablates tissue and our focus is on the response of the remaining tissues and not on wound healing per se. More specifically:
We showed that the dynamic geometry of the dorsal opening during closure is a consequence of four biological processes: the contractile force of an actomyosin-rich supracellular “purse-string” located at the leading edge of epidermis; the contractile force due to cortical actomyosin networks in amnioserosa cells; the resistive force due to movement and deformation of the lateral epidermis; and adhesive zipping. We also determined force ladders that specify the relative magnitude of the first three applied forces as compared to the drag force. We found that the vector sum of these applied forces acting on a point of the leading edge is only a small fraction of any one of the individual forces. Although these forces collectively drive a process that is, to a first approximation, quite symmetric, closer inspection makes it clear that various asymmetries are apparent. We contend that quantifying morphogenic asymmetries in native embryos is essential for understanding the spatial and temporal differences in the contributing processes. Moreover, we seek to investigate the extent to which asymmetric forces can vary and still result in successful closure. Ultimately, understanding asymmetry provides a basis for understanding changes that occur to compensate for genetic or laser perturbations.
We showed that dorsal closure is robust and surprisingly resilient to laser perturbations, as individual biological processes can be removed without blocking closure. Three specific examples are illustrative (4). First, when the force produced by the amnioserosa is removed by laser incision(s), the leading edges rapidly recoil away from the dorsal midline, and after reaching a maximum displacement, closure resumes. Second, when zipping is laser-inhibited at both canthi, the geometry changes dramatically—the dorsal opening distorts such that the leading edges constrict toward the dorsal midline and subsequently meet to form an interior seam that completes closure. Third, when zipping is inhibited at one canthus, closure progresses approximately on schedule, albeit asymmetrically, as zipping is essentially limited to the unperturbed canthus. Collectively, our observations demonstrated that when one of the cellular processes governing dorsal closure was laser-perturbed, the remaining processes could compensate through alterations in the force(s) they produced. In part, this robust and resilient behavior is due to redundancy—more than one force contributes to closure. We contend that having large applied forces combined with the ability to compensate for perturbations and for native variations in force-producing processes contributes to the stability underlying the robustness and the resiliency of closure. With regard to zipping, our observations suggest that while zipping contributes a key role in coordinating forces driving closure and is essential for seam formation, it is not required for the bulk of tissue movements during closure. Our results suggest that identifying specific processes that are upregulated as a consequence of perturbations can elucidate the dynamics that contribute to this compensation, the relationships between apparently independent biological processes, and their relative importance for closure with the potential to ultimately explain how complicated morphogenic movements result in a properly formed tissue.
We proposed an empirically derived rate equation to describe the zipping rate that incorporates the leading edges into the seam. This equation depends on representing the dorsal opening as symmetric about the anterior-posterior axis and assigning a single zipping rate constant for both canthi. Application of this model to the dynamic geometry of the dorsal opening of myospheroid embryos combined with a comparison to native and laser-perturbed closure indicated that βPS integrin has an early, important role in zipping. Extending this quantitative model to accommodate spatial, kinematic, and dynamic antero-posterior asymmetries to successfully quantify morphogenic asymmetries is another open research area.
As mentioned earlier, dorsal closure has been characterized as being coordinated in space, synchronized in time, and resilient to laser perturbations; however, the detailed mechanisms responsible for these attributes are not fully understood.
In this study, we extend our use of laser confocal microscopy, a steered UV microbeam, genetic strategies, and quantitative biophysical reasoning to advance our understanding of tissue dynamics during dorsal closure. A key objective is to further assess the resiliency of dorsal closure in response to laser perturbations and to identify the specific tissues where biological processes are upregulated. A second objective is to investigate the asymmetric dynamics of dorsal closure in the context of overall embryonic development for wild-type and mutant embryos. In particular, in this study, we:
Quantify spatial and kinematic asymmetries observed during dorsal closure in laser-perturbed wild-type and mutant embryos and compare them to the asymmetries of wild-type, unperturbed closure.
Interpret these asymmetries in terms of molecular and cellular dynamics.
Elucidate the regulatory consequences of laser-perturbed closure.
MATERIALS AND METHODS
Experimental design
The fly genetics and optical design are detailed elsewhere (2,15). All Drosophila melanogaster fly lines were homozygous for sGMCA, a transgene that encodes GFP fused to the actin binding region (GFP-moe) of moesin and is expressed under the control of the spaghetti squash promoter. GFP-moe renders F-actin fluorescent in vivo (2,3). We generated stocks in which bsk2 (12) and scb2 were balanced with CyO, TwiGal4, and UAS-GFP, and mys1 was balanced with FM7, TwiGal4, and UAS-GFP (all obtained from Bloomington Stock Center, Bloomington, IN). Hemizygous mys1 and homozygous scb2 and bsk2 embryos were distinguished from their siblings through the lack of Twi-driven GFP expression using a GFP-dissecting microscope. Wild-type, bsk (12,13), mys (14), and scb (15) mutant embryos were collected, dechorionated, and subsequently mounted in a modified chamber between a gas-permeable membrane (Teflon) and a glass coverslip that allowed development to proceed while time-lapsed confocal images were collected (24).
Fluorescent images were collected with either a Zeiss LSM410 or a LSM510 (488 nm excitation; Carl Zeiss, Minneapolis, MN) laser-scanning confocal microscope using a 40×, 1.3 NA oil-immersion objective or a 25×, 0.8 NA multi-immersion objective, respectively. Scanning time was either 1.08 or 1.14 s and either two or eight scans were averaged to produce an image. Sequences of images were stored for subsequent analysis.
The microbeam uses the third harmonic of a Continuum Q-switched Nd:YAG laser (355 nm; Continuum, Santa Clara, CA), either the YG571C or the Minilite II, which was interfaced to the confocal microscope to dissect the dorsal surface of the embryos with subcellular spatial resolution. It can be steered across the focal plane to make laser incisions of arbitrary shape while acquiring images with the confocal system. The UV laser light was focused onto the dorsal surface, where ∼4 ns pulses, 300–700 nJ per pulse at 10-Hz repetition rate, produced typical laser lesions of ∼2 μm in diameter and a lesion depth of <15 μm. The physical mechanism for UV laser lesions in tissue has been attributed to the disruption of chemical bonds, with the subsequent release of both chemical and mechanical energy, resulting in minimal collateral damage to surrounding tissue (25). For sufficient laser intensity, cell lysis is very fast relative to the collection time of the confocal microscope. The signature for ablation in our studies is tissue recoil, which is readily distinguishable from photobleaching effects alone.
Analysis
The contours of the fluorescent leading edges from the confocal images were digitized using a customized active contour algorithm (26) implemented in ImageJ (27). Once digitized, various geometrical parameters of the dorsal opening (Fig. 1 a) were obtained using custom programs in Mathematica (Wolfram Research, Champaign, IL) and analyzed further. W is the canthus-to-canthus length, LR is the arc length of the right leading edge (top in the image), and hi is the height as i is indexed through the digitized points. wA (wP) is the length of seam formed on the anterior (posterior) end, θA,R is the anterior angle between the right leading edge and the dorsal midline, and θPos is the total, posterior, angle between the two leading edges given by θPos ≡ θP,R + θP,L. Similarly, θA,L, θP,R, and θP,L (not shown) are defined by the dorsal midline and the remaining three segments of leading edges near the canthi while θAnt ≡ θA,R + θA,L. In the mathematical model, we treat the purse-string as a cable under tension, T, so a segment of the leading edge is subjected to a force per unit length from both the lateral epidermis, σLE, and the amnioserosa, σAS. The Appendices include detailed accounts of determination of the centroid, dynamic geometry of the dorsal opening, the zipping rate model and comparison to experiment, the asymmetric zipping rate model, analysis of mechanical jump experiments, determination of the recoil velocity, and an estimate of the increase in the force produced by the amnioserosa in the presence of a localized constriction. All results are reported as mean ± SE (n) where n is the number of trials.
RESULTS
Mechanics of the dorsal opening during native closure
Spatial asymmetries
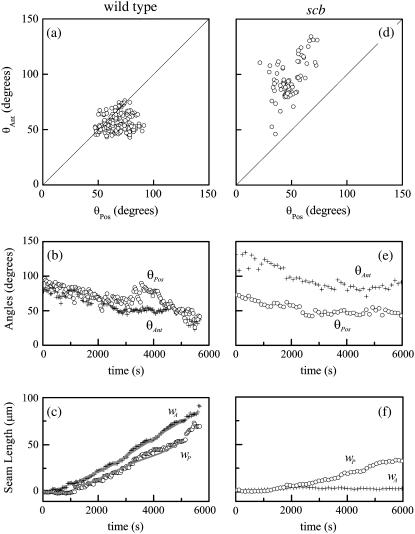
While the dorsal opening is approximately symmetric about the antero-posterior (A-P) and left-right (L-R) axes, it frequently exhibits asymmetric teardrop geometry. To quantify this A-P asymmetry, we evaluated the total angle at each canthus θAnt and θPos (Fig. 1 a). Typically θAnt < θPos (Fig. 2 a) and averaging over the duration of dorsal closure θAnt,avg is 86(±12)% of θPos,avg (n = 7) (Table 1). Fig. 2 b shows that the trend in both angles is to decrease as closure progresses.
FIGURE 2.
Geometric parameters of the dorsal opening for (a–c) a wild-type, unperturbed embryo, and (d–f) a scab mutant (see text). In panels a and d, each circle represents a time point. Solid lines in panel c are the result of the fit based on Eq. 5 and detailed in Appendix B. A fit was not possible in panel f due to complications in implementing Eqs. B-17–B-19 in the analysis; specifically, the data set was too sparse for numerical convergence.
TABLE 1.
Angles and length of seams during dorsal closure
| n | θAnt,avg (deg) | θPos,avg (deg) | wA,avg (μm) | wP,avg (μm) | |
|---|---|---|---|---|---|
| Wild-type | 7 | 46.5 ± 2.7 | 54.1 ± 3.2 | 33.9 ± 3.6 | 23.1 ± 2.8 |
| bsk | 6 | 68.6 ± 6.0 | 51.8 ± 4.2 | 2.4 ± 0.7 | 7.9 ± 1.8 |
| mys | 9 | 79.1 ± 3.6 | 71.5 ± 3.9 | 5.3 ± 0.9 | 10.8 ± 1.5 |
| scb | 5 | 86.6 ± 6.0 | 56.9 ± 4.8 | 2.7 ± 0.9 | 8.8 ± 2.4 |
Values are averages for n embryos, of a specific genotype, of the mean geometric parameters.
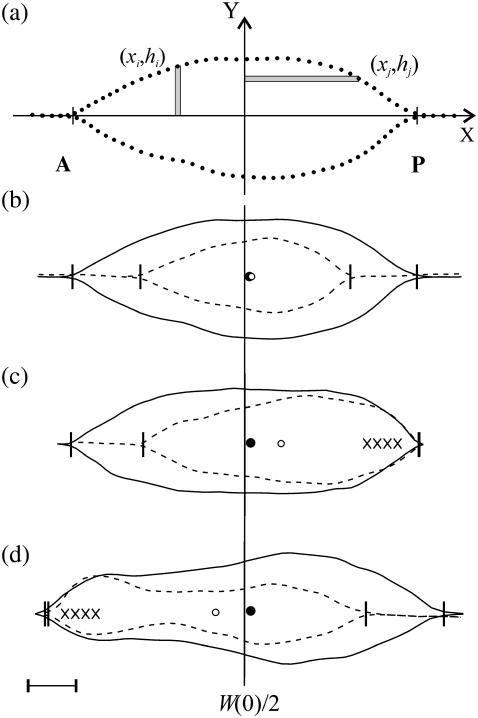
The location of the opening on the dorsal surface and the geometrical asymmetry of the opening can both be quantified in terms of the centroid rc = (xc, yc) (Appendix A, Fig. 3). In our application, rc is determined by the intersection of all lines that divide the dorsal opening into two areas of equal moment. The position of rc is given by
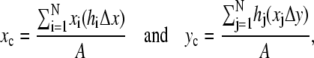 |
(1) |
where we define the x axis to lie along the dorsal midline and the (fixed) origin to be W(0)/2 where W(0) refers to the first image analyzed (Fig. 3 a), Δx and Δy are length increments and A is the area of the opening. Two moments are shown in Fig. 3 a; for example, the distance xi times the area hiΔx and the distance hj times the area xjΔy. The points (xi, hi) trace out the two leading edges as i is stepped from 1 to N = 100, as do the points (xj, hj) as j is stepped from 1 to N = 100. The coordinates xc and yc, respectively, quantify the A-P and L-R geometric asymmetries. Averaging xc and yc over the duration of dorsal closure imaged for each embryo and then averaging over n embryos, we obtain xc,avg = 1.3 ± 0.3 μm and yc,avg = 0.0 ± 0.3 μm (n = 7), with maximum values within 5 μm and 0.6 μm, respectively. This indicates a small but significant A-P asymmetry with the head of the teardrop located posteriorly throughout dorsal closure (Fig. 3 b), and essentially no L-R asymmetry.
FIGURE 3.
(a) Contour of the leading edges during native closure showing examples of hiΔx and xjΔy used in the calculation of the centroid xc. Points are the result of the active contour algorithm and indicate the stepping procedure (see text). (b) Contours of the leading edges during native, unperturbed closure, where the dashed contours were taken 1700 s after the initial solid contours. Circles indicate xc at the earlier (solid) or later (open) times. (c) Contours of the single-canthus nicking protocol targeted to the posterior canthus, where the initial contour is just before the first laser incision. (d) Contours of the single-canthus nicking protocol targeted to the anterior canthus, where the initial contour is ∼900 s after the first laser incision. The vertical line indicates the location of W(0)/2 and the vertical ticks locate the canthi. Scale bar is 20 μm.
Kinematic asymmetries
In wild-type, unperturbed embryos, the rate of change in the position of the centroid Δxc/Δt = 1.9 ± 0.4 nm/s (n = 7) (Table 2). Thus, xc moves ∼20 μm posteriorly during 3 h of closure. Inspection of Eqs. 1 indicates Δxc/Δt may be attributable to: 1), changing teardrop geometry, which influences the moment through hi; 2), asymmetric rates of seam formation, which influences the moment through both xi and hi; and 3), contraction of the purse-strings, which influences the moment through hi. Δxc/Δt will prove useful in analyzing laser-perturbed closure (Fig. 3, c and d).
TABLE 2.
Spatial and dynamic asymmetries
| n | Δxc/Δt (nm/s) | kz,A (nm/s) | kz,P (nm/s) | |
|---|---|---|---|---|
| Native closure | 7 | 1.9 ± 0.4 | 15.3 ± 0.7 | 10.6 ± 1.7 |
| Nick on posterior | 8 | 7.5 ± 0.6 | 17.5 ± 0.9 | blocked |
| Nick on anterior | 6 | −9.0 ± 0.7 | blocked | 15.8 ± 1.0 |
Using the t-test at a significance level of 0.05: kz,A native closure >kz,P native closure (t = 2.61; DoF = 12; P = 0.011); kz,A single-canthus nicking >kz,A native closure (t = 1.79; DoF = 13; P = 0.049); and kz,P single-canthus nicking >kz,P native closure (t = 2.56; DoF = 11; P = 0.013). We have excluded one embryo where the rate of anterior seam formation was smaller than that of the posterior seam; however, in this case the centroid was also located closer to the posterior end than the canthus-to-canthus midpoint. “Blocked” refers to values of <1 nm/s, where there is added uncertainty due to deviations from ideal geometry at the targeted canthus.
To evaluate asymmetry in the rates of seam formation, we measured the length of the seams in each image as defined in Fig. 1 a. The length on the anterior (wA) and posterior (wP) seems to satisfy the time-dependent relationship W(t) = W(0)−wA(t)−wP(t), where W(0) refers to the first image analyzed (Appendix B). Fig. 2 c indicates wA(t) > wP(t). Averaged over the duration of dorsal closure, wA,avg is 46(±23)% larger than wP,avg (n = 7) (Table 1). In the following two subsections, we investigate further dW/dt to account for the angular dependence in the rate equation and then generalize the equation for asymmetric rates of seam formation in terms of dwA/dt and dwP/dt.
Dynamic geometry of the dorsal opening
We summarize the derivation of dW/dt, based on a model for the dynamic geometry of the dorsal opening, confirming the previous empirically derived rate equation (Eq. 2 in (4)) and placing it on a firmer geometric foundation (Appendix B). The model idealizes the opening as two intersecting arcs symmetric about both the A-P and L-R axes, each constrained to remain a circular arc while allowing L, W, θ, the height at the symmetry point h, and the curvature κ to vary in time. We obtain dW/dt and dh/dt to analytically track the dynamic geometry, yielding
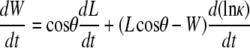 |
(2) |
and
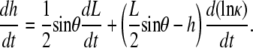 |
(3) |
Experimental values indicate that the first term on the right-hand side of Eqs. 2 and 3 is approximately an order-of-magnitude larger than the second term. Consequently, dividing Eq. 2 by Eq. 3 we find, to a good approximation (justified in Appendix B), that
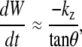 |
(4) |
where kz ≈ −2 dh/dt. Therefore, when applied to the dorsal opening, 1/tanθ is a consequence of circular arc geometry and kz ≈ −2vnative, where vnative = dh/dt.
Our analysis shows that κ(t) is not strictly constant; the dorsal opening measurably rounds up during the later stages of native dorsal closure (Appendix B). Inspection of Eqs. 2 and 3 indicate that both dW/dt and dh/dt are relatively insensitive to changes in curvature due to the d(ln κ)/dt dependence, which is a direct consequence of circular arc geometry.
Zipping rate constants
To quantify the asymmetry in the rates of seam formation, each canthus was treated independently by relaxing any constraints on A-P and L-R symmetry (Appendix B),
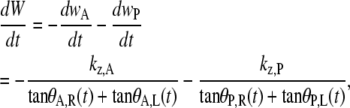 |
(5) |
where we have separated the anterior (kz,A, θA,R, θA,L) and posterior (kz,P, θP,R, θP,L) dependencies. Integrating numerically from the time the first image was taken to the time of the last image, we obtained kz,A and kz,P and accounted for the experimental observations, i.e., curves through the data in Fig. 2 c. In six of the cases analyzed, kz,A > kz,P (in one case kz,A = kz,P to within 1%) and, averaging over seven embryos, kz,A > kz,P by 45(±20)% (Table 2).
Dorsal closure in basket, myospheroid, and scab mutant embryos
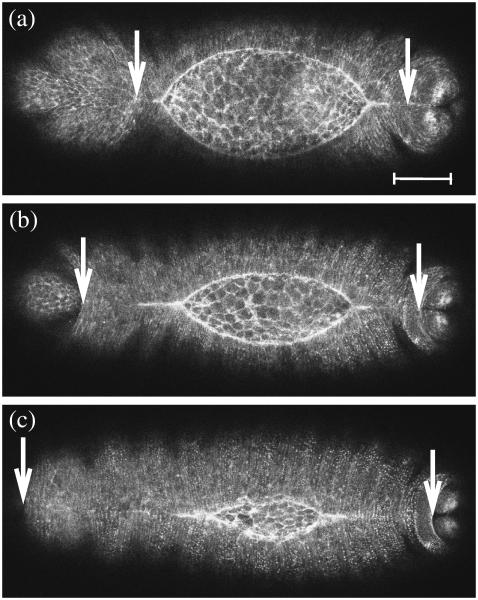
We confirmed that bsk, mys, and scb mutants fail to complete closure (12–17). Here we report the initial point of failure in all cases as the detachment between the lateral epidermis and the amnioserosa on the anterior side of the dorsal opening (bsk, n = 10; mys, n = 11; scb, n = 6) (Fig. 4; see Supplementary Material, Movies 1–3). For each of these mutants, W, LAvg ≡ (LR + LL)/2, and the ratio wA/wP have critical values that quantitatively predict the onset of failure (Table 3). Across mutants, the critical values for W and LAvg agree to within 4% while those for wA/wP agree to within 12%. In contrast, the critical values for h, wA, wP, θAnt, and θPos show variations that range from 34% to 105% across mutants. In Discussion, below, we will interpret these results in the context of head involution, another developmental process that occurs concomitant with dorsal closure.
FIGURE 4.
Dorsal closure in (a) bsk, (b) mys, and (c) scb mutant embryos shown at the onset of failure. The arrows locate the site of failure. Scale bar is 50 μm.
TABLE 3.
Critical values correlating to the onset of failure
| n | W (μm) | LAvg (μm) | wA / wP | h (μm) | wA (μm) | wP (μm) | θAnt (deg) | θPos (deg) | |
|---|---|---|---|---|---|---|---|---|---|
| bsk | 9 | 194.4 ± 6.5 | 205.8 ± 6.8 | 0.24 ± 0.11 | 50.9 ± 1.9 | 3.1 ± 0.6 | 13.2 ± 3.8 | 66.3 ± 6.7 | 46.1 ± 6.9 |
| mys | 9 | 203.1 ± 6.0 | 211.5 ± 6.4 | 0.27 ± 0.08 | 39.8 ± 2.3 | 6.4 ± 1.2 | 24.2 ± 2.8 | 68.3 ± 4.0 | 53.0 ± 3.3 |
| scb | 5 | 199.6 ± 8.8 | 207.9 ± 8.7 | 0.23 ± 0.12 | 37.4 ± 3.1 | 4.3 ± 1.1 | 18.3 ± 4.9 | 89.0 ± 8.4 | 38.9 ± 6.5 |
We also investigated closure before failure, where Fig. 2, a and d, is a representative comparison of A-P spatial asymmetry in one wild-type and one scb mutant embryo. As closure progresses, there is a tendency for θAnt < θPos for wild-type embryos, e.g., Fig. 2 a, while, in contrast, θAnt > θPos for all scb mutants, e.g., Fig. 2 d. Similarly, for bsk and mys mutants the angles were either symmetric (θAnt = θPos) or the asymmetry was opposite (θAnt > θPos) to that observed in wild-type embryos (Table 4).
TABLE 4.
Penetrance of the temporal asymmetry
| n | −dh/dt (nm/s) | θAnt > θPos | θAnt = θPos | wA < wP | wA = wP | |
|---|---|---|---|---|---|---|
| bsk | 6 | 6.0 ± 0.8 | 83% | 17% | 83% | 17% |
| mys | 9 | 5.6 ± 1.2 | 44% | 56% | 89% | 11% |
| scb | 5 | 3.5 ± 1.3 | 100% | 0% | 80% | 20% |
A representative comparison of A-P dynamic asymmetries is also included in Fig. 2. Throughout closure, θAnt in a typical scb mutant (Fig. 2 e) is significantly larger than in a typical wild-type embryo (Fig. 2 b). In addition, θAnt,avg is uniformly larger in embryos homozygous for each of the three mutations compared to wild-type, ranging from 47(±14)% to 86(±12)% larger depending on the mutant genotype (Table 1). In contrast, only for mys is θPos,avg >10% larger than θPos,avg in wild-type. There is a deficiency in seam formation at both canthi for scb mutants with respect to wild-type, where little if any zipping occurs at the anterior canthus for this scb embryo (Fig. 2, c and f). Mutant seam formation is uniformly deficient (Table 1): on average, wA,avg is reduced by factors of 6–14 and wP,avg by factors of 2–3, depending on the mutant genotype. In contrast to wild-type, wA < wP for all of the mutant genotypes (Table 4). In addition, dh/dt for bsk and mys mutants is comparable to that of wild-type, while the value for scb mutants is approximately half.
Upregulation during laser perturbed dorsal closure
Single-canthus nicking protocol
We targeted the microbeam to block zipping by nicking amnioserosa tissue close to either canthus with the aims of altering the inherent A-P asymmetry and elucidating changes that result from this perturbation. Zipping was blocked while leaving the leading edges intact, as was previously not the case (4). A nick was 10-μm long, took ∼1 s, and was repeated approximately every 30 s (Fig. 1, d and e).
Confocal images analyzed by using Eq. 5 indicate an upregulation in kz,A when targeting the posterior end, and in kz,P when targeting the anterior end (Fig. 1, d and e; Fig. 3, c and d; Table 2). The upregulation was asymmetric: when the embryos were nicked on the relatively slowly zipping posterior canthus, kz,A increased by 14(±10)% with respect to the anterior value during native, unperturbed closure; when the embryos were nicked on the relatively rapidly zipping anterior canthus, kz,P increased by 49(±22)% with respect to the analogous posterior value. In addition, the dorsal opening constricts as a consequence of the single-canthus nicking protocol applied to the anterior (67%; n = 6) or the posterior (25%; n = 8) canthus. An example is shown in Fig. 3 d (dashed contour). This constriction strongly suggests an upregulation of the force produced by the amnioserosa, which will be considered further in Discussion, and motivated the double-canthi nicking and edge-cut protocol described below.
During single-canthus nicking, xc moved toward the targeted canthus at about four times the speed observed during unperturbed closure (Fig. 3, b–d; Table 2). Δxc/Δt reverses its direction and is 21(±15)% larger when the anterior canthus is targeted relative to targeting the posterior canthus. We considered whether induced changes in teardrop geometry, asymmetric rates of seam formation, and/or contraction of the purse-strings could account for the change in Δxc/Δt. While it seems unlikely that the effects we observe are due to alterations in teardrop geometry, the average angle of the unperturbed canthus does increase by up to 20% relative to native dorsal closure (data not shown). However, this promotes xc movement away from the targeted canthus, contrary to experimental observations. Consequently, this indicates that seam formation and possibly contraction of the purse-strings dominate the angular contribution in determining xc during single-canthus nicking.
Double-canthi nicking and edge-cut protocols
The double-canthi nicking protocol alternately targeted the microbeam to the amnioserosa in the proximity of each canthi to completely block zipping (Fig. 5 a). Nicks were 10-μm long, required ∼1 s, and pairs of nicks were repeated every 30 s. As a consequence, a local constriction forms after ∼40 min such that the leading edges assume a region of reverse curvature (Fig. 5, a and b). In seven of these embryos, the constriction formed closer to the anterior end, and in one case, it formed near W/2.
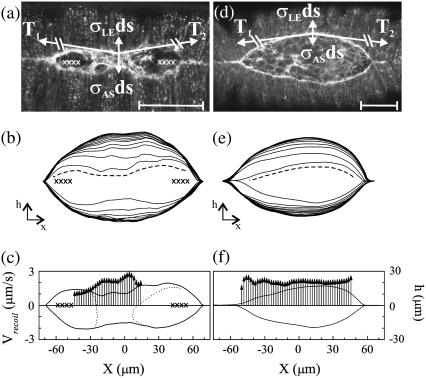
FIGURE 5.
Determination of vrecoil in the presence of a localized constriction due to the double-canthi nicking protocol (a–c) and in native, unperturbed closure (d–f). In panels a and d, confocal fluorescent images with free body diagrams superimposed. Scale bar is 50 μm. In panels b and e, digitized contours showing the recoil of the purse-strings after an edge-cut protocol (dashed lines), where the innermost contour is just before the edge-cut and subsequent contours progress from inside to outside in 10.8 s steps. The total time is 140 s. In panels c and f, vrecoil after edge-cuts. Vertical arrows represent vrecoil and correspond to the far-left axis. Bold lines indicate the contour of the purse-strings just before the edge-cut where height corresponds to the far-right axis. The X characters in panels a–c indicate the location and extent of the laser perturbations. In panel c, the dotted lines indicate the boundary of the intact amnioserosa.
The edge-cut protocol determines the relative force produced by the amnioserosa. The microbeam is targeted just inside one of the leading edges, it takes ∼10–15 s to steer depending on the length of the leading edge, and results in the recoil of the remaining tissues (Fig. 5, b and e; see Supplementary Material, Movies 4 and 5). As derived in Appendix C, the relative force exerted by the amnioserosa just before the cut can be determined from the initial recoil velocity of the leading edge, vrecoil. The edge-cut protocol and a more detailed analysis replaces our previous strategy of determining vrecoil based on a linear canthus-to-canthus incision (4). Due to more complete removal of the amnioserosa from the leading edge, higher sampling rates, and tracking the effective time of the cut along the leading edge (Appendix C), vrecoil determined by the edge-cut protocol is ∼2.4-times larger than reported after a linear canthus-to-canthus incision.
The recoil velocities determined by the edge-cut protocol are shown for embryos with (Fig. 5 c) and without (Fig. 5 f) a localized constriction, where the constriction was a consequence of double-canthi nicking (Fig. 5 a). Inspection of Fig. 5 c indicates: that vrecoil increases in a localized region that correlates with the constriction and the central band of intact amnioserosa; that local maxima (minima) in vrecoil are correlated with local minima (maxima) in h(x); and that there is a decrease in vrecoil toward the canthi. The average recoil velocity measured after an edge-cut following a constriction was vrecoil,1 = 3131 ± 215 nm/s (n = 8), as determined by selecting the maximum vrecoil within the region for each embryo. The average recoil velocity measured after an edge-cut in the absence of double-canthi nicking was vrecoil,2 = 2280 ± 104 nm/s (n = 6), as determined by averaging over a 20-μm window centered on the canthus-to-canthus midpoint. Both vrecoil,1 and vrecoil,2 far exceed vnative = dh/dt = −6.0 ± 0.3 nm/s (n = 8). Using the t-test at a significance level of 0.05, vrecoil,1 > vrecoil,2 (t = 3.20; DoF = 12; P = 0.004). Since vrecoil,1/vrecoil,2 is 1.37 ± 0.16, this comparison indicates that the response to the double-canthi nicking protocol caused the force per unit length produced by the amnioserosa σAS to increase by 37(±12)%. Appendix D analyzes the increase in σAS necessary to compensate for the reversal of the curvature as seen in Fig. 5, a and d, where the free body diagrams represent the forces just before the edge-cut. This analysis estimates σAS to increase by 60(±6)%, which compares favorably to the analysis of vrecoil. In the Discussion, we will consider molecular mechanisms that may trigger this upregulation in response to both the single-canthus and double-canthi nicking protocols.
The revised determination of σAS due to the edge-cut protocol necessitated a recalculation of the force ladder: ∼510:380:130:1 ≥ σLE:σAS:Tκ:bvnative ≥ ∼490:380:110:1, where σLE (σAS) is the force/unit length of the lateral epidermis (amnioserosa), T is the magnitude of the tension in the purse-string, and bvnative is the viscous drag/unit length (see Fig. 5 d). This updated force ladder is in qualitative agreement with that previously reported (4).
DISCUSSION
We have identified key regulatory features and provided further phenomenological characterization of morphogenesis in dorsal closure by applying new analytical tools to quantify the observed asymmetries during closure in wild-type, laser, and genetically perturbed embryos. We have derived dW/dt based on the dynamic geometry of intersecting circular arcs, identifying the correlation kz ≈ −2 vnative, finding that progress toward closure is relatively insensitive to changes in κ, and confirming our previous phenomenological assignment of the 1/tanθ dependence. In wild-type, unperturbed embryos, A-P asymmetries are manifest in measurements of the canthus angles (θAnt < θPos), the location and movement of the centroid, the rates of seam formation (wA > wP), and the zipping rate constants (kz,A > kz,P). The location of the centroid indicates no significant L-R asymmetries. In bsk, mys, and scb embryos, the A-P asymmetries are opposite that of wild-type embryos, including θAnt > θPos and wA < wP, and we observe that they invariably fail at their anterior ends during a critical time in dorsal closure as measured by W, LAvg, and wA/wP. In these mutants, θAnt is larger and wA is smaller relative to wild-type embryos. In the case of scb, there is a significant decrease in dh/dt, which lies along the L-R axis, relative to wild-type embryos. In addition, we observe two examples of upregulation that promote closure in response to laser perturbation in wild-type embryos: in response to laser inhibition of zipping at one canthus, there is an upregulation of the zipping rate constant at the other canthus, and when zipping is inhibited at both canthi, there is an upregulation of the force produced by the amnioserosa.
A mathematical feature of circular-arc geometry of the dorsal opening is the relative insensitivity of dW/dt and dh/dt to changes in κ. While it is an open research question as to whether this insensitivity relaxes any constraints for precise coordination and synchronization of the biological processes that produce forces and zipping during native closure, we have observed relatively large differences between kz,A and kz,P in wild-type, unperturbed closure. This is in contrast to both the relatively smaller differences in the canthus angles and the remarkable uniformity in dh/dt, where the canthi are moving anchors that influence the curvature of the purse-strings. The biological processes that account for kz ≈ −2vnative remain elusive and it is intriguing to consider whether this correlation is attributable solely to biological processes per se or to an additional mathematical property of circular-arc geometry. While circular-arc geometry is well understood mathematically, its application to describe the dorsal opening where the two leading edges are losing length both via zipping and via contraction is the subject of ongoing research.
The A-P asymmetries that we have observed suggest asymmetries in the molecular and/or cellular processes responsible for canthus dynamics. In the past, zipping processes have been attributed to filopodia and/or adhesion proteins (3,4,28–30) and possible explanations for the asymmetry in the zipping rate constants include an asymmetry in the number, distribution, or force-producing capabilities of these factors. In contrast to wild-type closure, bsk, mys, and scb phenotypes have a reversed and more pronounced A-P asymmetry. How these processes relate to previously characterized A-P asymmetries of the developing embryo that affect dorsal closure (31) is not clear, as are the biological processes responsible for the reduction of dh/dt in scb but not in bsk and mys genotypes. Homsy et al. (17) provide evidence that bsk and other components of the N-terminal jun kinase signaling pathway mediate zipping at least in part through their regulation of mys and scb expression, so the similarities described here are not surprising. On the other hand, differences in phenotype are likely due to defects in the expression of other jun transcriptional targets and differences in the perdurance of maternally loaded integrin (32). At this time, the detailed biological processes responsible for zipping are not known and any explanation of either the intrinsic or regulatory asymmetries in kz,A and kz,P would be speculative.
Both laser protocols produce lesions in the amnioserosa, apparently affecting biological process(es) that act as sensors. The lesions change the magnitude of stresses in the remaining amnioserosa, the purse-strings, and the lateral epidermis as well as releasing biochemical debris from damaged cells. These consequences of laser perturbation could affect adhesion molecules, signaling molecules, the contractile components, and mechanically gated channels in the various tissues, therefore triggering a chemical (33,34) and/or mechano-sensing response (35). In any event, the downstream effect of this response is the upregulation of the zipping rate constants in the single-canthus nicking protocol or the force of the amnioserosa in the double-canthi nicking protocol. Both compensatory processes occur in tissue remote from the amnioserosa targeted by the microbeam and therefore we do not consider them to be a local wound-healing response.
There is evidence that the mechanisms for these two regulatory processes are related through σAS. Targeting the microbeam to amnioserosal cells substantially reduces σAS near the canthus and inhibits zipping locally, where neither the seams nor the purse-strings were nicked. When a single-canthus was nicked, kz at the other canthus is upregulated. Apparently σAS near the canthus influences zipping in two ways, via canthus angle and zipping rate constants. Following both nicking protocols, we observe localized constrictions of the leading edges that, in the case of double-canthi nicking, correlate with regions of increased σAS. The increase in σAS likely generalizes to single-canthus nicking and kz may be proportional to local values of σAS. The upregulation of both the force produced by the amnioserosa and the zipping rate constant highlight the resiliency of dorsal closure to laser perturbations to ensure timely closure of the dorsal opening.
We propose that the anterior end of the dorsal opening is subject to relatively greater stresses due to head involution, which may contribute to the A-P asymmetries and would account for the observed anterior failure in the bsk, mys, and scb embryos. Head involution (Fig. 6; see Supplementary Material, Movie 6) is a developmental process that occurs concomitant with the end stages of dorsal closure and after its completion (28). During head involution, a region of the anterior-most tissue folds into the interior of the embryo while the adjacent lateral epidermis moves anteriorly to cover it. Cells closer to the anterior end of the embryo move a larger distance relative to those located more posteriorly (see arrows in Fig. 6)—we suggest the magnitude of movement correlates with the magnitude of the stresses in the embryo. Consider this correlation in light of the following observations. The dorsal opening in wild-type embryos generally has a teardrop geometry with the sharper angle located anteriorly, which reduces the extent of leading edge-amnioserosa interface exposed to relatively larger stresses. In addition, kz,A > kz,P results in the dorsal opening as a whole distancing itself from the region of larger stresses as it translates posteriorly across the dorsal surface as measured by xc. Furthermore, both the single-canthus nicking and double-canthi nicking protocols promote the movement of the opening away from the anterior end of the embryo by the formation of constrictions closer to the anterior end of the opening, possibly reducing the vulnerability to failure. In the single-canthus nicking protocol there is an upregulation of the zipping rate constants, with kz,P increasing proportionately more than kz,A. While upregulated zipping at the unperturbed canthus promotes the completion of closure approximately on schedule, the asymmetric upregulation of kz,P and kz,A promotes movement of the dorsal opening away from the anterior end of the embryo, reducing any vulnerability to the inhomogeneous stresses caused by head involution. In contrast, the reversal of the A-P asymmetries in bsk, mys, and scb genotypes exacerbate the vulnerability to relatively greater stresses at the anterior end due to the geometry and location of the opening, which we contend leads to failure during head involution.
FIGURE 6.
Confocal fluorescent images of native closure showing head involution. The arrows track the movement of anterior and posterior epidermal tissue boundaries. Images were taken 46 min apart. Scale bar is 50 μm.
In conclusion, we have characterized further the physical forces involved in cell sheet movements during dorsal closure in wild-type and genetic or laser-perturbed Drosophila embryos. Previously, we showed that the process of dorsal closure is resilient: neither all the tissues nor processes that contribute to closure are absolutely required, i.e., individual forces can be removed without blocking closure. This is in part due to redundancy in the multiple forces that contribute to closure and in part a consequence of our observation that individual forces that contribute are nearly two orders-of-magnitude greater than their vector sum. Here we have demonstrated that an additional contribution to resiliency is the capability of individual tissues to upregulate the forces they contribute. Thus, the zipping rate and the force produced by the amnioserosa increase in response to experimental manipulations that reduce or remove processes contributed by other tissues, namely laser perturbations at one or both canthi, respectively. These two upregulatory processes may both be mediated through alterations in the mechanical properties of the amnioserosa. We hypothesize that these features of closure, e.g., redundancy, resiliency, and the capacity to overcome defects in force production or transmission in one or another contributing tissue, characterizes morphogenesis throughout phylogeny. We have also quantified multiple A-P asymmetries during unperturbed wild-type closure, some of which indicate that closure progresses successfully with systematic variation in zipping rates. Such asymmetry, at one level or another, characterizes virtually all biological systems. Understanding how the dorsal opening remains approximately symmetric when subject to systematic asymmetric dynamical processes is important for understanding the regulation of the forces that contribute to morphogenesis. Moreover, when the embryos are subjected to genetic or laser perturbation, the asymmetries are modified: in bsk, mys, and scb mutant embryos they are opposite to those observed in wild-type embryos while in single-canthus nicking the asymmetries in zipping are exacerbated. These observations provide insights into the cellular and molecular processes involved in dorsal closure.
How forces contribute to morphogenesis throughout phylogeny is key to understanding the development of all metazoans, including humans (1). Moreover, it is a first step in understanding and subsequently ameliorating the suffering that is associated with such developmental defects as spina bifida, cleft palate, congenital heart or kidney diseases. In addition, because various features of dorsal closure are recapitulated in wound healing, our studies provide insight into the cellular and molecular processes that produce the forces responsible for this important biological process as well.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org. It includes a mathematical derivation of Eqs. B-4 and B-6, movies of dorsal closure in three representative mutant embryos (Movies 1–3), of the edge-cut both with (Movie 4) and without (Movie 5) a localized constriction, and of dorsal closure showing head involution (Movie 6).
Acknowledgments
We thank Fernando Boschini, Alice Rodriguez, and Adrienne Wells for useful discussions.
This research has been supported by the National Institutes of Health grants No. GM33830 and GM61240.
APPENDIX A: DETERMINATION OF THE CENTROID
The centroid of an enclosed surface in Cartesian coordinates, rc = (xc, yc), is sensitive to asymmetries in the geometry. The movement with time of rc gives information about how the enclosed area changes. The general expressions for rc are (37)
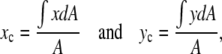 |
(A-1) |
where A is the total area. Discretizing in Eq. A-1 and applying them to the dorsal opening, we obtain the expressions
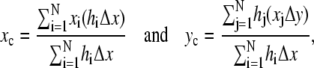 |
(A-2) |
where Δx and Δy are length increments. In Fig. 3 a, the digitized coordinates (xi, hi) trace out both of the leading edges as i is stepped from 1 to N = 100, as do the digitized coordinates (xj, hj) as j is stepped from 1 to N = 100. N = 100 is an empirically derived number of points needed to describe the leading edges with the active contour algorithm (see Analysis), although not so many as to become burdensome during the numerical analysis. An example of the segmentation hiΔx and xjΔy is shown in Fig. 3 a. Δx is found by taking W(0) divided by the smaller number of points along the right or left leading edge. Δy was found in an analogous manner but with the maximum height h in the first image taken. A comparison of the centroid's position with the canthus-to-canthus midpoint gives direct information about the A-P (a)symmetry of the dorsal opening.
APPENDIX B
Dynamic geometry of the dorsal opening
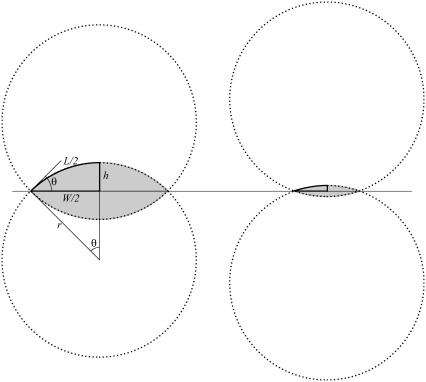
Previously we have reported a quantitative model that successfully accounts for many experimental observations of the geometry of the dorsal opening (4). This model was based on several mathematical assumptions that are well justified experimentally: 1) The shape of each leading edge was assumed to be a circular arc; 2), The height at the symmetry point, h(t), in Fig. 7 decreases linearly with time; 3), The rate of zipping at the canthi was accounted for with an empirical rate equation having the biologically reasonable attribute that the rate of zipping quickened as the angles at the canthi became more acute. Overall, the model provides a quantitative, albeit abstract, summary of the coordination in space and synchronization in time that is a consequence of four cellular processes that are responsible for the dynamics of dorsal closure.
FIGURE 7.
Schematic representation of the setting sun model. Two intersecting circular arcs representing native dorsal closure at earlier (left) and later (right) stages. Shown in bold are the arclength L/2; the half-horizontal opening W/2; the half-vertical opening at the symmetry point h; the half-opening angle θ; and the radius r.
Here we present a derivation of the zipping rate equation based on the dynamic geometry of the dorsal opening. Before delving into the mathematics, we will provide some geometric intuition and key background information by comparing the geometry of the dorsal opening during early-to-mid stages of closure (Fig. 1, b and c) to a sun setting over water (Fig. 7). The arc of the sun and its reflected image appear symmetric about the horizon. During later stages of sunset, the arc of the sun and its reflection provide an image of two intersecting circular arcs (shaded area in Fig. 7), reminiscent of the dorsal opening. As sunset progresses, the two arcs decrease in length as the sun sets, just as the lengths of the leading edges decrease as dorsal closure progresses.
Moving beyond this idealized image of a setting sun, during dorsal closure the length of the leading edges are reduced through two processes: active contraction of the purse-string and incorporation of the leading edges into the seam through zipping, a process that lengthens the seams as closure progresses (Figs. 1 c and 2 c).
Zipping rate model and comparison to experiment
Consider two intersecting circular arcs as shown in Fig. 7, which corresponds to a geometric model for the dorsal opening that is symmetric before both the A-P and L-R axes. The following three relations hold:
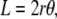 |
(B-1) |
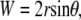 |
(B-2) |
 |
(B-3) |
As derived in the Supplementary Material, the time derivative of Eq. B-2 is given by
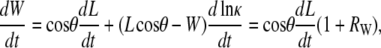 |
(B-4) |
where, by definition, the curvature κ ≡ 1/r and the following ratio RW will prove to be of particular interest when it is small relative to 1:
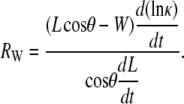 |
(B-5) |
Similarly, the time derivative of Eq. B-3 and the ratio Rh are given by
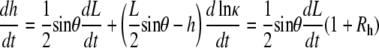 |
(B-6) |
and
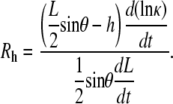 |
(B-7) |
Equations B-4 and B-6 generally describe changes in the geometry of a curve subject to the constraint that the curve remains a circular arc, where L, θ, h, and κ may be functions of time. Dividing Eq. B-4 by Eq. B-6 and recognizing that dh/dt = vnative, which has been shown empirically to be essentially constant during native closure, we obtain
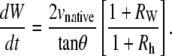 |
(B-8) |
When d(ln κ)/dt = 0, i.e., the constant curvature that characterizes the “setting sun,” then RW = Rh = 0, as seen in Eqs. B-5 and B-7. Consequently, Eq. B-8 exactly becomes
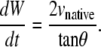 |
However, d(ln κ)/dt = 0 is not strictly realized experimentally. Instead, when the condition
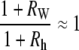 |
(B-9) |
is satisfied, which does not necessarily imply that RW and Rh are both ≈ 0 as will be discussed below, then Eq. B-8 is well approximated by
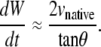 |
(B-10) |
Equation B-10 should be compared to Eq. 5, where wA and wP are the lengths of seam formed at the anterior and posterior ends. For the idealized geometry considered here, θ = θA,R = θA,L = θP,R = θP,L (Fig. 7) and the anterior and posterior zipping rate constants are equal, i.e., kz = kz,A = kz,P. Consequently,
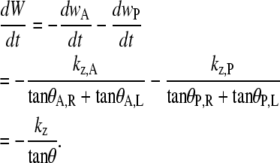 |
(B-11) |
Comparing this result with Eq. B-10 indicates kz ≈ −2 vnative, which is a geometric correlation between the zipping rate constant (kz) and the rate of movement of the symmetry point of the leading edges (vnative). The experimental value for vnative is −6.0 ± 0.3 nm/s (n = 7) and hence the value for −2 vnative falls between the experimental values of kz,A = 15.3 ± 0.7 nm/s and kz,P = 10.6 ± 1.7 nm/s (n = 7), which were reported in the main text. This analysis provides a geometric foundation for the 1/tanθ dependence in the formula for the rate of zipping.
We now compare this model with experimental results to justify the approximations. First we determine the curvature κ from experimental observations of native dorsal closure. In the following, the figures present the results for one embryo, while the averages were taken from four embryos (each with two leading edges). Experimental observations indicate that the leading edges form shallow circular arcs during native dorsal closure (Fig. 1), where the aspect ratio 2h/W decreases from 0.4 to 0.2. To quantify κ we fitted the digitized leading edges, excluding points near the two canthi where the curvature deviates from the arc geometry as the free leading edge joins the zipped seam. Consequently, κ was determined by fitting 90% of the points in the central region at each time. As a test of the circular arc assumption, we first fitted the digitized leading edge with a polynomial s(x), where κ was determined analytically at the symmetry point xsym using the expression (37)
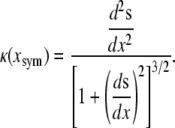 |
(B-12) |
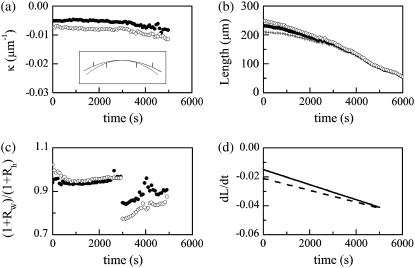
We then fitted the digitized leading edge with an arc of a circle. The two fitting procedures yielded curvatures that agreed to within 7(±2)%, providing experimental support for the circular arc assumption inherent in this model. Fig. 8 a summarizes the experimentally determined κ-values of the two leading edges for a typical embryo. κ is approximately, but not strictly, constant during much of dorsal closure, i.e., up to 3000 s in this case. At later times, κ increases in magnitude, i.e., there is a small but measurable rounding up of the dorsal opening, in this case after 3000 s, as shown in the inset to Fig. 8 a. Consequently, experimental observations indicate d(ln κ)/dt ≠ 0 and strictly speaking the setting sun model does not apply, although it can be a useful approximation.
FIGURE 8.
Time dependence of various parameters that describe changes in the geometry of the dorsal opening. The solid (open) circles are for the right (left) leading edge. (a) Curvature (κ) of the leading edge. (Inset) fitted arcs at 0, 3000, and 5000 s, where the extent of the upper arc corresponds to the length of the leading edge at 0 s. The arc at 3000 s essentially is superposed on the arc at 0 s. Tick marks correspond to the lengths of the leading edge at 3000 s (upper arc) and 5000 s (lower arc), respectively. (b) Arclengths of the leading edges L and canthus-to-canthus distance W (crosses). (c) Ratio of 1+RW to 1+Rh. (d) dL/dt for the right (solid line) and left (dashed line) leading edges.
We now consider the condition, Eq. B-9, introduced to the model to arrive at the approximate equation, Eq. B-10. Fig. 8 b plots the canthus-to-canthus distance W and the arclength of the leading edges LR and LL for dorsal closure in a typical native embryo. The curves were fitted with polynomials to facilitate taking derivatives. Fig. 8 c plots (1+RW)/(1+Rh) based on experimental values. The jump in the data is due to a segmentation at 3000 s in Fig. 8 a, where κ was approximated as two linear regions for the determination of d(ln κ)/dt. Averaging over eight data sets, (1+RW)/(1+Rh) ranges from 0.92 ± 0.10 at earlier stages to 0.88 ± 0.08 at later stages of native dorsal closure, which indicates Eq. B-10 is reliable to ∼10% during much of dorsal closure, which is comparable to biological variability.
Having shown that the experimental data supports the condition (Eq. B-9) used in deriving the rate equation, we next consider two biological insights that can be gained. For the two terms on the right-hand side of Eq. 2 to be comparable, i.e., RW ≈ 1, κ would have to increase by a factor of ∼30. Note that during the edge-cut protocols (Fig. 5, b and e) κ increases by a factor of ∼4 at the turning point, the point of largest curvature. Consequently, κ ≈ 30 is not biologically feasible during dorsal closure. In addition, after some straightforward algebra, it can be shown that
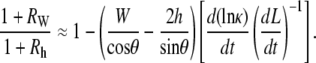 |
(B-13) |
Fig. 8 c plots the left-hand side of Eq. B-13. The second term on the right-hand side accounts, to leading order, for the deviations from 1. The key to the approximation is the term in the square brackets. Using the data presented in Fig. 8 a, d(ln κ)/dt is of the order of 10−5 s−1 until ∼3000 s (for this particular embryo), after which d(ln κ)/dt increases by less than a factor of 10 to a value of the order of 10−4 s−1. This increase in d(ln κ)/dt is partially compensated by dL/dt, which linearly decreases in value by a factor of ∼3 as plotted in Fig. 8 d. The functional form of d(ln κ)/dt is a direct consequence of maintaining circular-arc geometry.
This analysis accounts for the success of the rate equation, Eq. B-10, in quantitatively describing dorsal closure. The dynamics of native dorsal closure are not characterized by closure with approximately constant curvature per se, but instead are attributable to circular arc geometry, in particular due to the relative insensitivity to changes in curvature with time due to the d(ln κ)/dt dependence.
Asymmetric zipping rate model
To explore any possible asymmetry in the anterior and posterior zipping rates, we relaxed any constraints on ideal arclike geometry for the dorsal opening as well as either A-P or L-R symmetries and explicitly consider asymmetries in angles and zipping rate constants. W and the length of seams formed (wA and wP) are measured directly at each time step and satisfy the time-dependent relationship
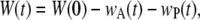 |
(B-14) |
where W(0) refers to the first image analyzed subject to the assumption that the length of the seam does not change once it is formed, which is valid to within an experimental resolution of <2 μm. Taking the time derivative of Eq. B-14, we treat zipping at each canthus with a rate equation,
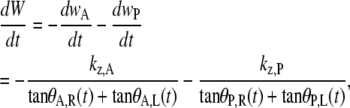 |
(B-15) |
where we have independent zipping rate constants for the anterior (kz,A) and posterior (kz,P) canthi. We explicitly considered whether the differences between dwA(t)/dt and dwP(t)/dt could be attributed to the angular dependence in Eq. B-15 by constraining kz,A to be equal to kz,P and correlating any changes in θAnt(t) and θPos(t) (Fig. 2 b) with corresponding changes in wA(t) and wP(t) (Fig. 2 c), thereby ruling out this possibility. In addition, in the limit that kz ≡ kz,A = kz,P, θA ≡ θA,R = θP,R, θB ≡ θA,L = θP,L and using the approximation that tanθA + tanθB ≈ 2(tanθA/2 + tanθB/2), we recover the more idealized Eq. B-10 as well as the empirical rate equation for zipping introduced in Hutson et al. (4):
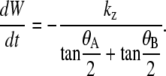 |
(B-16) |
Derivatives can lead to large uncertainties during the numerical analysis of data sets, so Eq. B-15 was integrated and the integrals were expressed as sums, where we use the simplifying notation Ti ≡ tanθA,R (ti) + tanθA,L(ti) to write the expression for seam growth at the anterior canthus as
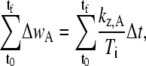 |
(B-17) |
where t0 and tf are the time of the initial and final images in the time series selected for the analysis, and Δt is the time between images and remains constant throughout a time series. We can estimate kz,A by using an average value for wA to obtain
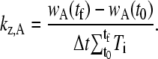 |
(B-18) |
There is an analogous expression for kz,P that allows us to determine kz,A and kz,P independently. In each case, a least mean-squares minimization procedure was used to minimize the difference between the measured data for wA and the values calculated from
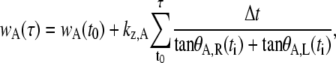 |
(B-19) |
where τ runs from t0 to tf in Δt increments. The initial value for the minimization procedure was chosen by plotting a histogram of the zipping rates as a function of tf from Eq. B-18 and finding the mean peak value. The reported values were determined by taking these initial values for the rate constants and allowing them to vary by up to 10%, subject to Eq. B-14, to minimize the least mean-squares analyses for both anterior and posterior ends.
The analyses of the centroid and the zipping rate constants depend on a fixed frame of reference determined by the confocal microscope. In other words, any movement of the dorsal opening as a whole on the surface of the embryo would compromise the analyses. To within experimental resolution (<2 μm), we observed no such effect.
APPENDIX C
Analysis of mechanical jump experiments
The initial recoil of the leading edge after the edge-cut protocol provides a direct measure of the relative force produced by the amnioserosa. For completeness we summarize the derivation, previously published as Supplementary Material (4). The purse-string can be treated as a one-dimensional, linearly elastic rod under tension, T, which is subjected to a force per unit length from both the lateral epidermis, σLE, and the amnioserosa, σAS (Fig. 5, a and d). Applying Newtonian dynamics to an infinitesimal segment of the leading edge ds, under the condition of low Reynolds number, we can express the vector force balance equation as
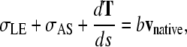 |
(C-1) |
where vnative is the native rate of closure and bvnative is the viscous drag per unit length. Assuming σAS vanishes as a consequence of the edge-cut protocol, which is a refinement of the protocol that targeted the amnioserosa from canthus-to-canthus along the dorsal midline used in reference 4, Eq. C-1 reduces to
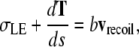 |
(C-2) |
where the leading edge recoils away from the dorsal midline with an initial speed vrecoil in contrast to the direction of vnative, which moves toward the dorsal midline. Idealizing the jump in the velocity from vnative to vrecoil to be instantaneous, subtracting Eq. C-2 from Eq. C-1 yields
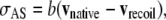 |
(C-3) |
where experiments demonstrate that |vrecoil| exceeds |vnative| by two orders of magnitude. Consequently, vrecoil provides a measure of σAS, subject to the idealization of an instantaneous edge-cut.
Determination of the recoil velocity
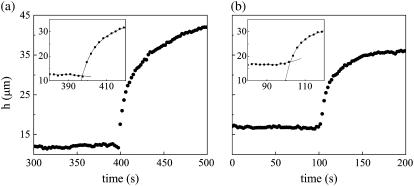
The key to experimentally determining vrecoil with precision is quantifying the effective time of the cut, teff(x), which was somewhat obscured by data sampling and the mechanical response of the tissue during the scanning of the microbeam. h for a fixed value of x is nearly linear as a function of time before laser perturbation (Fig. 9 b, t ≤ 100s). However, as the laser is scanned across the dorsal surface, e.g., from left to right, there is a region of amnioserosa to the immediate right of the location of the microbeam that begins to recoil, and in this region, h can deviate from linearity. To model this region of recoil, data points just before the cut, t < teff, were fit with a polynomial (see insets to Fig. 9, a and b). A double exponential was required to accurately fit the data after the cut, t > teff. The x-values that did not satisfy this double exponential fit rendered the analysis unreliable and were not analyzed further—essentially all such cases were near the canthi. The effective time of the cut, teff, was found using an iterative algorithm to estimate the intersection of the polynomial with the double exponential. Then the instantaneous recoil velocity, vrecoil(teff), was found from the analytical expression for the recoil, dh(x,t)/dt. This algorithm minimizes the consequences of averaging two images in the analysis of edge-cut protocols, where the largest uncertainty occurs for several points just after teff (inset to Fig. 9 a) and possibly for the point just before teff (inset to Fig. 9 b). In particular, determining the polynomial from seven points before teff and the double exponential by all points after teff takes advantage of the many data points that are known with greater certainty in this iterative algorithm. The results for vrecoil(teff) are reliable to within 10% due to the procedure for determining teff, but this effect is less than the variance due to averaging over embryos.
FIGURE 9.
Determination of the recoil velocity. (a,b) Analysis of the recoil in h(x, t) after the edge-cut protocols. Insets highlight the determination of teff at the intersection of the two fits. Plots of h(x, t) are at (a) x = 6 μm in Fig. 5 c, and (b) x = 28 μm in Fig. 5 f.
Inspection of the insets in Fig. 9, a and b, reveals the limitations of approximating vrecoil with differentials determined by two data points, as our group reported previously (4). The analysis presented here leads to larger recoil velocities, due to larger experimental values attributable to the edge-cut protocol as well as greater accuracy of the algorithm attributable to sampling rate and determination of teff. These factors combined allowed for a more accurate determination of the force of the amnioserosa.
We also determined the recoil velocity of the opposing leading edge. In the presence of localized constriction, vrecoil,3 = 1793 ± 284 nm/s (n = 7) and in the absence of a localized constriction, vrecoil,4 = 952 ± 95 nm/s (n = 4). These reduced values are consistent with the opposing edge dragging and deforming the bulk of the amnioserosa as it recoils. Since the amount of remaining amnioserosa is much larger in the absence of a localized constriction compared to when there is a localized constriction, it is not straightforward to draw conclusions from a comparison of these two recoil velocities.
APPENDIX D: ESTIMATE OF THE INCREASE IN THE FORCE PRODUCED BY THE AMNIOSEROSA IN THE PRESENCE OF A LOCALIZED CONSTRICTION
We estimate the increase required in σAS to account for the onset of a constriction as a consequence of the double-canthi nicking protocol. A comparison of the effect of curvature on the orientation of T1 and T2, as summarized in Fig. 5, a and d, provides a geometric distinction between closure in the region of a localized constriction and during unperturbed dorsal closure. While tensions of the purse-strings support dorsal closure in Fig. 5 d, in the region of the localized constriction of Fig. 5 a tensions of the purse-strings oppose closure and indeed σAS is the sole force-producing process that supports closure. The vertical component of Eq. C-1 can be applied at the symmetry points in the presence of a localized constriction (σAS), as shown in Fig. 5 a, and in the absence of a localized constriction (σAS0), as shown in Fig. 5 d, yielding
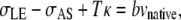 |
(D-1) |
 |
(D-2) |
where κ is the curvature of the leading edge, T is the magnitude of the tension, and the subscript 0 indicates values before any laser perturbation. The bvnative term is two orders-of-magnitude smaller than any of the other terms and can be ignored to a very good approximation (4,38). Setting vnative to zero in both equations, solving Eq. D-1 for σAS, and dividing by σAS0 from Eq. D-2, yields
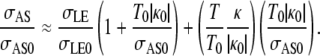 |
(D-3) |
Relative to native closure, the concavity changes sign with the onset of a localized constriction and the edge-cuts were performed when κ/|κ0| was well approximated by unity. The value σLE/σLE0 was estimated by experimental observations of the change in length of the cells of the lateral epidermis, σLE/σLE0 = 0.88 ± 0.01, and both T0|κ0|/σAS0 and T/T0 were determined by the updated force ladders, ∼510:380:130:1 ≥ σLE:σAS:Tκ:bvnative ≥ ∼490:380:110:1, and found to be 0.30 ± 0.01 and 2.06 ± 0.10, respectively. Using these values, σAS/σAS0 was estimated to be 1.6 ± 0.1, which compares favorably with vrecoil,1/vrecoil,2 obtained from the edge-cut experiments.
References
- 1.Keller, R., L. A. Davidson, and D. R. Shook. 2003. How we are shaped: the biomechanics of gastrulation. Differentiation. 71:171–205. [DOI] [PubMed] [Google Scholar]
- 2.Kiehart, D. P., C. G. Galbraith, K. A. Edwards, W. L. Rickoll, and R. A. Montague. 2000. Multiple forces contribute to cell sheet morphogenesis for dorsal closure in Drosophila. J. Cell Biol. 149:471–490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Jacinto, A., W. Wood, T. Balayo, M. Turmaine, A. Martinez-Arias, and P. Martin. 2000. Dynamic actin-based epithelial adhesion and cell matching during Drosophila dorsal closure. Curr Biol. 10:1420–1426. [DOI] [PubMed] [Google Scholar]
- 4.Hutson, M. S., Y. Tokutake, M.-S. Chang, J. W. Bloor, S. Venakides, D. P. Kiehart, and G. S. Edwards. 2003. Forces for morphogenesis investigated with laser microsurgery and quantitative modeling. Science. 300:145–149. [DOI] [PubMed] [Google Scholar]
- 5.Jacinto, A., S. Woolner, and P. Martin. 2002. Dynamic analysis of dorsal closure in Drosophila: from genetics to cell biology. Dev. Cell. 3:9–19. [DOI] [PubMed] [Google Scholar]
- 6.Harden, N. 2002. Signaling pathways directing the movement and fusion of epithelial sheets: lessons from dorsal closure in Drosophila. Differentiation. 70:181–203. [DOI] [PubMed] [Google Scholar]
- 7.Wood, W., A. Jacinto, R. Grose, S. Woolner, J. Gale, C. Wilson, and P. Martin. 2002. Wound healing recapitulates morphogenesis in Drosophila embryos. Nat. Cell Biol. 4:907–912. [DOI] [PubMed] [Google Scholar]
- 8.Kiehart, D. P. 1999. Wound healing: the power of the purse-string. Curr. Biol. 9:R602. [DOI] [PubMed] [Google Scholar]
- 9.Agnès, F., and S. Noselli. 1999. Dorsal closure in Drosophila. A genetic model for wound healing? C. R. Acad. Sci. III. Sci. Vie. 322:5–13. [DOI] [PubMed] [Google Scholar]
- 10.Martin, P., and S. M. Parkurst. 2004. Parallels between tissue repair and embryo morphogenesis. Development. 131:3021–3034. [DOI] [PubMed] [Google Scholar]
- 11.Franke, J. D., R. A. Montague, and D. P. Kiehart. 2005. Nonmuscle myosin II generates forces that transmit tension and drive contraction in multiple tissues during dorsal closure. Curr. Biol. 15:2208–2221. [DOI] [PubMed] [Google Scholar]
- 12.Riesgo-Escovar, J. R., M. Jenni, A. Fritz, and E. Hafen. 1996. The Drosophila Jun-N-terminal kinase is required for cell morphogenesis but not for DJun-dependent cell fate specification in the eye. Genes Dev. 10:2759–2768. [DOI] [PubMed] [Google Scholar]
- 13.Sluss, H. K., Z. Han, T. Barrett, R. J. Davis, and Y. T. Ip. 1996. A JNK signal transduction pathway that mediates morphogenesis and an immune response in Drosophila. Genes Dev. 10:2745–2758. [DOI] [PubMed] [Google Scholar]
- 14.MacKrell, A. J., B. Blumberg, S. R. Haynes, and J. H. Fessler. 1988. The lethal myospheroid gene of Drosophila encodes a membrane protein homologous to vertebrate integrin β-subunits. Proc. Natl. Acad. Sci. USA. 85:26–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Stark, K. A., G. H. Yee, C. E. Roote, E. L. Williams, S. Zusman, and R. O. Hynes. 1997. A noval α-integrin subunit associates with βPS and functions in tissue morphogenesis and movement during Drosophila development. Dev. 124:4583–4594. [DOI] [PubMed] [Google Scholar]
- 16.Brown, N. H. 1994. Null mutations in the αPS2 and βPS integrin subunit genes have distinct phenotypes. Development. 120:1221–1231. [DOI] [PubMed] [Google Scholar]
- 17.Homsy, J. G., H. Jasper, X. G. Peralta, H. Wu, D. P. Kiehart, and D. Bohmann. 2006. JNK signaling coordinates integrin and actin functions during Drosophila embryogenesis. Dev. Dyn. 235:427–434. [DOI] [PubMed] [Google Scholar]
- 18.Brouzés, E., and E. Farge. 2004. Interplay of mechanical deformation and patterned gene expression in developing embryos. Curr. Opin. Genet. Dev. 14:367–374. [DOI] [PubMed] [Google Scholar]
- 19.Hardin, J., and T. Walston. 2004. Models of morphogenesis: The mechanisms and mechanics of cell rearrangement. Curr. Opin. Genet. Dev. 14:399–406. [DOI] [PubMed] [Google Scholar]
- 20.Farge, E. 2003. Mechanical induction of twist in the Drosophila foregut/stomodeal primordium. Curr. Biol. 13:1365–1377. [DOI] [PubMed] [Google Scholar]
- 21.Shraiman, B. 2005. Mechanical feedback as a possible regulator of tissue growth. Proc. Natl. Acad. Sci. USA. 102:3318–3323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hove, J. R., R. W. Köster, A. S. Forouhar, G. Acevedo-Bolton, S. E. Fraser, and M. Gharib. 2003. Intercardiac fluid forces are an essential epigenetic factor for embryonic cardiogenesis. Nature. 42:172–177. [DOI] [PubMed] [Google Scholar]
- 23.Kiehart, D. P., Y. Tokutake, M-S. Chang. M. S. Hutson, J. Wiemann, X. G. Peralta, Y. Toyama, A. R. Wells, A. Rodriguez, and G. S. Edwards 2005. Cell Biology: A Laboratory Handbook, 3rd Ed. J. E. Celis, editor. Elsevier, San Diego, CA.
- 24.Kiehart, D. P., R. A. Montague, A. L. Rickoll, D. Foard, and G. H. Thomas. 1994. Methods in Cell Biology. L. S. B. Goldstein and E. A. Fyrerg, editors. Academic Press, San Diego, CA.
- 25.Srinivasan, R. 1986. Ablation of polymers and biological tissue by ultraviolet lasers. Science. 234:559–565. [DOI] [PubMed] [Google Scholar]
- 26.Kass, M., A. Witkin, and D. Terzopoulos. 1987. Snakes: active contour models. Int. J. Comput. Vis. 1:321–331. [Google Scholar]
- 27.Rasband, W. S. 1997. –2005. ImageJ. U.S. National Institutes of Health, Bethesda, Maryland. http://rsb.info.nih.gov/ij/.
- 28.Martin, P., and W. Wood. 2002. Epithelial fusions in the embryo. Curr. Opin. Cell Biol. 14:569–574. [DOI] [PubMed] [Google Scholar]
- 29.Bloor, J. W., and D. P. Kiehart. 2002. Drosophila RhoA regulates the cytoskeleton and cell-cell adhesion. Development. 129:3173–3183. [DOI] [PubMed] [Google Scholar]
- 30.Magie, C. R., M. R. Meyer, M. S. Gorsuch, and S. M. Parkhurst. 1999. Mutations in the Rho1 small GTPase disrupt morphogenesis and segmentation during early Drosophila development. Development. 126:5353–5364. [DOI] [PubMed] [Google Scholar]
- 31.Lawrence, P. 1992. The Making of a Fly. Blackwell Scientific, London, UK.
- 32.Roote, C. E., and S. Zusman. 1995. Functions for PS integrins in tissue adhesion, migration and shape changes during early embryonic development in Drosophila. Dev. Biol. 169:322–336. [DOI] [PubMed] [Google Scholar]
- 33.Bershadsky, A. D., N. Q. Balaban, and B. Geiger. 2003. Adhesion-dependent cell mechanosensitivity. Annu. Rev. Cell Dev. Biol. 19:677–695. [DOI] [PubMed] [Google Scholar]
- 34.Shemesh, T., B. Geiger, A. D. Bershadsky, and M. M. Kozlov. 2005. Focal adhesions as mechanosensors: a physical mechanism. Proc. Natl. Acad. Sci. USA. 102:12383–12388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hamill, O. P., and B. Martinac. 2001. Molecular basis of mechanotransduction in living cells. Physiol. Rev. 81:685–740. [DOI] [PubMed] [Google Scholar]
- 36.Campos-Ortega, J. A., and A. Hartenstein. 1985. The Embryonic Development of Drosophila melanogaster. Springer-Verlag, Berlin, Germany.
- 37.Gillett, P. 1988. Calculus and Analytic Geometry. D.C. Heath, Lexington, KY.
- 38.Tokutake, Y. 2003. PhD dissertation. Biophysical investigation of dorsal closure in Drosophila. Duke University, Durham, NC.