Abstract
Kinesin-1 is one of the motor proteins that drive intracellular transport in eukaryotes. This motor makes hundreds of 8-nm steps along a microtubule before releasing. Kinesin-1 can move at velocities of up to ∼800 nm/s, which means that one turnover on average takes 10 ms. Important details, however, concerning the coordination between the two motor domains have not been determined due to limitations of the techniques used. In this study, we present an approach that allows the observation of fluorescence intensity changes on individual kinesins with a time resolution far better than the duration of a single step. In our approach, the laser focus of a confocal fluorescence microscope is pointed at a microtubule and the photons emitted by fluorescently labeled kinesin motors walking through the spot are detected with submicrosecond accuracy. We show that the autocorrelation of a fluorescence time trace of an individual kinesin motor contains information at time lags down to 0.1 ms. The quality and time resolution of the autocorrelation is primarily determined by the amount of signal photons used. By adding the autocorrelations of several tens of kinesins, fluorescence intensity changes can be observed at a timescale below 100 μs.
INTRODUCTION
Molecular motors of the kinesin superfamily are microtubule-binding proteins that hydrolyze ATP to drive motility. The most widely studied family is kinesin-1, which is one of the motors that drives intracellular vesicle transport (1). Kinesin-1 consists of two identical motor domains and makes single steps of 8 nm along a microtubule (2) per ATP hydrolyzed (3). Furthermore, it is able to make hundreds of such steps during one encounter with a microtubule, a property called ‘processivity’ (4). It is believed that release of the motor from the microtubule is prevented by keeping the chemical cycles of the two motor domains out of phase (5). Consistent with this idea was the finding that each motor domain in turn steps 16 nm forward in a hand-over-hand fashion (6–8). The molecular details of the coupling between the motor domains remains unclear, but mechanical interactions play a role (9,10). The enzymatic cycle of ATP hydrolysis by each motor domain consists of at least four distinct states, each coupled to the conformation of the neck linker and the affinity for the microtubule. The ATP concentration dependence of kinesin's velocity follows Michaelis-Menten kinetics with a maximal velocity (vmax) of ∼0.8 μm/s. Consequently, under saturating ATP conditions, the average duration of a single catalytic cycle is ∼10 ms (11–13). To reveal the molecular details of the coupling between the chemical and mechanical cycles of the two motor domains of walking kinesin, it is essential to use techniques that allow discrimination of the chemical states with submillisecond time resolution.
Our understanding of kinesin's mechanism has benefited a great deal from the application of single-molecule techniques. The key advantages of applying single-molecule methods to kinesin are that the properties (e.g., velocity, step size, generated force) of single kinesin motors can be determined directly and that synchronization of many motors is not needed (such as in stopped-flow kinetics experiments). Two single-molecule techniques that have been used extensively to clarify kinesin's mechanism are optical tweezers and wide-field single-molecule fluorescence microscopy. Using optical tweezers, the force exerted by a single motor as well as its center-of-mass position can be measured with high time resolution (>5 kHz) and high force (<1 pN) and spatial resolution (<1 nm) (14). In general, the properties of the motor are measured while it is subjected to an external load; measurements at low load are difficult. A limitation of this technique is that the mechanics of the kinesin as a whole are studied and that it does not allow for direct measurement on individual motor domains. Furthermore, information on the kinetics of transitions in kinesin's chemomechanical cycle can only be inferred from fitting kinetic models to the data (11) but cannot be observed directly. The other frequently used technique is wide-field single-molecule fluorescence microscopy, which allows direct observation of the motion of single, fluorescently labeled motors. By attaching the label to different parts of the molecule, one can measure the motion of the center of mass of the whole dimeric motor (15) or one of the motor domains (6). Fluorescence microscopy has the advantage that other parameters besides location can also be measured, such as relative distances using Förster resonance energy transfer (FRET) (16), orientation using fluorescence polarization (17), and the presence of fluorescent substrate analogs (18). In most applications of wide-field fluorescence microscopy to kinesin, charge-coupled device (CCD) cameras are used for fluorescence detection (19). These severely limit the time resolution of the technique, since they require integration of the emitted photons over 50–500 ms to obtain images with a high enough signal/noise ratio for accurate localization of the motor (6). During such time intervals kinesin makes several steps, unless its velocity is lowered by limiting the ATP concentration. Both these techniques do not allow resolving the details of the coupling between the chemical and mechanical cycles of the two motor domains of walking kinesin. Wide-field single-molecule fluorescence microscopy does not have the time resolution required, whereas optical tweezers do not allow discrimination between the states of the individual motor domains.
In this study we introduce another fluorescence-based approach, with a time resolution high enough to allow resolution of the transitions between kinesin's chemical states. Our approach is based on fluorescence detection of individual, labeled kinesin motors walking through the focus of a confocal fluorescence microscope at saturating ATP concentrations without applying an external load. This article is structured as follows. First, we describe the technical details of our method. Next, we test the properties of our kinesin construct and motility assay with traditional, wide-field single-molecule fluorescence microscopy. Then we show that our confocal fluorescence microscopy method is compatible with the wide-field results. Finally, we show by applying autocorrelation analysis that our method allows resolving fluorescence intensity fluctuations that take place on a timescale of 10 μs, a 1000th of kinesin's average turnover time at saturating ATP concentrations.
MATERIALS AND METHODS
Construction of a single-cystein kinesin construct
We constructed a homodimeric kinesin with a single cys located in the tail (hK421C). We started with a human kinesin (KIF5B) construct of 560 amino acids with a single cys at position 174 in a Pet23b vector (20) and changed the only cys present to ala. An upstream primer 5′-GCGCCACAGAGCGTTTTGTAGCAAGTCCAGATGAAGTTATGGATA-3′ and a downstream primer 5′-TATCCATAACTTCATCTGGACTTGCTACAAAACGCTCTGTGGCGC-3′ were used to introduce the mutation and amplify the sequence with a site-directed mutagenesis kit (Quikchange II, Stratagene, La Jolla, CA). A cys was reintroduced at position 421 (cys in the wild-type sequence) using upstream primers 5′-GCTGAAAGAAGAAAGTGTGAAGAAGAAATTGCTAAATTATACAAACAGCTTGATG-3′ and downstream primers 5′-CATCAAGCTGTTTGTATAATTTAGCAATTTCTTCTTCACACTTTCTTCTTTCAGC-3′. The plasmids were stored in XL1-blue Escherichia coli cells.
For expression, the plasmid was introduced in E. coli Bl21(DE3) cells, grown to larger volumes (1 or 2l), and induced overnight at 22°C with isopropyl-β-D-thiogalactopyranoside (AppliChem, Darmstadt, Germany). Bacteria were spun down and the pellet was lysed by adding lysosyme and applying three brief periods of sonification. The lysate was loaded on a NiNTA column and the motor, tagged with a 6× his repeat on the N-terminus, was eluted with 300 mM imidazole.
The motor was labeled with Alexa Fluor 555 maleimide (Invitrogen, Carlsbad, CA) by adding the dye (dissolved in dimethylformamide and diluted in demineralized water) in a 1:1 fluorophore/kinesin monomer ratio and incubating for 3 h at 4°C. Unreacted dye was separated from the labeled kinesin by microtubule affinity centrifugation (21).
Sample chamber preparation
Coverslips (No. 1.5, MenzelGlaser, Braunschweig, Germany) and slides (MenzelGlaser) were cleaned before use by sonification in 0.1 M KOH (1×, 10′) and in demineralized water (3×, 10′). Coverslips were made positively charged by sonification in 0.1% (V/V) N1-[3-(Trimethoxysilyl)-propyl]diethylenetriamine (Sigma-Aldrich, St. Louis, MO) in water (1×, 10′) and subsequent washing in water (3×, 10′). The coverslips were dried in an oven at 130°C and were stored dry. In contrast, the slides were cleaned each day and dried immediately before use. Sample chambers with three lanes (volume ∼5 μl) were made by gluing a coverslip to a slide using double-stick tape.
Sample lane preparation
Microtubule seeds were polymerized by mixing 7.5 μM unlabeled tubulin, 2.5 μM tetramethyl rhodamine (TMR)-labeled tubulin and 1 mM GMPCPP (Guanosine-5′[(α,β)-methyleno]triphosphate (Jena Bioscience, Jena, Germany)) for 15′ at 36°C. Afterward they were stabilized with Pem80-taxol buffer (80 mM Pipes (1,4-piperazinediethanesulfonic acid), 1 mM EGTA (ethyleneglycol-bis(aminoethyl ether)-N,N′-tetraacetic acid), 2 mM MgCl2, pH 6.8, and 10 μM taxol) and were injected into the sample lanes. After 10′ the lanes were rinsed three times with 10 μl Pem80-taxol buffer. Casein (sodium salt from bovine milk, Sigma-Aldrich) at 0.4 mg/ml in Pem80-taxol buffer was flushed into the lane and incubated for 10′. The lane was again rinsed three times with 10 μl Pem12-taxol buffer (equivalent to Pem80-taxol but with 12 mM Pipes). After these steps the mix with kinesin motors was flushed into the sample lane, after which the sample was sealed with vacuum grease. In all experiments an oxygen scavenger system (20 μg/ml glucose-oxidase, 35 catalase μg/ml, and 25 mM glucose), 4 mM dithiothreitol, and 10 μM taxol were added. For samples at saturating ATP concentrations, 2 mM ATP was added. In other experiments kinesin's velocity was decreased by instead adding 100 μM ATP and an ATP regeneration system (10 mM phosphocreatine and 50 μg/ml creatine kinase) (22).
Experimental setup
The attenuated, 532-nm beam of a Verdi V10 (Coherent, Santa Clara, CA) laser was circularly polarized with a quarter-λ plate, expanded six times, and coupled into an inverted microscope (TE-2000-U Nikon, Tokyo, Japan) with a 100× oil immersion objective (Nikon Plan Fluor, numerical aperture 1.3) (Fig. 1 A). Fluorescence was collected through a dichroic mirror (Q545LP, Chroma, Rockingham, VT) and filtered with an emission filter (HQ575/50, Chroma). The fluorescence light was then imaged on a CCD camera (CoolsnapHQ, RoperScientific, Tucson, AZ) or focused onto a multimode optical fiber (100-μm core diameter), serving as a pinhole (23) and detected with an avalanche photodiode (APD) (SPQM-AQR-14, PerkinElmer, Vaudreuil, Quebec, Canada). Photons detected by the APD are converted to digital pulses, which were time tagged with electronic counterboard (6602, National Instruments, Austin, TX) with 12.5-ns time resolution. Arrival times of detected photons were stored on a computer using custom-built Labview software (Labview 7.1, National Instruments).
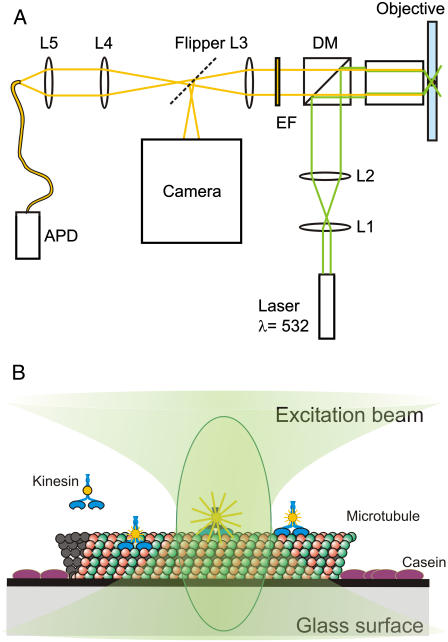
FIGURE 1.
Schematic representation of the experimental setup and the motility assay. (A) Light paths of excitation (green) and emission (yellow) are indicated. The beam expander is represented by L1 and L2. DM is the dichroic mirror and EM is the emission filter. L3 is a lens located inside the microscope, and L4 and L5 image the confocal spot onto the optical fiber. The dashed line represents the port selection of the microscope. (B) Several kinesins in or near the confocal spot. The microtubule is attached to the glass via a positively charged surface. Casein prevents nonspecific sticking of the kinesin to the glass.
To accurately position the confocal spot and scan the sample, we used a feedback controlled piezo translation stage (P-561, Physikalischer Instrumente, Karlsruhe, Germany) with a custom-built sample holder mounted on top of the scanner.
Positioning the confocal spot and acquiring high time-resolution data
Wide-field illumination and CCD camera detection were used to locate the fluorescently labeled microtubules. The sample was translated to position the confocal spot within 1 μm of a microtubule. Then, a 1 × 1 μm area was scanned and the microtubule was positioned within 20 nm of the center of the confocal spot. This positioning procedure was repeated every 10 min to compensate for mechanical drift. Fluorophores on the microtubules were bleached before measuring the fluorescence of kinesins moving through the confocal spot.
Determining the width of the confocal spot
The width of the confocal point spread function was obtained by fitting a two-dimensional Gaussian to a confocal image of fluorescent beads (40-nm diameter, excitation/emission = 565/580 nm, FluoSpheres, Invitrogen) stuck to the surface. The width (defined as σ of the Gaussian, i.e., the halfwidth at 1/√e) was corrected for the bead size by deconvolution and was determined to be 113 ± 5 nm (mean ± SE).
RESULTS AND DISCUSSION
Characterization of the kinesin construct with conventional wide-field fluorescence microscopy
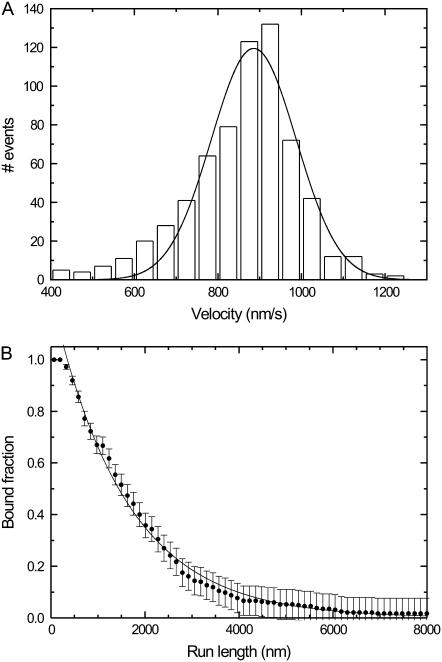
To test our kinesin construct (hK421C-Alexa 555), we measured run lengths and velocities of individual motors at saturating ATP concentrations with conventional wide-field fluorescence microscopy. In this assay, sparsely labeled microtubules (roughly 1 fluorophore per 1500 tubulin dimers) were bound to a positively charged surface, and kinesin was added. Movies were recorded and were analyzed using kymography (24) (not shown). Events were manually traced in the kymograph, and the velocity and run length of each event was determined. To reduce tracing inaccuracy and to discard binding events of nonfunctioning motors, only events longer than 0.6 s (two frames) were taken into account. Fitting a single Gaussian peak to the histogram of velocities of single motors (Fig. 2 A) yielded an average velocity of 886 ± 7 nm/s, similar to velocities published before (5). The average of all the velocities (860 ± 5 nm/s, N = 657) is comparable to the value found by fitting.
FIGURE 2.
Characterization of hK421C's motility on microtubules using single-molecule wide-field fluorescence microscopy assays. (A) Histogram of the velocities of individual motors (N = 657). The solid line is a Gaussian fit to the distribution with its center position at 886 ± 7 nm/s (mean ± SE). (B) Distribution of the probability of being bound after a given run length (N = 204). A single exponential fit (solid line) indicates that the average run length is 1550 ± 30 nm (not corrected for photobleaching). The error bars are calculated from the square root of the absolute number of already detached motors and normalized.
The average run length was determined by fitting a single exponential to a plot of the fraction of kinesin still bound as a function of run length (Fig. 2 B) (25). Using this method we found an average length of the runs of 1550 ± 30 nm. The amount of photobleaching under our experimental conditions was determined by measuring the fluorescence intensity as a function of time for labeled kinesins fixed to microtubules with adenylylimidodiphosphate. A single- exponential decay fitted to these data yielded an average bleaching time of 27 ± 1 s (data not shown). The run length was corrected for photobleaching with this value, yielding a corrected run length of 1680 nm. The run length is comparable to those in the literature (5,25). Taken together, these results show that we have an active construct that functions in single-motor assays equivalent to native kinesin-1.
Typical events observed with confocal microscopy
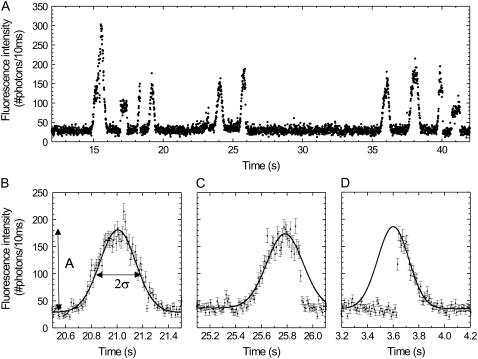
We then switched from wide-field to confocal microscopy. When the laser was focused on a microtubule (Fig. 1 B), we observed fluorescence time traces as shown in Fig. 3 A. Labeled kinesins walking through the confocal spot show up as Gaussian peaks, which can be explained as follows. The kinesin-bound fluorophore senses a laser intensity that is determined by its location in the laser spot (which can be approximated by a Gaussian with width σexc). Consequently, under our experimental conditions (see below) the fluorophore emits with a rate proportional to this local excitation intensity. In a confocal microscope, the efficiency of detecting a photon emitted by a fluorophore also depends on its location, as described by the collection efficiency profile (which can also be approximated by a Gaussian with width σCEF). As a consequence, the total detected fluorescence intensity is proportional to the product of the excitation profile and the collection efficiency function. The product is also a Gaussian (26) and is called the confocal point spread function. Therefore, the fluorescence of a labeled kinesin moving at constant velocity through the confocal spot will appear as a Gaussian peak in a binned fluorescence time trace. In Fig. 3 A, several Gaussian peaks can be discerned, all with nearly the same duration and amplitude except for one with an amplitude about twice as high. This latter signal is most probably due to a motor with two labels or two motors passing the focus at the same time. The time trace also shows two peaks with a constant, non-Gaussian fluorescence signal, which we attribute to fluorophores (loose or attached to kinesin) that get stuck somewhere in the confocal spot and detach or photobleach after some time.
FIGURE 3.
Fluorescence intensity traces obtained when the confocal spot was positioned on a locally bleached microtubule. (A) A time trace of 30 s shows several events, most with comparable amplitude. (B) A full event, which is due to a motor landing before the confocal spot, walking in and through it and consequently showing a complete Gaussian profile. The solid line is a Gaussian fit to the trace. The amplitude (A) and width (σ) of the event are indicated for clarity. (C) A vanish event, which is due to a kinesin walking into the confocal spot but abruptly photobleaching or detaching somewhere in the spot and consequently showing only the leading flank of a Gaussian. (D) A landing event, which is due to a kinesin landing on the microtubule somewhere in the spot and consequently showing only the trailing flank of a Gaussian. In (C) and (D) the Gaussian was fit to the points of the leading and the trailing flank, respectively. Each error bar in graphs B, C, and D is the square root of the corresponding intensity.
Closer examination of the apparent Gaussian peaks reveals that three types of events can be discerned. i) A large fraction of the events shows up like a complete Gaussian peak (Fig. 3 B). These events are due to labeled kinesins walking into and through the spot without detaching from the microtubule or photobleaching. We call this type of event ‘full events’. ii) The time traces of a second class of events show only the leading flank of a Gaussian (Fig. 3 C). We attribute such a signal to a kinesin walking into the spot but abruptly photobleaching or detaching somewhere in the spot. We call this type of event ‘vanish events’. iii) In the third type of events only the trailing flank of a Gaussian can be seen (Fig. 3 D). We attribute such a signal to a kinesin landing from solution on the microtubule somewhere in the spot and walking through the remainder of the spot. This type is referred to as ‘landing events’. Also shown in Fig. 3, B–D, are Gaussian fits to the time traces, used to determine the amplitude (A) and the width (σ) of each event, which were used for further analyses.
Determination of the velocity of kinesins walking through the confocal spot
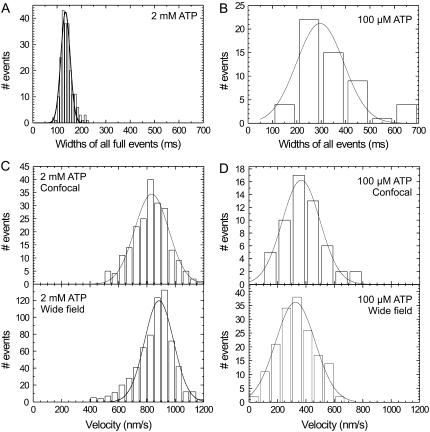
The Gaussian shape of the events indicates that the kinesin's velocity is constant during the passage through the confocal spot. Since the detected emission rate is proportional to the value of the confocal point spread function at the location of the motor, the motor's velocity equals the ratio of the spatial width of the point spread function and the temporal width of an event. A histogram of the temporal widths of all full events at a saturating ATP concentration of 2 mM is shown in Fig. 4 A. The distribution of the widths is Gaussian and peaks at 130.3 ± 1.7 ms (as determined with a Gaussian fit; the statistical average is 136.3 ± 1.5 ms). From this average temporal width an average velocity of 870 ± 40 nm/s can be calculated. The average value obtained in this way and the shape of the distribution compare very well to our wide-field fluorescence measurements, depicted in Fig. 4 C. To further validate our velocity determinations, confocal and wide-field measurements were also performed at 100 μM ATP, a concentration at which kinesin moves slower. The averaged temporal width of events at 100 μM ATP is larger (300 ± 20 ms) than at 2 mM. Furthermore, the distribution of the widths is wider as well (Fig. 4 B). Wide-field velocity determinations at the same ATP concentration show a similar average velocity (326 ± 9 nm/s) and distribution as the velocities calculated from the confocal measurements (344 ± 15 nm/s; Fig. 4 D).
FIGURE 4.
Wide-field and confocal velocity measurements at two different ATP concentrations. Histogram of the widths of full events at 2 mM ATP (A) and 100 μM ATP (B) (N = 213 for 2 mM and N = 55 for 100 μM, events at different excitation powers were pooled). The calculated velocities from these widths are plotted together with the velocities obtained from wide-field measurements for both 2 mM ATP (C) and 100 μM ATP (D). The solid lines represent Gaussian fits to the data.
Behavior of fluorophores at different excitation powers
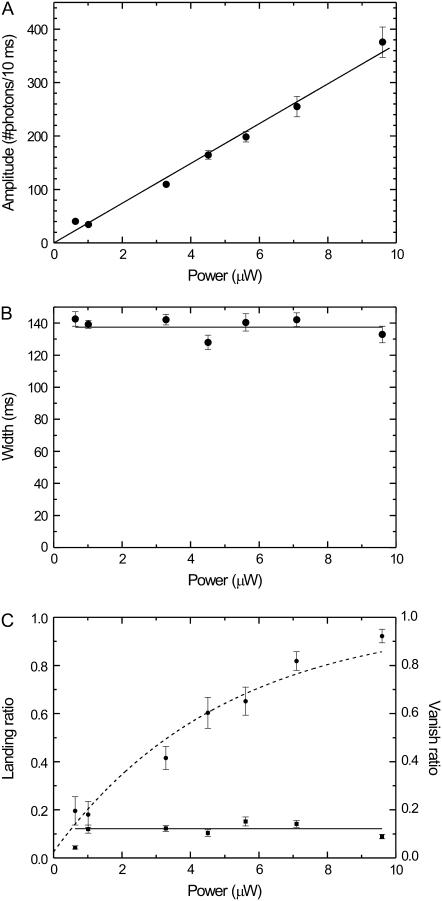
Next, we determined the laser power dependence of the emission time traces of labeled kinesins walking through the confocal spot. One would expect that high excitation powers lead to a higher rate of photon detection (improving photon statistics) but at the same time increase the probability of photobleaching (decreasing the number of full events). First, we determined the average amplitude as a function of laser power. Fig. 5 A shows that the amplitude depends linearly on the excitation power, as expected for the intensities used in our assay (27). Second, we determined that the width (of full events, i.e., kinesin's velocity) does not depend on the laser power (Fig. 5 B), as expected. Also the landing ratio, which we define as the number of landing events divided by the number of vanish and full events, does not depend on laser power (Fig. 5 C). In contrast, the vanish ratio, which we define as the ratio between vanish events and the sum of vanish and full events, depends in a nonlinear way on the excitation power (Fig. 5 C). These data can be described by exponential relaxation with an asymptote at a probability of one and an offset at zero power. The offset is caused by motor detachment due to the finite run length. The exponential relaxation can be explained by the exponential dependence of the probability of a fluorophore not having photobleached after emitting a given number of photons. The number of photons emitted during a full event is linearly proportional to the excitation power. Therefore, the probability of a kinesin completing a full event decays exponentially with excitation power. We chose to not perform a more quantitative analysis on these data, since that would strongly depend on an accurate estimation of the effective distance over which beginning or ending an event can be discriminated from background, which is problematic. In the following we will present a quantitative analysis of autocorrelated fluorescence time traces, which do not suffer from this problem.
FIGURE 5.
(A) The average amplitude of all full events as a function of excitation power. The solid line represents a linear fit (without offset) with a slope of 3700 ± 80 photons/(s μW). (B) The average width of all full events as a function of excitation power. The solid line represents a fit of a constant value (137 ± 2 ms). (C) Landing ratio (squares) and vanish ratio (dots) (see text) as a function of excitation power. The solid line represents a fit of a constant to the landing ratio data points (0.12 ± 0.01). The dashed curve represents a fit to an exponential decay (y = 1 − a exp(−x/P), where a = 0.97 ± 0.05 and P = 5 ± 0.5 μW).
Autocorrelation of fluorescence time traces
So far we have used 10-ms time binning of the photon arrival times in our data analysis. To determine the effective time resolution of our method, we performed autocorrelation analyses to fluorescence time traces with smaller bin widths (28). It should be noted that we do not expect the fluorescence intensity of the kinesin construct used for these experiments to change due to switches from one mechanical or chemical state to another because it is labeled in the tail.
Events due to individual kinesin dimers walking through the confocal spot were selected after visual inspection of the fluorescence time traces. The center point and background levels were determined for each event by fitting a Gaussian to 10-ms binned time traces. The autocorrelation was calculated from 2-s long, background-subtracted binned time traces containing an event with its center point in the middle. The time traces were binned with bin sizes of 1 ms or 10 μs, depending on the timescale of interest (the calculations at small time bins require substantial computation time). For the autocorrelations with 10-μs bins we applied a coarse-grained step afterward to improve the signal/noise ratio on the longer timescales: the correlation times were chosen to increase logarithmically with time (29). The correlation values within a bin were averaged.
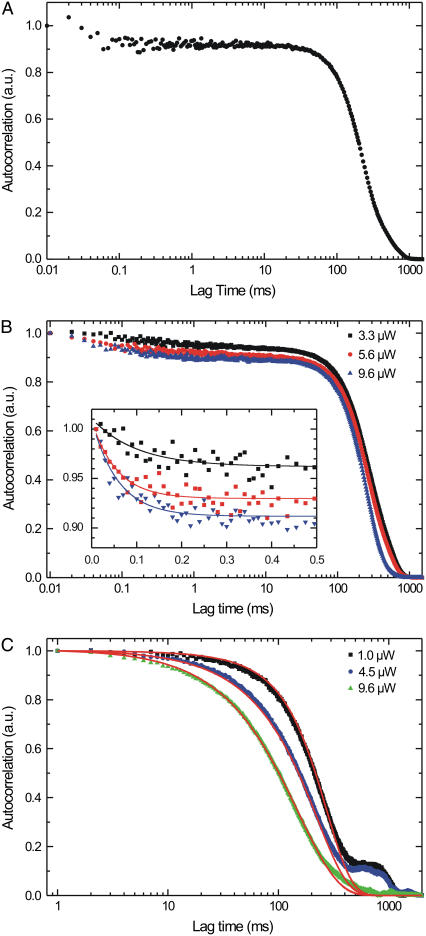
The normalized autocorrelation of the fluorescence trace of a single motor passing through the confocal spot (Fig. 6 A) is roughly Gaussian with a larger width than that of the time trace it was calculated from (as expected since the autocorrelation of a Gaussian is a Gaussian with a √2 larger width). The time-symmetric autocorrelation is shown only for positive lag times on a logarithmic timescale to more clearly represent the curve over 5 decades of time.
FIGURE 6.
Autocorrelation analysis of the time traces obtained with single-kinesin confocal microscopy. (A) Normalized autocorrelation of a single full event at an excitation power of 9.6 μW. (B) Normalized summed autocorrelation for three different excitation powers of only full events (time binned with 10 μs). Inset shows the exponential decay with their fits at the submillisecond timescale, probably due to triplet blinking of the fluorophore; the amplitudes increase with excitation power (0.049 ± 0.006, 0.079 ± 0.009, and 0.097 ± 0.008, respectively), whereas time constants of the fits are similar (0.10 ± 0.04, 0.056 ± 0.011, and 0.058 ± 0.010, respectively). (C) Normalized summed autocorrelations at three different excitation powers of vanish and full events (time binned with 1 ms). The small shoulders observed around 900 ms are due to small errors in the background correction and the finite time interval of the correlated trace (2000 ms in all graphs shown here). The red lines represent a simulation for the three different powers; see text for details of simulation.
Even with a limited number of photons (11,000 in this event) the autocorrelation function of a single event still contains information at 0.1 ms. The signal/noise ratio depends on both the distribution of times between consecutively detected photons and the total number of detected photons. The former can be improved by using higher fluorescence intensities. This leads, however, to an unwanted increase of the photobleaching. The number of photons detected and in that way the time resolution of the autocorrelation can be increased by summing the autocorrelations of multiple events, as shown for all full events at three different powers (Fig. 6 B). In this way, we obtain curves with relatively low noise down to 10 μs, showing that with our approach fluorescence fluctuations down to the 10-μs timescale can be observed. The traces show an exponential decay at lag times up to 0.1 ms (inset Fig. 6 B), which is probably due to the triplet state of Alexa 555, since its amplitude increases with excitation intensity and its decay time hardly changes for the relatively small range of changes in amplitude (30). The three curves measured with different excitation intensity have the same width of ∼200 ms (only full events were used, and kinesin's velocity does not depend on the excitation intensity; Fig. 5). When vanish events are also included in the summation (Fig. 6 C) the higher power curves turn out to be narrower than the lower power ones, which is indicative of increased photobleaching, leading to more and narrower vanish events.
Simulations of the autocorrelated fluorescence time traces
To fully understand the effects of photobleaching and detachment of the motor, we focused further analysis on the 1–1000 ms timescale of summed autocorrelations of all full and vanish events (Fig. 6 C) and simulated the autocorrelated fluorescence time traces. Simulations were performed as follows. The emission rate of a labeled motor moving with constant velocity (v) depends on its position in the Gaussian excitation profile with width σexc. The detection efficiency depends on the location of the motor in the collection efficiency profile, which we assume Gaussian with a width of σCEF. The number of detected photons (Ndet) between time interval t and t + Δt, due to such a motor, can be calculated using
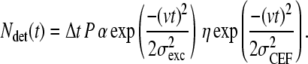 |
(1) |
Where P is the power of the excitation laser, α is the setup- and fluorophore-dependent factor that relates the excitation power to the rate of emitted photons, and η is the maximum collection efficiency. Here we assume that at t = 0 the motor passes the coinciding maxima of the excitation and collection profile.
Next, for each event photobleaching was introduced by assuming a constant probability of bleaching for each emitted photon (the reciprocal of the bleach constant, b). The probability of bleaching, pbleaching, during an interval between t and t + Δt can be expressed as
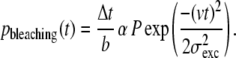 |
(2) |
Note that the probability of bleaching as a function of time depends only on the location of the fluorophore in the excitation spot and is not influenced by the location in the collection efficiency profile. For each step, this probability was compared to a randomly generated number (between 0 and 1) to decide whether photobleaching had occurred. In case of photobleaching, the signal was set to zero for the rest of the event.
In a similar way the finite length of kinesin runs was introduced. During each time interval the motor has a constant probability of detaching from the microtubule (pdetach), independent of its location:
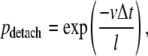 |
(3) |
where l is the average run length.
In this way, fluorescence time traces of 15,000 events were generated for different excitation powers using varying values for the other parameters. Subsequently, these traces were autocorrelated and summed. The measured autocorrelation curves can be simulated very well with a value for the run length (l) of 1700 nm, for the velocity (v) of 870 nm/s, for the width of the collection efficiency function (σCEF) of 220 nm, for the width of the excitation spot (σexc) of 150 nm, for the maximum collection efficiency (η) of 0.1, and for a bleach parameter (b) of 55,000 photons. Varying the value for the run length in the simulations (from 800 to 2000 nm) hardly altered the simulated correlation traces (data not shown), since the length scale of observing motion in our instrument (∼4σPSF ≈ 500 nm) is several times smaller than the run length. The overall good correspondence of the model to the data indicates that the behavior of labeled motor proteins walking through the confocal spot is sufficiently understood. The small shoulder around 900-ms lag time in the autocorrelation curve of 1.0 μW is due to small inaccuracies in the background correction of the events.
Simulation of a construct whose fluorescence fluctuates due to stepping
The ultimate goal of our approach is to observe transitions between the chemomechanical states of walking kinesin. For this, labeled kinesin constructs are needed with at least two states in the cycle with differing fluorescence intensities. To examine the potential of our approach to yield new information on kinesin's mechanochemistry, we have simulated time traces and intensity autocorrelations of a kinesin construct capable of FRET between its two motor domains. We assume a construct with a donor fluorophore on one motor domain and an acceptor fluorophore at the same position on the other motor domain. The stepwise behavior of the motor is taken into account, and each step is assumed to consist of two distinct fluorescent states. We assume that the FRET transfer efficiency between donor and acceptor is 0.16 when the two motor domains are attached to consecutive binding sites on the microtubule (8 nm apart). During a step, we assume that the two motor domains are closer and that the transfer efficiency equals 0.8. The proximity could be due to a substep but can also be due to the overtaking of the forward head by the rearward one. It is known that kinesin's stepping takes <1 ms (11).
Focusing on the intensity of the fluorescence emitted by the acceptor we assume that a single step consists of a short-lived high-fluorescent state and a longer lasting low-fluorescent state. We mimic the Poisson-like behavior of the motor by randomly selecting the occupation times of both states from an exponential distribution. In a first simulation we use an average occupation time of the high fluorescence state of 0.5 ms and of the low fluorescent state of 9.5 ms. The maximum emission rate of the acceptor is 20 photons/ms (as expected for the typical excitation powers used in our experiments), and the background signal is 1 photon/ms. The photon arrival times are generated from an exponential distribution with a decay time that depends on the fluorescent state and the position in the confocal spot.
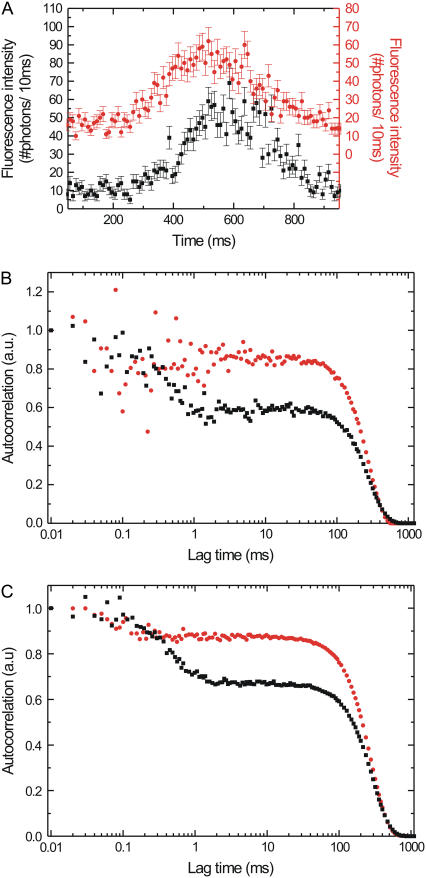
In the simulated, binned fluorescence intensity traces the short-lived high-fluorescent state is hidden in the amplitude fluctuations of the Gaussian envelope (Fig. 7 A, black curve). The autocorrelation of this single event shows a decay around 0.5 ms, a signature of short bursts of fluorescence with on average this duration (Fig. 7 B, black curve). Averaging the autocorrelations of 20 simulated full events (Fig. 7 C, black curve) yields a smooth curve with an even more clear decay at 0.5 ms. In a next set of simulations we decreased the time the molecule spends in the high state to on average 0.1 ms, whereas the low-fluorescent state lasts 9.9 ms. Comparison of the binned fluorescence traces for the two different sets of simulations shows no clear differences (Fig. 7 A, black and red curve). Moreover, in the autocorrelation of a single event, clear features on the 0.1-ms timescale cannot be discerned (Fig. 7 B, red curve). If we however average 20 events with these settings we observe a clear decay around 0.1 ms (Fig. 7 C, red curve), demonstrating that our approach can yield insight into chemomechanical transitions taking place in <0.1 ms. In the simulations, conservative estimates of the parameters are used. A further improvement of the detectable timescale could be obtained by averaging even more events.
FIGURE 7.
(A) Simulated fluorescence intensity traces of kinesin stepping through a Gaussian excitation profile switching between high and low FRET states. The red graph is shifted upward for clarity; its axis is on the right-hand side of the graph. Each error bar is the square root of the intensity. (B) Intensity autocorrelations of the events shown in A. (C) Summing the autocorrelation of 20 separately simulated events improves the signal/noise ratio, in particular on the short timescales. See text for details of the simulations. For all three graphs, the red circles represent a simulation with the low FRET state (emitting 4 photons/ms in the acceptor channel) lasting on average 9.9 ms, and the high FRET state (20 photons/ms) lasting 0.1 ms. Black squares represent a simulation, with the low FRET state lasting 9.5 ms and the high FRET state lasting 0.5 ms.
CONCLUSIONS
We have presented a new approach to study the motion of fluorescently labeled kinesin with submillisecond time resolution. In our approach labeled kinesins walk through the excitation spot of a confocal microscope, and the emitted photons are detected with nanosecond resolution. Fluorescence time traces measured in this way have an approximately Gaussian profile, the width of which is a signature of the motor's velocity. We find an average velocity of 870 ± 40 nm/s. Summed autocorrelations of the fluorescence time traces from individual motors allow discrimination of fluorescence intensity fluctuations on a timescale down to 10 μs. The autocorrelations and their excitation intensity dependence can be well described using a simple model taking into account the profiles of the excitation intensity and collection efficiency, the velocity of the motor, photobleaching, and detachment from the microtubule track.
Our approach is related to fluorescence correlation spectroscopy (31). Fluorescence correlation spectroscopy is often used to study freely diffusing labeled molecules, but it has also been applied to study flow inside cells (32) and microfluidic devices (33). In these studies, diffusion of the labeled biomolecules could be discriminated from drift with the solvent flow and flow velocities could be determined. Our approach is different in the key aspect that it is a truly single-molecule approach. We detect the trajectories of individual biomolecules walking through the confocal spot. This allows us to restrict our analysis to events with properties we expect for functional, singly labeled kinesin. We can select on properties such as width (a signature of velocity) and intensity (a signature of the amount of motors and labels).
For the labeled kinesin construct studied here, fluorescence fluctuations due to kinesin's mechanochemistry were neither expected nor observed. We have shown however that our approach allows for the observation of fluctuations on a timescale down to 10 μs, i.e., a thousand times faster than kinesin's stepping time. The confocal fluorescence approach shown here paves the way to study kinesin's mechanochemistry on the single-motor level, provided labeled kinesin constructs are used that report on chemical and conformational changes. One could, for example, think of fluorescence polarization as a reporter of conformational changes (17) or fluorescent ATP analogs to directly observe substrate binding and release (18). Another example would be a kinesin with a donor fluorophore on one motor domain and an acceptor on the other as a FRET reporter of the distance between the motor domains. We have performed a simulation with such a construct and shown that fluorescence intensity changes can be observed at timescales below 0.1 ms.
Acknowledgments
We thank J. Van Mameren for programming the kymograph software, I. Schaap for purifying microtubules, H. Sosa (Albert Einstein College of Medicine, Bronx, NY) for his generous gift of the kinesin plasmid, and J. Enderlein (Forschungszentrum Jülich, Germany) for generously sharing his fast correlation computing algorithm.
This research was supported by a VIDI fellowship from the Research council for Earth and Life Sciences (A.L.W.) and by a Projectruimte grant from the Dutch Foundation for Fundamental Research on Matter (F.O.M.).
References
- 1.Vale, R. D., T. S. Reese, and M. P. Sheetz. 1985. Identification of a novel force-generating protein, kinesin, involved in microtubule-based motility. Cell. 42:39–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Svoboda, K., C. F. Schmidt, B. J. Schnapp, and S. M. Block. 1993. Direct observation of kinesin stepping by optical trapping interferometry. Nature. 365:721–727. [DOI] [PubMed] [Google Scholar]
- 3.Schnitzer, M. J., and S. M. Block. 1997. Kinesin hydrolyses one ATP per 8-nm step. Nature. 388:386–390. [DOI] [PubMed] [Google Scholar]
- 4.Carter, N. J., and R. A. Cross. 2006. Kinesin's moonwalk. Curr. Opin. Cell Biol. 18:61–67. [DOI] [PubMed] [Google Scholar]
- 5.Visscher, K., M. J. Schnitzer, and S. M. Block. 1999. Single kinesin molecules studied with a molecular force clamp. Nature. 400:184–189. [DOI] [PubMed] [Google Scholar]
- 6.Yildiz, A., M. Tomishige, R. D. Vale, and P. R. Selvin. 2004. Kinesin walks hand-over-hand. Science. 303:676–678. [DOI] [PubMed] [Google Scholar]
- 7.Asbury, C. L., A. N. Fehr, and S. M. Block. 2003. Kinesin moves by an asymmetric hand-over-hand mechanism. Science. 302:2130–2134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kaseda, K., H. Higuchi, and K. Hirose. 2003. Alternate fast and slow stepping of a heterodimeric kinesin molecule. Nat. Cell Biol. 5:1079–1082. [DOI] [PubMed] [Google Scholar]
- 9.Vale, R. D., and R. A. Milligan. 2000. The way things move: looking under the hood of molecular motor proteins. Science. 288:88–95. [DOI] [PubMed] [Google Scholar]
- 10.Rosenfeld, S. S., P. M. Fordyce, G. M. Jefferson, P. H. King, and S. M. Block. 2003. Stepping and stretching. How kinesin uses internal strain to walk processively. J. Biol. Chem. 278:18550–18556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Schnitzer, M. J., K. Visscher, and S. M. Block. 2000. Force production by single kinesin motors. Nat. Cell Biol. 2:718–723. [DOI] [PubMed] [Google Scholar]
- 12.Leibler, S., and D. A. Huse. 1993. Porters versus rowers—a unified stochastic-model of motor proteins. J. Cell Biol. 121:1357–1368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Rice, S., A. W. Lin, D. Safer, C. L. Hart, N. Naber, B. O. Carragher, S. M. Cain, E. Pechatnikova, E. M. Wilson-Kubalek, M. Whittaker, E. Pate, R. Cooke, E. W. Taylor, R. A. Milligan, and R. D. Vale. 1999. A structural change in the kinesin motor protein that drives motility. Nature. 402:778–784. [DOI] [PubMed] [Google Scholar]
- 14.Neuman, K. C., and S. M. Block. 2004. Optical trapping. Rev. Sci. Instrum. 75:2787–2809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Vale, R. D., T. Funatsu, D. W. Pierce, L. Romberg, Y. Harada, and T. Yanagida. 1996. Direct observation of single kinesin molecules moving along microtubules. Nature. 380:451–453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ha, T., T. Enderle, D. F. Ogletree, D. S. Chemla, P. R. Selvin, and S. Weiss. 1996. Probing the interaction between two single molecules: fluorescence resonance energy transfer between a single donor and a single acceptor. Proc. Natl. Acad. Sci. USA. 93:6264–6268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sosa, H., E. J. G. Peterman, W. E. Moerner, and L. S. B. Goldstein. 2001. ADP-induced rocking of the kinesin motor domain revealed by single-molecule fluorescence polarization microscopy. Nat. Struct. Biol. 8:540–544. [DOI] [PubMed] [Google Scholar]
- 18.Funatsu, T., Y. Harada, M. Tokunaga, K. Saito, and T. Yanagida. 1995. Imaging of single fluorescent molecules and individual ATP turnovers by single myosin molecules in aqueous solution. Nature. 374:555–559. [DOI] [PubMed] [Google Scholar]
- 19.Peterman, E. J. G., H. Sosa, and W. E. Moerner. 2004. Single-molecule fluorescence spectroscopy and microscopy of biomolecular motors. Annu. Rev. Phys. Chem. 55:79–96. [DOI] [PubMed] [Google Scholar]
- 20.Peterman, E. J. G., H. Sosa, L. S. B. Goldstein, and W. E. Moerner. 2001. Polarized fluorescence microscopy of individual and many kinesin motors bound to axonemal microtubules. Biophys. J. 81:2851–2863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Case, R. B., D. W. Pierce, N. HomBooher, C. L. Hart, and R. D. Vale. 1997. The directional preference of kinesin motors is specified by an element outside of the motor catalytic domain. Cell. 90:959–966. [DOI] [PubMed] [Google Scholar]
- 22.Svoboda, K., and S. M. Block. 1994. Force and velocity measured for single kinesin molecules. Cell. 77:773–784. [DOI] [PubMed] [Google Scholar]
- 23.Haustein, E., and P. Schwille. 2003. Ultrasensitive investigations of biological systems by fluorescence correlation spectroscopy. Methods. 29:153–166. [DOI] [PubMed] [Google Scholar]
- 24.Waterman-Storer, C. M., A. Desai, J. C. Bulinski, and E. D. Salmon. 1998. Fluorescent speckle microscopy, a method to visualize the dynamics of protein assemblies in living cells. Curr. Biol. 8:1227–1230. [DOI] [PubMed] [Google Scholar]
- 25.Seitz, A., and T. Surrey. 2006. Processive movement of single kinesins on crowded microtubules visualized using quantum dots. EMBO J. 25:267–277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zander, C., J. Enderlein, and R. A. Keller. 2002. Single Molecule Detection in Solution. Wiley-VCH, Berlin.
- 27.Eggeling, C., J. Widengren, R. Rigler, and C. A. M. Seidel. 1998. Photobleaching of fluorescent dyes under conditions used for single-molecule detection: evidence of two-step photolysis. Anal. Chem. 70:2651–2659. [DOI] [PubMed] [Google Scholar]
- 28.Fleury, L., J. M. Segura, G. Zumofen, B. Hecht, and U. P. Wild. 2000. Nonclassical photon statistics in single-molecule fluorescence at room temperature. Phys. Rev. Lett. 84:1148–1151. [DOI] [PubMed] [Google Scholar]
- 29.Wahl, M., I. Gregor, M. Patting, and J. Enderlein. 2003. Fast calculation of fluorescence correlation data with asynchronous time-correlated single-photon counting. Opt. Express. 11:3583–3591. [DOI] [PubMed] [Google Scholar]
- 30.Widengren, J., U. Mets, and R. Rigler. 1995. Fluorescence correlation spectroscopy of triplet states in solution: a theoretical and experimental study. J. Phys. Chem. 99:13368–13379. [Google Scholar]
- 31.Magde, D., W. W. Webb, and E. Elson. 1972. Thermodynamic fluctuations in a reacting system—measurement by fluorescence correlation spectroscopy. Phys. Rev. Lett. 29:705. [Google Scholar]
- 32.Kohler, R. H., P. Schwille, W. W. Webb, and M. R. Hanson. 2000. Active protein transport through plastid tubules: velocity quantified by fluorescence correlation spectroscopy. J. Cell Sci. 113:3921–3930. [DOI] [PubMed] [Google Scholar]
- 33.Gosch, M., H. Blom, J. Holm, T. Heino, and R. Rigler. 2000. Hydrodynamic flow profiling in microchannel structures by single molecule fluorescence correlation spectroscopy. Anal. Chem. 72:3260–3265. [DOI] [PubMed] [Google Scholar]