Stiffness and Fraction of Myosin Motors Responsible for Active Force in Permeabilized Muscle Fibers from Rabbit Psoas

Abstract

The stiffness of the single myosin motor (ɛ) is determined in skinned fibers from rabbit psoas muscle by both mechanical and thermodynamic approaches. Changes in the elastic strain of the half-sarcomere (hs) are measured by fast mechanics both in rigor, when all myosin heads are attached, and during active contraction, with the isometric force (T₀) modulated by changing either [Ca²⁺] or temperature. The hs compliance is 43.0 ± 0.8 nm MPa⁻¹ in isometric contraction at saturating [Ca²⁺], whereas in rigor it is 28.2 ± 1.1 nm MPa⁻¹. The equivalent compliance of myofilaments is 21.0 ± 3.3 nm MPa⁻¹. Accordingly, the stiffness of the ensemble of myosin heads attached in the hs is 45.5 ± 1.7 kPa nm⁻¹ in isometric contraction at saturating [Ca²⁺] (e₀), and in rigor (e_r) it rises to 138.9 ± 21.2 kPa nm⁻¹. ɛ, calculated from e_r and the lattice molecular dimensions, is 1.21 ± 0.18 pN nm⁻¹. ɛ estimated, using a thermodynamic approach, from the relation of T₀ at saturating [Ca²⁺] versus the reciprocal of absolute temperature is 1.25 ± 0.14 pN nm⁻¹, similar to that estimated for fibers in rigor. Consequently, the ratio e₀/e_r (0.33 ± 0.05) can be used to estimate the fraction of attached heads during isometric contraction at saturating [Ca²⁺]. If the osmotic agent dextran T-500 (4 g/100 ml) is used to reduce the lateral filament spacing of the relaxed fiber to the value before skinning, both e₀ and e_r increase by ∼40%. ɛ becomes ∼1.7 pN nm⁻¹ and the fraction and the force of myosin heads attached in the isometric contraction remain the same as before dextran application. The finding that the fraction of myosin heads attached to actin in an isometric contraction is 0.33 rules out the hypothesis of multiple mechanical cycles per ATP hydrolyzed.

INTRODUCTION

Force and shortening in muscle are generated by cyclical ATP-driven interactions of the globular heads of myosin II, the molecular motor working in arrays in each half-sarcomere, with the actin filament. The fraction of myosin heads attached to actin during an isometric contraction (f) is a fundamental parameter for defining the mechanical properties of myosin II in situ and the kinetics of the myosin-actin interaction. Knowing f, it is possible to calculate, from the force developed in the isometric contraction (T₀), the force of the single myosin-actin interaction, a parameter required to define the efficiency of energy conversion by the myosin II motor. f corresponds to the “duty ratio” measured at the level of a single molecule, that is, to the fraction of the time of the ATPase cycle the myosin head spends attached to actin (1). A low duty ratio distinguishes muscle myosin II, a motor working in arrays, from motor proteins that work as single motors (kinesin, myosin V). In fact, because muscle myosin is organized in arrays in each half thick filament, detached heads are carried along as the thick filaments slide along the actin filaments due to the action of the attached heads. The sliding distance per ATP hydrolyzed by the average myosin head is several times larger than the sliding distance accounted for by a myosin head during its attached phase. The fraction of attached heads increases with the increase in the load that reduces the shortening velocity (2–4), so that at low velocity the force output is maximized by the sum of the forces exerted by the attached myosin heads working in parallel in the half-sarcomere.

The rate of regeneration of the mechanical working stroke in the myosin heads (5) is several times higher than the rate of ATP hydrolysis per myosin head (6). If f is large, the difference between the rate of the mechanical and the biochemical processes would suggest that there are several mechanical interactions for each ATP split (4). On the other hand, if f is ∼1/3 or less, the higher frequency of the mechanical process could be explained considering the repriming of the working stroke as a step in the whole ATPase cycle. In fact, with a sufficiently high fraction of detached heads, the repriming process could be due to the substitution of myosin motors that complete the working stroke with myosin heads entering the attached state (7,8). Thus, the value of f is fundamental in defining the kinetics and energetics of the chemomechanical coupling of muscle myosin II and the role of the ensemble of myosin heads in the half-sarcomere (hs).

The value of f reported for skeletal muscle varies widely depending on the methodological approach and the species used. The increased intensity ratio of the 1,1/1,0 x-ray equatorial reflections upon activation in frog muscle suggests that up to 90% of myosin heads stay in the vicinity of actin filaments (9–11). The intensity ratio during active contraction is as great as in rigor (a condition with all myosin heads attached to actin (12,13)). However, staying in the vicinity does not necessarily mean attachment to actin, and the intensity of actin layer lines during isometric contraction suggests that a much lower fraction of myosin heads (<0.3) are attached (14,15). In agreement with this, spectroscopic measurements in skinned fibers from rabbit psoas suggest that <20% of myosin heads are in the rigor configuration (16,17).

Fast length changes in single muscle fibers during an isometric contraction and in rigor produce estimates of f from the half-sarcomere stiffness. The myosin motors act in parallel in the half-sarcomere, and once the contribution of myofilament compliance is taken into account (18–20), the change in stiffness can be used to estimate the change in the number of myosin heads attached to actin. In single intact fibers from frog muscle, these studies yield values of f slightly higher than 0.4 (18). However, the myofilament compliance was likely underestimated by Linari and co-workers (18), especially in relation to the compliance of the myosin filament (21–23). To the best of our knowledge, a mechanical study with resolution at sarcomere level has not been performed in skinned fibers from mammalian muscle.

In this work, we reexamine the stiffness of the myosin heads in skinned fibers from rabbit psoas in rigor and during isometric contraction by two independent methods. We find that the stiffness is the same in both conditions, and we obtain an accurate estimate of the fraction of myosin motors attached to actin during an isometric contraction.

METHODS

Fiber preparation

The muscle fibers used in these experiments were obtained from the psoas muscles of six adult male rabbits (2.7–4.2 kg). Rabbits were killed by injection of an overdose of sodium pentobarbitone (150 mg kg⁻¹) in the marginal ear vein, in accordance with the official regulations of the European Community Council on use of laboratory animals (directive 86/609/EEC), and the study was approved by the Ethical Committee for Animal Experiments of the University of Florence. Small bundles (70–150 fibers) were stored in skinning solution (Table 1) containing 50% glycerol at −20°C for 3–4 weeks. For the experiments, a bundle of fibers was transferred to a petri dish with the bottom covered by Silgard (Dow Corning, London, UK) and kept at 4–6°C. Single fibers were dissected under a stereomicroscope (Stemi SV11, Zeiss, Oberkochen, Germany) with dark-field illumination and pinned down on the Silgard surface at both ends. Fibers were treated with relaxing solution (Table 1) containing Triton X-100 (1% v/v) for 1–2 min at ∼1°C to ensure complete removal of internal membranes. A segment 5–6 mm long was cut from the fiber and its extremities were loosely clamped by aluminum T-clips for attachment to transducer hooks.

TABLE 1.

Composition of solutions

(A) Solutions used during the experiments
	Na2ATP	MgCl2	EGTA	HDTA	CaEGTA	TES	Na2CP	GSH
Relaxing	5.44	7.70	25	—	—	100	19.11	10
Preactivating	5.45	6.93	0.1	24.9	—	100	19.49	10
Activating	5.49	6.76	—	—	25	100	19.49	10
Rigor	—	3.22	53	—	—	100	—	10
(B) Solutions used to prepare and store skinned fibers
	Na2ATP	MgCl2	EGTA	Imidazole	KP	NaN3	PMSF	Glycerol
Skinning solution	2.5	2.5	5	10	170	—	0.1	—
Storage solution	2.5	2.5	5	10	170	5	—	50%

All concentrations are in mM except glycerol (v/v). ATP, adenosine 5′-triphosphate; EGTA, ethylene glycol-bis-(β-aminoethyl ether)-N,N,N′,N′-tetraacetic acid; HDTA, 1,6 diaminohexane-N,N,N′,N′-tetraacetic acid; TES, N-tris[hydroxymethyl]methyl-2-aminoethanesulphonic acid; CP, N-[Imino(phosphonoamino) methyl]-N-methylglycine; GSH, glutathione; KP, potassium propionate; PMSF, phenylmethylsulphonyl fluoride. To all solutions were added 1 mg ml⁻¹ creatine phosphokinase, 10 μM transepoxysuccinyl-L-leucylamido-(4-guanidino)butane (E-64) and 20 μg ml⁻¹ leupeptin. pH (adjusted with KOH) was 7.1 at the different temperatures used (A) and 7.0 at 20°C (B). Ionic strength, 200 mM. HDTA was obtained from Fluka (Buchs, Switzerland), all other chemicals from Sigma (St. Louis, MO). In experiments with dextran, 4 g dextran T-500 (Pharmacia Biotech, Uppsala, Sweden) were added to 100 ml solution (4% w/v).

Experimental set-up

The fiber was mounted in a drop of relaxing solution between the lever arms of a loudspeaker motor, similar to that described by Lombardi and Piazzesi (24), and a capacitance force transducer with resonant frequency 40–50 kHz (25). A rapid solution exchange system driven by a stepper motor (speed ∼15 mm s⁻¹), similar to that already described (26, and references therein), allowed continuous recording of length changes of a selected population of sarcomeres (500–1200) by a striation follower (27). The solution exchange system consists of a movable platform carrying two aluminum plates that can be maintained at two different temperatures by means of two separated servocontrolled thermoelectric modules. Each plate carries two pedestals for the drops of solution confined between a bottom coverglass slit stuck to the pedestal and a top coverglass slit stuck to the revolving arm (18). The pedestals of the first plate (pedestals 1 and 2) were used to transfer the fiber between relaxing solution, preactivating solution, and activating solution at ∼1°C, and the pedestals of the second plate were used to transfer the fiber from activating solution at the test temperature (pedestal 3) to relaxing solution at the same temperature (pedestal 4). This system produces a rapid change of temperature when the activated fiber is transferred between pedestals 2 and 3, which are 4 mm apart. In this way, most of the force develops after the temperature jump, and the development of sarcomere nonuniformities relative to the diffusion-limited time of activation across the fiber is prevented (26).

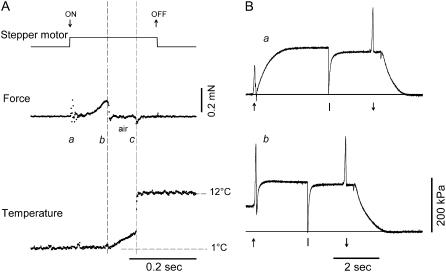
To estimate the speed of temperature change during the transition from pedestal 2 (∼1°C) to pedestal 3 (test temperature), a miniaturized unsheathed type K thermocouple (40.4 μV °C⁻¹, diameter 25 μm, Chal-001, Omega Engineering, Manchester, UK) was mounted in place of the fiber. The output signal was recorded via a monolithic thermocouple amplifier with cold junction compensation (AD595CQ, Analog Devices, Norwood, MA), to attain a sensitivity of 10 mV °C⁻¹ in the temperature range 0–50°C. As shown in Fig. 1 A, for a T-jump from 1 to 12°C, the temperature gradient in air is ∼2.2°C mm⁻¹ and 70% of the temperature jump occurs abruptly when the fiber enters the drop containing the test-temperature solution. The heat capacity of the thermocouple and of the layer of the surrounding water makes the temperature jump complete in 3–4 ms. With this set-up the time to get half-maximum force in the activating solution at the test temperature is one order of magnitude faster than transferring the fiber from preactivating solution to activating solution at the same temperature (Fig. 1 B).

FIGURE 1.

Temperature-jump protocol. (A) Temperature change (lower trace) measured by a miniaturized (diameter, 25 μm) fast thermocouple mounted in place of the fiber during the transition from the low-temperature (1°C) to the high-temperature drop (12°C). The upper trace indicates stepper motor start (↓) and stop (↑), and the middle trace is the force transducer signal. The artifacts in the force mark the start of the stepper motor motion for drop change (a) and the times when the probe leaves the first (b) and enters the second drop (c). The time of travel in air (∼90 ms) is marked by vertical dashed lines. The temperature gradient in air is ∼2.2°C mm⁻¹, 30% of the temperature difference between the two drops. The remaining 70% change in temperature occurs within 3–5 ms, at the interface of the high-temperature drop. (B) Force response to activation by Ca²⁺ at the test temperature (a) and at the low temperature followed by temperature jump (b). The arrow (↑) in a indicates the transition from preactivating to activating solution; in b, it indicates the transition from low- to high-temperature activating solution. A large release (∼8% of the initial fiber length, applied at the time marked in both panels by the vertical bar) was used to drop the force from the isometric tetanic force to zero. The arrow (↓) indicates the transition from activating solution to relaxing solution. The horizontal lines indicate zero force. Fiber length, 3.6 mm; average sarcomere length, 2.52 μm; CSA, 5740 μm².

Experimental protocol

Before starting the experiment, rigor was induced at ∼1°C and the fiber extremities (for ∼300 μm on either side) were then fixed with glutaraldehyde and glued to the clips with shellac dissolved in ethanol (18,28).

After gluing the fiber extremities to the clips, the fiber was transferred to relaxing solution and the sarcomere length (sl), width (w), and height (h) were measured at 0.5-mm intervals in the central segment of the fiber (2–4 mm) with a 40× dry objective (NA 0.60, Zeiss) and a 25× eyepiece. The sl was set to 2.50 ± 0.10 μm (mean ± SD, 17 fibers). The fiber cross-sectional area (CSA), determined assuming the cross-section to be elliptical, was π/4 × w × h = 4300 ± 810 μm².

The fiber was transferred from relaxing solution to preactivating solution at 1°C and, after 2 min, to activating solution at 1°C. Force rose to a steady value that was ∼0.4 of the isometric force developed at 12°C. The fiber was then transferred to the activating solution at the test temperature (12°C unless otherwise specified) for 2–3 s, and then to the relaxing solution at the same temperature.

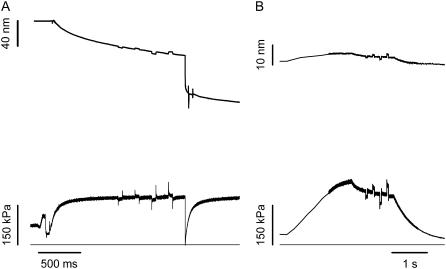
To measure half-sarcomere stiffness, small length changes (ranging from +3 to −3 nm hs⁻¹, stretch positive), completed in ∼110 μs, were imposed on the isometrically contracting fiber and in rigor (5,18,29). Half-sarcomere stiffness was estimated by the slope of the relation between the tension attained at the end of the step and the change in sarcomere length (T₁ relation (5)). To enhance the precision of stiffness measurements at the sarcomere level, a train of different-sized steps at 200-ms intervals was applied during each activation (Fig. 2 A). To maintain constant isometric tension before the test step, each test step was followed, after a 50-ms pause, by an equal but opposite step.

FIGURE 2.

Protocol for stiffness measurement during isometric contraction at saturating [Ca²⁺] (A) and at a similar tension in rigor (B). (Upper traces) Sarcomere length change in nm hs⁻¹. (Lower traces) Force. Horizontal lines are zero force. The same train of steps was imposed on the fiber in both activating and rigor solution. Force per CSA is expressed relative to the CSA in relaxing solution (4500 μm²). Fiber segment length, 2.3 mm; segment length under the striation follower, 0.87 mm. For active contraction, average segment sarcomere length, 2.60 μm; test temperature, 13.0°C. For rigor fiber, average segment sarcomere length, 2.50 μm; CSA, 4300 μm²; temperature, 13.0°C.

Stiffness measurements at different pCa

To modulate the number of interacting myosin heads and estimate, from the dependence of hs strain on isometric force, the contribution of myofilament compliance to the hs compliance (26,30–32), the isometric force and hs stiffness were measured in five fibers during isometric contraction at different pCa (range 6.0–4.5).

Stiffness measurements at different temperatures

To determine the dependence of hs strain on isometric force with a protocol that is not expected to change the number of myosin heads attached to actin and modulates the strain of all the elastic elements of the hs in relation to the isometric force (29,33), isometric force and hs stiffness were measured in seven maximally activated fibers (pCa 4.5) at different temperatures (range 4–20°C). The measurements were not extended below 4°C, because the water condensation on the coverglass slits precluded recording of sarcomere length changes.

Stiffness measurements in rigor

Rigor was induced, in four fibers by MgATP depletion (see Table 1) at low temperature (∼1°C). Stiffness in rigor was measured at different steady forces, similar to those developed by active fibers, obtained by slowly stretching the rigor fiber starting from the low level of force (∼0.1 the isometric force attained at saturating pCa) developed at the end of the rigorization procedure (Fig. 2 B). Stretch amplitude was adjusted to achieve the required force.

Stiffness measurements after fiber shrinkage by an osmotic agent

The hs stiffness decreases with fiber swelling after removal of the surface membrane (34–36). To investigate how this affects the stiffness of the attached myosin heads either in isometric contraction or in rigor, and how it affects the estimate of the fraction of heads attached in isometric contraction, the hs stiffness was measured in three fibers after addition of the osmotic agent dextran T-500. The dextran used, 4 g/100 ml, was capable of reducing the width of the relaxed fiber by ∼15%, to a value similar to that before skinning (18,34,35).

Data collection and analysis

Force, motor position, and sarcomere length signals were recorded with a multifunction I/O board (PCI-6110E, National Instruments, Austin, TX). A program written in LabVIEW (National Instruments) was used for signal recording and analysis. Data are expressed as mean ± SE, except in the case of CSA (mean ± SD). The experiments were made on a total of 43 fiber segments, but the planned protocol could be completed with preservation of sarcomere length signal on only 17 fibers, and the analysis and results reported here refer to these.

Solutions

The composition of the solutions are reported in Table 1. The concentrations of components were calculated with a computer program similar to that described by Brandt et al. (37). Cysteine and cysteine/serine protease inhibitors (trans-epoxysuccinil-L-leucylamido-(4-guanidino) butane, E-64, 10 μM; leupeptin, 20 μg ml⁻¹) were added to all solutions to preserve lattice proteins and, thus, sarcomere homogeneity.

Definitions

• β, fraction of myosin heads attached to actin in each half-sarcomere

• C_f, equivalent compliance of the myofilaments

• C_hs, compliance of the half-sarcomere

• C_hs,0, compliance of the half-sarcomere in isometric contraction at saturating [Ca²⁺]

• C_hs,r, compliance of the half-sarcomere in rigor

• e, stiffness of the myosin heads when all the heads are attached to actin

• e₀, stiffness of the myosin heads attached in isometric contraction

• e_r, stiffness of the myosin heads attached in rigor

• ɛ, stiffness of one attached myosin head

• f, fraction of myosin heads attached in an isometric contraction at saturating [Ca²⁺]

• k, stiffness of the half-sarcomere

• k₀, stiffness of the half-sarcomere in isometric contraction

• k_r, stiffness of the half-sarcomere in rigor

• s, average strain of the myosin heads in isometric contraction at saturating [Ca²⁺]

• T, steady force developed in rigor after a slow ramp of size L

• T₁, force attained at the end of a length step

• T₀, steady isometric force induced by Ca²⁺ activation

• T_0,s, steady isometric force at saturating [Ca²⁺]

• T_0,θ, steady isometric force at saturating [Ca²⁺] at temperature θ

• Y_0, strain in the half-sarcomere

RESULTS

Half-sarcomere strain in isometric contractions at different degrees of activation

The main structural components contributing to the half-sarcomere stiffness (k) during an isometric contraction are the myosin and actin filaments and the attached myosin heads (18,21–23,38,39). The summed compliances of these elements give the half-sarcomere compliance (C_hs, the reciprocal of k), and the individual contributions can be identified by determining how changes in the steady isometric force (T₀) induced by different activating [Ca²⁺] affect the half-sarcomere strain (Y₀ = C_hs × T₀) (26,30–32).

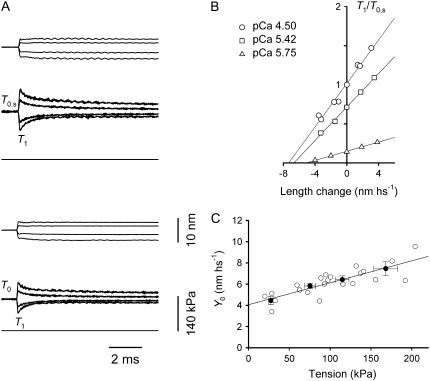
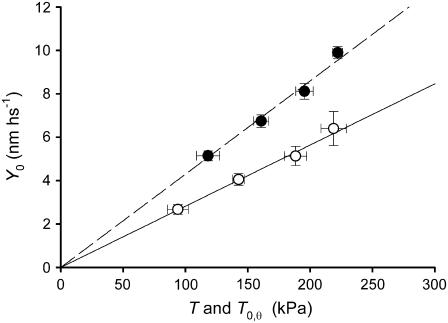
In the pCa range used in these experiments (6.0–4.5), T₀ varies from 27 ± 3 kPa to 168 ± 15 kPa at saturating pCa (T_0,s) (Table 2). Throughout the text, unless otherwise specified, force and half-sarcomere (hs) stiffness have been normalized for the CSA of the skinned fiber in relaxing solution. For each steady force, the hs stiffness (k₀) is estimated by the slope of the relation between the force attained at the end of the step and the size of the step (T₁ relation (5)) (Fig. 3, A and B). The linear fit to the T₁ points at any [Ca²⁺] (Fig. 3 B, solid lines) shows that k₀ decreases with the reduction of T₀, but the decrease is less than proportional. The abscissa intercept of the fitted line, Y₀, measures the strain in the hs elasticity during the isometric conditions preceding the step (5,38). Y₀ increases with T₀ (Table 2 and Fig. 3 C). The plot of the relation Y₀-T₀ for the five fibers fitted with a linear regression equation yields a slope of 21.0 ± 3.3 nm MPa⁻¹ and an ordinate intercept of 4.03 ± 0.38 nm. Both values are similar to those determined using the same method on fast skeletal fibers from human muscle (26).

TABLE 2.

Isometric force (T₀), strain of the half-sarcomere (Y₀), and strain of the attached myosin heads (s) measured in fibers activated at different pCa

pCa	T0 (kPa)	Y0 (nm hs−1)	s (nm hs−1)
5.68 ± 0.03	27 ± 3	4.45 ± 0.37	3.88 ± 0.39
5.53 ± 0.02	75 ± 7	5.82 ± 0.24	4.24 ± 0.19
5.36 ± 0.04	115 ± 9	6.43 ± 0.36	4.02 ± 0.30
4.50	168 ± 15	7.46 ± 0.64	3.93 ± 0.51

The data represent the mean ± SE from five fibres grouped in four classes of force. The temperature was 12.6 ± 0.3°C. SE in the pCa column is because the force classes are not necessarily taken from the same pCa.

FIGURE 3.

Equivalent myofilament compliance. (A) Superimposed length change per half-sarcomere (upper traces) and force response (lower traces) for steps of different size in a fiber activated at two pCas. (Upper) pCa 4.50; (lower) pCa 5.42. The horizontal line in each panel marks zero force. (B) T₁ relations for three pCas. The relations are obtained by plotting the extreme tension attained at the end of the length step, T₁ (relative to T₀ at pCa = 4.50, T_0,s), versus the step amplitude. Different symbols refer to different pCa values, as indicated in the inset. The lines are linear regressions fitted to the experimental points for each pCa. Fiber segment length, 3.88 mm; segment length under the striation follower, 1.08 mm; average sarcomere length, 2.58 μm; CSA, 4600 μm²; temperature, 12.1°C. (C) Relation of strain per half-sarcomere (Y₀) against the isometric force at different pCa. Solid circles are the mean values (± SE) from five fibers grouped in classes of forces (from Table 2). The solid line is the linear regression on the pooled data (open circles).

If the Ca²⁺ concentration modulates the isometric force by changing the number of attached myosin heads without a change in their strain (26), the slope of the Y₀-T₀ relation is an estimate of the equivalent compliance of the actin and myosin filaments (C_f), the elastic elements of the hs functionally in series with the myosin motors (18,20 (Appendix A)), whereas the ordinate intercept is an estimate of the average strain in the myosin heads. It must be noted that the slope of the Y₀-T₀ relation in Fig. 3 C is ∼1.5 times larger than that expected from mechanical and x-ray structural experiments in intact fibers from frog muscle (14–16 nm MPa⁻¹ (23,33,40)). However, for the correct comparison, the effect of swelling of the mammalian fibers after the permeabilization of the plasma membrane must be taken into account. Thus, C_f from skinned fibers must be divided by the ratio of the CSA attained after skinning to the CSA before skinning. This ratio in single fibers from frog muscle is ∼1.4 from the change in fiber width (18) and 1.3–1.6 from changes in lattice spacing measured by x-ray diffraction (34). Using a correction factor of 1.4, C_f from Fig. 3 C becomes 15.2 ± 2.4 nm MPa⁻¹, similar to the values in intact frog fibers.

Under the conditions above, the ordinate intercept is an estimate of the average strain in the attached myosin heads, s. s at any T₀ (and pCa) can be obtained by subtracting the filament strain (C_f × T₀) from the hs strain Y₀ (Table 2). In the range of T₀ and pCa investigated, s is similar (∼4 nm), indicating that the force per myosin head is the same, independent of the level of activating Ca²⁺.

Half-sarcomere strain in rigor

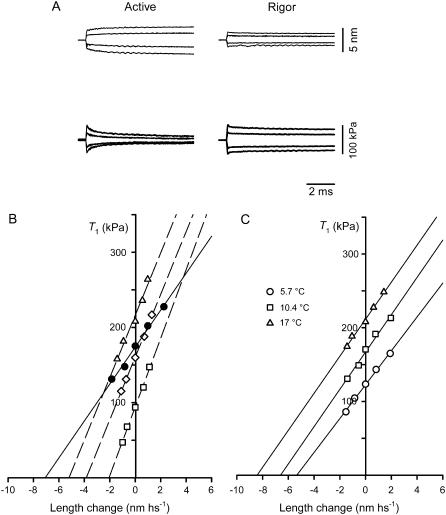
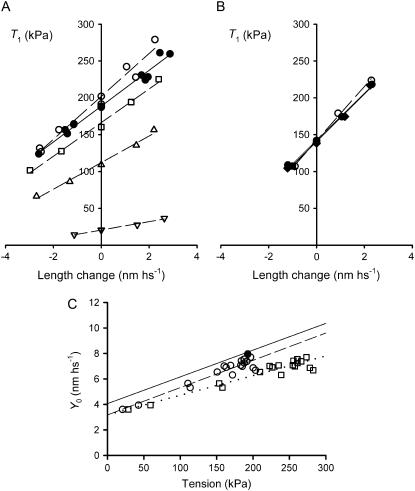
In four fibers, the half-sarcomere stiffness has been measured during the steady isometric force developed in activated fibers at saturating [Ca²⁺] (T_0,s, temperature 12°C) and in rigor at the same temperature (Fig. 4, A and B). In rigor, different levels of steady force T (range 0.5–1.2 T_0,s) were obtained by applying slow ramp stretches (ramp duration 2 s) of different amplitudes (L, 2–10 nm hs⁻¹) to the low-force rigor fiber. The tension responses to small length steps imposed on the same fiber during the isometric contraction and in rigor at a similar steady force are shown in Fig. 4 A. For comparison, considering that the number of myofilaments is the same independent of the reduced CSA in rigor (Table 3), force has been normalized to the CSA of the relaxed fiber. The change in force induced by the length step is larger in rigor than in the activated fiber, so that the hs stiffness (k), measured by the slope of the T₁ relation (Fig. 4 B), is larger (k_r, open diamonds) than in the activated fiber (k₀, solid circles). In the four fibers used, k₀ is 24.1 kPa nm⁻¹ and k_r is 35.3 kPa nm⁻¹ (+47%, Table 3). Correspondingly, Y₀ (equal to T₀/k) is reduced from 7.95 nm in the isometric contraction to 5.57 nm in rigor. As shown in Fig. 4 B (open symbols) and in Table 4, stiffness measurements in rigor at different levels of steady force T produced similar values of k_r. Consequently, in the whole range of rigor forces considered, Y₀ increases in proportion to T (Fig. 5, open circles). The linear regression equation fitted to pooled Y₀-T points, leaving the slope as the only parameter (solid line), gives a value of 28.2 ± 1.1 nm MPa⁻¹. Thus, as expected in rigor, all the elastic components of the half-sarcomere are strained in proportion to force, since no detachment/attachment of myosin heads occurs, and the slope of the relation represents the hs compliance (C_hs).

FIGURE 4.

Stiffness measurements in rigor at different steady forces and in active contraction at three temperatures. (A) Sample records of length changes per half-sarcomere (upper traces) and force responses (lower traces) in a fiber activated at saturating [Ca²⁺] (left column) and in rigor (right column) at a steady force, 0.91 T_0,s. Same fiber as in Fig. 2. (B) T₁ relations either during isometric contraction at saturating [Ca²⁺] (solid circles; T_0,s = 175 kPa) or in rigor (open symbols) at different steady forces (squares, 0.53 T_0,s; diamonds, 0.91 T_0,s; triangles, 1.19 T_0,s). The lines are linear regressions fitted to the experimental points. Isometric contraction, solid line; rigor, dashed lines. Same fiber as in Fig. 2. (C) T₁ relations during isometric contraction at three temperatures (symbol key in the inset). Solid lines are linear regressions fitted to the experimental points at each temperature. Fiber-segment length, 3.55 mm; segment length under the striation follower, 0.95 mm; average sarcomere length, 2.58 μm; CSA, 4450 μm².

TABLE 3.

Steady isometric force, hs stiffness (k), and hs strain (Y₀) during contraction at saturating [Ca²⁺] and in rigor

	Force (kPa)	k (kPa nm−1)	Y0 (nm hs−1)	CSA (μm2)
Active	190 ± 8	24.07 ± 1.72	7.95 ± 0.26	4630 ± 70
Rigor	193 ± 11	35.29 ± 2.04	5.57 ± 0.28	4190 ± 240

Steady force in rigor obtained after a slow ramp stretch of 7.4 ± 0.9 nm. The fourth column reports the CSA in the relaxed fiber (first row) and in rigor (second row). Force has been normalized to the CSA in the relaxed fiber. The values given are the mean ± SE from four fibers. In the case of CSA, the values are mean ± SD. Temperature, 12.8 ± 0.2°C.

TABLE 4.

hs stiffness (k_r), measured in rigor at different steady forces (T) attained after slow ramp stretches of different sizes (L)

L (nm hs−1)	T (kPa)	kr (kPa nm−1)
3.25 ± 0.46	94 ± 8	35.39 ± 2.52
5.38 ± 1.11	143 ± 5	35.74 ± 2.51
6.57 ± 1.38	188 ± 5	37.92 ± 5.11
9.35 ± 0.26	219 ± 10	34.95 ± 3.30

The force is normalized by the CSA of the relaxed fiber. Data represent the mean ± SE from four fibers. Temperature, 12.6 ± 0.3°C.

FIGURE 5.

Relation of half-sarcomere strain (Y₀) versus steady force either in maximally Ca²⁺ activated fibers at different temperatures (solid circles) or in rigor (open circles). Mean ± SE of data grouped in classes of force. The lines are the linear regressions forced through zero fitted to the pooled data.

After the procedure in Appendix A of Ford et al. (20) (see also Linari et al. (18)), the contribution of the myosin heads to hs elasticity can be calculated using the simplified equation (41)

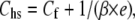(1)

where all terms are given in nm MPa⁻¹ and 1/(β × e) is the equivalent compliance of the array of myosin heads in each hs, with e the stiffness of cross-bridges when all heads are attached and β the fraction of attached heads. In rigor, β = 1 and C_hs= 28.2 ± 1.1 nm MPa⁻¹ (Fig. 5, solid line). With C_f = 21.0 nm MPa⁻¹ (from the slope in Fig. 3 C), 1/e (C_hs − C_f) is 7.2 ± 1.1 nm MPa⁻¹, that is, 0.26C_hs. The reciprocal of 1/e, which corresponds to the stiffness of myosin heads in rigor (e_r), is 138.9 ± 21.2 kPa nm⁻¹. The average stiffness per myosin head (ɛ) can be calculated by dividing e_r by (n × d), where d is the density of myosin filaments and n is the number of myosin heads per filament in a half-sarcomere. With d = 0.407 × 10¹⁵ myosin filaments m⁻² (from the distance between lattice planes formed by the myosin filaments in relaxed skinned fibers from rabbit psoas (see Discussion)), and n = 283, ɛ is 1.21 ± 0.18 pN nm⁻¹.

Half-sarcomere strain in isometric contractions at different temperatures

In intact fibers from frog muscle, it has been demonstrated that the increase in isometric force with temperature is due to an increase in average force per attached myosin head, without change in number (29,33). If this property is shared by Ca²⁺-activated skinned mammalian fibers, it will be possible to use the same temperature protocol to determine the strain of the myosin heads at different isometric force levels and apply thermodynamic considerations to estimate the stiffness of the myosin head during Ca²⁺-activated contraction.

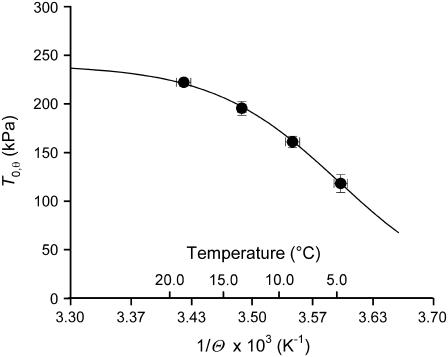
The temperature dependence of active isometric force (T_0,θ) and stiffness (e₀) at saturating [Ca²⁺] has been determined in seven fibers in the temperature range 4–20°C. T_0,θ monotonically increases with temperature and at the highest temperature attains a value 88% larger than that at the lowest temperature (Fig. 6 and Table 5).

FIGURE 6.

Relation of steady isometric force developed by maximally Ca²⁺-activated fibers versus the reciprocal of absolute temperature Θ. Circles are mean ± SE from Fig. 5. The line is the fit to the pooled data using the equation T_0,θ = T_0,max/(1 + exp(ΔH/(k_b·Θ) − ΔS/k_b)).

TABLE 5.

Temperature dependence of isometric force (T₀) and hs stiffness (k₀), and derived molecular parameters free-energy change (ΔG), strain (s), and force (F₀) per attached myosin head

Temperature (°C)	T0 (kPa)	k0 (kPa nm−1)	ΔG (zJ)	s (nm)	F0 (pN)
4.8 ± 0.6	118 ± 9	22.84 ± 1.09	0.08	2.67	3.34 ± 0.37
9.0 ± 0.6	161 ± 6	23.96 ± 0.68	−2.86	3.37	4.21 ± 0.47
13.5 ± 0.4	195 ± 7	24.11 ± 0.31	−6.07	4.01	5.02 ± 0.56
18.9 ± 0.7	222 ± 4	22.55 ± 0.89	−9.86	5.23	6.55 ± 0.73

Data represent the mean ± SE from seven fibers. The free-energy change is calculated as explained in the text.

T₁ relations obtained from tension responses to length steps imposed on the steady isometric force at different temperatures in one fiber are shown in Fig. 4 C. All the T₁ relations exhibit the same slope, indicating that the hs stiffness (k₀) is the same and that Y₀ increases in proportion with T_0,θ (Fig. 5, solid circles). In fact, in the seven fibers used, k₀ is 22.8 kPa nm⁻¹ at the lowest temperature and 22.6 kPa nm⁻¹ at the highest temperature (Table 5). The linear regression equation fitted to pooled Y₀-T_0,θ points leaving the slope as the only parameter (dashed line) gives a value of 43.0 ± 0.8 nm MPa⁻¹. In this case, as in rigor, all the elastic components of the half-sarcomere are strained in proportion to steady isometric force. The stiffness contributed by the attached myosin heads (and their number) remains constant at different temperatures and the slope of the Y₀-T_0,θ relation measures the hs compliance (C_hs).

According to Eq. 1, the contribution to C_hs of the array of myosin heads attached to actin during the isometric contraction (1/(β × e)) can be calculated by subtracting C_f (21.0 nm MPa⁻¹, the slope of the Y₀-T₀ relation in Fig. 3 C) from C_hs (43.0 ± 0.8 nm MPa⁻¹, the slope of the dashed line in Fig. 5). Thus, 1/(β × e) is 22.0 ± 0.8 nm MPa⁻¹ (0.51 C_hs) in the isometric contraction at saturating pCa and 12°C. The reciprocal of 1/(β × e), which represents the stiffness of the myosin heads attached to actin in the isometric contraction, e₀, is 45.5 ± 1.7 kPa nm⁻¹.

The analysis in the previous paragraph shows that in skinned fibers from rabbit psoas, as in the intact fibers from frog tibialis anterior muscle, increase in isometric force with temperature does not imply any increase in the number of attached myosin heads but can be fully explained as an entropically driven increase in the isometric force generated by the myosin motor (29,33). Under the above condition, as shown in Fig. 6, the plot of T_0,θ versus the reciprocal of absolute temperature (1/Θ) can be fitted with the equation (derived from the van't Hoff equation):

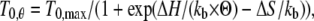(2)

where T_0,θ is the isometric force at temperature θ, T_0,max is the maximum isometric force, ΔH is the enthalpy change, k_b is the Boltzmann constant, ΔS is the entropy change, and ΔH − Θ × ΔS = ΔG. The result of the fit gives T_0,max = 240 ± 13 kPa, ΔH = 197.2 ± 40.4 zJ, and ΔS = 0.709 ± 0.146 zJ K⁻¹. The change in ΔG with temperature (Table 5) is an estimate of the mechanical energy accumulated in the elasticity at any isometric force T_0,θ (29,33), from which the stiffness of the attached myosin head ɛ can be calculated according to the equation

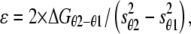(3)

where ΔG_θ2−θ1 is the change in free energy drop with the rise from temperature θ1 to temperature θ2 and s_θ1 and s_θ2 are the average strains per attached head at θ1 and θ2, respectively. s at any given temperature is obtained by subtracting the myofilament strain (C_f × T_0,θ) from the hs strain, Y₀ (Table 5). Assigning θ1 the lowest temperature used (4.8°C), the average value of ɛ, calculated using Eq. 3 for the three θ2 values 9.0, 13.5, and 18.9°C, is 1.25 ± 0.14 pN nm⁻¹. This value is in good agreement with that estimated for the stiffness of the myosin head attached in rigor (1.21 pN nm⁻¹).

From the analysis above, it can be concluded that the value of the parameter e in Eq. 1 is the same in isometric contraction as in rigor, and considering that in isometric contraction e₀ = β × e and in rigor β = 1, the ratio e₀/e_r gives an estimate of β. During isometric contraction β is f, the fraction of attached myosin heads, and f is 45.5/138.9 = 0.33 ± 0.05.

Osmotic compression and half-sarcomere strain

The fiber swelling after the permeabilization of the surface membrane is known to reduce the hs stiffness (36). Moreover, the swelling is partially reversed in rigor (Tables 3 and 6) (42,43). Therefore, it is important to evaluate how the lattice swelling caused by membrane permeabilization influences both the estimates of elasticity of the structural elements of the half-sarcomere and the conclusion about the fraction of myosin heads attached in the isometric contraction. In three fibers, the stiffness measurements during the isometric contraction were made both in the absence and in the presence of 4% dextran T-500. The concentration of the osmotic agent (42,43) was chosen to reduce the CSA of the relaxed fiber (Table 6) by ∼30%; this is enough to reverse the 1.4-fold increase after permeabilization of the plasma membrane (18,34,35).

TABLE 6.

Effect of 4% dextran T-500 on the mechanical parameters of the fiber during isometric contraction at saturating [Ca²⁺] and in rigor

(A) Isometric Contraction	CSA (μm2)	T0,s (kPa)	Y0 (nm hs−1)	k0,rel	e0,rel
Control	4070 ± 370	193 ± 4	7.94 ± 0.29	1	1
4% dextran	2920 ± 430 (0.72)	199 ± 1	7.01 ± 0.32	1.17 ± 0.02	1.41 ± 0.04
(B) Rigor	CSA (μm2)	T (kPa)	Y0 (nm hs−1)	kr,rel	er,rel
Control	3110 ± 450	167 ± 20	5.13 ± 0.41	1	1
4% dextran	2650 ± 450 (0.85)	168 ± 17	4.72 ± 0.44	1.09 ± 0.03	1.38 ± 0.14

(A) T_0,s, isometric force; Y₀, hs strain; k_0,rel and e_0,rel, hs stiffness and myosin head stiffness, respectively, normalized to their value in the absence of dextran. Force has been normalized to the CSA in relaxing solution in the absence of dextran. Values represent the mean ± SE from three fibers. (B) T, steady force attained after a slow stretch of 6.2 ± 1.2 nm; k_r,rel and e_r,rel, hs stiffness and myosin head stiffness, respectively, normalized to their value in the absence of dextran. Values represent the mean ± SE from three fibers other than those in (A); force has been normalized to the CSA in relaxing solution in the absence of dextran (3800 ± 390 μm²).

Fig. 7 A shows the T₁ relations determined in the same fiber during isometric contraction at saturating [Ca²⁺] in the absence of dextran (control conditions, solid circles) and during isometric contractions at different [Ca²⁺] in the presence of dextran (open symbols). The number of myofilaments in any given fiber is independent of the change in CSA; therefore, force is normalized to the CSA of the relaxed fiber in control conditions. As shown in Table 6, at saturating pCa the addition of dextran has almost no effect on the isometric force T_0,s (+3% in dextran) but increases the slope of the T₁ relation, and thus increases the hs stiffness, k₀, by 17%.

FIGURE 7.

Effect of 4% dextran T-500 on half-sarcomere stiffness in the active isometric contraction and in rigor. (A) T₁ relation in the isometric contraction at saturating Ca²⁺ (pCa, 4.50) either in the absence of dextran (solid circles) or in the presence of dextran (open symbols) at different pCa (circles, pCa 4.50; squares, pCa 6.00; triangles, pCa 6.25; inverted triangles, pCa 6.47). The lines are linear regressions fitted to the experimental points in the absence of dextran at pCa 4.50 (solid line) and in the presence of dextran at different pCa (dashed lines). Fiber segment length, 4.46 mm; segment length under the striation follower, 0.93 mm; average segment sarcomere length, 2.54 μm; CSA, 4540 μm² in control and 3580 μm² in the presence of dextran. Temperature, 11.7°C. (B) T₁ relations in rigor in 4% dextran (open circles) and in control (solid symbols) before (circles) and after (diamonds) dextran. The lines are linear regressions fitted to the experimental points in control (solid lines) and in the presence of dextran (dashed lines). Fiber segment length, 2.70 mm; segment length under the striation follower, 0.83 mm; average segment sarcomere length, 2.53 μm; CSA, 4020 μm² in relaxing solution in control, 3280 μm² in rigor solution in control, and 2800 μm² in rigor solution in the presence of dextran. Temperature, 11.8°C. (C) Relation of the half-sarcomere strain (Y₀) against the isometric force at different pCa in dextran with the isometric force normalized for the CSA in the control solution (circles) and in the presence of dextran (squares). The solid circle represents the mean value (± SE) in control at saturating Ca²⁺ (pCa 4.50). The solid line is the linear regression on the data in control solution from Fig. 3. Dashed and dotted lines are linear regressions on the circles and squares, respectively. Data are from three fibers. Temperature, 11.8 ± 0.1°C.

The effect of 4% dextran was tested also in rigor in three different fibers. As reported in Table 6, in rigor, at the same steady force, 4% dextran increases k_r by only 9%. Given the high structural and mechanical stability of the fiber in rigor, it was possible to determine the control T₁ relation before and after perfusion with dextran; Fig. 7 B demonstrates that the effect of dextran is reversible.

To separate the effects of osmotic shrinkage by dextran on the compliances of the myofilaments and of the myosin heads, the relation Y₀-T₀ of fibers activated at different pCa is plotted in Fig. 7 C (open circles). The slope (an estimate of C_f) and the ordinate intercept (an estimate of s) of the linear regression equation fitted to the Y₀-T₀ data (dashed line) are 21.5 ± 1.7 nm MPa⁻¹ and 3.17 ± 0.28 nm, respectively. As shown by comparing the dashed line with the solid line (from the fit in Fig. 3 C), the Y₀-T₀ relation in dextran is parallel to that in control but shifted downward, reducing the ordinate intercept by 0.88 nm. Thus lattice shrinkage by 4% dextran does not affect C_f but reduces s to 0.78 the control value.

When force is normalized to the CSA in dextran (Table 6), it increases by a factor of 1.39, shifting the T₀ coordinate of the Y₀-T₀ points to the right (Fig. 7 C, squares). The slope of the linear regression fit to the squares (dotted line) is reduced accordingly, so that the correct C_f is 15.4 ± 1.2 nm MPa⁻¹, a value in quite good agreement with both 1), the value calculated for the fibers activated in the absence of dextran when the lattice expansion induced by skinning in frog fibers is taken into account (18,34); and 2), the value found in intact fibers from frog muscle (23,33,40).

According to the analysis in Fig. 7 C, the increase in hs stiffness by osmotic shrinkage (Table 6) is completely accounted for by the increase in stiffness of the array of the attached myosin heads, as calculated from data in Table 6 by subtracting the filament compliance from the hs compliance. The results of this analysis show that the addition of 4% dextran increases e₀ by 41 ± 4% and e_r by 38 ± 14%. Thus, reducing filament lattice spacing of the relaxed fiber to that of the intact fiber increases the stiffness of the attached myosin heads by ∼40%, independent of their state, and, consequently, does not alter the fraction of heads attached in isometric contraction, estimated by the ratio e₀/e_r (0.33).

The changes in stiffness reported in Table 6 are normalized to the CSA of the relaxed fiber. Thus, the filament density d is, as in the control, 0.407 × 10¹⁵ myosin filaments m⁻². Consequently, the stiffness of a single myosin head, ɛ, calculated by dividing e_r by (n × d), is increased in 4% dextran by 40%, just like e_r. Taking ɛ in control to be 1.23 pN nm⁻¹ (the average of the values obtained in the isometric contraction and in rigor), ɛ in dextran becomes 1.72 pN nm⁻¹.

DISCUSSION

To define the elasticity of the two functionally distinct structural components of the half-sarcomere, the myofilaments, and the attached myosin heads, sarcomere-level mechanics is applied to skinned fibers from rabbit psoas in both isometric contraction and rigor. From this, we determine the stiffness of a single myosin head attached to actin and the fraction of heads attached during active isometric contraction.

The most significant findings are as follows:

• The equivalent compliance of actin and myosin filaments is 21.0 ± 3.3 nm MPa⁻¹.

• The half-sarcomere compliance (C_hs,0) is 43.0 nm MPa⁻¹ in isometric contraction of maximally Ca²⁺-activated fibers and is divided so that 50% is due to the attached myosin heads and 50% to the myofilaments.

• The half-sarcomere compliance (C_hs,r) is reduced to 28.2 nm MPa⁻¹ in rigor, with the contribution of attached myosin heads reduced to 26%.

• The stiffness of myosin heads attached to actin in each half-sarcomere is, accordingly, ∼46 kPa nm⁻¹ in isometric contraction at saturating Ca²⁺ (e₀) and rises to ∼140 kPa nm⁻¹ in rigor (e_r).

• The stiffness of a single myosin head attached to actin is ∼1.2 pN nm⁻¹, independent of the active or rigor condition.

• Addition of 4% dextran to the bathing solution reduces C_hs,0 and C_hs,r by 17% and 9%, respectively. These changes are due to a 40% increase in the stiffness of each attached myosin head (∼1.7 pN nm⁻¹). There are no effects of dextran on the compliance of the myofilaments.

• The fraction f of the myosin heads attached to actin during isometric contraction of maximally activated fibers is 0.33, and is not influenced by 4% dextran.

Separating the contributions of the myofilaments and myosin heads to half-sarcomere compliance

In a muscle fiber at full filament overlap the structural components of the half-sarcomere that are mechanically relevant in both active contraction and rigor are the myosin and actin filaments and the array of myosin heads attached to actin (18,20,38). The compliances of these components are distributed along the length of the half sarcomere. The analysis of Ford et al. (20 (Appendix A)) has provided a simplified equation (see also Eq. 4 in Linari et al. (18)) that describes the half-sarcomere compliance as the sum of the following three components: 1), the equivalent compliances of the actin filament (C_A); 2), the myosin filament (C_M); and 3), the attached myosin heads (1/(β × e)). For the purpose of this work, C_A and C_M can be added together as the equivalent myofilament compliance C_f; therefore, Eq. 1 relates the two relevant compliances.

C_f of this equation is extracted from the slope of the relation between half-sarcomere strain and T₀ at different [Ca²⁺] (Figs. 3 C and 7 B), where T₀ changes with the number of force-generating myosin heads, without change in strain per head (26,30–32). We find that, with force normalized to the CSA of the relaxed fiber, the slope of the Y₀-T₀ relation is 21.0 nm MPa⁻¹. However, C_f reduces to 15.4 nm MPa⁻¹ either by assuming that the skinning of psoas fibers increases the CSA by a factor of 1.4, as it does in frogs (18,34,35), or normalizing the force to the actual CSA measured in 4% dextran (adequate to reduce the CSA by a factor of 1.4 (Table 6)). C_f estimated in relation to the CSA in dextran, 15.4 nm MPa⁻¹, is therefore not affected by the osmotic agent per se, and is in good agreement with that from x-ray diffraction experiments on frog muscle (21–23). This indicates that the compliances of actin and myosin filaments are the same in the muscle of different vertebrate classes.

The strain in the attached myosin heads, s, represents the other component contributing to the strain of the half-sarcomere, Y₀. The average strain in the heads in the isometric contraction at 12°C is ∼4 nm and is independent of [Ca²⁺] (and T₀), demonstrating that [Ca²⁺] does not change the force but only the number of the attached myosin heads (Fig. 3 C and Table 2). At very low [Ca²⁺], the force in the half-sarcomere is correspondingly low and the main source of hs strain is s. As T₀ increases with [Ca²⁺] and the myofilament strain increases, the contribution of s to Y₀ is reduced, and at T_0,s, when Y₀ is ∼8 nm and the myofilament strain is ∼4 nm, s reduces to ∼50% of Y₀. In rigor, all myosin heads are attached; this reduces the hs compliance to 0.65–0.7 of that at T_0,s (Tables 3 and 4). Consequently, independent of the steady force level, the contribution of myosin heads to Y₀ is reduced to 26%.

The stiffness and force of myosin heads attached in the isometric contraction

All the myosin heads are attached to actin in rigor (12,13,19), producing a stiffness of 140 kPa nm⁻¹. This is reduced to 46 kPa nm⁻¹ during isometric contraction at saturating [Ca²⁺]. The ratio of the stiffness of the myosin heads in isometric contraction to those in rigor, e₀/e_r = 0.33, estimates the fraction of myosin heads attached during isometric contraction. This follows because the stiffness of a single attached myosin head, ɛ (∼1.2 pN nm⁻¹), is the same in the two states. In rigor, ɛ is calculated from the stiffness of the array of heads, e_r, and the lattice dimensions. In isometric contraction, ɛ is calculated from the temperature-dependent change in free energy that accounts for the change in mechanical energy stored in the myosin head (Eq. 3) (see also Decostre et al. (33)). A prerequisite for this analysis is the demonstration that the increase in isometric force with temperature does not result from an increase in the number of attached myosin heads (Fig. 5, solid circles), but is due to an entropically driven increase in the isometric force generated by the myosin motor. In terms of the Huxley and Simmons (5) model of force generation, force rises because the temperature increase shifts the equilibrium distribution of the attached myosin heads from a low to a high force-generating state (29,33,44,45).

Regarding the conclusion from this and previous works (29,33,46) that the temperature does not affect the number of myosin heads attached to actin, it must be noted that it contradicts the work by Kawai and collaborators (47 (and references therein)), reporting that a rise in temperature increases the number of strongly bound myosin heads without affecting the force per motor. The discrepancy with our results is likely to be due to both the absence of control at sarcomere level and the reduced time resolution of mechanical measurements: the number of attached heads is extrapolated from tension responses to length oscillations at frequencies up to a maximum of 100 Hz, more than one order of magnitude lower than the frequency characteristic of the length perturbations in our measurements. The evidence that the temperature does not affect the number of myosin heads attached to actin during an isometric contraction can be adjusted with the known temperature dependence of the actomyosin ATP-ase cycle if, in terms of a simplified scheme of the cross-bridge cycle (2), the apparent attachment and detachment rate constants have the same dependence on temperature. More specifically, the fraction of cross-bridge attached during an isometric contraction could be determined by steric and not by kinetic constraints.

The average isometric force developed by an attached myosin head (F₀), calculated in Table 5 at each experimental temperature as ɛ × s_θ, ranges from 3.3 pN at 4.8°C to 6.6 pN at 19°C. Comparing these values with those reported for frog fibers (Table 1 in Decostre et al. (33)), it is evident that, with allowance for the temperature difference, the isometric force developed by a myosin head is similar for the two different classes of vertebrates.

The finding that the stiffness, ɛ, of a single force-generating myosin head is the same as the average stiffness per head in rigor implies that the attachment of both heads of the same molecule in rigor exhibits a stiffness twice that of a single head attachment and confirms the x-ray evidence that the source of the elasticity of the myosin motor is in the head (the S1 portion), and not in the tail (the S2 portion), of the myosin molecule (19,48,49).

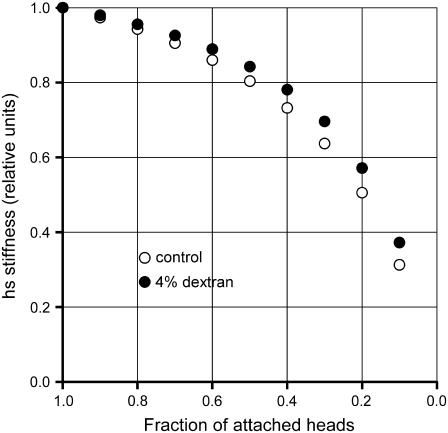
In previous work combining EPR spectroscopy and stiffness measurements in skinned psoas fibers, it was shown that up to 50% of rigor heads could be detached by the addition of ATP analogs, with only a small reduction in the fiber stiffness (50,51). This was used as evidence that only one of the pair of attached heads is stiff. However the effect of reduction in number of attached heads on stiffness is complicated by the contribution to the half-sarcomere compliance of myofilaments, an element of constant stiffness. As shown here, the contribution of myofilament compliance to half-sarcomere compliance in rigor is at least 75%, and this makes small the effect on stiffness of a reduction in the number of attached heads (Fig. 8, open circles). A larger compliance in series with attached heads (as in the study by Pate and Cooke (50), where, according to the Young modulus reported in their Fig. 7 legend, the hs stiffness in rigor is ∼25 kPa nm⁻¹, 30% lower than in our experiments, likely due to the contribution of compliance in series to sarcomeres), or a larger stiffness of the attached heads (our data in 4% dextran (Fig. 8, solid circles)) shifts the relation upward, making the stiffness even less sensitive to change in number of attached heads. Our findings that in rigor 1), the myofilaments contribute to at least 75% of the hs compliance; and 2), the two heads of the same myosin molecule have the same stiffness, are of crucial importance in the interpretation of the structural changes induced in the myosin heads by changes in length of the fiber: because most of the compliance is in the head itself, even if the two heads of the same myosin molecule are attached with different orientations, they will undergo the same axial motion after a length step (19,52,53).

FIGURE 8.

Relation between hs stiffness and fraction of attached heads. Stiffness is normalized to the value with all heads attached (rigor). Points are calculated with two different values for the contribution of myosin heads to the hs compliance in rigor: 24%, control (open circles); 18%, 4% dextran (solid circles).

Stiffness and force in relation to fiber width, density of filaments, and previous estimates

In a skinned psoas fiber in relaxing solution, the interfilament spacing, determined by x-ray diffraction as the distance between the lattice planes made of the myosin filaments (d_1,0), is 42 nm (42,43). Taking into account the filament hexagonal lattice and the above value for d_1,0, the density of myosin filaments (d) in the relaxed fiber is 0.407 × 10¹⁵ myosin filaments m⁻². d_1,0 decreases by 7% in rigor (43), which implies a reduction in CSA of 14%, comparable with the reduction reported in Table 3. Using the changes in fiber width after permeabilization of the membrane of the frog fiber (18,34,35), this work assumes that the CSA in the relaxed fiber is increased by a factor of 1.4 with respect to the original CSA of the intact fiber. Accordingly, the original d_1,0 in the intact psoas fiber would be 35 nm (16% smaller than in the relaxed fiber), in agreement with d_1,0 measured with x-ray diffraction in frog fibers at sarcomere length ∼2.4 μm (34).

Throughout this report, force has been normalized to the CSA of the skinned fiber in relaxing solution. To relate all the normalized mechanical parameters to the CSA of the intact fiber, force and stiffness must be increased and compliance reduced by a factor of 1.4 (see filament compliance conclusions in the first section of the Discussion). Thus, in Tables 3–5, the data in the T and k columns must be multiplied by 1.4. Consequently, the isometric force varies with temperature from 165 kPa at 5°C to 310 kPa at 19°C. Note that the data in the Y₀ and s columns are not affected by the choice of the normalization factor, as they are pure length signals. Note also that the stiffness (ɛ) and force (F₀) at the level of the single myosin head (Table 5) are not affected by CSA as long as the associated filament density d is correct. As an alternative to the thermodynamic approach reported in Table 5, F₀ can be calculated from purely mechanical data using the expression F₀ = T₀/(ndf), with f estimated by the ratio e₀/e_r. The values of F₀ obtained in this way at each temperature are very similar to those reported in Table 5, within the limits of the statistical error.

The expression above can be used to derive f for the intact fiber of the frog from published data (T₀ and F₀ from Table 1 of Decostre et al. (33)) and the filament lattice dimensions (6,34). f in that case is 0.22, which is 33% lower than that obtained in this work from the rabbit psoas fiber. A lower value of f in turn explains why, with a similar value of F₀, T₀ is lower in Rana esculenta (maximum 230 kPa at 17°C (33)) than in rabbit psoas (maximum 310 kPa at 19°C, see above).

Previous work based on stiffness measurements in fibers of Rana esculenta (18) reported a value of f about twice that calculated here. In that article, the myosin filament compliance assumed for calculating, from the change in hs stiffness, the change in number of attached myosin heads was 0.10%/T₀, derived from spacing changes of M3 x-ray reflection (49,54). However, recently it has been established that the signal more specifically related to the extension of the myosin filament is the spacing of the M6 x-ray reflection (23,40,55,56). Changes in spacing of M6 reflection indicate a compliance of the myosin filament 2.5 times larger than that assumed in Linari et al. (18). With this value, the difference in hs stiffness between isometric contraction and rigor reported by Linari et al. (18) gives f of 0.2, in agreement with the value estimated above from the force per myosin head (33).

The effects of changing the lattice spacing

The addition of 4% dextran to the bathing solution is intended to restore the lattice spacing to that of the intact fiber, as it reduces the CSA of the relaxed skinned fiber by 29% (Table 6). In fact, in the relaxed fiber, d_1,0 was decreased from 42 nm to 35–37 nm (42,43). In rigor, the reduction of CSA by 4% dextran is small (10%, Table 6) and statistically not significant, in agreement with the finding that d_1,0 is reduced by only ∼5% (from 39 nm to ∼37 (42,43)). The response to osmotic agents shown by the lattice spacing in the Ca²⁺-activated fiber is only slightly larger than in rigor; according to these authors, d_1,0 is reduced from 39 nm to ∼36 nm. These considerations suggest that the fiber width and the interfilamentary distance in our activated fibers are similar to those in rigor, in either the absence or presence of dextran.

The addition of dextran increases hs stiffness in both Ca²⁺-activated (17) and rigor fibers (9%) (Table 6). Both are explained by the 40% increase in stiffness of each myosin head attached to actin. This reduces the contribution of attached myosin heads to hs compliance from 50% to 43% in isometric contraction and from 26% to 20% in rigor. A change of 40% in the stiffness of the myosin head is much larger than that expected on the basis of the effect of change in the interfilamentary distance on the transmission of mechanical perturbation along the sarcomere. In fact, it can be calculated that the associated change in the angle of the S2 portion of the myosin molecule would change the force on the S1 portion by an amount two orders of magnitude smaller (57). However, the force per attached head is only slightly increased (3%) by dextran. Except in the work of Kawai and Schulman (58), reduction in lattice spacing in skinned fibers has been found to increase stiffness but not force (36,42). Our finding that the osmotic agent increases the myosin head stiffness similarly in rigor and in active contraction is in accord with the x-ray evidence that the lattice spacing is reduced by dextran similarly in either case. Thus, most of the data reported above support the view that the stiffness of the attached myosin head, but not the force, is quite sensitive to interfilamentary distance.

These conclusions, however, appear to contradict results from the effects of osmotic perturbations on active isometric force and stiffness in intact fibers (59–62). d_1,0 during isometric contraction of an intact fiber in the physiological solution with normal tonicity (1 R) is 34 nm. An increase in osmolarity of the solution to 1.4 R reduces d_1,0 in isometric contraction by 5% and the plateau tetanic force by 15–20%; a reduction in osmolarity to 0.8 R increases d_1,0 in isometric contraction by 6% and the plateau force by 9%. Over this same range of lattice-spacing changes, stiffness does not change significantly. The dependence of isometric force on the osmotic perturbation in intact fibers may be because in this preparation, but not in the skinned fiber, the change in volume involves change in the ionic strength of the internal milieu. When an intact fiber is placed in the hyperosmotic solution, there is an efflux of solvent and the ionic strength of the internal solution increases, which reduces the force of the myosin cross-bridges (63–65).

Two questions about the mechanics of skinned fibers remain: 1), why is stiffness so sensitive to changes in interfilament spacing? and 2), why is stiffness of myosin heads reduced, compared to the intact fiber, even at similar lattice spacing? Possible explanations, to be verified in future experiments, are that 1), the lattice-spacing-dependent reduction in stiffness in skinned fiber is a general property that in intact fibers is masked by the related change in ionic strength, which affects stiffness in the opposite direction (63); and 2), an intrinsic difference in stiffness of the myosin motor between mammalian and frog muscle contributes at least in part to the observed difference.

Consequences on the energetics and kinetics of the myosin-actin interaction

The finding that in the skinned fiber from psoas muscle the maximum isometric force exerted by the myosin head is ∼6.5 pN supports the conventional 1:1 coupling between mechanical and biochemical cycles of the myosin motor. Taking the sliding distance per myosin interaction at high load to be 6 nm (23), the mechanical work per interaction, 39 zJ, is ∼0.45 ΔG_ATP (the change in free energy of ATP hydrolysis) and thus is consistent with the known macroscopic efficiency of muscle at high load (66); this excludes the possibility of several mechanical cycles per ATP hydrolyzed.

In agreement with this conclusion, the finding that the fraction f of myosin heads attached to actin in isometric contraction of a maximally Ca²⁺-activated fiber is 0.33 supports the idea that the rate of repriming of the working stroke (measured by the rate of regeneration of the quick force recovery after a step release (6)) is higher than the ATPase rate per myosin head because the repriming is a step in the ATPase cycle, due to detachment of myosin heads at the end of the working stroke and attachment of new heads from the ∼0.7 fraction of detached heads.

The finding that the stiffness of the myosin motors (ɛ) in skinned rabbit psoas fibers, even in the presence of 4% dextran, is only 0.55 that of intact frog fibers (3.1 pN nm⁻¹ (33)), whereas the isometric force is the same, implies that the mechanical energy stored in the motor in the isometric contraction (½ɛ × s²) in rabbit muscle is 1.8 that in frog muscle. Therefore it will be important, especially for the energetic and comparative aspects, to establish whether the reduced stiffness of the myosin motor in mammalian muscle compared with frog muscle is due to skinning or, at least in part, to intrinsic differences in the myosin motors from different classes of vertebrates.