Abstract
The “primary hydration shell” method in molecular dynamics simulations uses a two- to three-layer thick shell of explicitly represented water molecules as the solvent around the protein of interest. We show that despite its simplicity, this computationally cheap model is capable of predicting acceptable water and protein behavior using the CHARMM22/CMAP potential function. For protein dynamics, comparisons are made with Lipari-Szabo order parameters. These have been derived from NMR relaxation parameters for pico-nano second motions of the NH groups in the main-chain and NH2 groups in Asn/Gln side chains in hen lysozyme. It is also shown that an even simpler, and therefore faster, water-shell model leads to results in similarly good agreement with experiments, and also compared with simulations using a full box of water with periodic boundary conditions or with an implicit solvation model. Thus, the primary hydration shell method should be useful in making larger systems accessible to extensive simulations.
Water plays a crucial role for the stability, dynamics, and function of proteins (1,2). For this reason molecular dynamics (MD) simulations must account for the effects that this solvent has, both on protein structure and on protein dynamics. Using a box full of explicitly represented water molecules with periodic boundary conditions (PBC) is the most common way to achieve this goal. However, even in favorable cases the majority of the calculations in such simulations involve water molecules alone. This high computational cost has resulted in several alternative approaches to account for water and water-protein interactions. They can be broadly classified into three categories. In one class, water molecules are entirely replaced by an implicit solvent model (e.g., Lazaridis and Karplus (3) and Im et al. (4)). The second category comprises methods that use only a thin shell of explicit waters around the protein (5–7). A hybrid explicit/implicit method (a thin shell of explicit waters surrounded by an implicit solvent representation) is used in the third class of models (8,9).
The “primary hydration shell” (PHS) method, developed by Beglov and Roux (5) and implemented in CHARMM, is a good representative of the second category of solvation approaches. In this method, the protein is solvated by a two- to three-layer thick shell of explicit waters, and a half-harmonic constraint is applied to the water molecules if their distance from the nearest protein atom is larger than a certain value (see Supplementary Material for details). Importantly, the force is applied toward the closest protein atom, which results in a water-shell that has the same shape as the protein and can adapt to protein conformational changes. Although the PHS method has been used, for example, for simulated annealing of a tripeptide conformation (10), reports of its application have been few. An explanation for this lack of popularity is that thin water shell models have been thought to lead to unrealistic water and protein behavior. Here we show that the PHS approach leads to acceptable water and especially protein behavior, and thus deserves more attention.
In this study we compare the PHS approach (5) with a simulation using the classical method of solvating the protein in a box full of explicitly represented waters under periodic boundary conditions (PBC). Comparisons are also made with results from an implicit solvent approach, using a recently developed generalized Born method with a simple smoothing function (GBSW) (4). Finally, we present an approach involving a simple harmonic constraint by use of the GEO facility in CHARMM. This approach is similar to the primary hydration shell method but saves on computer time as distances and forces are not calculated with respect to the nearest protein atom but relative to three perpendicular principal axes that follow the protein frame. Such a treatment of forces also allows waters to follow possible changes in protein shape (see Supplementary Material).
The simulations were carried out on hen lysozyme (Protein Data Bank identifier 6LYT), an ellipsoid-shaped protein that has been subject to extensive experimental (11) and computational (12) studies. The simulation details are described in the Supplementary Material and are briefly summarized as follows: For all simulations involving explicit waters, lysozyme was first immersed in a cubic box of water with a side length of 61.5 Å. In the reference simulation PBCs were used together with the particle-mesh Ewald method. Eight chloride atoms neutralized the system's net charge. All solvent molecules with distances from protein atoms <2.8 Å were deleted, eliminating solvent-protein overlap and resulting in 5749 waters. In the case of the PHS approach and its variant employing a simpler harmonic restraint (GEO, described in Supplementary Material), water molecules further than 5.8 Å from the nearest protein atom were also deleted, leaving 750 waters in a shell of approximately two- to three-layer thickness around the protein. The implicit hydration (GBSW) simulation is described in the Supplementary Material. In the production stage 25 ns or 50 ns trajectories were calculated. The CHARMM22/CMAP potential was used throughout.
Standard analyses of water dynamics and distributions were used to compare the PHS and GEO methods with the fully solvated protein simulation (PBC). Water motions are rapid, and so each trajectory frame was saved over a period of 100 ps (2-fs intervals) after 25 ns of simulation. Using the distance to the nearest protein surface atom, dnear, waters were classified as either belonging to the first shell (dnear < 4 Å), a second shell (4 Å < dnear < 7 Å) or beyond reach. To capture the essence of water behavior in a certain shell, only water molecules were considered that had continuous residency in that particular shell (for 20 ps in the first shell and 5 ps in the second). Diffusion coefficients derived from mean-square displacements are given in Table 1. They are similar for the three simulations involving water, although the first-shell solvent molecules diffuse slightly faster in the PBC simulation. First-shell molecules have a smaller diffusion coefficient than those in the second shell, in agreement with previous studies (13,14).
TABLE 1.
The diffusion coefficients of water oxygen atoms in 10−5cm2/A
| PBC | PHS | GEO | |
|---|---|---|---|
| First shell | 0.54 | 0.45 | 0.38 |
| Second shell | 3.32 | 3.54 | 2.89 |
The slower dynamics in the first shell is also obvious from Table 2, listing values from fitting the 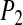 rotational correlation function and the quantity
rotational correlation function and the quantity 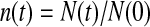 , the fraction of water molecules that still remain in a given shell after time
, the fraction of water molecules that still remain in a given shell after time 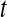 . The fitting function was
. The fitting function was 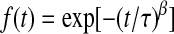 , except in the case of
, except in the case of 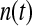 for the first shell, which was fitted to
for the first shell, which was fitted to 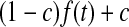 . Here
. Here 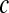 accounts for the fraction of waters that stay in the first shell for a long time, presumably because they are either in the protein interior or bound to the surface. The number of these molecules was found to be 58 (
accounts for the fraction of waters that stay in the first shell for a long time, presumably because they are either in the protein interior or bound to the surface. The number of these molecules was found to be 58 (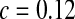 ), 71 (
), 71 (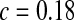 ), and 55 (
), and 55 (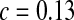 ) for PBC, PHS, and GEO, respectively. No fitting is reported here for the
) for PBC, PHS, and GEO, respectively. No fitting is reported here for the  correlation function as the decay timescale was longer than the analysis time intervals (20 and 5 ps). The decay functions (shown in the Supplementary Material), however, also suggest an acceptable agreement between the different models. Interestingly, ignoring the bound waters, exchange between the shells (mostly perpendicular to the protein surface) appears to be quite fast. This finding is, nevertheless, consistent with the diffusion and rotational correlation time as these are measured for waters that remain resident in a certain shell, preferentially sampling movement in parallel to the protein surface. In summary, we find that the solvent dynamics are overall very similar in the PHS and GEO calculations and close to those of the PBC simulation.
correlation function as the decay timescale was longer than the analysis time intervals (20 and 5 ps). The decay functions (shown in the Supplementary Material), however, also suggest an acceptable agreement between the different models. Interestingly, ignoring the bound waters, exchange between the shells (mostly perpendicular to the protein surface) appears to be quite fast. This finding is, nevertheless, consistent with the diffusion and rotational correlation time as these are measured for waters that remain resident in a certain shell, preferentially sampling movement in parallel to the protein surface. In summary, we find that the solvent dynamics are overall very similar in the PHS and GEO calculations and close to those of the PBC simulation.
TABLE 2.
Fit values for dynamics in the first and second shell
| Method | Function |
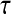 (ps)* (ps)*
|
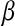 * *
|
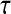 (ps)† (ps)†
|
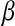 † †
|
|---|---|---|---|---|---|
| PBC | P2 | 3.0 | 0.31 | 0.5 | 0.57 |
| PHS | P2 | 4.7 | 0.25 | 0.7 | 0.50 |
| GEO | P2 | 3.3 | 0.25 | 0.6 | 0.50 |
| PBC | n | 3.3 | 0.67 | 1.5 | 0.77 |
| PHS | n | 3.9 | 0.72 | 1.5 | 0.80 |
| GEO | n | 3.8 | 0.69 | 1.5 | 0.76 |
First shell.
Second shell.
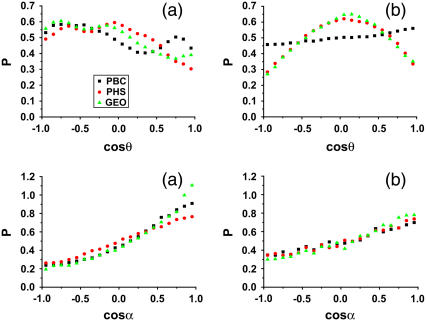
Distribution functions are a popular measure of solvent structure. It is known that the orientation of the water molecules close to a protein is not isotropic (13). In Fig. 1 we show the normalized distribution of two angles (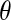 and
and 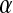 );
); 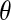 is the angle between the dipole moment of a water molecule and the vector connecting its oxygen to the center of geometry of the protein, indicating the orientation of waters with respect to the protein.
is the angle between the dipole moment of a water molecule and the vector connecting its oxygen to the center of geometry of the protein, indicating the orientation of waters with respect to the protein.
FIGURE 1.
Normalized distributions of the water-protein, 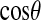 , and water-water orientation,
, and water-water orientation, 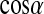 , for (a) first and (b) second shells.
, for (a) first and (b) second shells.
The distribution of water-protein angles, 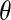 , shows small differences between the PBC and PHS/GEO simulations in the first shell. Second-shell waters show a slight orientational preference in the PBC simulation, favoring the oxygen to be closer to the protein (lysozyme has a net positive charge). A parallel or antiparallel dipole orientation, however, is not preferred for a noticeable fraction (∼10%) of second-shell waters in the PHS and GEO simulation. This behavior could arise from anisotropic hydrogen bonding that may exist at the solvent-vacuum boundary. Hybrid implicit/explicit solvation models have been developed to deal with this artifact (e.g., Lounnas et al. (8)). We describe the orientation of a water molecule relative to others within 5 Å by
, shows small differences between the PBC and PHS/GEO simulations in the first shell. Second-shell waters show a slight orientational preference in the PBC simulation, favoring the oxygen to be closer to the protein (lysozyme has a net positive charge). A parallel or antiparallel dipole orientation, however, is not preferred for a noticeable fraction (∼10%) of second-shell waters in the PHS and GEO simulation. This behavior could arise from anisotropic hydrogen bonding that may exist at the solvent-vacuum boundary. Hybrid implicit/explicit solvation models have been developed to deal with this artifact (e.g., Lounnas et al. (8)). We describe the orientation of a water molecule relative to others within 5 Å by 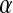 , which is the angle between its dipole moment and those of neighboring waters belonging to the same shell. The distribution of
, which is the angle between its dipole moment and those of neighboring waters belonging to the same shell. The distribution of 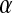 is similar in all cases and, as expected, is less anisotropic in the second shell as the influence of the protein surface decreases. Importantly, the orientation of waters toward each other does not appear to be affected by the solvent-vacuum boundary. Considering this and our analysis below, computationally costly approaches that randomize the dipole orientation of boundary waters may not be required.
is similar in all cases and, as expected, is less anisotropic in the second shell as the influence of the protein surface decreases. Importantly, the orientation of waters toward each other does not appear to be affected by the solvent-vacuum boundary. Considering this and our analysis below, computationally costly approaches that randomize the dipole orientation of boundary waters may not be required.
For comparison of the structural and dynamic behavior of the protein several parameters were calculated over the last 10 ns of the 25-ns trajectories. The main-chain root mean-square (RMS) deviations from the lysozyme crystal structure had equilibrated by then at 0.8, 1.4, 1.2, and 2.4 Å for the PBC, PHS, GEO, and GBSW methods, respectively. Although the RMS deviations in the PHS and GEO calculations are somewhat greater than in the PBC simulation, longer (50-ns) simulations showed that these systems were stable. RMS fluctuations of Cα atoms in the shell and in the implicit simulation were compared to those in the PBC calculation. The resulting correlation coefficients (0.75, 0.80, and 0.71 for the PHS, GEO, and GBSW, respectively) showed a comparatively high agreement of main-chain dynamics.
Comparison with experimental data (11) is made in Table 3, listing correlation coefficients (R) and RMS differences (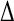 ) of the simulation-derived main-chain N-H and Asn/Gln side-chain NH2 Lipari-Szabo order parameters, S2 (data shown in Supplementary Material), with the corresponding experimental values.
) of the simulation-derived main-chain N-H and Asn/Gln side-chain NH2 Lipari-Szabo order parameters, S2 (data shown in Supplementary Material), with the corresponding experimental values.
TABLE 3.
The correlation coefficients (R), and the RMS differences (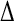 ) between the simulation-derived and experimental order parameters
) between the simulation-derived and experimental order parameters
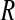 (main) (main) |
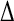 (main) (main) |
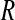 (side) (side) |
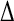 (side) (side) |
|
|---|---|---|---|---|
| PBC | 0.67 | 0.060 | 0.74 | 0.155 |
| PHS | 0.62 | 0.061 | 0.75 | 0.160 |
| GEO | 0.53 | 0.074 | 0.72 | 0.157 |
| GBSW | 0.50 | 0.089 | 0.58 | 0.185 |
Although the main-chain correlation coefficients for the PBC and PHS are similar, the GBSW and GEO results are less correlated with the experimental data. The GEO method, however, shows a good agreement with the experiment for Asn/Gln side-chain dynamics. As noted before, the comparison between simulation and experimentally derived order parameters are not yet perfect (12). Remarkably the three methods that involve explicit waters give very similar results for the amplitude (S2) and also timescale (τe not shown) of the protein motions. This validates the inclusion of explicit solvent in simulations, but also suggests that principal solvation shell models reproduce the behavior seen in a fully solvated system.
In summary the data suggest that by comparison with full solvation under PBC, simple water shell models (PHS and GEO) result in acceptable water and protein behavior at a much lower computational cost. Using eight 3.2 GHz Pentium 4 Xenon processors in parallel, 1.0 ns of simulation took 36.5, 4.5, 3.4, and 11.3 h for the PBC, PHS, GEO, and GBSW simulations, respectively. Water and protein behavior is almost identical between the water-shell and PBC approaches, whereas, as expected, there is a slight orientational preference of waters at the outer shell boundary. Overall, the results are encouraging for the further exploration of primary hydration-shell approaches in simulations of large proteins, protein docking, and protein-membrane systems.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Acknowledgments
We thank Mr. David Slochower for help with the early phases of the project.
The calculations were carried out on the High Performance Computing Cluster at Case Western Reserve University, supported with an award from the Provost's office, and at the Ohio Supercomputing Center.
Note added in proof: The PHS and GEO simulations were extended to a longer period of 150 ns, giving results closely similar to those reported.
References
- 1.Mattos, C. 2002. Protein-water interactions in a dynamic world. Trends Biochem. Sci. 27:203–208. [DOI] [PubMed] [Google Scholar]
- 2.Vitkup, D., D. Ringe, G. A. Petsko, and M. Karplus. 2000. Solvent mobility and the protein ‘glass’ transition. Nat. Struct. Biol. 7:34–38. [DOI] [PubMed] [Google Scholar]
- 3.Lazaridis, T., and M. Karplus. 1999. Effective energy function for proteins. Proteins. 35:133–152. [DOI] [PubMed] [Google Scholar]
- 4.Im, W., M. S. Lee, and C. L. Brooks. 2003. Generalized Born model with a simple smoothing function. J. Comput. Chem. 24:1691–1702. [DOI] [PubMed] [Google Scholar]
- 5.Beglov, D., and B. Roux. 1994. Dominant solvation effects from primary shell of hydration: approximation for molecular dynamics simulations. Biopolymers. 35:171–178. [Google Scholar]
- 6.Sankararamakrishnan, R., K. Konvicka, E. L. Mehler, and H. Weinstein. 2000. Solvation in simulated annealing and high-temperature molecular dynamics of proteins: a restrained water droplet model. Int. J. Quantum Chem. 77:174–186. [Google Scholar]
- 7.Steinbach, P. J., and B. R. Brooks. 1996. Hydrated myoglobin's anharmonic fluctuations are not primarily due to dihedral transitions. Proc. Natl. Acad. Sci. USA. 93:55–59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lounnas, V., S. K. Ludemann, and R. C. Wade. 1999. Towards molecular dynamics simulation of large proteins with a hydration shell at constant pressure. Biophys. Chem. 78:157–182. [DOI] [PubMed] [Google Scholar]
- 9.Lee, M. S., and M. A. Olson. 2005. Evaluation of Poisson solvation models using a hybrid explicit/implicit solvent method. J. Phys. Chem. B. 109:5223–5236. [DOI] [PubMed] [Google Scholar]
- 10.Rosenhouse-Dantsker, A., and R. Osman. 2000. Application of the primary hydration shell approach to locally enhanced sampling simulated annealing: computer simulation of thyrotropin-releasing hormone in water. Biophys. J. 79:66–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Buck, M., J. Boyd, C. Redfield, D. A. MacKenzie, D. J. Jeenes, D. B. Archer, and C. M. Dobson. 1995. Structural determinants of protein dynamics: analysis of 15N NMR relaxation measurements of main-chain and side-chain nuclei of hen egg white lysozyme. Biochemistry. 34:4041–4055. [DOI] [PubMed] [Google Scholar]
- 12.Buck, M., S. Bouguet-Bonnet, R. W. Pastor, and A. D. MacKerell Jr. 2006. Importance of the CMAP correction to the CHARMM22 protein force field: dynamics of hen lysozyme. Biophys. J. 90:L36–L38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bizzarri, A. R., and S. Cannistraro. 2002. Molecular dynamics of water at the protein-solvent interface. J. Phys. Chem. B. 106:6617–6633. [Google Scholar]
- 14.Schroder, C., T. Rudas, S. Boresch, and O. Steinhauser. 2006. Simulation studies of the protein-water interface. I. Properties at the molecular resolution. J. Chem. Phys. 124:234907:1–18. [DOI] [PubMed] [Google Scholar]