Attachment Conditions Control Actin Filament Buckling and the Production of Forces

Abstract

Actin polymerization is the driving force for a large number of cellular processes. Formation of lamellipodia and filopodia at the leading edge of motile cells requires actin polymerization induced mechanical deformation of the plasma membrane. To generate different types of membrane protrusions, the mechanical properties of actin filaments can be constrained by interacting proteins. A striking example of such constraint is the buckling of actin filaments generated in vitro by the cooperative effect of a processive actin nucleating factor (formin) and a molecular motor (myosin II). We developed a physical model based on equations for an elastic rod that accounts for actin filament buckling. Both ends of the rod were maintained in a fixed position in space and we considered three sets of boundary conditions. The model qualitatively and quantitatively reproduces the shape distribution of actin filaments. We found that actin polymerization counterpoises a force in the range 0.4–1.6 pN for moderate end-to-end distance (∼1 μm) and could be as large as 10 pN for shorter distances. If the actin rod attachment includes a spring, we discovered that the stiffness must be in the range 0.1–1.2 pN/nm to account for the observed buckling.

INTRODUCTION

Actin filament nucleation and elongation, which promotes lamellipodia formation, propulsion of pathogens or endosomes, and other processes controlling cell plasticity (for a general review, see Pollard and Borisy (1)), is controlled by a variety of accessory protein with diverse properties. The Arp2/3 complex is the best understood actin filament nucleation factor (1). However, a second nucleation factor has been a recent focus of intense study. Formin participates in the formation of a growing list of actin-based higher ordered structures (2), including actin cables in yeast (3), the cytokinetic ring (4), focal adhesions (5–7), cell migration and ruffling (8,9), endosome motility (10), and filopodia (11,12). Direct in vivo observations (10) and in vitro experiments (13–16) have shown that formins are processive nucleators, which remain continuously attached to the fast growing actin filament barbed end while directing insertion of actin monomers at that end (17).

Macromolecular assembly has the capacity to convert chemical energy into forces that can move intracellular endosomes, cell membrane, or experimental objects, like polystyrene beads. However, the molecular mechanisms underlying force generation is still under debate: for instance, Listeria propulsion, a well-documented experimental model for cell motility (2), is not totally understood, although different models have been proposed (17–21).

To elucidate the conversion of chemical energy into mechanical work, the use of total internal reflection fluorescence (TIRF) microscopy has been a valuable tool to study the properties of individual actin filament under ligand constraint (13). Indeed, this technique was utilized to evaluate the force induced by a single actin filament (13). In these experiments, the region near the pointed end of an actin filament is tethered to a rigid surface through side binding to an inactive myosin molecule whereas the barbed end is capped by a formin grafted to the surface. Actin polymerization continues at the formin-associated barbed end while the end-to-end distance of the filament is constrained in space. Therefore, the filament buckles and its configuration depends on the balance of the processive forces developed by actin polymerization and the spatial constraints imposed on the two ends.

We report the analysis of two-dimensional buckling by a mechanical model accounting satisfactorily for the spatial configurations of actin filaments and for the force/filament-length relationship. We propose a direct semiquantitative measure of the forces developed by a growing filament against its ends. We also show that the actin monomer concentration required to begin buckling is ∼1–10 μM for actin filament lengths above 0.5 μm. Shorter actin filaments (end-to-end distance between 0.2 and 0.5 μm) necessitate actin monomers concentration up to 10 μM to buckle. Finally, we predict that the stiffness of the bonds between the surface and actin filament should be in a 0.2–1.2 pN nm⁻¹ range, which is consistent with the experimental values obtained for the cross-bridge stiffness in acto-myosin cables. We also show that below a critical end-to-end length, actin filaments cannot buckle in realistic conditions regardless of the amount of free actin monomers or bond robustness.

MATERIALS AND METHODS

Total internal reflection fluorescence microscopy

Rhodamine actine polymerization was observed on an Olympus IX-71 inverted microscope equipped with a 60×, 1.45 NA Planapo objective (Olympus, Melville, NY), and modified as described (22) for TIRF illumination. The laser used for these experiments was an Omicron Laserage LAFE 1007 (Latronics, Aachen, Germany) emitting a 532-nm wavelength, and limited to 10 mW. The time course of actin polymerization was acquired with a Hamamatsu ORCA-ER camera (Hamamatsu Photonics Deutschland GmbH, Herrsching, Germany) using MetaMorph version 6.2r6 (Universal Imaging, Media, PA).

Glass flow cells were coated with a mixture of N-ethyl-maleimide (NEM)-myosin and mouse formin mDia1 or yeast Bni1p for 1 min, then washed extensively with 1% BSA for another minute (23). A mixture of 1 μM rhodamine actine bound to 5 μM profilin in fluorescence buffer (10 mM imidazole-HCl, pH 7.0, 50 mM KCL, 1 mM MgCl₂, 100 mM DTT, 20 μg/ml catalase, 100 μg/ml glucose oxidase, 15 mg/ml glucose, 0.5% methylcellulose) was injected into the flow cell. Actin polymerization and buckling events were observed a few minutes after injection.

RESULTS

Model

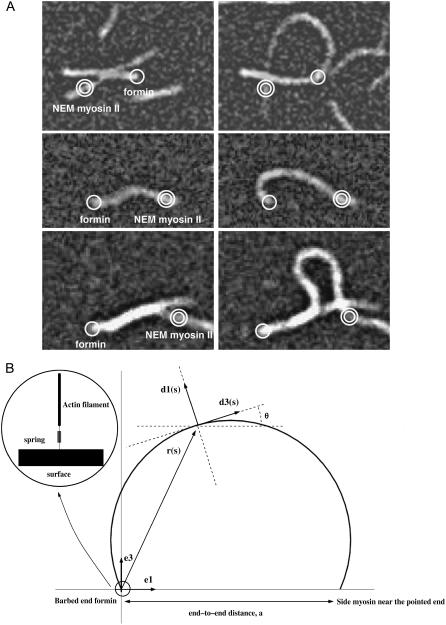
We used total internal reflection fluorescence microscopy (TIRFM) to observe the transition between initial (Fig. 1 A, left column) and buckled configuration (Fig. 1 A, right column) of growing actin filaments bound to the microscope slide by formin (barbed end filament) or by NEM myosin II (side binding near the pointed end filament). To analyze the part of attachment conditions in the production of the buckling force, we develop a mechanical model for filament bending, as shown in Fig. 1 B. The curve represents the filament centerline whose extremities are fixed in space and we note θ, the angle between the unit vector tangent to the curve and the horizontal axis; the other variables or parameters used in the model are listed in Table 1.

FIGURE 1.

Buckling of filaments and model. (A) The initial (left column) and buckled configurations (right column) for actin filaments are observed by total internal reflection fluorescence microscopy. Filaments are attached to the microscope slide either by formin (single circle) or NEM myosin II (double circle). (B) Schematic representation of the filament centerline by a curve. A point on the filament, at position r(s), where s is the arclength along the filament centerline, is characterized by the material frame (d₁, d₃), with d₃ tangent to the filament centerline at r(s). The fixed orthogonal set of unit vectors (e₁, e₃) defines the global orientation of the rod, with the end-to-end vector along the axis e₁. During filament buckling, the set of three vectors (r, d₁, d₃) remains in the plane spanned by (e₁, e₃). We also define, θ(s), the angle between d₃ and e₁. L is the total contour length of the filament and a its constant end-to-end distance. (Inset) We model the bond between the filament ends and the surface by an equivalent spring associated with the filament/formin junction.

TABLE 1.

Model parameters and variables

Symbol	Meaning	Value used in this study	Property or definition
kBT	Thermal energy	4.05 10−21 J
κ	Bending modulus	6.1 10−26 J m
Lp	Persistence length,	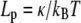15 μm
e1, e3	Constant unit orthogonal vectors defining the reference plane for bending.
L	Filament length	0.2–10 μm
a, a	End-to-end distance, end-to-end vector	0.2–1.5 μm	a = ae1
s	Arclength distance measured along the filament centerline
r(s)	Point position along the filament at arclength s		r(L) = r(0)+ ae1
x(s), z(s)	Horizontal and vertical coordinates of r(s)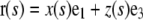
d3(s)	Unit vector tangent to the filament centerline at s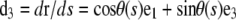
θ(s)	Angle between d3(s) and the horizontal axis at s
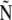	Buckling force
N	Normalized force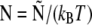

The theory of elastic rods (Kirchhoff equations, (24)) expresses the conditions for mechanical equilibrium of elastic rods given the geometrical and mechanical constraints on the extremities. In Appendix A, we present a derivation of the equations and boundary conditions, as well as the elementary properties of the solutions (Appendix B). The equations for the rod position and orientation read

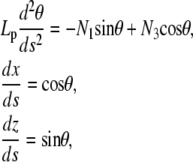(1)

where L_p is the persistence length of the actin filament and s is the arclength measured along the rod centerline; θ is the angle between the tangent to the filament centerline and the horizontal axis; x and z are the Cartesian coordinate of the point at arclength s (Fig. 1 B). In Appendix A, we show that the force vector that balances the surface reaction at s = 0 and s = L is constant. Its horizontal and vertical components denoted, respectively, N₁ and N₃, are unknown quantities that will be determined as part of the solution of equations in Eq. 1. The first equation in Eq. 1 expresses the balance between bending, due to local change of the filament centerline curvature, and the moment of the force (respectively, 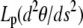and 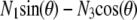). The second and third equations give the components of the unit vector tangent to the rod centerline.

The experimental setup imposes fixed positions to the two filament ends to which correspond four geometrical conditions associated with the position of actin filament extremities

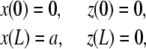(2)

where a is the constant end-to-end distance (a < L). Besides geometrical conditions (2), giving the location of filaments extremities, we impose conditions for the direction of the filament by specifying either the value of the angle θ or its derivative with respect to arclength 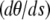. From observations of experimental actin filament buckling, all configurations close to the filament ends are amenable to two cases only. In the first situation, the filament changes its direction continuously while its length increases (see, e.g., left end of the filament, middle row in Fig. 1 A). The corresponding mathematical condition is 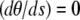, which allows free rotation of the filament end about the attachment point. A second situation is illustrated by the right end of the same filament (Fig. 1 A, middle row) where the direction is globally constant throughout elongation; the corresponding condition is θ = 0. Therefore, we are left with three possibilities for θ

(3)

Boundary condition of type 1 (BC1) represents a filament whose both ends can rotate about the attachment point; boundary condition of type 3 (BC3) imposes a horizontal tangent vector to the filament centerline; the third condition (boundary condition of type 2 or BC2) combines both constraints. The solution of Eq. 1, accompanied with conditions in Eq. 2 and one of the conditions listed in Eq. 3, gives the actin filament configuration and the force exerted on the surface.

Equilibrium configurations and force

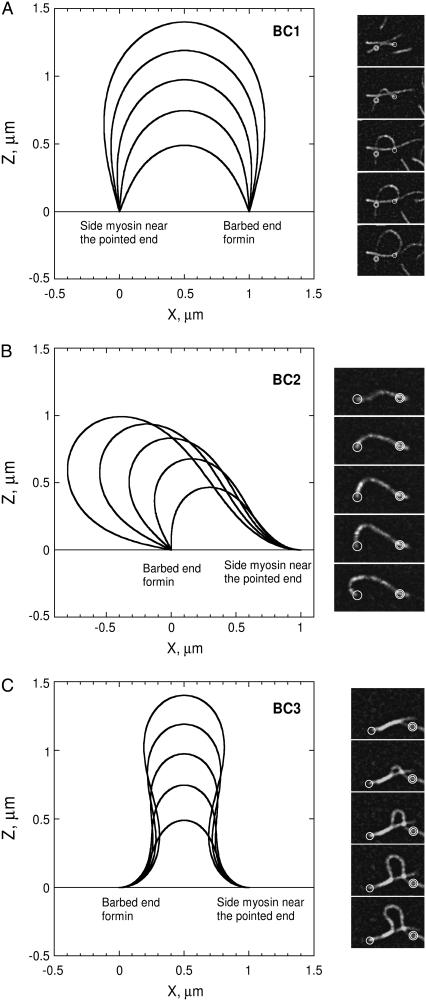
All rod configurations obtained with the boundary conditions listed in Eq. 3 (Fig. 2, A, B, and C) are in very good agreement with the experimental results (see also Fig. 3, A and B, in Kovar and Pollard (13)). The model shows that all boundary conditions BC1–3 can happen in realistic conditions and are sufficient to account for the variety of observed actin filament shapes.

FIGURE 2.

Side-by-side comparison of experimental and modeled actin filaments buckling configurations. Typical buckled configurations, calculated for boundary conditions of type 1 (BC1, A, left column), boundary conditions of type 2 (BC2, B, left column), and boundary conditions of type 3 (BC3, C, left column), are compared to their experimental counterpart. (A–C, right column) Time-lapse evanescent wave fluorescence microscopy of profilin/rhodamine actin polymerization in the presence of formin (single circle) and NEM-myosin II (double circle) attached to the coverglass. Images were taken every 15 s. All model configurations in panels A–C correspond to an end-to-end distance of 1 μm and contour lengths ranging from 1.5 to 3.5 μm. Right column in panel a shows experimental buckling with freely rotating ends (BC1 conditions, end-to-end distance of 3 μm). In panel B, only the left end rotates (BC2 conditions, end-to-end distance of 5 μm) whereas panel C illustrates buckling with fixed horizontal tangent at both ends (BC3 conditions, end-to-end distance of 2 μm).

FIGURE 3.

Force-contour length relation. (A) The force (boundary conditions BC1, BC2, and BC3, end-to-end distance of 1 μm) is maximal at short filament length, when the rod configuration is almost straight and eventually becomes weaker for longer filaments. (B) The normalized elongation rate, corresponding to curves in panel A (reference is elongation of the free barbed end), is shown as a function of the contour length. For BC1 and BC2 conditions, the tangent force exerted on the filament ends shifts from pushing against an obstacle (L < 2 μm, B) to pulling away from the attachment point (L > 2 μm). This transition occurs when the direction at the filament end is orthogonal to the horizontal end-to-end vector. Conversely, in BC3 conditions, the tangent force pushes the filament against the surface along constant directions and, therefore, the normalized elongation rate is always bounded by 1. We used L_p = 15 μm and end-to-end distance of 1 μm.

During actin filament elongation, bent actin filaments exert a force on the surface via the formin or myosin bond that is transduced to the slide surface (in vitro) or to cellular structures (in vivo). The magnitude of the force is not directly proportional to the amplitude of the actin filament curvature: instead, the maximal internal stress occurs for contour lengths just above the end-to-end distance, when actin filaments are almost straight (Fig. 3). For large filament lengths L, the surface reaction to actin filament bending decreases rapidly (scaling as L⁻²) and becomes negligible for contour lengths comparable to the persistence length (Fig. 3). The results in Fig. 3 bring out the role of boundary conditions in the transmission of forces from the actin filament to the surface. When actin filaments are almost straight, the force is directed along the end-to-end vector with a zero normal component (term N₃ in Eq. 1 and Appendix A). Therefore, the total force is approximately proportional to the horizontal component of the vector Ñ

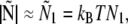where N₁ is the horizontal force component in normalized Eq. 1. BC1 conditions, which give an initial force of 0.4 pN (L = 1 μm; L_p = 15 μm), agree with the classical Euler condition for buckling beams (Eq. B-2, with k = 1)

For BC2 condition and because of the condition at s = L, which constrains the filament to be horizontal at one end, the yielded force is ∼0.8 pN for L ∼ a, as predicted by a linear analysis of Eq. 1 (Eq. B-4, with k = 1). Furthermore, since the BC3 condition imposes that both tangents are horizontal, in agreement with the analysis of linearized Eq. 1 in Appendix B (Eq. B-5), the force is high (∼1.6 pN).

In the presence of a large excess of actin monomer, actin filament elongation is mainly controlled by the k_on rate at the barbed end, which is 11.6 μM⁻¹s⁻¹ for free barbed ends (25); in the presence of the mouse formin mDia1, the k_on is ∼4× larger (26). When the barbed end is bound to a leaky capper, such as a processive formin like mDia1, the free energy associated to actin monomer insertion at the capped end, balances the work of the tangent force over a distance of one actin monomer size (27). Therefore, the actual k_on rate is modified according to

(4)

where k_on,0 is the on-rate of free barbed end (17,27). In the above expression, the force Ñ and the tangent vector d₃ are expressed at the barbed end of the actin filament; d is the radius of one actin monomer. At the onset of buckling, the ratio (k_on/k_on,0) is low and eventually reaches unity for large L, when the force imposed to the actin filament is weak (Fig. 3). In this latter case, the elongation rate is almost as fast as an actin filament with a free barbed end.

At intermediate contour lengths, the orientation of the actin filament end changes (BC1 and BC2 conditions, Fig. 2, A or B). In consequence, the barbed end experiences a transition from compression, when the force pushes the end against the formin, to extension, when the actin filament is pulled away from the surface. In the latter case, actin filament elongation becomes independent of the mechanical stress and is only limited by diffusion of actin monomer (Fig. 3, conditions BC1–2). In contrast, the BC3 condition cannot sustain such an acceleration of the elongation rate, because both tangents are fixed and the force remains compressive for all configurations.

The configurations adopted by a single actin filament during elongation provide a direct way to measure the buckling force (Appendix C). The solution of Eq. 1 compares well with the force magnitude determined from pooled experiments that correspond to different actin filament lengths and end-to-end distances (Fig. 4). Note also that the model is valid throughout the elongation period and accounts for both the initial and final phases.

FIGURE 4.

Experimental buckling and model validation. From 113 pooled filament contours (Fig. 3, A and B, in D. Kovar and T. Pollard (13) and unpublished data), we determined the force magnitude as solution of the moment balance equation with BC1 conditions and L_p = 15 μm (Appendix C). The end-to-end distance is ∼5 μm for all data; filament length is in the range 5–12 μm at the end of the elongation period.

Actin concentration and force at initial buckling

The energy necessary to buckle an actin filament is supplied by the addition of actin monomers at the formin-associated barbed end. The presence of an obstacle at the barbed end slows polymerization and actin filament elongation as

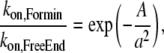where we adapt Eq. 4 to BC1 (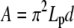, Eq. B-3), BC2 (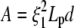, Eq. B-4) or BC3 conditions (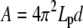, Eq. B-5); d is the fluctuation of the actin filament position allowing insertion of one actin monomer. If the off-rate is unaffected by the presence of the constraint, the minimal actin monomer concentration necessary to sustain buckling is

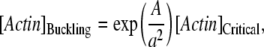where [Actin]_Critical is the critical concentration at the barbed end of an actin filament in absence of any obstacle (∼0.1 μM, (25)). This relationship predicts the minimal end-to-end distance as a function of the actin concentration present near the barbed end. For a concentration of 1 μM actin monomer, buckling is possible above 0.3 μm (BC1), 0.45 μm (BC2), or 0.7 μm (BC3) (Fig. 5 B); larger concentration (50 μM actin monomer) does not significantly move this minimum (0.2 μm for BC1, 0.25 μm for BC2, and 0.4 μm for BC3; Fig. 5 B).

FIGURE 5.

Actin concentration and force at onset buckling. The force (A) and the actin concentration (B) are plotted against the end-to-end distance, for different attachment conditions (BC1, solid line; BC2, dashed line; BC3, dotted line). We use L_p = 15 μm. To appreciate the role of actin in the buckling of short filaments, note that the critical actin monomer concentration for the free barbed end is 0.1 μM.

The model predicts that single actin filaments can produce buckling forces in the range of 5–10 pN (Fig. 5 A, end-to-end <0.5 μm). Moreover, this figure illustrates the significance of actin concentration, boundary conditions, and the distance between actin filament ends in buckling force. BC1 condition is associated with very loose connections between the actin filament and the cover glass; conversely, BC2, and even more BC3, represents tight constraint, because one or two ends have fixed directions. Therefore, for identical end-to-end distance, buckling with BC3 produces larger force than the one associated to BC2 or BC1 (Fig. 5 b).

Model for filament-surface junction

Bond robustness between the formin and the coverglass might limit the actual force developed by the actin filament, in particular, at short end-to-end distance and contour length (Fig. 5 A). To better understand the force transmission between the actin filament and the surface, we modeled the bond as a spring (Fig. 1, inset, and Appendix D). The equations remain unchanged (Eq. 1), but the condition for the rod position at s = 0 now gives the balance between the internal force developed by the actin filament and the spring extension (Eq. D-2)

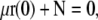(5)

where μ is proportional to the spring stiffness. Note that in condition BC3, both actin filament ends have fixed horizontal directions; thus, any relative displacement between the filament end and the surface is impossible. Therefore, we examine the consequences of Eq. 5 for BC1 or BC2 conditions only. We focus on the critical stiffness, μ_c, necessary to hold the filament end at a distance Δ from the surface (Fig. 6). Both BC2 and BC1 requires large bond robustness, in the range 0.2–1.2 pN nm⁻¹, when the end-to-end distance is about equal to the observation limit in TIRF (Fig. 6); conversely, μ_c goes under 0.2 pN nm⁻¹ for long filaments (above 1.5 μm, all combinations of Δ and boundary conditions). The bond stiffness necessary to maintain the actin filament ends close to the microscope slide becomes very large, as shown in Fig. 6, for an end-to-end distance below 0.2 μm.

FIGURE 6.

Critical bond stiffness. We determine the conditions necessary to hold the filament ends at a distance Δ from the surface for different end-to-end (a) and contour length (L); a is the control parameter and L is given by L/a = 1.1; L_p = 15 μm; Δ is chosen in the range 3–9 nm, i.e., the typical size of one actin monomer (∼6 nm). The curvilinear domain with blue (red) boundaries gives the bond stiffness compatible with the constraint 3 nm < Δ < 9 nm for conditions BC1 (BC2). For both kind of boundary conditions, the top (respectively, bottom) border, indicated by red and blue squares, is associated with Δ = 3 nm (Δ = 9 nm, red and blue dots). The vertical borders, indicated by blue and red triangles, are determined by the condition L_c < L (Eqs. D-3 and D-4); below this limit, no buckling occurs, whatever the bond robustness.

DISCUSSION

We have used a mechanical model for elastic rods, based on the equilibrium of forces and moments, to analyze single actin filament buckling events in vitro. Besides its simplicity, the model depends on a unique parameter, the persistence length for actin filaments, which ranges from 10 to 15 μm (28–30). With the help of the model, we can determine the role of external constraints imposed to actin filament, measure the forces, and predict the actin level necessary to develop forces against the mechanical constraints imposed at both filaments ends.

The solution of Eq. 1 depends only on the ratio of the end-to-end distance over the contour length, a/L, and on the conditions specifying the position and the orientation of the actin filament ends. The filament end positions are fixed in space (see Eq. 2, in the text). The orientation of the filament at its ends, which is the decisive factor in the determination of actin filament configuration, is given by a limited number of cases listed in Eq. 3. Boundary conditions 1 and 2 give the possibility to the filament end to change its direction in the course of elongation, as shown in Fig. 2, A (both ends) or B (left end). Conversely, in boundary conditions 2 and 3, we can also fix the value of the angle between the filament direction and the horizontal axis, as illustrated in Fig. 2, B (right end) or C (both ends).

Effect of actin filament configuration to force generation

Solutions of Eq. 1 associated with one of the boundary conditions BC1, 2, or 3 account satisfactorily for all configurations found in vitro. We observed the correlation between the type of boundary condition (BC1–BC3) and the magnitude of the force produced by the actin filament during buckling (Figs. 2, 3, and 5). If the vector tangent to the actin filament end can change its orientation, the case of boundary condition BC1 (Fig. 2 A), the buckling force is always smaller than the force developed under other conditions (BC2 or BC3). These two latter cases correspond to important constraints because the vector tangent to the actin filament centerline at one or both ends has a fixed direction.

The model helps us to trace the variety of actin filament configurations to the tightness of the connections between the actin filament and the formin or the myosin. For example, a single bond between the formin-associated filament end and the microscope slide allows freedom for the end to change its direction and corresponds to boundary conditions of type 1 or 2 in the model. Conversely, multiple attachment points along the side of the filament via NEM myosin II amount to maintain the vector tangent to the filament extremity in a fixed direction. This situation is the analog of boundary conditions 2 or 3 in the simulations.

To derive force-filament length relations, we used a persistence length of 15 μm and an end-to-end distance of 1 μm. For actin filament contour length just above the end-to-end distance the force is maximal and crucially depends on the kind of boundary condition at the actin filament ends: free rotation gives rise to gentle stress (∼0.4 pN). If one of the tangents is held fixed, the force is doubled (∼0.8 pN) and rises to 1.6 pN when both tangents are constrained. For shorter end-to-end distance, the force becomes important: single filaments can produce up to 10 pN for a ≤ 0.5 μm (Fig. 5 A).

We bring out a direct validation of Eq. 1 by confronting a modified version of the moment balance equation and reconstructed geometrical configurations of the actin filaments at different buckling stages (Fig. 4). In addition, Fig. 4 indicates that force fluctuations do not have an important part: the first harmonic of the buckled configuration is sufficient to account for the observations (discussion in Appendix A). For large filament length and end-to-end distance, the buckling force is only a fraction of pN (Fig. 4), in agreement with the linear theory for filament buckling (Eq. B-2).

Conditions for actin concentration, bond stiffness, and buckling formation

It has been suggested that insertion of actin monomers at the barbed end is limited by the presence of forces or loads (27). However, this is not a limiting factor, since 1 μM of actin is sufficient to initiate buckling for a wide range of end-to-end distances above 0.5 μm (all boundary conditions). For actin filaments initially shorter than 0.5 μm, the actin monomer concentration required for efficient polymerization increases abruptly. Due to the predicted high force (∼10 pN, Fig. 5, BC1–3 conditions) that constrains actin filament ends, it is necessary to have up to 50 μM of free actin monomers to elongate and efficiently deform actin filaments of 0.2 μm, (BC1 conditions). Although we cannot entirely rule out the possibility that the actin monomer supply is limiting for elongation of short actin filaments under constraint in vivo, the proximity of deformable structure (i.e., the cell membrane) near the site of nucleation allow us to predict that in most cases actin monomers concentration in vivo will be high enough to limit steric capping.

We modeled the interactions between the filament and the surface as a spring of stiffness μ. In the absence of data for this parameter, we constrained the model by requiring that both actin filament ends remains at a distance Δ from the surface; Δ is chosen in the range 3–9 nm, i.e., approximately the size of one actin monomer. We can compare the values for bond stiffness μ (Fig. 6) to the stiffness or chemical bonds in similar systems. Ishijima et al. (31) determined that the stiffness of the myosin head is in the range 0.14–0.28 pN nm⁻¹; a value of ∼0.69 pN nm⁻¹ was reported for the stiffness of the acto-myosin cross-bridges during movement (32). Therefore, the predicted stiffness, in the range 0.2–1.2 pN nm⁻¹ (Fig. 6), is compatible with the experimental values obtained in similar systems (acto-myosin cables). In consequence, actin monomer concentration and the bond stiffness necessary to observe buckling would not constitute a limitation for model predictions applied to in vivo situations.

Implication of the model for force generation in vivo

Formin-driven (re)arrangement of the actin cytoskeleton is essential to initiate new cell compartments (filopodia, yeast buds), to establish cell polarity before division, to assemble the cytokinetic contractile ring and to regulate cell-cell or cell-surface interactions during adhesion and motility (12). All these cellular processes require the right combination (in space and time) of chemical and physical factors operating within a cell of cellular compartment, including: filament size, actin monomers concentration, boundary conditions, and bond stiffness. Although our modeling approach is motivated by experiments in reconstituted systems, we can extend our results to in vivo conditions.

We have shown that over a wide range of conditions, a single filament can develop forces to move the membrane and/or organize the cell cytoskeleton. The buckling force per single filament can counterpoise resistance up to ∼10 pN (Fig. 5 A), which is on the order of magnitude of the force measured in thin highly curved structures such as experimentally driven tethers (33). In addition, our study shows that this deformation requires a high but plausible concentration of free actin monomers (∼10–50 μM, Fig. 5 A) and a bond stiffness in the range 0.1–0.5 pN nm⁻¹ (Fig. 6). Therefore, these two factors are not limiting in the generation of large forces at the cell scale level.

From Fig. 5, we can extrapolate the role of short actin filaments in vivo. A single actin filament is able to develop a force ∼10 pN only in a prebuckling state whereas its length remains relatively short (<0.5 μm). As illustrated in Figs. 5 and 6, prebuckling occurs when both actin filament ends are trapped by adjacent molecular complexes in the cell. Therefore, it is important to examine the different physical or molecular mechanisms keeping the filament configuration (its orientation and its length) in a prebuckled state. We will examine the consequences of two possibilities for controlling filament configuration by: a), severing filaments; or b), cross-linking filaments together.

Severing of filaments by ADF/cofilin could provide ways to expand the population in the prebuckling stage at the expense of long and old filaments. Experiments demonstrate that ADF/cofilin utilizes the mechanical properties of filaments to bind them before severing (34). Therefore, because the mechanical stress experienced by filaments during elongation is rapidly decreasing after the onset of buckling (Fig. 3), ADF/cofilin could use this differential property to bind preferentially to postbuckled filaments, whose mechanical stress is the lowest. After severing, only actin filaments in the prebuckling stage and of short contour length would survive while their turnover is maintained at a high rate.

Cross-linking proteins (e.g., fascin or α-actinin) and the Arp2/3 complex are extremely important for actin filament formation or actin cytoskeleton growth. In the presence of high cross-linking or branching activity, the size of the filament piece between the free barbed end and the first cross-link would be well below 1 μm while it lengthens rapidly by polymerization. Therefore, these short filaments are permanently kept in a prebuckling state and could provide a large part of the total force developed by actin filaments for cell deformation or lamellipodia progression.

Finally, we also hypothesize that the mechanical stress developed by growing actin filaments could represent a new way to convey information in the cell and achieve organization of the cytoskeleton. It is well accepted that information driving actin filament nucleation and elongation flows from external signaling molecules to their intracellular targets, via actin regulators at the membrane, including WASP, formins or the complex Arp2/3. However, the type of boundary conditions experienced by actin filament depends on the interactions between the filament end and the activator complex at the membrane. Therefore, if the force developed during filament elongation becomes large, it could, in turn, modify the molecular organization of the sites where actin filament nucleation and elongation occur. Our study illustrate the possibility that, in addition to on and off chemical switches, mechanical stress could take part in the self-organization of the cell cytoskeleton during movement by direct activation and/or inhibition of actin polymerization.

APPENDIX A: MECHANICAL EQUILIBRIUM EQUATIONS FOR A CONSTRAINED ROD

We use the Kirchhoff equations for elastic rods to model actin filaments, which are assumed inextensible and isotropic (24). The rod position (Fig. 1 A) is defined by a vector function

where s is the arclength of the rod centerline and L the total filament length. The local orientation of the filament is given by a set of two orthonormal vectors, (d₁(s), d₃(s)); d₁(s) is aligned with the principal flexure axis of the rod and prescribes the orientation of the cross section at s. The tangent vector to the rod centerline, denoted d₃(s), lines up with the torsion axis. d₃ is obtained by derivation of the rod position r(s) with respect to arclength s

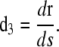Actin filaments are observed in the field of an evanescent wave (<500 nm) so that the rod remains in a plane during elongation. Moreover, as suggested by experimental evidences showing no accumulation of filament torsion along its centerline (Fig. 3 g in Kovar and Pollard (13)), the actin filament does not suffer out-of-plane deformation (Zajac phenomenon, (35)). Therefore, we demand that (r, d₁, d₃) be in a plane spanned by a set of two, constant, orthonormal vectors (e₁, e₃). Additionally, we assume that the end-to-end vector is along the horizontal axis

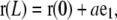where a is the end-to-end distance and 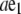the end-to-end vector (Table 1). Let θ(s) be the angle between d₃ and e₁. The vectors associated with filament position and orientation are

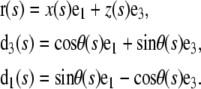To find model equations and boundary conditions, we start from the Lagrangian of the system, including contributions arising from the elastic energy stored in filament flexure, the inextensibility constraint and attachment conditions. The total elastic energy is

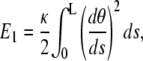where κ is the bending modulus of the rod, related to the persistence length, L_p, through 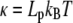; k_B and T are the Boltzmann constant and absolute temperature (Table 1). The internal force in the rod, Ñ, ensures inextensibility so that s is the arclength for all configurations. Therefore, any departure from equation 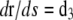contributes to change the potential energy by

The physical interpretation of the term 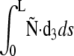in E₂ is a potential energy associated with a load applied to filament ends. Finally, the surface reaction ũ₀ (respectively ũ_L) at s = 0 (respectively L) is included via terms for the energetic contribution of Ñ at s = 0 or L

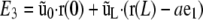Therefore,

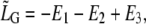is the Lagrangian function, which, after normalization by k_BT, reads

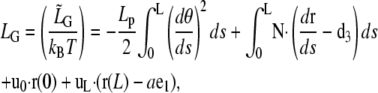(A-1)

with 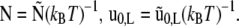The variation of L_G results into Euler-Lagrange equations

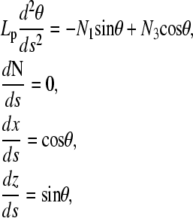(A-2)

and boundary terms

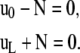The first equation in Eq. A-2 represents the balance between the bending moment and the constraints exerted by the fixed-rod end conditions. From the second equation, we note that the buckling force, N, is constant along the filament centerline. Finally, the second and third equations give the filament position. The unknown force components, N₁ and N₃, which are determined as part of the solution of (Eq. A-2), depend on the boundary conditions used for θ, x, and z. They give the surface reaction exerted on the rod during buckling (u₀ and u_L) and, consequently, the force exerted by the elongating filament on its ends. The boundary conditions for filament ends come as

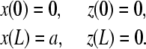We supplement these constraints by one condition for the angle θ chosen in the list

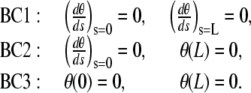The boundary conditions of type 1, 2, or 3 (BC1–3) refer to different behavior of the filament orientation at s = 0 or L. Nonlinear Eq. A-2 admit multiple solutions depending on resonance arising from the constraints on rod ends and boundary conditions BC1–3. Also, note that these nonlinear equations are valid for arbitrary large deviations of the tangent vector from the horizontal baseline, to the contrary of the fourth-order linear differential system classically used in models for semirigid polymers.

In the limit of slightly bent rods, x(s) approximates s and θ(s) equals the slope of z(s) (as function of x(s)). From Eq. A-2, one recovers the classical fourth-order differential linear equation valid for small amplitude bending solution

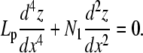Time relaxation constant for almost straight filaments

The hydrodynamics of actin filaments is controlled by fluid viscosity due to its low Reynolds number and can be modeled via drag forces distributed along the filament. However, we used a model without friction terms (see Eq. A-2), because relaxation to equilibrium is fast. To check the validity of this assumption, we look at the stability of the solutions of Eq. A-2 in the limit of almost straight configurations. The angle θ, which is function of space and time, obeys

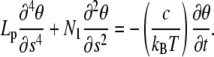(A-3)

In the above equation, c is the orthogonal drag coefficient for a filament moving at a constant altitude, h, near a planar surface (36)

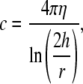where η is the fluid viscosity and r the filament radius. Solution of Eq. A-3, supplemented with four boundary conditions 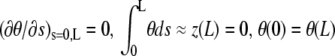, yields the relaxation time

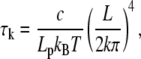where k is a positive integer. Using η = 0.07 Pa s, h = 500 nm (approximately the depth of the evanescent wave), r = 4 nm, and L in the interval 0.2–1 μm, we found that τ₁ ranges from 0.003 to 1.7 ms. (L_p = 15 μm). Therefore, this result proves that relaxation to equilibrium is very fast and the equilibrium Eq. A-2 account for the buckling of actin filaments. Note that the actin filament length L has the role of a pseudotime coding for the actin filament age.

Model validity

In this study, we assume that filament shape fluctuations are negligible and a deterministic description of actin filament bending accounts for in vitro experiments and in vivo observations. We discuss the validity of this assumption with respect to fluctuation of thermal origin.

On the one hand, the existence of multiple bending modes, solution of Eq. A-2, raises the possibility of rapid, noise-induced, transitions between them. We use the partition function, Z, which gives the number of configurations for semirigid polymers constrained by a constant end-to-end distance (37) to estimate the statistical distribution of filaments during elongation. Z depends only on three parameters, the filament contour length (L), the end-to-end distance (a), and the persistence length (L_p). If we keep a and L_p constant and vary L, >99% of the distribution is concentrated in the interval 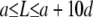, where d is the typical diameter of one actin monomer (∼6 nm); this conclusion is valid for all values of L_p ranging from 10 to 15 μm. Thus, for a/L ratio below 0.95 (or, equivalently, L > a + 10d), the number of rod configurations compatible with the constraints is extremely low. In consequence, the most probable filament shape corresponds to the one with the lowest energy level. On the other hand, the physics of semiflexible polymers predicts a rigid-to-flexible transition at high L/L_p ratio (∼2.85–3) (38). This implies a second limit, for large L, above which the configuration of very long actin filament (∼30–45 μm) cannot be accounted for by our approach. If we combine these two bounds, we see that model validity is limited to the interval .

In actin polymerization experiments followed by evanescent wave microscopy (13), buckling is observed for end-to-end distances as short as 0.7 μm up to a final length of ∼10 μm, hence, L/L_p ranges from 0.05 at beginning to ∼0.6, when elongation stops (L_p = 15 μm). Moreover, when incorporation of monomers into actin filaments is fast (26), the ratio a/L decreases rapidly below 0.95. Therefore, the experimental bounds for L are compatible with the use of a simple, deterministic model based on the mechanics of elastic rods.

APPENDIX B: DETERMINATION OF THE FORCE MAGNITUDE AT INITIAL BUCKLING

We derive an expression for θ and the internal force components, solution of Eq. A-2, in the case of a slightly bent rod, when the contour length is just above the end-to-end distance. Thus, we limit our search to solutions of Eq. A-2 with small amplitude: the variables (θ(s), N(s)) will be function of the “small” parameter , when L ∼ a.

BC1 conditions

A direct integration of Eq. A-2, using boundary conditions for the rod ends (Eq. 2) and BC1, gives

Because the end-to-end distance is nonzero, N₃ vanishes identically: the vertical force is zero. The linearized equation for θ(s)

(B-1)

has solutions of the form

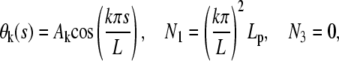(B-2)

where k is an integer; at this stage, the amplitudes A_k are arbitrary. The total extension x(L) is obtained by direct integration of equation

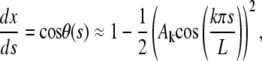which implies

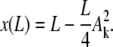(B-3)

Using the boundary condition x(L) = a, we obtain a relation between the unknown amplitudes A_k and δ

Because the condition z(L) = 0 is O(δ³), it is automatically fulfilled at O(δ). The amplitude of the first buckling mode increases with L as

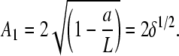BC2 conditions

Because boundary conditions BC2 are asymmetric, both components of the internal force are nonzero. The small amplitude solution for θ(s) reads

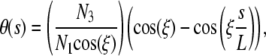where ξ is solution of

The solutions of the above equation begins with 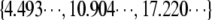and are asymptotically given by 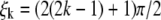for large integer k. From conditions x(L) = a, z(L) = 0, and assuming that N₃ is of order O(δ^1/2), one can check that

(B-4)

is solution of Eq. A-2 with BC2 conditions and .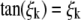

BC3 conditions

The last case, BC3, can be treated in a similar way. Because boundary conditions are symmetric (θ is zero at both ends), the component N₃ vanishes and we are left with

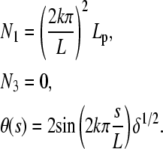(B-5)

Note that the condition z(L) = 0 selects even harmonic solutions. If we impose nonhorizontal tangents (i.e., 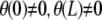), N₃ is generally nonzero, unless .

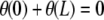APPENDIX C: ESTIMATION OF THE FORCE MAGNITUDE FROM FILAMENT CONFIGURATION

Integrating Eq. A-2 twice with respect to s and using conditions BC1, we show that the moment balance is a relation between θ and the rod position

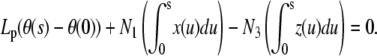(C-1)

with constant coefficients L_p, N₁, and N₃. If we express the relation (Eq. C-1) at n points of abscissas s_i, (i = 1, …n) along a particular filament, we obtain a linear system of (n − 1) equations and two unknown coefficients N₁ and N₃

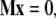(C-2)

with

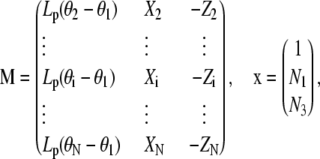where 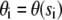, , 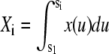and . Because the system of linear Eq. C-2 is overdetermined (two unknowns and n − 1 equations), we solve it in the least square sense by minimizing the norm 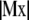. Therefore, the solution, x*, is proportional to the eigenvector associated with the minimal eigenvalue of the symmetric (3 × 3) matrix ^TMM

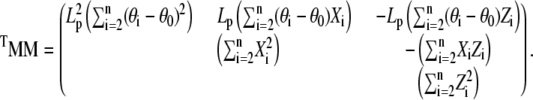The coefficients of ^TMM are determined from the B-spline representation of the functions θ(s), x(s), and z(s) extracted from a particular filament configuration. After normalization of the solution so that its first component is 1, the force components N₁ and N₃ read off from the second and third component of x*. The form of Eq. C-1 depends on the boundary conditions for θ at s=0, L. Other choices (e.g., conditions BC2 or 3) would give slightly different terms but the linearity of the final equation with respect to the unknown force components is preserved, hence, the procedure to find the actual force from filament configuration remains unchanged.

APPENDIX D: TRANSITION BETWEEN STRAIGHT AND BUCKLED CONFIGURATIONS

We examine the possibility that one of the rod ends is weakly attached to the formin by a spring, a situation directly relevant to the analysis of the bonds between formin-driven filaments and the cell membrane in vivo conditions. To derive the corresponding equations and boundary conditions, we use a slightly modified Lagrangian function (Eq. A-1)

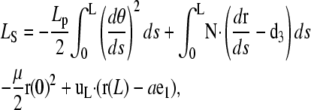(D-1)

where the reaction constraint at s = 0 is replaced by the harmonic potential of a spring of stiffness μ (the actual stiffness is 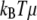). The variation of Eq. D-1 gives equations similar to Eq. A-2 but with different boundary terms

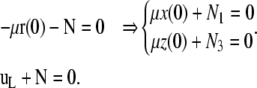(D-2)

The boundary condition at s = 0 represents the balance between the force due to spring extension and N. We look for small amplitude solutions (BC1 conditions), given by Eq. B-1, and constrained by the condition

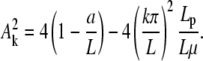Real solutions of the above equation exist for L above a critical length L_c, solution of

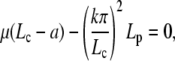(D-3)

In the interval 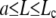, the most favorable configuration for filaments corresponds to straight rods; transition to buckling occurs for L = L_c, when the spring force balances the force of elastic origin, as given by Eq. D-3. Similar analysis for BC2 condition gives the expression for the amplitude and L_c

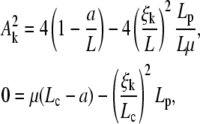(D-4)

with ξ_k is one of the positive solutions of (Eq. B-4).

Fluctuations of filament length at onset of buckling

Filament undulations, driven by thermal fluctuations, shorten the projected filament length along the end-to-end axis: therefore, the critical length given by conditions (Eqs. D-3 and D-4) can change dramatically. Before buckling, the spring constraint imposed to the filament is loose: the different bending modes are almost independent. Therefore, we use the elastic energy associated to the bending mode k (unit is k_BT)

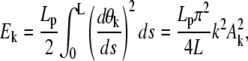to find the second and fourth moments of the fluctuating quantities A_k by application of the energy equirepartition theorem

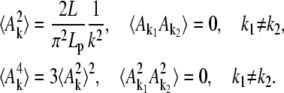From Eq. B-3, which gives the projection of the filament along the horizontal axis, we obtain the average of x(0) and x²(0)

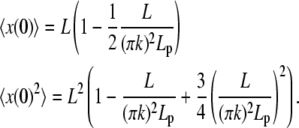(D-5)

The onset of buckling occurs for a new critical filament length, denoted 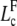, solution of an equation analogous to relation (Eq. D-3) with k = 1

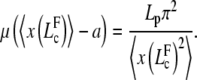We can prove that

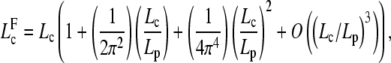where L_c is solution of Eq. D-3. We find for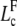

Thus, for L < 2L_p, we can use the deterministic Eq. D-3 to predict onset of buckling.